Combination of discrete wavelet packet transform with detrended fluctuation analysis using customized mother wavelet with the aim of an imagery-motor control interface for an exoskeleton

Abstract

One critical issue in brain computer interface (BCI) studies is to extract imaginary movement patterns from electroencephalograph (EEG). In this study, two different techniques —detrended fluctuation analysis (DFA) and discrete wavelet packet transform— are combined (DWPT-DFA) for feature extraction. Both approaches are known as self-similarity quantifier techniques. In wavelet technique, mother wavelets play an important role. Herein, A customized mother wavelet utilizing event related desynchronization (ERD) potential patterns are extracted and updated automatically for individual subjects. Also, three predefined mother wavelets are used, and the results are compared with the customized mother wavelet. The predefined mother wavelets are db4, db8 and coiflet 4. The soft margin support vector machine with the generalized radial basis function (SSVM-GRBF) is employed to classify the DWPT-DFA features. For the efficiency of the method, nine subjects have participated to record EEG based on the imaginary hand movements. The ERDs and features are extracted from FC1 and CP6 channels. Results show that the combination of the DWPT and DFA with the personalize ERD mother wavelet gives the best accuracy of 85.33% with p < 0.001. Based on the results, we conclude that the DWPT-DFA method using the ERD mother wavelets improves significantly the efficiency of the SSVM-GRBF classifier.

Introduction

A electroencephalograph (EEG) property is self-similarity, which means one part of an object or a signal is similar to the other parts of the object or signal [19]. The self-similarity concept is used in chaos theory for extracting features and detecting special mind disorder patterns from the EEG signal such as ADHD [3] and Autism [2]. Self-similarity features are also impressively used in the sleep science to detect sleep spindle or k-complex patterns automatically. These patterns are studied for quantifying learning, memory consolidation and detecting mental disorders [22, 30]. In our previous study [21], a combination of Katz, Higuchi, and Sevcick fractal dimensions is utilized to quantify the self-similarity, in order to detect sleep spindle patterns. Katz and Sevcick fractal dimensions are self-similarity quantifier algorithms based on the time space and Higuchi is based on the embedded space in signal processing [3]. The other method of quantifying self-similarity is the discrete wavelet transformation (DWT) [26]. The DWT approach is a powerful technique to extract the localized information in time-frequency space with the aim of diagnosing self-similarities. The flexibility of the DWT is provided by adding up different scales of a linear DWT, namely the discrete wavelet packet transform (DWPT) [6]. The DWPT algorithm is executed by selecting three inputs that include: scale, level and ideal pattern for diagnosis. The scaling is implemented by dividing signals into high and low frequency bands. The second input is the level, which is the number of times that a signal should be decomposed into sub-frequency bands. The third input is the mother wavelet, which plays a critical role. Mother wavelets are changed in different applications, such as in bio-signal processing [36], multi-fractal pattern detection [38] and diagnosing self-similarity in EEG processing [26]. Since now, many patterns are generated as a mother wavelet such as Daubechies [14] and Mexican Hat [34]. One method to improve the DWT functionality is to optimize the mother wavelets [10]. For instance, to diagnose fetal phonocardiography waves for higher accuracy, beside a mother wavelet a daughter wavelet is designed to add a property of finding the wavelet location to the mother wavelet [10]. In another study, the evolutionary algorithm is exploited to generate a mother wavelet pattern based on the predefined mother wavelet such as genetic algorithm for finding epilepsy seizure patterns [17].

The second reliable technique for quantifying self-similarity in signal processing is the detrended fluctuation analysis (DFA) [32]. The DFA is a well-promising method for predicting correlation, which can depict correlation property of a signal in a wide-range [12]. The DFA is not based on a specific pattern such as mother wavelet. Also, the DFA has been used on various fields such as human signal processing [7], financial [40], and geophysics [13]. In a recent study, a combination of the DFA and DWPT methods (named DWPT-DFA) is introduced as an accurate method to quantify self-similarity with high accuracy in complex cases and bio-signals [39]. In order to evaluate the efficiency of the DWPT-DFA, researchers compared it with the DFA, wavelet and other nonlinear features, such as Lyapunov Exponent. In our study, DFA approach is used and improved by automatic mother wavelet optimization with relative event related potentials (ERPs). The ERP is a useful pattern to find specific mental responses, such as visionary [9], auditory [27] or olfaction [35] stimulation.

In order to explore a stimulation response, EEG should be recorded in a repetitive task. For instance, researchers extracted auditory ERP components to early diagnose the disable children with auditory problems effectively [1]. Similar technique is exploit to extract event related desynchronization (ERD) pattern, which is a sign of neurons activation in sensory-motor cortical area, such as hand and ankle movements [4]. These patterns are specified by amplitude attenuation before real or imagination of right hand movement. Event related synchronization (ERS) patterns are related neuron’s activation that occur immediately after the ERD and are identified by the enlarging amplitude [33]. The ERS is a pattern that is used to diagnose the moment of real movement, whilst the ERD is an effective pattern that is employed to detect the imagery movement pattern for rehabilitation applications [25, 28].

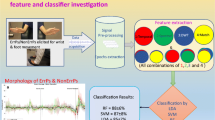
In this study, our contribution is the development of methods for features extraction using the DWPT-DFA with the ERD mother wavelet, and feature classification. In the main algorithm procedure, A task based on the imaginary right hand movement and no movement is designed to record the EEG signals. Then, the EEG signal is filtered and the ERD patterns are extracted and exploited as a mother wavelet. The obtained ERDs are assigned to each subject and updated automatically. The DWPT-DFA method is then integrated with the customized mother wavelet to extract the features. Finally, a soft margin support vector machine classifier with generalized radial basis function kernel (SSVM-GRBF) is utilized to classify the obtained features. Results are evaluated by accuracies and paired t-test. The complete procedure is depicted in Fig. 2.

Material and method

In this section, approaches utilized to detect right hand imagery movement patterns are presented as follow: 1- selecting a frequency band for filtering; 2- extracting the ERDs for individual subjects; 3- implementing the DFA algorithm; 4- combining the DWPT with DFA; 5- updating DWPT-DFA’s mother wavelet for individual subjects automatically; and 6- classifying the extracted features utilizing SSVM classifier with GRBF kernel.

Filtering

For the preprocessing, the EEG data consists of segments, and each segment is a time window, which starts at 200 msec before visual stimulation (displaying pictures) to the point of 2500 msec after the visual stimulation. The data is then filtered by applying the second order Butterworth filter in six frequency bands, which are 8-12Hz, 12-16Hz, 16-20Hz, 20-24Hz, 24-28Hz, and 28-32Hz [20, 23, 24]. The best frequency bands are selected from 8-12 Hz and 12-16Hz based on accuracies [24]. Finally, the 8-15Hz frequency band is selected by mixing the two frequency bands with try and test. After selecting the best frequency band, a customized mother wavelet using an ERD for the DWPT-DFA is attained as follows:

Event related desynchronization (ERD)

To obtain the ERD waves, a repetitive task is designed and depicted in Fig. 3, where of 280 trials are implemented. Subjects imagine the right hand movement after the hand pictures disappear from screen. In the procedure, a marker is sent to record the moment of the right hand movement imagination and displaying pictures. In Figs. 5 and 6, the y axes is the location of markers and is the zero point of our calculations in each EEG segments. The imaginary movement trials are extracted and filtered based on the location of the markers. The width of the window is 2700 msec. The window starts at the point of 200 msec before the stimulation and ends at 2500 msec after the stimulation. Finally, the filtered segments are averaged and obtained Figs. 5 and 6. Then, the ERD from FC1 channel is integrated with the DWPT as follows:

Wavelet

One well-known method to extract properties of a time series (TS) is Fourier Transform (FT). The FT does not have ability of specifying correspondence between time and frequency domains. Wavelet solved the constraint by decomposing TS to a frequency domain specified by time, i.e. time-frequency domain. The other property of wavelet is diagnosing self-similarity in frequency domain, which is based on mother wavelet function [16]. One wavelet constraint is that the predefined wavelets are not effectively useful in EEG studies. Our aim is to implement an automatic updateable mother wavelet method to diagnose the subject’s ERDs patterns. Hence, the ERD patterns of individual subjects are extracted and replaced. For instance, the ERD patterns of a subject are depicted in Figs. 5 and 6. The wavelets are defined into two main categories of discrete and continuous wavelets. The continuous wavelet is utilized when the high frequency ranges (or scales) are required for computations, whereas the discrete wavelet is useful when the low frequency bands are important for computations. The continuous wavelet is defined as follows [41]:

$$ \begin{array}{@{}rcl@{}} W{\!}_{\varphi }f(a,b)=\frac{1}{\sqrt{a}}\int\limits_{-\infty }^{+\infty }{f(t)\varphi \left( \frac{t-b}{a}\right)dt,} \end{array} $$

(1)

where φ, a, b symbols denote the mother wavelet, the scaling and shifting parameters, respectively [41]. To generalize the DWT, the DWPT is defined. The DWPT is a linear combination of the DWTs’ mother wavelet properties. The DWPT method has accessibility to low and high frequency bands at the same time as in Fig. 1. To design the diagram, the input signal is divided in low and high frequency components to reach the intended frequency bands (values in Fig. 1 are rounded, but in calculations values are accurate) [42].

Fig. 1

Wavelet decomposition diagram chart, values are in HZ unit

To implement the DWPT-DFA algorithm, the DFA approach is implemented as follows:

Detrended fluctuation analysis (DFA)

The DFA is an effective approach for evaluating self-similarity by predicting of long-term correlation and scaling algorithms in TS [39]. The self-similarity TS (x(j)) based on the DFA is calculated by integrating TS (y(i),i = 1,...,N) as follows [43]:

$$ \begin{array}{@{}rcl@{}} x(j)=\sum\limits_{i=1}^{n}{[y(i)-\left\langle y \right\rangle ],} \qquad \left\langle y \right\rangle =\frac{1}{N}\sum\limits_{i=1}^{N}{y(i)}, \end{array} $$

(2)

where x(j) is the input TS signal, which is divided into N_n equal segments with length n, ${{N}_{n}}=\text {int}(\frac {N}{n})$. Then, a least square error (LSE) method is utilized to fit an envelope on the x_n(j) sets of points for individual segments. Next, a mean square error (MSE) function ((S(n)) is applied on the detrended signals as follows:

$$ \begin{array}{@{}rcl@{}} & {{x}_{s}}(j)=x(j)-{{x}_{n}}(j),\\ & S(n)=\sqrt{\frac{1}{N}\sum\limits_{j=1}^{N}{{{[x(j)-{{x}_{n}}(j)]}^{2}}}}, \end{array} $$

(3)

where x_s(j) is the detrended TS. Thereupon, a logarithmic diagram named S(n) is computed. Based on exponential law the, S(n) is formed as S(n) ∝ n^α, in which, α is a parameter to obtain an envelope for fitting on the obtained logarithmic diagram. The slope of the fitted line is identified as self-similarity value. Regarding to α value, it is in the following categorized list:

• long-term anti-correlation for 0 < α < 0.5,

• long-term correlation for α > 0.5,

• white noise for α = 0.5,

• $\frac {1}{f}$ noise for α = 1,

• Brownian noise for α = 1.5.

In the final part of feature extraction calculations, the DFA is combined with the DWPT and ERD mother wavelets.

DWPT-DFA

To combine the DWPT-DFA with the ERD, the y(i) is decomposed into components in level l. In each level, the components are juxtaposing to make a new TS, called y^′(i). The complete procedure is presented as follows:

• I. Forming a new TS (y^′(i)) by computing and juxtaposing wavelet packet, components in each level,

• II. Constructing x(j) by integrating y^′(i) using (3),

• III. Dividing the achieved x(j) into N_n equal segments,

• IV. Fitting a line on the x(j) points utilizing the LSE method,

• V. Computing the S(n) using the MSE method and forming a logarithmic diagram,

• VI. Computing the slope (w) of the linear fitted line in the logarithmic diagram, which is drawn by S(n).

After extracting the DWPT-DFA features with different mother wavelets, features are classified using the SSVM-GRBF classifier. At this stage, db4, db8 and coif4 are the predefined mother wavelets that will be replaced with the ERD mother wavelet in order to extract the features classified through the SSVM-GRBF classifier. The SSVM-GRBF classifier algorithm is described in detail as follows:

Classifiers

The last section of the DWPT-DFA is to classify the imaginary movements and non-imaginary movement features. To classify the extracted features, the SSVM classifier with the GRBF kernel is utilized and is described in two parts, the GRBF kernel and the SSVM classifier:

Generalized radial basis function (GRBF)

The Generalized RBF is a successful kernel, which is utilized in our previous studies [21, 22, 30]. The flexibility of the GRBF is summarized in terms of width (w > 0), shape (τ > 0) and center (c) of the Gaussian distribution parameters, which leads the fashion to highly accurate and robust results. The procedure is described in detail as follows:

$$ \begin{array}{@{}rcl@{}} G(s;c,w,\tau )=\frac{\tau }{2w\gamma ({}^{1}/{}_{\tau })}\exp \left( -\frac{\left\| s-c \right\|}{{{w}^{\tau }}}\right), \end{array} $$

(4)

where the parameters w and γ are the width and factorial extension function, which are computed as follows:

$$ \begin{array}{@{}rcl@{}} w&=&\sigma \sqrt{\frac{\gamma ({}^{1}/{}_{\tau })}{\gamma ({}^{3}/{}_{\tau })}},\\ \gamma (k)&=&\int\limits_{0}^{\infty }{{{t}^{k-1}}{{e}^{-t}}dt} ,\qquad for \quad k>0, \end{array} $$

(5)

where σ, t and k symbols denote the standard deviation, positive values, and inputs number. The factorial extension function is developed in [42], which is a part of an approach for generalizing the Gaussian function in the extreme learning machine method. The key parameter for generalizing the RBF kernel is τ that is tuned by optimization in a wide range.

Soft margin support vector machine (SSVM)

The SSVM is a powerful binary supervised classifier, which has the ability of integrating with different kernels. The SSVM is based on the traditional SVM with modification in solving duality problem using Lagrange’s theorem when the number of W (features weight) is increased [8]. In the procedure, two classes of y = [− 1,+ 1] are defined for the training features (x_i ∈ Rⁿ,i = 1,...,l). Then the features are mapped into higher dimension with GRBF, which is defined in Section 2.6. Afterwards, a linear hyperplane W^Tx_i + b = 0 is employed to classify the data regarding to two criteria in decision boundary as follows:

$$ \begin{array}{@{}rcl@{}} & {{W}^{T}}{{x}_{i}}+b\ge 1\quad \qquad if\quad {{y}_{i}}=1, \\ & {{W}^{T}}{{x}_{i}}+b\le -1\qquad if\quad {{y}_{i}}=-1, \end{array} $$

(6)

where W, b, T symbols denote feature weight, bias, and the transpose operator, respectively[37]. The hyperplane is then fixed by choosing some features that maximizing the margin of the classes. The selected features are named as the support vectors and the margin center is fixed the decision boundary that are computed as follows:

$$ f(x)= sgn ({{W}^{T}}x+b). $$

(7)

In high dimension and complicated situations, a nonlinear map of ϕ(x_i) is defined for (7), W^Tϕ(x) + b = 0. The duality problem is observed, which is solved through the Lagrange’s theorem [5] in (10). The Lagrange’s theorem is employed to limit the number of used features. The final decision boundary is computed by (8):

$$ sgn ({{W}^{T}}\phi (x)+b)=sgn \left( \sum\limits_{i=1}^{l}{{{y}_{i}}{{\theta }_{i}}K({{x}_{i}},x)}+b\right), $$

(8)

where k is the kernel function, K(x_i,x_j) ≡ ϕ(x_i)^Tϕ(x_j). W is computed by $w=\sum \limits _{i=1}^{l}{{{y}_{i}}{{\theta }_{i}}\phi ({{x}_{i}})}$. The optimized values for (8) are obtained in (9). 𝜃 is the utilized Lagrange’s coefficient for high dimension feature space for the i^th trial (10).

$$ \mathop{\min_{W,b,\psi } } \left( \frac{1}{2}{{W}^{T}}W+Reg\sum\limits_{i=1}^{l}{{{\psi }_{i}}}\right)\quad \text{ Subject to }\quad \begin{array}{l} {{y}_{i}}({{W}^{T}}\phi ({{x}_{i}})+b)\ge 1-{{\psi }_{i}} \\ {{\psi }_{i}}\ge 0 \\ i=1,...,l, \end{array} $$

(9)

where ψ, (ψ(W;x,y) ≡ (1 − yW^Tx)²) is the loss function [8].

The Lagrange’s coefficient are computed as follows:

$$ \begin{array}{@{}rcl@{}} \mathop{\theta }{\mathop{\min }} \left( \frac{1}{2}\sum\limits_{i,j=1}^{N}{{{\theta }_{i}}^{T}{{y}_{i}}{{y}_{j}}K({{x}_{i}},{{x}_{j}}){{\theta }_{j}}}-\sum\limits_{i=1}^{N}{{{e}^{T}}{{\theta }_{i}}}\right) \text{ Subject to } \begin{array}{l} {{y}^{T}}\theta =0, \\ 0\le {{\theta }_{i}}\le Reg ,\\ i=1,...,l, \end{array} \end{array} $$

(10)

e_l×1 is a matrix unit (Fig. 2).

Fig. 2

The algorithm procedure diagram

Data acquisition and experiment setup

In this experiment, EEG is recorded from nine international students in Lappeenranta University of Technology (LUT). Data is recorded from non-alcoholic people who has no habits of smoking or drugs. Subjects did not drink caffeinated materials such as coffee or tea in four hours before the experiment. The average age of subjects is 27.3 years old. To record the EEG data, a task is designed regarding to the validated BCI competition III data IVa [37], which is presented in Fig. 3 and available in http://www.bbci.de/competition/iii/. Description of the task is presented in four stages as follows: I) displaying the cross sign (cross fixation) at the center of a black screen for 500 msec; II) presenting pictures of right hand movement for 500 msec; III) imagining right hand movement for 2500 msec; IV) and finally, resting from 3500 msec to 4000 msec randomly after stimulation. In this experiment, we used the ENOBIO 32 portable device EEG recorder with 32 gel electrodes that is connected with Matlab through Wi-Fi. The electrode locations are depicted in Fig. 4. The frequency rate was set to 500 Hz. Computations, simulations and task are implemented in Matlab 2017.

Fig. 3

Task’s flowchart for subject stimulation

Fig. 4

32 channel location map for EEG recording

Results

Nine subjects (S1 to S9) have participated in the experiment to record the imaginary EEG signals. The flowchart diagram of the task is shown in Fig. 3. After recording, the ERDs of S8 for 32 channels are extracted and depicted in Fig. 5. Only, the CP6 and FC1 channels (Figs. 5 and 6) are observed as the most informative channels for imagery right hand movements. Figures 6, 7 and 8 are the brain scalp map based on the average amplitude of the neuron activations (power of signal) with a window width of 1500 msec for S8. Tables 1, 2, 3 and 4 contains the classified results of the DWPT-DFA method with the Daubechie families, Coiflet4 (Coif4) and ERD mother wavelets, which are classified by the SSVM-GRB classifier. Accuracy and paired t-test evaluation is then utilized to evaluate the precision and the trustworthy of the DWPT-DFA methods in Tables 1–4. The paired t-test is applied between the hand movement imagination and no movement conditions for individual subjects. In order to study the features distribution competency, the number of SVs are presented in Tables 1–4 and the type of features scattering are depicted in Figs. 6, 7, 8, 9, 10, 11 and 12 for the conditions.

Fig. 5

Extracted ERDs for 32 channels. The best ERDs are seen in the FC1 and CP6 channels for S8

Fig. 6

Extracted ERD from the FC1 channel for S8

Fig. 7

Average power of EEG from a window width of 1500 msec before stimulation for S8

Fig. 8

Average power of EEG from a window width of 1500 msec after no movement imagination stimulation for S8

Table 1 SSVM-GRBF classifier results based on the DWPT-DFA with the db4 mother wavelet features in 8-15Hz from the CP6 and FC1 channels for nine subjects individually

Table 2 SSVM-GRBF classifier results based on the DWPT-DFA with the coif4 mother wavelet features in 8-15Hz from the CP6 and FC1 channels for nine subjects individually

Table 3 SSVM-GRBF classifier results based on the DWPT-DFA with the db8 mother wavelet features in 8-15 Hz from the CP6 and FC1 channels for nine subjects individually

Table 4 SSVM-GRBF classifier results based on the DWPT-DFA with the ERD mother wavelet features in 8-15Hz from the CP6 and FC1 channels for nine subjects individually

Fig. 9

Average power of EEG from a window width of 1500 msec after right hand movement imagination for S8

Fig. 10

Scattering of the two condition features using the DWPT-DFA with the db4 for subject S8

Fig. 11

Scattering of the two condition features using the DWPT-DFA with the db8 for subject S8

Fig. 12

Scattering of the two condition features using the DWPT-DFA with the coif4 for subject S8

In the design of the task, a cross sign is displayed on a black screen to attract the subject’s attention to the center of screen for 500 msec. The sketch of hand movement is then depicted for 500 msec, and simultaneously a trigger is sent to mark the data where code 1 and 2 are used to mark the imaginary hand movement and no movement pictures, respectively. Then, subjects have 2500 msec for the right hand movement imagination (Fig. 3). Markers are denoted as an index of zero for windowing signals, which are y axes in Figs. 5 and 6. In the ERD extraction and processing, ERPLAB toolbox is exploited effectively [15, 29]. To this end, body movement artifacts are removed from the EEG by the Butherworth filter order 2 with 0.1 to 40 Hz edges. Then, the EEG signals are segmented from the point of 200 msec before the stimulation and lasts for 2700 msec. The segmented signals are then arranged in a three-dimension matrix. Finally, segments are averaged and the obtained ERD is shown in Fig. 6. As an example, Fig. 5 is the extracted ERDs from 32 channels of S8, which are important for obtaining a mother wavelet and finding the most relative channels in the task (the FC1 and CP6 channels, Figs. 5 and 6). Therefore, regarding to Fig. 5, the most informative ERDs are observed in the FC1 and Cp6 channels for feature extraction and classification. Moreover, it is feasible to find the most appropriate frequency bands using the ERD extraction technique. The ERDs of the six frequency bands are extracted and the most informative frequency bands, namely 8-12Hz and 12-16Hz, are selected based on Fig. 5. The two frequency bands are mixed and one frequency band of 8-15Hz is selected to speed up the calculations.

Discussion

In the experiment of imaginary hand movement, nine subjects have participated in recording the EEG. An imagery movement task setup is designed, which is shown in Fig. 3. The presented method has seven steps (Fig. 2): I- designing a task using the Cogent2000 Matlab toolbox for stimulation [11]; II- extracting the ERDs from individual subjects; III- utilizing ERD; db4,db8 and coif4 as a mother wavelet; IV- implementing DFA algorithm; V- Combining DWPT with customizing mother wavelet with DFA (DWPT-DFA); VI- extracting features and classifying them; and VII- using paired t-test to evaluate the trustworthy of the results based on p-values.

Fig. 13

Scattering of the two condition features using the DWPT-DFA with the ERD for subject S8

To visualize the brain neuron’s activity, the scalp’s power map of the ERDs in 32 locations for three different states in the 8Hz-15Hz frequency range are shown in Figs. 7–9. Figure 7 is the average power of signal from a width window of 1500 msec before the stimulation (no stimulation) that depicts no high activation in the sensozry-motor cortex area of the brain. The red region is an artifact, which is not rejected completely. Figure 8 is the average power of the no movement pictures from 100 msec before the stimulation and lasted 1400 msec. Figure 8 shows that the visionary neurons located in the Occidental lobe are stimulated by the displayed pictures. Figure 9 is the average power of EEG in the processing of displaying the imagery hand movement picture. Figure 9 is the power EEG signal which is segmented at the point of 100 msec before stimulation and lasted for 1400 msec. The scalp map in Fig. 6 shows high neuron’s activation in the FC1 and CP6 channels. The ERDs in Fig. 5 also presents the noteworthy of the two channels. In addition, Fig. 6 depicts that the high neuron activation onset in the FC1 channel appears at approximately 800 msec after stimulation for S8. In other studies, usually the C3 and CZ area are reported as the activated area for imaginary right hand movements [4, 31]; whilst in our study, the FC1 and CP6 channels are known as the affected area.

For the feature extraction and classification, the DWPT-DFA algorithm decomposes the raw EEG signal in five levels, in order to reach the 8-15Hz frequency band. To reach the aim frequency band, the raw EEG signal is filtered with the second order Butherworth filter from 0.1 to 16Hz. Subsequently, a wavelet with one level decomposition is applied to reach the 8-15Hz band, and the results did not change significantly. Next, four different mother wavelets are utilized in the DWPT-DFA method to extract features based on the self-similarity theory. The four mother wavelets are Daubechies (db4, db8) and Coiflet (coif4) mother, which are similar to the ERPs, EEG waves, and have been used for the ERD detection [10, 23]. The last mother wavelet is provided by the ERD extraction method and updated automatically for different subjects. Since, individual subjects has different ERDs, the predefined mother wavelets are not efficient enough. Based on the DWPT-DFA method, the extracted features with different mother wavelets are fed into the SSVM classifier with the GRBF kernel. Regarding the previous studies [8, 21, 22, 30] on the classifiers of NN, K-NN, SVM, RBF and GRBF in the EEG signal processing, we employ a SSVM with a GRBF for classifying the imagin ary movement features. The SSVM and GRBF are the amended algorithms of the traditional SVM and RBF to solve the limitations and add flexibility, such as the curse of dimension in the SVM, and to add flexibility to the RBF for different cases of data distribution [8]. Based on our previous studies [22, 30], the GRBF has the ability of covering the data distribution widely in the feature space, compared to the traditional RBF. The advantage of the SSVM classifier is preventing the algorithm from the curse of dimension by employing the Lagrange theorem, when the number of features is increased. In addition, by adding three degrees of freedom in the RBF, it provides better flexibility for fitting the distributed features than the traditional RBF. Increased accuracy rate shows the efficiency of the approach. The SSVM-GRBF classifier is also suitable for the real-time EEG signal processing and other applications, such as the computer vision and the image processing applications. The main disadvantage of the SSVM-GRBF classifier is the limitation of classes, i.e., the SSVM-GRBF is suitable for only two conditions. Tables 1–4 present the SSVM-GRBF classifier efficiency for the four mother wavelets (db4, db8, coif4 and ERD), which are inserted into the DWPT-DFA approach.

For improving the quality of the DWPT-DFA feature and efficiency of the classifiers, the scattering and the number of selected SVs for the classifiers are evaluated. The feature scattering for the four mother wavelets in the two states is depicted in Figs. 6 to 12, respectively. The best scattering is denoted by the less overlap between two classes. And, the best classifier categorize the conditions with the less number of SVs. The scattering with the most overlap is shown in Fig. 11 (coif4). The best scattering with the less overlap is depicted in Fig. 12. The range and type of scattering in the four mother wavelets show a similarity between the ERD and db4 mother wavelets. It shows that the db4 pattern is approximately similar to the ERD for S8. Also, the number of SVs in the classifying shows the quality of data scattering. A lower number of selected SVs with higher amount of accuracy lead to a better mother wavelet. Tables 1–4 show that the selected number of SVs in the ERD is the lowest in comparison to the three mother wavelets.

Following evaluations are performed by taking account of accuracy and paired t-test values. In accuracy evaluation, four parameters, namely TP, TN, FN and FP play an important role. TP is related to condition true that is classified correctly. TN is related to the false condition that is classified correctly. FN is related to the false condition that is as true condition, and FP is the false condition that is classified as true condition [21]. Table 4 depicts that the highest amount of TP and TN, consequently the highest accuracies belong to the ERD mother wavelet with the DWPT-DFA. The paired t-test evaluation is utilized to find out if there is significant relation (p < 0.05) between hand movement imagination and no movement states for individual subjects. The paired t-test results between the two states are presented in Tables 1–4. The tables show that the extracted features from the DWPT-DFA method with db4, db8, coif4 and ERD mother wavelets have zero, two, one and three subjects with insignificant relation (p > 0.05) between the two states, respectively. Therefore, the DWPT-DFA with the ERD mother wavelet improves scattering with less overlap and a less number of SVs, which yield higher accuracies and significant p-values for nine subjects. Due to the heavy computation, this approach is time consuming for real-time processing, such as BCI applications, and needs to be optimized.

Conclusion

In order to identify the imagery hand movement and no movement states, a combination of DWPT and DFA methods with self-similarity concept is utilized. To produce appropriate mother wavelet and distinctive features, the best channels and frequency bands are determined by the ERD diagnosis method. The most informative information is extracted from the 8-15Hz frequency band in the FC1 and CP6 channels. The functionality of the DWPT-DFA method is improved by integrating the generated ERD mother wavelet and updating automatically for individual subjects. The results based on the ERD mother wavelet are compared to the db4, db8, and coif4 mother wavelets. Based on the accuracies, the paired t-test, and the number of selected SVs in the SSVM classifier, the combination of the DWPT-DFA with the ERD mother wavelet is deemed as the best method with the highest accuracy of 85.33% with p < 0.001.