Abstract
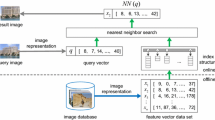
Content based image retrieval represents images as N- dimensional feature vectors. The k images most similar to a target image, i.e., those closest to its feature vector, are determined by applying a k-nearest-neighbor (k-NN) query. A sequential scan of the feature vectors for k-NN queries is costly for a large number of images when N is high. The search space can be reduced by indexing the data, but the effectiveness of multidimensional indices is poor for high dimensional data. Building indices on dimensionality reduced data is one method to improve indexing efficiency. We utilize the Singular Value Decomposition (SVD) method to attain dimensionality reduction (DR) with minimum information loss for static data. Clustered SVD (CSVD) combines clustering with SVD to attain a lower normalized mean square error (NMSE) by taking advantage of the fact that most real-world datasets exhibit local rather than global correlations. The Local Dimensionality Reduction (LDR) method differs from CSVD in that it uses an SVD-friendly clustering method, rather than the k-means clustering method. We propose a hybrid method which combines the clustering method of LDR with the DR method of CSVD, so that the vector of the number of retained dimensions of the clusters is determined by varying the NMSE. We build SR-tree indices based on the vectors in the clusters to determine the number of accessed pages for exact k-NN queries (Thomasian et al., Inf Process Lett - IPL 94(6):247–252, 2005) (see Section A.3 versus the NMSE. Varying the NMSE a minimum cost can be found, because the lower cost of accessing a smaller index is offset with the higher postprocessing cost resulting from lower retrieval accuracy. Experimenting with one synthetic and three real-world datasets leads to the conclusion that the lowest cost is attained at NMSE ≈ 0.03 and between 1/3 and 1/2 of the number of dimensions are retained. In one case doubling the number of dimensions cuts the number of accessed pages by one half. The Appendix provides the requisite background information for reading this paper.





Similar content being viewed by others
Notes
A sufficiently small standard deviation is achieved with a 1000 k-NN queries.
Some datasets are studentized by dividing the zero mean column by the standard deviation [9].
Abbreviations
- CBIR :
-
Content-based image retrieval
- CSVD :
-
Clustered singular value decomposition
- DR :
-
Dimensionality reduction
- KLT :
-
Karhunen-Loeve transform
- k-NN :
-
k-nearest-neighbor
- LBP :
-
Lower bounding property
- LDR :
-
Local dimensionality reduction
- MMDR :
-
Multi-level Mahalanobis-based dimensionality reduction
- NMSE :
-
Normalized mean square error
- SSQ :
-
Sum of squares
- SVD :
-
Singular value decomposition
References
Agrawal R, Gehrke J, Gunopulos D, Raghavan P (1998) Automatic subspace clustering of high dimensional data for data mining applications. In: Proc. ACM SIGMOD int’l conf. on management of data, Seattle, WA, June 1998, pp 94–105
Barbara W, DuMouchel W, Faloutsos C, Haas PJ, Hellerstein JM, Ioannidis Y, Jagadish HV, Johnson T, Ng R, Poosala V, Ross KA, Sevcik KC (1997) The New Jersey data reduction report. Data Eng Bull 20(4):3–42, December
Beckmann N, Kriegel H-P, Schneider R, Seeger B (1990) The R*-tree: an efficient and robust access method for points and rectangles. In: Proc. ACM SIGMOD int’l conf. on management of data, Atlantic City, NJ, May 1990, pp 322–331
Bergman LD, Castelli V, Li C-S, Smith JR (2000) SPIRE: a digital library for scientific information. Int J Digit Libr 3(1):85–99
Bohm C (2000) A cost model for query processing in high-dimensional data space. ACM Trans Database Syst 25(2):129–178
Bohm C, Berchtold S, Keim DA (2001) Searching in high-dimensional spaces – index structures for improving the performance of multimedia databases. ACM Comput Surv 33(3):322–373, September
Castelli V (2002) Multidimensional indexing structures for content-based retrieval. In: Castelli V, Bergman LD (eds) Image databases: search and retrieval of digital imagery. Wiley-Interscience, New York, pp 373–434
Castelli V, Bergman LD (eds) (2002) Image databases: search and retrieval of digital imagery. Wiley-Interscience, New York
Castelli V, Thomasian A, Li CS (2003) CSVD: clustering and singular value decomposition for approximate similarity search in high dimensional spaces. IEEE Trans Knowl Data Eng 14(3):671–685, June
Chakrabarti K, Mehrotra S (1999) The hybrid tree: an index structure for high dimensional feature spaces. In: Proc. 15th IEEE int’l conf. on data eng. - ICDE, Sidney, Australia, March 1999, pp 440–447
Chakrabarti K, Mehrotra S (2000) Local dimensionality reduction: a new approach to indexing high dimensional space. In: Proc. int’l conf. on very large data bases - VLDB, Cairo, Egypt, August 2000, pp 89–100
Faloutsos C (1996) Searching multimedia databases by content. Kluwer Academic, Boston, MA
Faloutsos C, Kamel I (1994) Beyond uniformity and independence: analysis of the R-tree using the concept of fractal dimension. In: Proc. ACM symp. on principles of database systems - PODS, Minneapolis, MN, June 1994, pp 4–13
Farnstrom F, Lewis J, Elkan C (2000) Scalability for clustering algorithms “revisited”. ACM SIGKDD Explor Newslett 2(1):51–57
Gaede V, Gunther O (1998) Multidimensional access methods. ACM Comput Surv 30(2): 170–231
Gonzalez TF (1985) Clustering to minimize the maximum intercluster distance. Theor Comp Sci 38:293–306
Han J, Kamber M (2006) Data mining: concepts and techniques. Morgan-Kaufmann, San Francisco
Hjaltason GR, Samet H (1995) Ranking in spatial databases. In: Proc. 4th symp. advances in spatial databases, lecture notes in computer science 951, Springer, Berlin Heidelberg New York, pp 83–95
Jin H, Ooi BC, Shen H, Yu C (2003) An adaptive and efficient dimensionality reduction algorithm for high-dimensional indexing. In: Proc. 19th IEEE int’l conf. on data engineering - ICDE, Bangalore, India, March 2003, pp 87–100
Jolliffe IT (2002) Principal component analysis. Springer, Berlin Heidelberg New York
Katayama N, Satoh S (1997) The SR-tree: an index structure for high dimensional nearest neighbor queries. In: Proc. ACM SIGMOD int’l conf. on management of data, Tucson, AZ, May 1997, pp 369–380
Kim B, Park S (1986) A fast k-nearest-neighbor finding algorithm based on the ordered partition. IEEE Trans Pattern Anal Mach Intell 8(6):761–766
Korn F, Jagadish HV, Faloutsos C (1997) Efficiently supporting ad hoc queries in large datasets of time sequences. In: Proc. ACM SIGMOD int’l conf. on management of data, Tucson, AZ, May 1997, pp 289–300
Korn F, Pagel B, Faloutsos C (2001) On the “dimensionality curse” and the “self-similarity blessing”. IEEE Trans Knowl Data Eng 13(1):96–111
Korn F, Sidiropoulos N, Faloutsos C, Siegel E, Protopapas Z (1996) Fast nearest neighbor search in medical image databases. In: Proc. 22nd int’l conf. on very large data bases - VLDB, Mumbai, India, September 1996, pp 215–226
Korn F, Sidiropoulos N, Faloutsos C, Siegel E, Protopapas Z (1998) Fast and effective retrieval of medical tumor shapes: nearest neighbor search in medical image databases. IEEE Trans Knowl Data Eng 10(6):889–904
Li Y (2004) Efficient similarity search in high-dimensional data spaces. Ph.D. dissertation, Computer Science Department, New Jersey Institute of Technology - NJIT, Newark, NJ, May
McCallum A, Nigam K, Unger LH (2000) Efficient clustering of high-dimensional data sets with applications to reference matching. In: Proc. 6th ACM SIGKDD int’l conf. on knowledge discovery and data mining, Boston, MA, 20–23 August 2000, pp 169–178
Niblack W, Barber R, Equitz W, Flickner M, Glasman EH, Petkovic D, Yanker P, Faloutsos C, Taubin G (1993) The QBIC project: querying images by content, using color, texture, and shape. In: Niblack W (ed) Proc. SPIE vol. 1908: storage and retrieval for image and video databases, SPIE, Bellingham, pp 173–187
Parsons L, Haque E, Liu H (2004) Subspace clustering for high dimensional data: a review. ACM SIGKDD Explor Newslett 6(1):90–105
Roussopoulos N, Kelley S, Vincent F (1995) Nearest neighbor queries. In: Proc. ACM SIGMOD int’l conf. on management of data, San Jose, CA, June 1995, pp 71–79
Samet H (2007) Fundamentals of multidimensional and metric data structure. Morgan- Kaufmann, San Francisco
Singh AK, Lang CA (2001) Modeling high-dimensional index structures using sampling. In: Proc. ACM SIGMOD int’l conf. on management of data, Santa Barbara, CA, June 2001, pp 389–400
Theodoridis Y, Sellis T (1996) A model for the prediction of R-tree performance. In: Proc. ACM symp. on principles of database systems - PODS, Montreal, Quebec, Canada, June 1996, pp 161–171
Thomasian A, Castelli V, Li CS (1998) RCSVD: recursive clustering and singular value decomposition for approximate high-dimensionality indexing. In: Proc. conf. on information and knowledge management - CIKM, Baltimore, MD, November 1998, pp 201–207
Thomasian A, Li Y, Zhang L (2003) Performance comparison of local dimensionality reduction methods. Technical report ISL-2003-01, Integrated Systems Lab, Computer Science Dept., New Jersey Institute of Technology
Thomasian A, Li Y, Zhang L (2005) Exact k-NN queries on clustered SVD datasets. Inf Process Lett 94(6):247–252, July
Thomasian A, Zhang L (2006) Persistent semi-dynamic ordered partition index. Comput J 49(6):670–684, June
White DA, Jain R (1996) Similarity indexing: algorithms and performance. In: Storage and retrieval for image and video databases SPIE, vol 2670. SPIE, San Jose, CA, pp 62–73
Yi BK, Faloutsos C (2000) Fast time sequence indexing for arbitrary Lp norms. In: Proc. 26th int’l conf. on very large data bases - VLDB, Cairo, Egypt, September 2000, pp 385–394
Zhang L (2005) High-dimensional indexing methods utilizing clustering and dimensionality reduction. Ph.D. dissertation, Computer Science Department, New Jersey Institute of Technology - NJIT, Newark, NJ, May
Acknowledgements
Discussions with Prof. Byoung-Kee Yi, Postech University of Science and Technology, Pohang, Korea, on determining the optimum dimensionality in the context of the “segmented means” method [40].
Author information
Authors and Affiliations
Corresponding author
Appendix: preliminaries
Appendix: preliminaries
We first describe the SVD method in Sectionref:SVD. In Section A.2 we specify the SVD-friendly clustering method developed in conjunction with the LDR method. Exact versus approximate k-NN query processing methods are discussed in Section A.3. Finally, in Section A.3 we specify an efficient method to compute Euclidean distances with dimensionally reduced data.
1.1 A.1 Singular value decomposition
The SVD of an M ×N matrix X for feature vectors is: X = USV T, where U is an M×N column-orthonormal matrix, V is an N×N unitary matrix of eigenvectors, and S is a diagonal matrix of singular values: s 1 ≥ s 2 ≥ ... ≥ s N . The mean values have been subtracted from the elements in each column, so that the columns of X have a zero mean. When N′ of the singular values are close to zero, then the rank of X is N − N′ [12]. The cost of computing eigenvalues using SVD is O ( M N 2 ).
PCA is based on the decomposition of the covariance matrix C = X T X/M = V ΛV T , where V is the matrix of eigenvectors and Λ is a diagonal matrix, which holds the eigenvalues of C. C is positive-semidefinite, so that its N eigenvectors are orthonormal and its eigenvalues are nonnegative. The trace (sum of eigenvalues) of C is invariant under rotation. We assume that the eigenvalues, similar to the singular values, are in nonincreasing order. The singular values are related to the eigenvalues by: \(\lambda_j = s^2_j /M \) or \(s_j = \sqrt{M\lambda_j}\). The eigenvectors constitute the principal components of X, hence the transformation below yields uncorrelated features:
Retaining the first n dimensions of Y minimizes the NMSE and maximizes the fraction of preserved variance:
Retaining the first n dimensions of Y minimizes the NMSE and maximizes the fraction of preserved variance:
1.2 A.2 Clustering
A large number of clustering algorithms, which are applicable to various domains have been developed over the years [17]. The k-means clustering method used [9, 35] can be specified succinctly [14]: (i) Randomly select H points from the dataset to serve as preliminary centroids for clusters. Improve centroid spacing using the method in [16]. (ii) Assign points to the closest centroid based on the Euclidean distance to form H clusters. (iii) Recompute the centroid for each cluster. (iv) Go back to step (ii), unless there is no new assignment. \({\cal C}^{(h)}\) denotes the h th cluster, with centroid C h with coordinates given by \(\vec{\mu}^{(h)}\), and a radius R h, which is the distance of the farthest point in the cluster from C h . Since the quality of the clusters varies significantly from run to run, the clustering experiment is repeated and the experiment yielding the smallest sum of squares (SSQ) distances to the centroids of all clusters is selected:
The k-means clustering method does not scale well to large high-dimensional datasets [28]. Subspace clustering methods take advantage of the fact that in high dimensional datasets many dimensions are redundant and hide clusters in noisy data. The curse of dimensionality also makes distance measures meaningless to an extent that data points are equidistant from each other. Subspace clustering methods find clusters in different, lower-dimensional subspaces of a dataset [30]. The weakness of the CLIQUE subspace clustering method [1] is that the subspaces are aligned with the original dimensions. Many others which are reviewed in [30]. The Multi-level Mahalanobis-based Dimensionality Reduction [19] clusters high dimensional datasets using the low-dimensional subspace based on the Mahalanobis [12] rather than the Euclidean distance, since it is argued that locally correlated clusters are elliptical shaped.
The LDR clustering method specified in [11] and utilized in this paper generates SVD-friendly clusters [35], which are amenable to DR at a small NMSE. The following discussion follows the Appendix in [9].
-
1-
Initial selection of centroids: H points with pairwise distances of at least threshold are selected.
-
2-
Clustering. Each point is associated to the closest centroid whose distance is ≤ ε, and ignored otherwise. Each cluster has now a centroid, the average of the associated points.
-
3-
Apply SVD to each cluster. Each cluster has now a reference frame.
-
4-
Assign points to clusters: Each point in the dataset is analyzed in the reference frame of each cluster. For each cluster determine the minimum number of retained dimensions so that squared error in representing points does not exceed MaxReconDist 2. The cluster requiring the minimum number of dimensions N min is determined. If N min ≤ MaxDim, the point is associated with that cluster, and the required number of dimensions is recorded, otherwise the point becomes an outlier.
-
5-
Compute the subspace dimensionality of each cluster. Find the minimum number of dimensions ensuring that at most FracOutliers of the points assigned to the cluster in Step 4 do not satisfy the MaxReconDist 2 constraints. Each cluster has now a subspace.
-
6-
Recluster points. Each point is associated with the first cluster whose subspace is at a distance less than MaxReconDist from the point. If no such cluster exists, the point becomes an outlier.
-
7-
Remove small clusters. Clusters with size smaller than MinSize are removed and the corresponding points reclustered with Step 6.
-
8-
Recursively apply Steps 1–7 to the outliers set. Make sure that the centroids selected in Step 1 have a distance at least threshold from the current valid clusters. The procedure terminates when no new cluster is identified.
-
9-
Create an outlier list. As in [23] this is searched using a linear scan.
The values for H, threshold, ε, MaxReconDist, MaxDim, FracOutliers, and MinSize need to be provided by the user. This constitutes the main difficulty with applying the LDR method. The invariant parameters are MaxReconDist, MaxDim, and MinSize. The method can produce values of H, threshold, and overall FracOutliers, which are significantly different from the inputs. The fact that the LDR method determines the number of clusters is one of its advantages with respect to the k-means method.
1.3 A.3 Exact versus approximate k-NN queries
k-NN search methods are classifiable into exact and approximate methods. We first define Recall and Precision, which are metrics of retrieval accuracy and efficiency, respectively. Since SVD is a lossy data compression method, in processing k-NN queries we retrieve k * ≥ k points. Given that k′ of the retrieved points are among the k desired nearest neighbors, it is easy to see that k′ ≤ k ≤ k * . Recall (accuracy) is defined as \({\cal R } = k' / k \) and precision (efficiency) as \( {\cal P} = k'/ k^* \). k-NN search on dimensionality reduced data is inherently approximate with a recall \({\cal R} < 1 \). Exact k-NN search returns the same k-NNs as would have been obtained without DR, i.e., \({\cal R}=1\).
Post-processing is required to achieve exact k-NN query processing on dimensionally reduced data. Post processing takes advantage of the lower-bounding property (LBP) [12] (or Lemma 1 in [25, 26]): Given that the distance of points in the subspace with reduced dimensions is less than the original distance, a range query guarantees no false dismissals.
False alarms are discarded by referring to the original dataset. Noting the relationship between range and k-NN queries, the latter can be processed as follows [25]: (i) Find the k-NNs of the query point Q in the subspace. (ii) Determine the farthest actual distance to Q among these k points (d max ). (iii) Issue a range query centered on Q on the subspace with radius ε = d max . (iv) For all points obtained in this manner find their original distances to Q, by referring to the original dataset and rank the points, i.e., select the k-NNs.
The exact k-NN processing method was extended to multiple clusters in [37], where we compare the CPU cost of the two methods as the NMSE is varied using two of the datasets in Section 3. An offline experiment was used to determine k *, which yields a recall R ≈ 1. The CPU time required by the exact method for a sequential scan is lower than the approximate method, even when \({\cal R}=0.8\). This is attributable to the fact that the exact method issues a k-NN query only once and this is followed by less costly range queries.
The LDR method also takes advantage of LBP to attain exact query processing [11]. It produces fewer false alarms by incorporating the reconstruction distance (the squared distance of all dimensions that have been eliminated as an additional dimension with each point.
1.4 A.4 Computing distances with dimensionality reduced data
The DR method in [9, 35] retains n < N columns of the Y matrix, which correspond to the largest eigenvalues, while the method described in [12, 23] retains the n columns of the U matrix corresponding to the largest eigenvalues. In both cases the eigenvalues or singular values are in nonincreasing order, so that columns with the smallest indices need to be preserved. We first show that retaining the n columns of the Y matrix results in the same distance error as retaining the same dimensions of the U matrix. We also show that our method is computationally more efficient than the other method. Retaining the first n dimensions (columns) of the transformed matrix Y = X V we have:
The rest of the columns of the matrix are set to the column mean, which is zero in our case.Footnote 2 The squared error in representing point \(P_i, \ 1 \leq i \leq M \) is then:
The elements of X are approximated as X′ ≈ U S V T by utilizing the first n dimensions of U [12, 23]:
Noting that Y = XV = US, the squared error in representing P i is:
To show that e i = e′ i , 1 ≤ i ≤ M, we use the definition δ k,k′ = 1 for k = k′ and δ k,k′ = 0 for k ≠ k′ .
Our method is more efficient from the viewpoint of computational cost for nearest neighbor, range, and window queries. In the case of nearest neighbor queries, once the input or query vector is transformed and the appropriate n dimensions are selected, we need only be concerned with these dimensions. This is less costly than applying the inverse transformation.
Rights and permissions
About this article
Cite this article
Thomasian, A., Li, Y. & Zhang, L. Optimal subspace dimensionality for k-nearest-neighbor queries on clustered and dimensionality reduced datasets with SVD. Multimed Tools Appl 40, 241–259 (2008). https://doi.org/10.1007/s11042-008-0206-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-008-0206-3