1 Introduction

In astronomy the research about the minor planets is an important branch. Since the first minor planet named as Ceres was found in 1801, the more and more minor planets are observed by hundreds of observatories located on the surface of Earth. As the main part of minor planets, Asteroids, called by Willian Herschel firstly, are a class of small solar system bodies in orbit around the Sun. The formation of asteroids are thought as the large planets (such as Mars, Jupiter) prevent the formation of a new large planet from the planetesimals and thousands of small bodies are left to orbit the Sun. Most of asteroids found now lie between the Jupiter and Mars called as Main Belt Asteroids (MBA) commonly. Almost all of the MBA has a stable orbit around the Sun with a distance about 2.1–3.3 AU from the Sun, with rare exception of the perturbation from the secular resonances of Jupiter, Mars and Saturn. The diameters of most MBA are less than 10 km although the mean diameter of the former 4 MBA is about 400 km. So the best research methods for asteroids will depend on the ground-based observations which can record abundant photometric data with a continuous period of time for a whole night. Until now there are thousands of lightcurves for about less than 300 asteroids collected in DAMIT (Ďurech et al. 2010). Besides, there is another large repository of lightcurves for asteroids in minor planet center(MPC) (Warner et al. 2009). Recently some large sky survey missions such as UVEX, VPHAS, SSS, LSST, SkyMapper, PanSTARRS, including the future mission Gaia launched in 2013 (Jordi et al. 2010), send tremendous amounts of photometric data from the space out of Earth. Ultimately the larger photometric data can be adopted to build up the model of asteroids.

Shape of asteroids, always irregular, can be applied to estimate the density of asteroids and deduce their origin. Furthermore, the accurate shape model can be applied to obtain more accurate physical parameters, such as period and pole orientation. The shape inverse problem was concerned firstly by Russell in 1906 with a pessimistic conclusion (Russell 1906). He thought it was impossible to reconstruct the original shape only from the lightcurves in the opposition. (Opposition is a position where the solar phase angle (α) is zero.) As technology in both the telescope and mathematical model is developed recently, more and more research about asteroids is made by others (Karttunen 1989; Karttunen et al. 1989; Cellino et al. 1985). Most of the methods for this inverse problem treat the shape of asteroids as an ellipsoid with three semi-axis. In this way some rough physical parameters such as spin axis, rotation period, albedo and other scattering factors, can be estimated simultaneously with the ellipsoid model from lightcurves, whereas it is very hard to simulate the scattering law of asteroids accurately. Fortunately laboratory experiments and radar photos confirm that the brightness variation of the asteroid mainly depends on the variation of its shape but the one of the scattering factor of its surface. Due to the simplicity of the ellipsoid model, many shape models and physical parameters of asteroids are obtained under the ellipsoid assumption and this method is still popular until now.

In order to reconstruct the irregular shapes of asteroids and get more accurate physical parameters, Kaasalainen and Lamberg presented a very efficient method to search the best fit solution totally including the arbitrary three-dimensional shape model and the related physical parameters of asteroids (Kaasalainen and Lamberg 1992a; Kaasalainen and Lamberg 1992b). The whole process to reconstruct the arbitrary shape is split into two steps. Firstly a set containing triangular facets with their areas is calculated to make sure their synthetic brightnesses are consistent with lightcurves. Then another process named Minkowski is employed to construct the shape from the facets set. The stability of Minkowski process can make the inverse problem converge in a feasible way (Lamberg and Kaasalainen 2001). Moreover this method is testified to perform very well in laboratory by Kaasalainen and they confirm that more or less about 10 lightcurves observed in various geometric positions are required to reconstruct the shape of asteroids with a good match in the laboratory environment (Kaasalainen et al. 2005).

Both ellipsoid model and Kaasalainen’s model are based on the lightcurves with various viewing aspect. According to many observed lightcurves of one specific asteroid, such as (6) HEBE, 39 lightcurves collected in DAMIT, one rough shape model with the pole orientation and spin period can be calculated by the inverse method. Basing on these obtained parameters, the geometric distribution of observed lightcurves can be analyzed and the cabins of viewing aspect without any lightcurve are picked out to guild the new observation plan. As the additional lightcurve in required viewing aspect is observed, the related parameters, such as pole orientation can be updated soon. It seems like a long-term ‘iteration’. However, a total shape model of asteroids can be refined in this way. If there would be a large center, such as DAMIT and MPC, to host the whole of lightcurves data and provide the future observing plan, the shape model of asteroids could be refined in an efficient way.

The details of this article are arranged as follows. Section 2 introduces the scattering law and Kaasalainen’s method in a simple way. Then in Section 3 the geometric distribution of recorded lightcurves will be shown for the specified asteroid, (6) HEBE. After that the detailed observation plan is made for (6) HEBE. The conclusion and future work will be mentioned in the Section 4.

2 Shape Model of Asteroids

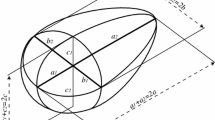
In order to build shape models of asteroids, some notations are introduced firstly as follows. Because the orbits of most MBA are stable only with a very rare probability of perturbation, the related physical characteristics are fixed during the most part of their orbital periods, such as the rotation period (P 0) and the orientation of the spin axis denoted as (λ0,β0) under the ecliptic coordinate system. The brightness in lightcurves observed by telescopes is the integration on the part of the asteroid’s surface illuminated by Sun. For example, published by Lagerkvist et al. 1995, the lightcurve of (6) HEBE containing 37 points scattering within 6 h is plotted in Fig.  1 with a relative brightness. There are totally 39 lightcurves dispersing in about 50 years, collected in DAMIT, which can be used to reconstruct the shape model of (6) HEBE by Kaasalainen’s method, shown in Fig. 2. Besides, the other physical parameters of (6) HEBE can be obtained simultaneously, such as the pole orientation is (340°, 40°) and the rotation period is P 0 = 7.27 h, which can be employed to make the observation plan.

Fig. 1
figure 1

one lightcurve of (6) HEBE

Full size image
Fig. 2
figure 2

Shape model of (6) HEBE

Full size image

The geometric positions will play a very important role in the variation of the brightness. Supposed that the unit vectors in the directions of illuminating and viewing are denoted as \(\omega_0, \omega \in {\mathbb R}^3\) respectively. Then the phase angle (α) can be calculated by cosα = ω0·ω. Generally the Julian day, relative brightness, position vectors ω0 and ω are recorded in the lightcurve under the same frame, ecliptic coordinate system with the origin laying on the asteroid.

The shape inverse method depends on the lightcurves with full observations on the surface of the asteroid. Two synthetic lightcurves are shown in Fig. 3 by simulating the rotation of (6) HEBE illuminated at the same phase angle α and viewed with different observing geometry. In order to illustrate the observing geometry better, we refer to the phase angle bisector(PAB) introduced firstly by Harris et al. (1984), which bisects the directions to sun(illumination) and earth(observing) as seen from the asteroid, and present a similar direction vector ‘PABS’ to PAB, which is not defined on the common ecliptic coordinate frame, but the asteroid-centric coordinate frame with the spin axis as its Z-axis. Under the definition, the PABS latitude (Θ), i.e., the angle between the direction of PAB and the orientation of the spin axis of asteroids, can be adopted to measure the observing geometry on the surface of asteroids. Apparently lightcurves with different PABS latitude (Θ) contain the corresponding surface information of the different part of the asteroid. Due to the rotation period of most asteroids is distributed in an interval from 2.2 to 24 h, generally several observations on one apparition with PABS latitude varying not too much, can cover most part of PABS longitudes. So in this meanings the more lightcurves with various Θ there are, the more accurately the shape model will express the real asteroid. Focusing on this we present the way how to make the observation plan to get much more lightcurves with various PABS latitude (Θ)

Fig. 3
figure 3

The comparison of two synthetic lightcurves with different PABS latitude (Θ) at the same phase angle α = 15° (Left: \(\Uptheta=45^\circ$ \hbox{Right:\,} $\Uptheta=5^\circ)\)

Full size image

Due to the development of the technologies in both telescope and mathematical theory the accurate position and velocity (called as the Ephemeris) of asteroids can be calculated with respect to the time in an acceptable precision level. Generally the position of any asteroid under the ecliptic coordinate system can be calculated from its six orbital elements with a small calibration of large planets perturbation. Besides, NASA/JPL also provides the ephemeris computation for most of numbered asteroids.

The position of the asteroid under the ecliptic coordinate system can be adopted to compute the geometry relationship of the asteroid, Sun(illumination direction) and Earth(viewing direction). If combining the spin axis of the asteroid, which can be computed by solving the previous shape inverse problem, the distribution of the PABS latitude (Θ) may be generated. When the asteroid is observed at a low Θ, more shape information at the equatorial area of the asteroid will be recored, while observed at a high (Θ) more shape information at the polar area of the asteroid will be recored. In Fig. 4 the distribution of PABS latitude (Θ) of (6) HEBE is shown. In order to build up an accurate shape model of the asteroid, lightcurves observed in various Θ will be required. But the Θ is also limited to the orbit of the asteroid and position of Earth. We will analyze the distribution of observed lightcurves and try to get the required lightcurves under the limitation of its orbit in next section.

Fig. 4
figure 4

Distribution of PABS latitude (Θ) of (6) HEBE

Full size image

3 Observation Plan

Since 1906 when Russell firstly started the research of shape inverse problem from the observed lightcurves, there have been tens of thousands of lightcurves recorded by the observatories and amateurs for many asteroids. Especially for some easy-to-be-observed asteroids, like (3)JUNO and (6)HEBE et. al, there are about more than tens of lightcurves collected now, which can be adopted to reconstruct their shape models and physical parameters. Nevertheless, due to the limitation of asteroid’s orbit and observing condition, the PABS latitudes (Θ) of collected lightcurves do not cover the asteroid evenly. Moreover, an accurate shape model needs the full surface information implied in the lightcurves with various viewing aspect. Herein to complement the lightcurves database with required PABS latitude (Θ) we try to present an observation plan for (6) HEBE and expect this method can be spread for more asteroids in the future.

3.1 Geometric Distribution of Lightcurves

Now about 39 lightcurves of (6) HEBE observed in the last decades are collected in DAMIT. The geometric distribution of the 39 lightcurves is present to make the new observation plan for (6) HEBE.

The distribution of phase angle (α) is illustrated in Fig. 5, showing that (6) HEBE has been observed evenly in various phase angle from \(0^\circ \sim 25^\circ \). The following figure will confirm the largest phase angle of (6) HEBE in its orbit is close to 25°. Although the brightness in the same phase angle can vary with respect to the illuminate direction due to the irregular surface of the asteroid, most MBA whose maximum phase angle is smaller than 30° especially (6) HEBE, are observable in any phase angle. As a result, the solar phase will not be the obstacle to make the observation plan for (6) HEBE.

Fig. 5
figure 5

Distribution of phase angle (α) of (6) HEBE

Full size image

In Table 1 the distribution of PABS latitude (Θ) of the 39 lightcurves is classified. Apparently the observed lightcurves are not distributed evenly on the intervals with a 10° increment. More than one-third lightcurves are observed on the same \(\mathrm{\Uptheta}$ \hbox{interval} $[40^\circ \sim 50^\circ]\) while there is none on the intervals \([30^\circ \sim 40^\circ]\) and \([0^\circ \sim -10^\circ] \). The accurate shape model of asteroids requests all kinds of lightcurves observed in various Θ. Physical experiments in laboratory have confirmed that about accurate 10 lightcurves distributed in different Θ are sufficient to obtain the shape model of the asteroid (Kaasalainen et al. 2005). The Table 1 shows that we have collected many lightcurves observed on the similar PABS latitude interval, while there is none lightcurves recored on some other intervals. So the future observation will be arranged better on the intervals with none lightcurve. According to the orbital data of the asteroid the observing dates with a required PABS latitude can be found.

Table 1 Distribution of PABS latitude Θ for all 39 lightcurves of (6) HEBE
Full size table

Besides, solar elongation of asteroid is better limited larger than 90° for a good observing condition. If the elongation is less than 90°, the observation can not guarante to obtain the high-quality photometric data.

3.2 Observable Dates

After analyzing the 39 observed lightcurves of (6) HEBE the desired PABS latitude (Θ) intervals are known, such as the intervals of [30°, 40°] and [0°, −10°]. The geometric relationship in its whole orbital period is shown in Fig. 6. Some notations are introduced firstly herein. The stars(*) stands for the solar phase angle (α) which will change from 0 to the largest angle 31.5°. For sketching the three angles in the same figure better, the diamond(\(\diamondsuit\)) represents the complement of PABS latitude i.e. \(90^\circ-\Uptheta\). And the plus(+) stands for the elongation which will change as both asteroid and Earth run around Sun. Ultimately the observable time intervals are sketched out on the bold lines of the ‘YEARS’ axis assuring that elongation is larger than 90°.

Fig. 6
figure 6

Observation Plan of (6) HEBE for its following whole orbital period from 2011.8–2015.5

Full size image

In Fig. 6 the geometric relationship of Sun, Earth and (6) HEBE in the following three year is presented. We obtain three observable date intervals under the condition of elongation larger than 90°, on which the phase angles are also available for (6) HEBE to be observed by the ground-based observatories.

In Table 2 the detailed observation plan is presented for (6) HEBE to obtain the lightcurves distributed on the desired PABS latitude intervals. Such as from 2012.3.20 to 2012.5.20 we could make the observation to get the lightcurves with the Θ on the interval of [\(30^\circ \sim 40^\circ\)] under a small phase angle within the interval of [\(9.6^\circ \sim 20.7^\circ\)]. This was a very good chance to complement the lightcurves database of (6) HEBE because it is very hard to get the lightcurves on this Θ interval. Fortunately Raoul Behrend et al. observed the lightcurves of (6) HEBE from 2012.2.25 to 2012.3.16 close to the best date interval. From Fig. 6 if we want to obtain the similar lightcurves maybe we have to wait until 2016. The detailed information of two other best observable data interval is listed in Table 2. Further more the PABS latitudes (Θ) corresponding with the best observing dates are also highlighted in Fig. 6 by the solid diamond.

Table 2 Observation plan of (6) HEBE in the following 3 years
Full size table

4 Conclusions

Through combining the shape inverse problem and the orbital calculation of asteroids we present an observation plan for (6) HEBE. By making the analysis of the existing 39 lightcurves of (6) HEBE collected in DAMIT, the distribution of PABS latitude is sketched and the desired PABS latitude intervals are found. At last limited by the geometric relationship of Earth, Sun and (6) HEBE in the following three years, the observable date intervals are tabled to obtain the desired PABS latitude. This plan can guide the observation to enrich the photometric database of (6) HEBE and the new additional lightcurves can be used to update the shape model and physical parameters furthermore.

Because our observation plan needs a prior estimation of the spin axis, for the asteroid with only several lightcurves it is better to collect as many lightcurves as possible firstly to obtain a rough orientation of its spin axis. The spin axis is mainly adopted to analyze the degree of concentration of observed lightcurves, which do not request an accurate spin axis. A spin axis with a 10° error can also be applied to classify the lightcurves and make the observation plan. The purpose of the scheme is to guild the observation for collecting more lightcurves to make the lightcurves database with an even distribution. However, for some asteroids with many lightcurves, such as (8) FLORA with more than 47 lightcurves and (21) LUTETIA with more than 50 lightcurves, the scheme presented in the article to make the observation plan can be applied to enrich the lightcurves database and refine their shape models.

We have introduced the whole process to make the observation plan for (6) HEBE and present it in Table 2. It is better to give out the best observing place, such as the longitude and latitude. We will make more detailed observation plan for asteroids and specify the observing place with the observing time in the future. Besides, now that we have known that the observation of (6) HEBE from 2013.3.1 to 2013.8.20 can fill the PABS latitude interval [\(0^\circ \sim -10^\circ\)], we will plan to make this observation at these dates using our observatory located on Nanjing, China.