1 Introduction

Electrostatic ion-cyclotron instability (EICI), observed in the auroral acceleration region by various satellites like S3-3, ISEE-1, Viking and recently by Polar, Freja and FAST satellites (Mozer et al. 1997; Carlson et al. 1998; Norqvist et al. 1998; Gavrishchaka et al 2000; Hamrin et al. 2001), has been of considerable interest to plasma physicists as the instability appears in almost all types of magnetized plasma and under a variety of physical conditions ranging from fusion and laboratory experiments to space plasma. Currents (Drummond and Rosenbluth 1962; Motley and D’Angelo 1963; Kindel and Kennel 1971), ion beams (Weibel 1970) and velocity shear (Ganguli et al. 1985; Koepke et al. 1994; Teodorescu et al. 2002; Agrimson et al. 2002) have all been proposed to provide free energy for the instability.

Inhomogeneties in plasma parameters such as the density and drifts, which are inescapable in both space and laboratory plasma, naturally affect the waves and the plasma properties. Sharp density gradients along the auroral acceleration region have been reported recently by the analysis of the four point cluster mission data (Darrouzet et al 2002) and FAST satellite data (Ergun et al. 2002). Density gradients in conjunction with shear flow configurations have been observed in and above the auroral acceleration region by the Freja satellite (Hamrin et al. 2001). Density gradient of the plasma particles has been observed to act as a source of free energy for many kind of instabilities e.g. drift cyclotron waves (Mikhailovskii and Timofeev 1963), lower hybrid drift waves (Davidson et al. 1977), drift-cyclotron loss-cone (DCLC) instability (Post and Rosenbluth 1966), dispersive Alfven waves etc (Guzdar et al. 2001; Stasiewicz et al. 2001).

The importance of using the loss-cone distribution function of the plasma particles for studying the DCLC modes in the active regions of the magnetosphere like the auroral acceleration region has been pointed out by various workers (Post and Rosenbluth 1966; Baldwin 1977; Gomberoff and Cuperman 1981; Koepke 1984; Summers and Thorne 1995). Mikhailovskii (1965) and Shima and Fowler (1965) first combined the free energy of a density gradient and a positive slope in the ion transverse velocity distribution function to predict an instability. The DCLC mode is a microinstability of a magnetized, collisionless, mirror confined plasma, which is driven by the radial density gradient and the loss-cone feature of the confined ions (Post and Rosenbluth 1966).

The observations of the DCLC instability is attributed to the PR-6 experiment in the Soviet Union and to the 2XII and 2XIIB experiments at the Lawrence Livermore Laboratory (Coensgen et al. 1975; Simonen, 1976; Turner et al. 1977) which were shown to be in reasonable agreement with predictions of a quasilinear model of anomalous ion diffusion into the loss-cone by the instability (Baldwin et al. 1976). A fully nonlinear treatment of the mode amplitude saturation (Myer and Simon 1981) was applied to PR-6 data with reasonable agreement. The DCLC mode has been extensively studied by Koepke (1984) and the unstable DCLC modes with fluctuations containing many frequency harmonics have been experimentally identified in axisymmetrical mirror machine, MIX 1 (Koepke 1984).

Post and Rosenbluth (1966) first derived the dispersion relation for the DCLC mode in an infinite, electrostatic limit. They evaluated the critically unstable density gradient and found it about an order of magnitude more restrictive than that for Mikhailovskii and Timofeev’s (1963) drift-cyclotron instability which can grow in an inhomogeneous Maxwellian plasma. The non-linear saturation of the instability including the effects of partially filled-in loss-cone has been studied by Myer and Simon (1980) and Cohen and Maron (1980). Baldwin (1977) has studied the mode’s contribution to the end losses. Baldwin et al. (1976), Berk and Stewart (1977) have developed a quasilinear model to describe the time evolution of a mirror confined plasma which is unstable to the DCLC mode. Stabilization of the DCLC mode by addition of warm plasma has been studied by Berk and Gerver (1976) and the stabilization of the mode by the cold plasma has been studied by Gerver (1976) and Baldwin and Jong (1979). Berk et al. (1969) have shown that the presence of spatial inhomogeneties along the magnetic field destabilizes the mode. Hershcovitch and Politzer (1979) have shown the stabilization of the DCLC mode by the injection of rf power. The mechanism as well as the first experimental observation of the Bounce-Resonance Landau Damping of the DCLC mode in an axisymmetrical mirror trap, MIX 1, has been reviewed by Koepke (1984) in his Ph.D. thesis. Three- dimensional mode structure of the DCLC mode in a mirror trap has been studied by Koepke (1984) and Koepke et al. (1986). Coupling between the harmonics of the unstable DCLC mode in an axisymmetric mirror trap by the electron bounce-resonance Landau damping has been predicted by Koepke et al. (1992).

The functional forms of the loss-cone distribution adopted in the aforementioned studies vary considerably depending on the angular width of the loss-cone or the sharpness of the loss-cone edge. In practice, a geometrical loss-cone region cannot be completely empty, on account of particle scattering and collisional processes. The loss-cone distribution used in the present study is the general loss-cone distribution function of the Dory-Guest-Harris type (1965), the most frequently used loss-cone distribution in plasma physics literature and is discussed in detail in Sect. 5.

The present work therefore, studies the generation of the DCLC mode in an inhomogeneous plasma using the general loss-cone distribution of the plasma ions. Both long and short wavelength modes of DCLC mode are considered. The analysis is based on the microscopic study of EICI first performed by Terashima (1967a) using the particle aspect analysis approach and further extended by Tiwari et al. (1985), Tiwari and Varma (1993) to study the drift wave instability. Mishra and Tiwari (2004, 2005, 2006) extended this method to study the EICI in homogeneous plasmas. Recently Duan et al. (2005) have used the same particle aspect analysis approach to study the kinetic Alfven wave in an inhomogeneous plasma.

2 Basic assumptions

The basic assumptions are the same as in earlier work by Terashima (1967a) and Mishra and Tiwari (2006). The plasma is considered to be weakly inhomogeneous, anisotropic and collisionless consisting of resonant and non-resonant particles. The non-resonant particles support the oscillatory motion of the wave while the resonant particles participate in energy exchange with the wave. The ions are supposed to have unit charge. An EIC wave is assumed to propagate almost perpendicularly to the static uniform magnetic field B 0 (which is along the z-direction). As the EICI is excited in low β plasma, the magnetic field inhomogeneity is ignored. In the present mathematical analysis the procedure adopted by Terashima (1967a) and Mishra and Tiwari (2006) is followed.

3 Particle trajectories and velocities

The trajectories of particles are evaluated within the framework of linear theory using the procedure adopted by Terashima (1967a) and Mishra and Tiwari (2006). The details of the mathematical model used are given in Mishra and Tiwari (2006).

The equation of motion of a particle is given by

$$ \hbox{m}\left({\frac{\hbox{dv}}{\hbox{dt}}}\right)= \hbox{q}\left[\hbox{E}+\left({\frac{1}{\hbox{c}}} \right)\hbox{v}\times \hbox{B}_0 \right] $$

where symbols have their usual meaning.

If E is considered to be a small perturbation i.e., E = E 0 + E 1, velocity v can be expressed in terms of unperturbed velocity V and perturbed velocity u.

Then the perturbed velocity of the plasma particles for an anisotropic and collisionless plasma with density gradient along the negative y-axis, is derived by Mishra and Tiwari (2006) and is given by

$$ \begin{aligned} \hbox{u}_{\rm x}\left(\hbox{r,t}\right) & =\frac{\hbox{qE}_1} {\hbox{m}}\sum\limits_{-\infty }^{+\infty}{\hbox{J}_{\rm n}(\mu)}\sum\limits_ {-\infty}^{+\infty}{\hbox{J}_\ell(\mu)} \left[{\frac{\Uplambda_\ell}{\Uplambda_\ell^2-\Upomega_{\rm i}^2}\sin\chi _{{\rm n}\ell}-\frac{\delta}{2\Uplambda_{\ell+1}}\sin\left({\chi_{\rm n\ell}-\Uplambda_{\ell+1}\rm t}\right)-\frac{\delta}{2\Uplambda_{\ell-1}}\sin \left({\chi_{\rm n\ell}-\Uplambda_{\ell-1}\rm t}\right)}\right] \\ \hbox{u}_{\rm y}\left(\hbox{r,t}\right) & =\frac{\hbox{qE}_1 }{\hbox{m}}\sum\limits_{-\infty}^{+\infty}{\hbox{J}_{\rm n}(\mu)} \sum\limits_{-\infty}^{+\infty}{\hbox{J}_\ell (\mu)}\left[ {\frac{\Upomega_{\rm i}}{\Uplambda_\ell^2-\Upomega_{\rm i}^2}\cos \chi_{{\rm n}\ell}+\frac{\delta}{2\Uplambda_{\ell +1}}\cos \left({\chi_{\rm n\ell}-\Uplambda_{\ell +1}\hbox{t}}\right)-\frac{\delta}{2\Uplambda_{\ell -1} }\hbox{cos}\left({\chi_{\rm n\ell}-\Uplambda_{\ell -1}\hbox{t}}\right)} \right] \\ \hbox{u}_{\rm z}\left({\hbox{r,t}}\right) & =\frac{\hbox{q}\kappa \hbox{E}_1}{\hbox{m}}\sum\limits_{-\infty}^{+\infty}{\hbox{J}_{\rm n} (\mu)}\sum\limits_{-\infty}^{+\infty}{\hbox{J}_\ell (\mu)} \frac{1}{\Uplambda_\ell}\left[{\sin \chi_{\rm n\ell}-\delta \sin \left({\chi_{\rm n\ell} -\Uplambda_\ell {\rm t}} \right)} \right] \end{aligned} $$
(1)

where \({{\chi_{\rm n\ell}}={\bf k.r}-\omega \hbox{t}+({\hbox{n}-\ell} )(\Upomega_{\rm i}\hbox{t}-\theta),{\Uplambda_{\ell}}(\hbox{V}_{\vert \vert}=\hbox{V}_{\rm r})=\hbox{k}_{\vert \vert}\hbox{V}_{\rm r}-\omega +\ell \Upomega_{\rm i}=0;\ell=\pm 1,\pm 2,\ldots\ldots}\) , Jℓ(μ) is the Bessel’s function which arise from the different periodical variations of charged particles trajectories and \({\mu =\frac{k_\bot V_\bot}{\Upomega_i}}\) · \({\delta =0}\) for non-resonant particles and δ = 1 for resonant particles is defined.

4 Density perturbation

Equation for the perturbed density, as derived by Terashima (1967b) and Duan et al. (2005), is given by

$$ \frac{\hbox{dn}_1 \left(\hbox{r,t}\right)}{\hbox{dt}}= -\hbox{N}\left({\hbox{r,V}} \right)\left[{\nabla.\hbox{u}}\left({\hbox{r,t}} \right) \right]-\hbox{u}_{\rm y}\left({\hbox{r,t}}\right)\frac{\hbox{dN}} {\hbox{dy}} $$
(2)

where n1(r,t) is the density perturbation associated with the velocity perturbation u(r,t), N(r,V) is the unperturbed density of the ions. Substituting Eq. 1 in Eq. 2 the perturbed density for the non-resonant and resonant particle is obtained as

$$ \hbox{n}_1 \left({\hbox{r,t}} \right)=-\frac{\hbox{qE}_1 \hbox{N}}{\hbox{m}} \sum\limits_{-\infty}^{+\infty}{\hbox{J}_{\rm n}(\mu)}\sum \limits_{-\infty}^{+\infty}{\hbox{J}_\ell(\mu)} \left[{\frac{\hbox{k}_\bot}{\Uplambda_\ell ^2 -\Upomega_{\rm i}^2 }+\frac{\kappa^2\hbox{k}_\bot}{\Uplambda_\ell ^2}-\frac{\hbox{mv}_ {\rm di}}{\hbox{T}_\bot \Uplambda_\ell}}\right]\sin \chi_{\rm n\ell} $$
(3)
$$ \hbox{n}_1 \left({\hbox{r,t}}\right)= -\frac{\hbox{qE}_1 \hbox{N}}{\hbox{m}}\sum\limits_{-\infty }^{+\infty} {\hbox{J}_{\rm n}(\mu)}\sum\limits_{-\infty}^{+\infty} {\hbox{J}_\ell(\mu)} \left[{\frac{\hbox{k}_\bot}{\Uplambda_\ell^2-\Upomega _{\rm i}^2}+\frac{\kappa^2\hbox{k}_\bot}{\Uplambda_\ell ^2}-\frac{ \hbox{mv}_{\rm di}}{\hbox{T}_\bot \Uplambda_\ell}}\right] \times \left[{\sin \chi_{\rm n\ell}-\sin \left({\chi_{\rm n\ell} -\Uplambda_\ell \hbox{t}}\right)-\Uplambda_\ell \hbox{t}\cos \left( {\chi_{\rm n\ell}-\Uplambda_\ell \hbox{t}}\right)} \right] $$
(4)

provided \({\omega \sim \ell\Upomega_{\rm i}}\) and \({\kappa ^2=\left( {\frac{\hbox{k}_{\vert \vert}}{\hbox{k}_\bot}}\right)^2\rangle \left| {\frac{\Uplambda_\ell ^2}{\Uplambda_\ell ^2 -\Upomega_{\rm i}^2}} \right|\approx \frac{\Uplambda_\ell^2}{\Upomega_{\rm i}^2}}\) .

Here \({\hbox{v}_{\rm di}}\) is the diamagnetic drift velocity of the ions in the crossed density gradient and magnetic field (B 0) and is given by (Terashima 1967b; Shukla and Stenflo 1998; Duan et al. 2005)

$$ \hbox{v}_{\rm di}=\frac{\hbox{T}_{\bot \rm i}}{\hbox{m}_{\rm i} \Upomega_{\rm i}}\frac{1}{\hbox{N}}\frac{\hbox{dN}}{\hbox{dy}} $$
(5)

with \({\frac{1}{\rm N}\frac{\rm dN}{\rm dy}}\) as the inverse of the density gradient scale length.

Equations 3 and 4 show that the term proportional to \({\frac{\hbox{k}_\bot}{\Uplambda_\ell^2-\Upomega_{\rm i}^2}}\) in n1 (r,t) denotes the density variation due to the oblique propagation of the wave, the term involving to \({\kappa^2=\frac{\hbox{k}_{\vert \vert}^2}{\hbox{k}_\bot^2}}\) is caused directly by the EZ component of the wave’s electric field and the one proportional to vdi is due to the ion density gradient drift.

5 Loss-cone distribution function

To calculate the dispersion relation and growth rate, the general loss-cone distribution function of the following form (Dory et al. 1965; Gomberoff and Cuperman 1981; Summers and Thorne 1995; Duan et al. 2005, Mishra and Tiwari 2006) is used

$$ \hbox{N}(\hbox{y,V})=\hbox{N}_0\left[{1-\varepsilon \left({\hbox{y}+ \frac{\hbox{V}_{\rm x}}{\Upomega}} \right)}\right]\hbox{f}_\bot (\hbox{V}_\bot)\hbox{f}_{\vert \vert} (\hbox{V}_{\vert \vert}) $$
(6)
$$ \hbox{where}\; \hbox{f}_\bot(\hbox{V}_\bot)=\frac{\hbox{V}_\bot^{2{\rm J}}} {\pi \hbox{V}_{\rm T\bot}^{2(\hbox{J}+1)} \hbox{J}!}\hbox{exp}\left\{{-\frac{\hbox{V}_\bot^2}{\hbox{V}_{\rm T\bot} ^2}}\right\} \hbox{with} \hbox{V}_{\rm T\bot}^2=\frac{1}{\left({\hbox{J}+1} \right)}\frac{2\hbox{T}_\bot} {\rm m} $$
$$ \hbox{f}_{\vert \vert}(\hbox{V}_{\vert \vert})=\frac{1}{\sqrt \pi \hbox{V}_{\rm T\vert \vert}}\hbox{exp} \left\{{-\frac{\hbox{V}_ {\vert \vert}^2}{\hbox{V}_{\rm T\vert \vert}^2}}\right\} \hbox{with} \hbox{V}_{\rm T\vert \vert}^2 =\frac{2\hbox{T}_{\vert \vert}} {\hbox{m}} $$
$$ \left({\frac{\hbox{T}_\bot}{\hbox{T}_{\vert \vert}}-1} \right)_{\rm eff}= \left({\hbox{J}+1}\right)\frac{\hbox{V}_{\rm T\bot}^2}{\hbox{V}_{\rm T\vert \vert}^2}-1 $$
(7)

N0 is the background plasma density, ɛ is a small parameter of the order of inverse of ‘density gradient scale length’, V 2T|| and V\({_{\rm T\bot}^{2}}\) are the squares of parallel and transverse thermal velocities of the particles with respect to the external magnetic field. J=0,1,2,..is the distribution index, also known as the steepness of the loss-cone. It is a measure of the angular size of the effective loss-cone region. For J = 0, this distribution represents a bi-Maxwellian distribution and for J=∞, this reduces to Dirac-Delta function. Moreover, f\({_{\bot}}\) (V\({_{\bot}}\)) is peaked about J\({^{1/2}\hbox{V}_{\rm T\bot}}\) and has a half width of \({\Delta \hbox{V}_{\bot}\sim \hbox{J}^{-1/2}\hbox{V}_{\rm T\bot}}\) (Gomberoff and Cuperman 1981; Summers and Thorne 1995).

6 Dispersion relation

To evaluate the disturbed density \(({\tilde{\rm n}_{\rm i,e}})\) we integrate the perturbed density for the non-resonant particles in the presence of the wave i.e., \({\tilde{\rm n}_{\rm i,e}=\int\limits_0^\infty {2\pi \hbox{V}_\bot \hbox{dV}_\bot \int\limits_{-\infty}^\infty {\hbox{dV}_{\vert \vert}}} \hbox{n}_1\left({\hbox{r,t}}\right)}\) . Using Eqs. 3, 6 and the identities

$$ \int\limits_0^\infty {2\pi \hbox{V}_\bot \hbox{dV}_\bot \hbox{J}_\ell^2 (\mu)\hbox{f}_{\bot \rm i} (\hbox{V}_\bot)}=\hbox{I}_\ell \left({\hbox{b}_{\rm i}}\right)\hbox{exp} \left({-\hbox{b}_{\rm i}}\right) \hbox{for the ions}. $$

and \({\int\limits_{-\infty}^\infty {\frac{1}{\sqrt \pi}}\frac{\exp \left({-\hbox{x}^2}\right)}{\left({\hbox{x-G}}\right)}\hbox{dx}=\hbox{Z} (\hbox{G})}\) where Z(G) is the dispersion function.

The integrated perturbed density for the non-resonant ions in an inhomogeneous plasma using the general loss-cone distribution function is obtained as

$$ \tilde{\rm n}_{\rm i}\cong \left[{-\frac{\hbox{k}_\bot \kappa^2}{\left( {\omega-\ell \Upomega_{\rm i}}\right)^2}-\frac{\hbox{mv}_{\rm di}} {\hbox{T}_{\bot \rm i}\left( {\omega-\ell \Upomega_{\rm i}}\right)}}\right]\omega_{\rm pi}^2\left[ {\hbox{I}_\ell \left({\hbox{b}_{\rm i}}\right)\hbox{exp}\left({\hbox{b}_ {\rm i}} \right)}\right]\frac{\hbox{E}_1}{4\pi\hbox{e}}\sin (\hbox{k.r}-\omega \hbox{t}) $$
(8)

where \({\omega_{\rm pi,e}^2 =\frac{4\pi \hbox{n}_0 \hbox{e}^2} {\hbox{m}_{\rm i,e}},\hbox{I}_\ell \left({\hbox{b}_{\rm i}}\right)}\) is modified Bessel function, \({\hbox{b}_{\rm i}=\frac{\hbox{k}_\bot^2 \rho_{\rm i}^2}{2},}\) and for the ions (Summers and Thorne 1995)

$$ \begin{aligned} \hbox{I}_\ell \left({\hbox{b}_{\rm i}}\right)\hbox{exp}\left({-\hbox{b}_{\rm i}} \right) & =\left({1-\left({\hbox{J}+1}\right)\hbox{b}_{\rm i}}\right) \hbox{for}\,\, \hbox{b}_{\rm i} < 1 \\ & =\frac{1}{\left({2\pi \left({\hbox{J}+1}\right)\hbox{b}_{\rm i}} \right)^{1/2}} \hbox{for}\,\, \hbox{b}_{\rm i} > 1 \end{aligned} $$
(9)

here J is the loss-cone distribution index.

And on using \({\int\limits_0^\infty {2\pi \hbox{V}_\bot \hbox{dV}_\bot \hbox{J}_\ell ^2 (\mu)\hbox{f}_{\bot \rm e} (\hbox{V}_\bot)} =1}\) for the electrons. The integrated perturbed density for the non-resonant electrons in an inhomogeneous plasma is derived as

$$ \tilde {\rm n}_{\rm e}\cong \left({\frac{1}{\hbox{k}_\bot \hbox{d}_{\vert \vert \hbox{e}}^2}}\right)\frac{\hbox{E}_1}{4\pi \hbox{e}}\sin \left( {\hbox{k.r}}-\omega \hbox{t} \right) $$
(10)

where \({\hbox{d}_{\vert \vert \hbox{e}}^2=\frac{\hbox{T}_{\vert \vert \hbox{e}}}{\hbox{m}_{\rm e}\omega_{\rm pe}^2}}\) is the Debye length corresponding to mean parallel energy.

Dispersion relation for the EICI in an inhomogeneous plasma using the general loss-cone distribution function is then obtained by using Poisson’s equation \({\varvec\nabla \cdot\mathbf{E}=-\hbox{k}_{\bot}(1+\kappa)\hbox{E}_{1} \hbox{sin}({\bf k.r}-\omega \hbox{t}) = 4\pi \hbox{e}(\tilde{n}_{\rm i}-\tilde{n}_{\rm e})}\) and Eqs. 8 and 10 and is derived as

$$ 1+\frac{1}{\left({1+\kappa}\right)\left({\hbox{k}_\bot ^2 \hbox{d}_{\vert\vert \hbox{e}}^2} \right)}-\left({1+\frac{2\hbox{k}_ \bot \hbox{v}_{\rm di}}{\left({\hbox{k}_{\vert \vert}\hbox{V}_{{\rm T}\bot {\rm i}}}\right)^2}} \right)\left({\frac{\kappa ^2}{1+\kappa}} \right)\left[{\hbox{I}_\ell \left({\hbox{b}_{\rm i}} \right)\hbox{exp}\left({\hbox{b}_{\rm i}}\right)} \right]\frac{\omega_{\rm pi}^2}{\left({\omega -\Upomega_{\rm i}}\right)^2}=0 $$
(11)

where

$$ \hbox{V}_{\rm T\bot i}^2 =\frac{1}{\left({\hbox{J}+1} \right)}\frac{2\hbox{T}_{\bot \rm i}}{\hbox{m}} $$
(12)

Equation 11 gives the dispersion relation for the DCLC mode driven unstable by the density gradient and the loss-cone distribution of ions. For vdi = 0 and J = 0 this dispersion relation reduces to that given by Terashima (1967a) and for vdi = 0 to that given by Mishra and Tiwari (2006). The dispersion relation derived by Post and Rosenbluth (1966) for the DCLC mode using the contribution of “loss-cone” ion-cyclotron motion to plasma permittivity considers the electron diamagnetic drift whereas the dispersion Eq. 11 derived here using the particle aspect analysis approach and the general loss-cone distribution function considers the ion diamagnetic drift and also includes the effects of the parallel propagation and the ion temperature anisotropy. For the given values of the parameters in the result and discussion section the frequency of the EIC wave is obtained to be 363 Hz which is of the order of the ion-cyclotron frequency in the auroral acceleration region and therefore, can be interpreted in terms of the DCLC instability.

Equation 11 also shows that loss-cone index (J) and the perpendicular thermal velocity affect the dispersion relation of the DCLC mode by virtue of their occurrence in the temperature anisotropy and not independently. The result obtained here on the EICI in an inhomogeneous plasma is thus an extension of the results of Summers and Thorne (1995) drawn on the obliquely propagating electrostatic waves in homogeneous plasma. Summers and Thorne (1995) have shown that for obliquely propagating electrostatic waves in homogeneous plasma the loss-cone indices and the perpendicular thermal velocity enter the dispersion relation via the temperature anisotropy.

7 Wave energy density

The wave energy density (Ww) per unit wavelength is the sum of pure field energy and the changes in the energy of the non-resonant particles i.e. \({\hbox{W}_{\rm w}=\frac{\lambda \hbox{E}_1^2}{8\pi}+ \hbox{W}_{\rm i}+\hbox{W}_{\rm e}}\) where \({\hbox{W}_{\rm i,e} =\int\limits_0^\lambda {\hbox{ds}\int\limits_0^\infty {2\pi \hbox{V}_\bot \hbox{dV}_\bot}}\int\limits_{-\infty}^\infty {\hbox{dV}_{\vert \vert}} \frac{\hbox{m}}{2}\left[{\left({\hbox{N}+\hbox{n}_1} \right)\left({\hbox{V+u}} \right)^2-\hbox{NV}^2}\right]_{\rm i,e}}\) is the change in the energy of the non-resonant ion and electrons respectively (Terashima 1967a; Mishra and Tiwari 2006). Following the analysis of Mishra and Tiwari (2006) the wave energy density in an inhomogeneous plasma is obtained as

$$ \hbox{W}_{\rm w}=\frac{\lambda \hbox{E}_1^2}{8\pi}+\frac{\lambda \hbox{E}_1^2 }{16\pi} \frac{\omega_{\rm pi}^2}{\left\{{\omega -\Upomega _{\rm i}} \right\}^2}\kappa ^2\left[{1+\frac{4{\rm k}_\bot {\rm v_{di}}}{\omega }\frac{1}{\left({1-\frac{\Upomega_{\rm i}}{\omega}} \right)}\frac{\hbox{V}^2_{\hbox{T}\vert \vert i}}{\left({\hbox{J}+1} \right)\hbox{V}^2_{\hbox{T}\bot \hbox{i}}}}\right]\frac{1}{2}\left[ {\hbox{I}_\ell \left({\hbox{b}_{\rm i}} \right)\hbox{exp}\left( {\hbox{b}_{\rm i}}\right)} \right]+\frac{\lambda \hbox{E}_1^2 }{16\pi }\left({\frac{1}{\hbox{k}_\bot ^2 \hbox{d}_{\vert \vert \hbox{e}}^2 }} \right) $$
(13)

where ω is given by Eq. 11.

As the ions contribution is dominant i.e., \({\hbox{k}_\bot ^2 \hbox{d}_{\vert \vert {\rm e}}^2 \langle 1,}\) therefore, Ww ≈ Wi. Thus, the major part of the energy is contained in the form of the oscillatory motion of the non-resonant ions.

8 Transverse and parallel energy of the resonant ions

The changes in the transverse energy and parallel energy of the resonant ions is obtained as (Terashima 1967a; Mishra and Tiwari 2006)

$$ \hbox{W}_{\rm r\bot,\vert \vert}=\int\limits_0^\lambda {\hbox{ds}\int\limits_0^\infty {2\pi \hbox{V}_\bot \hbox{dV}_\bot}} \int\limits_{\rm -L}^{\rm L} {\hbox{dV}_{\vert \vert}} \frac{\hbox{m}_{\rm i}}{2}\left[{\left( {\hbox{N}+\hbox{n}_1}\right)\left({\hbox{V+u}}\right)^2-\hbox{NV}^2} \right]_{\bot,\vert \vert}$$

where

$$\pm \hbox{L}=\frac{\left({\omega -\ell \Upomega_{\rm i}} \right)}{\hbox{k}_{\vert \vert}}\pm \hbox{dV}_{\vert \vert}$$

Following the analysis of Mishra and Tiwari (2006) these energies in the presence of the density gradient are obtained as

$$ \hbox{W}_{\rm r\bot}=\left({\frac{\lambda \hbox{E}_1^2}{8}}\right) \left({\frac{\omega_{\rm pi}^2}{\Upomega_{\rm i}^2}}\right)\left( {\frac{\omega}{\hbox{k}_{\vert \vert} \hbox{V}_{\rm T\bot i}}}\right)\frac{\Upomega_{\rm i} \hbox{t}}{\sqrt{2\pi}} \hbox{exp}\left\{{-\frac{1}{2}\left({\frac{\omega}{\hbox{k}_{\vert \vert} \hbox{V}_{\rm T\bot \hbox{i}}}}\right)^2\left({1-\frac{\Upomega_{\rm i}} {\omega}}\right)^2}\right\}\frac{1}{2}\left[{\hbox{I}_\ell \left({\hbox{b}_{\rm i}}\right)\hbox{exp}\left({\hbox{b}_{\rm i}} \right)}\right] \times \left[{1-\frac{\left({\hbox{J}+1}\right)\hbox{V}^2_{\rm T\bot i} }{\hbox{V}^2_{\rm T\vert \vert i}}\left( {\frac{\hbox{R}\left({\frac{\Upomega_{\rm i}}{\omega}-1} \right)}{\frac{\Upomega_{\rm i}}{\omega}}}\right)\left( {1+\frac{2\hbox{k}_\bot \hbox{v}_{\rm di}}{\omega}\left( {\frac{\omega}{\hbox{k}_{\vert \vert} \hbox{V}_{\rm T\bot i}}} \right)^2\left({1-\frac{\Upomega_{\rm i}}{\omega}}\right)}\right)} \right] $$
(14)

where

$$ \hbox{R}=\frac{\left\langle{\left({\hbox{J}_{\ell -1}+ \hbox{J}_{\ell +1}} \right)^2}\right\rangle}{\left\langle {\hbox{J}_{\ell -1}^2 +\hbox{J}_{\ell +1}^2}\right\rangle} $$
(15)

and

$$ \hbox{W}_{\rm r\vert \vert}=\left({\frac{\lambda \hbox{E}_1^2} {8}}\right)\left({\frac{\omega_{\rm pi}^2}{\Upomega_{\rm i}^2}}\right)\left({\frac{\omega}{\hbox{k}_{\vert \vert} \hbox{V}_{\rm T\bot i}}} \right)\frac{\Upomega_{\rm i}\hbox{t}} {\sqrt {2\pi}}\hbox{exp}\left\{{-\frac{1}{2}\left({\frac{\omega} {\hbox{k}_{\vert \vert} \hbox{V}_{\rm T\bot i}}}\right)^2\left({1-\frac{\Upomega_{\rm i}}{\omega}} \right)^2} \right\}\frac{1}{2}\left\langle {\left({\mathop {\mathbf{J}_{\ell -1} +\mathbf{J}_{\ell +1}}\nolimits}\right)^2}\right\rangle \times \left[{\frac{\left({1-\frac{\Upomega_{\rm i}}{\omega}} \right)^2}{\frac{\Upomega_{\rm i}}{\omega}}} \right]\frac{\left({\hbox{J}+1} \right)\hbox{V}^2_{\rm T\bot i}}{\hbox{V}^2_{\rm T\vert \vert i}}\left[ {1+\frac{\hbox{V}^2_{\rm T\vert \vert i}}{\left({\hbox{J}+1}\right) \hbox{V}^2_{\rm T\bot i}}\frac{\hbox{k}_\bot \hbox{v}_{\rm di}} {\omega}\frac{1}{\left({1-\frac{\Upomega_{\rm i}}{\omega}}\right)}}\right] $$
(16)

Equations 14 and 16 show that the change in the transverse and parallel energy of the resonant ions consists mainly of two terms: one is the usual term arising from the Landau mechanism. This term has contributions from the loss-cone distribution of particles as well. The other term arises from the drift motion of the ions due to density gradient across the magnetic field.

9 Growth rate of the wave

The expression for the growth rate of EICI is given by (Terashima 1967a)

$$ \gamma=\frac{1}{\hbox{E}_1}\left({\frac{\hbox{dE}_1}{\hbox{dt}}}\right) =-{\frac{\hbox{dW}_{\rm r}}{\hbox{dt}}}\mathord{\left/{\vphantom {{\frac{\hbox{dW}_{\rm r}}{\hbox{dt}}} {2\hbox{W}_{\rm w}}}}\right. {2\hbox{W}_{\rm w}}}. $$

Also

$$ \left|{\frac{\hbox{dW}_{\rm r\bot}^{\rm i}}{\hbox{dt}}} \right|\gg\left| {\frac{\hbox{dW}_{\rm r\vert \vert}^{\rm i}}{\hbox{dt}}} \right|. $$

Using the law of conservation of energy i.e.,\({\frac{\hbox{d}}{\hbox{dt}}(\hbox{W}_{\rm w}+\hbox{W}_{\rm r})=0}\) where Ww is given by Eq. 13 and \({\frac{\hbox{d}}{\hbox{dt}}(\hbox{W}_{\rm w}+\hbox{W}_{\rm r})=0}\) by Eqs. 14 and 16 the growth rate of the EICI is derived as

$$ \frac{\gamma}{\omega}=\sqrt {\frac{\pi}{2}} \left({\frac{\omega }{\hbox{k}_{\vert \vert} \hbox{V}_{\rm T\bot i}}}\right)\left( {1-\,\frac{\Upomega_{\rm i}}{\omega}}\right)^2\hbox{exp}\left\{{-\frac{1} {2}\left({\frac{\omega}{\hbox{k}_{\vert \vert}\hbox{V}_{\rm T\bot i}}} \right)^2\left({1-\frac{\Upomega_{\rm i} }{\omega}}\right)^2} \right\} $$
$$ \times \left[{R\left({\frac{\frac{\Upomega_{\rm i}}{\omega }-1}{\frac{\Upomega_{\rm i}}{\omega}}}\right)\frac{\left({\hbox{J}+1} \right)\hbox{V}^2_{\rm T\bot i}}{\hbox{V}^2_{\rm T\vert \vert i}} \left({1+\frac{2\hbox{k}_\bot \hbox{v}_{\rm di}}{\omega}\left({\frac{\omega}{\hbox{k}_{\vert\vert} \hbox{V}_{\rm T\bot i}}}\right)^2\left({1-\frac{\Upomega_{\rm i}} {\omega}}\right)}\right)-1} \right]\left[{1+\frac{4\hbox{k}_\bot \hbox{v}_{\rm di}}{\omega}\frac{1}{\left({1-\frac{\Upomega_{\rm i}}{\omega}} \right)}\frac{\hbox{V}^2_{\rm T\vert \vert i}}{\left({\hbox{J}+1} \right)\hbox{V}^2_{\rm T\bot i}}}\right] $$

where vdi, ω and R are given by Eqs. 5, 11 and 15. Here also it is observed that diamagnetic drift velocity (vdi) and the loss-cone distribution index (J) affect the growth rate through the thermal anisotropy. For vdi = 0 and J = 0 the result is the same as derived by Terashima (1967a) and for vdi = 0 result is the same as derived by Mishra and Tiwari (2006).

10 Marginal instability

For the marginally unstable condition γ = 0, we then obtain the result

$$ \hbox{v}_{\rm di}=\left({\frac{\omega}{2\hbox{k}_\bot}}\right)\times \left\{{\left({\frac{1}{\hbox{R}\left({1-\frac{\omega}{\Upomega_{\rm i}}} \right)\frac{\left({\hbox{J}+1} \right)\hbox{V}^2_{\rm T\bot i}} {\hbox{V}^2_{\rm T\vert \vert i}}}}\right)-1} \right\}\times \left\{ {\frac{1}{\left({\frac{\omega}{\hbox{k}_{\vert \vert}\hbox{V}_{\rm T\bot i} }}\right)^2\left({1-\frac{\Upomega_{\rm i}}{\omega}}\right)}}\right\} $$
(18)

which shows that the diamagnetic drift velocity due to the density gradient of the plasma particles may be a source of DCLC wave generation. The expression also shows that the phase velocity of the wave across the magnetic field \({\left({\frac{\omega}{\hbox{k}_\bot}} \right)}\) is nearly equal to the ions diamagnetic drift velocity (vdi). For the plasma parameters mentioned in the result and discussion and ω = 363Hz, the estimated value of vdi for the wave generation in the auroral acceleration region is of the order of 106 m/s.

11 Results and discussion

In the present analysis the expressions for the dispersion relation, resonant energies and growth rate are derived in the presence of diamagnetic drift velocity and the steepness of the loss-cone distribution of plasma ions. The following parameters relevant to the auroral acceleration region (Tiwari and Rostoker 1984; Mozer et al 1997; Duan et al. 2005, Mishra and Tiwari 2006) are used to evaluate the dispersion relation, resonant energies and growth rate. The density gradient is considered to be along the negative y-axis.

\({\hbox{B}_{0}=4300}\) nT at \({1.4\hbox{R}_{\rm E},\Upomega_{\rm i}=412\hbox{s}^{-1}, \ell =1, \lambda =300}\) m, \({\hbox{E}_{1}=50\,\hbox{mV/m}}\), \({\omega_{\rm pi}^{2}/ \Upomega_{\rm i}^{2}=2, \hbox{k}_{\vert \vert}=2\times 10^{-4}\hbox{m}^{-1}, \ \frac{1}{\rm N}\frac{\rm dN}{\rm dy}\approx k_{\bot} \approx 2.5\times 10^{-3}\,\hbox{m}^{-1}, \hbox{V}_{\rm T\bot i}/ \hbox{V}_{\rm {T}\vert \vert i} =5, \Upomega_{\rm i}/ \hbox{k}_{\vert\vert}\hbox{V}_{\rm {thi}}=0.2, \hbox{d}_{\vert \vert {\rm {e}}}=52.55}\) m and \({\Upomega_{\rm i}\hbox{t}=10.}\)

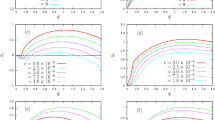
Figures 1 and 2 show the effect of the steep loss-cone distribution index (J) on the growth rate of the EICI for \({\hbox{k}_\bot \rho_{\rm i} \langle 1}\) and \({\hbox{k}_\bot \rho_{\rm i}\rangle 1}\) respectively in the presence of the diamagnetic drift velocity \(({\hbox{v}_{\rm {di}}=1\times 10^6}\) m/s). It is observed that the growth rate increases with \({k_\bot \rho_{\rm i}}\) . For both the regimes the effect of higher distribution index (J = 1,2) is to enhance the growth rate of the wave which may be due to the transfer of the ions energy to the EIC wave by the resonance interaction process. At the higher distribution indices J the energy of the mirroring ions parallel to the magnetic field may be transferred for perpendicular energisation leading to the resonance interaction with the wave. Thus, the EIC emission may be possible in ion conics observed in the auroral region.

Fig. 1
figure 1

Variation of \({\gamma/\omega}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of J for b\({_{\rm i} < 1}\) with \({\hbox{v}_{\rm {di}}=1\times 10^6}\)  m/s

Full size image
Fig. 2
figure 2

Variation of \({\gamma/\omega}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of J for b\({_{\rm i} > 1}\) with \({\hbox{v}_{\rm {di}}=1\times 10^6}\)  m/s

Full size image

From Fig. 1 it is observed that for J = 0 i.e., for the bi-Maxwellian distribution of the plasma ions the growth rate increases with \({\hbox{k}_\bot \rho_{\rm i}}\) and that the maximum growth rate occurs at \({\hbox{k}_\bot \rho_{\rm i}\approx 1}\) which is consistent with the previous work by Kindel and Kennel (1971). But with the introduction of the loss-cone distribution index (J = 1) the nature of the growth rate changes, the growth rate increases exponentially with \({\hbox{k}_\bot \rho_{\rm i}}\) , attains a peak and then decreases. The peak in the growth rate represents the resonance condition of the wave and it is observed to shift towards the lower side of the \({\hbox{k}_\bot \rho_{\rm i}}\) . With further enhancement in the loss-cone distribution index (J = 2) the nature of the growth rate remains same as that for J = 1 but the peak value shifts towards the lower side of \({\hbox{k}_\bot \rho_{\rm i}}\) and the maximum value of the growth rate attained also becomes smaller. This perhaps is in relation with the decreasing width of the loss-cone.

From Fig.2 it is observed that the growth rate increases with \({\hbox{k}_\bot \rho_{\rm i}}\) . The loss-cone distribution index (J=1,2) enhances the growth rate of the wave in the short wavelength regime as well. This may be due to the energy transfer from the ions to the wave. This is in accordance with the conservation of energy in mirror like devices.

Thus, the auroral acceleration region of the magnetosphere towards the ionosphere at the mirroring points with a steep distribution index may be unstable for the EIC wave emission giving rise to the DCLC instability. The steep loss-cone structures are analogous to mirror-like devices with higher mirror ratio that may accelerate the charged particles moving perpendicular to the magnetic field. Thus more energetic particles may be available to provide energy to the wave by resonance wave–particle interaction.

The effect of diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) on the growth rate and the resonant energies transferred for \({\hbox{k}_\bot \rho_{\rm i}\langle 1}\) is depicted in Figs. 3, 4 and 5. Figure 3 depicts the variation of growth rate \(({\gamma/\omega})\) with the perpendicular wave number \(({\hbox{k}_\bot \rho_{\rm i}})\) for different values of diamagnetic drift velocity \(({\hbox{v}_{\rm {di}}})\) in the presence of the loss-cone distribution index (J = 1). It is observed that for \({\hbox{k}_\bot \rho_{\rm i}\langle 0.75}\) the EIC wave is damped in the presence of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}}).\) The damping may be due to the local transfer of energy from the wave to the plasma by electron Landau damping mechanism. In the present analysis, however, we have not considered the electron Landau damping which may modify the results significantly in various experimental devices. Here, it is assumed that the auroral acceleration region is populated by hotter electrons of magnetospheric origin. Therefore, the electrons may not be the resonant particles to interact with the EICI in the auroral acceleration region. For \({\hbox{k}_\bot \rho_{\rm i}\rangle 0.75}\) the EIC wave grows. For \({\hbox{k}_\bot \rho_{\rm i}\rangle 0.75}\) effect of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) is to enhance the growth rate of the wave that may be due to the ion-density gradient drift wave interaction around ion-cyclotron frequency. Further a peak in the growth rate is also observed which represents the resonance condition of the ion-density gradient drift wave interaction. With the increasing values of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) the maximum growth rate attained by the wave enhances. At the higher \({\hbox{k}_\bot}\) the diamagnetic drift frequency \({\hbox{k}_\bot \hbox{v}_{\rm di}}\) exceeds the wave frequency \({\omega}\) around the ion-cyclotron frequency and ion-cyclotron drift waves are excited extracting energy from mirroring ions parallel to the magnetic field at finite \({\hbox{k}_{\vert \vert}}.\)

Fig. 3
figure 3

Variation of \({\gamma/\omega}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of\({\hbox{v}_{\rm di}}\) for b\({_{\rm i} < 1}\) and J = 1.

Full size image
Fig. 4
figure 4

Variation of Wr\({_{\bot}}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of \({\hbox{v}_{\rm di}}\) for b\({_{\rm i} < 1}\) and J = 1

Full size image
Fig. 5
figure 5

Variation of Wr\({_{\vert \vert}}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of \({\hbox{v}_{\rm di}}\) for b\({_{\rm i} < 1}\) and J = 1

Full size image

Figure 4 shows the variation of transverse resonant energy (Wr\({_{\bot}}\)) with the perpendicular wave number \(({\hbox{k}_\bot \rho_{\rm i}})\) for different values of diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) and for J = 1. It is observed that the transverse resonant energy (Wr\({_{\bot}}\)) decreases with \({\hbox{k}_\bot \rho _{\rm i}}\) which may be due to the transfer of energy from the transverse component of the plasma ions to the EICI. The effect of increasing diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) is to further decrease the transverse resonant energy. The decrease in the transverse energy of the ions due to the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) is supported by the increase in the growth rate of the EIC wave in the presence of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}}).\) Thus, the energy of the plasma ions is transferred to the EIC wave in the presence of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) through the ion-density gradient drift wave interaction.

Figure 5 depicts the variation of parallel resonant energy (Wr\({_{\vert\vert})}\) with perpendicular wave number \(({\hbox{k}_\bot \rho_i)}\) for different values of diamagnetic drift velocity (v\({_{\rm di})}\) and for J = 1. Here, it is observed that the parallel energy of the ions also decreases with \({\hbox{k}_\bot \rho_{\rm i}}\) which may be also due to the transfer of energy from the parallel component of the plasma ions to the EICI. The effect of increasing diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) is to decrease the parallel resonant energy. The decrease in the parallel energy of the ions due to the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) is supported by the increase in the growth rate of the EIC wave in the presence of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}}).\) Thus the parallel energy of the plasma ions is transferred to the EIC wave in the presence of the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) at finite k\({_{\vert \vert}}\) by the wave–particle interaction mechanism.

Thus, the density gradient of the plasma ions acts as a source of free energy for the EIC wave. It modifies the wave–particle resonance condition through the ion-density gradient drift wave resonance and enhances the growth rate of the wave. For the bi-Maxwellian distribution of the plasma ions the results are consistent with the findings of Alport et al. (1983), Shukla and Stenflo (1998) and Utsunomiya et al. (1998). Utsunomiya et al. (1998) have shown experimentally that in an ion beam-inhomogeneous plasma system the EIC waves are excited by the coupling with the drift waves.

Further, the results of the present study have shown that the use of the loss-cone distribution function for the plasma ions introduces a peak in the growth rate and shifts it towards the lower side of \({\hbox{k}_\bot \rho_{\rm i}}\) . For long wavelength mode the maximum growth rate of the EICI derived by the density gradient in the presence of the loss-cone distribution occurs at \({\hbox{k}_\bot \rho_{\rm i}\langle 1}\) . Effect of Landau damping due to the local transfer of energy between the plasma particles and the wave is also observed but this effect is for \({\hbox{k}_\bot \rho_{\rm i}\langle 0.75}\) . For \({\hbox{k}_\bot \rho_{\rm i}\rangle 0.75}\) effect of diamagnetic drift velocity \({\hbox{v}_{\rm di}}\) is prominent. Thus, the loss-cone distribution is important for describing the EICI in the auroral acceleration region.

Figures 6, 7 and 8 depict the effect of diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) on the growth rate and the resonant energies transferred for the short wavelength mode \(({\hbox{k}_\bot \rho_{\rm i}\rangle 1)}\) and for J = 1. Here, it is observed that the growth rate of the EICI increases to very large amplitudes with the diamagnetic drift velocity \(({\hbox{v}_{\rm di}})\) (Fig. 4) whereas the transverse (Fig. 5) and the parallel energy (Fig. 6) of the resonant ions decreases with the diamagnetic drift velocity \(({\hbox{v}_{\rm di}}).\) The decrease in the transverse and parallel energy of the resonant ions may be accounted for the increase in the growth rate of the EIC wave which may be due to ion-density gradient drift wave interaction.

Fig. 6
figure 6

Variation of \({\gamma/\omega }\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of \({\hbox{v}_{\rm di}}\) for b\({_{\rm i} > 1}\) and J = 1

Full size image
Fig. 7
figure 7

Variation of Wr\({_{\bot}}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of \({\hbox{v}_{\rm di}}\) for b\({_{\rm i} > }\) 1 and J = 1

Full size image
Fig. 8
figure 8

Variation of Wr\({_{\vert \vert }}\) with \({\hbox{k}_\bot \rho_{\rm i}}\) for different values of \({\hbox{v}_{\rm di}}\) for b\({_{\rm i} > 1}\) and J = 1

Full size image

Thus, the results have shown that for the short wavelength mode \(({\hbox{k}_\bot \rho_{\rm i}\rangle 1})\) the EICI in inhomogeneous plasma may attain very large amplitudes in the presence of the loss-cone distribution index (J = 1,2) which may then become non-linear. Shukla and Stenflo (1998) have recently presented a non-linear model for such large amplitude, drift EICI generated by sheared flow.

Thus in the auroral acceleration region, which has both the loss-cone distribution of the particles and the steep density gradient (Post and Rosenblutrh 1966; Gaelzer et al. 1997; Darrouzet et al. 2002; Duan et al. 2005), the DCLC wave with enhanced growth rate in both short and long wavelength regime may be generated by the converging magnetic lines of force and the density gradient on magnetic flux tube. The loss-cone distribution of the particles introduces peak in the growth rate due to the resonance interaction between the wave and the particles and shifts it towards the longer perpendicular perturbation.

The results are consistent with the findings of Post and Rosenbluth (1966) who have shown that unstable DCLC instability may be generated by the density gradient and loss-cone feature of the confined ions. The results are also consistent with the experimental findings of Turner et al. (1977) who have found that the dominant frequency of the EICI in a mirror machine occurs near the ion-cyclotron fundamental frequency and have perpendicular wave numbers consistent with ion diamagnetic drift wave. Recently, Cattell et al. (2002) using the FAST satellite data have observed EIC waves in association with down going ion beams (DFI) in the auroral acceleration region. But the waves at frequencies 300–600 Hz are not due to the DFIs since they began well before the ion event (Cattell et al. 2002). The waves in this frequency range may be interpreted in terms of the DCLC modes driven unstable by the EIC waves in the auroral acceleration region with density gradient (Ergun et al. 2002) and loss-cone distribution of the ions (Cattell et al. 2002).

Most turbulent heating experiments have been done in mirror like devices which in general allow loss-cone distribution and have density gradient (Turner et al. 1977; Summers and Thorne 1995). The theory developed in the present work may be also applicable to such hot particle mirror experiments. Charged particle trajectories can be used to obtain a detailed understanding of the ion-pickup processes, which are extensively studied in the present investigation. The present theory developed for the EICI in an inhomogeneous plasma using particle aspect analysis approach gives a fairly good explanation for the wave–particle interaction and Landau damping of the wave which has not been guaranteed by the other theories developed using kinetic approach for the electrostatic fluctuations in inhomogeneous plasma (pl. see conclusion of Silveria et al. 2004).

12 Conclusions

Thus, from the results of the present analysis following conclusions can be drawn:

  1. 1.

    The EICI can be driven unstable by ion density gradient in the presence of the general loss-cone distribution of the plasma ions in both long and short wavelength regimes leading to the DCLC instability. The result being consistent with the previous theories (Post and Rosenbluth 1966; Turner et al. 1977).

  2. 2.

    Dispersion relation for the DCLC mode derived here using the particle aspect analysis approach and the general loss-cone distribution function considers the ion diamagnetic drift and also includes the effects of the parallel propagation and the temperature anisotropy.

  3. 3.

    For long and short wavelength regimes the maximum growth rate attained by the EICI increases with the increase in the ion density inhomogeneity.

  4. 4.

    With the introduction of the general loss-cone distribution index the excitation of the EICI becomes easier and it attains maximum growth rate at longer perpendicular perturbations.

  5. 5.

    For both long and short wave length DCLC mode the loss-cone indices and the perpendicular thermal velocity affect the dispersion equation and the growth rate of the wave by virtue of their occurrence in the temperature anisotropy.

  6. 6.

    The particle aspect analysis approach used to study the EICI in inhomogeneous plasma gives a fairly good explanation for the wave–particle interaction.