1 Introduction

With the rapid development of mobile communication, the demand for multimedia services over heterogeneous networks has soared at a tremendous pace over recent years [10, 28,29,30,31]. However, the contradiction between the increasing service demands of users and the congested spectrum resource has become increasingly prominent [9]. Compared to 4G wireless communications, 5G wireless communication is expected to bring nearly a thousand times upgrade in data traffic [16]. Therefore, how to improve the system throughput has become the research hotspot of 5G wireless communication. To solve the problem, we need innovation in both technologies and mathematical tools.

Researchers in academia and industry therefore attempt to explore new valuable technologies that can improve the system throughput by spectrum reuse. As one of thealternative technologies of 5G communication, Device-to-device (D2D) technology has many advantages. Firstly, different from the traditional cellular networks (CNs), where all user equipments (UEs) transmit data signals through the base station (BS) directly, UEs may communicate directly via the D2D links by cellular spectrum resources under the control of the BS in D2D communication [33]. Secondly, the distance between two D2D users is closer, which can reduce the transmission power of the terminal and prolong the life of the battery [11]. Finally, the appropriate increase in the number of D2D users, not only offload the base station, but also enhance the system throughput [36]. Meanwhile, the research on wireless relaying has also made a breakthrough, from the early theoretic results to a practical stage in cellular networks. It is found that full-duplex (FD) relaying outperforms half-duplex (HD) relaying in spectrum and energy efficiency [24], since FD relays can transmit and receive simultaneously on the same frequency band. Therefore the combination of FD relaying and D2D technology can greatly improve the throughput.

In fact, few works have been carried out so far to explore FD relaying based D2D communication schemes. In [23], the authors propose an HD relaying-based D2D communication protocol that allows the D2D users to communicate bidirectionally with each other while assisting the two-way communication between the BS and the CU over the same time and frequency resources. However, the scheme decreases the reuse gain of spectrum resource due to the increase of interference. In [35], combining the FD relaying and D2D technology, the author propose an FD relaying-based D2D communication scheme that allows D2D links to underlay cellular downlink by assigning D2D transmitters as FD relays to assist cellular downlink transmissions. However, only the single user scenario is considered, where one D2D pair and one cellular user (CU) exist, whereas, the problem of resource allocation in multi-user scenarios isn’t addressed. Inspired by [35], we apply the FD relaying-based D2D communication scheme in a single cell multi-user scenario and consider the resource allocation problem in this scenario to further improve the throughput of D2D users.

Recently, most of the related research applied new mathematical tools such as game theory [22, 26], graph theory [32, 34] and matching theory [14, 15] to solve the resource allocation problems in D2D communications. In [22], considering a small-cell scenario in which full-duplex base station communicates with half-duplex D2D users, an iterative algorithm is proposed based on game theory by modeling the problem as a non-cooperative game between the uplink and downlink channels. In [26], the author apply the Stackerberg game framework in the resource allocation between D2D users and cellular users, which enhance the system throughput and user fairness. Previous works apply classic algorithm of graph theory such as the Hungarian (also refer to as Kuhn-Munkres, KM) algorithm [32, 34] to pairing D2D users and CUs, which achieves the optimal solution of the system throughput. However, the Hungarian algorithm only considers the optimal welfare instead of the stability. This stability notion implies robustness to deviations that can benefit both the resource owners(e.g. CUs in this paper) and the users (e.g. D2D pairs in this paper) [15]. In fact, an unstable matching may cause the case where D2D users switch to reuse other cellular users’ spectrum resource when the switch can benefit all of them. The case will cause the failure of the resource allocation scheme. Gu et al. [14, 15] implement matching theory to find a stable and efficient resource allocation method, which not only takes welfare into consideration but also guarantees stability in D2D communications. Moreover, the authors introduce the idea of cheating in matching to further improve D2D users’ throughput. However, the throughput performance of the algorithm in [14] is far from optimal and the complexity of the algorithm in [15] is too high to formulate.

Comparing with the above works, the main contributions of this paper are presented as follows:

  • We investigate resource allocation in multi-user heterogeneous cellular network with FD relaying-based D2D communication. In this model, we aim to maximize the throughput of D2D users on the premise of ensuring the QoS of CUs by allocating the power of the D2D transmitter. In addition, to further improve the throughput of D2D users, we solve this resource allocation problem by modeling it as a stable matching problem. The Gale-Shapley (GS) algorithm is utilized to find a stable matching between admissible D2D pairs and CUs.

  • Besides, we propose a Cheating algorithm based on cooperative game theory in order to further improve some D2D users’ throughput. It is proven that the cheating mechanism benefits a subset of D2D users without hurting the performance of the rest. Due to the NP-hardness of finding the cabal with biggest size, we cannot find the optimal solution within a polynomial time. Hence, using different colors to represent the different statements of D2D users, we develop a heuristic algorithm based on DFS to find a near-optimal solution of Cheating algorithm. Simulation results shows that our algorithm has better throughput and computation complexity performance compared with the existing algorithms.

The rest of this paper is organized as follows. Section 2 introduces the system model and formulate the resource allocation problem. The optimization problem is solved in Section 3 and the cheating problem is discussed in Section 4. Numerical results shown in Section 5 evaluate our proposed algorithms, while Section 6 concludes the paper.

2 System model and problem formulation

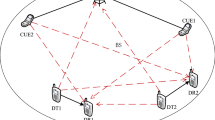
The heterogeneous cellular network model and FD relaying-based D2D underlaying cellular network model are shown in Figs. 1 and 2, respectively. The heterogeneous cellular network consists of a base station (BS), D2D pairs and cellular users(CUs) in a single cell. Here, we use \(\mathcal {D}=\left \lbrace {d}_{1},..., {d}_{i},..., {d}_{N}\right \rbrace \), 1 ≤ i ≤ N and \(\mathcal {C}=\left \lbrace {c}_{1},..., {c}_{j},..., {c}_{L}\right \rbrace \), 1 ≤ j ≤ L to denote the index sets of D2D pairs and CUs, respectively. Each D2D pair d i consists of a D2D transmitter UE- R i and a D2D receiver UE- D i .

Fig. 1
figure 1

The heterogeneous cellular network model

Full size image
Fig. 2
figure 2

FD relaying-based D2D communication model

Full size image

As for the D2D transmitter UE- R i , we make the following assumptions based on [35] and [25].

  • In this system model, each UE- R i operates in the FD relaying mode. In other words, UE- R i can transmit to UE- D i and receive-and-forward for c j over the same frequency band and same time, which indicates that the D2D transmission from UE- R i to UE- D i can underlay the cellular downlink transmission from BS to c j .

  • In addition, each UE- R i is equipped with isolated receive and transmit antennas. Therefore, the residual loop interference (LI, resulting from the relay transmission to the relay reception) at a D2D transmitter can be controlled at a certain level.

The cellular network operates in the frequency-division duplex mode. Since,the available downlink bandwidth for each CU c j is W j hertz. We assume that d i reuse the c j ’s spectrum resource and formulate the optimization problem step by step.

We consider both fast fading due to multi-path propagation effect and slow fading due to shadowing effect. Hence,the channel gain between UE- R i and BS can be expressed as \({h}_{B,R_{i}}=\textit {K}{\delta }_{B,R_{i}}{\zeta }_{B,R_{i}}{d}_{B,R_{i}}^{-\alpha } \), where K represents a system constant, \( {\delta }_{B,R_{i}} \) represents the fast fading gain as the exponential distribution with unit mean, \({\zeta }_{B,R_{i}} \) represents the slowing fading gain as the log-normal distribution [13], \( {d}_{B,R_{i}} \) represents the distance between BS and UE-\( {{R}}_{i}\), and α represents the path loss exponent. Similarly, \( {h}_{R_{i},C_{j}} \) denotes the channel gain from UE-\( {{R}}_{i}\) to CU j , \( {h}_{R_{i},D_{i}} \) denotes the channel gain from UE-\( {{R}}_{i}\) to UE-\( {{D}}_{i}\). \( {h}_{B,C_{j}} \) denotes the interference channel gains from BS to CU\(_{j}\). \( {h}_{B,D_{i}} \) denotes the interference channel gains from BS to UE- D i . Due to imperfect cancellation, we also denote the residual LI channel at UE-R by h LI . Assume that the BS transmit with power P B for each UE-R. Let P R denote the transmit power of each UE- D i . The transmission powers of all D2D pairs and BS are equal. Let \( {\sigma }^{2}\) denote the variance of the zero-mean additive white Gaussian noise on each channel.

The signal-to-interference-and-noise ratio (SINR) received by UE-Ri can be expressed as:

$$ \mathbf{\gamma}_{B,R_{i}}=\frac{{P}_{B}{h}_{B,R_{i}}}{{P}_{R}{h}_{LI}+{\sigma}^{2}} , $$
(1)

The signal transmitted by UE- R i consists of the following two components. The first is the regenerated signal that will be forwarded to the cellular user, i.e., CU j , and the second is the signal to be transmitted directly to the D2D receiver UE- D i [35]. We assume that UE-R adopts the decode-and-forward (DF) protocol [24] to assist the cellular downlink transmission for CU j , and UE- R i is willing to use the λ (0 ≤ λ ≤ 1) fraction of the power P R to forward the first signal component to CU j .In addition, UE- R i can use the remaining 1 − λ fraction power to transmit the second signal component to UE- D i . The SINRs received by CU j and UE- D i can be given by:

$$ \mathbf{\gamma}_{R_{i},C_{j}}=\frac{{\lambda}_{i,j}{P}_{R}{h}_{R_{i},C_{j}}}{{P}_{B}{h}_{B,C_{j}}+{\left( 1-{\lambda}_{i,j}\right)} {P}_{R}{h}_{R_{i},C_{j}}+{\sigma}^{2}} , $$
(2)
$$ \mathbf{\gamma}_{R_{i},D_{i}}=\frac{{\left( 1-{\lambda}_{i,j}\right)}{P}_{R}{h}_{R_{i},D_{i}}}{{P}_{B}{h}_{B,D_{i}}+{\lambda}_{i,j} {P}_{R}{h}_{R_{i},D_{i}}+{\sigma}^{2}} , $$
(3)

respectively. Based on the modulation and coding scheme in the DF protocol , the instantaneous end-to-end SINR of the link from BS to CU j via UE- R i should be determined according to the SINR of weakest hop. So we can get:

$$ \mathbf{\gamma}_{B,C_{j}}=\min\left( {\gamma}_{B,R_{i}}, {\gamma}_{R_{i},C_{j}}\right) , $$
(4)

Finally, we can get the throughput for the D2D user d i and cellular user c j , respectively, as

$$ \mathcal{R}_{i,j}^{D}={W}_{j}\log_{2}\left( 1+{\gamma}_{R_{i},D_{i}} \right) , $$
(5)
$$ \mathcal{R}_{i,j}^{C}={W}_{j}\log_{2}\left( 1+{\gamma}_{B,C_{j}} \right), $$
(6)

Although the FD relaying-based D2D communication scheme can dramatically improve the spectrum utilization, the unreasonable sharing of spectrum resources may increase the interference between D2D user and CU. If the BS assigns CUs to D2D users randomly, the QoS requirement will be not satisfied due to the interference caused by too close distance. Therefore, an effective resource allocation algorithm will play an important role in FD relaying-based D2D communication.

Considering the fairness of communication, one D2D user can only reuse the spectrum resources of one CU. Assuming that the final channel assignment matrix is X =[x ij ] N×L , where x ij is the resource indicator for CU and D2D pair. Here, x ij = 1 when D2D pair d i reuses CU c j ’s bandwidth W j , and x ij = 0 otherwise. W j is an equal share of spectrum for each CU. The system objective is to optimize the throughput of D2D users while satisfying the QoS requirements of the cellular users. Then, we can formulate the optimization problem and constraints as follows:

$$ \begin{array}{lllllll} \max_{\left\lbrace{\lambda}_{i,j},x_{ij}\right\rbrace}&\quad{\sum}_{i = 1}^{N}{\sum}_{j = 1}^{L}x_{ij}\mathcal{R}_{i,j}^{D} \\ s.t.\quad&\mathcal{C}1 : \mathcal{R}_{i,j}^{C}\geqslant\mathcal{R}_{\min}^{C},\\ &\mathcal{C}2 : {\sum}_{i = 1}^{N}x_{ij}\leqslant{1}; {\sum}_{j = 1}^{L}x_{ij}\leqslant{1}, \end{array} $$
(7)

Here, constraint \( \mathcal {C}1 \) guarantees the SINR requirement of each CU. \( \mathcal {C}2 \) presents that each CU can only share channel with one D2D user and each D2D user can only reuse one CU’s channel, respectively. In order to optimize the throughput of D2D users while satisfying the QoS requirements of CUs, we try to solve the resource allocation problem in two steps, i.e., power allocation of D2D transmitter and one-to-one matching between admitted D2D users and CUs. It can be seen from the Eq. 7 that a D2D pair can share with a CU only when the QoS requirements of this CU is satisfied. Hence, we need to control the power of D2D transmitter to meet the QoS requirements of CUs before matching D2D users and CUs. We will solve these two problems step by step in the next sections respectively.

3 Power allocation and stable matching

In previous section, we briefly introduce the FD relaying-based D2D communication scheme in a single cell multi-user scenario and formulate the optimization problem. In this section, we try to solve the above resource allocation problem in two steps. The first step is to satisfy the QoS requirement of CUs by power allocation. In the second step, the Gale-sharpley algorithm is adopted in order to find a stable matching. we take both CUs and D2D users’ preferences into consideration. Since our system objective is to maximize throughput, we measure the D2D users’ and the CUs’ preferences by throughput, respectively.

3.1 Power allocation

In cellular communication, QoS is related to the user experience [18]. SINR is an important indicator to measure the performance of QoS. It can be seen from the Eqs. 3 and 4 that the power allocation factor is proportional to the SINR of CUs and inversely proportional to the SINR of D2D links. Therefore, it is necessary to adjust the power allocation factor to meet the SINR requirements of CUs before pairing on D2D users and CUs. According to CUs’ minimum achievable rate requirement \(\mathcal {R}_{\min }^{C}={W}_{j}\log _{2}\left (1+{\gamma }_{\min }^{C} \right )\), we get the minimum SINR requirement of CUs \( {\gamma }_{\min }^{C} \). Hence, we should guarantee that the instantaneous end-to-end SINR of the link from BS to CU j via UE-\( {{R}}_{i}\) is \( {\gamma }_{R_{i},C_{j}} \), namely \({\gamma }_{R_{i},C_{j}}\leqslant {\gamma }_{B,R_{i}}\). So that we can adjust the power allocation factor to meet the SINR requirements of CUs. Since the self-interference is small enough, the equation \( {\gamma }_{B,R_{i}}\geq {\gamma }_{\min }^{C} \) is always guaranteed. So the \( {\gamma }_{R_{i},C_{j}} \) needs to meet the Eq. 8:

$$ {\gamma}_{\min}^{C}\leqslant {\gamma}_{R_{i},C_{j}}\leqslant{\gamma}_{B,R_{i}} , $$
(8)

The satisfaction of Eq. 8 needs to adjust the power allocation factor. So the λ i,j needs to meet the Eq. 9:

$$ \begin{array}{llllll} &\frac{{\gamma}_{\min}^{C}\left( {P}_{B}{h}_{B,C_{j}}+{P}_{R}{h}_{R_{i},C_{j}}+{\sigma}^{2} \right) }{{\gamma}_{\min}^{C}{P}_{R}{h}_{R_{i},C_{j}}+{P}_{R}{h}_{R_{i},C_{j}}}\leq{\lambda}_{i,j}\leq\\ &\min\left( 1,\frac{{P}_{B}{h}_{B,R_{i}}\left( {P}_{B}{h}_{B,C_{j}}+{P}_{R}{h}_{R_{i},C_{j}}+{\sigma}^{2} \right)}{{P}_{R}{h}_{R_{i},C_{j}}\left( {P}_{B}{h}_{B,R_{i}}+{P}_{R}{h}_{LI}+{\sigma}^{2} \right)} \right) \end{array} $$
(9)

It can be seen from Eq. 9 that the power allocation factor λ i,j is in a certain range. Then we select a feasible solution from the range. In this way, both the QoS requirement and matching requirement of CUs are satisfied. In order to further enhance the throughput of D2D users, a stable matching scheme between D2D users of CUs is necessary.

3.2 Stable matching

In step 2, we give the establishment process of the preference list, which is the critical component of matching model. The preference list is mainly based on maximizing the D2D users’ throughput. Here, we introduce a men-optimal (i.e., D2D users optimal) stable matching algorithm called Gale-Sharpley algorithm to further solve the resource allocation problem, which is beneficial to men (i.e., D2D users in this paper).

Since one D2D user can only reuse the spectrum resources of one CU and one CU can only be reused by one D2D user. This one-to-one matching problem can be formulated as the stable marriage problem with preference list in matching theory [21]. In a matching process, D2D pairs and CUs can be regarded as men and women, respectively. The following thing is to establish preference lists for CUs and D2D users. Since our system objective is to maximize throughput (i.e., achievable rate in this paper), we establish D2D users’ and the CUs’ preference lists by throughput. Let d i ’s throughput \( \mathcal R_{i,j}^{D} \) denote d i ’s preference value over c j , and likewise, c j ’s throughout \( \mathcal R_{i,j}^{C} \) as c j ’s preference value over d i . Hence, the preference list of d i over c j , denoted by \( \mathcal P{L_{i}^{D}} \) , is ranked by c j ’s preference value in a descending order,and similarly c j ’s preference list \( \mathcal P{L_{j}^{C}} \) over d i , is ranked by d i ’s preference value in a descending order. In order to further combine the resource allocation problem with stable marriage problem, we define the relation “prefer” in this paper as follows:

Definition 1

If \( \mathcal R_{i,j}^{C} > R_{i^{\prime },j}^{C}\), it indicates that c j prefers d i to d\(_{i^{\prime }} \), donated by \(d_{i} \succ _{c_{j}}d_{i^{\prime }} \). Similarly, if \( \mathcal R_{i,j}^{D} > R_{i^{\prime },j}^{D}\) , it indicates that d i prefers c j to c\(_{j^{\prime }} \), donated by \( c_{j} \succ _{d_{i}}c_{j^{\prime }} \).

D2D users will switch to reuse other cellular users in an unstable matching, where exists more than one blocking pairs. The blocking pair can be defined as follows:

Definition 2

(d i ,c\(_{j^{\prime }} \)) is a blocking pair in a one-to-one matching if \( c_{j^{\prime }} \succ _{d_{i}}c_{j} \) and \( d_{i} \succ _{c_{j^{\prime }}}d_{i^{\prime }} \), where c j is d i ’s partner and c\(_{j^{\prime }} \) is d \(_{i^{\prime }} \)’s partner.

The unstable matching will cause instability of network applications and user dissatisfaction. Hence, finding a stable matching by preference of D2D users and CUs ensures that neither D2D nor cellular users have a better choice than the current one, which is defined as follows:

Definition 3

A matching M without any blocking pair is one-to-one stable.

The Gale-Shapley algorithm can be used to solve the stable matching problem [12]. The main strategy of channel allocation based on GS algorithm can be formulated as follows: 1) Input the D2D users’ preference lists \( \mathcal P{L_{i}^{D}} \), \(\forall {d}_{i}\in \mathcal {D} \) and the celluar user’s preference list \( \mathcal P{L_{j}^{C}} \), \(\forall {c}_{j}\in \mathcal {C} \). 2) D2D user d i have a sequence of proposals to the c j . d i proposes, in order, to the c j in it’s preference list, pausing when c j agrees to consider d i ’s proposal, but continuing if the proposal is rejected. 3) When receiving a proposal, c j rejects if the CU already has a better choice, and otherwise agrees to hold it for consideration. 4) The progress ends until each D2D user find a partner. The computation complexity of GS algorithm is \( \mathcal O\left (n^{2}\right ) \), where n is the number of stable matching pairs .

GS algorithm is based on the non-cooperative game to find a stable matching. In other words, that is to pursue the maximization of personal interests. Thus, with the increase of the D2D users and CUs, more D2D users cannot be matched to their first choice according to the preferences list, which decreases the throughput of D2D users. Later in Section 4, the Cheating algorithm based on cooperative game is presented to solve the problem.

4 Cooperative game-based cheating algorithm

In Section 3, we have considered the stable matching problem and solve the problem using GS algorithm. In this section, we discuss some post-matching strategies under the result of GS algorithm, in which some D2D users can lie on their preference lists in order to be matched to more satisfied partners. Hence, we introduces a Cheating algorithm based on cooperative game, which can improve the whole interests by falsifying the D2D user’s preference lists. First, we introduce some notation, definitions and terminology of Cheating algorithm, which are the basis of falsifying D2D user’s preference lists. Afterwards, we propose a heuristic algorithm to further improve the performance of Cheating algorithm. Finally, we analyze the properties of our proposed algorithm.

4.1 Preliminaries

In this subsection, before developing our proposed Cheating algorithm in details, we establish some notation and terminology. We assume that the Gale-Sharpley men-optimal (i.e., D2D users optimal) algorithm is used and that we know the preference lists of all D2D users and CUs. When everyone is honest, M 0 is the men-optimal stable matching, and M S represents the men-optimal matching when some subset of people cheat. For any stable matching M and some subset of matching members \( S\subseteq \mathcal D\bigcup \mathcal C \), the partners of S can be represented as M(S). For instance, M 0(d i ) is the partner of D2D user d i in the men-optimal stable matching.

In addition, for D2D user d i , it’s preference list in men-optimal stable matching can be divided into \( (\mathcal PL(d_{i}), M_{0}(d_{i}),\mathcal PR(d_{i})) \), where \( \mathcal PL(d_{i}) \) and \( \mathcal PR(d_{i}) \) are respectively a set of CUs being more or less preferred than M 0(d i ) by D2D user d i . Since the preference list is ranked by a descending order, the set of CUs in \( \mathcal PL(d_{i}) \) (or \( \mathcal PR(d_{i}) \)) are on the left (right) of D2D user d i ’s preference list.

Assuming that A is a set of distinct objects, let π(A) denote the set of all |A|! permutations and π r (A) denote a random permutation from this set. Similar with the relation of “prefer” in definition 1, if for any D2D user \( d_{i}\in \mathcal D \), \( M(d_{i}) \succeq _{{d}_{i}}M_{0}(d_{i}) \), we can say stable matching M is “at least as good as” stable matching M 0, which is denoted as M ≽ M 0. Moreover, if there exists at least one D2D user and \( M(d_{i})\succ _{{d}_{i}}M_{0}(d_{i}) \), stable matching M is said to be strictly better than M 0, which is denoted as M ≻ M 0.

4.2 Falsifying preference list

The general idea of Cheating algorithm is presented as follows. 1) Find a cabal consisting of D2D user, in which each member prefers each other’s partner to its own. 2) Find the accomplices for the cabal, who need to falsify their preference lists in order to assist the cabal. 3) Run the men-optimal stable matching algorithm with the falsified preferences. Thus, in the resulting matching, all D2D users within cabal are better off while the rest of D2D users keep the same partners [15].

Before plunging into technical details, we present a Theorem and two definitions about Cheating algorithm and give a proof of them based on [17], which presented the Cheating algorithm for the first time.

Theorem 1

For a subset of D2D users \(\mathcal {D}=\{{d}_{1},...,\) d i ,...,d l }, 1 ≤ i ≤ l,if every member \( {d}_{i}\in \mathcal D\) ,falsifies preference list according to \((\pi _{r}(\mathcal PL(d_{i})-X), M_{0}(d_{i}),\pi _{r}(\mathcal PR(d_{i})+X)) \) then M S ≽ M 0 .

Proof

Theorem 1 introduces the way of falsifying preference list in Cheating algorithm. For a subset of CUs X, \( X\subseteq \mathcal PL(d_{i}) \). Since the members in X have already refused the proposal of D2D user d, shifting the set X from \(\mathcal PL(d_{i}) \) to \(\mathcal PR(d_{i}) \) and then giving a random permutation of \( (\mathcal PL(d_{i})-X) \) and \( (\mathcal PR(d_{i})+X) \), the current men-optimal matching after cheating M S is at least as good as the previous men-optimal matching M 0. We proceed by contradiction.

In M S , suppose at least one D2D user d i gets a worse partner than M 0(d i ). In general, assume that during the execution of the algorithm with unfalsified lists, d i is rejected by it’s M 0-partner. In other words, d i ’s M 0-partner has accepted another D2D user \( d_{i}^{\prime } \), who ranks higher than d i in M 0(d i )’s preference list. Now that \( d_{i}^{\prime } \) has not been accepted by \( M_{0}(d_{i}^{\prime }) \), he must prefer M 0(d i ) to \( M_{0}(d_{i}^{\prime }) \). Hence, (di′,M 0(d i )) compose a blocking pair in M 0. Since M 0 is a stable matching, the previous assumption is not established. Therefore, M S is at least as good as the previous men-optimal matching M 0. □

Definition 4

The cabal \(\mathcal {K}=\left \lbrace {d}_{1},...,{d}_{m},...,{d}_{k}\right \rbrace \), 1 ≤ k ≤ N, is a subset of \( \mathcal {D} \), within which each D2D pair \(d_{m}\), \(1\leq {m}\leq {k}\), \(m-1=k\) when m = 1, \( M_{0}(d_{m-1}) \succ _{{d}_{m}}M_{0}(d_{m}) \).

Definition 4 gives the requirement of cabal members. It indicates that any cabal member \( d_{m}\in \mathcal {K} \) prefers M 0(d m− 1) to M 0(d m ), where M 0(d m ) is d m ’s current partner and M 0(d m− 1) is d m ’s desired partner.In other words, that is to find a end to end loop with direction, where each member is eager to be matched to the partner of the member in previous position and the member in the first position is eager to be matched to the partner of the member in the end position.

Definition 5

The accomplices of cabal \(\mathcal K \) is a set of D2D pairs \(\mathcal H \), such that \( d\in \mathcal {H} \):

  1. 1:

    if \( d\notin \mathcal {K} \), for \( d_{m}\in \mathcal {K} \), \( M_{0}(d_{m}) \succ _{d}M_{0}(d) \& d\succ _{M_{0}(d_{m})}d_{m + 1}\);

  2. 2:

    if \( d=d_{l}\in \mathcal {K} \), for \( d_{m}\in \mathcal {K} \), m≠l, \( M_{0}(d_{m}) \succ _{d_{l}}M_{0}(d_{l-1}) \&d_{l}\succ _{M_{0}(d_{m})}d_{m + 1}\).

Definition 5 gives the requirements of the accomplices within or outside the cabal, respectively. It defines the subset of D2D users \(\mathcal H \) as the accomplices, who need to falsify their preference lists to assist cabal \(\mathcal K \) to get their desired partners. For any D2D user d outside the cabal, who would have prevented a cabal member d m from getting its desired partner, is defined as a accomplice of \(\mathcal K \). Here, we say d prevents d m when d prefers the M 0(d m ) to its own parter, while M 0(d m ) prefers d to d m . Similarly, for any D2D user d within the cabal, which is denoted as d l , who would have prevented another cabal member d m from getting its desired partner, is defined as an accomplice. Thus, we say d l prevents d m when d l prefers the M 0(d m ) to its desired partner M 0(d l− 1), while M 0(d m ) prefers d l to d m . Since d l would not get its desired partner d l− 1, we say d m prevents d l as well.

Briefly, we find a cabal by Definition 4 and the accomplices for the cabal by Definition 5. Then, we falsify the preference list of accomplices by Theorem 1. Finally, we run the men-optimal stable matching algorithm with the falsified preferences. In the resulting M S matching, D2D users outside the cabal can hold their M 0-partners and D2D users in the cabal can get their desired partners.

4.3 Cheating algorithm based on HLLSBD

From analysis above, users in cabal would improve their benefits by cheating, while other users’ benefits stay unchanged. Thus the larger the size of cabal is, the more users would have a performance improvement. Hence, to further improve the D2D users’ throughput, we try to find a cabal with bigger size. From the defination 4, if we let the D2D user d point to the other D2D users whose M 0-partners are preferred by the d to d’s M 0-partner, each user will have a directional relationship. Hence, the D2D pairs are represented as nodes and the directional relationships are denoted by edges, respectively. The cabal can be abstracted as a end to end loop in the graph containing different nodes and edges.

Therefore, the optimization problem can be abstracted as finding a largest loop in a directed graph [3, 8]. Due to the NP-hardness of finding the largest loop in a directed graph [1, 4, 7, 20], we cannot find a largest loop within a polynomial time. Hence, we can only find a near-optimal solution by improving the probability of finding the largest loop. The exist methods mostly use the color-coding technique to find loop with logarithmic length, if they exist. Using color-coding, the dependence on path length can be reduced to singly exponential [2, 6, 19, 27]. But this gives an approximation ratio of only \( \mathcal O(n/\log n) \) [2].

Inspired by above works, we want to find a largest loop with a relatively high probability and low complexity. It is proved that depth first search (DFS) [5] algorithm can also be used to find loop. However, the key problem is how to apply the DFS to finding the largest loop. To avoid traversing the directional relationship more than once, we propose the HLLSBD (Heuristic Largest Loop Searching Based on DFS) algorithm which using different colors to represent the different statements of D2D users. Since the proposed algorithm traverse the directional relationship only once, it can find a largest loop with higher probability and lower complexity. The computation complexity of the algorithm is \( \mathcal O(n+v) \), where n is the number of nodes, representing the number of D2D users; v is the number of edges, representing the number of all the directional relationship between the D2D users.

Compared with the algorithm in [15], which randomly find a loop for each possible D2D user and keep the loop with larger size each time after they finish one search, our algorithm can find a larger loop with lower complexity. Because the computation complexity of the algorithm in [15] is unpredictable. Now we present how to use the heuristic algorithm to find a larger loop in Algorithm 1.

figure a

The Algorithm 1 can be described briefly as follows.

  • First of all, we introduce the meaning of different colors. The white color represents the node has not been explored. Dyeing gray represents the node is being explored. Dying black represents the node has been explored.

  • Afterwards, we list all situations that can be encountered in traversal. 1) When finding a white node in traversal, we dye it gray. 2) When finding a gray node in travel, it indicates that the node has been explored before. So we find a end to end loop. Here, we rather backdate than traverse along the node, which ensuring that we don’t find a loop repeatedly and find a larger loop possibly. 3) When finding a black node, it indicates that the node is not in any loop or the loop containing the node has been explored. Here, the backtracking is necessary to avoid finding a loop repeatedly.

  • Finaly, the node whose children nodes have been explored is dyed black. The traversal ends until all nodes have been dyed black. We choose the largest loop from overall loops found as cabal.

After finding a cabal, we presents a Cheating algorithm with larger cabal in Algorithm 2. We know that M 0 is the men-optimal stable matching if and only if M 0 contains no cabal, which indicates that D2D users in M 0 not necessarily falsify their preference lists. To further reduce the computation complexity, we add a decision condition before finding accomplices.

figure b

In this way, we find a cabal with bigger size to benefit more D2D users with lower complexity, which achieves the optimization target.

4.4 Properties of the cheating algorithm based on HLLSBD

In this subsection, to evaluate the proposed algorithm, we analyze the properties in terms of effectiveness, stability, convergence and complexity in the following.

  1. 1)

    Effectiveness: The D2D users’ throughput increases after our proposed cheating algorithm.

Proof

Since we have proceeded the Theorem 1 by contradiction, the throughput performance of our proposed cheating algorithm is at least as good as the previous men-optimal GS algorithm. In addition, after the GS algorithm, some D2D users always can not be matched to their desired partners, which gives us the chance to outperform the GS algorithm in throughput. So we can conclude that our proposed algorithm can always increase the D2D users’ throughput. □

  1. 2)

    Stability: The proposed Algorithm 2 can obtain a one-to-one stable matching M S .

Proof

According to Definition 3, the matching M without any blocking pair is stable. In order to prove the stability of the proposed algorithm 2, we assume that there exists a blocking pair in the final matching M S satisfying that \( \exists d_{i},d_{i^{\prime }}\in \mathcal {D}\), \( M_{S}(d_{i^{\prime }}) \succ _{d_{i}}M_{S}(d_{i}) \&d_{i}\succ _{M_{S}(d_{i^{\prime }})}d_{i^{\prime }}\). According to algorithm 2, the cheating algorithm needs to run the GS algorithm in the end. If \( (d_{i},M_{S}(d_{i^{\prime }})) \) is an blocking pair, there will exist this two cases in matching process. Cases 1 is that d i never proposed to \( M_{S}(d_{i^{\prime }})\), which indicates that d i prefers M S (d i ) to \( M_{S}(d_{i^{\prime }})\). Case 2 is that d i has proposed to \( M_{S}(d_{i^{\prime }})\) while \( M_{S}(d_{i^{\prime }})\) rejected d i . The rejection also indicates that d i prefers M S (d i ) to \( M_{S}(d_{i^{\prime }})\). In either case \( (d_{i},M_{S}(d_{i^{\prime }})) \) can not compose a blocking pair, which causes conflict. Therefore, we conclude the proposed algorithm can reach the one-to-one stability in the end of the algorithm. □

  1. 3)

    Convergence: From the proof of effectiveness, we find that the D2D users’ throughput increases after each successful swap operation in cabal. Since the throughput has an upper bound due to limited spectrum resources, the swap operations stop when the maximum throughput is saturated. Therefore, within limited number of rounds, the matching will converge to the final state which is stable. However, there is little room for us to further increase the throughput after the first swap. In this case, it’s not worthwhile to sacrifice complexity performance in exchange for throughput performance. Hence, we just swap once rather than iterate to the final state.

  2. 4)

    Complexity: The computation complexity of Algorithm 2 consists of the following parts. The first part is finding cabal using Algorithm 1, whose computational complexity is \( \mathcal O(n+v) \). n is the number of D2D users and v is the number of all the relationship between the D2D users. However, the directional relationships among all D2D users are very simple after GS algorithm, which indicates that v is much less than n 2. The second part is finding accomplices, whose computation complexity is \( \mathcal O(n) \). The third part is falsifying preference lists, whose computation complexity is \( \mathcal O(n) \). The final part is GS algorithm, whose computation complexity is \( \mathcal O(n^{2}) \). Hence, the total computation complexity of Algorithm 2 is \( \mathcal O(n^{2}) \). More importantly, if M 0 is man-optimal stable matching, the computation complexity of Algorithm 2 is only \( \mathcal O(n+v) \). It is obvious that the computation complexity of our algorithm is lower than the Hungarian algorithm and the Cheating algorithm in [15].

5 Simulation result

In this section, considering a single cell multi-user scenario, we evaluate the performance our algorithms in the following way: how our algorithms work and where the advantages of our algorithm are shown. First, we show how much the D2D users’ throughput is improved by our algorithm compared to the GS algorithm [12], the existing Cheating algorithms [14, 15] and the Hungarian algorithm [32], respectively. Then we show how individual D2D user is improved by our cheating algorithm. Afterwards, to further illustrate the importance of cabal size, we compare the ratio of cabal members in D2D users using different algorithm. Finally, the probability of finding the largest cabal in a more complex case is presented to reflect the advantage of our algorithm. The benchmark algorithms can be briefly described as follows:

The Gale-Sharpley algorithm can obtain a stable matching in a lower computation complexity. The Cheating algorithm in [14] can be described as “Cheating with random cabal”, which random search for a cabal ends until a loop is found no matter how large this cabal is. The Cheating algorithm in [15] can be described as “Cheating with larger cabal”, which random search for a cabal for each D2D user and keep the loop with larger size each time after they finish one search. The Hungarian algorithm can achieve the theoretical maximum throughput in an unstable matching, which can be used as a benchmark. Simulation parameters are shown in Table 1.

Table 1 Simulation parameters
Full size table

In Fig. 3, we evaluate the D2D users’ throughput (i.e., the sum of all D2D users’ transmission rate) with different number of D2D users using different algorithms. The 10000 times Monte-Carlo simulation shows that with the increase of the number of D2D users/CUs, the total throughput of D2D users increases continuously. Since with the increase of the number, the average throughput is almost unchanged, but the increase in the number of D2D links improve the throughput. The Hungarian algorithm can find a maximum weight matching, which achieves the most D2D users’ throughput. The other four curves, i.e., the Gale-Sharpley curve, Cheating with random cabal [14] curve, Cheating with larger cabal [15] curve and Cheating based on HLLSBD curve, they achieve almost 87.01 %, 88.74 %, 92.18 % and 93.82 % of the optimal system throughput by Hungarian algorithm, respectively. With such performance, we could say that our algorithms are close optimal while ensuring the system stability. Besides, the computation complexity of our algorithm is less than the Hungarian algorithm and the Cheating with larger cabal [15]. Comparing the three Cheating curves to the one without Cheating, the most important is that with the increasing number of D2D users, the performance of our algorithm becomes better.

Fig. 3
figure 3

D2D user Throughput comparison with different number of D2D users

Full size image

Figure 4 shows how exactly an individual D2D user’s satisfaction (w.r.t. the ranking of partners) is improved using different algorithms. The 10000 times Monte-Carlo simulation give the average numbers of 20 D2D pairs that match to their kth choice in the preference list. If every user is honest, averagely 5.83 users get their favorite partners and 4.37 users match to the second choice. In case of cheating, we can have more than 7.53 users match to the first choice and 4.57 to the second. Comparing the three Cheating algorithm, our algorithm can make more users match to their first and second choice, which intuitively reflects the advantage of our algorithm.

Fig. 4
figure 4

D2D partners’ distribution with different algorithm

Full size image

To further illustrate the importance of cabal size, in Fig. 5, we compare the ratio of cabal members in D2D users between Cheating with random cabal, Cheating with larger cabal and Cheating based on HLLSBD. With the increase of the number of D2D users/CUs, the ratio of random cabal remains unchanged. The reason is that, the random search for a cabal in [14] ends until a loop is found no matter how large this cabal is. Although the number of D2D users increases, the cabal size with the random search not necessarily increases. As for the search for larger cabal in [15] (in their work, they have gone through all possible D2D members during the search), with the number of D2D users increase, the cabal size increases as well. It is obvious that the ratio increases a lot for exhaustive search. But the trend is increasing slowly. As for our algorithm, the Cheating based on HLLSBD yields a highest ratio among the three algorithm. Meanwhile, the ratio of cabal size keeps a substain increase, which indicates that our algorithm can always find a larger cabal.

Fig. 5
figure 5

The ratio of cabal member in D2D users with different number of D2D pairs

Full size image

In Fig. 6, we evaluate the probability of finding the largest cabal under different number of D2D pairs. It is not hard to understand that the directional relationships among all D2D users are very simple after men-optimal stable matching, which can be abstracted as the degree in graph theory. The degree of the vertex is defined as the number of all the edges containing the vertex. The lower the degree,the simpler the directional relationships. The mathematical expectation of each node degree accounts for 5 % of the number of all nodes. In this case, the probability of finding the largest cabal is almost 100 %. Therefore, we consider a more complex case. We evaluate the performance of our algorithm when the mathematical expectation of each node degree accounts for 20 % of all nodes. It can be seen from Fig. 6 that with the increase of the number of D2D users/CUs, the directional relationships become more and more complex, which resulting in the decrease in the probability of finding the largest cabal. Compared with the algorithm in [14] and [15], our algorithm can find the largest cabal with higher probability. It is proved that our algorithm has the advantage in the case of more complex directional relationships.

Fig. 6
figure 6

The probability of finding the largest cabal with different number of D2D pairs

Full size image

6 Conclusion

In this paper, we introduce the FD relaying-based D2D communication scheme in multi-user heterogeneous cellular network, which can improve the spectrum resource utilization dramatically. To further improve the throughput of D2D users, we implement matching theory into this scenario to solve the resource allocation problem. The GS stable matching algorithm is provided to solve the problem. The GS algorithm could reach 87.01 % (under our simulation set up) of the maximum D2D throughput by the Hungarian algorithm in polynomial time. In addition, We introduce a Cheating algorithm based on cooperative game in order to further improve some D2D users’ throughput. More importantly, due to the NP-hardness of our optimization target, we cannot find the optimal solution within a polynomial time. Hence, using different colors to represent the different statements of D2D users, we develop a heuristic algorithm with low complexity to find a near-optimal solution of Cheating algorithm.

The simulation results show that the throughput performance becomes better with the bigger cabal size. The performance increases by 5.08 % and 1.64 % for the D2D throughput, respectively, compared to the cheating algorithm in [14] and [15]. It is proved that our algorithm has better complexity and throughput performance compared with the existing algorithms.