Zero-Feedback, Collaborative Beamforming for Emergency Radio: Asymptotic Analysis

Abstract

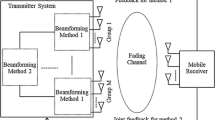
Collaborative beamforming among a set of distributed terminals is studied, assuming a) no specialized RF hardware for carrier frequency synchronization, and b) zero feedback from destination (either in the form of pilot signals or explicit messages). Our goal is to provide a solution for conventional radios (not necessarily wideband), when the link between a single source transmitter and destination is too weak, so that no signal can be reliably received at the destination. In such critical case, zero feedback messages from destination to the multiple transmitters cannot be assumed, even when the destination is equipped with powerful hardware. A solution is provided for conventional radios in relevant critical applications, such as in emergency radio. The proposed scheme simply exploits lack of synchronization among distributed carriers, operating at the same nominal carrier frequency. It is shown that such beamforming is possible and its performance is analytically quantified. Results include asymptotic analysis for the case of large number of transmitters.

Appendix

Theorem 3

Assume M independent, not identically distributed (i.n.i.d.) random variables X₁,  X₂, ...,  X _M , with probability density function (p.d.f.) $p_{X_i}{x}$ and cumulative distribution function (c.d.f.) $F_{X_i}{x}$ per X _i , $i \in \{1, 2,\ldots, M\}\equiv \mathcal{S}_{M}$. Denote Y₁ < Y₂ < ... < Y _M the ordered random variables {X _i }. The joint probability density function of the minimum and maximum of the i.n.i.d. random variables {X _i }

$$ p_{Y_1,Y_M}{Y_1=y=\min\limits_{i \in \mathcal{S}_{M} }\left\{ X_i\right\},Y_M=x=\max\limits_{i \in \mathcal{S}_{M} }\left\{ X_i\right\}} $$

is given by:

$$ p_{y,x}{y,x}= \left\{ \begin{array}{rl} &g_0(y,x), y<x\\ &0, \text{elsewhere,} \end{array} \right. \label{eq:joint_pdf} $$

(37)

where g₀(y, x) is given by Eq. 15.

Proof

$$ p_{y,x}{y,x} dy dx = \text{Pr}{Y_1 \in dy, Y_M \in dx} $$

(38)

$$ \begin{array}{rll} &=\Pr \left \{\text{one } X_i \! \in \!dy, \text{one } X_j \! \in \!dx (\text{with } y\!<\!x \text{ and } i \neq j)\right. \nonumber \\ &\left.\text{ and all the rest } \in (y,x) \right\} \end{array}$$

(39)

$$ \begin{array}{rll} &=\sum\limits_{k_1 \neq k_2}\left\{ \left[p_{X_{k_1}}{y} p_{X_{k_2}}{x} + p_{X_{k_1}}{x} p_{X_{k_2}}{y} \right] dy dx \right. \nonumber \\ &\left. \times \prod\limits_{k_3 \neq k_1, k_3 \neq k_2} \left(F_{X_{k_3}}{x} - F_{X_{k_3}}{y}\right) \right\}, \nonumber \\ &\text{ for } y<x. \end{array}$$

(40)

The double sum of $p_{X_{k_1}}{y} p_{X_{k_2}}{x} dy dx +$ $p_{X_{k_1}}{x} p_{X_{k_2}}{y} dy dx$ above stems from the fact that even though there are exactly $M \choose 2$ pairs among the set of M {X _i }’s, ordering among each pair matters. Simplifying the last line above concludes the proof. □

Lemma 2

Assume zero-mean uniform or normal carrier offset distribution p_Δf Δf with $\mathbb{E}{\Delta f^2}=\sigma^2$. The p.d.f. of $\{\ddot{\phi_j}\}$’s can be numerically calculated by:

$$ \begin{array}{rll} p_{\ddot{\phi_i}}{\ddot{\phi_i}} &= \frac{1}{2 \pi n T_s} \sum\limits_{k=-K_0}^{K_0} p_{\Delta f}{\frac{ \ddot{\phi_i} + 2 k \pi -\phi_i}{2 \pi n T_s}}, \\ &\ddot{\phi_i} \in [0,2\pi), \forall i \in \mathcal{S}_{M}, \nonumber \end{array}$$

(41)

where $K_0=\lfloor n T_s b +1 \rfloor$, $\lfloor x \rfloor$ is the floor function and $b=\sqrt{3} \sigma$ or b = 3 σ for uniform or normal carrier offset distribution, respectively.

Proof

For zero-mean uniform distribution p _Δf x in [ − b, b], the standard deviation σ is expressed through b as: $\mathbb{E}{\Delta f^2}=\sigma^2 = 4 ~b^2/12 \Rightarrow b=\sqrt{3} ~\sigma$. Given that p _Δf x is zero outside [ − b, b], the following holds:

$$ -b \leq \frac{ \ddot{\phi_i} + 2 k \pi -\phi_i}{2 \pi n T_s} ~\leq b \Rightarrow $$

(42)

$$ -1-n T_s b \leq \frac{\phi_i-\ddot{\phi_i}}{2\pi} - n T_s b \leq k, $$

(43)

$$ k \leq n T_s b + \frac{\phi_i-\ddot{\phi_i}}{2\pi} \leq n T_s b + 1, $$

(44)

where Φ _i  ∈ [0, 2π). Given that k is an integer, the above expression justifies the selected K ₀ = $\lfloor n T_s b +1 \rfloor$.

For zero-mean normal distribution p _Δf Δf, the justification is the same for b = 3 σ; about 99.7% of values drawn from a normal distribution are within 3 σ from the mean. □

Theorem 4

(Product of Densities (Joint PDF) Bound) Assume continuous carrier frequency offset probability density function p _Δf x with characteristic function $\chi_{\Delta f}(u)\stackrel{\triangle}{=}\mathbb{E}{e^{j u \Delta f}}$ and independent, non-identically distributed random variables $\{\ddot{\phi_j}\}$ , j ∈ {1, 2, .., M}, with

$$ \ddot{\phi_j}\stackrel{\triangle}{=} \left(2\pi n T_s \Delta f_j + \phi_j \right) \mod 2\pi = \widetilde{\phi_j} \mod 2\pi , $$

(45)

where n, T _s are positive constants, {Φ _j } constants in [0, 2π) and {Δf _j } independent and identically distributed, according to p _Δf (x).

For M→ ∞, the joint p.d.f. is lower-bounded by:

$$ \prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} \geq \frac{M!}{(2\pi)^M} \text{Pr}{\sum\limits_{j=1}^M \ddot{\phi_j} <2\pi}, $$

(46)

when

$$ \begin{array}{rll} &&\left|\chi_{\Delta f}(2\pi n T_s k)\right|^M \rightarrow 0, \text{for } M\rightarrow +\infty, \nonumber \\ && \forall k \in \Bbb{Z^*}=\{\pm 1, \pm 2,\ldots\}. \label{eq:cond} \end{array}$$

(47)

Proof

Given that $\{\ddot{\phi_j}\}$’s are independent, their joint pdf is given from the product $\prod_{j=1}^M p_{\ddot{\phi_j}}{x_j}$. We construct the random variables y and z such that:

$$ y= \sum\limits_{j=1}^M \ddot{\phi_j}=\sum\limits_{j=1}^M \left( \widetilde{\phi_j} \mod 2\pi \right), $$

(48)

$$ z= \left (\sum\limits_{j=1}^M \widetilde{\phi_j} \right) \mod 2\pi, $$

(49)

and observe that $z=y=\sum_{j=1}^M \ddot{\phi_j}$ when $\sum_{j=1}^M \ddot{\phi_j}<2\pi$. We also observe that the random variable z constitutes a random walk with distribution that could be estimated for M→ + ∞. Specifically, the Fourier-Stieltjes coefficients $\chi_z \left(\frac{2 k \pi}{2 \pi}\right)$ for $k \in \Bbb{Z}$ of random variable z can be shown to be

$$ \chi_z \left(k\right)= \prod\limits_{m=1}^M \chi_{\widetilde{\phi_m}}(k) = \left[\chi_{\Delta f}(2 \pi n T_s k)\right]^M \prod\limits_{m=1}^M e^{+i k \phi_m}. $$

(50)

By considering the Fourier-Stieltjes of the uniform distribution, we can see that the random variable z becomes uniform if and only if the Fourier-Stieltjes coefficients $\chi_z \left(k\right)$ become zero for any k ≠ 0 and M → ∞:

$$ \begin{array}{rll} && \Big | \chi_z(k) \Big | = \Big | \chi_{\Delta f}(2 \pi n T_s k) \Big |^M \rightarrow 0, \nonumber \\ && \forall k \in \{\pm 1, \pm 2, \ldots\}=\Bbb{Z^*}, M \rightarrow \infty. \label{eq:COND} \end{array}$$

(51)

The above condition is met by all characteristic functions $\chi_{\Delta f}(u)=\mathcal{O}(1/u)$. Thus, when y < 2π, the random variable $z=y=\sum_{m}^M \ddot{\phi_m}$ becomes uniform for M → ∞, even though $\{\widetilde{\phi_j}\}$’s are not identically distributed, provided that the above condition is met. A similar result regarding the limiting distribution of z was reported in [10] when the independent random variables $\{\widetilde{\phi_j}\}$ are identically distributed.

Assume that condition (51) is met and y < 2π. The random variable y (with 0 ≤ y < 2π) becomes uniform for M → ∞ according to the above. Therefore, the joint p.d.f. of $\ddot{\phi_m}$’s conditioned on y < 2π must be constant for any $\sum_{j=1}^M x_j =y \in [0,2\pi)$:

$$\begin{array}{rll} &\prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} dx_1 dx_2 \ldots dx_M \Big |_{y=\sum_{j=1}^M x_j < 2\pi} \nonumber \\ & = p_{y}{y} dy = \frac{1}{2\pi} dy = \text{constant}, \forall y \in [0, 2\pi) \Rightarrow \end{array}$$

(52)

$$ \begin{array}{rll} &\prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} \Big |_{y=\sum_{j=1}^M x_j < 2\pi} = \nonumber \\ & = \left\{ \begin{array}{rl} C_0=\text{constant}, & \quad\forall \sum_{j=1}^M x_j=y \in [0, 2\pi), \\ 0, & \quad\text{elsewhere.} \end{array} \right. \end{array}$$

(53)

Taking into account that for any β > 0:

$$ \begin{array}{rll} &\int_{(x_1, x_2,\ldots, x_M), \forall \sum_{j=1}^M x_j=y \in [0, \beta)} dx_1 dx_2 \ldots dx_M = \nonumber \\ & = \int_{x_M=0}^{\beta} \int_{x_{M-1}=0}^{\beta-x_{M}} \ldots \int_{x_1=0}^{\beta-x_{M-1}-x_{M-2}-\ldots-x_2} dx_1 \ldots dx_{M-1} dx_{M} \nonumber \\ & = \frac{\beta^M}{M!}, \label{eq:Hard_Integral} \end{array}$$

(54)

we conclude that $C_0=M!/(2\pi)^M$.

Finally, exploiting the following, we complete the proof:

$$\begin{array}{rll} \prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} &\geq& \prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} \Big |_{y=\sum_{j=1}^M x_j < 2\pi} \text{Pr}{\sum\limits_{j=1}^M \ddot{\phi_j} <2\pi} \nonumber \\ &=&\frac{M!}{(2\pi)^M} \text{Pr}{\sum\limits_{j=1}^M \ddot{\phi_j} <2\pi}. \end{array}$$

(55)

□

Lemma 3

Assume the special case of normal or uniform carrier offset distribution p_Δf Δf with $\mathbb{E}{\Delta f}=0$,  $\mathbb{E}{\Delta f^2}=\sigma^2$. For M→ ∞, the joint p.d.f. of $\{\ddot{\phi_j}\}$’s is lower-bounded by:

$$ \prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} \geq \frac{M!}{(2\pi)^M} \mathcal{O}\left(\left(\frac{\phi_0}{2\pi}\right)^{M}\right), $$

(56)

where 0 ≤ Φ₀ < π/2 and $\{\ddot{\phi_j}\}$’s are independent, not identically distributed (i.n.i.d.), defined in Theorem 4 above.

Proof

For the special case of normal or uniform distribution with $\mathbb{E}{\Delta f}=0$,  $\mathbb{E}{\Delta f^2}=\sigma^2$, the characteristic function of Δf becomes:

$$ \chi_{\Delta f}^{(normal)}(u) = e^{-\sigma^2 u^2/2}, $$

(57)

$$ \chi_{\Delta f}^{(uniform)}(u) =\frac{\sin\left(\sqrt{3} \sigma u\right)}{(\sqrt{3} \sigma u)}, $$

(58)

Both formulas adhere to Theorem 4 condition of Eq. 47.

Thus, according to Theorem 4,

$$ \prod\limits_{j=1}^M p_{\ddot{\phi_j}}{x_j} \geq \frac{M!}{(2\pi)^M} \text{Pr}{\sum\limits_{j=1}^M \ddot{\phi_j} <2\pi}, $$

(59)

when M→ ∞.

Additionally, uniform or normal carrier offset distribution p _Δf Δf amounts to finite moments for the i.n.i.d. $\{\widetilde{\phi_i}\}$’s and $\{\ddot{\phi_i}\}$’s. Thus, the Lyapunov conditions are met and $y=\sum_{j=1}^M \ddot{\phi_j}$ approaches normal distribution for M→ ∞. Given that $\mathbb{E}{y}=\mathcal{O}(M)$ and $\mathbb{E}{y^2 - \mathbb{E}{y}^2}= \mathcal{O}(M)$, it can be seen that

$$ \text{Pr}{\sum\limits_{j=1}^M \ddot{\phi_j} <2\pi}=\frac{1}{\sqrt{2\pi \mathbb{E}{y^2 - \mathbb{E}{y}^2}}} \times $$

$$ \times \int_{0}^{2\pi} \exp{\left[-\frac{\left(y-\mathbb{E}{y}\right)^2}{2\mathbb{E}{y^2 - \mathbb{E}{y}^2}}\right]} ~dy = \mathcal{O}\left(e^{-M} \right). $$

(60)

Since $e^{-1}> (\phi_0/2\pi)$ for Φ ₀ ∈ [0, π/2), it can be seen that $\text{Pr}{\sum_{j=1}^M \ddot{\phi_j} <2\pi} > \mathcal{O}\left(\left(\frac{\phi_0}{2\pi}\right)^{M}\right)$, completing the proof. □