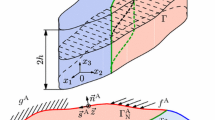
The stress-strain state that occurs in multilayered structures (for example, beams) significantly depends on the nature of the interaction of their layers. In practice, when calculating such structural elements, an ideal contact of the layers is most often considered, this implies the continuity of displacement vectors and stresses at the contact boundary. Strict elasticity theory solutions in this case inevitably lead to the appearance of infinite tangential stresses on the free surfaces at the angular points of structures at the layer interfaces. In this paper, the problem of the stress-strain state of a multilayered beam is considered in which the interaction of layers is assumed nonideal. For this aim, a layer interaction model with a thin contact layer between the adhesive and adherends is chosen. The equations obtained on the basis of this model allowed us to find non-singular solutions that describe the essentially inhomogeneous stress-strain state in each layer of the beam and at their interfaces.






Similar content being viewed by others
References
F. A. G. Giesteira, E. A. S. Marques, R. J. C. Carbas, and L. F. M. Da Silva, “Prediction of joint strength and effect of the surface treatment on the single overlap adhesive joints,” U. Porto J. Eng., 3, No. 3, 1-16 (2018).
Strength Prediction of Adhesively-Bonded Joints, Ed. D. S. Raul, Porto, CRC Press, Taylor & Francis Group (2016).
F. Guo and J. H. Wu, “Coupling resonance mechanism of interfacial stratification of sandwich plate structures excited by SH waves,” J. Low Frequency Noise, Vibration and Active Control, 40, No. 3, 1166-1193 (2021).
L. Goglio and M. Rossetto, “Evaluation of the singular stresses in adhesive joints,” J. Adhesion Sci. and Technol., 23, No. 10-11, 1441-1457 (2012).
P. Galvez, N. Noda, R. Takaki, Y. Sano, T. Miyazaki, J. Abenojar, and M. Martinez, “Intensity of singular stress field (ISSF) variation as a function of the Young’s modulus in single lap adhesive joints,” Int. J. Adhesion and Adhesives, 95, 102418 (2019).
T. J. Whitney, E. V. Iarve, and R. A. Brockman, “Singular stress fields near contact boundaries in a composite bolted joint,” Int. J. Solids and Structures, No. 41 (7), 1893-1909 (2004).
A. Barroso, F. París, and V. Mantič, “Representativity of the singular stress state in the failure of adhesively bonded joints between metals and composites,” Compos. Sci. and Technol., 69, No. 11, 1746-1755 (2009).
O. Volkersen, “Die nietkraftverteilung in zugbeanspruchten nietverbindungen mit konstanten laschenquerschnitten,” Luftfahrtforschung, No. 15, 41-47 (1938).
M. Goland and E. Reissner, “Stresses in cemented joints,” J. Appl. Mech., No. 11, A17-A27 (1944).
R. A. Turusov, K. T. Vuba, and A. S. Freidin, “Investigation of the influence of temperature and humidity factors on the strength and strain properties of adhesive joints of wood with steel reinforcement,” Trudy TsNIISK, No. 24, 86-124 (1972).
Z. Hashin, “Thermoelastic properties of particulate composites with imperfect interface,” J. Mech. and Physics of Solids, 39, No. (6), 745-762 1991.
R. Lipton and B. Vernescu, “Variational methods, size effects and extreme microgeometries for elastic composites with imperfect interface,” Math. Models and Methods in Appl. Sci., 5, No. 8, 1139-1173 (1995).
J. A. Nairn, Y. C. Liu, and C. Galiotis, “Analysis of stress transfer from the matrix to the fiber through an imperfect interface: application to Raman data and the single-fiber fragmentation test,” Fiber, Matrix, and Interface Properties, Ed. C. Spragg, L. Drzal, ASTM International, 47-66 (1996).
Hao Long, Yueguang Wei, and Lihong Liang, “A rigorous analytical solution of interfacial stresses and overall stiffness of beam structures bonded with partially covered plates,” Int. J. Mech. Sci., 167, 105284 (2020).
J. B. M. Sousa and A. R. Da Silva, “Analytical and numerical analysis of multilayered beams with interlayer slip,” Eng. Struct., 32, No. 6, 1671-1680 (2010).
R. A. Turusov, Adhesion Mechanics. Monograph [in Russian], Moscow, MGSU (2016).
R. Turusov, “Elastic and thermal behavior of a layered structure I. Experiment and theory,” Mech. Compos. Mater., 50, No. 6, 801-808 (2015).
H. Memarianfard and R. Turusov, “Multiscale analysis of the residual stresses occurring during curing and cooling of thick-wall cross-ply filament-wound cylinders,” Mech. Compos. Mater., 53, No. 1, 675-684 (2017).
S. Litvinov, S. Yazyev, A. Chepurnenko, and B. Yazyev, “Determination of rheological parameters of polymer materials using nonlinear optimization methods,” Lecture Notes in Civil Eng., 130, 587-594 (2020).
B. Yazyev, S. Litvinov, and S. Yazyev, “Thermoviscoelasticity problem for a multilayer inhomogeneous polymeric cylinder,” Int. Polymer Sci. and Technol., 36, No. 2, 49-51 (2009).
S. P. Timoshenko and D. Goodier Theory of elasticity [translated from English], Moscow, Nauka (1979).
Bo Zhao, Zhen-Hua Lu, and Yi-Ning Lu, “Two-dimensional analytical solution of elastic stresses for balanced single-lap joints. Variational method,” Int. J. Adhesion and Adhesives, 49, 115-126 (2014).
J. Zhengwen and W. Shui, “Improved one-dimensional beam model for unbalanced composite single-lap joint,” J. Adhesion Sci. and Technol., 32, No. 8, 854-873 (2018).
R. A. Turusov, “Adhesion interaction and adhesion mechanics. Theory and its application,” Polymer Science, Series D, 14, No. 4, 522-531 (2021).
A. Y. Sergeev, R. A. Turusov, and V. I. Andreev, “Determination of polymer-substrate joint adhesive strength by means method of pulling fiber from the matrix and normal avulsion,” IOP Conf. Series: Mater. Sci. and Eng., 1030, 012001 (2021).
V. I. Andreev, Mechanics of Inhomogeneous Bodies [in Russian], Moscow, Yurayt Publishing House (2020).
R. A. Kayumov Fundamentals of the Theory of Elasticity and Elements of the Theory of Elasticity of Plates and Shells [in Russian], Kazan, Publishing house of the Kazan State University of Architecture and Civil Engineering (2015).
A. L. Rabinovich, “On the elastic constants and strength of aviation materials,” Proceedings of TsAGI, No. 582, 1-56 (1946).
V. V. Bolotin and Yu. N. Novichkov, Mechanics of Multilayer Structures [in Russian], Moscow, Mashinostroenie (1980).
R. A. Turusov and L. I. Manevich, “Contact layer method: Determining parameters of rigidity and true strength of an adhesion bond for a contact layer,” Polymer Science Series D, 4, 4-11 (2011).
V. D. Tho, E. A. Korol, N. I. Vatin, and H. M. Duc, “The stress-strain state of three-layer precast flexural concrete enclosure structures with the contact interlayers,” Buildings, 11, No. 3, 88 (2021).
E. A. Korol and D. V. Tho, “Geometric and physicomechanical characteristics of the contact layer area of multilayer reinforced concrete structures,” IOP Conference Series Mater. Sci. and Eng., 1015, No. 1, 012034 (2021).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Tsybin, N.Y., Turusov, R.A., Sergeev, A.Y. et al. Solving the Stress Singularity Problem in Boundary-Value Problems of the Mechanics of Adhesive Joints and Layered Structures by Introducing a Contact Layer Model. Part 1. Resolving Equations for Multilayered Beams. Mech Compos Mater 59, 677–692 (2023). https://doi.org/10.1007/s11029-023-10124-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11029-023-10124-8