Skip to main content
SpringerLink
Log in

On Forced 3D Vibrations of Two Layered Plates under Periodic Tangential Impacts

  • Published:
Mechanics of Composite Materials Aims and scope

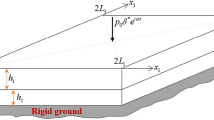
3D forced vibrations of two-layered plates under an influence of periodic in time tangential actions were studied. An asymptotic solution of the corresponding 3D problem of the theory of elasticity was obtained. The problem, in particular, models the seismic actions on the base-foundation of structures. All components of the stress tensor and displacement vector were determined. It is shown, that among these quantities tangential ones play the leading role. Cases, when found solution becomes mathematically exact, were indicated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.

Similar content being viewed by others

References

  1. L. A. Aghalovyan, Asymptotic Theory of Anisotropic Plates and Shells [in Russian], Nauka, Moscow (1977).

    Google Scholar 

  2. L. A. Aghalovyan, and R. S. Gevorgyan, Nonclassical Boundary-Value Problems of Anisotropic Layered Beams, Plates and Shells [in Russian], “Gitutyun”, NAS RA, Yerevan (2005).

  3. A. L. Gol’denveizer, Theory of Thin Elastic Shells [in Russian], Nauka, Moscow.

  4. K. O. Friedricks, “Asymptotic phenomena in mathematical physics,” Bulletin American Mathemathical Society, 61, No. 6, 485-504 (1955).

    Article  Google Scholar 

  5. K. O. Friedricks and R. F. Dressler, “A boundary-layer theory for elastic plates,” Communications on Pure and Appl. Math., 14, No. 1, 1-33 (1961).

    Article  Google Scholar 

  6. A. L. Gol’denveizer, “Derivation of an approximate theory of bending of a plate by the method of asymptotic integration of the equations of the theory of elasticity,” J. Appl. Math. and Mech., 26, No. 4,1000-1025 (1962).

  7. A. E. Green, “On the linear theory of thin elastic shells,” Proc. Royal Society Series A Math. and Physical Sci.. 266, No. 1325, 143-160 (1962).

  8. J. D. Kaplunov, I. V. Kirilova, and L. Yu. Kossovich, “Asymptotic integration of the dynamic equations of the theory of elasticity for the case of thin shells,” J. Appl. Math. and Mech., 57, No. 1, 95-103 (1993).

    Article  Google Scholar 

  9. S. M. Bauer, S. B. Filippov, A. L. Smirnov, and P. E. Tovstik, “Asymptotic methods in mechanics with applications to thin shells and plates,” In: R. Vaillancourt and A. L. Smirnov (eds) Asymptotic Method in Mechanics, American Mathematical Society, Providence, Phode Island, CAM Proceedings and Lectures Notes, 3, 3-140 (1993).

  10. P. E Tovstik, Stability of Thin Shells: Asymptotic Methods [in Russian]. Nauka, Moscow, (1995).

    Google Scholar 

  11. J. D. Kaplunov, L. Yu. Kossovich, and G. A. Rogerson, “Direct asymptotic integration of the equations of the transversely isotropic elasticity for a plate near cut-off frequencies,” Quartely J. Mech. and Appl. Math., 53, No. 2, 323-341(2000).

    Article  Google Scholar 

  12. P. E. Tovstik and A. L. Smirnov, Asymptotic Methods in the Buckling Theory of Elastic Shells. World Scientific Publishing Co Ltd., Singapore, New Jersey, London, Hong Kong (2001).

    Book  Google Scholar 

  13. G. I. Mikhasev and P. E. Tovstik, Localized Vibrations and Waves in Thin Shells. Asymptotic methods [in Russian], Fizmatlit., Moscow (2009).

  14. M. V. Vilde, J. D. Kaplunov, and L. Yu. Kossovich, Edge and Interface Resonance Phenomena in Elastic Bodies [in Russian], Fizmatlit., Moscow, (2010).

    Google Scholar 

  15. N. F. Morozov, P. E. Tovstik, and T. P. Tovstik, “A continuum model of a multilayer nanosheet,” Doklady Physics, 62, No. 11,567-570 (2016).

    Article  Google Scholar 

  16. L. A. Aghalovyan, “On asymptotic method in the solution of static and dynamic boundary value problems,” [in Russian], Proc. of NAS of Armenia, Mechanics, 57, No. 4, 3-14 (2004).

  17. M. L. Aghalovyan and T. V. Zakaryan, “The asymptotic solution of the first dynamic boundary value problem of the theory of elasticity for two-layered orthotropic plate,” [in Russian], Proc. of NAS of Armenia, Mechanics, 64, No. 2, 15-25 (2011).

  18. L. A. Aghalovyan, Asymptotic Theory of Anisotropic Plates and Shells, World Scientific Publishing, Singapore-London, (2015).

    Book  Google Scholar 

  19. L. A. Aghalovyan, “On some classes of 3D boundary-value problems of statics and dynamics of plates and shells,” In: H. Altenbach, G. I. Mihasev (Eds.) Shell and Membrane Theories in Mechanics and Biology, Cham. Advanced Structured Materials, 45, 1-23 (2015).

Download references

Author information

Authors and Affiliations

  1. Institute of Mechanics, National Academy of Sciences of Armenia (NAS RA), Yerevan, Armenia

    L. A. Aghalovyan & M. L. Aghalovyan

Authors
  1. L. A. Aghalovyan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. L. Aghalovyan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. A. Aghalovyan.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aghalovyan, L.A., Aghalovyan, M.L. On Forced 3D Vibrations of Two Layered Plates under Periodic Tangential Impacts. Mech Compos Mater 59, 393–402 (2023). https://doi.org/10.1007/s11029-023-10103-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-023-10103-z

Keywords

Search

Navigation