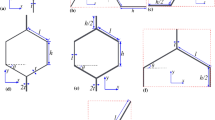
Due to the need for alternative materials for the realization of lightweight structures, the analysis of sandwich structures that have a semi-open thermoplastic honeycomb core as an internal support structure is of great technical and scientific interest. Sandwich components with a honeycomb-structured core layer between two continuous fiber-reinforced face sheets exhibit maximum weight-specific stiffnesses and strengths. The folded thermoplastic honeycomb cores have some characteristic properties not found in conventional honeycomb cores due to their special production, which causes the semi-open structure. As a result of the folding process, the cell walls of the honeycombs are not joined together in the folding direction, as would be the case, for example, with glued or expanded honeycombs. This specificity has a great influence on the structural mechanical behavior of the honeycomb. To characterize the mechanical material properties, one possibility is to examine the honeycomb structure based on data obtained by the computed tomography method and, building on this, to analyze these properties in more detail by means of modeling a representative volume element that reflects the cell geometry of the honeycomb core as closely as possible. The aim of this approach is to determine effective material parameters that can be applied to mechanical simulation using the finite element method. The validation of these characteristic values was carried out based on results that can be obtained through standardized, mechanical, quasi-static experiments.









Similar content being viewed by others
References
I. Verpoest and J. Pflug, Half Closed Thermoplastic Honeycomb, Their Production Process and Equipment to Produce”. AT DE FR GB IT Patent EP 1 824 667 B1, 21. 07. (2010).
H. Altenbach, J. Altenbach, and W. Kissing, Mechanics of Composite Structural Elements, 2nd ed., Springer Nature Singapore Pte. Ltd. (2018).
D. Gross, W. Hauger, und P. Wriggers, Technische Mechanik 4 - Hydromechanik, Elemente der höheren Mechanik, Numerische Methoden, Darmstadt: Springer Vieweg (2014).
R. Kienzler und R. Schröder, Einführung in die Höhere Festigkeitslehre, Bremen: Springer Vieweg (2019).
J. Hiller, S. Kasperl, U. Hilpert, und M. Bartscher, “Koordinatenmessung mit industrieller Röntgen-Computertomografie,” Technisches Messen, 74, No. 11, 553-564 (2007)
L. Gibson and M. Ashby, Cellular Solids — Structure and Properties, Cambridge: Cambridge University Press (1997).
V. G. Kouznetsova, Computational Homogenization for The Multi-Scale Analysis of Multi-Phase Materials, Technische Universiteit Eindhoven (2002).
Y. Rémond, S. Ahzi, M. Baniassadi, and H. Garmestani, Applied RVE Reconstruction and Homogenization of Heterogeneous Materials, London: ISTE Ltd. (2016).
R. Hill, “Elastic properties of reinforced solids: Some theoretical principles,” J. Mech. and Physics of Solids, 11, No. 5, 357-372 (1963).
O. van der Sluis, P. J. G. Schreurs, W. A. M. Brekelmans, and H. E. H. Meijer, “Overall behaviour of heterogeneous elastoviscoplastic materials: effect of microstructural modelling,” Mech. Mater., No. 32, 449-462 (2000).
K. Terada and N. Kikuchi, “A class of general algorithms for multi-scale analyses of heterogenous media,” Computer Methods in Appl. Mech. and Eng., No. 190, 5427-5464 (2000).
N. Goldberg, H. Donner, und J. Ihlemann, “Evaluation of hyperelastic models for unidirectional short fibre reinforced materials using a representative volume element with refined boundary conditions,” Technische Mechanik, 2, No. 35 (2014).
J. C. Michel, H. Moulinec, and P. Suquet, “Effective properties of composite materials with periodic microstructure: a computational approach,” Computer Methods in Appl. Mech. and Eng., No. 172, 109-143 (1998).
H. Donner, FEM-basierte Modellierung stark anisotroper Hybridcord-Elastomer-Verbunde, Technische Universität Chemnitz: Dissertation an der Fakultät für Maschinenbau (2017).
E. Nast, “Materialparameter für Sandwichkonstruktionen,” Technische Mechanik, Bd. Sonderheft, 55-62 (1997).
T. Oesch, In-Situ Röntgencompuertomographie für Mechanische, Thermische und Hydraulische Prozesse (2019).
E. Baur, G. Harsch, und M. Moneke, Werkstoff-Führer Kunststoffe - Eigenschaften - Prüfungen - Kennwerte, München: Hanser (2019).
H. Ijaz, W. Saleem, M. Zain-ul-Abdein, T. Mabrouki, S. Rubaiee, und A. Salmeen Bin Maahfouz, Finite element analysis of bend test of sandwich structures using strain energy based homogenisation method, Research Article: Hindawi Publishing Corporation (2017).
Acknowledgement
The results of this work were developed within the framework of the KMU-innovative / Production Research Project “HybridLFTSandwich” (funding code: 02P19K142). Our thanks go to the company ThermHex GmbH for the good cooperation and provision of the material.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Rusch, H., Horn, A. & Altenbach, H. Analysis and Modeling of Semi-Open Thermoplastic Honeycomb Core Structures for Mechanical Simulation with Representative Volume Elements. Mech Compos Mater 59, 381–392 (2023). https://doi.org/10.1007/s11029-023-10102-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11029-023-10102-0