Skip to main content
SpringerLink
Log in

Free Vibrations of a Nonlinearly Deformable Isotropic on the Average Composite Rectangular Membrane

  • Published:
Mechanics of Composite Materials Aims and scope

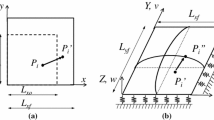
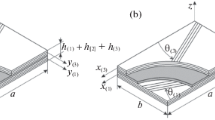
A refined vibration equation of a rectangular membrane is derived in this paper. It allows determining the natural frequencies as functions of the mechanical characteristics of an asymmetrically stretched membrane. The dynamic equation is generalized to the case of a nonlinearly deformable isotropic on the average composite material. An approximate analytical solution of the problem is found employing a new homogenization technique. This method is based on estimation of the effective deformation characteristics of the composite material. The range of its effective characteristics is obtained from the rule of mixtures for the stresses and strains found assuming Voigt and Reuss hypotheses. The nonlinear behavior of the material is modeled using the bilinear Prandtl diagrams as constitutive equations for components of the composite. The effective elastic moduli, hardening modulus, yield stress, and the natural frequencies as functions of elastoplastic characteristics of the composite are obtained analytically in a closed form.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

References

  1. S. T. Peters, Handbook of Composites, London: Chapman and Hall, 1998.

    Book  Google Scholar 

  2. P. A. A. Laura, L. Ercoli, R. O. Grossi, K. Nagaya, and G. S. Sarmiento, “Transverse vibrations of composite membranes of arbitrary boundary shape,” J. of Sound and Vibration, 101, No. 3, 299-306 (1985).

    Article  Google Scholar 

  3. D. V. Bambill, R. H. Gutierrez, P. A. A. Laura, and V. Jederlinic, “Vibrations of composite, doubly connected square membranes,” J. Sound and Vibration. 203, No. 3, 542-545 (1997).

    Article  Google Scholar 

  4. V. H. Cortinez and P. A. A. Laura, “Vibration of non-homogeneous rectangular membranes,” J. Sound and Vibration, 156, No. 2, 217-225 (1992).

    Article  Google Scholar 

  5. S. W. Kang and J. M. Lee, “Free vibration analysis of composite rectangular membranes with an oblique interface,” J. Sound and Vibration, 251, No. 3, 505-517 (2002).

    Article  Google Scholar 

  6. S. W. Kang, “Free vibration analysis of composite rectangular membranes with a bent interface,” J. Sound and Vibration, 272, 39-53 (2004).

    Article  Google Scholar 

  7. J. A. Masad, “Free vibrations of a non-homogeneous rectangular membrane,” J. Sound and Vibration, 195, No. 4, 674-678 (1996).

    Article  Google Scholar 

  8. P. A. A. Laura, R. E. Rossi, and R. H. Gutierrez, “The fundamental frequency of non-homogeneous rectangular membranes,” J. Sound and Vibration, 204, No. 2, 373-376 (1997).

    Article  Google Scholar 

  9. I. G. Aramanovich and V. I. Levin, Equations of Mathematical Physics [in Russian], M., Nauka, 1969.

  10. V. G. Bagrov, V. V. Belov, V. N. Zadorozhnyi, and V. Yu. Trifonov, “Methods of Mathematical Physics. IV, Equations of Mathematical Physics [in Russian], Tomsk, Izd. NTL, 2002.

    Google Scholar 

  11. I. A. Tarasyuk and A. S. Kravchuk, “Narrowing of the Voigt–Reuss range in the theory of elastic structurally nonuniform isotropic on the average composite bodies without the application of variational principles,” APRIORI, Ser. Estestv. Tekhn. Nauki, No. 3. URL: http://www.apriori-journal.ru/seria2/3-2014/Tarasyuk-Kravchuk.pdf (date of reference 11.11.2017)

  12. W. Voigt, Lehrbuch der Kristallphysik, Stuttgart, B.G. Teubner Verlag, 1966.

    Book  Google Scholar 

  13. A. Reuss, “Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle,” Zeitschrift für Angewandte Mathematik und Mechanik, 9, No. 1, 49-58 (1929).

    Article  Google Scholar 

  14. A. Lagzdiņš, G. Teters, A. Zilaucs, “Nonlinear deformation of composites with consideration of the effect of couple stresses,” Mech. Compos. Mater., 34, No. 5, 403-418 (1998).

    Article  Google Scholar 

  15. B. N. Zhemochkin, Theory of Elasticity [in Russian], M., Gostekhizdat, 1957.

  16. A. A. Ilyushin, Plasticity. Part 1. Elastic-plastic deformations [in Russian], M., Gostekhizdat, 1948.

  17. B. E. Pobedrya, Mechanics of Composite Materials [in Russian], M., Izd. Mosk. Univ., 1984.

  18. G. S. Pisarenko, and N. S. Mozharovskii, Equations and Boundary-Value Problems of Plasticity and Creep [in Russian], Kiev, Naukova Dumka, 1981.

    Google Scholar 

Download references

This work was performed at the support of Erasmus+ and the School of Computing and Mathematics (Keele University, Staffordshire).

Gratitude

I. A.Tarasyuk expresses his gratitude to Prof. Yu. D. Kaplunov and Dr. D. A. Prikazchikov for their invaluable help and support.

Author information

Authors and Affiliations

  1. Belarusian State University, Minsk, Belarus

    I. A. Tarasyuk, A. S. Kravchuk & G. I. Mikhasev

Authors
  1. I. A. Tarasyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. S. Kravchuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. I. Mikhasev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. A. Tarasyuk.

Additional information

Translated from Mekhanika Kompozitnykh Materialov, Vol. 54, No. 1, pp. 113-128, January-February, 2018.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tarasyuk, I.A., Kravchuk, A.S. & Mikhasev, G.I. Free Vibrations of a Nonlinearly Deformable Isotropic on the Average Composite Rectangular Membrane. Mech Compos Mater 54, 79–88 (2018). https://doi.org/10.1007/s11029-018-9720-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-018-9720-1

Keywords

Search

Navigation