Skip to main content
SpringerLink
Log in

Time-Harmonic Lamb Problem for a System Consisting of an Imperfectly Bonded Orthotropic Covering Layer and an Orthotropic Half-Plane

  • Published:
Mechanics of Composite Materials Aims and scope

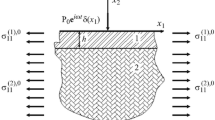
The time-harmonic Lamb problem for a system consisting of an imperfectly bonded covering layer and an orthotropic half-plane is studied. It is assumed that the materials of constituents of the system considered are orthotropic, and the imperfectness of contact conditions is modeled by using a shear-spring model. A plane strain state is considered, and an algorithm for calculating the dynamical stress field is developed and employed. Numerical results on the influence of the shear-spring imperfectness parameter on the distribution of normal contact stresses are presented and discussed. In particular, it is established that the numerical results obtained at limit values of the parameter coincide with the results obtained in the previous work of the authors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. S. D. Akbarov, “The influence of the third order elastic constants on the dynamical interface stress field in a half-space covered with a pre-strained layer,” Int. J. Non-Linear Mec. 41, 417- 425 (2006).

    Article  Google Scholar 

  2. S. D. Akbarov, “Dynamical (time-harmonic) axisymmetric interface stress field in a finite pre-strained half-space covered with a finite pre-stretched layer,” Int. J. Eng. Sci. 44, 93-112 (2006).

    Article  Google Scholar 

  3. S. D. Akbarov, “On the dynamical axisymmetric stress field in a finite pre-stretched bilayered slab resting on a rigid foundation,” J. Sound Vib. 294, 221- 237 (2006).

    Article  Google Scholar 

  4. S. D. Akbarov, “Frequency response of a axisymmetrically finite pre- stretched slab from incompressible functionally graded material on a rigid foundation,” Int. J. Eng. Sci. 44, 484-500 (2006).

    Article  Google Scholar 

  5. S. D. Akbarov, “The axisymmetric Lamb’s problem for a finite pre-strained half-space covered with the finite prestretched layer,” Int. Appl. Mech. 43 (3), 351-360 (2007).

    Article  Google Scholar 

  6. S. D. Akbarov and C. Guler, “Dynamical (harmonic) interface stress field in a half-plane covered by a pre-stretched layer under a strip load,” J. Strain Anal. Eng. Des. 40 (3), 225-236 (2005).

    Article  Google Scholar 

  7. S. D. Akbarov and C. Guler, “On the stress field in a half-plane covered by a pre-stretched layer under the action of arbitrary linearly located time-harmonic forces,” Appl. Math. Model. 31, 2375-2390 (2007).

    Article  Google Scholar 

  8. S. D. Akbarov and N. Ilhan, ‘Time-harmonic dynamical stress field in a system comprising a pre-stressed orthotropic layer and pre-stressed orthotropic half-plane,” Archive of Applied Mechanics, 80, 1271-1286 (2010).

    Article  Google Scholar 

  9. P. A. Martin, “Boundary integral equations for the scattering of elastic waves by elastic inclusions with thin interface layers,” J. Nondestructive, Eval 11, 167-174 (1992).

    Article  Google Scholar 

  10. J. P. Jones and I. S. Whitter, “Waves at a flexibly bonded interface,” Trans. ASME, Ser. E, Appl. Mech., 34, 905-909 (1967)

    Article  Google Scholar 

  11. J. R. Berger, P. A. Martin, and S. J. McCaffery, “Time-harmonic torsional waves in a composite cylinder with an imperfect interface,” J. Acoust. Soc. Amer, 107 (3), 1161-1167 (2000).

    Article  Google Scholar 

  12. T. Kepceler, “Torsional wave dispersion relations in a pre-stressed bi-material compounded cylinder with an imperfect interface,” Appl. Math. Model. 34, 4058-4073 (2010).

    Article  Google Scholar 

  13. S. D. Akbarov and C. Ipek, “The influence of the interface conditions on the dispersion of the axisymmetric longitudinal waves in the pre-strained compound cylinder,” CMES: Computer Modeling in Engineering and Sciences, 70 (2) 93-122 (2010).

    Google Scholar 

  14. S. I. Rokhlin and Y. J. Wang, “Analyses of boundary conditions for elastic wave interaction with an interface between two solids,” J. Acoust. Soc. Am. 89, 503-515 (1991).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Department of Mechanical Engineering, Yildiz Campus, Yildiz Technical University, 34349, Besiktas, Istanbul, Turkey

    S. Akbarov

  2. Institute of Mathematics and Mechanics of the National Academy of Sciences of Azerbaijan, 370141, Baku, Azerbaijan

    S. Akbarov

  3. Faculty of Civil Engineering, Department of Civil Engineering, Davutpasa Campus, Yildiz Technical University, 34220, Esenler, Istanbul, Turkey

    N. Ilhan

Authors
  1. S. Akbarov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. Ilhan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Akbarov.

Additional information

Russian translation published in Mekhanika Kompozitnykh Materialov, Vol. 50, No. 2, pp. 253-266, March-April, 2014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Akbarov, S., Ilhan, N. Time-Harmonic Lamb Problem for a System Consisting of an Imperfectly Bonded Orthotropic Covering Layer and an Orthotropic Half-Plane. Mech Compos Mater 50, 177–186 (2014). https://doi.org/10.1007/s11029-014-9405-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-014-9405-3

Keywords

Search

Navigation