Skip to main content
SpringerLink
Log in

Computational-experimental method to determine the averaged elastic and strength characteristics of fillers of multilayered structures in shear

  • Published:
Mechanics of Composite Materials Aims and scope

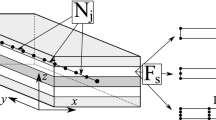
An analysis of known schemes of specimens for testing fillers of multilayered structures in shear to determine their stiffness and strength characteristics is presented. Based on results of a numerical simulation of the stress–strain state formed in the filler of test specimens in shear experiments, a refined scheme of their design, fastening, and loading is suggested, which ensures the realization of practically zero transverse compressive stresses and a constant tangential stress along the filler length (except for the short zones of edge effects). A computational-experimental method for determining the stiffness and strength characteristics of the fillers in shear is offered, which is based on a synthesis and combined use of data of physical experiment and results of computational simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. V. E. Bersudskii, V. N. Krysin, and S. I. Lesnykh, Manufacturing Technology of Honeycomb Aviation Structures, Mashinostroenie, Moscow (1975).

    Google Scholar 

  2. V. F. Panin and J. A. Gladkov, Structures with a Filler. Handbook, Mashinostroenie, Moscow (1991).

    Google Scholar 

  3. J. L. Grenestedt, “Effective elastic behavior of some models for ‘perfect’ cellular solids,” Int. J. Solid. Struct., No. 36, 1471–1501 (1999).

    Google Scholar 

  4. B. Lascoup, Z. Aboura, K. Khellil, and M. Benzeggagh, “On the mechanical effect of stitch addition in a sandwich panel,” Compos. Sci. Technol., No. 66, 1385–1398 (2006).

    Google Scholar 

  5. Q. M. Li, R. A. W. Mines, and R. S. Birch, “The crush behavior of Rohacell-51WF structural foam,” Int. J. Solid. Struct., No. 37, 6321–6341 (2000).

    Google Scholar 

  6. D. J. O’Conner, “A comparison of test methods for shear properties of the cores of sandwich constructions,” J. Test. Evaluat., 17, No. 4, 241–246 (1989).

    Article  Google Scholar 

  7. R. Garcia, T. A. Weisshaar, and R. R. McWithey, “An experimental and analytical investigation of the rail shear test method as applied to composite materials,” SESA Paper No. R79-105, Proc. 1979 SESA Spring Meeting, San Francisco, Calif., May 1979, Society of Experimental Stress Analysis (now, Society of Experimental Mechanics, SEM).

  8. ASTM C273/C273M - 07a Standard Test Method for Shear Properties of Sandwich Core Materials (2000).

  9. H. Toftegaard, “Initial fixture design for direct shear testing of sandwich core materials,” in: Risø (DK) (2006), pp. 337–347.

  10. H. Toftegaard and S. Goutianos, “Composite skin elastic constants from monolithic in-plane specimens and bonded out-of-plane specimens,” J. Sandw. Struct. Mater., No. 9, 239–259 (2007).

    Google Scholar 

  11. V. V. Bolotin and Yu. N. Novichkov, Mechanics of Multilayered Structures [in Russian], Mashinostroenie, Moscow (1980).

    Google Scholar 

  12. V. N. Paimushin, “Nonlinear theory of moderate bending of three-layer shells with defects in the form of areas of adhesion failure,” Prikl. Mekh., 23, No. 11, 32–38 (1987).

    Google Scholar 

  13. V. N. Paimushin and S. N. Bobrov, “Refined geometric nonlinear theory of sandwich shells with a transversely soft core of medium thickness for investigation of mixed buckling forms,” Mech. Compos. Mater., 36, No. 1, 59–66 (2000).

    Article  Google Scholar 

  14. M. B. Vakhitov, “Integrating matrices — a means for the numerical solution of differential equations of structural mechanics,” Izvest. Vuzov, Aviats. Tekhnika, No. 3, 50–61 (1996).

  15. R. Z. Dautov and V. N. Paimushin, “On the method of integrating matrices in solving boundary-value problems for ordinary differential equations of the fourth order,” Izv. Vuzov. Matem., No. 10, 13–25 (1996).

  16. A. V. Sachenkov, “Theoretical-experimental method for investigating the stability of plates and shells. Investigations into the theory of plates and shells,” Izdat. Kazan. Gos. Univer., Kazan’, Iss. 6-7, 391–433 (1970).

  17. V. N. Paimushin, “Analytical-computational-experimental method for determining the critical loads and free frequencies of deformable solid bodies,” Dokl. Akad. Nauk SSSR, 330, No. 1, 51–54 (1993).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Study of Dynamics and Stability, Tupolev Kazan State Technical University, Tatarstan, Russia

    V. N. Paimushin, I. M. Zakirov, S. A. Lukankin & I. I. Zakirov

Authors
  1. V. N. Paimushin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. M. Zakirov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. A. Lukankin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. I. I. Zakirov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. N. Paimushin.

Additional information

Translated from Mekhanika Kompozitnykh Materialov, Vol. 48, No. 4, pp. 521-538, July-August, 2012.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Paimushin, V.N., Zakirov, I.M., Lukankin, S.A. et al. Computational-experimental method to determine the averaged elastic and strength characteristics of fillers of multilayered structures in shear. Mech Compos Mater 48, 355–368 (2012). https://doi.org/10.1007/s11029-012-9293-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-012-9293-3

Keywords

Search

Navigation