Quantify the Effect of China’s Emission Trading Scheme on Low-carbon Eco-efficiency: Evidence from China’s 283 Cities

Abstract

The establishment of a carbon trading market is crucial for China to fulfil its carbon emission commitments through a market mechanism. As a market-based environmental regulation instrument, Emission Trading Scheme (ETS) has been attracted increasing attention worldwide, while the effect of ETS on low-carbon economy efficiency (LEE) has not been fully investigated, thus inspiring us to fulfil this research gap. Using the panel data of China’s 283 selected prefecture-level cities during 2006–2017, we adopted the difference-in-differences (DID) model, propensity-score-matched DID (PSM-DID) model, and the spatial DID model to model the direct and indirect effects of China’s ETS on LEE at national, regional, and local (resource-based cities with different development stages) levels. The robust results yield that ETS directly and significantly improved China’s LEE at the national level. Still, the LEE in ETS pilot region will increase by approximately 4.3% compared with untreated cities, while the spatial heterogeneity of this effect is captured at regional and local levels, which emphasises the necessity of a completed market construction and classified supervision. The results of this paper provide important insights for strengthening the policy design of a nationwide carbon market, and a reference point for other regions and countries, especially developing countries, in refining a carbon trading market.

1 Introduction

With the rapid development of economic growth and industrialisation in the world, global energy consumption is increasing year by year (see Fig. 1). Natural gas, oil, and coal are the main energy resources with the largest consumption, accounting for approximately 85% of the total energy consumption (Azadeh & Tarverdian, 2007; Aydin et al., 2016). Consequently, it has triggered adverse effects on the global environment and climate (Say & Yücel, 2006). China’s total energy consumption increased monotonically during 2008–2018. The consumption of oil, natural gas, and coal is gradually decreasing, and renewables and hydroelectricity are gradually increasing, while the consumption of oil, natural gas, and coal remains prominent (see Fig. 2).

Fig. 1

Global energy consumption in 2008–2018 (Unit: Million tons) (BP, 2019)

Fig. 2

China’s energy consumption in 2008–2019 (Unit: Million tons) (BP, 2019)

The international community has reached a consensus on the Copenhagen Accord that ‘climate change is one of the biggest changes of our times’ (Xu et al. 2021a, b). However, the massive emissions of carbon dioxide (CO₂) are the key driving force of the global warming (Bai et al. 2020), which will not only seriously affect socio-economic development, such as industrial production (Dell et al. 2012), agriculture (Chen & Gong 2021), immigration (Feng et al. 2010), and populations (Rehman et al. 2021), but also deteriorate ecological environment, thereby curbing the regional inclusive development (Xu et al. 2021a, b).

According to BP¹ (2019), China’s CO₂ emissions amounted to 9428.7 million tons in 2018, which was more than the sum of the European Union and the USA, and which accounted for 27.8% of the global total. To shoulder its responsibility in the process of global CO₂ emission mitigation, China promised to reduce its carbon emissions per unit of GDP by 60–65% by 2030 with respect to 2005 levels at the United Nations Climate Change Conference Paris 2015 and increase the share of non-fossil fuels in primary energy consumption to about 15% by 2020 (Dong et al. 2013).

The Chinese government has attached great importance to act on environmental issues by successively promulgating a series of environmental protection regulations. China has also introduced a series of laws and policies to prevent environmental and ecological degradation in its initial exploration since 1990, such as “The Laws of People’s Republic of China on the Prevention and Control of Atmospheric Pollution” (Feng et al. 2020). The implementation of the “Two-Control-Zone” policy enacted by the State Council in 1998 shows that the central government began to adopt a more strict environmental regulation policy (Sun et al. 2019).

Unfortunately, the aforementioned policies were mainly common-and-control regulations, and they were not strong enough for China to effectively achieve carbon emissions reduction commitment (Dong et al. 2017). This is because the regulated firms were forced by these common-and-control environmental regulations to either accept compliance cost or shut down stiffly, and thus suppressed their motivation eventually (Feng et al. 2019). In 2003, the launching of the “Regulations on the Collection and Use of Sewage Charges” in China marked the transformation of environmental policy from the common-and-control type to a market-oriented one (Tang et al. 2020b).

Fortunately, China’s carbon trading market is considered as the most remarkable achievement in achieving targets of energy conservation and CO₂ emissions reduction (Jiang et al. 2016; Gao et al. 2020). The “Decision of the State Council on Accelerating the Foresting and Development of strategic Emerging Industries²” released in October 2010 was the first official document to announce carbon trading. Subsequently, the National 12th Five-Year Plan further addressed the aforementioned issues. At the end of 2011, China issued a “The Work Plan for Greenhouse Gas Emission Control during the 12th Five-Year Plan Period³” aimed at exploring the establishment of China’s carbon trading market. Furthermore, on October 29, 2011, the NDRC released a “Notice on Carrying out the Carbon Emissions Rights Trading Pilot Work”. At the same time, this notice has approved seven carbon trading pilots: Beijing, Tianjin, Shanghai, Chongqing, Guangdong, Hubei, and Shenzhen.⁴

As an market incentive enabler, ETS plays a crucial role in realising cleaner production and sustainable development (Tang et al. 2020b). Coase’s property rights theory provides a solid theoretical support for Dales (1968) to propose the notion of emissions trading by defining the property rights of environmental resources in the case of environmental resources to realise the environmental target configured by the government. The essence of the ETS is that the environmental capacity is scarce resource, and emission qualification can be equalised under the absolute control and efficient allocation achieved by market means (Lyu et al. 2020). Or it can be seen as a tradable quota mechanism. In 1990, the “Clean Air Act Amendment” approved by the US Senate was the first emission trading program (Schmalensee & Stavins 2013). In 1997, the Kyoto protocol applied emission trading to the treatment of CO₂ emissions by imposing “quantitative emission reduction targets” for both developed and developing countries (Xuan et al. 2020). Subsequently, the EU constructed an ETS to aid its members to fulfil their emission reduction commitments, which was the first large-scale international emission trading system in the field of the environment (Skjærseth & Wettestad 2008).

Nevertheless, considering the superiority of cost saving, flexibility, and effectiveness, ETS, a market-oriented environmental regulation instrument, has arisen scholars’ interest in the field of environmental economics (Zhang et al. 2020a, b, c; Ma & Zhang 2019). Being different from the price instrument such as fiscal subsidy and carbon tax which only impose a bonus or cost on emissions, ETS operates through a set of policies and rules for various parities such as the government, third parity, firms, and markets (Yeo & Coleman 2019). Unlike the mandatory administrative environmental regulations, ETS acts on the emitters in a relatively roundabout way through a sound market mechanism (Du et al. 2020).

For simplicity, ETS is a vital mechanism to achieve environmental protection through the market economy. Based on the total CO₂ emission of a country, it permits firms to trade their carbon emissions obligations in the carbon emission trading market and thus progressively realises the specified carbon emission reduction targets (Zhao et al. 2018; Song et al. 2018). Given the aforementioned advantages, ETS has been given expectations of promoting the development of energy conservation and emission reduction, strengthening inclusive development of economic society (Du et al. 2018), and stimulating ecological and environmental governance. These expectations are consistent with the requirement of low-carbon economy⁵(LE), thus giving us an incentive to examine the effects of ETS on low-carbon economy efficiency (LEE). This is because the ETS is very important for China to reduce carbon emission and transit to a LE (Wu et al. 2019).

Not surprisingly, there is an abundant stream of studies focusing on such market-oriented environmental regulation tool based on different research themes, especially for emissions mitigation. The existing studies asserted that EU-ETS pilot is a successful trajectory after assessing its environmental effect. For example, employing a dynamic panel data model, Anderson & Di Maria (2010) demonstrated that the EU-ETS lowered the carbon emissions of the manufacturing industry. Besides, compared to those not participating in the ETS, emitters admitted to the market exert a greater potential for emission reduction. Schleich & Betz (2004) revealed that the EU-ETS is conducive to reducing emissions. As for China’s ETS practice, scholars addressed that the effect of China’s ETS has not yet made a consistent agreement. For example, using the panel data involved 37 industrial sub-sectors in each of China’s 26 provinces spanning from 2005 to 2015, Zhang et al. (2019) explored the influence of China’s ETS at the initial stage (2013–2015) by performing a DID model and PSM technique. The results demonstrate that China’s ETS pilot policy did reduce CO₂ emissions but failed to reduce carbon emission intensity. Similarly, taking Hubei pilot as a research case, Wen et al. (2020) concluded that the effect of China’s ETS on industrial CO₂ emissions, GDP, energy consumption intensity as well as carbon emission intensity is negligible. Shin (2013) proposed that China’s pilot project especially the sulphur dioxide (SO₂) has never been institutionalised in any of China’s provinces; thus, the system is a failure in China. Moreover, the implementation of environmental protection in most developing economies is endogenous (Wang & Wheeler 2000). Adopting some advanced techniques, scholars also discussed the efficiency of China’s carbon trading market. For example, based on the efficient market hypothesis, Wang et al. (2022) asserted that carbon prices follow mean reversion process by adopting the Sequential Panel Selection Method, designating that the inefficiency in Chinese carbon trading market (excluding Shanghai market). Employing GARCH (1, 1)-M model with state space time-varying parameter, modified Amihud illiquidity ratio, fixed effect variable intercept panel regression model, and panel impulse response analysis, Wu & Qin (2021) found that Shenzhen pilot has the highest market efficiency, followed by Beijing, Shanghai, Guangdong, while Hubei has the lowest efficiency.

While others held the opposite viewpoints with respect to the effects of China’s ETS, for example, taking Guangdong Province as an example, Cheng et al. (2016) constructed a regional CGE model with seven scenarios and demonstrated that provincial energy and carbon intensity can be achieved in the assumed carbon mitigation commitments with carbon cap, ETS, and clean energy development polices.

Chang et al. (2018) adopted a Generalised Autoregressive Conditional Heteroskedasticity model and proved that the launched China’s ETS market has significantly reduced CO₂ emissions. Wang et al. (2021) demonstrated that the implementation of ETS has significantly promoted the high-quality development of manufacturing industry⁶ in China. Still, the “Ecological Poverty Alleviation Work Plan” enacted by the Chinese government has arisen an interesting question that whether ETS aids China to combat poverty⁷? To this end, Zhang & Zhang (2020) pointed out that the ETS pilot policy has led to an increase in rural residential income and employment. Adopting the panel data of China’s A-share listed enterprises, Hu et al.(2020a, b) investigated the effect of China’s ETS on quantity and quality of innovation. The results show that ETS has a significant positive effect on the quantity and quality of firm’s innovation. However, the empirical results of Hu et al. (2020a, b) showed that ETS pilot policy has decreased energy consumption of the regulated industries in polit regions by 22.8% and the CO₂ emissions by 15.5%. Similarly, using a DID model, Zhang et al. (2020a, b, c) concluded that China’s ETS adopted in pilot regions has reduced carbon emissions by approximately 16.2% during 2004–2015.

Apart from the concerns in terms of carbon emissions, some studies also discussed the influence of ETS from an economic efficiency perspective. For example, aiming to verify whether China’s ETS pilot policy brings economic and environmental dividends, Dong et al. (2019) found that ETS did not generate Porter effect in the short term, in contrast, while it can significantly promote sustainable economic and environmental dividends in the long run, thereby producing Porter effect. Drawing on the panel data of A-share listed enterprises, Chen et al. (2021a, b, c) pointed out that ETS has significantly promoted TFP improvement (which was measured by OP and LP methods) of local enterprises. Based on provincial panel data and industrial enterprise panel data in China during 1998–2017, Zhang et al. (2021) found that ETS significantly contributed to green development efficiency and regional carbon equality. Further mechanism analysis shows that ETS significantly promoted regional carbon equality by improving green total factor productivity and reducing investments in the carbon-intensity industrial sectors in the pilot regions, thereby supporting the Porter hypothesis. In terms of the spatial spillover effects, ETS has generated a significant promoting effect on green innovation in pilot regions, but a significant inhibitory impact in the adjacent areas (Zhang et al., 2021).

However, whether and how China’s ETS pilot policy affects LEE remains in a black box,⁸ giving us an ideal quasi-natural experiment for investigating the ETS-LEE nexus by building a multi-stage DID model. Thus, a few points are devoured to be analysed further: First, current studies do not take the heterogeneity of the enablement time of the carbon trading market in different pilots into account to verify the effectiveness of ETS pilot policy in China. Second, China’s vastness determines remarkable differences among regions and cities, such as geographical locations, resource endowments, economic basis. The eastern China obtained the first-mover gains in economic development and therefore realised the importance of environmental regulation earlier, while the central and western areas still faced severe environment pollution in the process of economic model transformation and industrial re-articulation. Hence, the regional heterogeneous effects should be fully considered. Third, referring to Jia et al. (2021), the resource-dependent cities may emit more CO₂ as they are overdependent on resource exploitation and processing industries, thus facing a serious “carbon curse” (Friedrichs & Inderwildi, 2013). To this end, the heterogeneous effects at local (i.e. cities with different resource endowment) levels are also a good point for us to deal with.

Correspondingly, the objectives of this paper are threefold. First, to empirically examine the effect of China’s ETS on LEE by treating the enablement time of carbon trading market as a quasi-natural experiment based on prefecture-level cities.⁹ Second, to perform the spatial and non-spatial models to validate the potential spatial spillover effects. Third, to capture the potential spatial heterogeneity at the regional and local levels by applying estimations, thereby contributing to a theoretical basis and intellectual support for classified regulation based on local conditions. The reminder of this paper is structured as five parts; 1) a research methodology being used; 2) reports empirical results and conducts discussion; 3) conducts a spatial analysis; 4) conducts a heterogeneous analysis; 5) reports the research conclusions proposes policy implications.

2 Theoretical analysis

Excessive carbon emissions pollute the environment, resulting in negative externalities. Negative externalities can be handled by market transactions, according to Coase (1960), providing property rights are clearly stated. This provides the theoretical foundation for ETS. Dales (1968) goes on to say that defining pollution rights and making them marketable can help increase environmental pollution control efficiency. As a result, the ETS has become a key response to climate change as a market-based environmental regulation mechanism.

Environmental control based on the market is effective in reducing emissions and optimising the energy structure (Montgomery 1972). Improving green development efficiency entails pursuing a unified set of economic and environmental benefits, and it is supported as a way to increase environmental carrying capacity while also securing economic gains (Lin and Zhu 2019). First, assuming that enterprises make decisions based on profit maximisation, the ETS policy encourages companies to make optimal choice of their limited free carbon emission quotas to avoid extra expenses associated with excessive emissions (Xuan et al. 2020). As a result, China’s ETS policy can not only encourage polluting enterprises to improve their production technology, adjust product structure, and gradually adopt cleaner production technology, but also contribute to the optimisation and upgrading of polluting industries, resulting in improved environmental performance. Second, when the marginal cost of emission mitigation is lower than the carbon price, businesses are more likely to enhance emission mitigation in order to profit from the excess quota (Shakil et al. 2019).

ETS can incentivise businesses to cut emissions through market transactions in this way, benefitting the regional ecological environment. As a result, this research suggests that China's ETS policy can boost green development efficiency. Furthermore, because variations in the contribution rate of GDP and carbon sequestration are generally minor under the definition of regional carbon equality, the measurement of interprovincial carbon equality is mostly based on carbon emissions. First, an ETS drives businesses to innovate in green technology and build high-tech industries with clean advantages, whereas polluting businesses that refuse to update will eventually be phased out by the market (Calel and Dechezlepretre 2016). This will minimise resource use and traditional energy reliance, lowering pollution emissions and advancing regional carbon equity. Second, the ETS creates unseen green barriers that prevent polluting companies from expanding. The installation of an ETS raises sunk costs and production expenses for polluting businesses, limiting their entry and expansion. Third, regional disparities in environmental legislation may cause polluting businesses to relocate from pilot to non-pilot areas, lowering emissions in pilot areas and achieving “regional carbon equality,” and contributing to efficiency ultimately.

What is more, emissions limits in ETS trials may encourage regulated parties to adopt low-carbon, energy-saving, and emission-reducing technologies and equipment. These advancements may not only help to reduce carbon emissions, but also pollutant emissions, resulting in improved industrial and regional emission performance. The pilot regions, on the other hand, are more conducive to low-energy-intensive and new, high-growth businesses when compared to non-pilot regions. They are thought to be the driving force behind economic growth and productivity, as they help to decouple carbon emissions from traditional economic development, resulting in increased regional GDP. Due to the restrictions on emissions, the ETS adds additional expenses to the use of fossil energy. Manufacturers, particularly those in the energy-intensive industrial sector, will be advised on how to adapt their production input elements including capital, energy, labour, and information. Green productivity will increase as a result of the optimization procedure. Heavy polluting factories, on the other hand, that are unable to adapt their production habits to tolerate the additional costs imposed by the ETS must relocate to unregulated areas or close. This would result in the movement of production input elements across different sectors in pilot regions, thereby aiding pilot cities to enhance their eco-efficiency. Figure 3 presents the theoretical framework.

Fig. 3

Theoretical framework,

3 Materials and methods

3.1 Selections of variables

3.1.1 Low-carbon eco-efficiency

We perform the Super-SBM model taking CO₂ emissions (or the so-called undesirable) into consideration based on the SBM DEA methodology. In particular, we assume that technologies with more desirable outputs and less CO₂ emissions relative to less production factor inputs are considered as efficient (Chang et al. 2013). In the meantime, we also postulate that the LEE production system has $n$ DMUs (decision-making unit), and each unit has three crucial factors: inputs, desirable output (i.e. GDP), and undesirable outputs. Each DMU produces ${w}_{1}$ desirable outputs and ${w}_{2}$ undesirable outputs. We then present the relative factors by three crucial factors: $x\in {T}^{m},{y}^{do}\in {T}^{{w}_{1}}$, and ${y}^{udo}\in {T}^{{w}_{2}}$, and the matrices $X, {Y}^{do}$, and ${Y}^{udo}$ can be specified as follows:

$$\begin{array}{c}X=\left[{x}_{1},{x}_{2},\dots ,{x}_{3}\right]\in {T}^{m\times n}\\ {Y}^{do}=\left[{Y}_{1}^{do},{Y}_{2}^{do},\dots ,{Y}_{3}^{do}\right]\in {T}^{{w}_{1}\times n}\\ {Y}^{udo}=\left[{Y}_{1}^{udo},{Y}_{2}^{udo},\dots ,{Y}_{3}^{udo}\right]\in {T}^{{w}_{2}\times n}\end{array}$$

(1)

The PPS (production possibility set) is denoted as follows:

$$P\left(x\right)=\left({y}^{do},{y}^{udo}\right)|x can produce \left({y}^{do},{y}^{udo}\right),x\ge X\lambda ,{y}^{do}\le {Y}^{do}\lambda ,{y}^{udo}\ge {Y}^{udo}\lambda ,\lambda \ge 0$$

(2)

where $\lambda$ means the non-negative intensity vector, suggesting that the above definition is satisfied with CRS (constant returns to scale) assumption.

Based on PPS, and following Tone (2004), the SBM model dealing with undesirable outputs can be regulated as follows:

$$\begin{array}{c}\rho =min\frac{1-\frac{1}{m}\sum_{i=1}^{m}\frac{{w}_{i}^{-}}{{x}_{i0}}}{1+\frac{1}{{w}_{1}+{w}_{2}}\left(\sum_{r=1}^{{w}_{1}}\frac{{w}_{r}^{do}}{{y}_{r0}^{do}}+\sum_{t=1}^{{w}_{2}}\frac{{w}_{t}^{udo}}{{y}_{t0}^{udo}}\right)}\\ \begin{array}{c}s.t. {x}_{0}=X\lambda +{w}^{-}\\ {y}_{0}^{do}={Y}^{do}\lambda -{w}^{do}\\ {y}_{0}^{udo}={Y}^{udo}\lambda +{w}^{udo}\end{array}\\ {w}^{-}\ge 0,{w}^{do}\ge 0,{w}^{udo}\ge 0,\lambda \ge 0\end{array}$$

(3)

where the vector ${w}_{r}^{do}$ represents the shortage of desirable outputs, and vectors ${w}^{-}$ and ${w}^{udo}$ denote the excesses of inputs and undesirable outputs, respectively, while subscript $o$ means a DMU whose LEE is being measured. The range of objective function $\rho$ is [0, 1]. For a certain DMU, if $\rho =1$, and ${w}^{-}={w}^{do}={w}^{udo}=0$, then the DMU is considered efficient. In contrast, if $\rho <0$, the DMU is inefficient, that is, both inputs and outputs should be improved further.

We can see that the values derived from Eq. (3) are between 0 and 1. To effectively rank the efficiency of each DMU, Tone (2002) designed a Super-SBM model. However, the undesirable outputs are not incorporated in Tone’s Super-SBM. We finally adopt a Super-SBM model with CO₂ emissions to assess the DUM’s efficiency.

Assume that the ${DMU}_{k}({x}_{k},{y}_{k}^{do},{y}_{k}^{udo})$ is SBM-efficient, the Super-SBM model with undesirable outputs is regulated as follows:

$$\begin{array}{c}{\rho }_{SS}=min\frac{1+\frac{1}{m}\sum_{i=1}^{m}\frac{{w}_{i}^{-}}{{x}_{ik}}}{1-\frac{1}{{w}_{1}+{w}_{2}}\left(\sum_{r=1}^{{w}_{1}}\frac{{w}_{r}^{do}}{{y}_{rk}^{do}}+\sum_{t=1}^{{w}_{2}}\frac{{w}_{t}^{udo}}{{y}_{tk}^{udo}}\right)}\\ \begin{array}{c}s.t. {x}_{i}^{k}\ge \sum_{j=1,j\ne k}^{n}{x}_{ij}{\lambda }_{j}-{w}^{-}\\ {y}_{rk}^{do}\le \sum_{j=1,j\ne k}^{n}{y}_{rj}^{do}{\lambda }_{j}+{y}_{r}^{do}\\ {y}_{tk}^{udo}\ge \sum_{j=1,j\ne k}^{n}{y}_{tj}^{udo}{\lambda }_{j}+{y}_{t}^{udo}\end{array}\\ \begin{array}{c}1-\frac{1}{{w}_{1}+{w}_{2}}\left(\sum_{r=1}^{{w}_{1}}\frac{{w}_{r}^{do}}{{y}_{rk}^{do}}+\sum_{t=1}^{{w}_{2}}\frac{{w}_{t}^{udo}}{{y}_{tk}^{udo}}\right)>0\\ \lambda >0,{w}^{-}>0,{w}^{+}>0\\ i=1, 2,\dots ,m;j=1, 2,\dots ,n\left(j\ne k\right), r=\mathrm{1,2},..,{w}_{1};t=\mathrm{1,2},\dots ,{w}_{2}\end{array}\end{array}$$

(4)

where ${\rho }_{SS}$ represents the objective function whose value can be more than one, while other information is consistent with Eq. (3). The non-radial and non-angle Super-SBM model addressing undesirable outputs has the following advantages. First, it can rank the DMU’s efficiency score (because all SBM-efficient DMUs do not equal to one simultaneously). Second, it can address the slackness issues of inputs and outputs caused by angular and radial choices (Song et al. 2012). Third, it can solve the problems of input excess and output shortfall in efficiency estimations, which is particularly suitable for addressing undesirable outputs (Zhou et al. 2006).

Correspondingly, the Super-SBM model with undesirable output discussed above is applied to estimate LEE of China’s 283 cities from 2006 to 2017. More specifically, total population (P), city-level capital stock (K) represented by net value of fixed assets of industry (Zhu et al. 2018; Feng et al. 2018a), total energy consumption (E) are treated as input factors. The real gross domestic product (GDP) (Y) and CO₂ emissions¹⁰ (Chen & Jin 2020; Chen et al., 2021a, b, c) are used as desirable output and undesirable output, respectively, among which K is adjusted by the price index of the fixed assets to 2006 constant prices. Y is adjusted by GDP deflator to 2006 constant prices. It should be noted that there is no corresponding price index at the prefecture-city level; thus, the provincial price index of province where the city belongs will be used (Yang et al. 2021a, b). Besides, missing data for a few cities are supplemented by exponential translation and moving average.

3.1.2 Key explanatory variable

Different from the existing literature, this paper treats the enablement time of the carbon trading market as a quasi-natural experiment to build a multi-stage DID model. Specifically, two dummy variables are selected incorporating the event dummy variable $\left(\mathrm{Treat}\right)$ and time dummy variable $\left(\mathrm{Post}\right)$. Particularly, the $\mathrm{Treat}$ is assigned to 1 if the region belongs to the pilot, such as Beijing (2013), Shenzhen (2013), Tianjin (2013), Shanghai (2013), Guangdong (2013), Hubei (2014), Chongqing (2014), and Fujian (2016),¹¹ otherwise 0. The $\mathrm{Post}$ is assigned to 1 in the corresponding years, and subsequent years, otherwise 0. Thus, the interaction term $\mathrm{Treat}\times \mathrm{Post}$ regulates whether or not a specific city is affected by the ETS in a certain year, which is exactly what we pay attention to.

3.1.3 Control variables

To accommodate the heterogeneity of each city, this paper selected several interference variables following the existing literature: (1) economic structure (ECS), which is regulated by the ratio of total retail sales of consumer goods to GDP; (2) marketisation index (MI), which is denoted by marketisation index; (3) employment structure (ES), which is represented by the ratio of number of industrial and commercial registered employed persons in private enterprises and self-employed individuals in urban areas to total employed persons; (4) technological innovation (TI), which is given by the number of patents granted in the natural logarithm; (5) foreign direct investment¹² (FDI), which was measured by the total amount of foreign investment actually utilised to GDP; (6) financial deepening (FD), which is represented by the ratio of total balance of deposits and loans to GDP (Xiong et al. 2017); (7) clean energy (CE), which is calculated by the ratio of hydroelectricity to GDP. Moreover, the CO₂ emission reduction targets stipulated by the 11th, 12^th, and 13th National Five-Year Plans are also controlled, which are regulated by the multiplication between the specific targets and years in corresponding cities, denoted as ${\mathrm{Target}}_{1}$, ${\mathrm{Target}}_{2}$, and ${\mathrm{Target}}_{3}$. Table 1 reports the descriptive statistics.

Table 1 Descriptive statistics

3.2 Data sources

After the exclusion of cities with administrative modifications and missing data, a balance panel data with a total number of 283 prefecture-level and above cities were adopted as a sample, yielding 3396 observations for each variable. The data were collected from the China City Statistical Yearbook (2007 ~ 2018), China Urban Construction Statistical Yearbook (2007 ~ 2018), China Energy Statistical Yearbook (2007 ~ 2018), China Industry Statistical Yearbook (2007 ~ 2018), China Electric Power Statistical Yearbook (2007 ~ 2018), National Bureau of Statistics of China and Provincial Statistical Yearbook. Additionally, the carbon emission reduction target comes from 11th, 12^th, and 13th National Five-Year Plans (see http://www.gov.cn/).

3.3 Modelling specification

3.3.1 Benchmark regression

It is plausible to consider the public policy implementation as a quasi-experiment because its impacts on subject can be regarded as an exogenous “instrument”. DID proposed by Ashenfelter (1978) was used to capture the net effect of policy implementation by comparing the coefficient changes between the treatment and control groups before and after the policy implementation. Thus, it has been widely used to estimate the causal effects of specific policies (See Gu et al. 2021; Yang & Wang 2021; Chen et al. 2021a, b, c). The model used to verify the average treatment effect of ETS on LEE is specified as follows:

$${\mathrm{LEE}}_{\mathrm{it}}={\mathrm{\alpha }}_{0}+{\mathrm{\alpha }}_{1}{\mathrm{Treat}}_{\mathrm{it}}\times {\mathrm{Post}}_{\mathrm{it}}+{\mathrm{\alpha }}_{2}{\mathrm{Control}}_{\mathrm{it}}+{\upgamma }_{\mathrm{t}}+{\updelta }_{\mathrm{i}}+{\mathrm{city}}_{\mathrm{j}}\times {\mathrm{year}}_{\mathrm{t}}+{\upvarepsilon }_{\mathrm{it}}$$

(5)

where ${\mathrm{LEE}}_{\mathrm{it}}$ represents the low-carbon economy efficiency in city $\mathrm{i}$ at year $\mathrm{t}$. ${\mathrm{\alpha }}_{0}$ denotes the intercept; ${\mathrm{\alpha }}_{1}$ and ${\mathrm{\alpha }}_{2}$ are the regression coefficients. ${\mathrm{Treat}}_{\mathrm{i}}$ denotes the treated dummy variable, which equals to 1 if the city belongs to the treatment groups, otherwise 0. ${\mathrm{Post}}_{\mathrm{it}}$ regulates the time dummy variable, which equals to 1 after policy implementation, otherwise 0. ${\mathrm{Treat}}_{\mathrm{i}}\times {\mathrm{Post}}_{\mathrm{it}}$ represents the dynamic dummy variables. ${\mathrm{Control}}_{\mathrm{it}}$ denotes the selected control variables. ${\upgamma }_{\mathrm{t}}$ denotes the time fixed effect; ${\updelta }_{\mathrm{i}}$ denotes the city fixed effect, while ${\mathrm{city}}_{\mathrm{j}}\times {\mathrm{year}}_{\mathrm{t}}$ denotes the city-year fixed effect; ${\upvarepsilon }_{\mathrm{it}}$ is the error term. To avoid potential serial correlation and heteroskedasticity, we cluster the standard errors at the provincial level.

3.3.2 Parallel trend detection

The precondition for implementing the DID approach is that if the treatment group is not shocked by the policy intervention, the tendency of its results should be consistent with that of the control group (it may be the latter of time effects are controlled for), which is known as the so-called parallel trend assumption (Beck et al. 2010). Therefore, to meet the parallel trends assumption, it is necessary to ensure that the LEE of the treatment group and of the control group maintain the same trends before the policy implementation. Thus, the event study model (Jacobson et al. 1993) for validating the precondition is as follows:

$$\begin{array}{c}\begin{array}{c}{\mathrm{LEE}}_{\mathrm{it}}={\mathrm{\alpha }}_{0}+\sum_{\mathrm{t}=-6}^{-1}{\mathrm{\alpha }}_{\mathrm{pre}\_j}{\mathrm{Treat}}_{\mathrm{it}}\times pre\_j+{\mathrm{\alpha }}_{\mathrm{current}}{\mathrm{Treat}}_{\mathrm{it}}\times \mathrm{current}\\ +\sum_{\mathrm{t}=1}^{4}{\mathrm{\alpha }}_{\mathrm{pre}\_l}{\mathrm{Treat}}_{\mathrm{it}}\times \mathrm{Post}\_l+{\mathrm{\alpha }}_{2}{\mathrm{Control}}_{\mathrm{it}}+{\upgamma }_{\mathrm{t}}+{\updelta }_{\mathrm{i}}+{\mathrm{city}}_{\mathrm{j}}\times {\mathrm{year}}_{\mathrm{t}}+{\upvarepsilon }_{\mathrm{it}}\end{array}\end{array}$$

(6)

where variables $pre\_j$, $\mathrm{current}$ and $\mathrm{post}\_l$ are the time dummy variables.¹³ For instance, because 2006 is the first six years before policy implementation, the variable $\mathrm{pre}\_6=1$, while for other years, $\mathrm{pre}\_6=0$; because 2013 is the year of policy implementation, thus, $\mathrm{current}=1$, while it is assigned to 0 for other years; because 2014 is the year after policy implementation, $\mathrm{post}\_1=1$, while $\mathrm{post}\_1=0$ for other years. ${\mathrm{\alpha }}_{\mathrm{pre}\_j}$, ${\mathrm{\alpha }}_{\mathrm{current}},$ and ${\mathrm{\alpha }}_{\mathrm{pre}\_l}$ are the parameters being estimated, while the other information is consistent with Eq. (5). If the pilot regions and the non-pilot regions have common time trends during the period of 2006 ~ 2017, the coefficient of ${\mathrm{Treat}}_{\mathrm{it}}\times \mathrm{pre}\_j$ should be statistically insignificant.

3.3.3 Validation of spatial spillover effect

Following Chagas et al. (2016), we validate the potential spatial spillover effect by constructing a spatial difference-in-differences (SDID) model:

$$\begin{array}{c}\begin{array}{c}{\mathrm{LEE}}_{\mathrm{it}}={\upbeta }_{0}+{\upbeta }_{1}{{\mathrm{Treat}}_{\mathrm{it}}\times \mathrm{Post}}_{\mathrm{it}}+{\sum }_{\upkappa -1}^{\upkappa }{\upbeta }_{\upkappa }{\mathrm{Control}}_{\mathrm{it},\upkappa }+{\upgamma }_{1}{\mathrm{W}}_{\mathrm{T},\mathrm{T}}{\mathrm{D}}_{\mathrm{it}}+{{\upgamma }_{2}\mathrm{W}}_{\mathrm{NT},\mathrm{T}}{\mathrm{D}}_{\mathrm{it}}+\\ {\sum }_{\upkappa -1}^{\upkappa }{\upbeta }_{\upkappa +2}\times {\mathrm{W}}_{\mathrm{ij}}\times {\mathrm{Control}}_{\mathrm{it},\upkappa }+{\upgamma }_{\mathrm{t}}+{\updelta }_{\mathrm{i}}+{\mathrm{city}}_{\mathrm{j}}\times {\mathrm{year}}_{\mathrm{t}}+{\upvarepsilon }_{\mathrm{it}}\end{array}\end{array}$$

(7)

where ${\mathrm{W}}_{\mathrm{T},\mathrm{T}}{\mathrm{D}}_{\mathrm{it}}$ represents the spatial spillover effects on treated cities, ${\upgamma }_{1}$ is the coefficient of ${\mathrm{W}}_{\mathrm{T},\mathrm{T}}{\mathrm{D}}_{\mathrm{it}}$; ${\mathrm{W}}_{\mathrm{NT},\mathrm{T}}{\mathrm{D}}_{\mathrm{it}}$ represents the spatial spillover effects on the untreated cities surrounding the treated cities, and ${\upgamma }_{2}$ is the coefficient of ${\mathrm{W}}_{\mathrm{NT},\mathrm{T}}{\mathrm{D}}_{\mathrm{it}}$. ${\mathrm{W}}_{\mathrm{ij}}$ denotes the spatial weight matrix. ${\upbeta }_{\upkappa +2}$ is the coefficients of ${\mathrm{Control}}_{\mathrm{it},\upkappa }$, while the meanings of the other parameters are consistent with Eq. (5).

An economic–geographical spatial weight matrix is constructed by this paper based on the gravitational model by taking economic and geographical elements into consideration (Zhang et al. 2018):

$${\mathrm{W}}_{\mathrm{ij}}=\left\{\begin{array}{c}\begin{array}{cc}\frac{{\mathrm{pgdp}}_{\mathrm{i}}*{\mathrm{pgdp}}_{\mathrm{j}}}{{\mathrm{d}}_{\mathrm{ij}}^{2}}& \mathrm{i}\ne \mathrm{j}\end{array}\\ \begin{array}{cc} 0& \end{array}i=j\end{array}\right.$$

(8)

where ${\mathrm{pgdp}}_{\mathrm{i}}$ and ${\mathrm{pgdp}}_{\mathrm{j}}$ represent the per capital GDPs of cities $\mathrm{i}$ and $\mathrm{j}$, respectively; ${\mathrm{d}}_{\mathrm{ij}}$ is the geographical distance between cities $\mathrm{i}$ and $\mathrm{j}$.

4 Empirical findings

4.1 Spatial distribution of LEE

Considering the large sample size, we visualise LEE scores in China’s 283 prefecture-level cities in the selected years (i.e. 2006, 2010, 2014, and 2017), as displayed in Fig. 4. On the whole, the average city-level LEE presents an N-shaped trend during 2006–2017. China has been currently experiencing a crucial period of economic transformation, as known the new normal stage, since 2014.¹⁴ The Chinese economic growth momentum with a slower growth rate¹⁵ is the fundamental characteristic to portray the new normal stage (Dong et al. 2018). As a result, since 2006, the LEE has shown a substantial increasing trend. Following that, it reached its maximum in 2011, with an average value of 0.2557, and reached its lowest point in 2015, after which it has showed an exponential increase. It should be noted that the past remarkable achievements of China’s economy made are at heavy expense, suggesting but only limited to severe overcapacity, low energy efficiency and economic structure imbalance, and massive resource wasting, while in the new normal stage, the government will treat the high-quality development as a core guiding ideology to promote the sustainable development of China’s economy by strongly carrying out supply-side structural reform. Therefore, economic structure will be adjusted and re-articulated, and overcapacity issues will be overcomed progressively, thereby contributing to LEE eventually. Additionally, the LEE score of Shanghai, Beijing, and Shenzhen is significantly higher than that of other cities, among which Shenzhen has the largest level of LEE, with the average value of 1.356. In contrast, Dingxi, Lijiang, Xinzhou ranked in the bottom. In the meantime, all cities mentioned above come from Western China. In conclusion, the results show that the LEE performance of the cities in the central and western regions is in a backward position compared with the eastern cities, and there is still greater room for LEE improvement in China.

Fig. 4

Spatial distribution characteristics in the selected years

Based on the DID model, the net effect of China’s ETS pilot policy on city-level LEE is determined. First, the coefficient of $\mathrm{Treat}\times \mathrm{Post}$ is positive but insignificant without controlling for interference variables (see column 1 in Table 2). Second, the coefficient of $\mathrm{Treat}\times \mathrm{Post}$ becomes statistically significant at a 1% significance level (see columns 2–4) after considering interference variables and year and city fixed effects. Third, the coefficient of $\mathrm{Treat}\times \mathrm{Post}$ increases monotonically after controlling the city-specific time trends, while the corresponding coefficient is still significant positive at a 1% significance level, designating that the ETS pilot policy significantly improved the LEE and the LEE in ETS pilot region will increase by approximately 4.3% compared with untreated cities.

Table 2 Results for baseline regression

From the estimation results, one can infer that China’s ETS pilot is undergoing a greener transformation to reduce pollution emissions while enhancing economic efficiency. When taking the common origin of fossil fuels into consideration, the synergistic effect of energy conservation and pollution mitigation induced also sustains LEE improvement (Ohno et al. 2021). Our findings are consistent with the conclusions of Zhu et al. (2020) and Yang et al. (2021a, b). As a matter of fact, the improvement of LEE is determined by several factors, such as capital investment, industrial structure re-articulation, human capital. More investment inputs in those low-carbon and energy-efficient technologies could contribute to economic efficiency improvement. In the meantime, some energy-intensive industrial sectors with outdated production techniques should be phased out. Thus, the government environmental regulation policy could enhance LEE, while the relevant policy should be designed and adjusted in practice.

4.2 Robustness check

4.2.1 Validity test: Parallel trend

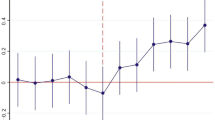
Using Eq. (6), we first conduct a parallel trend estimation. As depicted in Fig. 5, the results show the common trend for LEE from 2006 to 2017. The y-axis captures the influential coefficient of ETS on LEE, and x-axis represents the year. Before the policy is introduced, the estimated coefficients on the dummy variable denoting the policy’s implementation are insignificant in the former six years excluding the coefficient of $\mathrm{pre}\_1$. The possible explanation is that China in the 12th Five-Year Plan (2011–2015) has declared the carbon reduction targets.¹⁶ Subsequently, the pilot regions such as Shenzhen, Beijing, Shanghai took the lead in reducing CO₂ emissions, accelerating low-carbon economic transformation, and sustaining LEE improvement. Thus, the corresponding coefficient is statistically significant, which is caused by the “anticipation effect¹⁷” (Diao et al., 2017). Therefore, herein the parallel trend assumption is supported.

Fig. 5

Parallel trend in LEE before and after policy implementation

4.2.2 Placebo test

We then carry out a placebo test to eliminate the potential interference caused by other factors in the selection of pilot regions by randomly selecting a set of dummy trail groups from all samples. Specifically, 2000 times of random sampling are implemented to conduct regression consistent with baseline regression in 283 prefecture-level cities, with 10 provinces randomly selecting as the treatment group, while the remaining 20 provinces taking as the control group. Figure 6 displays that all the absolute t-values of the sampling coefficients are less than 0.2 and the estimated coefficient (column 4 in Table 1) is distributed in the right tail. The placebo test results show that the influence of the unobserved factors on the estimated results is negligible.

Fig. 6

Placebo test

4.2.3 Transforming matching approach

The robustness tests are further carried out from three aspects. One is to change the radius value of radius matching in baseline regression, changing the radius from 0.05 to 0.01. Another is to change matching method, adopting the nearest neighbours matching approach (the matching ratio is 1:4). The last one is the kernel matching approach. However, no matter what matching method is applied, the results will not be varied significantly (Vandenberghe & Robin, 2004). Table 3 reports the results of radius matching, nearest neighbours matching, and kernel matching. As we can see, all coefficients are positively significant at a 1% significance level, implying that the selected matching methods exhibit high robustness. To ensure the robustness of the selected matching methods, we then examine whether there is a significant difference in the average value of each covariable between the treatment and control groups, as shown in Appendix D.

Table 3 The estimation results of three matching methods

4.2.4 Excluding the interference from other environmental policies

First, the Chinese government put forward SO₂ emission pilot trading program in 2007, covering 11 provincial areas, such as Tianjin, Hebei, Shanxi, Chongqing, Inner Mongolia, Zhenjiang, Jiangsu, Hubei, Hunan, Shaanxi, and Henan (Ye et al. 2020). Second, the “Air Pollution Prevention in Key Regions during the 12th Five-Year Plan” (see Sect. 2) released by the Chinese government in 2013 also outlined 13 key areas for the prevention and control of the air pollution (Miao et al. 2021). The above-mentioned relevant policies may have a certain effect on LEE improvement of the pilot and non-pilot regions, thus resulting in the biased estimation. Fortunately, Table 4 shows that the effects of ETS on LEE are all positive in statistics, implying that ETS has exerted a promoting effect on LEE and thus consolidating the benchmark regression results.

Table 4 Results of excluding other environmental policies

4.2.5 IV method

The core explanatory variable in Eq. (5) should satisfy strict exogeneity. If ETS cities are not randomly selected, then $Treat\times Post$ is endogenous, thus resuting in biased estimation. To deal with this problem, we choose an IV method to further check the feasibility of the benchmark regression results. More specifically, the IV in our paper is constructed with an interaction term between the number of newspaper types in a given city and a time dummy variable that is treated as 1 after ETS and 0 otherwise. A proper IV should meet two vital requirements: relevance and exogeneity. As for the relevance requirement, more newspaper in a city means higher levels of information flow in that city. Therefore, the more quickly public demands and news are disseminated, and the greater possibility that the city will positively react the environmental regulation information released by the government. As for the exogeneity requirement, the number of newspaper types is not directly related to the LEE improvement of that city.

Table 5 reports the IV-estimation results, as we can see that the estimated coefficient of Newspaper_Type_IV in column 1 of Table 5 is statistically positive. This suggests that if there are more newspaper types in a given city, the probability of that city becoming a ETS city is higher, thus supporting that Newspaper_Type_IV meets the relevance requirement. The coefficient of $Treat\times Post$ in column 2 is significantly positive, which is consistent with the previous findings. To sum up, even considering the endogeneity issue of the core explanatory variable, ETS pilot policy still significantly contributes to LEE improvement, thus highlighting the robustness of the estimated results.

Table 5 Results of IV method

4.3 Results of spatial spillover effects

Since herein the SDID model is nested by the spatial econometric model, the prerequisite for applying it is to meet the condition of spatial autocorrelation. Thus, we conduct both global and local spatial autocorrelation tests for LEE. If, Moran’s I > 0 suggesting that there will be the positive spatial correlation. If, Moran’s I < 0 suggesting that there will be the negative spatial correlation. Table 6 shows that all Moran’s indexes are significantly positive at a 1% significance level. Therefore, the application of the SDID model is reasonable.

Table 6 Global Moran’s index of LEE over years

We further draw the scatter plot of Moran’s indexes of LEE for the selected years, as shown in Fig. 7. The scatter points located in the first and third quadrants regulate the characteristics of high–high and low–low agglomerations of LEE, respectively, while the points distributed in the second and fourth quadrats regulate those of low–high and high–low agglomerations of LEE, respectively. Evidently, most cities are mainly distributed in the first and third quadrants, designating a significant positive spatial autocorrelation for LEE among cities. That is, cities with higher LEE are spatially adjacent to each other, while cities with lower LEE tend to be concentrated.

Fig. 7

Scatter plots of local Moran indexes of LEE in China’s cities

By comparison, we report economic weight and first-order adjacent weight matrices simultaneously, as shown in Table 7. With the consideration of spatial spillover effect, the estimated coefficients of $\mathrm{Treat}\times \mathrm{Post}$ in columns 1 and 2 are statistically positive at a 1% significance level. It can be seen that the magnitude of core explanatory variable is greater under the economic–geographical weight matrix. By inspection, only the coefficient of ${W}_{T,T}D$ and ${W}_{NT,T}D$ is statistically positive under the economic–geographical weight matrix, implying that the spatial spillover effects of ETS on LEE in China are valid, while the spatial spillover effect of ETS pilot policy on the treated cities is greater than that effect of the untreated cities neighbouring the treated cities. This is because that compared to the ETS policy implemented in developed countries, the implementation of ETS pilot policy in China is still in its infancy, and both market liquidity and market maturity are low. Therefore, it is necessary for local government in polit regions to vigorously refine and carry out such a market-based environmental regulation tool, as well as give fully play to the decisive role of the ETS, so as to strengthen its spillover effects, thereby contributing to LEE.

Table 7 The estimation results of the SDID model

Logically, the spatial correlations of variables will decrease progressively as the geographical locations between cities increase, and therefore, the significant spatial spillover effects of ETS on LEE may exist only in a certain spatial range. Thus, to capture the spatial attenuation boundary, we then construct a distance threshold for the spatial weight matrix. The initial threshold value ${d}_{th}=$ 0 km and gradually increase the step size by 200 km until ${d}_{th}=$ 1800 km. As shown in Fig. 8, the spatial spillover effects of ETS on LEE present an inverted “V-shaped” trend over 0 km to 1800 km, which are consistent with our expectations: the spillover effects diminish with distance. In detail, the changes in the spatial spillovers of ETS on LEE can be divided into two stages. In the first stage, when ${d}_{th}<600$ km, ETS has exerted a significant promoting effect on LEE in neighbouring cities. In particular, the coefficient increases dramatically between 0 and 600 km. We hold that under the fixed carbon trading quota, firms who first adopt energy-intensive production techniques and conduct a cleaner production will receive the economic gains by trading their extra carbon emission quotas. Subsequently, the “demonstrating effect” of reducing pollution emissions generated by the treated cities could attract neighbouring cities to imitate and set up their own carbon trading market. In the second stage, the spillover effects show a significant downward trend (albeit gradually increasing and peaking at 1400 km). The possible explanation is that the implementation of China’s ETS pilot policy spills over the walls of local units to surrounding areas and is itself a crucial driver of efficiency enhancement.¹⁸

Fig. 8

Spatial attenuation boundary of ETS’s pilot policy

4.4 Heterogeneity analysis

4.4.1 Regional heterogeneity analysis

Based on the classification standard stipulated by the National Bureau of Statistics of China (NBSC), this paper divided research sample into three major economic zones (i.e. eastern, central, and western regions) and conducted the spatial and non-spatial estimations using Eq. (1) and Eq. (3), as shown in Table 8. The results show that all the coefficients of $\mathrm{Treat}\times \mathrm{Post}$ are positive in columns 1–6, while only the coefficients in columns 1, 3, and 4 are statistically significant, suggesting that ETS has effectively contributed to LEE in eastern region, in the western region without consideration of spatial spillover effect. The other insignificant coefficients of $\mathrm{Treat}\times \mathrm{Post}$ (i.e. in the western region with the consideration of spatial spillover effect, in the central region with and without consideration of spatial spillover effect) can also demonstrate the weak promoting effect of ETS on LEE in China at the regional level to some extent. Moreover, all the spatial coefficients of ${W}_{T,T}D$ are not significant, indicating that China’s ETS has failed to directly improve LEE in the treated groups at the regional level. Concerning the spatial coefficients of ${W}_{NT,T}D$, the coefficients in columns 4 and 6 are insignificant in statistic, but the coefficient in column 5 is significantly positive at a 5% significance level, designating that the positive spatial spillover effects of ETS on the LEE of the untreated cities surrounding the treated cities only can be captured in the central region under the economic–geographical spatial weight matrix. Overall, the spatial spillover effect of China’s ETS on LEE at the regional level is relatively poor, especially in the eastern China. Besides, Appendix D reports the influential degree of ETS on LEE in the pilots.

Table 8 The estimation results of regional heterogeneity

4.4.2 Heterogeneous analysis for resource-based and non-resource-based cities

To capture the potential heterogeneous effect of ETS on LEE for cities with different resource features, this paper divided the whole sample into two groups, i.e. resource-based, and non-resource-based cities following the “Notice on Promoting the Sustainable Development of Resource-dependent Cities (2013–2020)” issued by the State Council in 2013. Table 9 reports the empirical results estimated based on the resource and non-resource-based cites. Evidently, the coefficients of $\mathrm{Treat}\times \mathrm{Post}$ are all significantly positive, and the magnitude of the coefficients in columns (3) & (4) increases monotonically with the consideration of spatial spillover effects, meaning that ETS could help resource-based and non-resource-based cities to achieve CO₂ mitigation and develop a LE. The coefficient of ${W}_{T,T}D$ in column (2) is significantly positive at a 1% significance level, suggesting that ETS has directly contributed to the LEE of the resource-based cities in the treated samples. However, the spatial spillover effects of ETS on the LEE of the untreated samples neighbouring treated samples are not evident.

Table 9 The estimation results for the resource and non-resource-based cities

Why ETS pilot policy is beneficial for enhancing LEE in both resource-based and non-resource-based cities? First, resource-based cities mainly are developed and formed by processing and exploiting locally abundant resources (Kim & Lin, 2017). Over the past forty years, China’s resource-based cities have made substantial contributions to sustain national economic growth by providing a wide range of raw materials to the production process. Undoubtedly, long-term extensive development model has inevitably triggered a series of issues, such as increased unemployment, a gradual exhaustion of natural resources, and unbalanced economic structure (He et al., 2017). Consequently, resourced-based cities have gradually lot their investment attractiveness and their competitiveness, which may impede economic development further (Liu et al., 2018). Second, the economic development of these resource-based cities is still restricted by the legacy of the planned economy in the form of the path dependency of the steel and iron industry (i.e. Anshan in Liaoning is dubbed the “capital of iron and steel”). In other words, we should expect these cities through the same lens as Guangdong, Beijing, Zhejiang, Jiangsu, and other developed cities in China. Last but not least, the implementation of ETS could force firms to re-articulate production layout and thus upgrade industrial structure, while the advancement of industrial structure could shift the production factors from low-productivity industrial sectors to those sectors with high-level productivity. Such economic transformation could improve production efficiency and reduce pollution emissions ultimately in resource-based cities. Importantly, with the gradual improvement market efficiency, such promoting effect will be definitely improved in those non-resource-based cities.

4.4.3 Heterogeneous analysis for cities with different growth types

Furthermore, the resource-based cities were then divided into four groups with respect to their development stages, i.e. growing type, mature type, recessionary, and regenerating type. As we can see in Table 10, all the coefficients of $\mathrm{Treat}\times \mathrm{Post}$ are positive, and the coefficients in columns (3), (4), (7), and (8) are statistically significant, indicating that ETS has effectively boosted LEE for cities with maturity type and regeneration type, while the corresponding promoting effect on the other types is relatively weak. Unfortunately, the spatial coefficients of ${\mathrm{W}}_{\mathrm{T},\mathrm{T}}\mathrm{D}$ and ${\mathrm{W}}_{\mathrm{NT},\mathrm{T}}\mathrm{D}$ are insignificant, and thus the spatial spillover effects of ETS on LEE improvement are not significant across four types of cities.

Table 10 The estimation results considering cities with different four growth types

Resource-based cities refer to those whose leading industries include the processing and exploitation of natural resources, such as forests, fossil fuel, and materials.¹⁹ Resource-intensive industries are the dominating component of their economic structure (Li & Dewan, 2017), while the heavy resource dependence of resource-based cities would cause a large demand for fossil fuel, a massive quantity of CO₂ emissions, and a series of socio-economic issues, such as a lack of technological innovation, a high unemployment rate, and a monolithic industrial structure (Li et al., 2013; Shao & Qi, 2009). This is because over-dependence on resource-based industries in local economy could produce a crowding-out effect on the important economic factors (i.e. human capital) (Shao et al., 2020), thus triggering “resource curse” (Zhang et al., 2009).

While technological innovation plays a crucial in such process, on the one hand, under the ETS, environmental protection and energy saving enterprises can acquire economic gains by selling their surplus emission right in a paid way. On the other hand, ETS can provide insight information with enterprises on the technology market through the resource re-articulation effect, thereby reducing the search cost of the technology market and improving technological capability simultaneously. Moreover, the pollution control and production cost of environmental polluters will increase under the constraint of limited quota, and enterprises that aim to maximise their profits will be forced to improve their production equipment through vigorously conducting R&D activities (Yu et al., 2020).

As a typical environmental regulation deployed to control carbon emissions through market means, ETS has promoting effect on cities with different development stages, while the effects on growth type and recession type are negligible. Given this, resource-based cities should vigorously advance their industrial structure, especially for cities with growth and recession types. Evidently, the enhancement of technological innovation driven by ETS is the internal force for industrial structure upgrading. More specifically, technological innovation could help enterprises re-articulate original industrial sectors and forming the new industrial sectors. At the same time, it also can accelerate the adjustment and transformation of industry from the labour-intensive to capital- and technological-intensive industries. Correspondingly, production factors (i.e. capital, labour) can be shifted from low-productivity to high-productivity sectors (Aghion; & Howitt, 1994).

5 Conclusions and policy recommendations

Special attention has been attached on the LE in the process of rapid urbanisation and industrialisation. ETS has been introduced in China for many years, and it is quite necessary and important to investigate the effects of ETS on LEE. Employing a panel data of the selected 283 prefecture-level cities in China, this paper treated the enablement time of carbon trading market as a quasi-natural experiment, adopted the no-spatial econometric model (i.e. DID and PSM-DID) and spatial econometric model (i.e. SDID), and comprehensively examined the effects of ETS on LEE based on different spatial scales (national, regional, and local). Firstly, spatial distribution characteristics show that the LEE performance in China is extremely uncoordinated. Shenzhen plays a leading role in the national LEE improvement, and the development status of eastern region is better than the central and western regions. Second, the robustness results yield that ETS has significantly aided China to mitigate CO₂ emissions and boosted LEE at the national level. Third, the potential spatial spillover effects of ETS’s polit policy under the economic–geographical weight matrix are significant, while the corresponding effect on the treated cities is greater than that effect of the untreated cities neighbouring the treated cities. Also, such spatial spillover effects exist significant spatial attenuation. In particularly, a radius of 600 km is the concentrated range of the spatial spillover effect, whereas the spatial attenuation boundary is at 1800 km, beyond which the effect is no longer statistically significant. Fourth, as for the regional heterogeneity, ETS has directly and significantly improved LEE in the eastern and western areas without consideration of spatial spillover effect, in the eastern region with the consideration of spatial spillover effect. Overall, the promoting effect of ETS on LEE in China’s central region is very weak. What is more, the spatial spillover effects of ETS on the LEE of the untreated cities surrounding the treated cities can be captured only in central China under the economic–geographical spatial weight matrix. Fifth, no matter considering and non-considering the spatial spillover effect, ETS has directly improved LEE in the resource and non-resource-based cities. Additionally, the results show that ETS only has significantly promoting effects on cities with maturity type and regeneration type. Last but not least, the spatial spillover effects of ETS on LEE are quite poor in four kinds of cities.

Based on the empirical findings, several policy implications can be derived. First, to better develop a low-carbon economy and thus promote low-carbon efficiency, the role of ETS as a market-based tool to reduce CO₂ emissions and enhance eco-efficiency should be encouraged, and enhancement of the design of the ETS mechanism should be improved. Refining market-based environmental supervision and developing a low-carbon economy are not contradictory, but unified and compatible. Promoting the quality improvement of economic development and improving low-carbon efficiency requires stringent environmental regulations, while the implementation of environmental regulation (especially the market-based regulation, such as, ETS) will help to mitigate CO₂ emissions and improve LEE. Obviously, as an effective enabler, ETS is worthy of implementation throughout country further. Second, to reduce carbon leakage and avoid pollution heaven effect, a top-level design of a sound and unified national ETS market should be established as soon as possible. At the same time, to better play the spatial spillover effects of ETS on neighbouring LEE improvement, the regional sharing mechanisms should be well constructed, so as to reduce information asymmetry. Third, market regulators should fully consider the heterogeneity of resource endowments, economic strength, and industrial characteristics in resource-based and non-resource-based cities when allocating emission quota and price setting. On the one hand, the resource-based regions could produce a considerable amount of “resource bonus,” absorbing capital, labour, and other production factors into the mining industry. Consequently, the mining industry accounts for a large share of the local industrial structure in most resource-based regions (Shao et al., 2020). However, the larger proportion of the mining industry is expected to consume more energy and produce more CO₂ emissions (Ma et al., 2019). Moreover, the mining industry has long been criticised for its adverse effects on environment (Shen et al., 2015). On the other hand, resource-based industries could generate a crowding-out effect on some crucial factors of the long-term economic development (i.e. technological innovation, human capital) and thus induce the so-called resource curse (Shao & Qi, 2009). Therefore, it is necessary for those resource-based cities (especially in the central and western areas) to achieve economic development model transformation and improve LEE simultaneously. Finally, the implementation of ETS should take into account the specific stage of development cycle. A number of resource-based cities in Anshan and Changzhi are ferrous metal-based and coal-based mature or recessionary cities. Most importantly, the economic adjustment and transformation of ferrous metal-based and coal-based cities facilitate the driver for decarbonisation in China. Fortunately, a significant improvement of LEE in those cities is achievable (based on the accounting perspective) through ETS. Top-down environmental policies directive reducing pollution emissions without meticulous examination of the negative externalities and supported by the general public could lead to “shrinking cities” eventually.

Although China’s ETS has a promoting effect on LEE, several key practical and theoretical issues still should be addressed in the future exploration, including is there a synergy effect between China’s administrative intervention and market mechanism for mitigating CO₂ emissions and improving LEE, how to ensure the effectiveness and equity of the initial allocation of emission obligations in terms of the city’s resource carrying capacity. Further study can reveal the mechanism between ETS and LEE at a firm level (Joltreau & Sommerfeld, 2019). Moreover, by adopting big data, the application of the artificial intelligence technology will significantly smoothen the empirical analysis process and thus derive a more robust result.