Abstract
The problem of algorithmic fairness is typically framed as the problem of finding a unique formal criterion that guarantees that a given algorithmic decision-making procedure is morally permissible. In this paper, I argue that this is conceptually misguided and that we should replace the problem with two sub-problems. If we examine how most state-of-the-art machine learning systems work, we notice that there are two distinct stages in the decision-making process. First, a prediction of a relevant property is made. Secondly, a decision is taken based (at least partly) on this prediction. These two stages have different aims: the prediction is aimed at accuracy, while the decision is aimed at allocating a given good in a way that maximizes some context-relative utility measure. Correspondingly, two different fairness issues can arise. First, predictions could be biased in discriminatory ways. This means that the predictions contain systematic errors for a specific group of individuals. Secondly, the system’s decisions could result in an allocation of goods that is in tension with the principles of distributive justice. These two fairness issues are distinct problems that require different types of solutions. I here provide a formal framework to address both issues and argue that this way of conceptualizing them resolves some of the paradoxes present in the discussion of algorithmic fairness.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
In many domains, decision-making is nowadays supported by machine learning algorithms. These algorithms generate models that attempt to predict or estimate relevant unobserved properties on the basis of historical data. These predictions, in turn, inform the decision-making process. Automating decision-making processes in this manner, however, runs the risk of systematizing morally problematic decision patterns. In particular, when minority groups are the ones who could experience disproportionate negative consequences of algorithmic decision-making, this is cause for concern as it could potentially reinforce existing biases and structural inequalities. The recognition of this problem has led to a wide-ranging discussion about algorithmic fairness.
Typically, the problem of algorithmic fairness is presented as the problem of defining a unique formal criterion that guarantees that a given algorithmic decision-making procedure is morally permissible. In this paper, we argue that this is conceptually misguided and that we should replace the problem thus formulated with two more specific sub-problems. An algorithmic decision system can be conceptualized as operating in two stages: first, it predicts a relevant property, and second, it recommends a decision based (at least partly) on this prediction. It is important to notice that predictions are subject to different normative constraints than decisions. While predictions ought to be unbiased with regards to certain protected characteristics, decision-making based on these predictions ought to ensure that the resulting allocation of goods and opportunities is in line with the relevant principles of distributive justice. Current approaches to algorithmic fairness have failed to make this distinction. We here provide a formal framework to address both ethical issues and argue that this way of conceptualizing them resolves some of the paradoxes present in the discussion of algorithmic fairness.
The paper is organized as follows. In Section 2, we introduce the problem of algorithmic fairness and explain why all of the proposed solutions to it are unsatisfactory. In Section 3, we explicate the concept of algorithmic decision systems, and argue for a model of algorithmic decision systems which explicitly distinguishes between the predictive and the decision component of such systems. In Section 4, we turn to the ethical aspects of algorithmic decision-making, first examining the ethics of public decision-making more generally, before applying the conclusions of this analysis to algorithmic decision systems. In Section 5, we provide a formal framework for addressing the sub-problems obtained in the foregoing analysis, which we call the problem of predictive fairness and the problem of allocative fairness. In Section 6, we demonstrate how this bifurcation of algorithmic fairness problems can help to resolve a number of counterarguments to existing criteria of algorithmic fairness. Two potential objections are addressed in Section 7.
2 The Problem of Algorithmic Fairness
The topic of algorithmic fairness became known to the wider public when in 2016 an article was published which analyzed the risk predictions of a tool called COMPAS, which is used to support bail and sentencing decisions in some US courts. It was shown that the false positive rates of COMPAS’ predictions were much higher for African-American than for Caucasian defendants, and that, on the other hand, false negative rates were much higher for Caucasian than for African-American defendants (Angwin et al., 2016). In other words, African-Americans were much more often falsely accused of committing future crimes, while Caucasians were much more often falsely deemed innocent. It was concluded that COMPAS is racially biased. A discussion ensued about the question of whether disparities in error rates do indeed indicate bias, or whether there is a more appropriate criterion by which algorithmic decision systems such as COMPAS could be assessed (Flores et al., 2016). This marked the beginning of the field of fair machine learning.
While it is rarely made explicit, the problem addressed in much of the literature on fair machine learning is in fact a demarcation problem. The aim is to provide a precise criterion that constitutes a necessary and sufficient condition for the moral permissibility of an algorithmic decision-making process. This means, a formal criterion that, given a specific state of the world, allows us to rigorously distinguish algorithmic decision systems that are morally problematic from those that are unproblematic. The problem of algorithmic fairness can hence, preliminarily, be stated as follows:
The problem of algorithmic fairness For which formal criterion \(\phi\) is it the case that the application of algorithmic decision system S in world W is morally permissible if and only if \(\phi\) is satisfied?
Proposals for \(\phi\) abound (see, e.g., Verma & Rubin 2018). Typically, proposals are formulated as conditions involving the following variables: the input features \(\mathbf {X}\)Footnote 1 that are fed into the algorithmic system in order for it to arrive at a decision; the relevant protected characteristic A, which typically denotes a trait such as ethnicity, gender, or religion; the target variable Y, that is, the relevant property that is being estimated by the algorithm, and which is unknown at the time of application; and lastly, the outcome C, which denotes the value the algorithm returns after execution.
To illustrate with an example what these variables could stand for, think of a bank that uses an algorithmic decision system to determine who to grant a loan to. The vector of variables \(\mathbf {X}\) could here represent a set of variables containing a person’s income level (\(X_1)\), credit repayment history (\(X_2\)), and the like. The variable A could represent the applicant’s religion, while Y would most likely stand for whether the applicant would pay back their loan. The variable C represents the categories that the algorithm can assign to an applicant: creditworthy or not creditworthy.
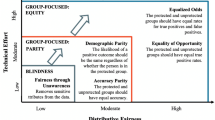
Table 1 contains brief descriptions of five of the most widely discussed fairness criteria. For the sake of simplicity, the criteria are presented as prose descriptions instead of mathematical definitions. We will later, where necessary, introduce their precise mathematical formalizations. For the moment, however, the prose descriptions should suffice to provide a conceptual exposition of the most important fairness criteria.
Despite the initial plausibility of each of these criteria, they come with a number of problems. First, none of the criteria seems to adequately capture the moral permissibility of the application of an algorithmic decision-making process. Often, the criteria are motivated by a handful of hypothetical or actual scenarios of algorithmic decision-making for which they give the right verdict, but are not shown to generally guarantee the absence of a particular moral wrong. For each criterion, forceful counterexamples can be constructed which demonstrate that moral permissibility and the satisfaction of the formal criterion can come apart. A counterexample can be a clearly permissible case of algorithmic decision-making that fails to satisfy the criterion, or a clearly impermissible case that does satisfy it. This means that none of the criteria provides both, a necessary and sufficient condition, and, as a matter of fact, many provide neither.
Second, the three so-called “statistical criteria”—statistical parity, equalized odds, and predictive parity—were shown to be pairwise incompatible when the target variable Y is correlated with the protected characteristic A (Kleinberg et al., 2016; Chouldechova, 2017). This means that, in most realistic scenarios, whenever one of the three criteria is satisfied, the other two criteria will be violated. This is an unfortunate result for a set of individually plausible fairness criteria.
Third, some of the criteria are constraints on individual algorithmic decisions (fairness through awareness, counterfactual fairness), while others are constraints on the population-level patterns of decision outcomes (statistical parity, equalized odds, predictive parity). This raises the question whether the moral wrongs inherent in certain algorithmic decision procedures are constituted at the individual or at the collective level, and if on both, how they relate to each other.
These three problems cast doubt on the possibility of solving the problem of algorithmic fairness as formulated above. A potential candidate for \(\phi\) would have to (1) guarantee that whenever the application of a given algorithmic decision system in a given context is wrongful, \(\phi\) is violated, and vice versa, that whenever the application is permissible, \(\phi\) is satisfied; (2) be grounded in a moral theory that explains away the mutual incompatibility of statistical parity, equalized odds, and predictive parity, by specifying the conditions under which the more fundamental fairness criterion \(\phi\) implies statistical parity, equalized odds, or predictive parity, respectively, and showing that under given conditions, it implies at most one of the three; and (3) said theory either shows that, fundamentally, the objects of algorithmic fairness are individuals, or that they are groups, and explains away intuitions to the contrary. Altogether, this is much to ask of a single fairness criterion.
It seems that the best explanation for the occurrence of the three problems is that in fact there are different types of moral wrongs that can occur in a given application of an algorithmic decision system, even though the unified use of the term algorithmic fairness misleadingly suggests the opposite. This, in turn, implies that different moral norms are relevant to algorithmic decision-making.
The apparent inability to specify universally applicable necessary and sufficient conditions for the absence of moral wrongs in algorithmic decision-making suggests that whether a given moral norm applies might depend on factors outside the mere specification of how the algorithm moves from input data to the resulting output. It might, first, depend on which aspect of the algorithmic decision-making process one is concerned with, and, second, on contextual factors that have a moral bearing on a given decision. This would mean that it is impossible to define a single, universally applying formal criterion of algorithmic fairness.
Now, if one accepts this explanation, this calls for a principled way of fine-graining the problem of algorithmic fairness, such that for each aspect of algorithmic decision-making that is bound to different normative constraints, we separately look for a (possibly context-relative) formal fairness criterion. This will be the task for the remainder of the paper.
3 Algorithmic Decision Systems
We begin by specifying what we take algorithmic decision systems to be. This will, first, help identify what the relevant normative questions about such systems are, and, secondly, delimit the scope of application of our framework. While these days algorithms are used in a variety of different ways, we are here concerned with one specific, but commonly used type of algorithmic system: a system, deployed in the public or semi-public sphere, that recommends or autonomously takes decisions affecting individuals, where these decisions are made on the basis of predictions from available information about these individuals.
Algorithmic decision systems of this sort are becoming increasingly popular in areas such as credit lending, criminal justice, hiring, and fraud detection. Returning to the example from the previous section, a bank could, for instance, use such a system to make a decision about whether and at what conditions to offer a loan to a loan applicant. The decision would (at least partly) be based on a prediction about the probability that the applicant would, if granted, default on the loan. To generate the prediction, the system might, as mentioned above, take as input data information about the applicant’s repayment history, education, and employment (see Lee & Floridi 2020). Many algorithmic decision systems deployed in other fields work in a similar fashion.
Before outlining our model of algorithmic decision systems, it is necessary to highlight an important conceptual distinction. In the discussion of algorithmic fairness it is rarely acknowledged that there is a morally relevant difference between algorithmic predictions and algorithmic decisions. Even though some authors explicitly distinguish between predictions and decisions (see, e.g., Hedden 2021, Kleinberg et al., 2018, Corbett-Davies & Goel 2018), the terms are, especially with regard to their moral aspects, often used interchangeablyFootnote 2. A plausible explanation for this is that algorithmic decisions are, as a matter of fact, almost always closely tied to predictions, so that one might conclude that there is no need to distinguish between them. This is, however, a misguided line of reasoning. A prediction—broadly understood as inference of an unknown proposition from a body of evidence—and a decision—understood as a choice of an act from a set of alternatives—differ in which properties can meaningfully be applied to each. While we can, for instance, speak of the accuracy of a prediction, it would be a category mistake to speak of the accuracy of a decision. By the same token, we can speak of the expected utility of a decision, but it would be a category mistake to speak of the expected utility of a prediction. The same, I contend, is true for moral properties. Consequently, we need to apply a model of algorithmic decision systems that is sensitive to this distinction in order to consistently discuss ethical aspects of algorithmic decision-making.
Algorithmic decision systems, according to the model proposed here, have two components (see Figure 1): a predictive model and a decision function. The predictive model takes the feature values \(\mathbf {x}\) as input, and, given a vector of learned parameters \(\varvec{\theta }\), outputs a probability assignment to the prediction \(\hat{y}\). The decision function, on the other hand, takes this probability assignment \(\hat{f}_{\varvec{\theta }}(\mathbf {x})\) as an input (and possibly the input values \(\mathbf {x}\) as well, as the dashed arrow indicates), and, given a cardinal utility function u over different possible outcomes, determines a decision o. This can be made mathematically precise. Let \(\mathbf {X}\) be a random vector (with domain \(D_{\mathbf {X}}\)) of input variables, \(\hat{Y}\) a random variable (with domain \(D_{\hat{Y}}\)) representing predictions of a target variable Y, and O a non-empty set of decision options. We can then define the notion of an algorithmic decision system as follows:
Definition 1
(Algorithmic decision system) An algorithmic decision system is an ordered pair \(S = (\hat{f}_{\varvec{\theta }}, d_u)\), consisting of a predictive model \(\hat{f}_{\varvec{\theta }}: \mathbf {X} \rightarrow [0,1]\), where \(\hat{f}_{\varvec{\theta }}(\mathbf {x})\) is interpreted as the conditional probability of \(\hat{y}\) given \(\mathbf {x}\), and a decision function \(d_u: [0,1] \times D_{\mathbf {x}} \rightarrow O\), where \(d_u(\hat{f}_{\varvec{\theta }}(\mathbf {x}), \mathbf {x})\) is interpreted as the decision option assigned to the combination of prediction \(\hat{f}_{\varvec{\theta }}(\mathbf {x})\) and input \(\mathbf {x}\).
A few remarks are in order. The predictive model is defined as a function from the input features \(\mathbf {x}\) to a real number in the interval [0, 1]. The output of the function represents an estimation of how likely it is that feature values \(\mathbf {x}\) make the prediction \(\hat{y}\) true, and it coincides with the conditional probability of the prediction \(\hat{y}\) given input features \(\mathbf {x}\). The reason for introducing a new function symbol \(\hat{f}\) is to highlight that we consider the predictive model to be a function of \(\mathbf {x}\) for fixed \(\hat{y}\). This is conceptually distinct from a probability function \(P_{\varvec{\theta }}(\hat{y} \mid \mathbf {x})\), which is a function of \(\hat{y}\) for fixed \(\mathbf {x}\). This definition of a predictive model is conceptually in line with common practice in machine learning, where models are typically conceptualized as functions of the input vector together with a quantification of the uncertainty of a given prediction (see Deisenroth et al., 2020, Ch. 8.2). On our definition, the predictive model encompasses simple models, such as logistic regression, but also more complex ones, such as deep neural networks (see Goodfellow et al., 2016, p. 174).
The decision function \(d_u(\cdot )\) is defined in analogy to choice functions in decision and game theory (see, e.g., Bradley 2017, p. 247; Sen 1971, p.2, Suzumura 2009, pp. 20ff). It differs, however, in that the set of available decision options O is held fixed, as we assume that a given algorithmic decision system will only be applied to one specific type of decision situation. Generally, the decision function is a function of the probabilistic prediction \(\hat{f}_{\varvec{\theta }}(\mathbf {x})\), and possibly further information encoded in the input vector \(\mathbf {x}\). The output is a decision option o from the set of available decision options O. The decision function can embody principles such as maximize expected utility or the maximin rule, relative to a fixed cardinal utility function u which assigns numerical utilities to outcomes. As is standard in decision theory, outcomes are defined as combinations of a given decision option o, input values \(\mathbf {x}\), and a value y of the target variable (the latter two representing mutually exclusive and jointly exhaustive possible states of the world).
To illustrate this with our previous example, imagine an algorithmic system for lending decisions. The system will proceed as follows: it will take as input data on the applicant’s income (\(x_1\)) and their repayment history (\(x_2\)), on the basis of which the predictive model estimates how probable it is the applicant defaults on the loan. On the basis of this probabilistic prediction \(\hat{f}_{\varvec{\theta }}(\mathbf {x})\), the decision function then outputs a decision, namely whether to grant the applicant the loan or not. Obviously, this is an unrealistically simplified model for making lending decisions but it helps clarify the concept of an algorithmic decision system.
More formally, the set of input variables \(\mathbf {X} = \{X_1, X_2\}\) contains the two variables \(X_1\) (income in thousands of dollars), and \(X_2\) (repayment history), with respective domains
-
\(D_{X_1} = \mathbb {N}\),
-
\(D_{X_2} = \{0, 1, 2\}\), where 0 stands for “No late payments”, 1 for “Some late payments”, and 2 for “Many late payments”
Assume that the predictive model is a logistic regression model, which estimates the probability that a given applicant will default on their loan according to the following equationFootnote 3:
Now imagine an applicant, Alice (A), who earns \(\$35,000\) annually, and who never had any late payments in her repayment history. That is, her input values are \(x^{(A)}_1 = 35\) and \(x^{(A)}_2 = 0\). We can hence calculate her probability of defaulting on the loan according to the predictive model as follows:
According to the predictive model, Alice has a \(14.8\%\) probability of defaulting. In the next step, this prediction is used to inform the decision on whether to grant Alice a loan. To this end, we have to specify the decision function \(d_u(\cdot )\). We will assume that there is only one type of loan in terms of credit amount and conditions. The set of decision options O hence contains exactly two possible decisions: to reject an applicant (“Reject”), or to grant them a loan (“Grant”). The decision function could then look as follows:
Recall that by the definition of algorithmic decision systems, the first argument of the decision function is the output of the predictive model, that is, \(p = \hat{f}_{\varvec{\theta }}(\mathbf {x})\). This means a loan is granted if the applicant has less than \(30\%\) probability of defaulting. Since in our example, Alice’s estimated probability of defaulting is \(14.8\%\), the decision function’s output is “Grant”. To sum it up, the algorithmic decision system would make the decision to grant her a loan, based on the information that she earns \(\$35,000\) per year and that she has no late payments in her repayment history.
The model introduced in this section is an idealized representation of algorithmic decision systems intended to be general enough to subsume most of the impactful systems that are used in the public and semi-public sphere, and yet specific enough to allow for a sufficiently deep analysis that does justice to the complexity of the ethical questions we attempt to address. We will now turn to the ethical questions that arise when a system of the above form is applied to make decisions about individuals.
4 Ethical Aspects of Algorithmic Decision-Making
In order to examine the relevant ethical aspects of algorithmic decision-making, it will be useful to take a step back and think about the ethical aspects of public decision-making more generally. We will use the term public decision in a relatively loose sense, denoting two different types of decisions. First, any act or policy implemented by a public body, such as central and local governments, courts, or police departments, which allocates certain benefits or incurs certain harms on individual persons. Secondly, acts by private actors that involve access to goods which can reasonably be expected to be regulated by the government, such as education, housing, employment, or transport. For the purposes of this analysis, we can disregard the difference between the two.
There are two ethical concerns about decisions in the public sphere, which persist even if we assume that the decisions are taken without objectionable intentions. First, the decisions might be based on biased beliefsFootnote 4, which can result in discriminatory decisions. Secondly, the decisions might produce unjust distributions of benefits and burdens among different groups in societyFootnote 5. While discrimination is closely connected to distributive injustice, it is important to distinguish between the two concepts.
A few words are in order about the normative commitments made in this article. The aim of this article is to provide a framework that is compatible with many different moral theories. Hence, we try to only make minimal normative commitments. We do, however, make a few commitments about concepts relevant to moral theory, namely the (non-normative) aspects of what discrimination is, and the (non-normative) aspects of what distributive justice is. Yet, this leaves open under which circumstances discrimination is wrongful, and what constitutes an unjust distribution of goods. When more specific moral theories are considered, this is done in order to illustrate our argument with examples. Where this is the case, this is made explicit.
Discrimination can broadly be understood as wrongfully disadvantaging someone because they belong to a certain salient social group (see, e.g., Moreau 2010 Eidelson 2015; Lippert-Rasmussen 2014). The property of belonging to such a group is what we call a protected characteristic, the group constituted by this shared property a protected group. Whether an individual is treated disadvantageously is determined relative to some other (actual or hypothetical) individual, who is not a member of that group, and who is, by some standard, suitable for comparison. When a decision-maker takes an individual’s social group membership as a reason for intentionally treating them in a disadvantageous way, we speak of direct discrimination. However, not all forms of discrimination require an intention to discriminate. When rules and policies are set up in a way such that, despite the absence of any intentions to this effect, being a member of the group results in experiencing certain disadvantages, we speak of structural discrimination. Under which conditions exactly disadvantageous treatment of the above form is wrong, and why it is when it is, is widely debated (see, e.g., Alexander 1992; Eidelson 2015). We will here not take a stance on this issue.
Unintentional discrimination can come about when decisions are informed by beliefs that are defective in particular ways (see, e.g., Eidelson 2015; Ch. 5, Lippert-Rasmussen 2014, p. 41 ff). This is the case when beliefs are biased, either in that they are inferred from inaccurate generalizations about the properties or behaviors of individuals who belong to a specific social group (i.e. stereotyping), or in that they are grounded in, for instance, a decision-maker’s emotional reaction to members of a specific group, rather than in adequate evidence (i.e. prejudice). When decisions in the public sphere are taken, it is hence obligatory to ensure that beliefs that inform the decision at hand are arrived at in an appropriate way.
On the other hand, we can say that a decision contributes to creating or amplifying distributive injustice, when the decisions, which typically allocate certain benefits or burdens, do so in a way that disrespects the distributive principle relevant in a given context. A strict egalitarian principle, for instance, would require that certain goodsFootnote 6 be distributed equally among different groups, while an equality of opportunity principle would require that economic and educational opportunities be equally distributed among those with the same level of talent and diligence. It is plausible to think that different goods ought to be distributed according to different distributive principles. Which principle applies to the distribution of a given good depends on the social meaning attributed to the good in question (see, e.g., Walzer 1983).
We can hence say that whether a decision is to count as discriminatory is, at least in part, determined by procedural aspects of how the decision came about. Distributive injustice, in contrast, refers only to the resulting distribution of goods. To make this distinction more tangible, consider the following two scenarios. In both, we assume that a company is looking to hire a suitable employee. In the first scenario, we assume that in order to decide between two applicants, the employer estimates how much profit an applicant would generate for the company, were they employed. One applicant is female, has a relevant degree from a renowned university, and has a track record of prestigious jobs which evidence her willingness to work hard. The other applicant is male, has no university degree, and has an employment record of rather unimpressive jobs. In estimating their profitability, the employer considers the first applicant’s gender to be a point against employing her, as the employer thinks that women are generally not capable of hard work. Nonetheless, due to the male applicant’s lack of relevant education and work experience, the female applicant is estimated to be slightly more profitable for the company and is hence offered the job. In this scenario, the employer’s decision is informed by a false stereotypical belief about women, which, according to many theories of discrimination (see, e.g, Halldenius 2017; Eidelson 2015) has to be considered wrongful. This means the procedural aspects of the decision-making process are such that they could result in a potentially discriminatory decision. Nonetheless, this does in this case not result in an unjust distribution of employment opportunities.
To contrast the previous example, consider the second scenario (inspired by Eidelson 2015, p. 53). In this scenario, we assume the employer knows that if an employee has a parent who has herself been a long-term employee of the company, this has a positive effect on the new employee’s productivity, and hence the profitability for the company. Assume this is due to the fact that having a parent who is a senior employee facilitates certain things for new employees—it might, for instance, allow them to get acquainted with the processes within the company more quickly, or to get to know people in important roles at a more personal level, and so on. For this reason, the employer prefers, all else being equal, applicants who have a parent who has been working for their company. Now assume further that non-Christian applicants are less likely to have a parent who has been working in the employer’s company—possibly because many of the non-Christian applicants happen to be children of recent immigrants. This means that the employer’s hiring policy disproportionately denies non-Christians the opportunity to work for the company, even if they are, on average, equally talented and diligent. According to a theory of equality of opportunity along the lines of, for instance, Rawls (1971), this would hence constitute a case of distributive injustice against the group of non-Christians, despite the fact that the decision is not informed by biased beliefs about non-Christians.
In both scenarios, we can criticize the employer’s decision-making procedure as wrongful (given we accept the aforementioned moral theories). However, we do so on different grounds. In the first case, we can criticize the decision as being made on the basis of a belief that is, in a morally relevant way, defective. We cannot, however, criticize the outcome of the decision. In the second case, we can criticize the decision as producing an unfair distribution of economic opportunities among different social groups. We cannot, however, criticize that the employer’s belief about the profitability of potential employees is defective, since, by assumption, the belief is true.
Let us now transfer the above analysis to algorithmic decision systems. When algorithmic decision systems are deployed in order to make or recommend decisions in the public sphere, they are bound to the same normative constraints as public decisions taken by human decision-makers. Hence, it is necessary to ensure that they do not make decisions on the basis of biased beliefs and that they do not make decisions that allocate goods in a way that violates the relevant distributive principle.
While algorithmic decision systems do not have beliefs in any literal sense, they do possess representations of real-world properties. Those are encoded in the input features \(\mathbf {x}\), and the estimation of the probability that the unobserved property y is present. Consequently, the first normative constraint on algorithmic decision systems is that the probabilistic estimation of y on the basis of \(\mathbf {x}\) must not be biasedFootnote 7. This, unsurprisingly, is a constraint on the first component of an algorithmic decision system, the predictive model.
When an algorithmic decision system makes a decision that allocates goods, allocating these goods according to the probabilistic prediction of property y and background information \(\mathbf {x}\) must be compatible with the relevant distributive principle. This means that, for a given decision, the variable Y has to be chosen such that distributing a good according to it (possibly together with some of the input variables in \(\mathbf {X}\)) is permissible in the light of the principle. Think, for instance, of the second scenario discussed above. Assume that we accept a Rawlsian equality of opportunity principle. This principle demands that everyone with the same talent and diligence should have the same chance to be offered a given job. If we accept this principle, then in the scenario above, hiring decisions cannot (merely) be based on a prediction of the profitability of an applicant, because profitability is influenced by factors beyond talent and diligence—namely having a parent who also works for the employer’s company. Put differently, in the above case predicted profitability alone does not provide a permissible reason for a hiring decision. So, the second normative constraint on algorithmic decision systems is that a decision must be determined on the basis of properties (or predictions thereof) that are permissible for a given allocation of goods. This, on the other hand, is a constraint on the second component of an algorithmic decision system, the decision function.
We can conclude by summarizing that there are two aspects of algorithmic fairness, which are both necessary but individually insufficient for guaranteeing that the application of an algorithmic decision system is morally permissible. Consequently, we are confronted with two problems of algorithmic fairness: (1) finding a constraint on predictive models that ensures that probabilistic predictions are generated in an unbiased way, and (2) finding a constraint on decision functions that ensures that decisions about the allocation of a given good are based on information and estimations of adequate properties. These two problems will be made more precise in the next section.
5 Two Concepts of Algorithmic Fairness: A Formal Framework
The above analysis suggests a way to replace the problem of algorithmic fairness we presented in Section 2 with two separate subproblems. Rather than finding a single formal criterion that guarantees that, if satisfied, the application of a given algorithmic decision system is morally permissible, we turn the attention to finding two different criteria: one criterion that guarantees the absence of biased predictions, and another criterion that guarantees that decisions are made in a way such that no unjust distribution of goods results. While it seemed infeasible to find a single criterion that guarantees the intuitive permissibility of algorithmic decision systems, the bifurcation of the problem into two sub-problems aligns well with moral theory and allows us to explain away seeming contradictions.
Begin with the problem of finding a constraint on an algorithmic decision system’s predictive model that guarantees the absence of discriminatory bias. We say that predictive models are biased when their predictions exhibit specific patterns of errors. In other words, biased predictions deviate from the truth in systematic ways. To determine whether a predictive model is biased, it is thus necessary to not only take the probabilistic predictions themselves into consideration but moreover what is actually the case in (some relevant aspect of) the world. The constraint on the algorithmic decision system must hence be formulated relative to a specification of the relevant aspects of the world. How informationally rich this specification needs to be depends on how exactly one defines the notion of bias. In order to make the present framework compatible with as many different approaches as possible, we will here not take a stance on which technical notion of bias is to be chosen. To provide two examples, however, note that the world could simply be specified as the set of all the (relevant) true propositionsFootnote 8, or as a causal model which not only specifies what is true, but which also represents mechanisms and processes active in the worldFootnote 9. We can now formulate the first subproblem as follows:
The problem of predictive fairness. For which formal criterion \(\phi\) is it the case that the predictive model \(\hat{f}_{\varvec{\theta }}(\cdot )\) is unbiased if and only if \(\hat{f}_{\varvec{\theta }}(\cdot )\) satisfies \(\phi\) relative to world W and protected characteristic A?
Next, consider the problem of allocative algorithmic fairness. The task here is to find a constraint that ensures that the distribution of goods resulting from the application of the algorithmic decision system is in line with the relevant distributive principle. More technically speaking, this means that we want to constrain which properties are allowed or need to be correlated with receiving the specific good. For example, a strict gender parity principle would require that there be no correlation between an individual’s gender and receiving the good in question. Applied to, say, a hiring context, this would ensure that the proportion of female applicants offered a job is equal to the overall proportion of female applicants. An equality of opportunity principle, on the other hand, would require that receiving the good be perfectly correlated with talent and diligence, even if this means that receiving the good is to some degree correlated with a protected characteristic. Applied to the hiring example, equality of opportunity would ensure that the applicants which score the highest on features such as education, professional experience, or performance on relevant tests, are the ones who are offered the job.
As argued above, we assume that how a good ought to be distributed depends on the type of good in question. In order to define a formal framework for determining whether a decision function produces unfair allocations of a given good G, we hence have to specify two sets of properties. The first, \(\mathbf {I}_G\), denotes the set of properties for which it is impermissible to be correlated with the decision outcome \(d_u\). The second, \(\mathbf {O}_G\), denotes the set of properties for which it is obligatory that they be correlated with the decision outcome \(d_u\). Since an impermissible property cannot be obligatory, we assume that the set of impermissible properties and the set of obligatory properties are disjoint, i.e. \(\mathbf {I}_G \cap \mathbf {O}_G = \emptyset\). We can now formulate the second subproblem of algorithmic fairness as followsFootnote 10:
The problem of allocative fairness. For which pair of property sets \((\mathbf {I}_G, \mathbf {O}_G)\) is it the case that the decision function \(d_u(\cdot )\) is allocatively fair with regards to a given good G if and only if, under the assumption of perfectly accurate predictions, the outcomes of \(d_u(\cdot )\) are sufficiently correlated with all variables \(V_i \in \mathbf {O}_G\), and are sufficiently uncorrelated with all variables \(V_j \in \mathbf {I}_G\)?
In order to operationalize any concrete definition of allocative fairness, we need to make precise what we mean by saying that two variables are sufficiently (un)correlated. One natural way to do this would be to define two variables to be sufficiently correlated whenever the absolute value of some correlation coefficient, such as Pearson’s correlation coefficient (see, e.g., Lee Rodgers & Nicewander 1988), is above a certain threshold. Conversely, we could define two variables to be sufficiently uncorrelated whenever the absolute value of their correlation coefficient is below a certain threshold. There are, however, many different ways in which these notions could be explicated, and we will here leave the question open which is the most adequate.
Note that we always evaluate predictive and allocative fairness relative to a specific protected characteristic. This means we decide on the protected characteristic relative to which we want to evaluate a given algorithmic decision system beforehand, and then check whether the chosen criteria of predictive and allocative fairness hold for this specific characteristic. The framework presented here is agnostic about what counts as a protected characteristic and how to choose which protected characteristics are of special importance in a given situation. These are complex questions of their own, in particular in light of the fact that sometimes we care about intersectional characteristics, like for instance being a woman of a particular ethnicity. While the present framework cannot provide answers to these questions, it is general enough to be compatible with different theories about protected characteristics.
Let us now illustrate the distinction between the two problems with two hypothetical examples. As a first example, consider an algorithmic decision system that estimates how probable it is that a given, previously criminal individual, will commit another crime within some specified time frame in the future. On the basis of this prediction, the system then recommends whether to subject the individual to increased monitoring measures.
In this example, we assume that the only input the predictive model of the algorithmic decision system takes is information about which neighborhood a given individual lives in. We can further assume that it is known that there is a correlation between living in a given neighborhood and exhibiting criminal behavior, so that this choice of input data has, at least at first glance, some plausibility. The predictive model assigns a 0.2 probability of criminal behavior if the individual lives in neighborhood 1, and 0.8 probability if the individual lives in neighborhood 2. The decision function of the system is equally simple: it outputs the decision to increase monitoring (“\(\checkmark\)”) of an individual whenever the prediction is greater than 0.7, and the decision to stay with a regular level of monitoring (“\(\times\)”) otherwise. While this is certainly an unrealistically simplistic algorithmic decision system, its simplicity allows us to focus on those aspects that we aim to illustrate without getting caught up in technical details.
Table 2 contains information on eight fictitious individuals for whom predictions of criminal behavior were generated. In particular, we have information on each individual’s ethnicity, which is the protected characteristic relative to which we will assess the fairness of the system; on the neighborhood an individual lives in, which is the (only) input feature to the predictive model in this example; and on whether an individual actually exhibited criminal behavior, which is the target variable for which the predictive model estimates a probability. Note that, from the perspective of the predictive model, the value of the target variable is not known. Additionally, the table describes the probabilistic prediction \(\hat{f}_{\varvec{\theta }}(\cdot )\) of the algorithmic decision system and the decision output generated by the decision function \(d_u(\cdot )\)
In order to assess whether the algorithmic decision system is fair according to our proposed framework, we have to fill in the variables in the two fairness schemata to obtain concrete fairness criteria. Begin with predictive fairness. The protected characteristic relative to which we evaluate whether the predictive model is biased is ethnicity (denoted by variable A). The relevant aspect of the world W, relative to which we check whether the predictions make systematic errors, is whether an individual does in fact commit a crime (denoted by variable Y). As the criterion that ensures that the predictive model is not biased with regards to ethnicity, we choose equalized odds (Hardt et al., 2016). This means we require that the average predicted probability that an individual will not commit a crime, given she does in fact commit a crime (and, likewise, the average predicted probability that an individual will commit a crime, given that she does not, in fact, commit a crime) be equal among white and non-white individuals. These metrics can be considered the analogs of the false positive and the false negative rates for probabilistic predictions. Hence, we substitute \(\phi\) in the schema with the condition that for all \(\hat{y} \in D_{\hat{Y}}, y \in D_Y\), and \(a_1,a_2 \in D_A\):
Having specified a concrete predictive fairness criterion, we can now assess whether the predictive model is biased. A quick look at the data set in Table 2 shows that of the four white individuals, two turned out to commit criminal offenses (rows 3 and 4), as did two of the four non-white individuals (rows 6 and 7). This means the prevalence of criminal behavior is equal among the two groups according to our data. If, however, we look at the summary statistics of the predictive model \(\hat{f}_{\varvec{\theta }}(\cdot )\), we can see that on average, the non-white individuals received a probabilistic prediction of crime above 0.6, while the white individuals received on average predictions below 0.4 (Figure 2(i)). More specifically, we note that the average predicted probability of absence of criminal behavior among those who did in fact commit a crime is much higher for white individuals than for non-white individuals (Figure 2(ii)). At the same time, the average predicted probability of criminal behavior among those who do in fact not commit a crime is much higher for non-white individuals than for white individuals (Figure 2(iii)). Intuitively speaking, this means that for white individuals it is much more probable to be deemed innocent while actually going on to commit a crime, whereas for non-white individuals it is much more probable to be deemed criminal while actually being innocent. This clearly violates the fairness criterion specified above—the predictive model is biased on our definition.
Next, we have to choose a criterion according to which we can examine whether the decision function allocates the good in question in a fair way. The “good” at issue is in fact an “economic bad”—a burden that comes with negative utility for the individual—namely, to be subjected to an increased level of monitoring. Assume, hypothetically, that we take the position that a burden such as increased monitoring should be allocated according to a desert-based principle—in other words, the individuals subjected to increased levels of monitoring should be those who deserve so due to their inclination towards criminal behavior. In accordance with our formal framework, this can be formalized as the requirement that Crime \(\in \mathbf {O}_{Monitoring}\). This means that, assuming that the predictive model generates perfectly accurate predictions, the target variable Crime (that is, whether an individual did actually exhibit criminal behavior) ought to be correlated with the outcome of the decision function \(d_u(\cdot )\). Apart from this, there are no further constraints.
If the predictions were perfectly accurate, then every individual who will in fact go on to commit a crime would have received a predicted probability of 1, and every individual who will not would have received a predicted probability of 0. Since the decision rule \(d_u(\cdot )\) recommends increased monitoring for those individuals who have a predicted probability of criminal behavior above 0.7, every criminal would be subjected to increased monitoring, whereas no innocent individual would. Hence, the decision outcomes would be perfectly correlated with criminal behavior, and we can conclude that the decision function satisfies our criterion of allocative fairness.Footnote 11
To summarize, the algorithmic decision system in this example produces unfair decisions. As our analysis has shown, this is due to a biased predictive model. Hence, in this case the predictive model should be adjusted so as to not produce such biased predictions. There is, however, no reason to change the decision function.
Let us now turn to the second example. Here, we are considering university admission decisions. The predictive model of the algorithmic decision system estimates how likely it is that a given individual would be successful at the university they apply to, where success will be defined as achieving a grade average above a specific threshold. The decision function then recommends an admission decision on the basis of this estimation. Similar to the previous example, the predictive model \(\hat{f}_{\varvec{\theta }}(\cdot )\) assigns a predicted probability of university success of 0.8 whenever the individual had a high school grade of A or B, and 0.4 whenever the high school grades were below that. The decision function \(d_u(\cdot )\) recommends the decision to admit an individual whenever the predicted probability of success if greater than 0.7 (“\(\checkmark\)”). Table 3 depicts a fictitious data set with information on whether an individual has dyslexia (the protected characteristic in this example), their high school grades (the input data), and whether they actually turned out to be successful at university (the target variable), and what the algorithmic decision system would have predicted and decided for each individual.
Examining Figure 3, we notice that individuals without dyslexia have, on average, a higher predicted probability of academic success. Yet, the average predicted probability of not being successful, given that the student would actually have been successful, as well as the average predicted probability of being successful, given that the student would actually not succeed, are equal across the two groups. By our notion of predictive fairness (equalized odds), the predictive model would hence count as fair. Assume, for the sake of argument, that we adopt a normative position regarding the distribution of educational opportunities that entails that a learning difficulty such as dyslexia should not affect one’s chances of being accepted to a university programme. Dyslexic students, on this view, should have the same overall admission rate as students without dyslexia. More precisely, the decision outcomes should not be correlated with the variable Dyslexia, i.e. Dyslexia \(\in \mathbf {I}_{Admission}\). This allocative fairness criterion is clearly violated by the decision function. Out of four students with dyslexia, only one is admitted to the university, as compared to two out of the four students without dyslexia. This means, the decision outcomes are not statistically independent of the variable DyslexiaFootnote 12. Moreover, this would still be the case if the probabilistic predictions were perfectly certain and accurate.
What these two examples show is that two intuitively unfair algorithmic decision systems can suffer from fundamentally different flaws, and hence require different approaches to rectify these flaws. In the first example, the predictive model is biased against non-white individuals, and consequently, the appropriate response to this assessment would be to put effort into increasing the predictive accuracy for data points of non-white individuals. Changing the decision function would not help in any way, and presumably lead to further unforeseen and undesirable consequences. In contrast, in the second example, the predictive model is not biased against dyslexic individuals. Yet, basing decisions solely on the predictions of success at a given university creates a distribution of admissions which conflicts with our principle of allocative fairness. This, however, calls for a very different approach than the first example. Here, increasing predictive accuracy would not help to make the system fair. What would potentially help, in contrast, would be to change the decision function such that it takes not only an individual’s predicted probability of success into account but moreover whether the individual has a learning difficulty. A fair decision function could, for instance, implement different cut-off thresholds for individuals with dyslexia and for individuals without learning disorderFootnote 13. This would counteract the unequal initial conditions for individuals with dyslexia and those without.
6 Explaining Away Counterexamples
In this section, we will discuss to which extent the proposed bifurcation of the problem of algorithmic fairness into the two sub-problems of predictive and allocative fairness allows us to resolve or explain away counterexamples to some widely discussed criteria of algorithmic fairness.
Recall that by stating that none of the proposed constraints capture the notion of moral permissibility adequately, we meant that none of the constraints provides a necessary and sufficient condition for the moral permissibility of a given algorithmic decision system. More precisely, this means that for each of the criteria, we can either show that it is not a necessary condition of moral permissibility, by providing a counterexample of an algorithmic decision system that is morally permissible, but which does not satisfy the constraint in question, or we can show that it is not a sufficient condition of moral permissibility, by providing a counterexample of an algorithmic decision system that is not morally permissible, but which satisfies the constraint. In the case of some proposed fairness criteria, both types of counterexamples can be constructed.
While the bifurcation of fairness notions will certainly not be able to completely resolve the issue that many fairness constraints face plausible counterexamples, it may provide an explanation for why, despite the existence of a multitude of plausible fairness constraints, it seems that it is relatively easy to construct tenacious counterexamples for each of them. This is so because the constraints were implicitly intended to simultaneously play two distinct and incompatible roles, namely to act as a fairness constraint on predictions and as a fairness constraint on decisions. As argued above, predictions and decisions are subject to different normative constraints. Consequently, applying a fairness constraint that is plausible for predictions to decisions, or vice versa, will in most cases conflict with our moral judgment. This, in turn, means that we have a simple recipe for constructing counterexamples. We only need to figure out whether a given constraint is intuitively plausible for predictions or decisions, and then construct an example in which we apply the constraint to the other.
A second potential explanation can be made with regard to allocative fairness. As argued above, allocative algorithmic fairness constraints should be indexed by goods, since for different goods different distributive principles hold. This means that an allocative fairness constraint that is plausible for an algorithmic decision system that allocates one good might not be plausible for an algorithmic decision system that allocates a different good. So, a second recipe for constructing counterexamples to fairness constraints is to apply an allocative fairness constraint to an algorithmic decision system that is used for a good that is subject to a different distributive principle than the one corresponding to the fairness constraint.
So, our claim is that if the scope of a given fairness constraint is restricted according to the bifurcation of fairness problems proposed above, many counterexamples will lose their argumentative force. It would be tedious to check for every alleged counterexample whether the above pair of explanations can in fact rebut it, and it would be impossible to show more generally that we can do so for every conceivable counterexample. To illustrate the point, however, we can look at a number of prominent counterexamples in order to see whether the explanations are any good.
Let us first consider the fairness criterion statistical parity, which requires that the members of different protected groups be equally likely to receive a certain algorithmic outcome, or, in other words, that the algorithmic outcome ought to be statistically independent of the protected characteristic. Statistical parity was criticized as a formal algorithmic fairness criterion in a number of ways. Hardt et al. (2016), for instance, argue that statistical parity is too strict a requirement for fairness. Their argument is based on the observation that whenever there is a correlation between the target variable and the protected characteristic, a perfect predictor, that is, a predictive model which predicts the target variable with perfect accuracy, will not satisfy statistical parity. If one assumes that perfectly accurate predictions are always morally permissible, it follows that statistical parity is not a necessary condition for fairness. The example they mention to illustrate this argument is credit lending. Imagine a predictive model which predicts with perfect accuracy whether an applicant will default on a loan or not. It would not be reasonable, Hardt et al. contend, to consider this model discriminatory and hence unfair, even if the proportion of positive predictions were slightly different for loan applicants of different ethnicities.
Another counterexample was put forward by Corbett-Davies et al. (2017), who argue that applying statistical parity to decision-making in an area such as criminal justice is not morally optimal. In their example, which is based on the COMPAS data setFootnote 14, statistical parity is applied to an algorithmic decision system for pretrial release decisions, that is, for decisions as to whether to detain or release a defendant for the time leading up to the trial. Corbett-Davies et al. compare two different decision functions: one that maximizes expected social utility without any fairness constraints, and one that maximizes expected social utility subject to statistical parity with regard to ethnicity. In this scenario, it is assumed that positive utility is assigned to detaining defendants who would otherwise commit violent crimes, while negative utility is assigned to the social and economic costs incurred through detention. It can be shown that in this specific case a decision function that satisfies statistical parity yields a lower expected overall utility: such a function can be expected to lead to a higher number of violent crimes committed by released defendants as well as a higher rate of detentions of individuals who would not have committed violent crimes had they been released. If we assume, as Corbett-Davies et al. seem to do, that in the domain of criminal justice the expected social utility of a decision has a bearing on its moral evaluation, it follows that ensuring statistical parity alone is not sufficient for the moral permissibility of an algorithmic decision system.
We can make sense of these two counterexamples with our conceptual distinction between predictive and allocative algorithmic fairness. Statistical parity clearly only makes sense as an allocative fairness criterion. It only takes into account whether the protected characteristic is correlated with the algorithmic outcome. This would not be plausible for a constraint on predictions. As argued above, we have to check whether predictions deviate from the truth in systematic ways in order to determine whether they are biased. To do so, we obviously have to take information about the relevant aspect of the world (that is, at least the individual truth values of the target variable) into account. Statistical parity does not do this—it merely considers whether outcomes are uniformly distributed across protected groups. It is hence misguided to interpret statistical parity as a criterion of predictive fairness. But this is exactly what Hardt et al. did: they argued against statistical parity on grounds that it possibly prohibits the perfect predictor. This, however, is wrong—statistical parity can at best constrain how to move from perfectly accurate predictions to decisions. So, the first counterexample loses its force when viewed through the lens of our conceptual distinction.
In order to address the second counterexample, we have to keep in mind that criteria of allocative fairness are indexed by goods. Statistical parity can be represented as the pair of property sets \((\mathbf {I}_G, \mathbf {O}_G) = (\{A\},\emptyset )\). This means that for a certain class of goods G, it is impermissible that the decision outcomes are correlated with the protected characteristic A, but that there are no requirements as to which variables the outcomes must be correlated with. So, the counterexample of Corbett-Davies et al. cannot be taken as an argument against statistical parity per se, but at best as an argument that, if statistical parity is interpreted as an allocative fairness criterion for a certain class of goods, legal punishment does not fall into this category of goods.
Let us now consider an alleged counterexample to equalized odds. Recall that equalized odds is the fairness criterion that requires that the probability of a prediction of some target variable, given the actual value of the target variable, be equal for all protected groups. This is a generalization of the requirement that the false positive and false negative rates of the algorithmic decision system be equal for all protected groups. An example of a context in which equalized odds can plausibly be applied is criminal sentencing. The criterion was, for example, used to evaluate whether algorithmic assignments of risk scores, measuring a defendant’s risk of violent reoffence, are biased in discriminatory ways. The intuition behind this criterion is that if one protected group has a higher false positive rateFootnote 15 than another, meaning that it is more likely for members of one group to actually be innocent and yet be deemed to be at high risk of violent reoffence by the algorithm, this reflects a discriminatory bias on part of the model underlying the algorithm.
Gölz et al. (2019) argue against applying equalized odds as a criterion of algorithmic fairness on grounds that under some circumstances, equalized odds conflicts with certain game-theoretic axioms of fair division. Most strikingly, they contend, equalized odds is largely incompatible with a principle called population monotonicity. This principle states that when a finite amount of goods is to be distributed among a number of individuals, removing one individual (for instance because the individual decides not to be interested in the goods to be allocated anymore) should not negatively affect the allocation of goods to the remaining individuals. This means any individual who would previously have received the good in question should, after the removal of the other individual, still receive the good. Gölz et al. put forward an example along the following lines: imagine a number of student loans can be given out to applicants of a given university. Assume further that the algorithmic decision system which recommends whether to grant a loan to a student or not satisfies equalized odds. That is, for each protected group it is the case that of those students in that group who are in fact capable of paying back their loan, an equal proportion is granted a loan. Analogously, for each protected group, of those students in that group who would in fact default on the loan, an equal proportion are denied the loan. Now, if a student from one group, who was granted a loan and is in fact capable of paying it back, decides to reject the loan—maybe because the student decided to attend a different university -, this might require withdrawing the initially granted offer of a loan from students of the other protected groups in order to restore equalized odds. It is counterintuitive to think that this would be morally permissible, let alone morally required. In other words, it seems that this shows that equalized odds is not a necessary condition for moral permissibility.
Whether this argument goes through, however, depends on how equalized odds is interpreted. One could interpret it as an allocative fairness criterion: among those that fall into something designated as the positive class (in this case, this might be the class of students who possess adequate qualifications and are from suitable economic circumstances), the probability of a positive or negative prediction ought to be the same. (Analogously, this ought to be the case for the negative class as well.) Nonetheless, it seems that the more plausible interpretation in this example is to take equalized odds as a criterion of predictive fairness. Moreover, this seems to be in line with the general conception of the criterion. Many articles discussing equalized odds understand it as requiring equal false positive and false negative rates for different protected groups (see, e.g., Moritz et al., 2016; Hedden 2021). The very notion of a true or false positive, however, can not be meaningfully applied to decision settings. Predictions can turn out to be true or false (or, in the probabilistic case, accurate), but decisions can not.
Under this interpretation of equalized odds, this counterexample, too, can be explained away using the bifurcation of fairness problems. While the cited axiom of fair division, population monotonicity, is concerned with the fair allocation of goods, equalized odds can here plausibly be interpreted as a criterion of predictive rather than allocative fairness. Since equalized odds is a criterion of which one parameter takes into account what is actually the case in the world (by considering the truth value of the target variable Y), it nicely fits the schema of the problem of predictive fairness.
The counterintuitive consequence of the example arises only under the assumption that equalized odds here acts as a fairness constraint on decisions to allocate goods. When applying a predictive model to determine whether a student would pay back their loan, equalized odds can be used to ensure that predictions are not biased. The predictions then act as an input to the decision function in order to determine whom to grant a loan. If one of the students who is initially granted a loan rejects the offer, this has an effect on the distribution of loans, but not on the predictions made by the predictive model. So, it does not affect whether the predictive model satisfies equalized odds or not. Once again, the counterexample potentially only emerged due to a failure to distinguish between normative constraints on predictions on the one hand and normative constraints on the allocation of goods on the other.
These three examples should suffice to show that the conceptual distinction between predictive fairness and allocative fairness can help to rebut many of the arguments put forward against specific notions of algorithmic fairness. Many of the counterexamples arise simply because the scope of the proposed fairness criteria is not appropriately delineated. The above examples should count as evidence for the claim that at least part of the difficulty of defining adequate criteria of algorithmic fairness can be explained by the inappropriate framing of the problem of algorithmic fairness as the problem of finding a unique formal criterion for the moral permissibility of an algorithmic decision system.
7 Potential Objections
We will now address a number of potential objections to the proposed framework or the assumptions on which it is built. The first objection is that the problem of algorithmic fairness was not presented in an adequate form. The second objection is that one central premise, namely that we can clearly distinguish predictions from decisions, is false. Let us discuss both potential objections in turn.
7.1 Misrepresentation of the Problem of Algorithmic Fairness
One could argue that the way the problem of algorithmic fairness is presented in this paper—namely as an attempt to find a single formal criterion that is a necessary and sufficient condition for the moral permissibility of an algorithmic decision system—does not correspond to the reality of what researchers in the field of algorithmic fairness are actually doing. Instead of trying to find a single formal criterion that provides a necessary and sufficient condition for fairness, they aim to identify individually necessary conditions of moral permissibility, with the greater goal of being able to find the list of all those individually necessary conditions which are jointly sufficient for the moral permissibility of algorithmic decision systems. Formally represented, we could say that on this alternative view, researchers are trying to find some \(\phi _i\), such that \(\phi \equiv \phi _1 \wedge ... \wedge \phi _n\), with \(i \in {1, ..., n}\).
The first thing to be said about this is that, clearly, many of the seminal papers in the field of algorithmic fairness can be understood to have the aim to formulate a definition of fairnessFootnote 16. Giving a definition typically means providing necessary and sufficient conditions. But granted that indeed most authors’ goal is to provide only necessary conditions for fairness, would this invalidate the argument made in this paper?
The central point this paper is trying to establish is that when considering criteria of algorithmic fairness, be they intended as necessary and sufficient, or as necessary conditions only, one has to take into account whether these criteria are reasonable constraints on the predictive model or on the decision function. This determines whether in evaluating the algorithmic decision system, we take the output to be the prediction \(\hat{y}\) or the decision option o. Given an algorithmic decision system and a criterion of algorithmic fairness, we might come to different conclusions about whether it satisfies the criterion depending on whether we take \(\hat{y}\) or o to be the relevant output. The aim of proposing a framework for distinguishing between predictive and allocative fairness criteria is to eliminate this kind of ambiguity.
While the assumption that the problem of algorithmic fairness is the search for a single formal necessary and sufficient condition of moral permissibility provides a motivation for the present project, the value of the proposed framework does not hinge on this assumption.
7.2 The Distinction Between Predictions and Decisions
The argument outlined in this paper builds on the assumption that we can, at least in most cases, clearly distinguish between predictions—interpreted as forming an epistemic attitude towards an unobserved event or property—and a decision—interpreted as the choice to pursue one specific course of action. But while in theory the distinction can be upheld, there are some arguments to the effect that this distinction is less strict. This involves some major philosophical projects such as epistemic utility theory (see, e.g., Pettigrew 2016), or the theory of epistemic democracy (see, e.g., List & Goodin 2001; Goodin & Spiekermann 2018). Let us discuss both in turn.
The central idea of epistemic utility theory is to apply the mathematical machinery of decision theory to the evaluation of epistemic norms. At its foundation sits the assumption that, from an epistemic point of view, all we care about is coming to believe true (and only true) propositions. Epistemologists are hence concerned with finding norms of belief formation that are optimal with regard to this goal. The gist of epistemic utility theory is that the structure of the epistemic problem—forming beliefs in a way that is optimal with regard to the goal of accuracy—is similar to the problem of practical rationality—taking decisions in a way that is optimal with regard to one’s personal preferences or values. Since the structure is similar, the methods used to evaluate decision strategies can also be used to evaluate epistemic norms. Nonetheless, epistemic utility theory is about norms of rational belief formation, not about rational decision-making, even though it applies the formal framework of the latter. On our more orthodox interpretation of what a decision is, making predictions cannot be seen as a species of decision-making, since, as Pettigrew (2016, p. 207) puts it, “we don’t choose our doxastic states”. Moreover, adopting a doxastic state does not allocate any goods—and this is, at least in the present context, the central type of decision from which we wish to distinguish predictions. The project of epistemic utility theory, then, does not seem to put into doubt the feasibility of the distinction between predictions and allocative decisions in the context of algorithmic decision-making.
Another philosophical project which seems to blur the lines between decision-making and belief formation is the theory of epistemic democracy. Here, the central notion is that in collective decision-making, there is some fact of the matter about which choice can be considered to be correct. This, however, has to be understood in the following way. For each of the options available to the collective, it is possible to assign an objective utility. On the basis of this objective utility assignment, we can say that it is true (or false) that a given option is the best option available. Choosing the best option can be considered the correct decision, choosing any other option an incorrect decision. While this view introduces some epistemic aspects into collective decision-making, it would be an overstatement to say that the view implies that we cannot clearly distinguish between (purely) epistemic practices (like making predictions) and the act of making a decision to allocate some good.
Now, even if one were to concede that we can understand belief formation as a species of decision-making, or that one can call some decisions (in some epistemic sense) correct and others incorrect, this would still not necessarily invalidate our thesis. The minimal premise needed in order for the argument outlined in this paper to work is that in the context of algorithmic decision-making, it is clear when we are concerned with predicting an event or a property, and when we are concerned with allocating a good. This does not seem to be put into doubt by either of the two projects described above.
8 Conclusion
We have argued that the way the problem of algorithmic fairness is commonly presented is misleading and unlikely to be solvable. This, as we have argued, is due to the fact that it conflates two different realms of ethical consideration, namely predictions and decisions. An algorithmic decision system typically makes (or recommends) decisions on the basis of predictions of some variable of interest. Here, two distinct morally problematic phenomena can occur: first, the predictions can exhibit discriminatory bias, and second, the decisions can lead to unfair distributions of goods or opportunities. We have provided a general formal schema that helps to diagnose and address each of these two problems—the problem of predictive algorithmic fairness, and the problem of allocative algorithmic fairness—individually. We concluded this paper with a demonstration of how this bifurcation of fairness criteria enables us to (at least partially) resolve many of the paradoxes that beset the original problem of algorithmic fairness.
Notes
Since algorithmic predictions are often based on a large number n of input variables \(X_1, ..., X_n\), it is convenient to use vector notation to denote the input variables and their values. This will be indicated by denoting random vectors and their respective values in boldface. Consequently, the input will be denoted by the random vector \(\mathbf {X} = (X_1, ..., X_n)\), and, accordingly, a particular realization of \(\mathbf {X}\) by \(\mathbf {x} = (x_1, ..., x_n)\) (Deisenroth et al., 2020, p. 370). The domain \(D_{\mathbf {X}}\) of the random vector \(\mathbf {X}\) is simply the Cartesian product \(D_{X_1} \times ... \times D_{X_n}\) of the respective domains of the individual random variables \(X_1, ..., X_n\).
This is, for instance, evidenced by the following quotes: “It is always possible to construct a trivial predictor satisfying equalized odds by making decisions independent of X, A, and R” (Hardt et al., 2016, p. 6), “If we think of the decision as a binary prediction of the outcome, then \(b_{00}\) and \(b_{11}\) are the values of true negatives and true positives, respectively.” (Corbett-Davies 2018, p. 7), “we use the following notations: [...] d: predicted decision (category) for the individual (here, predicted credit score for an applicant—good or bad)” (Verma & Rubin 2018, p. 2), and Kusner et al. (2017), who first write “predictor \(\hat{Y}\) is counterfactually fair if (...)” (p. 3) but then “while \(\hat{Y}\) is the actual decision of giving the loan” (p. 5).
The function \(S(\cdot )\) stands for the logistic function. This detail is of no importance to the subsequent arguments in this paper, and only serves the purpose of illustration.
Note that the term bias is here used in the sense of cognitive bias (as opposed to behavioral or emotional bias), and refers to a systematic error in forming propositional attitudes.
This is sometimes (e.g. in legal texts) called indirect discrimination, even though, as some have argued (see, e.g., Eidelson 2015, Ch. 1.2), this is a misleading use of the term discrimination. For this reason, we will give preference to the term distributive injustice.
For the sake of brevity, we use the term good to denote any material object or service that is assumed to have a (positive or negative) utility to individual persons. This includes what is sometimes called economic bads (see, e.g., Varian 2006, p. 41)
Note that the notion of a distinction between biased and unbiased beliefs presupposes that there is an epistemically accessible ground truth from which beliefs can deviate systematically. This is, in particular with regards to concepts such as race or gender, not uncontentious (see, e.g., Malinsky & Bright 2021; Hu 2021). The discussion of this issue, though, is beyond the scope of this article.
Examples of criteria that take into account whether certain propositions are true are equalized odds and group-wise calibration
Examples of criteria for the absence of bias that take the relevant causal mechanisms into account are counterfactual fairness and no-proxy discrimination (Kilbertus et al., 2017)
Note that for full generality, we would need to adjust how we frame the problem of allocative fairness in two respects. First, we would need to frame it in terms of partial/conditional correlations, rather than unconditional correlations. This would mean that \(\mathbf {I}_G\) and \(\mathbf {O}_G\) would contain tuples of properties rather than individual properties. This would allow us to express conditional requirements, for instance, that it is impermissible that the decision outcome \(d_u\) is correlated with \(V_i\) given \(U_i\). Formally, this requirement would be expressed by stating that \((V_i,U_i) \in \mathbf {I}_G\). While it would still hold that the two sets of tuples are disjoint, it would be possible that variables appear in tuples in both, \(\mathbf {I}_G\) and \(\mathbf {O}_G\). It would thus be possible to define allocative fairness conditions in terms of even complex interactions between variables. Secondly, while in the present framework, correlation is defined as a binary property—either two variables are sufficiently correlated or not—we would need to allow the framework to capture different degrees of correlation for different variables. For the sake of conceptual clarity, however, and due to the fact that most distributive principles can be expressed in the framework presented here, we restrict the discussion to unconditional single-threshold correlations.
We could, for instance, use the Pearson correlation coefficient to measure the degree of correlation. As we here have a perfect correlation between criminal behavior and increased monitoring, the coefficient would take the maximum value \(+1\). This would trivially be considered a sufficiently strong correlation.
More precisely speaking, the absolute value of the Pearson correlation coefficient of admission and dyslexia is 0.26, while we would expect it to be 0 (or close to 0) in a fair algorithmic decision system.
The idea of implementing different cut-off thresholds for different protected groups was explored in more detail by Kleinberg et al. (2018)
The data set can be found here: https://github.com/propublica/compas-analysis
A higher false negative rate, on the other hand, reflects a reverse bias: it means that it is more likely to actually be a violent reoffender and yet be deemed to be at low risk of reoffending.
References
Alexander, L. (1992). What makes wrongful discrimination wrong? Biases, preferences, stereotypes, and proxies. University of Pennsylvania Law Review, 141(1), 149–219.
Angwin, J., Larson, J., Mattu, S., & Kirchner, L. (2016). Machine bias: there’s software used across the country to predict future criminals. And it’s biased against blacks. ProPublica.
Bickel, P. J., Hammel, E. A., & O’Connell, J. W. (1975). Sex bias in graduate admissions: Data from Berkeley. Science, 187(4175), 398–404.
Binns, R. (2020). On the apparent conflict between individual and group fairness. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, (pp. 514-524).
Bradley, R. (2017). Decision theory with a human face. Cambridge University Press.
Chouldechova, A. (2017). Fair prediction with disparate impact: A study of bias in recidivism prediction instruments. Big data, 5(2), 153–163.
Cleary, T. A. (1966). Test bias: Validity of the scholastic aptitude test for Negro and white students in integrated colleges. ETS Research Bulletin Series, 1966(2), i–23.
Corbett-Davies, Sam, Pierson, Emma, Feller, Avi, Goel, Sharad, & Huq, Aziz. (2017). Algorithmic Decision Making and the Cost of Fairness. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’17). Association for Computing Machinery, New York, NY, USA, (pp. 797-806).
Corbett-Davies, S., & Goel, S. (2018). The measure and mismeasure of fairness: A critical review of fair machine learning. arXiv preprint arXiv:1808.00023.
Deisenroth, M. P., Faisal, A. A., & Ong, C. S. (2020). Mathematics for machine learning. Cambridge University Press.
Dwork, C., Hardt, M., Pitassi, T., Reingold, O., & Zemel, R. (2012, January). Fairness through awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference (pp. 214–226).
Eidelson, B. (2015). Discrimination and disrespect. Oxford University Press.
Flores, A. W., Bechtel, K., & Lowenkamp, C. T. (2016). False positives, false negatives, and false analyses: A rejoinder to machine bias: There’s software used across the country to predict future criminals. and it’s biased against blacks. Fed. Probation, 80, 38.
Gölz, P., Kahng, A., & Procaccia, A. D. (2019). Paradoxes in fair machine learning. NeurIPS’19.
Goodfellow, I., Bengio, Y., Courville, A., & Bengio, Y. (2016). Deep learning (Vol. 1, No. 2). MIT Press.
Goodin, R. E., & Spiekermann, K. (2018). An epistemic theory of democracy. Oxford University Press.
Halldenius, Lena. (2017). Discrimination and Irrelevance.
Hardt, M., Price, E., & Srebro, N. (2016). Equality of opportunity in supervised learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS’16). Curran Associates Inc., Red Hook, NY, USA, (pp. 3323–3331).
Hedden, B. (2021). On statistical criteria of algorithmic fairness. Philosophy and Public Affairs, 4949(2), 209–231.
Hertweck, C., Heitz, C., & Loi, M. (2021). On the moral justification of statistical parity. In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency (pp. 747–757).
Hu, L. (2021). What is “race” in algorithmic discrimination on the basis of race. Journal of Moral Philosophy.
Kilbertus, N., Rojas-Carulla, M., Parascandolo, G., Hardt, M., Janzing, D., & Schölkopf, B. (2017). Avoiding discrimination through causal reasoning. arXiv preprint arXiv:1706.02744.
Kleinberg, J., Mullainathan, S., & Raghavan, M. (2016). Inherent trade-offs in the fair determination of risk scores.
Kleinberg, J., Ludwig, J., Mullainathan, S., & Rambachan, A. (2018). Algorithmic fairness. In Aea papers and proceedings, (Vol. 108, pp. 22-27).
Kusner, M., Loftus, J., Russell, C., & Silva, R. (2017). Counterfactual fairness. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17). Curran Associates Inc., Red Hook, NY, USA, (pp. 4069-4079).
Lee Rodgers, J., & Nicewander, W. A. (1988). Thirteen ways to look at the correlation coefficient. The American Statistician, 42(1), 59–66.
Lee, M. S. A., & Floridi, L. (2020). Algorithmic fairness in mortgage lending: from absolute conditions to relational trade-offs. Minds and Machines, 1–27.
Lippert-Rasmussen, K. (2014). Born free and equal?: a philosophical inquiry into the nature of discrimination. Oxford University Press.
List, C., & Goodin, R. E. (2001). Epistemic democracy: Generalizing the Condorcet jury theorem. Journal of political philosophy, 9(3).
Malinsky, D., & Bright, L. K., (2021). On the causal effects of race and mechanisms of racism. Unpublished manuscript.
Moreau, S. (2010). What is discrimination?. Philosophy & Public Affairs, 143-179.
Pettigrew, R. (2016). Accuracy and the Laws of Credence. Oxford University Press.
Sen, A. K. (1971). Choice functions and revealed preference. The Review of Economic Studies, 38(3), 307–317.
Rawls, J. (1971). A theory of justice. Belknap Press/Harvard University Press.
Suzumura, K. (2009). Rational choice, collective decisions, and social welfare. Cambridge University Press.
Varian, H. R. (2006). Intermediate microeconomics with calculus: a modern approach (7th ed.). WW Norton & Company.
Verma, S., & Rubin, J. (2018). Fairness definitions explained. In 2018 ieee/acm international workshop on software fairness (fairware), (pp. 1-7). IEEE.
Walzer, M. (1983). Spheres of justice: A defense of pluralism and equality. Basic books.
Acknowledgements
I am grateful for detailed feedback on earlier drafts of the manuscript from Christian List, Richard Bradley, and Liam Kofi Bright. I would also like to thank two anonymous reviewers at Minds and Machines, as well as the audience members at the Algorithmic Fairness Workshop Copenhagen for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beigang, F. On the Advantages of Distinguishing Between Predictive and Allocative Fairness in Algorithmic Decision-Making. Minds & Machines 32, 655–682 (2022). https://doi.org/10.1007/s11023-022-09615-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11023-022-09615-9