1 Introduction

The topic of representations is one of the most debated topics in philosophy of cognitive science. Despite the fact that the representational debate has been around for a long time there is only little agreement on what exactly representations are, how they gain their contents, whether representations even exist and, if they exist, whether they play a functional role in cognitive processing (Ramsey, 2007; Gładziejewski, 2016; Dolega, 2017; O’Brien & Opie, 2004; Hutto & Myin, 2012). The latter query casts into doubt whether it is necessary to evoke the notion of representation to understand different aspects of action, planning, and cognition (Ramsey, 2007; Hutto & Myin, 2012).

Here, we use the claim that genuine representations exist as a background assumption. We argue that an important part of what makes representations explanatorily relevant are the degrees to which representational features (i.e., features of representations – more on this in the following section) are expressed. We will call this the “gradual features hypothesis”. A similar proposal, i.e., “representational gradation”, has been implicitly present in the representation debate for some time (see for example Clark & Toribio, 1994). However, both the empirical grounding of this idea as well as the consequences of adopting a gradual hypothesis remain greatly underspecified.

Our thesis that representational features come in degrees will be explored within the framework of predictive processing (PP from now on). Embedding our thesis in this neuroscientific framework will enable us to connect the “gradual features hypothesis” to relevant theoretical and empirical work. In developing our proposal, we evaluate two features of (structural) representations, structural similarity and decoupling. We argue that structural similarity can be cast in terms of the number of exploitable internal relations and state space granularity. We show that both of these dimensions can occupy multiple values which in turn implies that structural similarity is a graded notion. We further argue that decoupling is gradual in two ways. First, we show that different brain areas are involved in decoupled cognitive processes to a greater or lesser degree depending on the cause (internal or external) of their activity. Second, and more importantly, we show that the degree of decoupling can be further regulated in some brain areas through precision weighting of prediction error. Lastly, we argue that regulating the degree to which each representational feature is expressed importantly contributes to successful behavioural performance. Conversely, inflexible or inappropriate (for the situation) regulation of representational features underlies suboptimal behavioural performance such as echopraxia, overgeneralisation in category learning in children, and hallucinations under the influence of psychedelics.

The paper is structured as follows. First, we introduce the framework of PP and some of its key principles that are relevant for our thesis. Second, we present two conflicting accounts of the existence of representations and their arguments. Third, the concept of structural representation is introduced and two of its core features are discussed, structural similarity and decoupling. Then, we briefly discuss three existing accounts of gradual representations, which we build on in several ways in our “gradual features hypothesis”. Finally, we present our main thesis, i.e., that representational features are gradual and need to be regulated. We discuss what makes representational features gradual and then we suggest what PP mechanisms might be involved in modulating the gradation of these features. Following this, we argue that behavioural success of cognitive systems depends on the gradation of representational features. We round off with concluding remarks and present some avenues for future research. We suggest that our “gradual features hypothesis” may be relevant both for existing representationalist as well as for non-representationalist accounts.

2 Predictive processing in a nutshell

2.1 The problem of underdetermination in perception

Our brains are continuously presented with a stream of sensory observations which is ambiguous and noisy. For one sensory input there are multiple possible underlying causes, a problem that has been called “perceptual underdetermination” (e.g., Orlandi, 2016). The brain also needs to integrate sensory observations from multiple modalities as well as cope with internal noise that is present in biological systems (Rescorla, 2016). In other words, the brain is confronted with the causal inference problem: it must infer the causes generating the noisy and ambiguous sensory observations across modalities. In cognitive science the process of causal inference has been cast as Bayesian inference, i.e., a normative method of combining prior expectations (formed through learning) and sensory observations via Bayes’ rule (e.g., Perfors, 2011). Importantly, whilst Bayesian cognitive science postulates that the brain conducts Bayesian inference it does not explain how it does it (Williams, 2018). What is needed is an algorithmic-level explanation of how the brain implements Bayesian inference (Colombo & Seriès, 2012) – PP is an attempt at filling this gap. PP is a very influential paradigm in computational cognitive neuroscience (e.g., Clark, 2013a, 2016; Hohwy, 2013; Rao & Ballard, 1999) which postulates that Bayesian inference is carried out by hierarchically organised generative models where, importantly, only the difference between expected and sensory observations is propagated through the levels of the hierarchical generative model (Friston et al., 2016). Building on these basic cognitive mechanisms, PP aims to provide a unifying framework for understanding cognition, action and perception (Friston, 2010).Footnote 1 As a consequence, various cognitive domains have been explored through the lens of PP such as perception (den Ouden et al., 2012), action (Yon et al., 2018), planning (Kaplan & Friston, 2018), communication (Friston & Penny, 2011), learning (da Costa et al., 2020) and mentalizing (Koster-Hale & Saxe, 2013).

2.2 The functionality of hierarchical generative models

Generative models encode sensory observations and model underlying processes that generate these observations (Clark, 2013a, 2016). At the higher, cortical areas of the brain, top-down predictions are made about the distal causes underlying sensory observations which are then sent to the lower levels of the hierarchy, triggering an expected pattern of activation. Lower areas of the hierarchical generative model receive sensory observations and compare them to the expected pattern of activation (SanMiguel et al., 2013). Based on the difference between the predicted observation reflected in the expected activation pattern and the actual sensory observation, prediction error is computed (Friston & Kiebel, 2009; Clark, 2013a).

Prediction error however is not only a difference between the predicted and the actual sensory observation. Prediction error has to be weighted by its precision, which signals how important the error is for learning, and how reliable the prediction error is (Feldman & Friston, 2010; Clark, 2013b). Based on this the brain estimates how the prediction error should affect learning and hence to what extent the error should be used for updating the generative model. Errors that are expected to be noisy or unimportant will be down-weighted by having low precision. In such situations changing the internal model to minimise prediction error will not reliably increase perceptual accuracy. Conversely, important and reliable prediction errors will be up-weighted by having high precision. Only prediction errors with high precision will be accumulated and assimilated in higher levels of the generative model (Kanai et al., 2015).

From the point of view of PP, minimising prediction error is the primary goal of computations in the brain (e.g., Friston & Kiebel, 2009). Prediction error can be minimised in one of two ways; either through action (sometimes also referred to as “active inference”) or perception (also referred to as “perceptual inference”) (Friston et al., 2011; Clark, 2016). In what follows, we will be using the terms “perception” and “action”, instead of “perceptual inference” and “active inference”, so as not to confuse action with active inference as a theoretical framework (which is, roughly, constituted by a class of models that extend PP in certain respects). When prediction error is detected, the error-indicating activity is propagated to the level above, which results in an adjustment of the parameters of probabilistic representations at that level. This in turn allows top-down predictions to explain away prediction error at lower levels. This process is characteristic of perception (Friston et al., 2011). The alternative process of minimising prediction error through action is aimed at changing sensory input, in order to make it conform to top-down predictions (Friston et al., 2011). In doing so, future prediction error will be smaller.

3 Representation wars in predictive processing and the job description challenge

Whilst central to cognitive science and philosophy of mind, the characterisation of representations and the attribution of representational status has been a controversial topic for a long time. Here, we briefly describe what has come to be labelled as the “representation wars” (Williams, 2018; Clark, 2015) in the context of PP.

To assess whether a representational posit deserves its label, Ramsey (2007) identifies a challenge that every purported representation needs to pass, the job description challenge. The job description challenge consists of showing that the cognitive structures in question have a genuinely representational function. For something to function as a representation it needs to play a causal role in a cognitive system, where causal relevance constitutes explanatory relevance. Furthermore, the roles played by representations must “provide us with conditions that delineate the sort of job representations perform, qua representations, in a physical system.” (Ramsey, 2007, p. 27). In particular, a structure or a state needs to be not just explanatorily relevant, but it must be explanatorily relevant in virtue of functioning as a representation.

One way in which the job description challenge can be met is via what Gładziejewski (2016) calls the compare-to-prototype strategy. The first step in applying this strategy is to think of a prototypical representation, a structure “that can be pretheoretically categorized as a representation in an uncontroversial way. In particular, one concentrates on the functions served by the structure in question—on what it does for its users that makes it a representation. This is our representational prototype” (Gładziejewski, 2016, p. 564). The second step involves a functional comparison between a representational prototypeFootnote 2 and a cognitive structure in question. In doing so, one evaluates whether the cognitive structure under consideration plays a functional role that is similar enough to the functional role of the chosen representational prototype (Gładziejewski, 2016).

By applying this strategy Gładziejewski shows that generative models in PP play a map-like and hence representational functional role in the following way. Generative models can be modelled as Bayesian networks (Pearl, 2000) whose structure resembles the causal structure of the environment. Specifically, generative models capture the causal structure in three ways: by hidden or latent variables, their relations (this is how the dynamics of causal-probabilistic relations in the world is encoded), and by prior probabilities. Generative models further afford action guidance as they can be exploited for guiding action in virtue of them correctly representing the environmental structure. Generative models can also be decoupled – brain areas that are usually engaged in perception and action control can give rise to fully offline cognitive processes such as imagining (Moulton & Kosslyn, 2009) and thinking (Williams, 2020). Lastly, generative models detect errors where the source of misrepresentation can be two-fold. Error either arises from an inaccurate model or due to a model misapplication in light of an unreliable, noisy signal (Gładziejewski, 2016). Thus, generative models in PP, like the representational prototype of cartographic maps, function as genuine structural representations (Gładziejewski, 2016; Gładziejewski & Miłkowski, 2017; Wiese, 2018; Williams, 2018; Kiefer & Hohwy, 2018). We present structural similarity and decoupling more in detail in the next section as they are central to our proposal.

The line of reasoning presented above supports the representationalist stance. Three historic and foundational challenges have been posed to representationalism: concerning representational content, cognitive function and representational function (Williams, 2018). The first challenge, also called the “content determination problem” (Von Eckardt, 2012), is to “identify the natural properties, relations and processes that determine the intentional properties of internal representations without circularity” (Williams, 2018, p. 145, see also Wiese, 2017). The second challenge is grounded in ecological perception (Gibson, 2014), and presents the pragmatic turn away from representation-centred cognition to cognition for action. Here, the brain is primarily understood as a control system for interaction with the environment as opposed to reconstructing the structure of the environment. Hence, the question is whether representations are needed at all (Anderson, 2017; Chemero, 2009; Pezzulo, 2016). The third challenge is to show that representational content is causative, i.e., for a cognitive structure to qualify as a representation it needs to be exploited to guide behaviour of the cognitive system to which it belongs (Shea, 2018; Ramsey, 2007). More recently, in relation to the third challenge, opponents of representationalist views have objected that structural representations do not meet the job description challenge (Facchin, 2021b; van Es & Myin, 2020), that they do not differ in kind from (non-representational) detectors (Nirshberg & Shapiro, 2021), and that generative models are not structural representations (Facchin, 2021a).

For ease of exposition, our proposal is aligned with the representationalist position. However, importantly, our argument does not constitute an argument in favour of a representalionalist position. In the conclusion we even suggest that our contribution may be of relevance to anti-representationalist positions (but we do not defend that claim in this paper). Here, we argue that degrees of structural similarity and decoupling need to be taken into account.

4 Structural representations

For the purposes of our research we will only examine two functional properties of structural representations; structural similarity and decoupling (note, decoupling is different from detachment, which we explain more in detail in Sect. 4.2 Decoupling). In the following, we present more in detail what structural similarity and decoupling of representations pertain to, according to the received view. Note that we elaborate on and refine the classical treatment of these two functional properties in later parts of the manuscript.

4.1 Structural similarity

Structural similarity pertains to representations sharing (to a sufficient degree) a relational structure with whatever they represent (i.e., a target object). In other words, structural similarity is a result of relations between the parts of a target object being preserved under a mapping (Shea, 2018; Gładziejewski, 2016; Gładziejewsky & Miłkowski, 2017). A cartographic map is an example that illustrates structural similarity. Cartographic maps consist of points and spatial relations between them. Points A’, B’, and C’ on a map may, for instance, correspond to buildings A, B and C. If we observe that building A is closer to building B than it is to C, then points on the map should preserve this relation: point A’ on the map should be closer to B’ than it is to C’ (O’Brien & Opie, 2004). If spatial relations between buildings in an area are preserved by the spatial relations that hold between the corresponding parts on the map, then we can say that the map is structurally similar to the area.Footnote 3

Defining structural similarity more rigorously is a challenging task. Intuitively, we can judge whether two cartographic maps are similar to each other or not. However, making the intuitive notion of similarity precise is non-trivial for at least two reasons. First, identifying structural similarity with the existence of a structure-preserving mapping trivialises the notion of structural similarity, because it seems that arbitrary mappings can be defined by an observer (a version of this problem is known as Newman’s problem, see Newman, 1928, p. 144). Second, whether one representation is (structurally) more similar to the representandum than another representation can depend on the purpose for which the representation is used.Footnote 4 This suggests that measuring structural similarity independently of the context is impossible (Goodman, 1972, p. 445).

Because of considerations like these, structural similarity needs to be defined not only in terms of the existence of a structure-preserving mapping between two systems. The standard way of enriching this definition is to require that the structure preserved under the mapping be exploitable (e.g., Shea, 2007, 2018). That is, it must be possible to use the structural information contained to guide action (Gładziejewski, 2016). Take for example a cartographic map. Users of cartographic maps successfully navigate the environment due to structural similarity between the spatial structure of the map and the spatial structure of the area it represents (Gładziejewsky & Miłkowski, 2017; Gładziejewski, 2016). In this case, a mere existence of a structure-preserving mapping is not sufficient to account for a successful navigation. The users must also be able to take advantage of the structure embodied by the map. Furthermore, the use-condition specifies a context for determining which relations are relevant when it comes to evaluating structural similarity. For instance, if a person is unable to make sense of contour lines, they will not even be able to use information about elevation in a cartographic map (that features contour lines). Consequently, such a map will be highly similar to a map lacking contour lines for this person (at least when it comes to using the map to navigate; things may be different when the person is asked to judge if the maps “look” similar to one another).

4.2 Decoupling

For a representation to be called decoupled it needs to be independent of specific stimulus conditions (e.g., Ramsey, 2007; Shea, 2018). Decoupled representations operate independently of external stimulation and as such they can generate behavioural responses based on internal stimulation alone. A decoupled representation can be distinguished from a detector or a causal mediator (Ramsey, 2007). Whilst information afforded by a genuinely decoupled representation can be used independently of external stimulation, a causal mediator presents merely a stage in the processing of the sensory stimulus. In short, decoupled representations play an information-carrying role and mediators do not have such a role (Ganson, 2020). In that context it is important to further distinguish decoupled representations from detached representations that “stand for objects or events that are neither present in the situation nor triggered by some recent situation” (Gärdenfors, 1995, p.1, see also Gładziejewski, 2016 who subscribes to the detachment requirement as well). A decoupled representation, by contrast, can be about currently present objects; however, the causal connection to the current environment must be at least loosened for the representation to count as decoupled.

Early empirical evidence of what is now known as decoupled representations comes from studying rodent navigation (Tolman, 1938)Footnote 5. In one of his experiments Tolman (1938) found that the experimental rats that had previously learnt the roundabout route to a goal point switched to a more direct path immediately if the familiar route was blocked. Based on this, Tolman reasoned that rodents must “have access to spatial knowledge about the environment, akin to the spatial knowledge obtainable from a map, that could be used to guide behaviour in a flexible manner” (Epstein et al., 2017). Building on these initial findings it has been found more recently that place cells in hippocampus, which are “normally associated with the animal’s spatial position, can also fire when the animal is outside its standard “place field,” especially during periods of rest or sleep, and at decision points” (Pezzulo, 2016, p. 2). There is another kind of internally produced neuronal sequence which is signified by a specific theta rhythm (8–12 Hz). The latter is activated when animals are engaged in decision tasks and when they are anticipating the consequences of their choices. More broadly, these internally generated sequences have been suggested as plausible neural correlates of “what-if” scenarios and forward-modelling processes (Johnson & Redish, 2007; Wikenheiser & Redish, 2015).

Relating these two complementary examples to the discussion on decoupled representations, we can say that cognitive structures that support spatial navigation carry relevant information about the structure of the external environment. This information plays an important role for the cognitive system as it can be further exploited to guide its behaviour even in the absence of external stimulation (or, in the case of rats, the so-called mental map can be used for finding an alternative path when the previously used path has been blocked).

So far, this characterisation of decoupling has focused on extreme cases (i.e., either completely decoupled or coupled). However, this overlooks that the degree to which one part causally influences another can vary. For instance, a mechanism computing a weighted average will produce a representation of a value (i.e., the weighted average), and the result will be influenced to varying degrees by different parts of the mechanism (i.e., the values that are weighted and averaged). The degree to which a given part affects the result will be specified by the weight associated with the represented value of that part. In this example, the causal influence (and hence, coupling), is proportional to the relative weight associated with the represented value. We will come back to the point that causal coupling comes in degrees in the later sections.

4.3 Existing accounts of gradual representations

Before unpacking our “gradual features hypothesis” we provide a brief overview of accounts according to which either representations or representational features are gradual. This will enable us to point out how our proposal differs from existing accounts and to clarify what our proposal entails (and what it does not).

To the best of our knowledge, Clark and Toribio (1994) were the first to propose that representations might be gradual. In trying to reconciliate anti-representational with representational accounts, Clark and Toribio argue for a “rich continuum of degrees and types of representationality” (Clark & Toribio, 1994, p. 1). They suggest that at the one end of the continuum there are cognitive processes that arise as a result of a direct coupling between the cognitive system and the environment (hence are barely representational) and at the other end of the continuum there are cognitive processes that function independently of external stimulation and are as such fully dependent on internal representations. The continuum, according to Clark and Toribio (1994), is differentiated based on the computational effort needed to transform the sensory input into a form usable by a cognitive system.

In contrast to Clark and Toribio (1994), we shall argue that the benefit of taking gradation seriously is not primarily that it allows a synthesis of representationalist and anti-representationalist accounts, but rather that it puts gradual features of structural representations at the centre stage. In particular, we do not argue that representationality itself is gradual, but only that the ability to flexibly modulate degrees of representational features is explanatorily relevant.

In his seminal paper on the nature of representations in PP Gładziejewski (2016) notes that detachment can be gradual: internal models guide action in a similar way as an electronic map connected to the GPS system that is guiding a car. The action guidance achieved by means of an internal model though is attuned to the environmental input at all times. Therefore, even though it might appear as if the cognitive system operates based on the internally driven processes, these processes are constantly being updated on the basis of external input. Hence, internal models do not operate in a fully detached manner due to them receiving a “constant corrective feedback” to use Gładziejewski’s term. In a related vein, Gładziejewski and Miłkowski (2017) argue that: “[…] structural similarity can be easily construed as a gradable relation, depending on the degree to which the structure of one relatum actually preserves the structure of the another [sic] relatum (see note 1; for another account that explicitly defines similarity as coming in degrees, see: Tversky, 1977; Weisberg, 2013). This way we can treat X as capable of taking a range of values {X1, X2,…, Xn}, where each increasing value corresponds to an increased degree of similarity between the vehicle and the target. Therefore, between the lack of any similarity and a complete structural indistinguishability, there is a range of intermediate possibilities” (2017, p. 342). The mechanisms that regulate gradation of structural similarity (Gładziejewski & Miłkowski, 2017) and detachment (Gładziejewski, 2016), as well as the explanatory value of this gradual idea, are not explored further in either of the two accounts therefore leaving the “gradual features hypothesis” with a familiar but underspecified status.

A slightly different take on the gradual argument has also been proposed. Namely, some authors have suggested that structural representations and detectors are not different in kind but only gradually differ in terms of their state space granularity (Morgan, 2014; Nirshberg & Shapiro, 2021; see the following section for more on state space granularity). According to this view, detectors are very simple structural representations. An example would be a collision warning system in a car that signals the presence of a potential collision object in front of the car. A simple system could generate a single sound whenever a collision object is within a certain distance from the car (depending on the car’s current speed). Such a system would function as a detector that indicates only that there is a collision object. A more sophisticated system could use different types of sound (say, a louder or higher-pitched sound if the collision object is closer to the car). Such a system would have a higher state space granularity (see below). Within the state space, differences between the volume (and pitch) of the sounds would correspond to differences in the spatial distance between the car and the collision object. At some point, the structural similarity (and state space granularity) could be sufficiently rich, so as to render the system a genuine structural representation.

Although this emphasises that the level of state space granularity is relevant to understanding structural representations, it does not amount to the claim that regulating state space granularity (and other gradual features of structural representations) is explanatorily relevant. We will clarify and argue for this point in more detail below. As a guide for intuition, consider the following extension of the example just given. If the same system is also used to aid during parking, it is useful to signal the distance to other parked cars in a more fine-grained manner (i.e., increasing state-space granularity), because that enables the driver to use the available space more efficiently. By contrast, an increased state-space granularity at high speed on a highway would be unnecessary or even confusing.

5 Thesis: Representational features are gradual, and their gradation underlies behavioural success of cognitive systems

In the following, we unpack the main thesis of our paper: representational features are gradual, and gradation has important implications for the behavioural success of cognitive systems. We first provide an account of what PP mechanisms might underlie representational features (i.e., structural similarity and decoupling) and then we show that representational features are gradual. Next, we argue that representational features, in virtue of being gradual, underlie behavioural success of cognitive systems.

5.1 Gradual structural similarity

5.1.1 Regulating state space granularity and number of exploitable relations as mechanisms of gradual structural similarity

In general, structural similarity pertains to a representation sharing the structure with a target object where the preserved structure is exploitable (Shea, 2007, 2018; Gładziejewski, 2016). In the example of a cartographic map, the preservation of structural properties is most readily explained in terms of spatial relations between points on the map (which resemble spatial relations between points in the represented territory). Call such structural properties “exploitable internal relations”. One way of increasing structural similarity – or, rather, level of detail – is to increase the number of exploitable internal relations (that track relations in the representational target). In addition to this, structural similarity can also be defined in terms of another dimension, i.e., state space granularity, which we describe next.

Traditionally, generative models in PP have been operationalised in terms of Gaussian densities (or, more generally, continuous distributions). However, recently Friston and colleagues (2015) introduced a distinction between models that use Gaussian densities and models that use categorical probability distributions. Taking this on board, Kwisthout and van Rooij (2015) argued that a crucial difference between the two is that in categorical distributions the notion of granularity plays a vital role. While the amount of precision in a Gaussian distribution is sufficiently described by its variance, precision in categorical distributions must be described in terms of entropy (Shannon, 1948) – where the latter is a function of variance and state space granularity. It is the granularity of a probability distribution that specifies the level of detail of that distribution (Kwisthout & van Rooij, 2015). By clustering the values that a given distribution can take, the level of detail is changing. That is, the more clusters the distribution has, the more detailed it is and the other way around. The level of detail is a context-dependent property. Which level of detail will be recognised in the model and further utilised in a particular context is determined by context-dependent hyperparameters (Kwisthout et al., 2017)Footnote 6.

Below, we provide a practical example that illustrates the notion of state space granularity. Imagine you are meeting a friend in a cafeteria and the only thing that you know about her drinking preferences is that she likes drinking tea. In making a guess about her order you can employ two strategies: you can either increase the state space granularity of your prediction by predicting that she will order green jasmine tea or decrease the state space granularity by predicting that she will drink tea. In other words, you can sample your guess from models that are more or less specific. A specific model has a high state space granularity (bottom part of the flow chart in Fig. 1) and a less specific model has lower state space granularity (top part of the flow chart in Fig. 1).

Fig. 1
figure 1

Visual depiction of different levels of state space granularity. Grey boxes present hypotheses/predictions that are increasing in their state space granularity.

Full size image

Note that it is important not to confuse the level of detail with accuracy as they are orthogonal terms.Footnote 7 Whilst the level of detail depends on the grain at which the representation can structurally resemble its target (how many relations could in principle be encoded in the representation), accuracy corresponds to how many relations are correctly preserved between the representation and the target. To showcase the difference between accuracy and the level of detail consider again the tea example above. In one scenario you make a prediction about your friend’s order at a high level of detail, so you predict that she will drink green jasmine tea. It turns out that she will in fact have black tea with vanilla. Despite the fact that your prediction had a high level of detail it was not accurate. In another scenario you make a prediction at a low level of detail so you only predict that your friend will order tea. She does indeed order tea, a black tea with vanilla. Although your prediction was low in detail it was entirely accurate.

Next, we provide an example showing that two dimensions of structural similarity, i.e., state space granularity and the number of exploitable internal relations, are distinct in important ways and hence cannot be subsumed by one another.Footnote 8 Imagine two cartographic maps x and y which both depict locations of five cities (Fig. 2). Spatial relations between the cities as well as differences in their size are the same on both maps. The one difference between the two maps is that in map y the variable colour comes in three different values whereas colour in map x comes only in two values – the former has a higher level of detail compared to the latter, and in this sense can be regarded as more “structurally similar” to the actual city. In both maps the darkness of the colour indicates the size of the city (the darker, the bigger). If we compare cities D and E on both maps, the representations are the same in terms of the number of exploitable internal spatial relations. Based on both maps we can also infer that city D is bigger than city E. However, map y conveys more information about the cities than map x; based on map y we can infer that city D is indeed big but not the biggest (city A and B are bigger). Map x does not afford this information as it is only able to differentiate between small and big cities but nothing in between.

Fig. 2
figure 2

State space granularity and the number of exploitable relations are distinct concepts. The number of exploitable internal relations in maps y and map x is the same. However, they are different in terms of the state space granularity, i.e., map y is more detailed than map x in this respect.

Full size image

In sum, structural similarity can be defined with regards to two dimensions. On the one hand, it can be thought of in terms of relations between parts of a representational vehicle that are used in a way that is conducive to the success of a cognitive system. This is what we call the number of exploitable internal relations. On the other hand, the parts of a structural representation can themselves carry information for the system, independently of relations to other parts that are currently tokened. This is what we call state space granularity. Both of these features are gradual, i.e., a structural representation can have a higher or lower state space granularity than another representation, and the number of exploitable internal relations can also vary.

5.1.2 Empirical evidence for the regulation of state space granularity in the brain

Empirical evidence on the regulation of state space regularity in the brain is scarce. One suggestion has been recently put forward that the 5-HT2A receptors in layer V pyramidal neurons are involved in the regulation of the level of detail (Pink-Hashkes et al., 2017). Hyper-activation of the said receptors has been proposed to lead to the so-called decomposition of predictions, i.e., a broad categorical prediction is broken down into sub-categories (Pink-Hashkes et al., 2017). So called “decomposed predictions” originate in the prefrontal, parietal and somatosensory cortex and are fed back to the lower levels of the cortical hierarchy.

5.2 Gradual decoupling

Here, we describe two ways in which neural representations can differ in their degree of decoupling. On the one hand, some brain areas are farther away from the sensory periphery than others and are therefore less directly affected by the environment, whereas other brain areas are closer to the sensory periphery. In other words, there are neural structures whose activation (and hence their causal involvement in the cognitive system’s behaviour) is largely dependent on external stimuli (e.g., retina), but also representations whose activation relies on external stimulation only to a small degree (e.g., prefrontal cortex). We provide some empirical evidence that supports the idea that there are differences in how much neural structures depend on internal vs. external stimulation. This provides a “default” decoupling of each neural structure, which broadly determines the range of their decoupling.Footnote 9 On the other hand, the decoupling of some neural representations can be further regulated through precision weighting of prediction error. The challenge then is to show that neural structures at different levels of the hierarchical generative model are affected by precision weighting – the ones that are will have this extra flexibility with regards to decoupling. We provide empirical evidence in support of both of these forms of gradual decoupling.

5.2.1 Different brain areas afford different degrees of decoupling

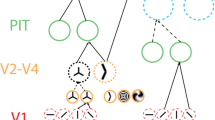
Retina.

While one might think that the retina only receives and relays visual sensory signals, one of its main functions is actually to filter the incoming signals (lateral and temporal inhibition; for an overview of information processing in retina see Dowling, 2012). Here, we discuss lateral inhibition through the prism of predictive coding, which is used as a procedure that reduces the signal amplitude by getting rid of predictable and therefore redundant elements in the sensory stimulus. In that way sensory signals coming to the system are easily recognisable from the intrinsic noise (which limits information capacity of neurons) coming from the central nervous system (Srinivasan et al., 1982). Lateral inhibition reduces the range of inputs presented to a neuron by making use of the correlation between adjacent points in a visual scene. The signal from the centre of the receptive field is estimated based on the weighted linear sum of the signals from the surrounding receptors. The weighted sum defines an inhibitory surrounding that is subtracted from the arriving signal and thereby minimises its amplitude (Srinivasan et al., 1982).

What the above example showcases is that even the activity of structures involved in early visual processing (e.g., retina) is not entirely externally driven. Namely, the interneurons compute the estimate of the coming signal based on the activity of the surrounding neurons and their activity is also influenced by the top-down internal noise. Still, early visual processing largely depends on the external sensory influx. Therefore, we suggest that the retina is an example of a structure that is very low on the decoupling continuum.

Primary visual cortex.

One example of a neural structure that has a moderate degree of decoupling is V1, also known as primary visual cortex. Whilst traditionally thought of as being entirely dependent on external stimulation, it has been recently proposed that neural activity at V1 can be partly explained by the top-down processing. In other words, V1 can get activated in the absence of visual sensory stimulation (Petro, 2016; Muckli et al., 2015; Edwards et al., 2017). In their experiment, Chong and colleagues (2016) used inducer stimuli to showcase that the motion prediction that was projected back to V1 contained information about textural detail. The information that they could read out from V1 was about an object’s rotational movement as it moved through the visual field. Importantly though, sensory input that the brain received did not contain information about the rotation. Instead, the rotational information was made out by the brain based on its prior experience and accumulated knowledge. Drawing on these experimental findings Petro and colleagues (2016) suggest that the activity of V1 depends on two information streams; external (i.e., it carries information coming from the environment) and internal (i.e., it carries internally generated signals) stream. The external stream provides highly detailed input coming from the retina that is processed with high spatial acuity. The internal stream carries more abstract information and provides less precise, internally generated cortical feedback.

Default mode network.

The default mode network constitutes an example of a highly decoupled neural structure. The default mode network includes the medial temporal lobe, a subsystem of the medial prefrontal, posterior cingulate cortex, and inferior parietal lobe (Buckner et al., 2008). It is well-known for being active when people are not attending to the external world (Shulman et al., 1997; Mazoyer et al., 2001; Raichle et al., 2001). It is thus involved in more or less temporally distant internally simulated cognitive processes such as daydreaming, imagining, mind-wandering, thinking about the past and planning the future (e.g., Buckner & Carroll, 2007; Buckner et al., 2008). Important for our thesis is the fact that the brain areas constitutive of the default brain network are, at all points, highly influenced by top-down expectations (since the said network is activated in the absence of attention to sensory stimulation).

More generally, activity of the brain areas that are associated with higher order cognitive functioning relies to a large extent on prior knowledge and experience, thus being less dependent on a direct sensory stimulation. Therefore, we make a schematic suggestion that the brain areas involved in higher cognition (such as brain areas constitutive of the default mode network) are largely decoupled. This puts them on the other end of the decoupling continuum.

The examples above are by no means supposed to represent an exhaustive overview of the decoupling continuum. Rather, they serve as an illustration of how to think about a continuum of “default decoupling” and what differences in the degree of decoupling pertain to.

5.2.2 Precision weighting of prediction error as a mechanism of gradual decoupling

Clark (2013b) suggests that precision weighting of proprioceptive prediction error could be involved in the regulation of offline and online cognitive processes. When we imagine an action our motor actions are “entrained by proprioceptive expectations and cannot here ensue” (Clark, 2013b, p. 3), whereas all other parts of the generative model are ready to engage in action. This means that during imagining, the motor parts of the generative model get activated as if the action was carried out. What blocks the action and hence enables imagination is the weight of proprioceptive prediction error being dampened. By setting the precision of proprioceptive prediction error low, a cognitive system is free to deploy a generative model offline. Only if exteroceptive prediction error is low (attenuated) in relation to the proprioceptive prediction error, can proprioceptive prediction error be sustained and ultimately decreased by moving. Clark (2016, p. 158) concludes: “For according to PP it is the minimisation of proprioceptive prediction error that directly drives our own actions, as those high-precision predictions become fulfilled by the motor plan.” This suggests that certain prediction error units that are given increased weight become likely candidates for driving response, learning, and action. Conversely, if proprioceptive prediction errors have low precision weights (relative to other sensory prediction errors), action is inhibited and a cognitive system can engage in offline motor simulations.

Whilst Clark’s (2013b) proposal is about the role of precision weighted proprioceptive prediction error, we argue that precision weighting of any type prediction error has a similar function. That is, by downplaying the effect of prediction error at a given level, a cognitive system disengages from sensory stimulation, such that representations at that level are relatively more strongly affected by top-down signals. Important for our argument about the role of precision weighting in decoupling is that precision weighting plays an important role in deciding to what degree a cognitive system is free to disengage from the sensory stimulation and rely on internal simulation instead. We provide concrete examples (i.e., echopraxia) of this under 5.3.

5.2.3 Empirical evidence for precision weighting of prediction error in the brain

Empirical evidence of precision weighted prediction error has been found in different brain areas. Pulvinar, the largest nucleus of the thalamus, has been suggested to encode and regulate expected precision of prediction errors at different levels of the cortical hierarchy (Kanai et al., 2015). The pulvinar has specifically strong connectivity with the visual cortex. Saalmann and colleagues (2012) found direct evidence for the pulvinar’s key role in precision weighting in their study of the spike-field coherence. They showed that the spike field coherence between the neurons of the pulvinar and alpha oscillations in V4 and TEO (brain area situated at the junction between the occipital and temporal lobes) was amplified when attention was allocated to the receptive field of the pulvinar neurons. As the authors point out, this “provides empirical evidence that the pulvinar serves as a gain control system […] to adjust effective synaptic gain transiently across cortical regions [Crick, 1984; Saalman et al., 2012]” (Kanai et al., 2015, p. 8). Another study (Purushothaman et al., 2012) found that the inactivity of the lateral pulvinar suppressed the activity of the V1 neurons in response to the visual input. Conversely, excitation of the pulvinar neurons increased the responsiveness of the V1 neurons. Evidence for the precision-weighted prediction errors has also been found in the cortical areas such as superior frontal cortex (Haarsma et al., 2020). The activity of the dopaminergic neuromodulatory system mediates the precision weighting in these cortical areas. Conversely, dysfunctions in the dopaminergic neuromodulatory system result in impaired precision-weighing in these areas and has been reported to result in psychotic symptoms (Adams et al., 2013; Fletcher et al., 2009).

5.3 Behavioural performance depends on the gradation of representational features

Next, we present a few examples in which regulating either decoupling (via precision weighting of prediction error) or structural similarity (via state space granularity) is compromised and we discuss the effects this has on behavioural performance of cognitive systems. Given the importance of representational features for behavioural success, we propose that a significant part of the explanatory work is done by determining how representational features are regulated.

The first example is given by echopraxia (involuntary movements). Normally, when observing others, we are able to refrain from involuntarily mimicking them. Mirror neurons that are involved in action observation can be divided into two kinds. The first kind responds to action and action observation and the second kind is activated by action and is suppressed during action observation (Kraskov et al., 2009). Action observation goes along with lowering precision in units that thereby attenuate spinal prediction error (Friston et al., 2014). This in turn will attenuate spinal reflexes and preclude echopraxia (i.e., motor representations will be decoupled; Vigneswaran et al., 2013; Shipp et al., 2013). Conversely, if precision of prediction error was accidentally set high when observing an action, the latter would turn into an actual action.

An example where regulating the level of detail is of primary importance is development of (category) learning in children. Children’s category learning follows a U-shaped curve (e.g., Siegler, 2004). The U-shaped learning denotes learning where a child seems to have correctly acquired some pieces of knowledge initially thus making error-free categorical predictions; this phase is then followed by a period where a child is making incorrect categorical predictions (a period known as overgeneralisation); the U-shaped learning is concluded by a child eventually learning to make categorical predictions at the right level of detail by self-correcting. What explains the curious case of children being able to make predictions at the right level of detail initially is that, if the learning data set is small enough, they “can simply memorize individual data points in addition to choosing among hypotheses about them” (Perfors et al., 2011, p. 11). At the end of the U-shaped learning, however, children have acquired a theory that equips them with a true understanding of the entities it consists of. Hence, children are able to correctly adjust the level of detail of categorical predictions based on the context once they have undergone this developmental process.

In the previous section we explained how the 5-HT2A receptors in layer V pyramidal neurons are involved in regulating of the level of detail (Pink-Hashkes et al., 2017). Specifically, hyperactivation of the cells in layer V is supposed to decompose a broad prediction (that is encoded by this neural population) into an overly detailed prediction, i.e., “decomposed prediction”. Pink-Hashkes and colleagues further suggest that the hyperactivation of the said receptors can explain various effects of psychedelics, such as hallucinations, synaesthesia, “ego-death”, time dilation and more (Pink-Hashkes et al., 2017; Deane, 2020). Here is an example of how, according to Pink-Hashkes and colleagues’ proposal, psychedelics can lead to “decomposed predictions”. In comparison to normal predictions, they elicit larger prediction errors, which the brain attempts to minimise by continuously changing predictions. However, since these “decomposed predictions” remain overly detailed, large prediction errors will persist and the brain will not settle on a stable percept. Instead, objects and scenes will appear to rapidly change and morph (Pink-Hashkes et al., 2017, p. 2910).

The examples above illustrate how an inflexible or inappropriate regulation of the two representational features, decoupling and structural similarity via the proposed PP mechanisms, can result in suboptimal behavioural performance. Substantial involvement of representational features in behavioural performance of cognitive systems suggests that representational features bear an explanatory role.

6 Concluding remarks and future research

The main aim of the present paper was to examine gradual features of representations within the confinements of PP. We focused on two features of representations, structural similarity and decoupling, and identified candidate mechanisms that underlie their gradation. We argued that structural similarity can be analysed in terms of two, rather than one, dimension: number of exploitable internal relations and state space granularity. Both dimensions can take on different values and hence render structural similarity gradual. Furthermore, we argued that decoupling is gradual in two ways. First, we showed that different brain areas are involved in decoupled cognitive processes to a greater or lesser degree depending on their proximity to the sensory and motor periphery. Second, and more importantly, we argued that the degree of decoupling can be further regulated in some brain areas through precision weighting of prediction error. Finally, we argued that gradation of decoupling (via precision weighting) and gradation of structural similarity (via state space granularity) are conducive to behavioural success.

Whilst the notion of representational gradation is not entirely novel (see Clark & Toribio, 1994; Gładziejewski & Miłkowski, 2017; Gładziejewski, 2016), our take on gradation is different from existing accounts and, crucially, extends them. First, we do not assume that representationality itself comes in degrees, in contrast to Clark and Toribio (1994), but rather argue that representational features are gradual. Hence, the explanatory potential is carried by gradual representational features. Second, we provided potential mechanisms that are involved in the regulation of feature gradation, and third, we have argued that representational gradation is related to behavioural success of cognitive systems.

We have argued that distinguishing between degrees of representational features is not just a conceptual distinction. In our paper we put forward the idea that representational gradation has implications for the behavioural success of cognitive systems. Computational simulations could more formally nuance this idea. For example, we propose that representational features as cast in PP terms can be implemented in artificial agents where one group of agents is equipped with gradational representational features and the other one has representational features that are fixed. The task of agents would be two-fold, to survive in an artificial environment and to achieve a certain goal. The hypothesis following from our theoretical proposal is that agents that can dynamically change the degree to which representational features are expressed would be better off at surviving and achieving the goal than the ones that have fixed representational features.

Besides this, we propose that the next research step should be to explore what consequences our gradational account has for the debate on representations in (philosophy of) cognitive science more generally. Although we have, as a background assumption, presupposed that the structures posited by PP play a genuinely representational role, one might be able to make a case for the claim that the actual explanatory burden is carried by the degrees to which representational features are expressed, rather than by a representation itself. That is, one could argue that the regulation of structural similarity and of decoupling is explanatorily relevant, while denying that the regulation of these features contributes to genuine representational processes in the brain. For ease of exposition, we have described our gradational account as a contribution to a specific representationalist position (as defended by Gładziejewski, 2016). However, it may be equally valuable for non-representationalist interpretations of PP (Hutto & Myin, 2012; van Es & Myin, 2020; Nirshberg & Shapiro, 2021), as long as they agree that the regulation of structural similarity and decoupling plays an important role in understanding the performance of cognitive systems. Conversely, our account may also serve to refine existing representationalist interpretations of PP, for instance, by facilitating a nuanced account of the difference between structural representations and detectors (Nirshberg & Shapiro, 2021), or by offering conceptual tools to further clarify how structural representations can play a genuine representational role (thereby responding to Facchin, 2021b). Lastly, our account might even inspire new accounts of how representationality itself can come in degrees (in the spirit of Clark & Toribio, 1994), where the idea would be that the more granular and decoupled the more representation-like a cognitive structure is. To flesh out this proposal in detail, a full research program is needed. However, our goal here has been much more modest: we only hope to have shown that the regulation of structural similarity and decoupling is explanatorily relevant, and that PP offers a perspective through which these processes can be better understood.