1 Introduction

Contemporary architecture frequently addresses the demand for dynamic structures capable of spatial transformation to accommodate ephemeral or changing needs. The rapidly emerging field of deployable structures provides solutions for adaptive and sustainable architectural applications. Deployable structures are defined as structures capable of large morphological changes in an autonomous way, due to their geometric, material, and mechanical properties [1,2,3]. They embody characteristics such as flexibility, transportability, and reconfigurability, offering innovative solutions across various scenarios requiring spatial adaptation to climatic conditions, natural disasters, or changes in use.

Upon reviewing the various existing classifications of deployable structure types in literature [4], it becomes evident that two general categories emerge: strut structures and surface structures, as proposed by Merchan [5]; or lattice structures and continuous structures, as identified by Hanaor and Levy [6]. The category of lattice deployable structures includes scissor-hinged, reciprocal, four-bar linkages, and tensegrity structures, among others. Conversely, the classification of continuous surface deployable structures comprises rigid origami, pneumatic structures, tensioned membranes, and similar thin-shell elements.

In the application of lattice deployable structures for architectural solutions there is typically a need to cover the space they enclose, often addressed by integrating external surface elements when fully deployed. On the other hand, continuous surface deployable structures are generally not characterized by high mechanical strength and usually require attachment to fixed lattice supports in their deployed configurations.

The present study, part of an ongoing research effort by the authors, addresses the kinematic coupling of topologically related kinetic elements from the two aforementioned categories. The main objective is to develop hybrid deployable structures that ensure structural integrity and space enclosure, and also maintain their transformability as kinematically paired mechanisms.

Earlier research conducted by the authors [7,8,9] has explored the coupling of origami folded surfaces, utilized as space-covering elements, with planar scissor linkages serving as structural retractable frames. Figure 1 illustrates the deployment sequences of selected physical models of the previously proposed coupled mechanisms.

Fig. 1
figure 1

Earlier research by the authors: Kinetic physical models of origami folded surfaces coupled with scissor-hinged linkage frames (deployment sequences) [7, 8]

Full size image

This paper builds upon earlier research by the authors, extending it to explore and develop hybrid deployable structures characterized by vaulted geometry. The proposed structures utilize rigid thick origami surfaces in conjunction with a combination of planar scissors and four-bar linkage retractable frames. The aim is to provide novel solutions for adaptable and sustainable architectural applications, contributing to the advancement in the field of deployable structures.

2 Methodology

The methodological approach utilized for developing the hybrid deployable vaulted structures proposed in this paper involves a series of sequential steps. Firstly, the origami Crease Pattern (CP) is selected from existing ones, by considering the desired vaulted deployed configuration of the covering surfaces. Subsequently, the unit geometry and kinematic equations of the selected CP are parameterized within the Grasshopper visual programming environment. To enhance the rigidity and functionality of the origami plates, the tapered panels' thickness accommodating technique, as outlined in prior research [10], is employed and embedded in the algorithm. The following step involves the development of a retractable linkage frame mechanism that mirrors the geometry and motion path of the origami surface in space. Establishing precise relations between the dependent variables of the rigid origami surfaces and the corresponding linkages is crucial in this phase for achieving seamless integration between the two components. The developed Grasshopper algorithm is then utilized to generate several morphological variations of the proposed hybrid deployable vault structure, by iteratively adjusting selected parameters. Throughout this form-finding process, derivative variations of the CP are explored, leveraging the origami inverse design method to optimize the developed vaulted structures in terms of compactness, optimal deployed form, and stability criteria. An integral part of this process is the construction of small-scale physical models, which are subject to kinematic and loading tests, providing valuable insights into the practical feasibility and performance of the proposed hybrid deployable vaulted structures.

3 Thick origami surface development

Folding gives structure to matter [11]. A thin sheet of paper acquires mechanical strength and load-carrying capacity when properly folded, as illustrated in Fig. 2. Origami, the ancient Japanese art of paper folding, can be described as the sequential creasing of paper into various geometric forms without stretching or cutting. Folding techniques inspired by origami can be applied to sheets of other materials with similar properties to paper, notably significantly high in-plane stiffness compared to out-of-plane stiffness. The rapidly developing field of structural origami investigates the correlation between forms emerging from sheet folding and their structural performance [12]. Numerous pioneers have made substantial contributions to the field of structural origami, including mathematicians [13], computer scientists [14], physicists [15], astrophysicists [16], architects and engineers [17, 18], as well as origami artists and designers [19, 20].

Fig. 2
figure 2

A thin sheet of paper (a) acquires mechanical strength and load-carrying capacity when properly folded (b) [21]

Full size image

Two distinct approaches are commonly employed in designing origami structures: the direct design method, which involves applying existing CPs to address particular design challenges, and the inverse design method, which involves modifying existing CPs or creating new ones to solve more demanding design problems [22]. Through the utilization of origami design methodologies and thickness accommodating techniques [10], rigid and thick origami structures can be manufactured for architectural applications requiring adaptability to changing needs in space configuration [23, 24]. Rigid origami structures are characterized as scalable mechanisms composed of stiff plates and hinges, capable of deploying and retracting with a unified and synchronous movement of all creases [17].

3.1 Crease pattern

The rigid-foldable Miura-ori and its derivative CPs are commonly employed in structural origami applications owing to their unique property of representing an overconstrained case of a general 4-degree vertex with only one degree of freedom (DOF) [25]. Moreover, they possess useful characteristics such as flat-foldability, where panels are co-planar when fully folded, and developability, which allows them to be folded from a continuous flat sheet of material [26]. For the direct origami design phase of this research, the Arc Pattern CP is selected, which is a Miura-ori first-level derivative CP, as outlined in reference [25]. This pattern is chosen for its ability to achieve single-curvature geometries, particularly vaulted surfaces.

The basic unit of the Arc Pattern CP, depicted in Fig. 3a, consists of four identical trapezoidal plates and can be geometrically defined by three parameters: side lengths a1 and b, and sector angle φ. Two more dependent parameters, side length a2, and panel width w, are derived to describe the CP base unit geometry. Their values are determined by Eqs. (1) and (2), with the constraint that a1 < a2.

Fig. 3
figure 3

Unit geometry of the Arc Pattern CP [25]

Full size image
$${a}_{2}={a}_{1}+2 b{\text{cos}}\varphi$$
(1)
$$w=b{\text{sin}}\varphi$$
(2)

Four additional parameters, namely the dihedral angles ηA and ηZ, as well as the edge angles θA and θZ, are essential in determining any specific folded configuration of a rigid unit, as illustrated in Fig. 3b. The values of these parameters vary according to the folding state of the CP unit and can be algebraically calculated using Eqs. (3)–(5), provided any one of the four parameters is treated as an input variable for the folding motion. Furthermore, the varying folded width parameter \(\overline{w}\), obtained from Eq. (6), is also significant in this context.

$$\left(1+{\text{cos}}{\eta }_{z}\right)\left(1-{\text{cos}}{\eta }_{A}\right)=4{{\text{cos}}}^{2}\varphi$$
(3)
$${\text{cos}}{\eta }_{\rm A}= {{\text{sin}}}^{2}\varphi {\text{cos}}{\theta }_{\rm Z}-{{\text{cos}}}^{2}\varphi$$
(4)
$${\text{cos}}{\eta }_{Z}={{\text{sin}}}^{2}\varphi {\text{cos}}{\theta }_{\rm A}+{{\text{cos}}}^{2}\varphi$$
(5)
$$\overline{w }=b{\text{sin}}({\eta }_{\rm Z}/2)=w \mathit{sin}({\eta }_{\rm Z}/2)/{\text{sin}}\varphi$$
(6)

As shown in Fig. 3c, the vertices of a partially folded Arc Pattern CP unit lie along an arc profile characterized by a radius R, which can be determined using Eqs. (7) - (9). Here, ξ1 and ξ2 denote the central angles formed by creases a1 and a2 of the CP unit, respectively.

$${\xi }_{1}+{\xi }_{2}=2 (\pi -{\eta }_{\rm A})$$
(7)
$$R={a}_{1}/[2{\text{sin}}\left({\xi }_{1}/2\right)]$$
(8)
$$R={a}_{2}/[2{\text{sin}}\left({\xi }_{2}/2\right)]$$
(9)

In a rigid Arc Pattern tessellation with m straight and n zigzag CP lines (rows and columns), the precise position of all vertices can be determined using a 3D cylindrical coordinate system. This coordinate system, depicted with its specified orientation and origin in Fig. 3c, serves as the essential framework for accurately specifying the location of each vertex in any folded configuration of the CP. By employing kinematic Eqs. (10) and (11), every Vi,j vertex of an Arc Pattern tessellation can be defined.

$${V}_{i,j}=\left(x,y,z\right)=(R{\text{cos}}\theta , i b{\text{sin}}\left({\eta }_{\rm Z}/2\right), R{\text{sin}}\theta )$$
(10)
$$\theta = \left\{ {\begin{array}{*{20}l} {j \left( {\xi_{1} + \xi_{2} } \right)/2} \hfill & {for\;even\;i\;and\;even\;j} \hfill \\ {j \left( {\xi_{1} + \xi_{2} } \right)/2 + \left( {\xi_{2} - \xi_{1} } \right)/2} \hfill & {for\; even\;i\; and\;odd\; j} \hfill \\ {\left( {j - 1} \right) \left( {\xi_{1} + \xi_{2} } \right)/2 + \xi_{2} } \hfill & {for\;odd\;i\;and\;even\;j} \hfill \\ {\left( {j - 1} \right)\left( {\xi_{1} + \xi_{2} } \right)/2 + \xi_{1} + \left( {\xi_{2} - \xi_{1} } \right)/2} \hfill & {for\;odd\;i\;and\;odd\;j} \hfill \\ \end{array} } \right.$$
(11)

To summarize, an Arc Pattern tessellation can be geometrically and kinematically defined using fifteen parameters. Seven of these parameters (a1, a2, b, φ, w, m, n) maintain constant values regardless of the folded state of the CP. Conversely, the remaining eight parameters (θA, θZ, ηA, ηZ,\(\overline{w}\), ξ1, ξ2, R) vary for each distinct folded configuration of the same CP. The spatial deployment of a rigid CP is depicted in Fig. 4 for an Arc Pattern tessellation with parameters a1 = 1.4, b = 3.2, φ = 30°, m = 13, n = 6, and a sequence of variable edge angles θA = 180°, 125°, 75°, 20° as input.

Fig. 4
figure 4

Folding sequence of a rigid Arc Pattern tessellation

Full size image

3.2 Thickness accommodation

The selected technique for accommodating the thickness of the origami surfaces in this study is the layered tapered panels’ technique [10]. This method is chosen primarily because it maintains the kinematics of an ideal zero-thickness model while also being easily fabricated using laser cutting or 2-axis CNC routing methods.

In order to achieve the desired total thickness, an equal amount of thickness is added to each side of the ideal origami surface, as illustrated in Fig. 5a. To avoid self-intersection, the necessary taper length T for each panel in the CP is calculated using Eq. (12), where t represents the half thickness of the panel, and η the dihedral angle (ηA/ηZ) of the embedded zero-thickness surface at the maximum retracted folded state. It’s important to note that to maintain a non-zero panel thickness, the maximum fold angle of the thick origami mesh cannot reach 180°. Employing the described technique, thickness is applied to both sides of the Arc Pattern tessellation, as depicted in a darker tone in Fig. 5b, for both the convex and concave sides of the origami surface.

Fig. 5
figure 5

Layered tapered panels’ thickness accommodating technique: a taper detail, b thickness addition to the convex and concave sides of the CP [9]

Full size image
$${\rm T}=t{\text{cot}}(\eta /2)$$
(12)

4 Linkage retractable frame development

We observe that by constraining the boundary edges of folded surfaces, their stability and load-carrying ability can be enhanced [21], as illustrated in Fig. 6. This can be achieved by integrating a complementary mechanism whose motion aligns with the deployment path in space of the origami surface edges. An essential criterion for this mechanism is its capability to be constrained or locked into selected configurations.

Fig. 6
figure 6

The stability and load-carrying ability of folded surfaces can be enhanced by constraining their boundary edges [21]

Full size image

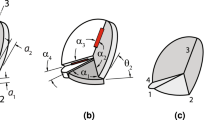
Previous studies by the authors [7, 8] have investigated planar scissor-hinged linkages as a suitable mechanism for this purpose. However, due to the variable curvature of this specific CP during deployment, a different linkage type is needed to address the curvilinear boundary edges of the Arc pattern. Therefore, a modified linkage is proposed for the retractable frame mechanism of the developed origami vaults, as shown in Fig. 7. This frame consists of two pairs of distinct linkages: one scissor-hinged rectilinear linkage (lengthwise), and one four-bar curvilinear linkage (widthwise). The geometric construction and parameterization, tailored to the Arc Pattern CP, of these two types of linkages constituting the developed retractable frame mechanism are elaborated upon in the subsequent sections.

Fig. 7
figure 7

Parameter relations and coupling detail between a thick Arc Pattern tessellation with a retractable frame mechanism consisting of scissor-hinged (blue) and four-bar (red) linkages

Full size image

4.1 Scissor-hinged linkages

For the lengthwise rectilinear boundary edges pair of the Arc Pattern CP, a translational scissors linkage of two distinct bar lengths is utilized, as depicted in Fig. 8b, showcasing three deployment configurations. The longer bar length of the scissors linkage corresponds to side length b of the Arc Pattern CP and is aligned with the lengthwise opposite boundary edges of the CP. Conversely, deliberately shorter lengths are chosen for half of the scissor bars of this linkage to hinder the unfolding of the origami surface, thereby limiting its mobility. This shorter length is set equal to half the folded width \(\overline{w}\) parameter in the desired fully deployed configuration of the Arc Pattern CP, as depicted in Fig. 7. This design decision guarantees that the hybrid mechanism achieves and maintains the intended space-covering configuration upon deployment.

Fig. 8
figure 8

Hybrid deployable vault visualization in Rhino: retracted, intermediate, and deployed configurations in a front, b side, and c top views

Full size image

4.2 Four-bar linkages

To address the widthwise curvilinear boundary edges pair of the Arc Pattern CP, a customized four-bar linkage with specific sliding joints is implemented, as depicted in Fig. 7 in red and Fig. 8a in three deployment configurations. This linkage is specifically designed to align with the geometry and folding motion of the Arc Pattern CP, comprising bars with lengths equivalent to the CP side lengths a1 and a2. The pivots situated at the intersecting points of the linkages feature sliding capability to adapt to the variable curvature of the widthwise opposing edges of the CP, while also preventing the origami surface from further unfolding at the desired deployed configuration.

5 Form-finding

In order to facilitate the kinematic study, form-finding and design optimization of the proposed hybrid deployable vaulted structures, an algorithm was developed within the Rhino Grasshopper visual programming environment. The developed parametric model utilizes the equations and methods described in Sects. 3 and 4 of this paper for the generation of the CP tessellation, thickness accommodation, and the creation of the complementary linkage frame mechanism. The algorithm performs necessary computations based on the provided input and offers a visual representation of the hybrid vault model and its deployment in space. Parameterization of the geometry and motion of the elements of the proposed vaulted structure enables the creation of diverse morphological variations, each possessing unique characteristics, through the manipulation of input parameters. Analyzing the resultant morphologies enables the assessment of crucial aspects such as compactness, structural integrity, performance, as well as form and aesthetic qualities.

The primary parameters influencing the geometry of the proposed vault structure include the initial input values of the Arc Pattern a1, b, φ, m, and n. These parameters not only define the vault's overall shape but also influence the ratio between its retracted and deployed states. This ratio denotes the proportional relationship between its dimensions when it is in a compact state compared to when it is fully expanded. For example, the hybrid vault variation shown in Fig. 8 is generated with a1 = 2, b = 2, φ = 45°, m = 9, and n = 4, resulting in a compact design with minimum moving parts. In contrast, the vault variation shown in Fig. 9, with a1 = 1.5, b = 1, φ = 35°, m = 41, and n = 6, exhibits a larger span and greater curvature changes upon deployment. The same set of parameters defines the kinetic physical model depicted in Fig. 10, with the only difference being m = 21 in this case.

Fig. 9
figure 9

Large variation hybrid deployable vault visualization in Rhino: a side view of retracted and deployed configurations, b front view of retracted and deployed configurations, and c perspective view of deployed configuration

Full size image
Fig. 10
figure 10

Small-scale kinetic physical model of a hybrid vault variation in retracted (left) and deployed (right) configurations [9]

Full size image

During experimentation with different input parameter values, we encountered self-intersection occurrences between the opposing rectilinear edges of the origami surface under certain conditions. The probability of self-intersection instances rises with an increase in the number of n counts or the value of the φ angle. Through a process of trial and error, we observed that improved variations of the developed hybrid vaults could be achieved by modifying some aspects of the original origami CP. Utilizing the origami inverse design methodology, we redesigned the CP to enable retraction into a more compact configuration while avoiding self-intersection. Another objective of this form-finding process was to ensure that the "wall" surfaces of the vault when fully deployed, meet the ground at a 90° angle to enhance its stability. The proposed modification of the CP, depicted in Fig. 11, includes six distinct widthwise side lengths a instead of two, and two different lengthwise side lengths b instead of one. The kinematic simulation of the new CP was conducted using the rigid-folding motion solver provided by the Crane plugin for Grasshopper [27]. Subsequently, thickness was added to the origami plates following the method outlined in Sect. 3.2.

Fig. 11
figure 11

Crease Pattern modification

Full size image

The design of the linkage frame for the new CP follows a similar approach to the previous case, with the only difference being that the lengthwise scissor-hinged linkages comprise equal-length bars in this instance, forming a truss base when fully deployed. The hybrid deployable vault depicted in Fig. 12 is generated through the inverse design methodology described above and can retract into a packed configuration while avoiding self-intersection. Its deployed configuration offers enhanced structural integrity, since the origami plates meet the ground vertically and the pair of scissor-hinged linkages act as truss bases.

Fig. 12
figure 12

Modified CP hybrid deployable vault visualization in Rhino: retracted, intermediate, and deployed configurations in a front and b isometric views

Full size image

Through iterative refinement of the design via this process, it becomes feasible to generate origami CP variations that best suit the requirements of specific architectural applications. This method of form-finding and optimization streamlines the decision-making process, enabling the development of structures that effectively meet the criteria of each unique usage scenario.

6 Conclusion and future research

The research presented in this paper investigates the development of hybrid vaulted structures that integrate topologically related kinetic elements from lattice and continuous surface deployable structures. The developed hybrid deployable vault variations are comprised of thick origami surfaces and retractable structural frames consisting of four-bar and scissor-hinged linkages.

The methods employed for developing the proposed hybrid deployable vaults presented in this study include both the direct design process, wherein an existing CP is employed and the inverse design process, wherein the CP is redesigned to fulfill specific requirements. In both cases, thickness is incorporated into the surfaces using one of the existing thickness accommodating techniques. The kinematically paired linkage retractable frames are specifically designed to align with the geometric and kinematic characteristics of the origami surfaces.

Future research will focus on developing a unified and generalized algorithm for inverse origami design and form-finding, capable of accommodating various and complex target geometries of such hybrid deployable structures. Additionally, further research and experimentation can build upon the findings of this work by focusing on joint design and materials selection, which are pivotal for ensuring structural integrity, ease of construction, and functionality of the kinematically coupled mechanisms. Furthermore, the utilization of finite element analysis can assess stress distribution and deformation across varying loading scenarios, offering valuable insights into structural performance and potential design optimizations.

The hybrid deployable structures described in this paper could find application in challenging architectural scenarios where flexibility, lightweight design, transportability, mechanical strength, and sustainability are essential considerations.