1 Introduction

Vibrations occur in practically every machine, structure and mechanical device, and they are usually seen as unwanted and harmful phenomena. Continuous oscillations and repetitive motions can damage machinery; they may lead to the fissure and eventual breakage of shafts, gears, brake disks, and other machine elements due to wear and material fatigue. Apart from causing the failure of mechanical constructions, unwanted vibration and deformation could spoil their capability to function properly; for example, in the case of wings, oscillations could result in poor aerodynamic performance [1, 2]. These vibrations also create noise and heat, which reduces efficiency and may cause discomfort to anyone exposed to it for an excessive amount of time [3, 4]. Therefore, it is essential for engineers to mitigate these vibrations as much as possible.

Passive vibration absorbers are commonly used, easily implementable and well-researched solutions to the aforementioned problem. The tuned mass damper (TMD)—the most commonly implemented type of dynamic vibration absorber—is a simple passive absorber consisting of a secondary mass-spring-damper oscillator attached to the host system in order to absorb its vibrational energy. TMDs are tuned to mitigate vibrations at well-defined frequencies by exploiting a modal interaction between the host system and the absorber [5]. These vibration absorbers first appeared at the end of the 19th century, intending to mitigate the rolling motion of ships [6, 7]. Later, the design method of TMDs was generalized and formalized by Den Hartog in the 1930s [5]. Den Hartog’s equal-peak method is still popular and extensively used nowadays, 90 years later [8]. TMDs are extensively used in everyday applications, with examples ranging from aircraft engines [9, 10], spectator stands [11], long-span suspended bridges [12,13,14] and transmission lines [15, 16].

Although the TMD was originally designed as a linear system, several types of nonlinear vibration absorbers have been developed in the last decades. Particularly renowned are the nonlinear energy sink [17, 18], where a purely nonlinear restoring force is adopted for providing a broad frequency band of operation, and the nonlinear tuned vibration absorber [19,20,21], which is a nonlinear extension of the TMD, particularly effective in the case of nonlinear host systems.

As dynamic vibration absorbers are passive structures, their main problem is that they are fine-tuned for specific scenarios, disturbances or frequencies. An active mass damper (AMD) is a possible solution for introducing a vibration absorber capable of mitigating vibrations at different frequencies and amplitudes [22,23,24]. AMDs achieve their goal using actuators that are controlled with a closed-loop control strategy. Common types use proportional (displacement), derivative (velocity), or acceleration feedback, but more advanced solutions exist, such as sliding mode control [24, 25]. Active vibration absorption can also be achieved using the existing actuators in the host system, such as the actuators at the joints of robot arms [26, 27].

A hybrid vibration absorber (HVA) is a combination of a TMD and an AMD [24]. They are used in a variety of systems, suggesting that their implementation can be advantageous compared to a passive TMD or AMD [28]. For instance, Cheung et al. [29] presented an optimal design of an HVA applied to a single-degree-of-freedom (DoF) structure to minimize the control effort. In [30], Tso et al. show that a pole placement control technique can be used for global structural vibration attenuation. In [24], Collette and Chesné propose another control law for HVAs, the \(\alpha\)-HMD, which involves an adequate placing of zeros to create an unconditionally stable controller. They discussed its performance on a 3 DoF mechanical model and showed that this control strategy requires less control effort than a TMD or an AMD for better vibration suppression performance. In [31], the performance of an HVA against forced and shock vibrations is investigated numerically and experimentally. In [32], a passive electromagnetic shunt damper is augmented with an active controller. Its performance is then compared with a purely active one (in terms of energetic cost) and a passive one, highlighting the advantages of the hybrid design.

Even though time delay is usually undesirable and harmful (it could very well be the primary source of the oscillations), sometimes it can also have beneficial effects, just like in the case of the delayed resonator (DR). A DR contains an appropriately designed feedback loop, where time delay is intentionally included such that the DR absorbs emerging vibrations [33]. Olgac and Holm-Hansen first proposed the concept of using a delayed resonator for vibration mitigation. They demonstrated its advantages, such as the fact that a DR is tunable in real-time and can also eliminate oscillations for a wide range of harmonic excitation frequencies [33]. In [34], Wang and Xu propose a DR for changing excitation frequency using analytical and experimental methods and conclude that the DR greatly improves absorption performance.

In [35], stability analysis and design of a delayed resonator with acceleration feedback are presented. As it is pointed out, one of the main advantages of using the acceleration signal in the feedback loop is that accelerometers are reliable and low-cost. In [36], Mohanty and Dwivedy consider a nonlinear vibration absorber with delayed acceleration feedback as well, suggesting that time delay can lead to better vibration suppression performance depending on the system parameters when nonlinearity is present in the system. A DR is proposed in [37] with delayed acceleration feedback, and both analytical and experimental results show that the absorber mitigates vibrations on a wide bandwidth, and, additionally, the appropriately tuned delayed feedback control can successfully facilitate the recovery of the stability of the system, if the passive absorber fails.

As this summary hints, the existing literature extensively covers the application of various dynamic vibration absorbers to mitigate forced and shock oscillations. Conversely, the suppression of self-excited oscillations is relatively less studied. Examples of works addressing the implementation of dynamic vibration absorbers for suppressing self-excited oscillations are still numerous [38,39,40,41,42]. However, to the authors’ knowledge, HVAs were never implemented for this purpose. The main scope of this paper is to fill this gap.

Self-excited oscillations are a particular type of vibrations that develop due to the systems’ inherent tendency to lose stability without explicit and time-dependent external excitation. Therefore, they are intrinsically different from forced and shock vibrations, and their mitigation or suppression requires different approaches.

Friction-induced vibrations are one of the most common types of self-induced vibrations. They mainly occur due to the Stribeck effect, meaning that the friction coefficient decreases with the increase of the relative velocity for some part of the characteristics [43,44,45]. In its mathematical formulation, the Stribeck effect generates a negative damping term around the equilibrium, causing instability.

Fluid–structure interactions and aeroelasticity are other common sources of self-induced vibrations, such as in the cases of flutter, galloping, and vortex-induced vibrations [46,47,48]. The instability is usually related to the dynamic interaction between the fluid’s and the structure’s periodic motion, which reciprocally sustain each other. Owing to a different phenomenon, but still related to fluid–structure interactions, instabilities and self-excited oscillations are also experienced in pressure relief valves [49,50,51]. Another type of self-excited oscillation due to fluid–structure interaction is the porpoising motion affecting high-speed planing vessels [52] and, recently, F1 cars.

Lateral oscillations of towed wheels, usually called shimmy [53, 54], are another example of self-excited vibrations. Shimmy is an unwanted and potentially dangerous phenomenon, which is typically observable in towed vehicles [55], landing gears [56, 57], shopping trolleys [58] and the front wheel of motorcycles and bicycles [59]. These oscillations are usually driven by the interaction between the tires and the ground [60]. Special dampers, called shimmy dampers, are often implemented to counteract these vibrations [61].

The presence of time delay in a system can also lead to the loss of stability, generating self-excited oscillations. Usually, time delay is introduced to the system by a feedback controller, as it takes a finite amount of time for the controller to process the information coming from the sensors, and it also takes additional time for the actuator to intervene and exert its effect [62]. This phenomenon affects human-controlled systems as well [63]. A prominent example of self-induced vibrations related to time delay is the so-called regenerative chatter [64, 65]. A noteworthy aspect of this phenomenon is that, in this case, the time delay is related to the mechanical system itself and not to the control system.

This paper aims to address the problem of the suppression of self-excited oscillations through the implementation of an HVA. In particular, we consider a simple host system (single-DoF) undergoing an instability related to a negative damping term. The system’s general character and the instability considered make the model representative of a large range of engineering applications. For instance, the mathematical model adopted is locally equivalent to the one often used for modeling friction-induced vibrations [44] and aeroelastic instabilities [38], if limited to the neighborhood of the equilibrium solution. On the one hand, this paper investigates the potential improvement of adding an active controller to an already existing TMD. On the other hand, it aims at analytically identifying the parameter values of the passive and active components, which maximize the stable region owing to an optimal set of parameter values.

The remaining part of the paper is organized as follows. Section 2 describes the mechanical model used to investigate the effects of an HVA on a system susceptible to self-induced vibrations. Section 3 contains the stability analysis and optimization. First, we briefly present the stability analysis for a purely passive TMD (Sect. 3.1), then we investigate the possible advantages of augmenting a finalized TMD with acceleration feedback control (Sect. 3.2), while Sect. 3.3 provides the stability analysis for the HVA. In Sect. 4, two case studies are considered: suppression of friction-induced and galloping vibrations. In Sect. 5, we will discuss practical considerations and provide suggestions for the possible tuning procedure for the parameters of the HVA in practice. Finally, conclusions are given in Sect. 6.

2 The mechanical model

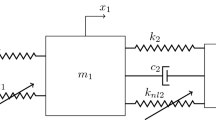
The mechanical system under study comprises two parts: the host, or primary system, and the vibration absorber. The primary system is modeled as a classical single-DoF oscillator with a lumped mass \(m_1\) and stiffness \(k_1\). The damping coefficient is assumed to be negative (\(c_1 < 0\)) to model a simple case of dynamic instability and self-excited oscillations (Fig. 1). As a result, the trivial solution of the primary system is unstable. Although this model is relatively simple, it is representative of various mechanical systems relevant to engineering, such as the mass-on-moving-belt with a weakening friction law at low belt speed [44], or galloping instabilities [38, 39, 66], which will be discussed in more detail later.

The HVA is an attached single-DoF oscillator, where \(m_2\), \(k_2\) and \(c_2\) are its lumped mass, stiffness and damping coefficients. \(m_1\), \(k_1\), \(m_2\), \(k_2\) and \(c_2\) are assumed as positive real numbers. The last part of the system is the controller, which accounts for the active part of the HVA. Its effect is represented by the force \(F_{\rm C}\) exerted between the two masses.

The control law implemented by the active controller is a simple linear acceleration feedback. This control law is inefficient compared to much more sophisticated techniques, such as sliding mode or model-predictive control techniques [67]. However, because of the low cost and easy implementation of acceleration sensors, combined with its simplicity, it is commonly adopted in industrial environments [27, 68, 69]. We note that adding terms proportional to the relative displacement or velocity to the control law would not provide any theoretical advantage over a passive system, as these terms correspond to spring and damping components, which are already included in the TMD. The control force \(F_{\rm C}\) is given by

$$\begin{aligned} F_{\rm C} = a_1\ddot{x}_1 + a_2\ddot{x}_2, \end{aligned}$$
(1)

where \(x_1\) and \(x_2\) are the absolute displacements of masses \(m_1\) and \(m_2\), while \(a_1\) and \(a_2\) are the control gain parameters. The analysis of more advanced control strategies is beyond the scope of this paper.

Fig. 1
figure 1

The mechanical model

Full size image

The dynamics of the two-DoF system is described by the following system of linear second-order ODE:

$$\begin{aligned}&m_1\ddot{x}_1 + (c_1+c_2){\dot{x}}_1 + (k_1+k_2)x_1 - c_2{\dot{x}}_2 - k_2x_2 = -F_{\rm C}, \end{aligned}$$
(2)
$$\begin{aligned}&m_2\ddot{x}_2 + c_2{\dot{x}}_2 + k_2x_2 - c_2{\dot{x}}_1 - k_2x_1 = F_{\rm C}. \end{aligned}$$
(3)

By substituting (1) into the equations above, we obtain:

$$\begin{aligned}&(m_1+a_1)\ddot{x}_1 + (c_1+c_2){\dot{x}}_1 + (k_1+k_2)x_1 \nonumber \\&\quad + a_2\ddot{x}_2 - c_2{\dot{x}}_2 - k_2x_2= 0, \end{aligned}$$
(4)
$$\begin{aligned}&(m_2-a_2)\ddot{x}_2 + c_2{\dot{x}}_2 + k_2x_2 - a_1\ddot{x}_1 - c_2{\dot{x}}_1 - k_2x_1 = 0. \end{aligned}$$
(5)

To reduce the number of parameters, it is advantageous to non-dimensionalize the equations of motion. After dividing (4) and (5) by \(m_1\) and introducing the following parameters

$$\begin{aligned} \alpha _1= & {} \frac{a_1}{m_1}, \quad \omega _{\textrm{n}1} = \sqrt{\frac{k_1}{m_1}}, \quad \psi = -\frac{c_1}{2\omega _{\textrm{n}1}m_1}, \quad \varepsilon = \frac{m_2}{m_1}, \end{aligned}$$
(6)
$$\begin{aligned} \alpha _2= & {} \frac{a_2}{m_2}, \quad \omega _{\textrm{n}2} = \sqrt{\frac{k_2}{m_2}}, \quad \zeta _2 = \frac{c_2}{2\omega _{\textrm{n}2}m_2}, \end{aligned}$$
(7)

the resulting equations are

$$\begin{aligned}&(1+\alpha _1)\ddot{x}_1 + 2(-\psi \omega _{\textrm{n}1}+\varepsilon \zeta _2\omega _{\textrm{n}2}){\dot{x}}_1\nonumber \\&\quad + (\omega _{\textrm{n}1}^2+\varepsilon \omega _{\textrm{n}2}^2)x_1 + \varepsilon \alpha _2\ddot{x}_2\nonumber \\&\quad - 2\varepsilon \zeta _2\omega _{\textrm{n}2}{\dot{x}}_2 -\varepsilon \omega _{\textrm{n}2}^2x_2= 0, \end{aligned}$$
(8)
$$\begin{aligned}&-\alpha _1\ddot{x}_1 - 2\varepsilon \zeta _2\omega _{\textrm{n}2}{\dot{x}}_1 - \varepsilon \omega _{\textrm{n}2}^2x_1 \nonumber \\&\quad + \varepsilon (1-\alpha _2)\ddot{x}_2 + 2\varepsilon \zeta _2\omega _{\textrm{n}2}{\dot{x}}_2 +\varepsilon \omega _{\textrm{n}2}^2x_2= 0\,. \end{aligned}$$
(9)

We then introduce the dimensionless time \(T = \omega _{\textrm{n}1}t\). From here on, derivations with respect to the dimensionless time of a function f(T) are denoted by

$$\begin{aligned} \frac{{\textrm{d}}f(T)}{{\textrm{d}}T} = f'(T) = f'. \end{aligned}$$
(10)

Performing this transition, then dividing both equations by \(\omega _{\textrm{n}1}^2\) and defining the ratio of natural angular frequencies as

$$\begin{aligned} \gamma = \frac{\omega _{\textrm{n}2}}{\omega _{\textrm{n}1}}, \end{aligned}$$
(11)

we obtain the final form of the equations of motion in dimensionless time:

$$\begin{aligned}&(1+\alpha _1)x_1'' + 2(\varepsilon \gamma \zeta _2-\psi )x_1' + (1+\varepsilon \gamma ^2)x_1 \nonumber \\&\quad + \varepsilon \alpha _2x_2'' - 2\varepsilon \gamma \zeta _2x_2' -\varepsilon \gamma ^2x_2= 0, \end{aligned}$$
(12)
$$\begin{aligned}&-\alpha _1x_1'' - 2\varepsilon \gamma \zeta _2x_1' - \varepsilon \gamma ^2x_1 + \varepsilon (1-\alpha _2)x_2''\nonumber \\&\quad + 2\varepsilon \gamma \zeta _2x_2' + \varepsilon \gamma ^2x_2= 0\,. \end{aligned}$$
(13)

3 Stability analysis

To carry out the stability analysis, we will reformulate the problem as a linear system of first-order ODEs:

$$\begin{aligned} {\textbf{y}}' = {\textbf{A}}{\textbf{y}}, \end{aligned}$$
(14)

where the vector \({\textbf{y}}\) contains the general coordinates and their time derivatives

$$\begin{aligned} {\textbf{y}} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ x_1' \\ x_2' \end{bmatrix}, \end{aligned}$$
(15)

and \({\textbf{A}}\) is the system matrix:

$$\begin{aligned} {\textbf{A}} = \begin{bmatrix} 0 &\quad 0 &\quad 1 &\quad 0 \\[6pt] 0 &\quad 0 &\quad 0 &\quad 1 \\[6pt] -\frac{1+\varepsilon \gamma ^2-\alpha _2}{1+\alpha _1-\alpha _2} &\quad \frac{\varepsilon \gamma ^2}{1+\alpha _1-\alpha _2} &\quad -2\frac{(\alpha _2-1)\psi +\varepsilon \gamma \zeta _2}{1+\alpha _1-\alpha _2} &\quad 2\frac{\varepsilon \gamma \zeta _2}{1+\alpha _1-\alpha _2} \\[6pt] \frac{\varepsilon \gamma ^2-\alpha _1}{\varepsilon (1+\alpha _1-\alpha _2)} &\quad -\frac{\gamma ^2}{1+\alpha _1-\alpha _2} &\quad 2\frac{\psi \alpha _1+\varepsilon \gamma \zeta _2}{\varepsilon (1+\alpha _1-\alpha _2)} &\quad -2\frac{\gamma \zeta _2}{1+\alpha _1-\alpha _2} \end{bmatrix}. \end{aligned}$$
(16)

The system’s stability can be determined by checking its characteristic exponents (denoted by \(\lambda\)): the system is asymptotically stable if and only if all of its characteristic exponents have negative real parts. The characteristic exponents are the roots of the characteristic polynomial \(p(\lambda )\)

$$\begin{aligned} p(\lambda ) = \det (\lambda {\textbf{I}}-{\textbf{A}}), \end{aligned}$$
(17)

where \({\textbf{I}}\) is the 4-by-4 identity matrix. As the system matrix is a 4-by-4 matrix, the characteristic polynomial is a 4th-degree polynomial, so it takes the following general form:

$$\begin{aligned} p(\lambda ) = b_4\lambda ^4 + b_3\lambda ^3 + b_2\lambda ^2 + b_1\lambda + b_0, \end{aligned}$$
(18)

where

$$\begin{aligned} b_4&= 1, \end{aligned}$$
(19)
$$\begin{aligned} b_3&= \frac{2 \left( \alpha _2 \psi +\gamma (\varepsilon +1) \zeta _2-\psi \right) }{\alpha _1-\alpha _2+1}, \end{aligned}$$
(20)
$$\begin{aligned} b_2&= \frac{-\alpha _2+\gamma ^2 \varepsilon +\gamma ^2-4 \gamma \zeta _2 \psi +1}{\alpha _1-\alpha _2+1}, \end{aligned}$$
(21)
$$\begin{aligned} b_1&= \frac{2 \gamma \left( \zeta _2-\gamma \psi \right) }{\alpha _1-\alpha _2+1}, \end{aligned}$$
(22)
$$\begin{aligned} b_0&= \frac{\gamma ^2}{\alpha _1-\alpha _2+1}. \end{aligned}$$
(23)

To determine whether any of the characteristic roots have positive real parts, using the Liénard-Chipart criterion is sufficient instead of solving the 4th-degree polynomial [70]. This means that the following inequalities related to the coefficients in (18) need to be fulfilled:

$$\begin{aligned} b_4>0:\qquad&1>0, \end{aligned}$$
(24)
$$\begin{aligned} b_2>0:\qquad&\frac{-\alpha _2+\gamma ^2 \varepsilon +\gamma ^2-4 \gamma \zeta _2 \psi +1}{\alpha _1-\alpha _2+1}>0, \end{aligned}$$
(25)
$$\begin{aligned} b_0>0:\qquad&\frac{\gamma ^2}{\alpha _1-\alpha _2+1}>0, \end{aligned}$$
(26)

It is also necessary to examine the Hurwitz matrix

$$\begin{aligned} {\textbf{H}} = \begin{bmatrix} b_3 &\quad b_1 &\quad 0 &\quad 0\\ b_4 &\quad b_2 &\quad b_0 &\quad 0\\ 0 &\quad b_3 &\quad b_1 &\quad 0\\ 0 &\quad b_4 &\quad b_2 &\quad b_0\\ \end{bmatrix}. \end{aligned}$$
(27)

The corresponding determinantal inequalities, together with the previously discussed inequalities related to the coefficients, provide a necessary and sufficient condition for the system’s stability:

$$\begin{aligned} h_1 = \det ({\textbf{H}}_1)&= b_3 >0, \end{aligned}$$
(28)
$$\begin{aligned} h_3 = \det ({\textbf{H}}_3)&= b_1b_2b_3 - b_0b_3^2 - b_1^2b_4>0, \end{aligned}$$
(29)

where \({\textbf{H}}_i\) is the i-th leading principal minor of \({\textbf{H}}\). The expanded formulations of (28) and (29) can be seen in the Appendix.

3.1 Stability of the passive system

The case in which one was to use only a passive TMD corresponds to \(\alpha _1 = 0\) and \(\alpha _2 = 0\), for which the system matrix simplifies to

$$\begin{aligned} {\textbf{A}} = \begin{bmatrix} 0 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ -1-\varepsilon \gamma ^2 &\quad \varepsilon \gamma ^2 &\quad 2\psi -2\varepsilon \gamma \zeta _2 &\quad 2\varepsilon \gamma \zeta _2 \\ \gamma ^2 &\quad -\gamma ^2 &\quad 2\gamma \zeta _2 &\quad -2\gamma \zeta _2 \end{bmatrix}. \end{aligned}$$
(30)

The objective of the vibration absorber is to stabilize the system for the possible largest \(\psi\) value; in fact, the larger \(\psi\) is, the ‘more unstable’ the host system is. The TMD is characterized by three parameters: \(\gamma\), \(\zeta _2\) and \(\varepsilon\), which characterize its stiffness (or natural frequency ratio), damping coefficient and mass ratio, respectively. Several studies illustrate that the larger the mass ratio is, the better the TMD performance is [71], so the \(\varepsilon\) value is usually limited by practical constraints. Conversely, the correct choice of \(\gamma\) and \(\zeta _2\) values critically affects the TMD performance.

In [72], it is shown that the parameter values

$$\begin{aligned} \zeta _2= & {} \zeta _2^{\textrm{TMD}}:= \frac{1}{2}\sqrt{\frac{\varepsilon }{1+\varepsilon }}, \end{aligned}$$
(31)
$$\begin{aligned} \gamma= & {} \gamma ^{\textrm{TMD}}:= \frac{1}{\sqrt{1+\varepsilon }}, \end{aligned}$$
(32)

provide an excellent approximation of the set of parameter values leading to the maximal \(\psi ^*\), resulting in

$$\begin{aligned} \psi ^*=\psi _{\textrm{cr}}:= \frac{\sqrt{\varepsilon }}{2}, \end{aligned}$$
(33)

where \(\psi ^*\) is the maximal \(\psi\) value such that the system is stable for any \(\psi <\psi ^*\). Figure 2 shows the sections of the stable region corresponding to the passive system in the \(\zeta _2 - \psi\) and \(\gamma - \psi\) planes.

Fig. 2
figure 2

Stability charts of the passive system

Full size image

3.2 Augmenting the passive system with acceleration feedback control

A simplistic but relatively common approach towards HVA is first to optimize the HVA’s passive components and then adjust the control gains to improve stability performance. In this section, we illustrate the limitations of this approach by considering the case of adding an active component (an acceleration feedback control) to an already optimally designed passive TMD. This means that the values of \(\gamma\) and \(\zeta _2\) are fixed to the ones shown in (31) and (32) for this part of the stability analysis.

Fig. 3
figure 3

Evolution of the stable region of the applied acceleration feedback control

Full size image

Figure 3 shows the evolution of the stable region as \(\psi\) approaches \(\psi _{\textrm{cr}}\) in the \(\alpha _1 -\alpha _2\) plane, where \(\alpha _1\) and \(\alpha _2\) are the two control gains. The choice of the mass ratio \(\varepsilon\) is arbitrary (as long as \(\varepsilon >0\), otherwise its meaning would be unphysical). For all figures, \(\varepsilon = 0.05\) is used, partly since this makes practical sense and also for the sake of easier comparison, as it is the value used in [72]. As it can be observed in the figures, as \(\psi\) approaches its critical value, the stable region shrinks, and it seems as if it disappears exactly when \(\psi = \psi _{\textrm{cr}}\). This suggests that applying an acceleration feedback control on a system that already has a TMD attached to it cannot extend the range of stable parameters compared to the system without the active control.

To prove this observation, we will analytically investigate the evolution of the stable region. As it can be seen on the stability charts above, the left boundary of the stable region is given by a straight line, which is related to the sign of \(b_0\), that is

$$\begin{aligned} b_0>0\,\iff \,\alpha _2 < \alpha _1 + 1. \end{aligned}$$
(34)

This inequality is independent of \(\psi\); therefore, it is not related to the loss of stability for \(\psi >\psi _{\textrm{cr}}\).

The right boundary of the stable region is a parabola, which corresponds to the implicit equation \(h_3 = 0\). The shrinkage and eventual disappearance of the stable region are due to the fact that this parabola is closing as \(\psi\) is increased. \(h_3 = 0\) corresponds to

$$\begin{aligned}{} & {} \sqrt{\varepsilon } \left( -\alpha _2 \left( \varepsilon ^{3/2}+8 \sqrt{\varepsilon } \psi ^2-4 \varepsilon \psi -8 \psi ^3\right) \right. \nonumber \\{} & {} \left. \quad -2 \alpha _2^2 (\varepsilon +1) \psi +\left( \sqrt{\varepsilon }-2 \psi \right) ^3\right) \nonumber \\{} & {} \quad -\alpha _1 \left( \sqrt{\varepsilon }-2 \psi \right) ^2 = 0. \end{aligned}$$
(35)

Equation (35) can be solved for \(\alpha _1\), resulting in the following quadratic equation:

$$\begin{aligned} \alpha _1 = c_2\alpha _2^2 + c_1\alpha _2 + c_0, \end{aligned}$$
(36)

where

$$\begin{aligned} c_2&= -\frac{2 \sqrt{\varepsilon } (\varepsilon +1) \psi }{\left( \sqrt{\varepsilon }-2 \psi \right) ^2}, \end{aligned}$$
(37)
$$\begin{aligned} c_1&= \frac{\sqrt{\varepsilon } \left( -\varepsilon ^{3/2}+4 \varepsilon \psi -8 \sqrt{\varepsilon } \psi ^2 +8 \psi ^3\right) }{\left( \sqrt{\varepsilon }-2 \psi \right) ^2}, \end{aligned}$$
(38)
$$\begin{aligned} c_0&= \sqrt{\varepsilon } \left( \sqrt{\varepsilon }-2 \psi \right) . \end{aligned}$$
(39)

In order to investigate the system’s behavior, we will take the limits of coefficients \(c_0\), \(c_1\), and \(c_2\) as \(\psi\) approaches \(\psi _{\rm cr}\). Let us introduce

$$\begin{aligned} {\widetilde{\psi }} = \psi - \psi _{\rm cr}. \end{aligned}$$
(40)

With the help of the new variable \({\widetilde{\psi }}\), we can determine the limits by substituting \({\widetilde{\psi }} + \psi _{\rm cr}\) for \(\psi\). Since

$$\begin{aligned} c_2= & {} \frac{-2\sqrt{\varepsilon }\left( \varepsilon + 1\right) \left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) }{\left( \sqrt{\varepsilon }-2\left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) \right) ^2}\nonumber \\= & {} \frac{-2\sqrt{\varepsilon }\left( \varepsilon + 1\right) \left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) }{4{\widetilde{\psi }}^2}, \end{aligned}$$
(41)

this means that

$$\begin{aligned} \lim _{{\widetilde{\psi }}\rightarrow 0} c_2 = -\infty , \end{aligned}$$
(42)

as the numerator is a finite negative number and the denominator approaches 0. The coefficient \(c_1\) can be reduced to

$$\begin{aligned} \begin{aligned} c_1&= \frac{\sqrt{\varepsilon } \left( -\varepsilon ^{3/2}+4 \varepsilon \left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) -8 \sqrt{\varepsilon } \left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) ^2 +8 \left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) ^3\right) }{\left( \sqrt{\varepsilon }-2 \left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) \right) ^2}, \\&=\frac{2 \sqrt{\varepsilon } \left( \varepsilon {\widetilde{\psi }} +2 \sqrt{\varepsilon } {\widetilde{\psi }}^2+4 {\widetilde{\psi }} ^3\right) }{4{\widetilde{\psi }}^2},\\&=\frac{\varepsilon ^{3/2}}{2 {\widetilde{\psi }} }+\varepsilon + 2 \sqrt{\varepsilon } {\widetilde{\psi }} , \end{aligned} \end{aligned}$$
(43)

so its limit is indeterminate; however, one-sided limits exist. The limit from the left is

$$\begin{aligned} \lim _{{\widetilde{\psi }}\rightarrow 0^-} c_1 = -\infty , \end{aligned}$$
(44)

since the dominant term in the sum is \(\varepsilon ^{3/2} / \left( 2{\widetilde{\psi }}\right)\), which becomes an increasingly large negative number as \({\widetilde{\psi }}\) gets closer to 0 from below. When the limit is taken from the right, the dominant term becomes an increasingly large positive number:

$$\begin{aligned} \lim _{{\widetilde{\psi }}\rightarrow 0^+} c_1 = \infty . \end{aligned}$$
(45)

Finally,

$$\begin{aligned} c_0 = \sqrt{\varepsilon } \left( \sqrt{\varepsilon }-2\left( {\widetilde{\psi }}+\frac{\sqrt{\varepsilon }}{2}\right) \right) = -2\sqrt{\varepsilon }{\widetilde{\psi }}, \end{aligned}$$
(46)

so

$$\begin{aligned} \lim _{{\widetilde{\psi }}\rightarrow 0} c_0 = 0. \end{aligned}$$
(47)

Equation (47) implies that, as \(\psi\) approaches \(\psi _{\rm cr}\), the vertex of the parabola gets closer and closer to the origin in the \(\alpha _1 - \alpha _2\) plane. Equation (42) means that the parabola closes as \(\psi\) reaches the critical value, which inevitably results in the shrinkage and, ultimately, the disappearance of the stable region. The results expressed in (44) and (45) related to the coefficient of the linear part (\(c_1\)) point out that there is a singularity when \(\psi\) reaches \(\psi _{\rm cr}\), which is in accordance with the notion of the closure of the parabola.

This proves that, selecting \(\gamma\) and \(\zeta _2\) according to Eqs. (31) and (31), any arbitrarily small values of \(\alpha _1\) and \(\alpha _2\) cannot stabilize the system for \(\psi > \psi _{cr}\) and \(\psi -\psi _{cr}\ll 1\). A numerical investigation (not presented here) suggests that this result is generally valid also for any \(\alpha _1\) and \(\alpha _2\) values, and also if \(\psi \gg \psi _{cr}\).

From a physical perspective, this result is probably related to the detuning effect of the active control. In fact, the passive vibration absorber is very sensitive to variations of \(\gamma\), whose optimal value depends on the mass ratio (see Eq. (32)). Accordingly, if \(\alpha _1\ne 0\) or \(\alpha _2\ne 0\), the system’s effective inertia varies, causing a sort of detuning, which deteriorates vibration suppression performance.

3.3 HVA optimization

Although simply adding the active component to an already optimized TMD cannot increase the stable region, simultaneously tuning both the active and passive system parameters might expand the stable region. This possibility is evaluated in this section. To reiterate, the parameters that can be adjusted are \(\gamma\), \(\zeta _2\), and \(\varepsilon\) for the passive component, and \(\alpha _1\) and \(\alpha _2\) for the active component. First, let us define the meaning of optimum in this specific context. The combination of parameters \(\gamma\), \(\zeta _2\), \(\varepsilon\), \(\alpha _1\), and \(\alpha _2\) is considered optimal if and only if they yield the largest value of \(\psi _{\textrm{max}}\) while ensuring the stability of the system for all \(\psi < \psi _{\textrm{max}}\).

Initially, we perform a numerical optimization through matlab’s fminsearch function and simulated annealing from the Global Optimization Toolbox, which exploits the simplex search method of Lagarias et al. [73]. Several attempts provided similar results regarding the maximal achievable \(\psi\) value. However, depending on the initial conditions of the numerical optimization, we obtained different values for the parameters. In particular, the optimal values were always just below the \(\alpha _1 - \alpha _2 + 1 = 0\) line in the \(\alpha _1 - \alpha _2\) plane.

Notice that as we approach the \(\alpha _1 - \alpha _2 + 1 = 0\) line, the denominators of the Routh–Hurwitz coefficients and some entries in the system matrix approach 0; thus, the coefficients explode. Furthermore, as soon as the line is crossed, the system loses stability because \(b_0\) becomes negative while \(b_4= 1\) is always positive. Since the coefficients cannot have the same sign, this implies instability.

To verify if our observation from the numerical analysis is accurate—specifically, that there exists an entire set of optimal parameter combinations instead of just one—and to identify this set, we will perform an analytical stability analysis.

As it is discussed in the previous section, \(\alpha _2 < \alpha _1 + 1\) is a necessary condition for stability; on the other hand, the optimum is close to the \(\alpha _2 = \alpha _1 + 1\) line. Therefore, we investigate the Routh–Hurwitz coefficients as \(\alpha _2\) approaches \(\alpha _1 + 1\) from below. The denominator of the coefficients approaches \(0^+\) as \(\alpha _2 \rightarrow (\alpha _1 + 1)^-\), which means that, in order to satisfy conditions (25) and (26), the numerators should be positive, too. Let \(n_i\) denote the numerator of \(b_i\) (for \(i \in {0,2}\)). Then,

$$\begin{aligned} n_0 = \gamma ^2 > 0 \end{aligned}$$
(48)

is trivially satisfied. The condition from \(b_2 > 0\) becomes

$$\begin{aligned} \lim _{\alpha _2 \rightarrow (\alpha _1 + 1)^-}n_2> 0: \qquad \gamma ^2(1 + \varepsilon ) - \alpha _1 - 4\zeta _2\gamma \psi > 0. \end{aligned}$$
(49)

It is also necessary to satisfy the positivity constraints on the Hurwitz-determinants. As \(h_1 = b_3\), condition (28) translates to

$$\begin{aligned} \lim _{\alpha _2 \rightarrow (\alpha _1 + 1)^-}n_3> 0: \qquad \alpha _1\psi + \gamma (1 + \varepsilon )\zeta _2 > 0. \end{aligned}$$
(50)

Moreover, condition (29) becomes

$$\begin{aligned} \lim _{\alpha _2 \rightarrow (\alpha _1 + 1)^-}{h_3} = \lim _{\alpha _2 \rightarrow (\alpha _1 + 1)^-}\left( b_1b_2b_3 - b_0b_3^2\right) , \end{aligned}$$
(51)

as the third term (that contains \(b_4 = 1\)) is dominated by the first two terms. Since \(b_3 > 0\) has to hold true, the inequality simplifies to

$$\begin{aligned} \lim _{\alpha _2 \rightarrow (\alpha _1 + 1)^-}\left( b_1b_2 - b_0b_3 \right) > 0, \end{aligned}$$
(52)

thus

$$\begin{aligned} \lim _{\alpha _2 \rightarrow (\alpha _1 + 1)^-}\left( n_1n_2 - n_0n_3\right) > 0, \end{aligned}$$
(53)

from which

$$\begin{aligned} 4\gamma ^2\zeta _2\psi ^2 - (\gamma ^3(1 + \varepsilon ) + 4\gamma \zeta _2^2)\psi - \alpha _1\zeta _2 > 0. \end{aligned}$$
(54)

Inequality (54) is a quadratic inequality in \(\psi\) with a positive leading coefficient, which means that the inequality is satisfied if \(\psi\) is lower than the smaller root or higher than the larger root. The roots are:

$$\begin{aligned} \psi _{1,2} = \frac{\gamma ^3(1 + \varepsilon ) + 4\gamma \zeta _2^2 \pm \sqrt{(\gamma ^3(1 + \varepsilon ) + 4\gamma \zeta _2^2)^2 + 15\gamma ^2\zeta _2^2\alpha _1}}{8\gamma ^2\zeta _2}. \end{aligned}$$
(55)

By setting the discriminant to 0, the region between the roots vanishes, and the condition is essentially always satisfied (except if \(\psi\) coincides perfectly with the root of the quadratic expression, but that is irrelevant from a practical point of view). The discriminant is

$$\begin{aligned} \Delta = (\gamma ^3(1 + \varepsilon ) + 4\gamma \zeta _2^2)^2 + 16\gamma ^2\zeta _2^2\alpha _1, \end{aligned}$$
(56)

so

$$\begin{aligned} \Delta =0\,\iff \,\alpha _1 = -\frac{(\gamma ^3(1 + \varepsilon ) + 4\gamma \zeta _2^2)^2}{16\gamma ^2\zeta _2^2}. \end{aligned}$$
(57)

If we substitute this result into the remaining two inequalities (49) and (50), we attain the following conditions on \(\psi\):

$$\begin{aligned} \psi&< f_2(\gamma ,\zeta _2,\varepsilon ) \end{aligned}$$
(58)
$$\begin{aligned} \psi&< f_3(\gamma ,\zeta _2,\varepsilon ), \end{aligned}$$
(59)

where

$$\begin{aligned} f_2(\gamma ,\zeta _2,\varepsilon )&= \frac{\gamma ^3(1 + \varepsilon )^2}{64\zeta _2^3} + \frac{3\gamma (1 + \varepsilon )}{8\zeta _2} + \frac{\zeta _2}{4\gamma } \end{aligned}$$
(60)
$$\begin{aligned} f_3(\gamma ,\zeta _2,\varepsilon )&= \frac{16\gamma (1 + \varepsilon )\zeta _2^3}{(\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^2}. \end{aligned}$$
(61)

To obtain the correct relation sign for (59), we had to use the fact that according to (57), \(\alpha _1 < 0\) always.

It can be shown that, given \(\gamma > 0\), \(\zeta _2 > 0\) and \(\varepsilon > 0\), the following relation exists between \(f_2\) and \(f_3\):

$$\begin{aligned} f_2(\gamma ,\zeta _2,\varepsilon ) \ge f_3(\gamma ,\zeta _2,\varepsilon ). \end{aligned}$$
(62)

In other words, if \(\psi < f_3(\gamma ,\zeta _2,\varepsilon )\), then (58) is necessarily satisfied as well. The proof of (62) is the following. It is known that

$$\begin{aligned} (p^2 + 4pq - q^2)^2 \ge 0 \end{aligned}$$
(63)

for any p and q real numbers. Therefore,

$$\begin{aligned} p^4 + 8p^3q + 14p^2q^2 - 8pq^3 + q^4 \ge 0. \end{aligned}$$
(64)

If we choose

$$\begin{aligned} p&= \gamma ^2(1 + \varepsilon ), \end{aligned}$$
(65)
$$\begin{aligned} q&= 4\zeta _2^2 \end{aligned}$$
(66)

we get

$$\begin{aligned}{} & {} \gamma ^8(1 + \varepsilon )^4 + 32\gamma ^6(1 + \varepsilon )^3\zeta _2^2 + 224\gamma ^4(1 + \varepsilon )^2\zeta _2^4 \nonumber \\{} & {} - 512\gamma ^3(1 + \varepsilon )\zeta _2^6 + 256\zeta _2^8 \ge 0. \end{aligned}$$
(67)

From this:

$$\begin{aligned}{} & {} (\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^4 + 16\gamma ^2(1 + \varepsilon )\zeta _2^2(\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^2 \nonumber \\{} & {} \quad \ge 1024\gamma ^2(1 + \varepsilon )\zeta _2^6, \end{aligned}$$
(68)

which implies

$$\begin{aligned}{} & {} (\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^2 + 16\gamma ^2(1 + \varepsilon )\zeta _2^2 \nonumber \\{} & {} \quad \ge \frac{1024\gamma ^2(1 + \varepsilon )\zeta _2^6}{(\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^2} \end{aligned}$$
(69)

and therefore

$$\begin{aligned}{} & {} \gamma ^4(1 + \varepsilon )^2 + 24\gamma ^2(1 + \varepsilon )\zeta _2^2 + 16\zeta _2^4 \nonumber \\{} & {} \quad \ge \frac{1024\gamma ^2(1 + \varepsilon )\zeta _2^6}{(\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^2}. \end{aligned}$$
(70)

Since all the parameters are positive, we obtain

$$\begin{aligned}{} & {} \frac{\gamma ^3(1 + \varepsilon )^2}{64\zeta _2^3} + \frac{3\gamma (1 + \varepsilon )}{8\zeta _2} + \frac{\zeta _2}{4\gamma } \nonumber \\{} & {} \quad \ge \frac{16\gamma (1 + \varepsilon )\zeta _2^3}{(\gamma ^2(1 + \varepsilon ) + 4\zeta _2^2)^2}. \end{aligned}$$
(71)

This inequality is exactly (62). The surfaces corresponding to \(f_2=0\) and \(f_3=0\) can be seen in Fig. 4a. Looking at the figure, one might get the impression that there are regions where \(f_3\) exceeds \(f_2\). However, the surfaces only touch each other without crossing. Namely, if \(\zeta _2 = \frac{\gamma }{2}\sqrt{2+\sqrt{5}}\sqrt{1+\varepsilon }\), then \(f_2=f_3\).

As a consequence, the stability of the system entirely boils down to \(f_3\): as long as \(\psi < f_3\), the system is stable. Accordingly, the optimal parameter values of the HVA correspond to the maximum of \(f_3\).

For any given value of \(\varepsilon\), \(f_3\) is a different surface. For any local maximum of this surface, it must hold that

$$\begin{aligned} \frac{\partial f_3}{\partial \gamma }&= 0, \end{aligned}$$
(72)
$$\begin{aligned} \frac{\partial f_3}{\partial \zeta _2}&= 0. \end{aligned}$$
(73)

The partial derivatives are

$$\begin{aligned} \frac{\partial f_3}{\partial \gamma }&= -\frac{16(1 + \varepsilon )\zeta _2^3(3\gamma ^2(1 + \varepsilon ) - 4\zeta _2^4)}{\gamma ^2(1 + \varepsilon + 4\zeta _2^2)^3}, \end{aligned}$$
(74)
$$\begin{aligned} \frac{\partial f_3}{\partial \zeta _2}&= \frac{16\gamma (1 + \varepsilon )(3\gamma ^2(1 + \varepsilon )\zeta _2^2 - 4\zeta _2^4)}{\gamma ^2(1 + \varepsilon + 4\zeta _2^2)^3}. \end{aligned}$$
(75)

The only solution to this system of equations (given the positivity of the parameters) is

$$\begin{aligned} \zeta _2^\star = \frac{\sqrt{3}}{2}\gamma \sqrt{1 + \varepsilon }, \end{aligned}$$
(76)

meaning that the optimal parameters for the passive part are on a (half-)line passing through the origin in the \(\gamma - \zeta _2\) plane for a given \(\varepsilon\). This result is illustrated by Fig. 4b. This result implies that, if \(\alpha _1\) and \(\alpha _2\) are correctly selected, any combination of \(\gamma\) and \(\zeta _2\) values satisfying (76) corresponds to an optimal set.

By substituting (76) into the expression for \(\alpha _1\) (see (57)) we obtain the simpler expression

$$\begin{aligned} \alpha _1^\star = -\frac{4}{3}\gamma ^2(1 + \varepsilon ). \end{aligned}$$
(77)

It is important to note, however, that (77) can be used only if \(\zeta _2\) is chosen according to (76). Setting the parameters of the controller this way leads to the following value for the maximal stable \(\psi\):

$$\begin{aligned} \psi _{\textrm{max}} = \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon } \end{aligned}$$
(78)

regardless of \(\gamma\). In comparison to a purely passive TMD, the HVA can always provide better performance in terms of the size of the stable region:

$$\begin{aligned} \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon } > \frac{\sqrt{\varepsilon }}{2} \end{aligned}$$
(79)

for all \(\varepsilon\). Indeed, differently from the TMD, the HVA works also for a theoretical vibration absorber with no mass (\(\varepsilon =0\)).

Fig. 4
figure 4

a Surfaces \(f_2\) and \(f_3\) (\(\varepsilon = 0.05\)). b Surface \(f_3\) (with \(\varepsilon = 0.05\)) and the line corresponding to the optimal parameters

Full size image
Fig. 5
figure 5

Sections of the stability map of the system supplemented by an HVA. a \(\alpha _2\) varies together with \(\alpha _1\) according to Eq. (34), \(\gamma =1\) and \(\zeta _2=0.8874\); b, c \(\alpha _1=-1.4\), \(\alpha _2=-0.4\) and \(\gamma =1\); c \(\alpha _1=-1.4\), \(\alpha _2=-0.4\) and \(\zeta _2=0.8874\)

Full size image

The different sections of the stable region with respect to the various HVA parameters are illustrated in Fig. 5. The optimal values of the parameters and the resulting maximal \(\psi\) are shown, too. All the various sections highlight that \(\psi _{\text {max}}\) is not the maximal \(\psi\) value for which we can have stability, but it is the maximal \(\psi\) such that the system is stable for any \(\psi >\psi _{\text {max}}\). The significant improvement related to the additional active controller—i.e., the difference between \(\psi _{\text {max}}\) and \(\psi _{\text {cr}}\)—can be visually appreciated.

Figure 6 illustrates the evolution of the stable region, assuming that \(\alpha _1\) and \(\alpha _2\) are chosen optimally. The stable region clearly shrinks and approaches the derived line in the \(\zeta _2 - \gamma\) plane (Eq. 76) as \(\psi\) approaches \(\psi _{\rm max}\).

Fig. 6
figure 6

Evolution of the stable region in the \(\zeta _2 - \gamma\) plane

Full size image

Figure 7 illustrates the time histories of simulations for different cases. Comparing Fig. 7a and b highlights that the HVA does not only greatly extend the stable region but also provides a much better performance in terms of the speed of convergence. With a properly tuned HVA, the system is stable with large values of \(\psi\) (Fig. 7c). However, as it is illustrated by Fig. 7d, as soon as \(\psi\) exceeds \(\psi _{\rm max}\), the system loses stability.

Fig. 7
figure 7

Time histories of numerical simulations

Full size image

To recapitulate, the optimal tuning of the parameters can be theoretically done as follows:

  1. 1.

    Choose \(\gamma\) and \(\varepsilon\) arbitrarily (a larger \(\varepsilon\) corresponds to a larger stable region)

  2. 2.

    Set \(\zeta _2^\star = \frac{\sqrt{3}}{2}\gamma \sqrt{1 + \varepsilon }\) (Eq. (76))

  3. 3.

    Set \(\alpha _1^\star = -\frac{4}{3}\gamma ^2(1 + \varepsilon )\) (Eq. (77))

  4. 4.

    \(\alpha _2\) should be as close as possible to \(\alpha _1 + 1\), but it is crucial to make sure that \(\alpha _2 < \alpha _1 + 1\) holds true

The resulting maximal \(\psi\) is \(\psi _{\textrm{max}} = \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon }\) (Eq. (78)). Alternatively, \(\zeta _2\) can be chosen arbitrarily, and \(\gamma\) according to Eq. (76). Several practical implications should be considered while selecting the parameter values, as discussed in Sect. 5.

It is not trivial to provide a physical interpretation of the obtained results. The most important result is that the active part can significantly improve stability if the passive components are properly tuned. This observation suggests that the detuning effect of the modified inertial terms can be compensated for if properly taken into account. Equation (78) highlights that the active controller does not need an additional mass to work (\(\varepsilon =0\)), but it helps to have one. It is surprising that, to obtain optimal performance, a linear relationship between the absorber’s damping (\(\zeta _2\)) and stiffness (\(\gamma\)) should be satisfied (Eq. (76)), as this is not the case for a purely passive absorber. Equation (77) implies that, the stiffer the absorber, the larger the control gains should be, which is consistent with intuition since a stiffer absorber requires a larger force to be moved.

4 Case studies

This section demonstrates the effect of applying an HVA on real mechanical systems with the help of two case studies.

4.1 Mass-on-moving-belt model

The first system considered is the mass-on-moving-belt model [44]. The dynamics of the system is described by

$$\begin{aligned} m_1 \ddot{x}_1 + {\tilde{c}}_1 {\dot{x}}_1 + k_1 x_1 = F, \end{aligned}$$
(80)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} F = \mu (v_{\rm rel})\ mg &\quad v_{\rm rel} \ne 0, \\ |F| \le \mu _{st}mg &\quad v_{\rm rel} = 0, \end{array}\right. } \end{aligned}$$
(81)

represents the friction force, \(v_{\rm rel} = v_{\rm belt} - {\dot{x}}\) is the relative velocity, \(\mu (v_{\rm rel})\) denotes the friction coefficient that depends on the relative velocity, and \(v_{\rm belt}\) is the belt velocity. We consider a velocity-weakening friction law of the form

$$\begin{aligned} \mu (v_{\rm rel}) = \left( \mu _{\rm d} + (\mu _{\rm st} - \mu _{\rm d})\textrm{exp}\left( -\frac{|v_{\rm rel}|}{v_0}\right) \right) \textrm{sign}(v_{\rm rel}), \end{aligned}$$
(82)

where \(v_0\) is a constant representing a reference velocity, and \(\mu _{\rm st}\) and \(\mu _{\rm d}\) denote the static and dynamic friction coefficients, respectively. Linearizing (80) around the static equilibrium \(x = \frac{mg}{k}\mu (v_{\rm belt})\) yields

$$\begin{aligned} m_1 \ddot{x}_1 + c_1{\dot{x}}_1 + k_1 x_1 = 0, \end{aligned}$$
(83)

where

$$\begin{aligned} c_1 = {\tilde{c}}_1 - mg\frac{\mu _{\rm st} - \mu _{\rm d}}{v_0}\textrm{exp}\left( -\frac{v_{\rm belt}}{v_0}\right) . \end{aligned}$$
(84)
Table 1 Problem data for the mass-on-moving-belt example
Full size table

Consider the problem data shown in Table 1, where the values of \(\mu _{\rm st}\) and \(\mu _{\rm d}\) correspond to the case where both the oscillating mass and the belt are made of cast iron (see [44]). The system is stable if and only if

$$\begin{aligned} c_1 \ge 0 \iff {\tilde{c}}_1 \ge m_1g\frac{\mu _{\rm st} - \mu _{\rm d}}{v_0}\textrm{exp}\left( -\frac{v_{\rm belt}}{v_0}\right) . \end{aligned}$$
(85)

Thus, without an HVA, the minimum allowed belt velocity to keep the equilibrium stable is

$$\begin{aligned} v_{\rm belt} \ge v_0 \ln \left( \frac{m_1g(\mu _{\rm st} - \mu _{\rm d})}{v_0{\tilde{c}}_1 }\right) = 1.462\, \mathrm{m/s}. \end{aligned}$$
(86)
Fig. 8
figure 8

Time histories of numerical simulations for the system in Eq. (80) without and with HVA

Full size image

Figure 8a illustrates that, for \(v_{\rm belt}<1.462\) m/s, the system experiences a periodic stick–slip motion because of the instability of the equilibrium.

An HVA can significantly decrease this lower bound and extend the stable region. According to (78),

$$\begin{aligned} \psi _{\textrm{max}} = \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon }. \end{aligned}$$
(87)

That is, by designing the HVA following Sect. 3.3, the system is stable for all \(\psi \le \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon }\), where

$$\begin{aligned} \psi = -\frac{c_1}{2\omega _{\textrm{n}1}m_1} = \frac{m_1g\frac{\mu _{\rm st} - \mu _{\rm d}}{v_0}\textrm{exp}\left( -\frac{v_{\rm belt}}{v_0}\right) - {\tilde{c}}_1}{2\omega _{\textrm{n}1}m_1} \end{aligned}$$
(88)

and \(\omega _{\textrm{n}1}=\sqrt{k_1/m_1}\). Therefore, the equilibrium is stable if

$$\begin{aligned} \frac{m_1g\frac{\mu _{\rm st} - \mu _{\rm d}}{v_0}\textrm{exp}\left( -\frac{v_{\rm belt}}{v_0}\right) - {\tilde{c}}_1}{2\omega _{\textrm{n}1}m_1} \le \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon }. \end{aligned}$$
(89)

Using a secondary oscillator in the HVA with mass \(m_2 = 0.5\ \textrm{kg}\) (resulting in \(\varepsilon = 0.05\)), the minimum allowed belt velocity keeping the equilibrium stable is reduced to

$$\begin{aligned} v_{\rm belt}\ge & {} v_0 \ln \left( \frac{m_1g(\mu _{\rm st} - \mu _{\rm d})}{v_0\left( {\tilde{c}}_1 + \frac{3\sqrt{3}}{4}\omega _{\textrm{n}1}m_1\sqrt{1 + \varepsilon } \right) }\right) \nonumber \\= & {} 0.637\, {\mathrm{m/s}}. \end{aligned}$$
(90)

Figure 8b and c illustrates that the trivial equilibrium is stable for \(v_{\rm belt}>0.637\) m/s and unstable below this belt velocity, leading the system to stick–slip vibrations. We note that the mass-on-moving-belt typically loses stability through a subcritical Hopf bifurcation [44, 74]; therefore, the stable equilibrium near the stability boundary may have limited dynamical integrity.

With an optimally tuned passive TMD with the same mass (\(\varepsilon =0.05\)), the minimal velocity cannot be reduced below

$$\begin{aligned} v_{\rm belt} \ge v_0 \ln \left( \frac{m_1g(\mu _{\rm st} - \mu _{\rm d})}{v_0\left( {\tilde{c}}_1 + \omega _{\textrm{n}1}m_1\sqrt{\varepsilon } \right) }\right) = 1.195\, {\mathrm{m/s}}. \end{aligned}$$
(91)

4.2 Galloping vibrations

Galloping is the unstable aeroelastic oscillation of one-DoF bluff structures in winds and currents [38, 66]. Similarly to the mass-on-moving-belt example presented in Sect. 4.1, where the velocity-dependent friction force caused the development of self-excited oscillations, a velocity-dependent aerodynamic force often results in unstable galloping vibrations. The system dynamics is described by the differential equation

$$\begin{aligned} m_1\ddot{x}_1 + {\tilde{c}}_1{\dot{x}}_1 + k_1 x_1 = F, \end{aligned}$$
(92)

where

$$\begin{aligned} F = -\frac{1}{2}\rho U^2_{\rm rel} D (c_L \cos \alpha + c_D \sin \alpha ) \end{aligned}$$
(93)

is the aerodynamic force. The relative velocity \(U_{\rm rel}\) satisfies

$$\begin{aligned} U^2_{\rm rel} = U^2 + {\dot{x}}_1^2, \end{aligned}$$
(94)

and the angle of attack \(\alpha\) can be obtained by

$$\begin{aligned} \tan \alpha = \frac{{\dot{x}}_1}{U}. \end{aligned}$$
(95)

U represents the steady flow velocity and \(\rho\) is its density, \(c_L\) and \(c_D\) denote the lift and drag coefficients, respectively. Finally, D denotes the characteristic length of the cross-section, e.g., in the case of a square cross-section, it corresponds to the length of the sides of the square. Expressing the nonlinear force as a Taylor series in \({\dot{x}}_1/U\) yields

$$\begin{aligned} F = \frac{1}{2}\rho U^2 D \sum _{k = 0}^{\infty } A_k \left( \frac{{\dot{x}}_1}{U}\right) ^k. \end{aligned}$$
(96)

Linear stability can be investigated by neglecting the higher-order terms, resulting in the form

$$\begin{aligned} F = \frac{1}{2}\rho U D A_1 {\dot{x}}_1. \end{aligned}$$
(97)

Consequently, the equation of motion takes the form

$$\begin{aligned} m_1\ddot{x}_1 + c_1{\dot{x}}_1 + k_1 x_1 = 0, \end{aligned}$$
(98)

where

$$\begin{aligned} c_1 = {\tilde{c}}_1 - \frac{1}{2}\rho U D A_1. \end{aligned}$$
(99)

The Taylor coefficient takes the value \(A_1 = 1.833\) m for a rectangular cross-section, where the side lengths are D and 3/2D for the sides perpendicular and parallel to the flow, respectively, provided that the flow is turbulent (see [66]).

Table 2 Problem data for the galloping example
Full size table

The system is stable if and only if

$$\begin{aligned} c_1 \ge 0 \iff {\tilde{c}}_1 \ge \frac{1}{2}\rho U D A_1, \end{aligned}$$
(100)

therefore, using the problem data summarized in Table 2, the maximal flow velocity keeping the trivial solution stable is

$$\begin{aligned} U \le \frac{2{\tilde{c}}_1}{\rho D A_1} = 8.445\, {\mathrm{m/s}} \end{aligned}$$
(101)

if no absorber is implemented. Figure 9a shows how the system settles on a periodic attractor for \(U>8.445\) m/s. At the maximal velocity, the Reynolds number is

$$\begin{aligned} \textrm{Re} = \frac{\rho U D}{\mu } = 63106, \end{aligned}$$
(102)

meaning that the flow is turbulent indeed.

Fig. 9
figure 9

Time histories of numerical simulations for the system in Eq. (92) without and with HVA

Full size image

Implementing the HVA following the design method proposed in Sect. 3.3 guarantees stability if

$$\begin{aligned} \psi \le \psi _{\rm max} = \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon }, \end{aligned}$$
(103)

where

$$\begin{aligned} \psi = -\frac{c_1}{2 m_1\omega _{\textrm{n}1}} = \frac{\frac{1}{2}\rho U D A_1 - {\tilde{c}}_1}{2 m_1\omega _{\textrm{n}1}}, \end{aligned}$$
(104)

meaning that the system is stable if

$$\begin{aligned} \frac{\frac{1}{2}\rho U D A_1 - {\tilde{c}}_1}{2 m_1\omega _{\textrm{n}1}} \le \frac{3\sqrt{3}}{8}\sqrt{1 + \varepsilon }. \end{aligned}$$
(105)

If \(m_2\) is chosen such that \(\varepsilon = 0.05\) (i.e. \(m_2 = 0.05\ \textrm{kg}\)), the maximal flow velocity using an HVA is

$$\begin{aligned} U \le \frac{2 \left( {\tilde{c}}_1 + \frac{3\sqrt{3}}{4}\omega _{\textrm{n}1}m_1\sqrt{1 + \varepsilon } \right) }{\rho D A_1} = 43.994\, {\mathrm{m/s}}. \end{aligned}$$
(106)

The accuracy of the stability boundary obtained for the system encompassing the HVA is demonstrated by the time series in Fig. 9b and c, where the system converges to the trivial solution and to a periodic attractor, respectively.

Utilizing a passive TMD with the same mass, the maximal flow velocity keeping the system stable would be

$$\begin{aligned} U \le \frac{2 \left( {\tilde{c}}_1 + \omega _{\textrm{n}1}m_1\sqrt{\varepsilon } \right) }{\rho D A_1} = 14.417\, {\mathrm{m/s}}. \end{aligned}$$
(107)

The results of the case studies are summarized in Table 3.

Table 3 Summary of the results of the case studies
Full size table

5 Practical considerations about parameter tuning

In real engineering cases, the tuning of the parameters can hardly follow the steps suggested at the end of Sect. 3. Conversely, practical aspects must be considered. In general, the control gain values can be freely chosen, and their tuning is straightforward. However, it is usually complicated to identify the exact value of \(\alpha _1\) and \(\alpha _2\) because the modal mass of the primary system is typically unknown. The natural frequency ratio \(\gamma\) can be designed with quite a good accuracy based on geometrical considerations, numerical models of the absorber, and measurements of the host system’s natural frequency. Once the system is realized, \(\gamma\) can be measured relatively easily by disassembling the two subsystems and usually adjusted by increasing or reducing the absorber mass \(m_2\). The absorber damping \(\zeta _2\) can be measured through free vibrations of the host subsystem [75]. However, it is practically impossible to define its value by design, if not with a very rough accuracy, in most engineering applications [76]. Also, the assumption that damping is linear is often largely inaccurate [77].

Despite these difficulties, the stability and optimization analyses performed in Sect. 3 provides an interesting result from a practical point of view. Namely, from the stability point of view, there is not a single set of optimal parameter values; instead, a full line of the parameter space provides the same optimal stability properties. This means that a designer has some freedom in choosing the parameter values, depending on technical constraints, without necessarily having suboptimal performance. Considering this result, and the practical limitations mentioned above, a possible optimization strategy, implementable in real cases, is suggested.

  1. 1.

    Define the “optimal line” \(\alpha _2=\alpha _1+1\): although it is quite complicated to identify the exact values of \(\alpha _1\) and \(\alpha _2\), they are both proportional to some control gains applied digitally or analogically to the controller. In most cases, their tuning is very simple. Besides, theoretical results show that the system is always unstable on the left side of the “optimal line”. By selecting a negative arbitrarily small (in absolute value) \(\alpha _1\), and by slowly sweeping the \(\alpha _2\) value for the system without forcing (\(\psi =0\)), one point of the “optimal line” can be found by marking the point for which stability is lost. Then, repeating the procedure for \(\alpha _2=0\), by sweeping \(\alpha _1\), another point of the line is identified. These two points enable us to uniquely define the line \(\alpha _2=\alpha _1+1\), even without knowing the values of \(\alpha _1\) and \(\alpha _2\). In the case of a digital controller, it can be easily set such that \(\alpha _2\) is slightly smaller than this line, reducing the number of parameters to be tuned. Referring to the two case studies considered in Sects. 4.1 and 4.2, this strategy can be implemented in the absence of belt motion (\(v_{\text {belt}}=0\)) and for no wind (\(U=0\)). Accordingly, it is technically easy to apply it.

  2. 2.

    Setting \(\zeta _2\) and\(\gamma\): we consider the case when the value of \(\zeta _2\) can be roughly estimated before the realization of the device, but its exact value cannot be precisely tuned. In this case, it is often convenient to design \(\gamma\) according to the estimated \(\zeta _2\) value (according to Eq. (76)), then realize the device, measure the actual \(\zeta _2\) value and, based on that, fine-tune \(\gamma\) by adjusting the absorber mass (or by changing the stiffness if the specific application allows doing so).

  3. 3.

    Identifying \(\varepsilon\): in step 1, we were able to identify the line \(\alpha _2=\alpha _1+1\). By remaining on this line and setting \(\alpha _2=0\), we can identify the \(a_1\) value corresponding to \(\alpha _1=-1\); therefore, we can find \(m_1\) through the relation \(\alpha _1=a_1/m_1\). Analogously, by setting \(\alpha _1=0\) and exploiting that \(\alpha _2=a_2/m_2\), we can find \(m_2\). Accordingly, we can find \(\varepsilon =m_2/m_1\). This procedure cannot be implemented if \(a_1\) and \(a_2\) cannot be directly identified. However, if the tuning control gains have the same proportionality law with respect to \(a_1\) and \(a_2\) (\({{\tilde{a}}}_1=K a_1\) and \({{\tilde{a}}}_2=K a_2\)), then their ratio for \(\alpha _2=0\) and \(\alpha _1=0\) can be used for identifying \(\varepsilon\). In fact, for \(\alpha _2=0\), \(\alpha _1=-1\) and \({{\tilde{a}}}_1=-K m_1\), while for \(\alpha _1=0\), \({{\tilde{a}}}_2=K m_2\), thus their ratio is equal to \(-\varepsilon\). The knowledge of K is not required.

  4. 4.

    Setting \(\alpha _1\): once \(\gamma\) and \(\varepsilon\) are known, the required \(\alpha _1\) value to have optimal performance can be identified based on Eq. (77). Since the \({{\tilde{a}}}_1\) value corresponding to \(\alpha _1=-1\) is known, assuming the linear proportionality \({{\tilde{a}}}_1=K a_1\) the required value of \({{\tilde{a}}}_1\) such that \(\alpha _1=-4\gamma ^2(1+\varepsilon )/3\) can be found.

Each case might have its specific complications. However, their analysis is beyond the scope of this paper. Points 2, 3 and 4 of the suggested procedure strictly refer to the technical properties of the absorber implemented; thus, no specific indication can be given even referring to the case studies in Sect. 4, since only the primary system is specified for those cases.

Figures 4b and 6 provide other important information for practical applications. Namely, the smaller \(\gamma\) and \(\zeta _2\) are, the more they have to be accurately tuned to have close to optimal performance.

Energy requirements, possible problems of saturation of the actuator, limitations in the stroke of the absorber, and the speed of convergence are other important aspects of practical relevance not investigated in this study.

6 Conclusions

In this paper, we have investigated the performance of an HVA for suppressing self-excited oscillations of a generic single-DoF mechanical system. While there are various real-life and practical examples of mechanical and mechatronic features and systems that lead to self-induced vibrations, we focused on modeling these specific cases by including a linear ‘damper’ with a negative damping coefficient.

After discussing the effect of a purely passive TMD on the stability of the host system, we demonstrated that augmenting an already designed TMD (optimal in the sense that it has the largest possible stable region) with acceleration feedback control does not extend the stable region. However, we showed that if we optimize both the active and passive parameters simultaneously by completely retuning the HVA parameters, the extent of the stable region can be greatly increased compared to a TMD. The optimal set of parameter values was found fully analytically, and a practical tuning strategy was proposed. The optimized HVA was numerically implemented in two case studies, namely, for suppressing friction-induced and galloping vibrations.

The paper’s topic is open to further research in many different directions. The optimal sets of parameter values are on the boundary of the stable region. Consequently, either high accuracy is required for the tuning, or a compromise with the optimal stable region should be accepted. Also, being close to the stability boundary, nonlinear effects might limit the robustness of the solution; in particular, the saturation of the control force might have important consequences in this respect [78,79,80]. Possible nonlinearities in the viscoelastic elements of the system were also overlooked but might have important effects. However, improving linear stability tends to prevent unwanted nonlinear behaviors as well, as shown by several studies [38, 55, 81], which makes this study engineering relevant even if nonlinearities were neglected.

Time delay in the feedback loop often plays a significant role in stability [62]. Since time delay is always present in real cases, it should be considered in future studies. Moreover, more advanced controllers could be considered instead of the suggested acceleration feedback control. Experimental validation of this paper’s analytical and numerical results should also be carried out.