Turbulent statistics and interface dynamics in a lubricated channel flow at $Re_{\tau }=100$

Abstract

In this work we aim to study, through the use of Direct Numerical Simulations (DNS), the turbulent drag reduction (DR) that occurs in a lubricated channel during the transport of a fluid at a low Reynolds number. In this situation, one of the two fluids separates the second from the wall forming a thin layer in contact with it. In our configuration the thin lubricating layer is adjacent to one of the wall, which will be called lubricated side and and we consider the same density $(\rho _1=\rho _2)$ for the two fluids, while for  the viscosity ratio $(\lambda = \nu _1/\nu _2)$ we will consider  two different values: $\lambda = 1$ and $\lambda = 0.5$. Moreover to assess the role of the surface tension we have duplicated the two simulations at We number of $We=0.055$ and $We=0.5$. As expected the DR mechanism is strongly related to the viscosity ratio, in particular the flow rate increase when decreasing $\lambda$ due to a relaminarization of the lubricated layer. Moreover, the parametric analysis on the effect of viscosity ratio and surface tension allows us to highlight very interesting modulations of the dynamics of the interface and of the turbulent kinetic budgets. To date, the latest studies in this area have been carried out using the Phase Field Method for the description of the interface. One of the scopes of the present study is to confirm and extend the existing results by exploring the dynamics of the flow with the use of the volume of fluid method.

1 Introduction

Experimentally it has been demonstrated that the presence of lubrication by a low viscosity fluid inside a pipeline produces a significant reduction of the wall shear stress and, therefore, of the energy spent for the transport of the fluid [3,4,5,6]. Our current understanding is that this reduction can be mainly explained by the action of viscous forces. Particularly, in the situation in which the lubricated layer has a lower viscosity the resulting increase of the volume flow rate suggests the establishment of a friction loss. This mechanism has been explored in several directions. As an example, the physics of stratified viscous fluid has been largely investigated through the analysis of the flow instabilities, an extensive review can be found in [7]. In general the phenomenon has been investigated qualitatively in its global aspects, such as pressure drop and flow rate, and a satisfactory description of the flow characteristics has not yet been achieved. This is partly due to experimental limitations and partly to the limited number of DNS conducted. The latter in particular represents the best tool for the detailed characterization of both phases as well as the evolution of the interface. Some of most recent studies adopt the Phase Field Method for capturing the interface [8,9,10].

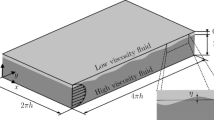
Ahmadi et al. [9] for instance considered a turbulent channel flow with two immiscible stratified layers at a shear Reynolds number $Re_{\tau }=100$ with the aim to explore the role of the surface tension in the observed the drag reduction. In this paper we will address the same set up i.e. we will consider a channel, with the height of 2h, where one interface is located at 1.85h, separating a lubricating layer of fluid with kinematic viscosity $\nu _1$ from a thicker main layer of fluid with kinematic viscosity $\nu _2$. The results that we will discuss in the paper come from the balance of the pressure gradient and a redistribution of momentum due to the asymmetry of the set up. While a model for the friction losses in a fully lubricated case is still missing, the approach presented here allows for an immediate comparison between the different dynamics of turbulence at the two walls. Ahmadi et al. [9] used the same density but different viscosity ratio for the two fluids. According to their results a non negligible contribution to DR is related to the energy spent to deform the interface and the effect increases when the viscosity ratio decrease. In a following study [8] the same authors explored the correlation between the shear stress distribution at the lubricated wall and the the interface elevation, in order to confirm the previous observations.

In the present study we aim to extend those findings simulating the flow with the Volume of Fluid method. This numerical approach shares with phase field method some of the characteristics of the front capturing schemes even if it allows for a sharper variation of the flow properties across the interface. The DR is here examined in a channel where a thin layer with equal or lower viscosity is flowing on the top of a thicker layer. Specifically we selected two values for the viscosity ratio, namely $\lambda =0.5$ and $\lambda =1$. We observed a considerable DR as the viscosity ratio is smaller than one. In particular for the case with $\lambda = 0.5$ we see a complete relaminarization of the thin layer. DR is also observed for $\lambda =1$ and we report that in this case its value is slightly larger for the larger Weber number we simulated i.e. $We=0.5$. We did not find here any appreciable effect related to the capillary forces generated by the surface tension, namely we do not observe turbulence reduction due to energy spent in deforming the interface. For all the simulation we adopted $Re_{\tau } = 100$.

The paper is structured as follows. We start with a recap of the conditions and parameters, then we cover the main aspects of the Volume of Fluid method. After that we show the results we obtained through statistics aimed at highlighting those aspects that can reveal the mechanism of the DR.

2 Methodology

We consider here a configuration with two immiscible fluids in a plane channel. The governing equations, namely mass conservation and non-dimensional Navier–Stokes equation, for two phase incompressible Newtonian fluids can be written as

$$\begin{aligned}{} & {} \nabla \cdot {\textbf {u}} = 0, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \frac{\partial {\textbf {u}}}{\partial t} + {\textbf {u}} \cdot \nabla {\textbf {u}} = \frac{1}{\rho } \left[ -\nabla p + \frac{1}{Re} \nabla \cdot {\textbf {T}} + \frac{1}{We}{} {\textbf {f}}_{\sigma }\right] \end{aligned}$$

(2)

where the velocity field, ${\textbf {u}}=\bar{{\textbf {u}}}({\textbf {x}})+{\textbf {u}}^{'}({\textbf {x}},t)$, is divided into a mean component and a fluctuation term (marked with the apex $'$). Since we are considering a fully developed turbulent flow, for our purposes the mean velocity field here is the average over time, streamwise and spanwise directions. We will assume the following notation for the components of the velocity field

$$\begin{aligned} {\textbf {u}}({\textbf {x}},t)= \begin{pmatrix} u({\textbf {x}},t)\\ v({\textbf {x}},t)\\ w({\textbf {x}},t) \end{pmatrix}. \end{aligned}$$

(3)

The other quantities in Eq. 2 are $p=p({\textbf {x}},t)$ which represents the pressure, $\rho =\rho ({\textbf {x}},t)$ the density, $\mu = \mu ({\textbf {x}},t)$ the dynamic viscosity, ${\textbf {f}}_{\sigma }={\textbf {f}}_{\sigma }({\textbf {x}},t)$ the force per unit volume due to surface tension. ${\textbf {T}}=2\mu {\textbf {S}}$ is the viscous stress tensor, where ${\textbf {S}} =[\nabla {\textbf {u}} + \nabla {\textbf {u}}^{T}]/2$ is the strain-rate tensor. Re and We are respectively the Reynolds number and the Weber number, defined as

$$\begin{aligned} Re = \frac{\widetilde{U}\widetilde{L}{\widetilde{\rho }}}{{\widetilde{\mu }}}, \quad We = \frac{{\widetilde{\rho }}\widetilde{U}^2h}{{\widetilde{\sigma }}}, \end{aligned}$$

(4)

where $\widetilde{U}$, $\widetilde{L}$, ${\widetilde{\rho }}$, ${\widetilde{\mu }}$, ${\widetilde{\sigma }}$, are the reference quantities used to obtain the non-dimensional governing equations. In order we have velocity, length, density, dynamic viscosity, surface tension.

The force per unit volume due to surface tension is defined as

$$\begin{aligned} {\textbf {f}}_{\sigma }=\sigma k {\textbf {n}} \delta , \end{aligned}$$

(5)

where k the curvature of the interface, ${\textbf {n}}$ the normal vector, $\delta$ the Dirac function. This latter can be approximated by $\nabla \phi$, in which $\phi$ is the $\textit{Volume of Fluid}$ (VOF) fraction across the interface that will be discussed in detail later in this section. In particular $\phi =0$ in fluid 1, while $\phi =1$ in fluid 2 and $0<\phi <1$ at the interface. The $\textit{Volume of Fluid}$ Method has been developed for locating and advecting a fluid interface. This method can be described introducing a Color Function $H({\textbf {x}},t)$ such that $H({\textbf {x}},t)=1$ in the presence of a fluid or $H({\textbf {x}},t)=0$. As the fluid moves due to the velocity flow, the color function is updated by the advection equation

$$\begin{aligned} \frac{\partial H}{\partial t} + {\textbf {u}} \cdot \nabla H = 0. \end{aligned}$$

(6)

The volume fraction of the Volume of Fluid can be defined as

$$\begin{aligned} \phi ({\textbf {x}},t)=\frac{1}{V_0}\int _{V} H({\textbf {x}},t)dV', \end{aligned}$$

(7)

where $V_0$ is the volume of a specific cell. Within this framework the $\textit{MTHINC}$ (multidimensional tangent of hyperbola for interface capturing) method for the interface reconstruction [12, 13] has been used. In this method the color function H is approximated using a multidimensional hyperbolic tangent function given by

$$\begin{aligned} H({\textbf {x}}) \approx \widetilde{H({\textbf {x}})} = \frac{1}{2}(1+tanh(\beta (P({\textbf {x}}))+d), \end{aligned}$$

(8)

in which ${\textbf {x}} \in [0,1]$ is a local coordinate system in each cell, $\beta$ is a constant parameter that represents the slope of the approximate Heaviside function, d a normalization parameter and $P({\textbf {x}})$ a linear or quadratic surface function. The linear expression is given as

$$\begin{aligned} P(x_j) = a_j x_j, \end{aligned}$$

(9)

where the $a_j$ coefficients can be algebraically determined imposing the components of the normal values and the curvature tensor for P. The d parameter can be obtained through the constraint

$$\begin{aligned} \int _{{\textbf {x}} \in (0,1)} \widetilde{H({\textbf {x}})} d{\textbf {x}} = \phi . \end{aligned}$$

(10)

Once the normal vector defined as $\textbf{n}=\nabla \phi / \Vert \nabla \phi \Vert$ is known, the curvature k is given by $\partial n_i / \partial x_i$. Approximating the interface location $\delta \approx \Vert \nabla \phi \Vert$, the surface tension force can be written as

$$\begin{aligned} f_{j\sigma }=\sigma k n_j \delta \approx \sigma k \frac{\partial \phi }{\partial x_j}. \end{aligned}$$

(11)

It has been proved that in most cases VOF results are more accurate compared to the Phase field at the same resolution [14]. The computational cost of the Diffusive Interface is instead typically of an order of magnitude less than VOF at the same resolution.

2.1 Data set

For all the simulations the flow is periodic in the streamwise x and spanwise y directions, with no-slip conditions in the normal direction z and it is driven by a constant pressure gradient. The channel dimensions are $L_x\times L_y\times L_z = 8\,h\times 4h\times 2h$, with h the half-channel height, the grid we used is $N_x\times N_y\times N_z =384\times 192\times 284$. The reference position of the interface is located at 1.85h, which separates a lubricating layer of fluid with kinematic viscosity $\nu _1$ from a thicker main layer of fluid with kinematic viscosity $\nu _2$. The two fluids have the same density. Starting with a single phase flow, all simulations are performed with an initial Poiseuille profile perturbed by a finite amplitude disturbance. The film is added once reached the statistically steady state condition. In two fluid flows the value of the surface tension characterizes the behaviour of the interface. In our simulations the variations in surface tension appears in terms of a Weber number (see the definition below), that represents a ratio between deforming inertial forces and cohesive forces, namely surface tension force. In this way for high values of We we get more easily deformable interfaces, while for low We more stable interfaces. All our simulations are run at a shear Reynolds number $Re_{\tau }=u_{\tau }h/\nu _2=100$, where, as customary, $u_{\tau }= \sqrt{{\overline{\tau }}/\rho }$ (with $\sqrt{{\overline{\tau }}}$ being the wall shear stress) is the friction velocity and $\nu _2=\mu _2/\rho _2$ is the kinematic viscosity of the fluid in the thicker layer. The extension of the domain is not extremely large however the inspection of the spanwise and streamwise velocity correlations have not reveal a pathological behaviour. Unless otherwise stated, we have used as friction units those obtained considering for the value of the wall shear stress that calculated as average between the two wall. This procedure has the effect that the normalization is the same for all the simulations regardless of the fact that locally at each of the two walls the viscous units would be different. One of the goals of the present work has been to investigate the coupling between the interface and the turbulent modulation in particular when decreasing the viscosity ratio a larger the drag reduction is observed. In order to better investigate the dynamic of the interface, for both the cases at $\lambda =1$ and $\lambda =0.5$ , we have performed simulations with two different Weber numbers, $We = 0.055$ and $We=0.5$. When considering a flow in a channel of the height of 5.12 centimeters with the same Reynolds number of the simulations and a $\sigma =44 \times 10^{-3} N m^{-1}$ that is quite appropriate for water and oil we would obtain a $We=0.14$. Hence, we have decided to study the effect of the surface tension by varying the Weber number by one order of magnitude around this physically sound one.

The amount of data considered for the statistics are selected to ensure the statistical convergence. For the simulation has been run the open source code developed by KTH Royal Institute of Technology in Stockholm [11]. During our analysis we will refer for comparison to the aforementioned work by Ahmadi et al. [8, 9], which reports results of a turbulent channel flow with a lubricating film on one wall. It is worth pointing out that the parameters explored in their study are slightly different and we will address the implications further on.

Fig. 1

Cross-section $(y-z)$ of the instantaneous streamwise velocity u. In the top panel the case with $\lambda =0.5$. Middle panel refers to the case with $\lambda =1$. Bottom panel the case $\lambda =1$, $We=0.5$. The white line marks the position of the interface

3 Results and discussion

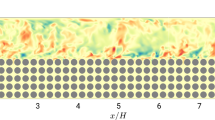
In Fig. 1 we report the contours of the streamwise velocity u in a cross-section of the channel for three of the four cases with the lubricating layer together with the position of the interface identified with a white line. The top panel shows the case with $\lambda =0.5$ while the middle and bottom panels refer to the case with $\lambda =1$. Already at first glance, the analysis of the top panel seems to suggest that in the lubricating layer we have a laminar behaviour with no evidence of turbulence. This can be related to the DR mechanism that damping the turbulent fluctuations produces a relaminarization of the layer. When the viscosity for the two fluids is the same in the case with $We=0.055$ (Fig. 1, mid panel), we can still appreciate how the presence of an interface affects the dynamics near the lubricated wall. Comparing the two cases at $\lambda =1$, in the case with $We=0.5$ (Fig. 1, bottom panel), we can  observe a larger deformation of the interface.

Fig. 2

Normalized mean streamwise velocity ${\overline{u}}^+$ as a function of the wall-normal direction for all the simulated cases. The dotted line at $z = 1.85 h$ marks the mean interface position

We continue the analysis reporting the wall normal behavior of the mean streamwise velocity profile (Fig. 2). The first thing that we notice for all studied cases is that the presence of the lubricating layer produces an asymmetric velocity profile. When considering simulations with constant pressure gradient, this is balanced by the viscous shear stress at the walls. By observing that the gradient in the non-lubricated wall increases for both $\lambda$ values we expect that the value of the shear stress should in both cases decreased at the other wall (see also Fig. 4). What we see is that for the case with the lower viscosity at the lubricated wall ($\lambda =0.5$) this is compatible with an increase of the velocity in the region close to the lubricated layer, while for the case when the viscosities are the same ($\lambda =1$) this has to come with a smaller velocity gradient at the wall. The cases with $We=0.5$ are not reported here because basically identical to the other cases at smaller Weber.

Table 1 Volume flow rate $Q/Q_{SP}$ normalized by the reference Single Phase along with the wall shear stress for the different cases (SinglePhase(SP), $\lambda =1$, $\lambda =0.5$) at the bottom wall (${\overline{\tau }}_{w,b}$) and top wall (${\overline{\tau }}_{w,t}$)

In Table 1 we show the behavior of the total volume flow rate Q of the two layers and the wall shear stress $\tau _w$ at both walls taking the Single Phase value as a reference. As a consequence of the presence of the interface there is a gain of the volume flow rate. This increase reaches its maximum $(\simeq 22 \%$) for $\lambda = 0.5$ without a large sensitivity to the Weber number. When the viscosity of the two fluids is the same, the increase of the volume flow rate ($\simeq 7 \%$) for lower Weber, while for $We=0.5$ is slightely higher ($\simeq 8 \%$). This suggests that the drag reduction is already in place, so that the mechanism stems from the presence of the interface. Compared to the work of Ahmadi et al. [9], we do not observe here any inflection point close to the interface.

Fig. 3

Root-mean square velocity fluctuations for single phase and viscosity stratified flows along the z axis. Streamwise component $u_{rms}$ panel above, spanwise component $v_{rms}$ middle panel, wall-normal component $w_{rms}$ bottom panel. The dotted line at $z = 1.85 h$ marks the mean interface position

To better understand the connection between the dynamic of turbulence and the viscosity, we analyse the root mean square (RMS) velocities in the homogeneous and wall normal directions. The velocity fluctuation intensities can provide an idea of the structure of turbulence. We start by examining the streamwise velocity fluctuations, $u_{rms}$, in the top panel in Fig. 3. The profile of the SP presents its maximum close to the walls and is symmetrical to the center line, as expected when the statistics has reached the steady state. Fluctuations are higher at the vicinity of the walls, where the velocity gradients are larger. The behavior at the non lubricated wall does not change remarkably varying the parameters, in particular we can see that values in that region increase as $\lambda$ decreases as we expected from the observation of the mean velocity. On the other hand the behavior at the lubricated wall is very different. Regardless the viscosity, we observe a strong reduction of turbulence. We can therefore confirm that relaminarization is taking place in this region. Somehow surprisingly this process intensifies as $\lambda$ decreases. We can only speculate that this effect comes from the interplay between the inhibition of turbulent transport due to the presence of the interface and the increase of local dissipation due to the higher gradient in the low viscosity region. It is worth noting that the $u_{rms}$ profile does not show the presence of the interface when the two fluids have the same viscosity, on the hand we observe an inflection point when viscosity changes across the interface. We present the values of the spanwise component $v_{rms}$ in the middle panel of Fig. 3. As for the streamwise one, the fluctuations are minimal when the value of the viscosity in the lubricating layer is halved. Regarding the cases at $\lambda =1$, we see that the fluctuating component overcomes that of the single phase at the lubricated wall for the smaller Weber number. The behaviour of the wall-normal component $w_{rms}$ (bottom panel of Fig. 3) is again qualitatively close to that of the spanwise one, with larger fluctuations for the case with $\lambda =1$, $We=0.055$. It worth observing that in this component we do have an inflection point when the Weber number is small suggesting that a larger surface tension might be responsible for this behaviour. These results differ widely from the ones obtained by Ahmadi et al. [9], where a local minimum close to the reference location of the interface is observed in most of the components.

Fig. 4

Profile of the viscous shear stress ${\overline{\tau }}^+_v$ in the top panel. Turbulent shear stress ${\overline{\tau }}^+_t$ and the two contributions together ${\overline{\tau }}^+_v+{\overline{\tau }}^+_t$, respectively continuous and dashed line on the panel below. The dotted line at $z = 1.85 h$ marks the mean interface position

To gain further understanding on the observed DR, we start looking at the contributions to the shear stress. In Fig. 4 top panel we can see the trend of the viscous shear stress. At the not-lubricated wall layer, profiles have qualitatively the same trend of the SP case, with larger values of the shear as expected from the behaviour of the mean velocity, Fig. 2. As $\lambda$ decreases, the decrease of the shear stress at the lubricated wall produces an equal increase at the non lubricated wall due to the fact that the the total shear stress must balance with the applied pressure gradient, which in all our simulations has a constant value. It is interesting to note that for $\lambda = 0.5$ in the low viscosity layer we can observe a basically linear profile, typical of laminar fluids. This is an evidence that of a relaminarization effect. We can now extend the analysis to the other stress contributions. In general, the total stress in two-phase flows is given by the sum of three contributions, the viscous shear stress, the turbulent stress and a further contribution produced by the surface tension. We display in the bottom panel of the Fig. 4 the turbulent stress profile along with the sum of this with the viscous term for the different cases examined,

$$\begin{aligned} {\overline{\tau }}^+_v(z)+{\overline{\tau }}^+_t(z) = \nu ^+(z)\frac{\partial \bar{u}^+}{\partial z^+} - (\overline{u^{'}w^{'}})^+. \end{aligned}$$

(12)

In a fully developed turbulent channel flow, the integral of the momentum equation with respect to the wall normal direction, produces a linear relation between the constant pressure gradient and the total shear stress. It is therefore possible to estimate the contribution of the capillary stress as a difference from the other two. The deviation form this straight line then gives us a measure of the magnitude of this quantity. We can accordingly infer from Fig. 4 that this contribution in our numerical results is basically negligible. The variation of the Weber number does not produce here any significant change of the trend at $\lambda =1$ or $\lambda =0.5$, so for simplicity we decided not to report the relative profiles. It is important to mention that this behaviour is again different from the one reported in Ahmadi et al. [9], leading us to conclude that in our case even if we observe a similar effect in terms of Drag Reduction we cannot directly link the observed changes to the presence of strong capillary stress contribution in the mean momentum.

We continue our analysis taking into account the vorticity field which is defined as $\varvec{\omega }=\nabla \times {\textbf {u}}$. In particular we will analyse the wall normal behaviors of the fluctuating components along homogeneous and wall-normal directions defined as

$$\begin{aligned} \varvec{\omega '_{rms}}= \begin{pmatrix} \frac{\partial w'}{\partial y} - \frac{\partial v'}{\partial z}\\ \frac{\partial u'}{\partial z} - \frac{\partial w'}{\partial x}\\ \frac{\partial v'}{\partial x} - \frac{\partial u'}{\partial y} \end{pmatrix}. \end{aligned}$$

(13)

Fig. 5

Root-mean square vorticity fluctuations for all the simulated cases along the normal axis. Streamwise component $\omega '_{x}$ panel above, spanwise component $\omega '_{y}$ middle panel, wall-normal component $\omega '_{z}$ below. The dotted line at $z = 1.85 h$ marks the mean interface position

In Fig. 5 we report the rms vorticity profiles. For the single phase all profiles are again symmetric to the centreline of the channel as they are supposed to be when the flow has reached the statistically steady state. We see again that the symmetry is lost by introducing the lubricated layer due to the change of the dynamic behaviour of the flow. As for the turbulent fluctuations, at the not-lubricated wall, we see that the amplitudes of the vorticity fluctuations exhibit larger values, compatibly with larger shear at the wall. At the lubricated wall, the homogeneous components of the vorticity, $\omega '_{x, rms}$ and $\omega '_{y, rms}$, can be described in a similar terms. An effect of the interface is clearly observable. In particular, for the two cases with the larger value of the Weber number, we can observe that at the interface the behavior of the fluctuations recalls somehow the one at the wall in the non lubricated case. This occurrence is particularly true for the case at $\lambda =0.5$, reported with the dash-dotted curves in Fig. 5. Indeed the top panel, showing the streamwise component we observe a local maximum at $z/h=1.7$ followed by a local minimum. On the other hand, in the middle panel the $\omega '_{y, rms}$ just before the interface shows an inflection point followed by an increase at interface location. A much smoother behaviour of the curves is indeed observed for the larger Weber number. Finally, in the lubricating layer for $z/h>1.85$, the dynamics of the fluctuations in the homogeneous directions show basically the same behavior. Starting from the value of the fluctuations at the interface location, we can appreciate a sharp drop followed by a recovery at the wall. Those extrema represent vortices with opposite sign and their location corresponds to the location of the centre of the vortices [15]. Generally speaking, the presence of the interface (the dotted line in the figure) seems to decouples the dynamics of the vorticity between the two layers. This observation seems to apply specially to the cases with the smaller value of the Weber number, where the larger value of the surface tension inhibits large excursions of the interface. The wall-normal component of the vorticity, $\omega '_{z, rms}$, instead is not influenced by the presence of the interface as much as the other components arguably because associated to wall-parallel motions which are less affected by the surface tension forces for limited interface deformations. Only the case with $\lambda = 0.5$ shows at the top wall an inflection point near the interface.

In order to discuss some overall characteristics of the interface dynamics in Fig. 6 we present spatial correlation of the fluctuations of the interface elevation $\eta '=\eta -{\overline{\eta }}$ only for the two simulations at $We=0.5$. Observing the correlation is the streamwise direction as a function of the separation $r_x$ we can easily appreciate that for the case at $\lambda =1$, where according to Fig. 3 the fluctuations have not been completely damped, the interface shows a marked spatial modulation that is smaller than the streamwise extension of the domain. Analyzing instead the correlation in the spanwise direction we confirm for the case $\lambda =1$ the very large correlation visible already from Fig. 1. The same behavior is also confirmed for the case at smaller $\lambda$.

Fig. 6

Profiles of the correlation of the fluctuations of interface elevation for the cases at $We=0.5$: $\lambda =1$ (solid line) and $\lambda =0.5$ (dashed line). The top panel reports the correlation along the streamwise direction x and bottom panel that along the spanwise direction y

Fig. 7

Probability density function (PDF) divided by the local mean shear stress of the normalized Wall-Shear stress fluctuations $\tau _w^{'} = (\tau _w-{\overline{\tau }}_w) / {\overline{\tau }}_w$ for all cases. Profiles at the non lubricated wall are on top panel, while the the bottow panel refers to the lubricated wall

3.1 Probability density functions

To understand the dynamics of the flow in the presence of the interface we computed the Probability Density Function (PDF) of the shear stress at both walls. In Fig. 7 we show in semi-logarithmic scale the PDF of the wall shear stress fluctuations $\tau _w^{'}$ defined as

$$\begin{aligned} \tau _w^{'} = \frac{\tau _w-{\overline{\tau }}_w}{{\overline{\tau }}_w} \end{aligned}$$

(14)

where ${{\overline{\tau }}_w}$ is the mean value calculated at the wall we are considering and the PDFs are divided by the value of ${{\overline{\tau }}_w}$ itself.

At the non lubricated wall all profiles are asymmetrical with a larger ratio of positive values that implies a higher probability occurrence of positive fluctuations. In general, we notice that the shape of the PDF for the two-phase flow do not significantly differ from the single-phase case, this means that the presence of the interface does not affect the dynamic near the opposite wall. We only appreciate a slightly different behavior of the tails of the PDFs. The increase probability of larger fluctuations can be traced back to the mean shear stress at the wall as discussed in the previous paragraph. At the lubricated wall the PDFs are instead drastically different from those of the single-phase case. While the latter is statistically identical to the non lubricated wall, the shape shows substantial differences as $\lambda$ and We change [9]. In the case when the two fluids have the same viscosity and $We=0.055$ the profile is shifted towards negative values. In particular when $\tau _w^{'}<-1$, the change of sign with respect to the average, suggests the presence of reverse recirculation areas in which $\tau _w$ locally changes sign. It is interesting to notice that this large negative fluctuations disappear in the case in which the We number is higher, namely $We=0.5$. Notwithstanding this observation the presence of positive fluctuations seem to suggests that the turbulence activity is still in place compared to the case with lower viscosity ratio. In fact, as $\lambda$ decreases we see that the curve is confined around the value $\tau _w=0$. The reduction of the shear stress fluctuations confirms the presence of a relaminarization mechanism.

Fig. 8

Probability density function (PDF) of the interface elevation $\eta /h$ at $\lambda =1$ with two different Weber number ($We=0.055$, We=0.5) and $\lambda =0.5$ with $We=0.055$ using a logarithmic scaling. The dotted line at $z = 1.85$ marks the reference interface position

We compare in Fig. 8 the PDF of the interface elevation $\eta$ for the different cases, taking into account the effects of the viscosity ratio and the Weber number. For all the cases the PDF of the interface is nearly symmetric around the value $z/h=1.85$, namely the reference position of the interface. The effect of the Weber number is consistent with the expectations.

When $We=0.055$ the the PDF is slightly taller and narrower close to the most probable value. A lower surface tension instead, allows a more deformable interface, so the PDF widens for the case We=0.5, see also the instantaneous position in Fig. 1. Decreasing the viscosity ratio to $\lambda =0.5$ with $We=0.055$ instead the shape of the pdf is sharper and constrained around the average position of the interface where it takes its maximum vale. This behavior occurs as a consequence of the turbulence reduction when decreases the viscosity ratio.

To better investigate the correlation between the interface deformation and the shear stress we show in Fig. 9 the Joint Probability Density Functions (JPDF) between the normalized interface elevation $\eta ^+=u_{\tau }(\eta - {\overline{\eta }})/\nu$ and the normalized wall-shear stress fluctuations $\tau _w^{'} = (\tau _w-{\overline{\tau }}) / {\overline{\tau }}$ for $\lambda = 1$ and the two values of the Weber number under consideration. The contour plot of the two-dimensional JPDF are shown only for the lubricated wall. We observe that the different value of the Weber number has a strong effect on the structure of the correlation. For the case with $We=0.055$ there is an anti-correlation between the shear and the interface deformation mostly when the $\eta ^+$ takes positive values. This means that crests of the interface elevation are correlated with negative fluctuations of the wall shear stress. This behaviour is in agreement with the work of Ahmadi et al. [9] who report a strong correlation between the crests of the interface and the shear stress inversion. The situation changes completely when $We=0.5$ where, consistently with the PDF of the wall shear stress fluctuations at the lubricated wall in Fig. 7, the range of the wall shear stress fluctuations is narrowed. Interestingly, in this case we do not see any flow recirculation ($\tau _w^{'}<-1$) associated with the interface deformation.   Such observation goes against the hypothesis that  larger excursion around the mean position due to the lower surface tension should enhance the geometrical situation described in Ahmadi et al. [9].

Fig. 9

Joint probability density function (JPDF) of the normalized Wall-Shear stress fluctuations $\tau _w^{'} = (\tau _w-{\overline{\tau }}) / {\overline{\tau }}$ over the interface elevation $\eta ^+$ in viscous units for increasing Weber number at $\lambda = 1$. Top: $We=0.055$, bottom: $We=0.5$

3.2 Turbulent kinetic energy budgets

Lastly, we examine the Turbulent Kinetic Energy (TKE) budget. The equation of the TKE for the two-fluid case, considering the symmetries of the channel flow at statistically steady state, can be written as

$$\begin{aligned} -\overline{u'w'}\frac{d{\overline{u}}}{dz}= & {} -\frac{1}{2}\frac{d}{dz}\overline{u_i'u_i'w'}+\frac{d}{dz}\overline{u'_iT'_{i3}} \nonumber \\{} & {} -\frac{1}{\rho }\frac{d}{dz}\overline{p'w'}-\epsilon +\psi _\sigma . \end{aligned}$$

(15)

In the equation above we have production on the left-hand side and turbulent convection, viscous diffusion, pressure transport, dissipation $\epsilon =\overline{T'_{ij}\frac{\partial }{\partial x_j}u'_i}$ and the contribution due to the surface tension $\psi _\sigma =\frac{1}{We}\overline{u'_jf'_{\sigma ,j}}$ on the right-hand side.

Fig. 10

Profiles of the contributions to the TKE budget near the lubricated wall region for the cases $\lambda =1$ (top panel $We=0.0055$ and middle panel $We=0.5$, respectively) and for $\lambda =0.5$ bottom panel

Profiles of the various component of the TKE budget for the three simulations are reported in Fig. 10. The contributions at the non lubricated wall normalized considering the friction velocity related to the thicker fluid does not present any significant deviation from the standard well known trends for the single phase turbulent channel flow, for this reason we did not report the plots of those profiles. In Fig. 10 we show instead the various terms of the equation (15) close to the lubricated wall normalized by $u_{\tau }^4/\nu$. We start analyzing the cases where two fluids have equal viscosity i.e. $\lambda =1$ (top and middle panels of Fig. 10). Similarly to classical turbulent channel flow, in the bulk only dissipation and production present a significant contribution to the balance. Approaching the interface for increasing values of the wall-normal direction, production starts to decrease. In both cases (but also for the lower viscosity case that we will discuss later) the peak of the production has been moved far away from the lubricated wall, suggesting that the turbulence is sustained by fluctuations occurring in the non lubricating layer but close to the interface. This observation is in agreement with the dynamics of vorticity discussed in Fig. 5. As expected, in correspondence of the maximum of production we observe negative values of convection, diffusion and pressure terms which are related with the redistribution of the turbulence kinetic energy via these three processes starting from the production layer. Looking at the surface tension term we observe that its value is substantially negative, reaching its lowest value in the vicinity of the interface. This result suggests that the effect of the interface in energetic terms is that of a sink. Comparing the two results at $\lambda =1$ we can try to infer the role of the interface dynamics. Our results suggest that even if in the case with larger We the interface excursion is larger, its explicit dynamic role is mostly controlled by the surface tension that is one order of magnitude larger for the case shown in the top panel of Fig. 10. It is worth mentioning that even if, according to our data, the magnitude of the contribution of the surface tension on the TKE budget is very small compared to the previous study by Zonta et al. [10], we still observe the same overall effect in terms of Drag Reduction. Continuing our analysis of the various terms in the lubricating layer we report that the most of the terms become not relevant, with the exception of the pressure term which presents a larger peak for the case at $We=0.0055$.

We conclude our analysis of the turbulent kinetic energy budget looking at the case with $\lambda =0.5$ in the bottom panel of Fig. 10. As mentioned before, also in this case we observe a peak of the turbulent production in the proximity of the interface in the side far from the wall. However its numerical value is nearly halved with respect to the previous cases, consistently with the observation that a nearly complete relaminarization is occurring for this case. On the other hand, examining the term due to the surface tension we see that the value of this contribution is lower than that shown for the case without viscosity difference at the same Weber. In line with the previous discussion, it is possible to explain this result considering that the forces due to surface tension are also modulated by the deformation that we expect smaller in this case because of the absence of turbulence.

4 Conclusions

In this work we performed a Direct Numerical Simulation of a two-phase turbulent channel flow to investigate the drag reduction associated to the presence of a thin layer of a lubricating fluid near one of the two walls. To the best of the author’s knowledge this is the first study where such flow is conducted using the Volume of Fluid. We considered a configuration of the two immiscible fluids with same density. For the viscosity ratio, two different values were selected, $\lambda =1$ and $\lambda =0.5$ and for each case two simulations with different Weber number, $We=0.055$ and $We=0.5$ have been reported. Compared to the single phase case the presence of a lubricating layer strongly modify the mean statistics analyzed. In particular we observe a strong increase of the flow rate. In the case of $\lambda =0.5$, a nearly complete relaminarization of the lubricated layer was observed, while the increase in the volume flow rate reached a value of $20\%$ for both values of the Weber number. Even when keeping the viscosity ratio $\lambda =1$, an increase in the volume flow rate was observed, which proves that the drag reduction mechanism is already in place, with a slightly higher value when the Weber number is larger. The simulations were conducted at a relatively small shear Reynolds number, $Re_\tau =100$, however the parametric analysis on the effect of viscosity ratio and surface tension allowed us to highlight very interesting modulations of the dynamics of the interface and of the turbulent kinetic budgets. Our results show some differences compared to the previous the work of Ahmadi et al. [8, 9], which can be easily traced back to the method used for the interface capturing method.