1 Introduction

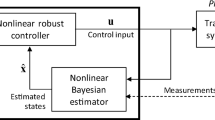
Hybrid simulation can be described as a hardware-in-the-loop simulation for deformable mechanical systems. It consists of performing numerical simulation and experimental testing simultaneously and exchanging data between them in real time. The technique typically applies to structures of too large dimensions for experimental testing as a whole or structures with local high nonlinearities (nonlinear elements that are too difficult or impossible to model numerically). Part of the mechanical system (typically the nonlinear part) is tested experimentally using actuators and sensors, while the rest of the structure is modeled numerically. During hybrid simulation, data is exchanged between the numerical computations and the experiment. The goal is to obtain the time-dependent response of the system to a certain dynamic load. The part tested experimentally is strained by the actuators exactly as it would be strained within the mechanical system under load [1, 2].

Hybrid simulation is performed in time step iterations. In every time step i, displacement ui+1 of the whole structure in the next time step i + 1 is computed from the equation of motion of the whole system (using an integration scheme) [3]. Calculated displacements of degrees of freedom related to the interface between the simulated and the physical part of the structure are imposed by actuators in the experiment. After imposing these displacements, the developed forces at the same DOFs rEi+1 are measured by sensors. The values of the measured forces must be sent back to the simulation to compute the displacement of the whole system for the next time step [3].

In order to catch the full dynamic behavior of the physical substructure tested experimentally, hybrid simulation is performed in real time, which means that the computations, actuator movements, sensor measurements, and data acquisition in each time step i is performed in less than the length of the time step. The most time-consuming part are the computations.

The numerical simulation is based on finite element (FE) model of the structure. Finite element method (FEM) is relatively computationally demanding therefore, performing it in real time can be problematic. In hybrid simulation, there is a conflict between accuracy and computational time. Normally, the finer the FE model is, the more accurate results are obtained. However, in hybrid simulation with this relation also comes an increase of required time for solution in each time step. If the computational time cannot meet the real-time regime, the length of the time step must be increased which causes a decrease in the accuracy of the obtained dynamic responses.

Hybrid simulation found its application in civil engineering where structural responses to seismic excitations are investigated [4,5,6], as well as in automotive and aerospace industries [7,8,9]. Other applications concern mechanical systems with nonlinear dampers (e.g. magneto-rheological) [10,11,12].

Because of the numerical complexity of the method and the necessity to perform the calculations in real time, the models of the tested structures are usually rather simple. The model is often a few-DOFs system of connected masses, springs, and dampeners [13] representing e.g. train-track interactions [14] or wheel-suspension system [15]. When the finite element method is used, the models are usually simple, built only of 1D beam, truss, or frame elements. Papers [4,5,6, 10, 16, 17] present modern (2013–2021) examples of hybrid simulations of frames and beams containing highly nonlinear elements (like magnetorheological dampeners). Because of the non-linear part of the structure, classical model order reduction methods do not apply to hybrid simulation.

In order to deal with the problem of numerical complexity in real-time processing, the most common trend is to involve devices with great computing power for hybrid simulations. A common approach is to build systems of real-time microcontrollers for actuator control and data acquisition and powerful PCs for performing computations [14, 16, 18]. This leads to communication challenges. Bas and Moustafa [19, 20] describe a system built of several data processing devices including one providing shared memory locations for real-time communications. When mechanical systems with large numbers of degrees of freedom are tested in hybrid simulation, computer clusters and supercomputers outside the laboratory can be used for calculations, where the communication between simulation and experiment is achieved by peer-to-peer networks [21,22,23,24]. The communication delays must be compensated by extrapolation methods to ensure a smooth motion of the actuators in the experiment. This makes the whole procedure even more complicated.

The presented research aims in an opposite direction—to reduce the model order and perform all the data processing tasks (including numerical computations, actuator control, and data acquisition) in one device, a real-time microcontroller. This approach allows for eliminating some of the communications and environment setup inconveniences. A single real-time microcontroller is of significantly less computing power than a modern PC. In order to make this simplification possible, the model needs to be reduced offline, on a PC. This can be a time-consuming process however, it is irrelevant as long as a reduction in real-time computations is achieved. An algorithm to prepare the reduced model, of optimized accuracy, for hybrid simulation, on a fully substructured FE model is presented in the paper. The algorithm is based on a dynamic condensation process. Numerical and experimental examples are provided, proving the effectiveness of the proposed algorithm. The size of the model was reduced over 12 times without a noticeable decrease in accuracy. Fully-dynamical real-time hybrid simulations were performed on a test stand built of just a small microcontroller with implemented LabVIEW program, and a dynamic universal testing machine.

The author presented the first idea of applying dynamic condensation to hybrid simulation in the conference paper [25] however, no details of the reduction algorithm are presented there. Another model order reduction approach was previously published by the author [26] where the FE model was substituted by an artificial neural network in the hybrid simulation, which was followed by the research of Bas and Moustafa [27] who utilized deep learning algorithms instead of artificial neural networks. The encountered problem was that it was difficult to find a neural network that would successfully work in such application and training networks of different architectures took thousands of trials. The approach presented in the following paper does not have this drawback as the algorithm for creating the reduced model is deterministic.

The novelty of the presented research is a new approach, based on a dynamic condensation algorithm, that allows to reduce the number of DOFs of the numerical model of the tested structure by orders of magnitude. Additionally, by implementing evolutionary optimization for the selection of DOFs to be kept after model order reduction, the accuracy loss of hybrid simulation results is minimal.

The paper is organized as follows: Sect. 2 presents the fundamental equations in hybrid simulations; Sect. 3 contains all the details of the developed algorithm for model order reduction applied to hybrid simulations, in Sect. 4 an example is provided where model order reduction is applied and the accuracy and times of computations are compared to the full model, Sect. 5 is the conclusion.

2 Equation of motion in hybrid simulation

In order to perform numerical analysis and experimental testing at parts of the same structure, the model of the structure has to be divided into two parts. Because of that, the equation of motion for the system takes a non-standard form that is derived in the following section.

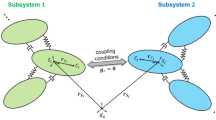
A mechanical system Ω, presented in Fig. 1a is considered. The boundary of Ω is Γ, and on the part of that boundary displacements u0 are known. On the rest of the boundary exciting forces are known. The motion of Ω is described by its displacement u(x, t) where x ∈ Ω and t denotes time. The equation of motion of the system Ω is as follows:

$$ {\mathbf{M\ddot{u}}}\left( t \right) + {\mathbf{C\dot{u}}}\left( t \right) + {\mathbf{K}}\left( t \right){\mathbf{u}}\left( t \right) = {\mathbf{f}}\left( t \right) $$
(1)

where M, C, and K are the mass, damping, and stiffness matrices, respectively, and f is the vector of exciting forces.

Fig. 1
figure 1

Considered mechanical system: a whole system, b substructuring for hybrid simulation

Full size image

In hybrid simulation, the mechanical system is divided into two subsystems—the physical subsystem, tested experimentally, ΩE (with the boundary ΓE), and the virtual (analytical) subsystem, simulated numerically ΩA (with the boundary ΓA)—as presented in Fig. 2b. I is the interface between the two substructures. It is assumed that ΩE ∪ ΩA =  Ω, IE = I ∩ ΓE, and IA = I ∩ ΓA. On the boundaries of the substructures ΓA ∩ Γ and ΓE ∩ Γ, the boundary conditions are the same as on the boundary Γ. The boundary conditions on the interface boundaries IA and IE are defined by the actuators and force sensors—on IA forces are known (measured by sensors) and on IE displacements are known (imposed by actuators).

Fig. 2
figure 2

Idea of model order reduction with dynamic condensation applied to hybrid simulation

Full size image

When taking into account the substructuring in hybrid simulation, Eq. (1) takes the form:

$$ \left( {{\mathbf{M}}^{{\mathbf{A}}} + {\mathbf{M}}^{{\mathbf{E}}} } \right){\mathbf{\ddot{u}}}\left( t \right) + \left( {{\mathbf{C}}^{{\mathbf{A}}} + {\mathbf{C}}^{{\mathbf{E}}} } \right){\dot{\mathbf{u}}}\left( t \right) + \left( {{\mathbf{K}}^{{\mathbf{A}}} + {\mathbf{K}}^{{\mathbf{E}}} \left( t \right)} \right){\mathbf{u}}\left( t \right) = {\mathbf{f}}\left( t \right) $$
(2)

where matrices with superscript A describe the virtual subsystem and matrices with superscript E describe the physical subsystem. The method of model order reduction being the object of this paper applies only to mechanical systems where ΩA is linear elastic therefore KA is constant, in contrast to the stiffness matrix of the nonlinear physical subsystem ΩE.

As the forces in the virtual subsystem are measured, Eq. (2) can be written in a more approachable form:

$$ {\mathbf{M}}^{{\mathbf{A}}} {\mathbf{\ddot{u}}}\left( t \right) + {\mathbf{C}}^{{\mathbf{A}}} {\dot{\mathbf{u}}}\left( t \right) + {\mathbf{K}}^{{\mathbf{A}}} {\mathbf{u}}\left( t \right) + {\mathbf{r}}^{{\mathbf{E}}} \left( t \right) = {\mathbf{f}}\left( t \right) $$
(3)

where rE is the vector of forces in the physical subsystem, that are dependent on the current and past displacements:

$$ {\mathbf{r}}^{{\mathbf{E}}} \left( t \right) = {\mathbf{M}}^{{\mathbf{E}}} {\mathbf{\ddot{u}}}\left( t \right) + {\mathbf{C}}^{{\mathbf{E}}} {\dot{\mathbf{u}}}\left( t \right) + {\mathbf{K}}^{{\mathbf{E}}} {\mathbf{u}}\left( t \right) $$
(4)

During hybrid simulation, the equation of motion (3) is solved step-by-step using explicit or implicit integration schemes. The details for both types of these numerical algorithms are well described by Shing [28]. Implicit integration schemes are significantly more computationally expensive than explicit however, there are unconditionally stable. This means that the time step can be freely adjusted to the computing power of the utilized hardware for the real-time regime to be met. When using explicit integration schemes, there is a critical (maximal) time step. For Central Difference Method (utilized in the following research) it is defined as:

$$ \Delta t_{{{\text{cr}}}} = \frac{{T_{{{\text{min}}}} }}{\pi } $$
(5)

where Tmin is the period corresponding to the highest eigenfrequency of the mechanical system. According to Chopra [29] to ensure high accuracy, the time step Δt must often be considerably smaller than the stability limit (5), e.g. Tmin/10. In many cases, the critical time step is several orders of magnitude lower than the lowest possible time step for real-time computations on typical portable hardware. For stiff structures with a relatively high number of degrees of freedom (DOFs), implementing explicit integration schemes to hybrid simulation is usually impossible. The greater the stiffness of the structure, the higher eigenvalues are obtained when solving the eigenproblem. When considering, for example, the maximal eigenvalue of a structure expressed in MHz, the critical time step would be expressed in microseconds or nanoseconds. Performing real-time finite element computations for hybrid simulation with such a small time step would probably not be possible using hardware of normal processing power.

3 Model order reduction algorithm using dynamic condensation

In the following section details of the proposed algorithm for model order reduction of a substructured system, dedicated to hybrid simulation, are presented.

Condensation is a model order reduction technique that consists on removing a subset of DOFs of the mechanical subsystem and modifying the structural matrices (M, C, and K). The method was proposed for the first time by Guyan [30] and Irons [31]. The numerical procedure is quite simple however, the inertia effects are neglected during the reduction. Therefore the reduced model only produces accurate results in static cases, and the method is also called static condensation. Dynamic condensation techniques do not have this drawback, inertia effects are partially or entirely taken into account [32].

The idea of model order reduction with dynamic condensation applied to hybrid simulation is presented in Fig. 2. Full FE model is built, and substructured, the number of DOFs in the virtual subsystem ΩA is reduced, and then the hybrid simulation is performed [25]. The proposed algorithm concerns mechanical systems where the virtual subsystem is linear elastic with proportional damping, and the physical subsystem is of small size compared to the virtual subsystem.

In order to perform the condensation, the set of all DOFs must be divided into two subsets: masters (indicated by subscript m) and slaves (indicated by subscript s). The equation of motion (3) now takes the form:

$$\begin{aligned} &\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{{\mathbf{mm}}}}^{{\mathbf{A}}} } & {{\mathbf{M}}_{{{\mathbf{ms}}}}^{{\mathbf{A}}} } \\ {{\mathbf{M}}_{{{\mathbf{sm}}}}^{{\mathbf{A}}} } & {{\mathbf{M}}_{{{\mathbf{ss}}}}^{{\mathbf{A}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{u}}}_{{\mathbf{m}}} \left( t \right)} \\ {{\mathbf{\ddot{u}}}_{{\mathbf{s}}} \left( t \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{{{\mathbf{mm}}}}^{{\mathbf{A}}} } & {{\mathbf{C}}_{{{\mathbf{ms}}}}^{{\mathbf{A}}} } \\ {{\mathbf{C}}_{{{\mathbf{sm}}}}^{{\mathbf{A}}} } & {{\mathbf{C}}_{{{\mathbf{ss}}}}^{{\mathbf{A}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}_{{\mathbf{m}}} \left( t \right)} \\ {{\dot{\mathbf{u}}}_{{\mathbf{s}}} \left( t \right)} \\ \end{array} } \right]\\ &\quad+ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{mm}}}}^{{\mathbf{A}}} } & {{\mathbf{K}}_{{{\mathbf{ms}}}}^{{\mathbf{A}}} } \\ {{\mathbf{K}}_{{{\mathbf{sm}}}}^{{\mathbf{A}}} } & {{\mathbf{K}}_{{{\mathbf{ss}}}}^{{\mathbf{A}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{u}}_{{\mathbf{m}}} \left( t \right)} \\ {{\mathbf{u}}_{{\mathbf{s}}} \left( t \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{r}}_{{\mathbf{m}}}^{{\mathbf{E}}} \left( t \right)} \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{{\mathbf{m}}} \left( t \right)} \\ {{\mathbf{f}}_{{\mathbf{s}}} \left( t \right)} \\ \end{array} } \right]\end{aligned}$$
(6)

As one can see in Eq. (6), all the DOFs of the physical subsystem where the forces are measured (nonzero elements of vector rE), must be classified as masters. This simplifies real-time computations (eliminating the need to transform the vector rE after every measurement).

The slave DOFs are now eliminated and the equation of motion is reduced only to the master DOFs:

$$ {\mathbf{M}}_{{\mathbf{R}}}^{{\mathbf{A}}} {\mathbf{\ddot{u}}}_{{\mathbf{m}}} \left( t \right) + {\mathbf{C}}_{{\mathbf{R}}}^{{\mathbf{A}}} {\dot{\mathbf{u}}}_{{\mathbf{m}}} \left( t \right) + {\mathbf{K}}_{{\mathbf{R}}}^{{\mathbf{A}}} {\mathbf{u}}_{{\mathbf{m}}} \left( t \right) + {\mathbf{r}}_{{\mathbf{m}}}^{{\mathbf{E}}} \left( t \right) = {\mathbf{f}}_{{\mathbf{R}}} \left( t \right) $$
(7)

The reduced system matrices of the virtual subsystem are denoted as \({\mathbf{M}}_{{\mathbf{R}}}^{{\mathbf{A}}}\), \({\mathbf{C}}_{{\mathbf{R}}}^{{\mathbf{A}}}\), and \({\mathbf{K}}_{{\mathbf{R}}}^{{\mathbf{A}}}\). The elements of the Eq. (7) are computed as follows:

$$ \left\{ {\begin{array}{l} {{\mathbf{M}}_{{\mathbf{R}}}^{{\mathbf{A}}} = {\mathbf{T}}^{{\text{T}}} {\mathbf{M}}^{{\mathbf{A}}} T = {\mathbf{M}}_{{{\mathbf{mm}}}}^{{\mathbf{A}}} + {\mathbf{R}}^{{\text{T}}} {\mathbf{M}}_{{{\mathbf{sm}}}}^{{\mathbf{A}}} + {\mathbf{M}}_{{{\mathbf{ms}}}}^{{\mathbf{A}}} R + {\mathbf{R}}^{{\text{T}}} {\mathbf{M}}_{{{\mathbf{ss}}}}^{{\mathbf{A}}} R} \\ {{\mathbf{C}}_{{\mathbf{R}}}^{{\mathbf{A}}} = \alpha {\mathbf{M}}_{{\mathbf{R}}}^{{\mathbf{A}}} + \beta {\mathbf{K}}_{{\mathbf{R}}}^{{\mathbf{A}}} } \\ {{\mathbf{K}}_{{\mathbf{R}}}^{{\mathbf{A}}} = {\mathbf{T}}^{{\text{T}}} {\mathbf{K}}^{{\mathbf{A}}} T = {\mathbf{K}}_{{{\mathbf{mm}}}}^{{\mathbf{A}}} + {\mathbf{R}}^{{\text{T}}} {\mathbf{K}}_{{{\mathbf{sm}}}}^{{\mathbf{A}}} + {\mathbf{K}}_{{{\mathbf{ms}}}}^{{\mathbf{A}}} R + {\mathbf{R}}^{{\text{T}}} {\mathbf{K}}_{{{\mathbf{ss}}}}^{{\mathbf{A}}} R} \\ {{\mathbf{f}}_{{\mathbf{R}}} \left( t \right) = {\mathbf{T}}^{{\text{T}}} f\left( t \right) = {\mathbf{f}}_{{\mathbf{m}}} \left( t \right) + {\mathbf{R}}^{{\text{T}}} {\mathbf{f}}_{{\mathbf{s}}} \left( t \right)} \\ \end{array} } \right. $$
(8)

where α and β are the Rayleigh coefficients, T is the transformation matrix, and R is the dynamic condensation matrix [33]. The relationship between T and R is:

$$ {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ {\mathbf{R}} \\ \end{array} } \right] $$
(9)

Dynamic condensation matrix R can be defined as the relation of eigenvector between master and slave DOFs:

$$ {{\varvec{\Phi}}}_{{\mathbf{s}}} = {\mathbf{R\Phi }}_{{\mathbf{m}}} $$
(10)

where Φs and Φm are subvectors of eigenvector Φ at the master and slave DOFs.

After the real-time hybrid simulation is performed (on the reduced model) and the vector rE(t) is known, the displacement results for all the DOFs of the full model can be calculated numerically.

An important advantage of the proposed method is that when utilizing explicit integration schemes, the critical time step increases with the reduction of DOFs. After condensation, Tmin in Eq. (5) is the oscillation period corresponding to the highest eigenfrequency of the reduced model. After performing condensation, it may turn out that the real-time calculations are possible using an explicit integration scheme, which would not be feasible for the full model.

3.1 Finding dynamic condensation matrix

In order to reduce the model order, dynamic condensation matrix R must be found that will provide high accuracy of the reduced model. The algorithm is based on the iterative scheme by Qu and Fu [33] that was adapted for the substructured models used in hybrid simulation and is presented in Fig. 3.

Fig. 3
figure 3

Iterative algorithm for finding dynamic condensation matrix for hybrid simulation

Full size image

The algorithm presented in Fig. 3 is based on the mass matrix of the whole mechanical system and the initial stiffness matrix K0:

$$ {\mathbf{K}}_{0} = {\mathbf{K}}^{{\mathbf{A}}} + {\mathbf{K}}_{0}^{{\mathbf{E}}} $$
(11)

Since the physical subsystem is considered to be nonlinear, where in hybrid simulations the nonlinearities are often hard or impossible to define numerically, \({\mathbf{K}}_{0}^{{\mathbf{E}}}\) is the linear approximation of stiffness matrix of the physical subsystem, for relatively small displacements. When the physical subsystem is considerably smaller than the virtual subsystem (of constant stiffness KA), such approximation will not have an important influence on the accuracy of the reduced model.

Matrix Q is calculated as inversed initial stiffness matrix multiplied by the mass matrix of the whole system:

$$ {\mathbf{Q}} = \left( {{\mathbf{K}}_{0} } \right)^{ - 1} {\mathbf{M}} $$
(12)

The initial approximation of the dynamic condensation matrix is calculated as:

$$ {\mathbf{R}}^{0,n} = {\mathbf{Q}}_{{{\mathbf{sm}}}} \left( {{\mathbf{Q}}_{{{\mathbf{mm}}}} } \right)^{ - 1} $$
(13)

The subsequent approximations of the dynamic condensation matrix are calculated in double iterations j and i. Constant n must be assumed, where i = 1, 2, …, n. If iteration i did not exist, iteration j would also lead to a convergent solution but slower. Rj,i is determined as:

$$ {\mathbf{R}}^{j,i} = \left( {{\mathbf{Q}}_{{{\mathbf{sm}}}} + {\mathbf{Q}}_{{{\mathbf{ss}}}} {\mathbf{R}}^{j,i - 1} } \right)\left( {{\mathbf{Q}}_{{{\mathbf{mm}}}} + {\mathbf{Q}}_{{{\mathbf{ms}}}} {\mathbf{R}}^{j,i - 1} } \right)^{ - 1} $$
(14)

j-th approximation of the reduced system matrices is given as:

$$ {\mathbf{M}}_{{\mathbf{R}}}^{j} = {\mathbf{M}}_{{{\mathbf{mm}}}} + \left( {{\mathbf{R}}^{j,n} } \right)^{{\text{T}}} {\mathbf{M}}_{{{\mathbf{sm}}}} + {\mathbf{M}}_{{{\mathbf{ms}}}} {\mathbf{R}}^{j,n} + \left( {{\mathbf{R}}^{j,n} } \right)^{{\text{T}}} {\mathbf{M}}_{{{\mathbf{ss}}}} {\mathbf{R}}^{j,n} $$
(15)

and

$$ {\mathbf{K}}_{{\mathbf{R}}}^{j} = {\mathbf{K}}_{{0,{\mathbf{mm}}}} + \left( {{\mathbf{R}}^{j,n} } \right)^{{\text{T}}} {\mathbf{K}}_{{0,{\mathbf{sm}}}} + {\mathbf{K}}_{{0,{\mathbf{ms}}}} {\mathbf{R}}^{j,n} + \left( {{\mathbf{R}}^{j,n} } \right)^{{\text{T}}} {\mathbf{K}}_{{0,{\mathbf{ss}}}} {\mathbf{R}}^{j,n} $$
(16)

The convergence criterion is that the relative error for m first eigenvalues (k = 1, 2, …, m) between the current and previous iteration of the algorithm must be lower than ε:

$$ \left| {\frac{{\omega_{k}^{j} - \omega_{k}^{j - 1} }}{{\omega_{k}^{j} }}} \right| < \varepsilon $$
(17)

When the stop condition is met after f iterations (j = f) then the final value of dynamic condensation matrix R is considered as its f-th approximation:

$$ {\mathbf{R}} = {\mathbf{R}}^{f,n} = \left( {{\mathbf{Q}}_{{{\mathbf{sm}}}} + {\mathbf{Q}}_{{{\mathbf{ss}}}} {\mathbf{R}}^{f,n - 1} } \right)\left( {{\mathbf{Q}}_{{{\mathbf{mm}}}} + {\mathbf{Q}}_{{{\mathbf{ms}}}} {\mathbf{R}}^{f,n - 1} } \right)^{ - 1} $$
(18)

3.2 Selecting master degrees of freedom

Selection of the subset of DOFs from the virtual subsystem to be kept as masters in the condensation process is crucial as it has a huge impact on the accuracy of the reduced model. Let the total number of DOFs of the mechanical system be denoted as n and the number of master DOFs as r. Then there are q combinations of selecting the subset of DOFs as masters:

$$ q = \frac{n!}{{r!\left( {n - r} \right)!}} $$
(19)

If the set of all the DOFs (of length n) is described as D then the k-th subset of D, which contains r entities selected as masters, can be denoted as Dr,k (where k = 1, 2, …, q). If the accuracy of the reduced model based on subset Dr,k is quantified by an error value e (between results obtained from the full and reduced model), then e is a function of the number of kept DOFs and the chosen combination of them:

$$ e = {\text{f}}\left( {r,k} \right) $$
(20)

The general rule regarding (20) is that the more DOFs we keep in the condensation process (r → n) the higher the accuracy of the reduced model is (e → 0). However, choosing different subsets of the same size for master DOFs can have a significant influence on the accuracy of the reduced model. Therefore selecting an optimal subset of DOFs to be kept as masters is crucial when performing real time hybrid simulation on a reduced model.

The well-known heuristic rule is that all the massless DOFs (rotational DOFs when using lumped mass matrix) can be classified a priori as slaves, as their influence on accuracy is negligible. Even if the mass matrix is consistent, eliminating rotational DOFs is usually advisable as they only influence high eigenvalues [34, 35].

The utilized algorithm for the optimal selection of master DOFs for dynamic condensation problems is based on evolutionary optimization and was described in detail by the author in his previous work [36]. Evolutionary optimization is a biologically inspired, nondeterministic algorithm where potential solutions are treated as individuals, and their adaptation to the environment is assessed by the objective function, where the most adapted individuals have the highest chance to survive. In subsequent generations, new individuals are created by crossover and mutation. In the end, the set of individuals in the final generation are possible optimal solutions to a given problem [37,38,39].

Among other known methods for optimal selection of master DOFs [34, 35, 40,41,42], the proposed method is the only one that optimizes not only which subset k to choose but also optimizes the size of the reduced model (number of masters r). For all other methods, r must be specified before optimization.

Multicriterial evolutionary optimization is utilized, with the following two criteria:

$$ r \to {\text{min}} $$
(21)

and

$$ e = \mathop \sum \limits_{h = 1}^{b} \frac{{\omega_{{h,{\text{R}}}} - \omega_{h} }}{{\omega_{h} }} \to {\text{min}} $$
(22)

Criterion (21) is the minimal number of masters and criterion (22) is the minimum error of the reduced model that is defined as the relative error between b first eigenvalues of the full ωh and reduced model ωh,R. For computing the value of e, the following eigenproblems must be solved:

$$ \left( {{\mathbf{K}}^{{\mathbf{A}}} + {\mathbf{K}}_{0}^{{\mathbf{E}}} } \right){{\varvec{\Phi}}} = {{\varvec{\upomega}}}^{2} \left( {{\mathbf{M}}^{{\mathbf{A}}} + {\mathbf{M}}^{{\mathbf{E}}} } \right){{\varvec{\Phi}}} $$
(23)

and

$$ {\mathbf{K}}_{{\mathbf{R}}} {{\varvec{\Phi}}}_{{\mathbf{R}}} = {{\varvec{\upomega}}}_{{\mathbf{R}}}^{2} {\mathbf{M}}_{{\mathbf{R}}} {{\varvec{\Phi}}}_{{\mathbf{R}}} $$
(24)

ωh is the h-th diagonal element of the matrix ω and ωh,R is the h-th diagonal element of the matrix ωR.

In order to maximize the accuracy of the reduced model in the whole range of frequencies of excitation forces applied in hybrid simulation, the following heuristic rule is assumed for proper choice of the number of considered eigenvalues b: the b-th eigenvalue must be at least three times higher than the maximal frequency ωmax of external exciting forces applied to the system in hybrid simulation:

$$ \omega_{b} \ge \, 3\omega_{{{\text{max}}}} $$
(25)

The design variables are all the DOFs considered to be eliminated. Binary coding is applied which is natural to the given problem (either a DOF is kept or eliminated). All the DOFs related to the physical subsystem ΩE are classified a priori as masters, as indicated in Eq. (6).

After the evolutionary algorithm finishes, a Pareto front from the final generation can be created. The final solution can be intuitively chosen from the Pareto front, by taking into account the required accuracy and size of the reduced model.

4 Example

The proposed algorithm for model order reduction was validated. The substructured model of an example structure has been reduced using the dynamic condensation approach. Numerical tests, as well as experimental testing by real-time hybrid simulations, were performed. Details and obtained results are presented in this section. Section 4.1 contains a descriptioofut model order reduction by applying the dynamic condensation procedure, three models with different reduction levels were obtained. Before real-time experimental testing, as a pretest, a series of virtual hybrid simulations were performed (where the physical subsystem is also simulated by external non-linear functions) to measure the accuracy and computing time of the reduced models—Sect. 4.2. Finally, real-time hybrid simulations with experimental testing were performed with a chosen reduced model, using a universal testing machine and real-time microcontroller—details and obtained results are given in Sect. 4.3.

A steel frame of a mountain bicycle, with a nonlinear shock absorber, is considered an example of hybrid simulation with reduced model order by dynamic condensation. This example was originally described by the author in [43] where real-time hybrid simulation was performed without dynamic condensation or any other model order reduction technique. Figure 4 presents the photograph and dimensions of the frame.

Fig. 4
figure 4

Bicycle frame for hybrid simulation: a photograph, b dimensions. Reprinted from [43], with the permission of AIP Publishing

Full size image

The division into substructures is as follows:

  • the non-linear shock absorber is the physical substructure (tested experimentally),

  • the rest of the frame (linear-elastic) is the virtual substructure (simulated numerically).

The material parameters of the virtual substructure are as follows: Young modulus is 200 GPa and the density is 7800 kg/m3.

The finite element model of the bicycle frame is presented in Fig. 5. The model consists of 27 finite elements (numbered in circles) and 25 nodes (marked as grey dots, numbered in grey). In node 18 there is a rotary joint, element 17 is connected to node 15 by a rotary joint (elements 15 and 16 are bonded), and element 17 is connected to node 16 by a rotary joint (elements 21 and 27 are bonded). The model has got 73 DOFs. Every node has got 3 DOFs (horizontal displacement, vertical displacement, and rotation), except node 1 (rotation only), node 23 (horizontal displacement and rotation), and node 18 (horizontal displacement, vertical displacement, rotation from the side of element 18, rotation from the side of element 19).

Fig. 5
figure 5

Finite element model of the bicycle frame

Full size image

For further consideration, the DOFs of the mechanical system will be described by the node number and symbol H, V, or R (for horizontal, vertical, or rotational DOF, respectively). For example, 17H denotes the horizontal DOF of node 17.

The bicycle frame is loaded in two places: on the handlebar (by force Fh) and on the saddle (by force Fs). The cross-section properties of the virtual subsystem are listed in Table 1.

Table 1 Cross-section properties of the analytical subsystem of the bicycle frame. Reprinted from [43], with the permission of AIP Publishing
Full size table

4.1 Model order reduction

The order of the finite element model of the considered example was reduced using the procedures described in Sect. 3. The subset of master DOFs was selected using the evolutionary optimization approach, with two optimization criteria—maximal accuracy and minimal size of the reduced model. The system matrices of the reduced model were calculated (Eq. 8) using the dynamic condensation matrix R that was found with the iterative procedure from Fig. 3.

The full numerical model assumes lumped mass matrices. The Rayleigh damping coefficients are α = 2 and β = 0.1. The initial stiffness of the shock absorber was measured as k0 = 131.35 N/mm. The system of consistent units adapted in the numerical analyses is: N, mm, MPa, ms, g. Table 2 lists the eight lowest frequencies obtained from the eigenproblem formulated in Eq. (23).

Table 2 Eight first eigenfrequencies of the mechanical system, obtained from the full model
Full size table

For the model order reduction, all the rotational DOFs were classified a priori as slaves. Four DOFs (15H, 15 V, 16H, 16 V) related to the physical substructure tested experimentally were classified a priori as masters. Also, two DOFs where loads Fh and Fs are applied (6 V and 13 V, respectively) were classified as masters (this is not a necessity, just a convenience as the exciting forces do not have to be transformed—fR(t) = fm(t)). This leaves 41 DOFs for classification, therefore, 41 binary design variables for the evolutionary algorithm. It is assumed, that the frequency of the forces Fh(t) and Fs(t) will not exceed 150 Hz, therefore the number of eigenvalues from Table 2 taken into consideration for error estimation using Eq. (22) is b = 5 (according to the heuristic rule from Eq. 25).

Evolutionary optimization was performed, with parameters suggested in [36]: 400 individuals in a population, tournament selection, uniform crossover probability of 0.8, mutation probability of 0.1, two alternative stop conditions (maximum number of iterations of 4100 and average relative change in the best fitness function value over 100 generations is less than or equal to 10−4.

The Pareto front as the result of the optimization is presented in Fig. 6. It presents the number of DOFs of the reduced model r and their error value e (calculated from Eq. 22) of five nondominated results from the final population. For further comparison, reduced models with 6, 8, and 11 DOFs will be taken into consideration, which will be denoted as RM1, RM2, and RM3, respectively. RM1 has got only the master DOFs from the a priori classification, RM2 additionally has got 11H and 12 V, and in RM3 2H, 8 V, 10 V, 21H, and 22H were kept by the optimization process.

Fig. 6
figure 6

Pareto front—the result of the optimization

Full size image

4.2 Virtual hybrid simulations

Virtual hybrid simulation is often a preparatory simulation before real-time hybrid simulation. In the virtual hybrid simulation, the experiment is also numerically simulated, two simulations are carried out simultaneously (of the virtual and physical substructures) and data is exchanged between the two models [44]. In the presented example, a series of virtual hybrid simulations was performed in order to test and compare the accuracy and the numerical complexity of the reduced models.

Newmark implicit integration scheme [28] was used in the numerical simulations, the time step was 1 ms, and the time of simulations was 5 s. The virtual hybrid simulations were carried out in MATLAB software, the experiment was simulated using an external function. Three variants were considered: (a) the shock absorber is linear elastic with a stiffness of 131.35 N/mm (simulation A), (b) the elasticity of the shock absorber is described by Eq. (23) (simulation B), (c) the elasticity of the shock absorber is described by Eq. (24) (simulation C).

In variants B and C, the nonlinear behavior of the shock absorber is given as the normal force value Nsa that is developed while the shock absorber is subjected to elongation Δlsa. The two alternative functions are:

$$ N_{{{\text{sa}},{\text{B}}}} = 120\Delta l_{{{\text{sa}}}} + \left( {\Delta l_{{\text{s}}} } \right)^{3} $$
(26)

and

$$ N_{{{\text{sa}},{\text{C}}}} = 150\Delta l_{{{\text{sa}}}} - 0.2\left( {\Delta l_{{\text{s}}} } \right)^{3} $$
(27)

The time plot of the forces Fh(t) and Fs(t) is presented in Fig. 7. In all the simulations displacement of DOF 15H is considered as an example result, for which accuracy will be measured. Table 3 lists mean squared errors (MSEs) between the displacement calculated from the full and reduced models RM1, RM2, and RM3, for simulations A, B, and C. Example displacement results, for simulation B, are presented in Fig. 8.

Fig. 7
figure 7

Time courses of the acting forces in virtual hybrid simulations

Full size image
Table 3 Mean squared errors of the obtained displacement 15H from reduced models
Full size table
Fig. 8
figure 8

Time courses of displacement 15H: a whole range, b close-up on a sample fragment

Full size image

For the linear simulation (variant A), the differences in accuracy between models with 6, 8, and 11 DOFs are relatively large, of different orders of magnitude. For nonlinear simulations (B and C), the MSEs are sometimes of the same order of magnitude. Nevertheless, all the models are of high accuracy, the MSE values are insignificantly small. The reduced model with only 6 DOFs, RM1, is considered sufficient for performing the real hybrid simulation.

The time of computations for all 5000 time steps was measured for the full and reduced models, as the average from 100 runs on a PC (Intel Core i7-8700 CPU, 24 GB DDR4 RAM), and compared in Table 4. Although the computations were not performed in real time, the time of computations can be considered a reliable measurement of the model order reduction. As one can see in Table 4, the time for models RM1-RM3 was very similar. When comparing RM1 with the full model, by applying dynamic condensation, the time required for computations was reduced by over 17 times, while maintaining high accuracy (displacement MSE with the order of magnitude of 10−5 mm2).

Table 4 Time of computations for the considered models
Full size table

4.3 Real-time hybrid simulation

A series of real-time hybrid simulations of the bicycle frame was performed. The hardware configuration is presented in Fig. 9. All the computations were performed on a microcontroller with a real-time operating system, National Instruments myRIO-1900 [45]. The microcontroller is equipped with a dual-core processor, which allowed two deterministic jobs to run simultaneously: FE computations were performed in real time on one core, and the experiment control and data acquisition was running on the other core. The nondeterministic job was to communicate with a Windows PC, which was performed whenever one of the threads was available. The experiment was executed using a universal dynamics testing machine Instron ElectroPuls E10000 [46] where displacement imposing and force and displacement measurements took place. The microcontroller and testing machine communicated by three analog signals (± 10 V).

Fig. 9
figure 9

Hardware configuration for real-time hybrid simulation

Full size image

When performing real-time hybrid simulation, implementing an explicit integration scheme is much more convenient than an implicit scheme, as the algorithm is significantly simpler [28, 43]. Therefore it is a good practice to check whether the maximum time step condition (5) can meet the real-time regime. Critical times steps for full and reduced models were calculated using Eq. (5) and are listed in Table 5. For the full model, implementing an explicit integration scheme is not possible, as the highest eigenfrequencies are infinite (due to lumped mass matrix). The presented critical time steps for the reduced models were tested on the real-time microcontroller, and only the RM1 model can be utilized (the time of FE computations for a single time step is less than the critical time step value). Therefore the real-time hybrid simulations were performed with the RM1 model, the time step was set to Δt = 0.64 ms, and explicit integration (central difference method, described in [28]) was implemented.

Table 5 Critical time step for explicit integration
Full size table

Two load cases are discussed. In both it was assumed that the force acting on handlebar Fh is equal to 40% of the force acting on saddle Fs at every moment of time:

$$ F_{h} \left( t \right) = 0.4 \cdot F_{s} \left( t \right) $$
(28)

The time plots of the force Fs for both load cases are presented in Fig. 10 with the results of real-time hybrid simulations—elongation of the shock absorber measured in the experiment, and displacement of an example DOF, 15H.

Fig. 10
figure 10

Results of real-time hybrid simulations—time plots of: a force Fs for load case 1, b imposed elongation of shock absorber Δlsa for load case 1, c displacement of DOF 15H u15H for load case 1, a force Fs for load case 2, b imposed elongation of shock absorber Δlsa for load case 2, c displacement of DOF 15H u15H for load case 2

Full size image

Introducing dynamic condensation allowed to use explicit integration in the numerical analysis of the hybrid simulation which would be impossible for the full model.

5 Conclusion

The paper presents an algorithm for implementing dynamic condensation to real-time hybrid simulation, in order to significantly reduce the model and speed up real-time computations. The paradox in real-time hybrid simulation is that by model order reduction, the accuracy of the final results may increase, as with the model order the time step of the simulation can be decreased, which allows capturing the dynamic behavior of the tested mechanical system more precisely.

The proposed algorithms for (a) optimal selection of master DOFs and, then (b), finding the dynamic condensation matrix are quite computationally expensive, as they require multiple solutions of eigenproblems. However these algorithms are performed offline to prepare the model for real time computations, therefore the offline computational effort is considered of secondary importance, as long as it leads to further speeding up hybrid simulation.

The presented goal was to reduce the model for real-time FE computations, in order to simplify the hardware configuration for hybrid simulation. Therefore, the model order reduction can be performed on a machine with much higher computational power than the structure testing. As in the presented example, by using a modern PC, the model with 73 DOFs could be reduced to 6 DOFs in less than an hour, which allowed to perform real-time hybrid simulations on a small microcontroller, that could run FE computations and control the experiment simultaneously. Such simple hardware configuration for real-time hybrid simulations of mechanical systems with similar complexity is not seen, based on the described state of the art.

Regarding the algorithm for optimal mater DOFs selection, the proposed one that involves evolutionary optimization has the advantage of suggesting the number of DOFs to which the model could be reduced (can be chosen from the Pareto front). There are algorithms of less computational complexity, like the Matta scheme [40], and there are no contraindications to implement them however, they require setting a priori the size of the reduced model, which can be misleading (like in the presented example, reduction to 9 DOFs would be pointless, as one can see on the Pareto front). Moreover, in [36] the author proved that the proposed algorithm usually leads to more accurate reduced models than the Matta scheme (assuming reduction to the same number of DOFs).

Figure 11 presents how dynamic condensation affects real-time FE computations when explicit and implicit integration is implemented. In the first case, the critical time steps are often so close to zero, that real-time computations are impossible as the time of calculations for a single time step exceeds the critical value. Or, as in the presented example, explicit integration is absolutely impossible, when the highest eigenvalues are infinite (due to lumped mass matrix). By introducing dynamic condensation, the critical time step increases (with the decrease of master DOFs number) therefore, the time step in hybrid simulation can be adjusted between the necessary time for calculations and critical value (as it took place in the presented example of real-time hybrid simulations). In the second case, when implicit integration is involved, the time step value is usually set as slightly more than the maximum time required for calculations in a single step. By applying dynamic condensation, the required computational time decreases therefore, the time step can also be set lower. This often allows to increase the accuracy of the results when dynamic excitation forces are acting on the tested structure.

Fig. 11
figure 11

Influence of dynamic condensation on real-time finite element computations

Full size image

In the presented example, the accuracy of the reduced models RM1-RM3 was relatively very high, as indicated by the MSEs (when considering displacement of an example DOF). The obtained reduction can be considered significant, as in virtual offline simulations with implicit integration, the computational time decreased over 17 times, and in real-time hybrid simulations, it allowed utilization of explicit integration, which would most certainly not be possible without the reduction.