1 Introduction

Time decay of solutions in thermomechanics has deserved much attention. One aspect corresponds to the thermoelasticity. Dafermos [4] started this study showing the asymptotic stability for the one-dimensional case and the existence of undamped isothermal solutions for dimension greater than one. Several authors proved the exponential decay later [16, 22] as well as the polynomial decay (but not exponential) in higher dimensions [12, 14, 15]. Similar results were also obtained for other thermoelastic theories which are not based on the Fourier law [1, 18,19,20,21].

Recently, in [6] Fernández and Quintanilla studied the problem determined by the elasticity with \(n^2\) dissipative mechanisms, where n is the dimension of the domain. They showed that, whenever the matrix of the coupling coefficients is of the rank \(n^2\), the decay of the solutions is exponential, but different issues need to be considered. One could be if the number \(n^2\) of the dissipative mechanisms is optimal. Another one could be to clarify how the number of dissipative coupling mechanisms affects to the decay of the solutions. This paper is addressed to deal with these two questions.

The contribution [6] applies to the linearized theory [5, 9, 10, 13], where we note that few symmetries are satisfied by the constitutive coefficients. More symmetries are hold in the linear case. We will prove that, whenever the matrix of coupling coefficients satisfies the symmetries \(A_{ij}^l=A_{ji}^l\) (see system (4)), we can reduce the necessary number of coupling dissipation mechanisms to obtain the exponential decay. We point out that the linear theory satisfies these conditions. To be precise, we only need three dissipative mechanisms in dimension two and six in dimension three.

The mathematical aim of the contribution [6] was analytical. So, it will be suitable to provide a numerical study to the problem of the elasticity with several dissipative mechanisms. In this sense, we will introduce some fully discrete approximations of the general case involving four dissipative mechanisms (the two temperatures and the two mass diffusions), providing a priori error estimates which lead to the linear convergence of the algorithm. Later, we will carry out some simulations (always in dimension two) referring to the different problems when the coupling matrix has rank one, two, three and four, respectively. Since we work with simulations, we will be able to see the (numerical) exponential decay in all cases. This result should be interpreted as an approximation since the simulations correspond to numerical approximations, but we note that the introduction of an increasing number of dissipative mechanisms provides that the rate of the exponential decay (obtained from the numerical approach) also increases. This fact is not surprising, but this is the first mathematical contribution in this aspect. We show a numerical proof that the decay of the solution increases when we increase the number of coupling dissipative mechanisms.

The plan of this article is as follows: in the next section we recall the basic equations of the problem as well as the results obtained in [6] in this sense. Then, we focus on the case that we consider three dissipation mechanisms and the coupling coefficients satisfy a certain symmetry and we verify that, in this case, there is also an exponential decay. The numerical study of the problem is carried out in the fourth section, obtaining some a priori error estimates and deriving the linear convergence under adequate regularity conditions. In the fifth section, we carry out some simulations when we incorporate different dissipation mechanisms and we check how the decay rate increases as we introduce new mechanisms.

2 Basic equations and assumptions

In this section, we describe the model and the required assumptions on the data, and we recall some results regarding the existence and uniqueness or the energy decay (see [6] for further details).

Let us consider a two-dimensional bounded domain B with a sufficiently smooth boundary which is made of an elastic material coupled with (in general) four dissipative mechanisms. From a physical point of view, we can think that they are determined by two temperatures and two mass diffusion processes. For the sake of simplicity in the modeling, we assume that the material is homogeneous and isotropic in the mechanical, thermal and mass diffusion parts, but we do not impose this requirement on the coupling coefficients. Therefore, the general system is written as follows (see [6]):

$$\begin{aligned} \begin{array}{l} \rho \ddot{u}_i= \mu \varDelta u_{i}+ (\lambda +\mu ) u_{j,ji}+A_{ik}^l\theta _{l,k},\\ m_{lp} \dot{\theta }_p= \kappa _{lp}\varDelta \theta _p+A_{ik}^l\dot{u}_{i,k}+\xi _{pq}^l (\theta _p-\theta _q), \end{array} \end{aligned}$$
(1)

where \(i,j,k=1,2\) and \(l,q,p=1,\ldots ,4\), \(u_i\) denotes the displacement, \(\theta _1, \theta _2\) are the two temperatures, \(\theta _3,\theta _4\) are the other two dissipative variables which can be seen as two mass diffusions (see [13]), \(\rho\) is the mass density, \(\lambda , \mu\) are the Lamé constants, \(\kappa _{ij}\) are related with the thermal and diffusive conductivity, \(m_{ij}\) are related with the thermal and diffusive capacity, \(A_{ij}^l\) are the coupling terms and \(\xi _{kj}^l\) corresponds to the coefficients associated to the relative temperatures (or concentrations).

We will impose the boundary conditions, for a.e. \({\varvec{x}}\in \partial B\),

$$\begin{aligned} u_i({\varvec{x}},t)=0,\quad \theta _{k,j}({\varvec{x}},t)n_j({\varvec{x}})=0, \end{aligned}$$
(2)

where \(n_j\) is the outward normal vector to the boundary \(\partial B\), for \(i=1,2\) and \(k=1,\ldots , 4\), and some initial conditions, for a.e. \({\varvec{x}}\in B,\)

$$\begin{aligned} \begin{array}{l} u_i({\varvec{x}},0)=u_i^0({\varvec{x}}),\quad \dot{u}_i({\varvec{x}},0)=v_i^0({\varvec{x}}),\\ \theta _k({\varvec{x}},0)=\theta _k^0({\varvec{x}}), \end{array} \end{aligned}$$
(3)

for \(i=1,2\) and \(k=1,\ldots , 4\), where functions \(u_1^0\), \(u_2^0\), \(v_1^0\), \(v_2^0\), \(\theta _1^0\), \(\theta _2^0\), \(\theta _3^0\) and \(\theta _4^0\) represent the initial data of the problem. We note that conditions (2) imply that there is not displacement on the boundary and that the dissipative mechanisms are isolated with respect to the exterior.

We will impose the following conditions on the data:

  1. (i)

    \(\rho >0\), \(\mu >0\), \(\lambda +\mu >0\).

  2. (ii)

    The matrices \((m_{ij}),\, (\kappa _{ij})\) are symmetric, that is, \(m_{ij}=m_{ji}\) and \(k_{ij}=k_{ji}\) for \(i,j=1,\ldots ,4\).

  3. (iii)

    The matrices \((m_{ij})\), \((\kappa _{ij})\) and \((l_i)\) are positive definite, that is, there exist three positive constants \(C_1\), \(C_2\) and \(C_3\) such that

    $$\begin{aligned} \begin{array}{l} m_{ij}\xi _i\xi _j\ge C_1\xi _i \xi _i \quad \hbox {for every vector}\quad (\xi _i),\\ \kappa _{ij}\xi _i\xi _j\ge C_2\xi _i \xi _i \quad \hbox {for every vector}\quad (\xi _i),\\ l_1\xi _1^2+2l_2\xi _1\xi _2+l_3 \xi _2^2\ge C_3(\xi _1^2+\xi _2^2). \end{array} \end{aligned}$$

Let \(W_0^{1,2}(B)\) and \(L^2(B)\) be the well-known Sobolev spaces and

$$\begin{aligned} \begin{array}{l} \displaystyle L^2_*(B)=\{f\in L^2(B)\, ; \, \int _B f\, da=0\},\\ W^{1,2}_*(B)=W^{1,2}(B)\cap L^2_*(B). \end{array} \end{aligned}$$

Then, in [6] we proved the following.

Theorem 1

If \(u_i^0\in W^{2,2}(B)\), \(v_i^0\in W^{1,2}(B)\) and \(\theta _k^0\in W^{2,2}(B)\cap L^2_*(B)\), for \(i=1,2\) and \(k=1,\ldots ,4\), then problem (1–3) has a unique solution.

Moreover, if the coupling matrix defined, from the coefficients given in system (1), as

$$\begin{aligned} \begin{pmatrix} A_{11}^1&{}A_{12}^1&{}A_{21}^1&{}A_{22}^1 \\ A_{11}^2&{}A_{12}^2&{}A_{21}^2&{}A_{22}^2 \\ A_{11}^3&{}A_{12}^3&{}A_{21}^3&{}A_{22}^3 \\ A_{11}^4&{}A_{12}^4&{}A_{21}^4&{}A_{22}^4 \end{pmatrix} \end{aligned}$$

has rank 4, then the solutions to problem (1–3) decay in an exponential way.

3 Case \(A_{ij}^l=A_{ji}^l\) and three dissipative mechanisms

As we pointed out before, four coupling mechanisms are sufficient to guarantee the exponential decay for the elasticity. The natural question is if we can relax the number of couplings. A possible answer is that it will be positive whenever we assume that \(A_{ij}^l=A_{ji}^l\) for every i, j, l and we consider three dissipative mechanisms. The proof of this fact is very easy from the analysis proposed in [6]. For this reason, we are going to sketch the proofs and to follow the similar steps proposed there.

3.1 The problem

In this case, we consider the system (see Ieşan [11]):

$$\begin{aligned} \begin{array}{l} \rho \ddot{u}_i= \mu \varDelta u_{i}+ (\lambda +\mu ) u_{j,ji}+A_{ik}^l\theta _{l,k},\\ m_{lp} \dot{\theta }_p= \kappa _{lp}\varDelta \theta _p+A_{ik}^l\dot{u}_{i,k}-\xi _{pq}^l (\theta _p-\theta _q), \end{array} \end{aligned}$$
(4)

where \(i,j,k=1,2\) and \(l,q,p=1,\ldots ,3\), which is similar to system (1). It is relevant to say that, in contrast to the reference [6], we assume that l, p, q can be \(1,\,2\) or 3 and \(\xi _{12}^2=-\xi _{12}^1=l\) but the other combinations vanish. From a physical point of view, we can think that the dissipative mechanisms are determined by the two temperatures and one mass dissipation mechanism.

We will assume again conditions (i)-(iii) but now i, j vary between 1 and 3, without the condition on \(l_i\) since it now leads to a unique positive value l.

We combine system (4) with the initial conditions (3) and the boundary conditions (2), but in the case that \(k=1,2,3\) for a.e. \({\varvec{x}}\in B\).

We can study the problem (4), (3) and (2) in the Hilbert space:

$$\begin{aligned} {\mathcal {H}}=[W_0^{1,2}(B)]^2\times [L^2(B)]^2\times [L^2_*(B)]^3. \end{aligned}$$

We can define the inner product associated with the norm:

$$\begin{aligned} \Vert (u_i,v_i,\theta _d)\Vert ^2=\int _B \Big (\rho v_i\overline{v_i}+m_{kl}\theta _k\overline{\theta _l} +2\mu e_{ij}\overline{e_{ij}}+\lambda e_{ii}\overline{e_{jj}}\Big )\, da, \end{aligned}$$

where \(e_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}).\) As usual, the bar denotes the conjugated complex.

If \(U=(u_i,v_i,\theta _d)\) we can write our problem in the following abstract from:

$$\begin{aligned} \frac{dU}{dt}={\mathcal {A}}U,\quad U(0)=(u_i^0,v_i^0,\theta _d^0), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {A}}\left( \begin{array}{c} u_i\\ v_i \\ \theta _d\end{array}\right) = \left( \begin{array}{c} v_i\\ \rho ^{-1}(\mu \varDelta u_i+(\lambda +\mu )u_{j,ji}+A_{ik}^p\theta _{p,k}) \\ n_{dl}(\kappa _{lp}\varDelta \theta _p+A_{ik}^lv_{i,k}+\xi _{pq}^l(\theta _p-\theta _q))\end{array}\right) , \end{aligned}$$

and \(n_{dl} m_{lp}=\delta _{dp},\) with \(\delta _{dp}\) being the Kronecker symbol.

At is was pointed out in [6] the domain of the operator \({\mathcal {A}}\) is made by the elements of the Hilbert space \({\mathcal {H}}\) such that \(v_i\in W^{1,2}_0(B)\), \(\mu \varDelta u_i+(\lambda +\mu )u_{j,ji}\in L^2(B)\) and \(\theta _i\in W^{2,2}(B)\cap L^2_*(B)\). Therefore, the domain of the operator is dense.

At the same time, we have that

$$\begin{aligned} \begin{array}{l} \displaystyle Re <{\mathcal {A}}U,U>\\ \qquad \displaystyle =-\int _B\Big (\kappa _{ij}\theta _{i,m}\overline{\theta _{j,m}}+l(\theta _1-\theta _2)\overline{(\theta _1-\theta _2)} \Big )\, da\le 0. \end{array} \end{aligned}$$

Following the arguments used in the proof of Lemma 2 in [6] we can develop (word by word) a proof in the sense that zero belongs to the resolvent of the operator \({\mathcal {A}}\) in our case.

Therefore, we can obtain the following.

Theorem 2

The operator \({\mathcal {A}}\) generates a \(C^0\)-semigroup of contractions.

3.2 Exponential decay

In this subsection, we prove the exponential decay of the solutions to our problem. It is relevant to say that we assume that \(A_{ij}^l=A_{ji}^l\), for every \(i,j=1,2\) and \(l=1,2,3\), and that the matrix

$$\begin{aligned} \left( \begin{array}{c c c} A_{11}^1 &{} A_{12}^1 &{} A_{22}^1\\ A_{11}^2 &{}A_{12}^2 &{} A_{22}^2\\ A_{11}^3 &{} A_{12}^3 &{} A_{22}^3 \end{array}\right) \end{aligned}$$
(5)

has rank 3.

Then, we get the exponential decay of the solutions that we state as follows.

Theorem 3

The solutions to problem (2–4) decay in an exponential way.

Proof

The proof follows the same steps of the arguments used in the proof of Theorem 2 in [6]. That is, we need to prove that the imaginary axis is contained in the resolvent of the operator \({\mathcal {A}}\) and that the condition

$$\begin{aligned} \limsup _{|\beta |\rightarrow \infty }\Vert (i\beta I-{\mathcal {A}})^{-1}\Vert <\infty \end{aligned}$$

holds.

In order to show the first condition, we use a contradiction argument. Let us assume that this condition does not hold and we will arrive to a contradiction. Assuming that there exists \(\beta \ne 0\) such that \(i\beta\) belongs to the spectrum, there will exist a sequence of real numbers \(\beta _n\rightarrow \beta\) and a sequence of elements \(U_n\) of unit norm, at the domain of the operator \({\mathcal {A}}\),  such that

$$\begin{aligned} \begin{array}{l} i\beta _n u_{jn}-v_{jn}\rightarrow 0 \quad \hbox {in}\quad W^{1,2}(B),\\ i\rho \beta _nv_{jn}-(\mu \varDelta u_{jn}+(\lambda +\mu )u_{kn,kj}+A_{jk}^l\theta _{ln,k})\\ \qquad \qquad \rightarrow 0\quad \hbox {in}\quad L^2(B),\\ i\omega _n m_{pq}\theta _{qn}-(\kappa _{pq}\varDelta \theta _{qn}+\xi _{rs}^p(\theta _{rn}-\theta _{sn}) +A_{ml}^pf_{mln}) \\ \qquad \qquad \rightarrow 0\quad \hbox {in}\quad L^2(B), \end{array} \end{aligned}$$

where

$$\begin{aligned} f_{ml}=\frac{1}{2}(v_{m,l}+v_{l,m}). \end{aligned}$$

From the energy inequality, we see that \(\theta _{in}\rightarrow 0\) in \(W^{1,2}(B)\) for \(i=1,2,3\). Then, we obtain

$$\begin{aligned} \omega _n^{-1}\kappa _{jl}\varDelta \theta _{ln}+iA_{pq}^je_{pqn}\rightarrow 0 \quad \hbox {in} \quad L^2(B), \end{aligned}$$

where

$$\begin{aligned} e_{pqn}=\frac{1}{2}(u_{pn,q}+u_{qn,p}). \end{aligned}$$

We multiply by \(A_{pq}^je_{pqn}\) the jth-convergence and we note that

$$\begin{aligned} \begin{array}{l}<\omega _n^{-1}\varDelta \theta _{in},A_{pq}^j e_{pqn}>\\ \qquad =-<\nabla \theta _{in},\omega _n^{-1}\nabla (A_{pq}^j e_{pqn})>\rightarrow 0, \end{array} \end{aligned}$$

as far as the \(H^2-\)norm of \(\omega _n^{-1}u_{in}\) is bounded.

It then follows that

$$\begin{aligned} e_{pqn}\rightarrow 0 \quad \hbox {in}\quad L^2(B). \end{aligned}$$

If we use the Korn inequality we also obtain that

$$\begin{aligned} u_{pn,q}\rightarrow 0 \quad \hbox {in}\quad L^2(B), \end{aligned}$$

we deduce that \(v_{pn}\rightarrow 0\) in \(L^2(B)\) and we arrive to a contradiction.

We also note that we can use the same argument to prove the asymptotic condition and the theorem is derived. \(\square\)

Remark 1

We have developed the analysis in the two-dimensional case. For the three-dimensional one, we would need that the corresponding coupling matrix has rank six.

Remark 2

Two recent papers [7, 8] have extended the decay results obtained in [6] to the type III and the hyperbolic cases. It is worth saying that we can also extend Theorem 3 to these alternative theories. That is, it is possible to obtain the exponential decay in two dimensions for the type III or the hyperbolic cases in the case that \(A_{ij}^l=A_{ji}^l\) and the matrix (5) has rank three.

4 Numerical analysis of a fully discrete scheme

In the rest of this work, we will simplify the system (1) considerably in order to better demonstrate our results. So, we will take particular values of tensors \(A_{ik}^l\), \(m_{lp}\), \(\kappa _{lp}\) and \(\xi _{pq}\) to obtain the following system:

$$\begin{aligned} \begin{array}{l} \rho \ddot{u}_1= \mu \varDelta u_1+ (\lambda +\mu ) u_{j,j1}+\beta _1 \theta _{1,1}+\beta _2\theta _{2,2}\\ \qquad +\beta _3\theta _{3,2}+\beta _4\theta _{4,1},\\ \rho \ddot{u}_2= \mu \varDelta u_2+ (\lambda +\mu ) u_{j,j2}+\beta _1 \theta _{1,2}+\beta _2\theta _{2,1}\\ \qquad -\beta _3\theta _{3,1}-\beta _4\theta _{4,2},\\ c_1\dot{\theta }_1= \kappa \varDelta \theta _1 + \beta _1\dot{u}_{1,1}+\beta _1 \dot{u}_{2,2}-l_1(\theta _1-\theta _2),\\ c_2\dot{\theta }_2= \kappa \varDelta \theta _2 + \beta _2\dot{u}_{1,2}+\beta _2 \dot{u}_{2,1}+l_1(\theta _1-\theta _2),\\ c_3\dot{\theta }_3= \kappa \varDelta \theta _3 + \beta _3\dot{u}_{1,2}-\beta _3 \dot{u}_{2,1}+l_3(\theta _3-\theta _4),\\ c_4\dot{\theta }_4= \kappa \varDelta \theta _4 + \beta _4\dot{u}_{1,1}-\beta _4 \dot{u}_{2,2}-l_3(\theta _3-\theta _4). \end{array} \end{aligned}$$
(6)

In this case, we will impose the following conditions on the constitutive coefficients in order to guarantee assumptions (i)-(iv)Footnote 1:

$$\begin{aligned} \begin{array}{l} \rho>0,\quad c_1>0,\quad c_2>0,\quad c_3>0,\quad c_4>0,\quad \\ \mu>0,\quad \lambda +\mu>0,\quad \kappa>0,\quad l_1>0,\quad l_3>0. \end{array} \end{aligned}$$
(7)

In this section, we present a fully discrete approximation of the simplified problem given by the system (6) with boundary conditions (2) and initial conditions (3), and we perform an a priori error analysis. As usual, we will study the deformation of the body over a finite time interval [0, T], for a given final time \(T>0\).

First, we provide the variational formulation of problem (6), (2) and (3). So, let us denote the two components of the velocity by \(v_1=\dot{u}_1\) and \(v_2=\dot{u}_2\), respectively. Let \(Y=L^2(B)\) and \(H=[L^2(B)]^2\) and let \((\cdot ,\cdot )_Y\) and \(\Vert \cdot \Vert _Y\) (resp. \((\cdot ,\cdot )_H\) and \(\Vert \cdot \Vert _H\)) be the usual scalar product and the norm defined in Y (resp. H). Moreover, let V be the variational space given by \(V=H^1_0(B)\) and denote by \(\Vert \cdot \Vert _V\) its usual norm.

Multiplying the equations of system (6) by adequate test functions, using the Green’s formula and the boundary conditions (2), we obtain the following weak form.

Find the first component of the velocity \(v_1:[0,T]\rightarrow V\), the second component of the velocity \(v_2:[0,T]\rightarrow V\), the first temperature \(\theta _1:[0,T]\rightarrow V\), the second temperature \(\theta _2:[0,T]\rightarrow V\), the first mass diffusion \(\theta _3:[0,T]\rightarrow V\) and the second mass diffusion \(\theta _4:[0,T]\rightarrow V\) such that \(v_1(0)=v_1^0\), \(v_2(0)=v_2^0\), \(\theta _1(0)=\theta _1^0\), \(\theta _2(0)=\theta _2^0\), \(\theta _3(0)=\theta _3^0\), \(\theta _4(0)=\theta _4^0\) and, for a.e. \(t\in [0,T]\) and for all \(w,r,s,z,m,l\in V\),

$$\begin{aligned}&\displaystyle \rho (\dot{v}_1(t),w)_Y+\mu (\nabla u_1(t),\nabla w)_H\nonumber \\&\qquad + (\lambda +\mu )(\hbox { div\,}{\varvec{u}}(t),w_{,1})_Y=\beta _1 (\theta _{1,1}(t),w)_Y\nonumber \\&\qquad +\beta _2 (\theta _{2,2}(t),w)_Y +\beta _3(\theta _{3,2}(t),w)_Y\nonumber \\&\qquad +\beta _4(\theta _{4,1}(t),w)_Y, \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle \rho (\dot{v}_2(t),r)_Y+\mu (\nabla u_2(t),\nabla r)_H\nonumber \\&\qquad + (\lambda +\mu )(\hbox { div\,}{\varvec{u}}(t),r_{,2})_Y=\beta _1 (\theta _{1,2}(t),r)_Y\nonumber \\&\qquad +\beta _2 (\theta _{2,1}(t),r)_Y -\beta _3(\theta _{3,1}(t),r)_Y\nonumber \\&\qquad -\beta _4(\theta _{4,2}(t),r)_Y, \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle c_1(\dot{\theta }_1(t),s)_Y+\kappa (\nabla \theta _1(t),\nabla s)_H +l_1(\theta _{1}(t)-\theta _2(t),s)_Y \nonumber \\&\qquad =\beta _1 (v_{1,1}(t),s)_Y+\beta _1 (v_{2,2},s)_Y , \end{aligned}$$
(10)
$$\begin{aligned}&\displaystyle c_2(\dot{\theta }_2(t),z)_Y+\kappa (\nabla \theta _2(t),\nabla z)_H +l_1(\theta _{2}(t)-\theta _1(t),z)_Y \nonumber \\&\qquad =\beta _2 (v_{1,2}(t),z)_Y+\beta _2 (v_{2,1}(t),z)_Y , \end{aligned}$$
(11)
$$\begin{aligned}&\displaystyle c_3(\dot{\theta }_3(t),m)_Y+\kappa (\nabla \theta _3(t),\nabla m)_H +l_3(\theta _{3}(t)-\theta _4(t),m)_Y \nonumber \\&\qquad =\beta _3 (v_{1,2}(t),m)_Y-\beta _3 (v_{2,1}(t),m)_Y , \end{aligned}$$
(12)
$$\begin{aligned}&\displaystyle c_4(\dot{\theta }_4(t),l)_Y+\kappa (\nabla \theta _4(t),\nabla l)_H +l_3(\theta _{4}(t)-\theta _3(t),l)_Y \nonumber \\&\qquad =\beta _4 (v_{1,1}(t),l)_Y-\beta _4 (v_{2,2}(t),l)_Y , \end{aligned}$$
(13)

where \({\varvec{u}}(t)=(u_1(t),u_2(t))\) represents the displacement field and its components are recovered from the relations:

$$\begin{aligned} \begin{array}{l} \displaystyle u_1(t)=\int _0^tv_1(s)\,ds+u_1^0,\\ \displaystyle u_2(t)=\int _0^t v_2(s)\,ds+u_2^0. \end{array} \end{aligned}$$
(14)

Now, we provide the fully discrete approximation of the variational problem (8–14). This is done in two steps. First, in order to obtain the spatial approximation we assume that the domain \(\overline{B}\) is polyhedral and let us denote by \({{{\mathcal {T}}}}^h\) a regular finite element triangulation in the sense of [3]. Thus, we construct the finite dimensional space \(V^h\subset V\) given by

$$\begin{aligned} \begin{array}{l} V^h=\{w^h\in C(\overline{B})\cap V \; ; \; w^h_{|Tr}\in P_1(Tr)\\ \qquad \qquad \quad \forall Tr\in {{\mathcal {T}}}^h\}. \end{array} \end{aligned}$$
(15)

In the above definition, \(P_1(Tr)\) represents the space of polynomials of degree less or equal to one in the element Tr, i.e. the finite element space \(V^h\) is made of continuous and piecewise affine functions, and \(h>0\) is the spatial discretization parameter. Moreover, we assume that the discrete initial conditions, denoted by \(u_i^{0h}\), \(v_i^{0h}\) and \(\theta _j^{0h}\) (for \(i=1,2\) and \(j=1,\ldots , 4\)), are given by

$$\begin{aligned} \begin{array}{l} u_1^{0h}={\mathcal {P}}^{h} u_1^0,\quad u_2^{0h}={\mathcal {P}}^{h} u_2^0,\quad v_1^{0h}={\mathcal {P}}^{h} v_1^0,\\ v_2^{0h}={\mathcal {P}}^{h} v_2^0,\quad \theta _1^{0h}={\mathcal {P}}^{h} \theta _1^0,\quad \theta _2^{0h}={\mathcal {P}}^{h} \theta _2^0,\\ \theta _3^{0h}={\mathcal {P}}^{h} \theta _3^0,\quad \theta _4^{0h}={\mathcal {P}}^{h} \theta _4^0, \end{array} \end{aligned}$$
(16)

where \({\mathcal {P}}^{h}\) is the classical finite element interpolation operator over \(V^h\) (see, e.g., [3]).

In order to obtain the discretization of the time derivatives, we use a uniform partition of the time interval [0, T], denoted by \(0=t_0<t_1<\cdots < t_N=T\), with step size \(k=T/N\) and nodes \(t_n=n\,k\) for \(n=0,1,\dots ,N\). For a continuous function z(t), we use the notation \(z^n=z(t_n)\) and, for the sequence \(\{z^n\}_{n=0}^N\), we denote by \(\delta z^n=(z^n-z^{n-1})/k\) its corresponding divided differences.

Thus, applying the well-known implicit Euler scheme, the fully discrete approximations of problem (8–14) are the following.

Find the discrete first component of the velocity \(\{v_1^{hk,n}\}_{n=0}^N\subset V^h\), the discrete second component of the velocity \(\{v_2^{hk,n}\}_{n=0}^N\subset V^h\), the discrete first temperature \(\{\theta _1^{hk,n}\}_{n=0}^N\subset V^h\), the discrete second temperature \(\{\theta _2^{hk,n}\}_{n=0}^N\subset V^h\), the discrete first mass diffusion \(\{\theta _3^{hk,n}\}_{n=0}^N\subset V^h\) and the discrete second mass diffusion \(\{\theta _4^{hk,n}\}_{n=0}^N\subset V^h\) such that \(v_1^{hk,0}=v_1^{0h}\), \(v_2^{hk,0}=v_2^{0h}\), \(\theta _1^{hk,0}=\theta _1^{0h}\), \(\theta _2^{hk,0}=\theta _2^{0h}\), \(\theta _3^{hk,0}=\theta _3^{0h}\), \(\theta _4^{hk,0}=\theta _4^{0h}\) and, for \(n=1,\ldots , N\) and for all \(w^h,r^h,s^h,z^h,m^h,l^h\in V^h\),

$$\begin{aligned}&\displaystyle \rho (\delta {v}_1^{hk,n},w^h)_Y+\mu (\nabla u_1^{hk,n},\nabla w^h)_H\nonumber \\&\qquad + (\lambda +\mu )(\hbox { div\,}{\varvec{u}}^{hk,n},w_{,1}^h)_Y=\beta _1 (\theta _{1,1}^{hk,n},w^h)_Y\nonumber \\&\qquad +\beta _2 (\theta _{2,2}^{hk,n},w^h)_Y +\beta _3(\theta _{3,2}^{hk,n},w^h)_Y\nonumber \\&\qquad +\beta _4(\theta _{4,1}^{hk,n},w^h)_Y, \end{aligned}$$
(17)
$$\begin{aligned}&\displaystyle \rho (\delta {v}_2^{hk,n},r^h)_Y+\mu (\nabla u_2^{hk,n},\nabla r^h)_H\nonumber \\&\qquad + (\lambda +\mu )(\hbox { div\,}{\varvec{u}}^{hk,n},r_{,2}^h)_Y=\beta _1 (\theta _{1,2}^{hk,n},r^h)_Y\nonumber \\&\qquad +\beta _2 (\theta _{2,1}^{hk,n},r^h)_Y -\beta _3(\theta _{3,1}^{hk,n},r^h)_Y\nonumber \\&\qquad -\beta _4(\theta _{4,2}^{hk,n},r^h)_Y, \end{aligned}$$
(18)
$$\begin{aligned}&\displaystyle c_1(\delta {\theta }_1^{hk,n},s^h)_Y+\kappa (\nabla \theta _1^{hk,n},\nabla s^h)_H \nonumber \\&\qquad +l_1(\theta _{1}^{hk,n}-\theta _2^{hk,n},s^h)_Y \nonumber \\&\quad =\beta _1 (v_{1,1}^{hk,n},s^h)_Y+\beta _1 (v_{2,2}^{hk,n},s^h)_Y , \end{aligned}$$
(19)
$$\begin{aligned}&\displaystyle c_2(\delta{\theta }_2^{hk,n},z^h)_Y+\kappa (\nabla \theta _2^{hk,n},\nabla z^h)_H \nonumber \\&\qquad +l_1(\theta _{2}^{hk,n}-\theta _1^{hk,n},z^h)_Y \nonumber \\&\quad =\beta _2 (v_{1,2}^{hk,n},z^h)_Y+\beta _2 (v_{2,1}^{hk,n},s^h)_Y , \end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle c_3(\delta {\theta }_3^{hk,n},m^h)_Y+\kappa (\nabla \theta _3^{hk,n},\nabla m^h)_H\nonumber \\&\qquad +l_3(\theta _{3}^{hk,n}-\theta _4^{hk,n},m^h)_Y \nonumber \\&\quad =\beta _3 (v_{1,2}^{hk,n},m^h)_Y-\beta _3 (v_{2,1}^{hk,n},m^h)_Y , \end{aligned}$$
(21)
$$\begin{aligned}&\displaystyle c_4(\delta {\theta }_4^{hk,n},l^h)_Y+\kappa (\nabla \theta _4^{hk,n},\nabla l^h)_H\nonumber \\&\qquad +l_3(\theta _{4}^{hk,n}-\theta _3^{hk,n},l^h)_Y \nonumber \\&\quad =\beta _4 (v_{1,1}^{hk,n},l^h)_Y-\beta _4 (v_{2,2}^{hk,n},l^h)_Y , \end{aligned}$$
(22)

where \({\varvec{u}}^{hk,n}=(u_1^{hk,n},u_2^{hk,n})\) represents the discrete displacement field and its components are recovered from the relations:

$$\begin{aligned} \begin{array}{l} \displaystyle u_1^{hk,n}=k\sum _{j=1}^n v_1^{hk,j}+u_1^{0h},\\ \displaystyle u_2^{hk,n}=k\sum _{j=1}^n v_2^{hk,j}+u_2^{0h}. \end{array} \end{aligned}$$
(23)

It is worth noting that, under conditions (7), by using Lax-Milgram lemma it is easy to show that the above fully discrete problem has a unique solution.

In the rest of this section, our aim will be to obtain some a priori error estimates for the numerical errors \(v_i^n-v_i^{hk,n}\) and \(\theta _j^n-\theta _j^{hk,n}\) for \(i=1,2\) and \(j=1,\ldots ,4\).

Subtracting variational Eq. (8) at time \(t=t_n\) for a test function \(w=w^h\in V^h\), and discrete variational Eq. (9) we find that, for all \(w^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \rho (\dot{v}_1^n-\delta {v}_1^{hk,n},w^h)_Y+\mu (\nabla (u_1^n-u_1^{hk,n}),\nabla w^h)_H\\ \quad + (\lambda +\mu )(\hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n}),w_{,1}^h)_Y\\ \quad -\beta _1 (\theta _{1,1}^n-\theta _{1,1}^{hk,n},w^h)_Y-\beta _2 (\theta _{2,2}^n-\theta _{2,2}^{hk,n},w^h)_Y \\ \quad -\beta _3(\theta _{3,2}^n-\theta _{3,2}^{hk,n},w^h)_Y -\beta _4(\theta _{4,1}^n-\theta _{4,1}^{hk,n},w^h)_Y=0, \end{array} \end{aligned}$$

and so, it follows that, for all \(w^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \rho (\dot{v}_1^n-\delta {v}_1^{hk,n},v_1^n-v_1^{hk,n})_Y\\ +\mu (\nabla (u_1^n-u_1^{hk,n}),\nabla (v_1^n-v_1^{hk,n}))_H\\ + (\lambda +\mu )(\hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n}),(v_1^n-v_1^{hk,n})_{,1})_Y \\ -\beta _1 (\theta _{1,1}^n-\theta _{1,1}^{hk,n},v_1^n-v_1^{hk,n})_Y \\ -\beta _2 (\theta _{2,2}^n-\theta _{2,2}^{hk,n},v_1^n-v_1^{hk,n})_Y \\ -\beta _3(\theta _{3,2}^n-\theta _{3,2}^{hk,n},v_1^n-v_1^{hk,n})_Y \\ -\beta _4(\theta _{4,1}^n-\theta _{4,1}^{hk,n},v_1^n-v_1^{hk,n})_Y\\ = \rho (\dot{v}_1^n-\delta {v}_1^{hk,n},v_1^n-w^h)_Y\\ +\mu (\nabla (u_1^n-u_1^{hk,n}),\nabla (v_1^n-w^h))_H\\ + (\lambda +\mu )(\hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n}),(v_1^n-w^h)_{,1})_Y\\ -\beta _1 (\theta _{1,1}^n-\theta _{1,1}^{hk,n},v_1^n-w^h)_Y\\ -\beta _2 (\theta _{2,2}^n-\theta _{2,2}^{hk,n},v_1^n-w^h)_Y \\ -\beta _3(\theta _{3,2}^n-\theta _{3,2}^{hk,n},v_1^n-w^h)_Y\\ -\beta _4(\theta _{4,1}^n-\theta _{4,1}^{hk,n},v_1^n-w^h)_Y. \end{array} \end{aligned}$$

Now, keeping in mind that

$$\begin{aligned} \begin{array}{l} \rho (\dot{v}_1^n-\delta {v}_1^{hk,n},v_1^n-v_1^{hk,n})_Y=\rho (\dot{v}_1^n-\delta {v}_1^{n},v_1^n-v_1^{hk,n})_Y\\ \qquad + \rho (\delta {v}_1^n-\delta {v}_1^{hk,n},v_1^n-v_1^{hk,n})_Y,\\ \displaystyle \rho (\delta {v}_1^n-\delta {v}_1^{hk,n},v_1^n-v_1^{hk,n})_Y\\ \qquad \displaystyle \ge \frac{\rho }{2k}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y^2-\Vert v_1^{n-1}-v_1^{hk,n-1}\Vert _Y^2\Big \},\\ \mu (\nabla (u_1^n-u_1^{hk,n}),\nabla (v_1^n-v_1^{hk,n}))_H\\ \qquad =\mu (\nabla (u_1^n-u_1^{hk,n}),\nabla (\dot{u}_1^n-\delta u_1^{n}))_H\\ \qquad + \mu (\nabla (u_1^n-u_1^{hk,n}),\nabla (\delta u_1^n-\delta u_1^{hk,n}))_H,\\ \displaystyle \mu (\nabla (u_1^n-u_1^{hk,n}),\nabla (\delta u_1^n-\delta u_1^{hk,n}))_H\\ \displaystyle \qquad \ge \frac{\mu }{2k}\Big \{ \Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2-\Vert \nabla (u_1^{n-1}-u_1^{hk,n-1})\Vert _H^2\Big \},\\ (\theta _{l,i}^n-\theta _{l,i}^{hk,n},v_j^n-w^h)_Y=-(\theta _{l}^n-\theta _{l}^{hk,n},(v_j^n-w^h)_{,i})_Y, \end{array} \end{aligned}$$

where \(\delta v_1^n=(v_1^n-v_1^{n-1})/k\) and \(\delta u_1^n=(u_1^n-u_1^{n-1})/k\), after some algebraic manipulations and using several times Cauchy-Schwarz inequality and Cauchy’s inequality \(ab\le \epsilon a^2+\frac{1}{4\epsilon } b^2\), we find that, for all \(w^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\rho }{2k}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y^2-\Vert v_1^{n-1}-v_1^{hk,n-1}\Vert _Y^2\Big \}\\ \qquad \displaystyle +\frac{\mu }{2k}\Big \{ \Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2-\Vert \nabla (u_1^{n-1}-u_1^{hk,n-1})\Vert _H^2\Big \}\\ \qquad + (\lambda +\mu )(\hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n}),(\delta u_1^n-\delta u_1^{hk,n})_{,1})_Y \\ \qquad -\beta _1 (\theta _{1,1}^n-\theta _{1,1}^{hk,n},v_1^n-v_1^{hk,n})_Y -\beta _2 (\theta _{2,2}^n-\theta _{2,2}^{hk,n},v_1^n-v_1^{hk,n})_Y \\ \qquad -\beta _3(\theta _{3,2}^n-\theta _{3,2}^{hk,n},v_1^n-v_1^{hk,n})_Y-\beta _4(\theta _{4,1}^n-\theta _{4,1}^{hk,n},v_1^n-v_1^{hk,n})_Y\\ \quad \le C\Big ( \Vert \dot{v}_1^n-\delta v_1^n\Vert _Y^2+\Vert \dot{u}_1^n-\delta u_1^n\Vert _V^2+\Vert v_1^h-w^h\Vert _V^2\\ \qquad +\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2 + \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2\\ \qquad +\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2 +\Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2\\ \qquad +\Vert \hbox { div\,}({\varvec{u}}_n-{\varvec{u}}_n^{hk})\Vert _Y^2+(\delta u_1^n-\delta u_1^{hk,n},u_1^n-w^h)\Big ). \end{array} \end{aligned}$$

Proceeding in a similar form, we obtain the error estimates for the second component of the velocity field, for all \(r^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\rho }{2k}\Big \{ \Vert v_2^n-v_2^{hk,n}\Vert _Y^2-\Vert v_2^{n-1}-v_2^{hk,n-1}\Vert _Y^2\Big \}\\ \quad \displaystyle +\frac{\mu }{2k}\Big \{ \Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2-\Vert \nabla (u_2^{n-1}-u_2^{hk,n-1})\Vert _H^2\Big \}\\ \qquad + (\lambda +\mu )(\hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n}),(\delta u_2^n-\delta u_2^{hk,n})_{,2})_Y \\ \quad -\beta _1 (\theta _{1,2}^n-\theta _{1,2}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \quad -\beta _2 (\theta _{2,1}^n-\theta _{2,1}^{hk,n},v_2^n-v_2^{hk,n})_Y \\ \quad +\beta _3(\theta _{3,1}^n-\theta _{3,1}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \quad +\beta _4(\theta _{4,2}^n-\theta _{4,2}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \,\; \le C\Big ( \Vert \dot{v}_2^n-\delta v_2^n\Vert _Y^2+\Vert \dot{u}_2^n-\delta u_2^n\Vert _V^2+\Vert v_2^n-r^h\Vert _V^2\\ \quad +\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2+ \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2\\ \quad +\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2+\Vert v_2^n-v_2^{hk,n}\Vert _Y^2 \\ \quad +\Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2+\Vert \hbox { div\,}({\varvec{u}}_n-{\varvec{u}}_n^{hk})\Vert _Y^2\\ \quad +(\delta u_2^n-\delta u_2^{hk,n},u_2^n-r^h)\Big ), \end{array} \end{aligned}$$

where \(\delta v_2^n=(v_2^n-v_2^{n-1})/k\) and \(\delta u_2^n=(u_2^n-u_2^{n-1})/k\).

Combining the previous two estimates and taking into account that

$$\begin{aligned} \begin{array}{l} \displaystyle (\lambda +\mu )(\hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n}),\hbox { div\,}(\delta {\varvec{u}}^n-\delta {\varvec{u}}^{hk,n}))_Y\\ \quad \displaystyle \ge \frac{\lambda +\mu }{2k}\Big \{ \Vert \hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n})\Vert _Y^2\\ \qquad \qquad -\Vert \hbox { div\,}({\varvec{u}}^{n-1}-{\varvec{u}}^{hk,n-1})\Vert _Y^2\Big \}, \end{array} \end{aligned}$$

it leads, for all \(w^h,r^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\rho }{2k}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y^2-\Vert v_1^{n-1}-v_1^{hk,n-1}\Vert _Y^2\Big \}\\ \displaystyle \quad +\frac{\mu }{2k}\Big \{ \Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2\\ \qquad -\Vert \nabla (u_1^{n-1}-u_1^{hk,n-1})\Vert _H^2\Big \}\\ \quad \displaystyle + \frac{\lambda +\mu }{2k}\Big \{ \Vert \hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n})\Vert _Y^2\\ \qquad -\Vert \hbox { div\,}({\varvec{u}}^{n-1}-{\varvec{u}}^{hk,n-1})\Vert _Y^2\Big \} \\ \quad -\beta _1 (\theta _{1,1}^n-\theta _{1,1}^{hk,n},v_1^n-v_1^{hk,n})_Y\\ \quad -\beta _2 (\theta _{2,2}^n-\theta _{2,2}^{hk,n},v_1^n-v_1^{hk,n})_Y\\ \quad -\beta _3(\theta _{3,2}^n-\theta _{3,2}^{hk,n},v_1^n-v_1^{hk,n})_Y\\ \quad \displaystyle -\beta _4(\theta _{4,1}^n-\theta _{4,1}^{hk,n},v_1^n-v_1^{hk,n})_Y\\ \quad \displaystyle +\frac{\mu }{2k}\Big \{ \Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2-\Vert \nabla (u_2^{n-1}-u_2^{hk,n-1})\Vert _H^2\Big \}\\ \displaystyle \quad +\frac{\rho }{2k}\Big \{ \Vert v_2^n-v_2^{hk,n}\Vert _Y^2-\Vert v_2^{n-1}-v_2^{hk,n-1}\Vert _Y^2\Big \}\\ \quad -\beta _1 (\theta _{1,2}^n-\theta _{1,2}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \quad -\beta _2 (\theta _{2,1}^n-\theta _{2,1}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \quad +\beta _3(\theta _{3,1}^n-\theta _{3,1}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \quad +\beta _4(\theta _{4,2}^n-\theta _{4,2}^{hk,n},v_2^n-v_2^{hk,n})_Y\\ \,\; \le C\Big ( \Vert \dot{v}_1^n-\delta v_1^n\Vert _Y^2+\Vert \dot{u}_1^n-\delta u_1^n\Vert _V^2+\Vert v_1^h-w^h\Vert _V^2\\ \quad +\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2+ \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2\\ \quad +\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2+\Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2\\ \quad +\Vert \hbox { div\,}({\varvec{u}}_n-{\varvec{u}}_n^{hk})\Vert _Y^2+(\delta v_1^n-\delta v_1^{hk,n},v_1^n-w^h)\\ \quad + \Vert \dot{v}_2^n-\delta v_2^n\Vert _Y^2+\Vert \dot{u}_2^n-\delta u_2^n\Vert _V^2+\Vert v_2^n-r^h\Vert _V^2\\ \quad +\Vert v_2^n-v_2^{hk,n}\Vert _Y^2 +\Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2\\ \quad +(\delta v_2^n-\delta v_2^{hk,n},v_2^n-r^h)\Big ). \end{array} \end{aligned}$$

Now, we obtain the error estimates for the first temperature. If we subtract variational Eq. (10) at time \(t=t_n\) for a test function \(s=s^h\in V\), and discrete variational Eq. (19), we obtain, for all \(s^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle c_1(\dot{\theta }_1^n-\delta {\theta }_1^{hk,n},s^h)_Y+\kappa (\nabla (\theta _1^n-\theta _1^{hk,n}),\nabla s^h)_H\\ \quad +l_1(\theta _1^n-\theta _{1}^{hk,n}-(\theta _2^n-\theta _2^{hk,n}),s^h)_Y \\ \quad -\beta _1 (v_{1,1}^n-v_{1,1}^{hk,n},s^h)_Y-\beta _1 (v_{2,2}^n-v_{2,2}^{hk,n},s^h)_Y=0, \end{array} \end{aligned}$$

and therefore, we find that, for all \(s^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle c_1(\dot{\theta }_1^n-\delta {\theta }_1^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y\\ \quad +\kappa (\nabla (\theta _1^n-\theta _1^{hk,n}),\nabla (\theta _1^n-\theta _1^{hk,n}))_H\\ \quad +l_1(\theta _1^n-\theta _{1}^{hk,n}-(\theta _2^n-\theta _2^{hk,n}),\theta _1^n-\theta _1^{hk,n})_Y \\ \quad -\beta _1 (v_{1,1}^n-v_{1,1}^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y\\ \quad -\beta _1 (v_{2,2}^n-v_{2,2}^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y\\ \,\;= c_1(\dot{\theta }_1^n-\delta {\theta }_1^{hk,n},\theta _1^n-s^h)_Y\\ \quad +\kappa (\nabla (\theta _1^n-\theta _1^{hk,n}),\nabla (\theta _1^n-s^h))_H\\ \quad +l_1(\theta _1^n-\theta _{1}^{hk,n}-(\theta _2^n-\theta _2^{hk,n}),\theta _1^n-s^h)_Y \\ \quad -\beta _1 (v_{1,1}^n-v_{1,1}^{hk,n},\theta _1^n-s^h)_Y\\ \quad -\beta _1 (v_{2,2}^n-v_{2,2}^{hk,n},\theta _1^n-s^h)_Y. \end{array} \end{aligned}$$

Since

$$\begin{aligned} \begin{array}{l} c_1(\dot{\theta }_1^n-\delta {\theta }_1^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y=c_1(\dot{\theta }_1^n-\delta {\theta }_1^{n},\theta _1^n-\theta _1^{hk,n})_Y\\ \qquad + \rho (\delta {\theta }_1^n-\delta {\theta }_1^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y,\\ \displaystyle c_1(\delta {\theta }_1^n-\delta {\theta }_1^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y\\ \quad \displaystyle \ge \frac{c_1}{2k}\Big \{ \Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2-\Vert \theta _1^{n-1}-\theta _1^{hk,n-1}\Vert _Y^2\Big \},\\ (v_{i,1}^n-v_{i,1}^{hk,n},\theta _1^n-s^h)_Y=-(v_{i}^n-v_{i}^{hk,n},(\theta _1^n-s^h)_{,1})_Y \end{array} \end{aligned}$$

using again several times Cauchy-Schwarz inequality and the above commented Cauchy’s inequality, we obtain, for all \(s^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{c_1}{2k}\Big \{ \Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2-\Vert \theta _1^{n-1}-\theta _1^{hk,n-1}\Vert _Y^2\Big \} \\ \quad -\beta _1 (v_{1,1}^n-v_{1,1}^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y\\ \quad -\beta _1 (v_{2,2}^n-v_{2,2}^{hk,n},\theta _1^n-\theta _1^{hk,n})_Y\\ \,\; \le C\Big (\Vert \dot{\theta }_1^n-\delta \theta _1^n\Vert _Y^2+ \Vert \theta _1^n-s^h\Vert _V^2+\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2\\ \quad +\Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2+\Vert v_2^n-v_2^{hk,n}\Vert _Y^2\\ \quad +(\delta \theta _1^n-\delta \theta _1^{hk,n},\theta _1^n-s^h)_Y\Big ), \end{array} \end{aligned}$$

where \(\delta \theta _1^n=(\theta _1^n-\theta _1^{n-1})/k\).

In a similar way, we obtain the error estimates for the other temperature \(\theta _2\) and the two mass diffusions \(\theta _3\) and \(\theta _4\) (we skip the details for the sake of clarity):

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{c_2}{2k}\Big \{ \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2-\Vert \theta _2^{n-1}-\theta _2^{hk,n-1}\Vert _Y^2\Big \} \\ \quad -\beta _2 (v_{1,2}^n-v_{1,2}^{hk,n},\theta _2^n-\theta _2^{hk,n})_Y\\ \quad -\beta _2 (v_{2,1}^n-v_{2,1}^{hk,n},\theta _2^n-\theta _2^{hk,n})_Y\\ \,\; \le C\Big (\Vert \dot{\theta }_2^n-\delta \theta _2^n\Vert _Y^2+ \Vert \theta _2^n-z^h\Vert _V^2+\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2\\ \quad +\Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2+\Vert v_2^n-v_2^{hk,n}\Vert _Y^2\\ \quad +(\delta \theta _2^n-\delta \theta _2^{hk,n},\theta _2^n-z^h)_Y\Big ), \end{array} \\ \begin{array}{l} \displaystyle \frac{c_3}{2k}\Big \{ \Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2-\Vert \theta _3^{n-1}-\theta _3^{hk,n-1}\Vert _Y^2\Big \} \\ \quad -\beta _3 (v_{1,2}^n-v_{1,2}^{hk,n},\theta _3^n-\theta _3^{hk,n})_Y\\ \quad +\beta _3 (v_{2,1}^n-v_{2,1}^{hk,n},\theta _3^n-\theta _3^{hk,n})_Y\\ \,\; \le C\Big (\Vert \dot{\theta }_3^n-\delta \theta _3^n\Vert _Y^2+ \Vert \theta _3^n-m^h\Vert _V^2+\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2\\ \quad +\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2+\Vert v_2^n-v_2^{hk,n}\Vert _Y^2\\ \quad +(\delta \theta _3^n-\delta \theta _3^{hk,n},\theta _3^n-m^h)_Y\Big ),\\ \displaystyle \frac{c_4}{2k}\Big \{ \Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2-\Vert \theta _4^{n-1}-\theta _4^{hk,n-1}\Vert _Y^2\Big \} \\ \quad -\beta _4 (v_{1,1}^n-v_{1,1}^{hk,n},\theta _4^n-\theta _4^{hk,n})_Y\\ \quad +\beta _4 (v_{2,2}^n-v_{2,2}^{hk,n},\theta _4^n-\theta _4^{hk,n})_Y\\ \,\; \le C\Big (\Vert \dot{\theta }_4^n-\delta \theta _4^n\Vert _Y^2+ \Vert \theta _4^n-l^h\Vert _V^2+\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2\\ \quad +\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2+\Vert v_2^n-v_2^{hk,n}\Vert _Y^2\\ \quad +(\delta \theta _4^n-\delta \theta _4^{hk,n},\theta _4^n-l^h)_Y\Big ), \end{array} \end{aligned}$$

where \(\delta \theta _2^n=(\theta _2^n-\theta _2^{n-1})/k\), \(\delta \theta _3^n=(\theta _3^n-\theta _3^{n-1})/k\) and \(\delta \theta _4^n=(\theta _4^n-\theta _4^{n-1})/k\).

Combining all the estimates of the two components of the velocity, the two temperatures and the two mass diffusions, it follows that, for all \(w^h,r^h,s^h,z^h,m^h,l^h\in V^h\),

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\rho }{2k}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y^2-\Vert v_1^{n-1}-v_1^{hk,n-1}\Vert _Y^2\Big \}\\ \displaystyle +\frac{\mu }{2k}\Big \{ \Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2-\Vert \nabla (u_1^{n-1}-u_1^{hk,n-1})\Vert _H^2\Big \}\\ \displaystyle + \frac{\lambda +\mu }{2k}\Big \{ \Vert \hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n})\Vert _Y^2-\Vert \hbox { div\,}({\varvec{u}}^{n-1}-{\varvec{u}}^{hk,n-1})\Vert _Y^2\Big \} \\ \displaystyle +\frac{\mu }{2k}\Big \{ \Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2-\Vert \nabla (u_2^{n-1}-u_2^{hk,n-1})\Vert _H^2\Big \}\\ \displaystyle +\frac{\rho }{2k}\Big \{ \Vert v_2^n-v_2^{hk,n}\Vert _Y^2-\Vert v_2^{n-1}-v_2^{hk,n-1}\Vert _Y^2\Big \}\\ \displaystyle + \frac{c_1}{2k}\Big \{ \Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2-\Vert \theta _1^{n-1}-\theta _1^{hk,n-1}\Vert _Y^2\Big \} \\ \displaystyle +\frac{c_2}{2k}\Big \{ \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2-\Vert \theta _2^{n-1}-\theta _2^{hk,n-1}\Vert _Y^2\Big \} \\ \displaystyle +\frac{c_3}{2k}\Big \{ \Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2-\Vert \theta _3^{n-1}-\theta _3^{hk,n-1}\Vert _Y^2\Big \}\\ \displaystyle +\frac{c_4}{2k}\Big \{ \Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2-\Vert \theta _4^{n-1}-\theta _4^{hk,n-1}\Vert _Y^2\Big \}\\ \le C\Big (\Vert \dot{v}_1^n-\delta v_1^n\Vert _Y^2+\Vert \dot{u}_1^n-\delta u_1^n\Vert _V^2+\Vert v_1^n-w^h\Vert _V^2\\ +\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2 + \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2\\ +\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2+\Vert v_1^n-v_1^{hk,n}\Vert _Y^2 +\Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2\\ +\Vert \hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n})\Vert _Y^2+(\delta u_1^n-\delta u_1^{hk,n},u_1^n-w^h)\\ + \Vert \dot{v}_2^n-\delta v_2^n\Vert _Y^2+\Vert \dot{u}_2^n-\delta u_2^n\Vert _V^2+\Vert v_2^n-r^h\Vert _V^2\\ +\Vert v_2^n-v_2^{hk,n}\Vert _Y^2 +\Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2\\ +(\delta u_2^n-\delta u_2^{hk,n},u_2^n-r^h) +\Vert \dot{\theta }_1^n-\delta \theta _1^n\Vert _Y^2 \\ +(\delta \theta _1^n-\delta \theta _1^{hk,n},\theta _1^n-s^h)_Y+ \Vert \dot{\theta }_2^n-\delta \theta _2^n\Vert _Y^2\\ + \Vert \theta _2^n-z^h\Vert _V^2+(\delta \theta _2^n-\delta \theta _2^{hk,n},\theta _2^n-z^h)_Y\\ + \Vert \dot{\theta }_3^n-\delta \theta _3^n\Vert _Y^2+(\delta \theta _3^n-\delta \theta _3^{hk,n},\theta _3^n-m^h)_Y\\ +\Vert \dot{\theta }_4^n-\delta \theta _4^n\Vert _Y^2+(\delta \theta _4^n-\delta \theta _4^{hk,n},\theta _4^n-l^h)_Y\\ + \Vert \theta _1^n-s^h\Vert _V^2+ \Vert \theta _3^n-m^h\Vert _V^2+ \Vert \theta _4^n-l^h\Vert _V^2\Big ). \end{array} \end{aligned}$$

Multiplying the above estimates by k and summing up to n, we find that, for all \(\{w^{h,j}\}_{j=1}^n,\) \(\{r^{h,j}\}_{j=1}^n,\) \(\{s^{h,j}\}_{j=1}^n,\) \(\{z^{h,j}\}_{j=1}^n,\) \(\{m^{h,j}\}_{j=1}^n,\) \(\{l^{h,j}\}_{j=1}^n\subset V^h\)

$$\begin{aligned} \begin{array}{l} \displaystyle \Vert v_1^n-v_1^{hk,n}\Vert _Y^2+ \Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2+ \Vert \hbox { div\,}({\varvec{u}}^n-{\varvec{u}}^{hk,n})\Vert _Y^2\\ \displaystyle + \Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2 + \Vert v_2^n-v_2^{hk,n}\Vert _Y^2+ \Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2\\ \displaystyle + \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2+ \Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2 + \Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2\\ \displaystyle \le Ck\sum _{j=1}^n\Big (\Vert \dot{v}_1^j-\delta v_1^j\Vert _Y^2+\Vert \dot{u}_1^j-\delta u_1^j\Vert _V^2+\Vert v_1^j-w^{h,j}\Vert _V^2\\ +\Vert \theta _1^j-\theta _1^{hk,j}\Vert _Y^2 + \Vert \theta _2^j-\theta _2^{hk,j}\Vert _Y^2+\Vert \theta _3^j-\theta _3^{hk,j}\Vert _Y^2\\ +\Vert \theta _4^j-\theta _4^{hk,j}\Vert _Y^2+\Vert v_1^j-v_1^{hk,j}\Vert _Y^2 +\Vert \nabla (u_1^j-u_1^{hk,j})\Vert _H^2\\ +\Vert \hbox { div\,}({\varvec{u}}^j-{\varvec{u}}^{hk,j})\Vert _Y^2+(\delta v_1^j-\delta v_1^{hk,j},v_1^j-w^{h,j})\\ + \Vert \dot{v}_2^j-\delta v_2^j\Vert _Y^2+\Vert \dot{u}_2^j-\delta u_2^j\Vert _V^2+\Vert v_2^j-r^{h,j}\Vert _V^2\\ +\Vert v_2^j-v_2^{hk,j}\Vert _Y^2 +\Vert \nabla (u_2^j-u_2^{hk,j})\Vert _H^2+\Vert \dot{\theta }_1^j-\delta \theta _1^j\Vert _Y^2\\ +(\delta v_2^j-\delta v_2^{hk,j},v_2^j-r^{h,j}) + \Vert \theta _1^j-s^{h,j}\Vert _V^2 \\ +(\delta \theta _1^j-\delta \theta _1^{hk,j},\theta _1^j-s^{h,j})_Y + \Vert \dot{\theta }_2^j-\delta \theta _2^j\Vert _Y^2\\ + \Vert \theta _2^j-z^{h,j}\Vert _V^2+(\delta \theta _2^j-\delta \theta _2^{hk,j},\theta _2^j-z^{h,j})_Y\\ + \Vert \dot{\theta }_3^j-\delta \theta _3^j\Vert _Y^2+ \Vert \theta _3^j-m^{h,j}\Vert _V^2\\ +(\delta \theta _3^j-\delta \theta _3^{hk,j},\theta _3^j-m^{h,j})_Y +\Vert \dot{\theta }_4^j-\delta \theta _4^j\Vert _Y^2\\ + \Vert \theta _4^j-l^{h,j}\Vert _V^2+(\delta \theta _4^j-\delta \theta _4^{hk,j},\theta _4^j-l^{h,j})_Y\Big )\\ + C\Big ( \Vert v_1^0-v_1^{0h}\Vert _Y^2+ \Vert u_1^0-u_1^{0h}\Vert _V^2+ \Vert u_2^0-u_2^{0h}\Vert _V^2\\ + \Vert v_2^0-v_2^{0h}\Vert _Y^2 + \Vert \theta _1^0-\theta _1^{0h}\Vert _Y^2+ \Vert \theta _2^0-\theta _2^{0h}\Vert _Y^2\\ + \Vert \theta _3^0-\theta _3^{0h}\Vert _Y^2 + \Vert \theta _4^0-\theta _4^{0h}\Vert _Y^2 \Big ). \end{array} \end{aligned}$$

Finally, taking into account that

$$\begin{aligned} \begin{array}{l} \displaystyle k\sum _{j=1}^n (\delta v_1^j-\delta v_1^{hk,j},v_1^j-w^{h,j})\\ \quad = (v_1^n-v_1^{hk,n},v_1^n-w^{h,n})+(v_1^{0h}-v_1^0,v_1^1-w^{h,1})\\ \displaystyle \qquad + \sum _{j=1}^{n-1} (v_1^j-v_1^{hk,j},v_1^j-w^{h,j}-(v_1^{j+1}-w^{h,j+1})), \end{array} \end{aligned}$$

where similar estimates can be found for \(v_2\), \(\theta _1\), \(\theta _2\), \(\theta _3\) and \(\theta _4\), applying a discrete version of Gronwall’s inequality (see [2]) we obtain the following a priori error estimates result.

Theorem 4

Let the assumptions (7) still hold. If we denote by \((v_1,v_2,\theta _1,\theta _2,\theta _3,\theta _4)\) the solution to Problem (8–14) and by \(\{v_1^{hk,n},v_2^{hk,n},\theta _1^{hk,n},\theta _2^{hk,n},\theta _3^{hk,n},\theta _4^{hk,n}\}_{n=0}^N\) the solution to Problem (17–23), then we have the following a priori error estimates, for all \(\{w^{h,j}\}_{j=0}^N,\) \(\{r^{h,j}\}_{j=0}^N,\) \(\{w^{h,j}\}_{j=0}^N,\) \(\{z^{h,j}\}_{j=0}^N ,\) \(\{m^{h,j}\}_{j=0}^N,\) \(\{l^{h,j}\}_{j=0}^N\subset V^h\),

$$\begin{aligned}&\displaystyle \max _{0\le n\le N}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y^2+ \Vert \nabla (u_1^n-u_1^{hk,n})\Vert _H^2\\&\displaystyle + \Vert v_2^n-v_2^{hk,n}\Vert _Y^2 + \Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y^2+ \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y^2\\&+ \Vert \nabla (u_2^n-u_2^{hk,n})\Vert _H^2 + \Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y^2+ \Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y^2\Big \} \\& \displaystyle \le Ck\sum _{j=1}^N\Big ( \Vert \dot{v}_1^j-\delta v_1^j\Vert _Y^2+\Vert \dot{u}_1^j-\delta u_1^j\Vert _V^2\\&+\Vert v_1^j-w^{h,j}\Vert _V^2+ \Vert \dot{v}_2^j-\delta v_2^j\Vert _Y^2+\Vert \dot{u}_2^j-\delta u_2^j\Vert _V^2\\&+\Vert v_2^j-r^{h,j}\Vert _V^2 +\Vert \dot{\theta }_1^j-\delta \theta _1^j\Vert _Y^2+ \Vert \theta _1^j-s^{h,j}\Vert _V^2 \\&+ \Vert \dot{\theta }_2^j-\delta \theta _2^j\Vert _Y^2+ \Vert \theta _2^j-z^{h,j}\Vert _V^2+ \Vert \dot{\theta }_3^j-\delta \theta _3^j\Vert _Y^2\\&+ \Vert \theta _3^j-m^{h,j}\Vert _V^2 +\Vert \dot{\theta }_4^j-\delta \theta _4^j\Vert _Y^2+ \Vert \theta _4^j-l^{h,j}\Vert _V^2\Big )\\&+C\max _{0\le n\le N}\Big \{\Vert v_1^n-w^{h,n}\Vert ^2_Y+\Vert v_2^n-r^{h,n}\Vert ^2_Y\\&+\Vert \theta _1^n-s^{h,n}\Vert ^2_Y+\Vert \theta _2^n-z^{h,n}\Vert ^2_Y+\Vert \theta _3^n-m^{h,n}\Vert ^2_Y\\&+\Vert \theta _4^n-l^{h,n}\Vert ^2_Y\Big \}\\&+\frac{C}{k}\sum _{j=1}^{N-1}\Big [\Vert v_1^j-w^{h,j}-(v_1^{j+1}-w^{h,j+1})\Vert ^2_Y\\&+\Vert v_2^j-r^{h,j}-(v_2^{j+1}-r^{h,j+1})\Vert ^2_Y\\&+\Vert \theta _1^j-s^{h,j}-(\theta _1^{j+1}-s^{h,j+1})\Vert ^2_Y \\&+\Vert \theta _2^j-z^{h,j}-(\theta _2^{j+1}-z^{h,j+1})\Vert ^2_Y\\&+\Vert \theta _3^j-m^{h,j}-(\theta _3^{j+1}-m^{h,j+1})\Vert ^2_Y\\&+\Vert \theta _4^j-l^{h,j}-(\theta _4^{j+1}-l^{h,j+1})\Vert ^2_Y\Big ]\\&+ C\Big ( \Vert v_1^0-v_1^{0h}\Vert _Y^2+ \Vert u_1^0-u_1^{0h}\Vert _V^2+ \Vert u_2^0-u_2^{0h}\Vert _V^2 \\&+ \Vert v_2^0-v_2^{0h}\Vert _Y^2+ \Vert \theta _1^0-\theta _1^{0h}\Vert _Y^2+ \Vert \theta _2^0-\theta _2^{0h}\Vert _Y^2\\&+ \Vert \theta _3^0-\theta _3^{0h}\Vert _Y^2 + \Vert \theta _4^0-\theta _4^{0h}\Vert _Y^2 \Big ), \end{aligned}$$

where C is a positive constant which does not depend on parameters h and k.

It is worth noting that, from the above estimates we can derive the convergence order of the approximations provided by the fully discrete problem (17–23). For instance, under the additional regularity, for \(i=1,2\) and \(l=1,2,3,4\),

$$\begin{aligned} \begin{array}{l} u_i\in C^1([0,T];H^2(B)) \cap H^3(0,T;Y)\cap H^2(0,T;V),\\ \theta _l \in C([0,T];H^2(B))\cap H^1(0,T;V)\cap H^2(0,T;Y), \end{array} \end{aligned}$$

the algorithm is linearly convergent, that is, there exists a positive constant C, independent of the discretization operators h and k, such that

$$\begin{aligned} \begin{array}{l} \displaystyle \max _{0\le n\le N}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y+ \Vert u_1^n-u_1^{hk,n}\Vert _V+ \Vert u_2^n-u_2^{hk,n}\Vert _V\\ \quad \displaystyle + \Vert v_2^n-v_2^{hk,n}\Vert _Y + \Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y+ \Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y\\ \quad + \Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y+ \Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y\Big \}\le C(h+k). \end{array} \end{aligned}$$

5 Numerical results

In this final section, we present a numerical example to show the accuracy of the approximations and the dependence on the number of dissipation mechanisms.

The numerical scheme obtained in Problem \(VP^{hk}\) was implemented on a 3.2 GHz PC using MATLAB, and typical run (using parameters \(h=\sqrt{2}/8\) and \(k=0.01\)) took about 0.12 s of CPU time.

First, we will demonstrate the numerical convergence of the algorithm. As a simple example, in order to show the accuracy of the approximations, we consider the two-dimensional domain \(B=(0,1)\times (0,1)\) and we will divide it into \(2nd^2\) triangles.

We have employed the following data in these simulations:

$$\begin{aligned} \begin{array}{l} \rho =1, \quad \mu =1, \quad \lambda =3, \quad \kappa =2, \quad \beta _1=5,\quad \beta _2=1, \\ l_1=1, \quad \beta _3=2,\quad \beta _4=1, \quad l_3=2. \end{array} \end{aligned}$$

By using the following initial conditions, for all \((x,y)\in B=(0,1)\times (0,1)\),

$$\begin{aligned}&u_i^0(x,y)=v_i^0(x,y)=x(x-1)y(y-1)\quad \hbox {for }i=1,2,\\&{\theta _l^0(x,y)=x(x-1)y(y-1) \quad \hbox {for }l=1,2,3,4}, \end{aligned}$$

considering homogeneous Dirichlet boundary conditions in the boundaries and the (artificial) supply terms, for all \((x,y,t)\in B\times (0,1)\),

$$\begin{aligned} \begin{array}{l} F_1(x,y,t)=-e^t(2x(x - 1) + 10y(y - 1) \\ \qquad + 4(2x - 1)(2y - 1) + 2x(2y - 1)(x - 1) \\ \qquad + y(14x - 7)(y - 1) - (xy(x - 1)(y - 1))/2),\\ F_2(x,y,t)=-e^t(10x(x - 1) + 2y(y - 1) \\ \qquad + 4(2x - 1)(2y - 1) + 3x(2y - 1)(x - 1)\\ \qquad - (xy(x - 1)(y - 1))/2),\\ F_3(x,t)=-e^t(4x(x - 1) + 4y(y - 1) + 5x(2y - 1)(x - 1) \\ \qquad + 5y(2x - 1)(y - 1) - xy(x - 1)(y - 1)),\\ F_4(x,t)=-e^t(4x(x - 1) + 4y(y - 1) + x(2y - 1)(x - 1) \\ \qquad + y(2x - 1)(y - 1)- xy(x - 1)(y - 1)),\\ F_5(x,t)=-e^t(4x(x - 1) + 4y(y - 1) + x(2y - 1)(x - 1) \\ \qquad - y(2x - 1)(y - 1) - xy(x - 1)(y - 1)),\\ F_6(x,t)=-e^t(4x(x - 1) + 4y(y - 1) - 2x(2y - 1)(x - 1) \\ \qquad + 2y(2x - 1)(y - 1) - xy(x - 1)(y - 1)), \end{array} \end{aligned}$$

the exact solution to the above two-dimensional problem can be found and it has the form, for \((x,y,t)\in B\times [0,1]\):

$$\begin{aligned}&u_1(x,y,t)=u_2(x,y,t)=e^tx(x-1)y(y-1),\\&\theta _1(x,y,t)=\theta _2(x,y,t)=e^tx(x-1)y(y-1),\\&\theta _3(x,y,t)=\theta _4(x,y,t)=e^tx(x-1)y(y-1). \end{aligned}$$

Thus, the approximation errors estimated by

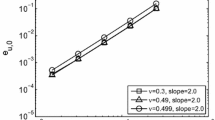
$$\begin{aligned} \begin{array}{l} \displaystyle \max _{0\le n\le N}\Big \{ \Vert v_1^n-v_1^{hk,n}\Vert _Y+\Vert u_1^n-u_1^{hk,n}\Vert _V+\Vert v_2^n-v_2^{hk,n}\Vert _Y\\ \qquad +\Vert u_2^n-u_2^{hk,n}\Vert _V+\Vert \theta _1^n-\theta _1^{hk,n}\Vert _Y +\Vert \theta _2^n-\theta _2^{hk,n}\Vert _Y\\ \qquad +\Vert \theta _3^n-\theta _3^{hk,n}\Vert _Y+\Vert \theta _4^n-\theta _4^{hk,n}\Vert _Y \Big \}\end{array} \end{aligned}$$

are shown in Table 1 (multiplied by 10) for some values of the discretization parameters h and k. Moreover, by using the diagonal of this table the evolution of the error depending on the parameter \(h+k\) is plotted in Fig. 1. As can be seen, the convergence of the algorithm is achieved, although the linear convergence obtained in the previous section under some additional regularity conditions, does not seem to be found.

Table 1 Numerical errors \((\times 10)\) for some values of h and k
Full size table
Fig. 1
figure 1

Asymptotic constant error

Full size image

Now, our aim is to compare the effect of the number of dissipation mechanisms in the evolution of the discrete energy. We assume now that there are not supply terms, and we use the final time \(T=10\), the following data (common for the four problems described later):

$$\begin{aligned} \rho =0.1, \quad \mu =1, \quad \lambda =3, \quad \kappa =2, \quad \beta _1=5, \end{aligned}$$

and the initial conditions, for all \((x,y)\in B\),

$$\begin{aligned} \begin{array}{l} u_i^0(x,y)=v_i^0(x,y)=x(x-1)y(y-1)\quad \hbox {for}\quad i=1,2,\\ {\theta _l^0(x,y)=x(x-1)y(y-1)\quad \hbox {for }l=1,2,3,4}. \end{array} \end{aligned}$$

We define the following four problems:

  • Problem 1 the problem with a unique dissipation mechanism. In this case, we only consider the temperature \(\theta _1\) and the data \(\beta _1=1\).

  • Problem 2 the problem with two dissipation mechanisms. Now, we consider the two temperatures \(\theta _1\) and \(\theta _2\) and the data \(\beta _1=\beta _2=l_1=1\).

  • Problem 3 the problem with three dissipation mechanisms. The case with the two temperatures \(\theta _1\) and \(\theta _2\), and one mass diffusion \(\theta _3\), where we use the data \(\beta _1=\beta _2=l_1=\beta _3=1\).

  • Problem 4 the problem studied in the previous section, which is solved with the data \(\beta _1=\beta _2=l_1=\beta _3=\beta _4=l_3=1\).

Taking the discretization parameter \(k=0.001\) and a very fine finite element mesh, the evolution in time of the discrete energy of the above four problems is plotted in Fig. 2 (in both natural and semi-log scales). As can be seen, every energy converges to zero and an exponential decay seems to be achieved in the four cases. Moreover, it is clear that, when the number of dissipation mechanisms increases, the energy decay seems to be faster.

Fig. 2
figure 2

Evolution in time of the discrete energy for different dissipation mechanisms (natural and semi-log scales)

Full size image

6 Conclusions

In this paper, we have analyzed a problem of elasticity with several dissipative mechanisms from the analytical and numerical points of view.

From the analytical point of view, we have seen that, if we assume that the coupling coefficients satisfy the symmetry \(A_{ij}^l=A_{ji}^l\), we only need three dissipative mechanisms (in dimension two) to guarantee the exponential energy decay; however, to know if three mechanisms are sufficient when this symmetry does not hold is an open question yet.

From the numerical point of view, we have provided a fully discrete approximation of a weak form of the above thermomechanical problem, and we have proved a main a priori error estimates result. In a numerical example, we have also shown the discrete energy decay of the solutions and we have seen that, when the number of dissipative mechanisms increases, the rate of the decay of the solutions also increases.