Dynamics and phase coordination of multi-module vibration-driven locomotion robots with linear or nonlinear connections

Abstract

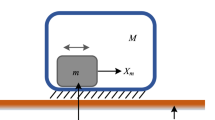
Earthworm-like locomotion robots have great potential for applications in areas such as pipeline inspection and disaster rescue. The vibration-driven mechanism, due to its simplicity in design and ease of miniaturization, is promising to be employed in earthworm-like robot development. Note that the coordination of actuation and the connection between adjacent robot modules play an important role in determining locomotion performance. In this paper, without applying any prerequisite and aiming at improving locomotion performance, we investigate the coordination of the actuation phases in a multi-module vibration-driven robot with linear or nonlinear connections, thereby advancing the current state of the art. Specifically, the optimal phase-difference coordination pattern corresponding to the maximal average steady-state velocity is sought via the particle swarm optimization algorithm. For an n-module vibration-driven robot with linear connections and working around the resonant frequencies, we discover that the optimal phase differences between adjacent modules can be determined based on their relative position relationship in the corresponding mode shape. For an n-module vibration-driven locomotion robot with nonlinear connections, the identical-phase-difference pattern is preferred in implementation because it not only reduces the number of independent phase-difference variables to one, but also achieves an average steady-state velocity very close to the maximum. Moreover, dynamic analysis shows that the bent frequency–response curve caused by the cubic nonlinearity can substantially improve the maximum average steady-state velocity level of the robot while acquiring the unique merits of multiple locomotion modes and broadband characteristics. The findings of this paper would provide useful guidelines for the design and control of earthworm-like vibration-driven robots.

Appendices

Appendix 1

1.1 The PSO algorithm used in this research

In this research, the PSO algorithm is selected to solve the optimization problem. The PSO is a metaheuristic with the following unique merits: PSO requires few or no assumptions about the problem being optimized; PSO can search a very large space of candidate solutions; PSO does not use the gradient of the problem being optimized (i.e., the optimization problem is not required to be differentiable). As a result, PSO is well suited for the optimization problem given in Eq. (17) with the following characteristics: the n-module system possesses discontinuous characteristics originating from the anisotropic resistance forces, the space of the high-dimensional candidate solution ($\Delta \varphi_{i(i + 1)} \, (i = 1,2,...,n - 1)$) is vast, and no prerequisite assumption is applied on $\Delta \varphi_{i(i + 1)} \, (i = 1,2,...,n - 1)$.

Figure 10 shows the flow chart of the PSO algorithm. Let $S$ be the number of particles in the swarm, each particle is described by its position ${{\varvec{\upmu}}}_{j}^{k}$ and its velocity ${\mathbf{v}}_{j}^{k}$ in the k-th iteration. The velocity term ${\mathbf{v}}_{j}^{k}$ is updated based on the best-know position (${\mathbf{p}}_{{{\mathbf{b}}j}}$) of the particle and the best-know position of the entire swarm (${\mathbf{p}}_{{\mathbf{g}}}$), i.e.,

$${\mathbf{v}}_{j}^{k} = w{\mathbf{v}}_{j}^{k - 1} + c_{1} r_{1} ({\mathbf{p}}_{{{\mathbf{b}}j}} - {{\varvec{\upmu}}}_{j}^{k - 1} ) + c_{2} r_{2} ({\mathbf{p}}_{{\mathbf{g}}} - {{\varvec{\upmu}}}_{j}^{k - 1} ),$$

(20)

where $w$ is the inertial weight, $c_{1}$ and $c_{2}$ are the cognitive coefficient and social coefficient, respectively, $r_{1}$ and $r_{2}$ are the random numbers between 0 and 1. To avoid getting trapped in a local optimum, the inertia weight $w$ is set to be linearly decreasing, i.e.,

$$w = w_{1} - (w_{1} - w_{2} ) \cdot \left( \frac{k}{G} \right),$$

(21)

where $w_{1}$ and $w_{2}$ are constants, and $G$ is the preset number of iterations. The particle position is updated by

$${{\varvec{\upmu}}}_{j}^{k} = {{\varvec{\upmu}}}_{j}^{k - 1} + {\mathbf{v}}_{j}^{k - 1} .$$

(22)

Two parameters are modified to ensure the convergence of the optimal solution. First, the number of particles $S$ is set as a dimension-dependent variable, i.e., $S$ is 100 times the dimension, so that a small number of particles are used when the number of dimensions is low to improve the efficiency; the number of particles will be increased as the number of dimensions increases, thus ensuring that the optimal solution of the problem can be obtained with guaranteed computational performance. Second, to avoid getting trapped in a local optimum, the inertia weight $w$ is defined as a decreasing function of the number of iterations $k$. This agrees with the findings of Xin et al. [67] that the use of dynamic inertia weight could improve convergence, and Wang et al. [68] that the use of large inertia weights at the beginning is beneficial for the algorithm to conduct a global search, and smaller weights are conducive to the algorithm to perform a local search as the number of iterations increases to find the global optimal value.

The maximum number of iterations $G$ is set as 100, which has been demonstrated to be sufficient to reach the optimal solution. The cognition of the particle $c_{1}$ and the social influence of the swarm $c_{2}$ represent the weights of the acceleration terms that pull each particle toward the best know position for that particle $j$ (${\mathbf{p}}_{bj}$) and the swarm as a whole (${\mathbf{p}}_{{\text{g}}}$), respectively. Marini and Jordehi et al. [69, 70] have pointed out that large values of $c_{1}$ and $c_{2}$ may increase the oscillations of particles near the optimum, while small values of $c_{1}$ and $c_{2}$ may cause the particles to move too slowly, greatly increasing the computational effort and preventing the algorithm from converging. In many cases, $c_{1} = c_{2} = 2$ allow the algorithm to search in the region centered on ${\mathbf{p}}_{{\text{g}}}$ and ${\mathbf{p}}_{bj}$ to ensure that the global optimum can be found [68].

In [71] and [72], the Lyapunov stability analysis and the von Neumann stability criterion have been used for demonstrating the stability of PSO, which provides us with the basis for selecting the PSO parameters.

As an example, based on parameters $\Omega = 2.14$, $n = 3$, $\hat{k}^{*} = 15000{\text{ (N/m}}^{{3}} )$, Fig. 11 displays the convergence process of the three-module vibration-driven locomotion robot connected by nonlinear springs in 100 iterations. The result indicates that the optimum solution can be reached within 20 iterations. Moreover, with different sets of randomly distributed particles, the optimization is carried out for 10 times, and the results are listed in Table 8, including the average values and the standard deviations of the phase-difference values and the maximum average steady-state velocity. It shows that the optimal phase-difference values and the corresponding maximum average steady-state velocities are very concentrated over the 10 optimization attempts, thus verifying the stability of the PSO algorithm.

Appendix 2

2.1 Optimization results of the 10-module system with Coulomb’s dry friction

For the 10-module vibration-driven locomotion robot subject to Coulomb’s dry friction, the maximum average steady-state velocity $\overline{V}_{{\text{s - max}}}$ obtained by the PSO algorithm and the average steady-state velocity $\overline{V}_{{\text{s - rule}}}$ determined via the general rules are listed in Table 9.

Appendix 3

3.1 Verification of the conclusion obtained in section 4

To verify the validity of the conclusions obtained in Sect. 4, a different set of system parameters is selected ($m^{*} = 0.05{\text{kg}}$, $M^{*} = 0.8{\text{kg}}$, $k^{*} = 200{\text{N/m}}$, and $\hat{k}^{*} = 30000{\text{ N/m}}^{{3}}$), and the three patterns of phase differences are examined. For $n = 3$, the dimensionless frequency $\Omega$ is swept between 0.7 and 2.5, with a step of 0.04; for $n = 4$ and 5, $\Omega$ is swept between 0.5 and 2.7, with a step of 0.04. The relative displacement between modules 1 and 2 (denoted by $\hat{x}_{12}$) and the average steady-state velocity $\overline{V}_{{\text{s}}}$ are examined in detail, and their evolution with respect to the actuation frequency $\Omega$ is shown in Fig. 12, 13, and 14 for $n = 3$, 4, and 5, respectively. For comparison purposes, $\hat{x}_{12}$ and $\overline{V}_{{\text{s}}}$ of the corresponding linear system (Eq. 9) are also plotted. In addition, the optimal phase differences $\Delta \varphi_{i(i + 1)} (i = 1,{ 2, } \ldots , \, n - 1)$ corresponding to $\overline{V}_{{\text{s - max}}}$ are listed in Table 10.

Figures 12, 13, 14, as well as Table 10 together, indicate that the results obtained in Sect. 4 are valid despite the different parameters of the system. First, the IPD pattern can still be considered optimal, which gives rise to a very high level of the average steady-state velocity with the peak that is almost identical to the global optimum. Second, the characteristics and merits brought by the introduced nonlinearity are again observed, including the improvement of the global maximum average steady-state velocity, the expansion of frequency bandwidth with high locomotion performance, and the potential to achieve multi-mode locomotion.