On the structure of isothermal acoustic shocks under classical and artificial viscosity laws: selected case studies*

Abstract

Assuming Newton’s law of cooling, the propagation and structure of isothermal acoustic shocks are studied under four different viscosity laws. Employing both analytical and numerical methods, 1D traveling wave solutions for the velocity and density fields are derived and analyzed. For each viscosity law considered, expressions for both the shock thickness and the asymmetry metric are determined. And, to ensure that isothermal flow is achievable, upper bounds on the associated Mach number values are derived/computed using the isothermal version of the energy equation.

1 Introduction

In a celebrated paper published in 1845, Stokes [1] appears to have been the first to consider the impact of shear viscosity on the 1D propagation of linear acoustic waves in gases. Six years later, Stokes [2] went on to examine the propagation of linear, time-harmonic, acoustic plane waves in a gas whose only loss mechanism is its ability to radiate heat to its surroundings, the process of which he modeled using Newton’s law of cooling; see Appendix A. In 1910, Rayleigh [3, pp. 270–271] presented a partial analysis of the isothermal¹ propagation of an infinite (1D) “wave of condensation” in a constant viscosity, but thermally non-conducting, gas, the process of radiation being invoked to maintain the flow’s isothermal nature. Later, Truesdell [5, p. 687], in 1953, generalized Stokes’ [2] radiant propagation model to include the effects of both viscosity and thermal conduction; see also Hunt’s [6] 1955 contribution, wherein is formulated a nonlinear theory of thermoviscous compressible flow with thermal radiation. In 2004, LeVeque [7], seeking to model the collision of dust clouds composed of “sticky particles” and surrounded by vacuum, investigated the propagation of 1D “delta shocks” in lossless perfect gases under the isothermal assumption. Because he did not consider the energy equation, however, LeVeque’s analysis, like Rayleigh’s [3, pp. 270–271], must be considered as only partially complete.

The primary aim of the present study is to not only complete, but also extend Rayleigh’s analysis, wherein only the equation of motion (EoM) for the specific volume was derived and integrated, by considering the effects of various viscosity laws on the propagation and structure of dispersed shocks, i.e., those of nonzero “thickness” (or “width”), in the setting of the isothermal piston problem. Specifically, we determine and analyze 1D traveling wave solutions (TWS)s, under the assumption that the temperature of the gas in question is held constant, based on the following four viscosity laws: (i) constant shear viscosity (i.e., the case considered in Ref. [3, pp. 270–271]), (ii) shear viscosity proportional to mass density, (iii) von Neumann–Richtmyer artificial viscosity, and (iv) Evans–Harlow–Longley artificial viscosity. These particular laws were selected primarily because all lead to model systems that are amenable to study by analytical means.

To provide a mechanism for achieving isothermal propagation, we, like Rayleigh, invoke the process of radiation, which like Stokes [2] we model via Newton’s law of cooling. To ensure that isothermal conditions are not only mathematically but also physically possible, under each of the four cases considered, we also determine, based on the full form of the isothermal energy equation, the upper bound on the range of (piston) Mach number values corresponding to each case.

In the next section, we begin our investigation with a review of the thermodynamics of perfect gases and the formulation of our governing system of equations. Before doing so, however, we first present a brief review of applications involving isothermal compressible flow phenomena.

Perhaps the best known example of isothermal flow involves a piston-cylinder-gas arrangement in which the period of the piston’s reciprocating motion is so long that the gas is always able to maintain thermal equilibrium with its surroundings; see Refs. [2] and [8, p. 26]. In contrast, the propagation in inviscid gases of linear acoustic plane waves of sufficiently high frequency is, provided certain conditions (e.g., $r=0$; see Sect. 2.2) are satisfied, essentially isothermal [9, § 1-10]. In general, as noted by Delany [10, p. 204], “Only in the neighbourhood of a heat-conducting boundary (as, for instance, when dealing with a sound field within a cavity or with porous absorbents) does propagation depart progressively from adiabatic to isothermal as the sound frequency is decreased.” With regard to the transition from adiabatic to isothermal propagation at low frequencies, Jensen [11] emphasizes how this is related to the smallness of the device in question because “the thermal boundary layer stretches over the full device and is important in, for example, condenser microphones . . .”; see also Fletcher’s [12] analysis of this transition in small (e.g., capillary) tubes, where we note that the (low) frequency range over which the isothermal assumption holds is defined by Ref. [12, Eq. (16)] with the inequality sign reversed.

And, along with the rather ordinary applications just described, it should be noted that the isothermal approximation also arises when modeling certain astrophysical phenomena; recall Refs. [4, 7]; see also Ref. [13].

2 Formulation of mathematical model

2.1 Thermodynamical aspects of perfect gases

As defined by Thompson [14], a perfect gas is one in which $p(>0)$, the thermodynamic pressure, $\rho (>0)$, the mass density, and $\vartheta (> 0)$, the absolute temperature, obey the following special case of the ideal gas law [14, § 2.5]:

$$\begin{aligned} p =c_{\textrm{v}} (\gamma -1)\rho \vartheta \qquad (c_{\textrm{p}}, c_{\text {v}} := \text {const.}). \end{aligned}$$

(1)

Here, $c_{\textrm{p}}> c_{\textrm{v}} > 0$ are the specific heats at constant pressure and constant volume, respectively, and $\gamma =c_{\textrm{p}}/c_{\text {v}}$, where $\gamma \in (1,5/3]$ in the case of perfect gases. Furthermore, a zero (“0”) subscript attached to a field variable identifies the uniform equilibrium state value of that variable; i.e., in the present investigation, the gas is assumed to be homogeneous when in its equilibrium state.

With regard to the perfect gas assumption we note that the equilibrium state values of the adiabatic and isothermal sound speeds in the gas are given by

$$\begin{aligned} c_{0}=\sqrt{c_{\textrm{p}} (\gamma -1)\vartheta _{0}} \end{aligned}$$

(2)

and

$$\begin{aligned} b_{0}= c_{0}\gamma ^{-1/2}=\sqrt{c_{\text {v}}(\gamma - 1)\vartheta _{0}}, \end{aligned}$$

(3)

respectively, where we observe that $b_{0}\in (0, c_{0})$. That is, $c_{0}$ and $b_{0}$ are, respectively, the speeds of infinitesimal-amplitude acoustic signals under the adiabatic and isothermal assumptions; see, e.g., Ref. [15, § 278], wherein $b_{0}$ is referred to as the “Newtonian velocity of sound”.

In this study we will also make use of the thermodynamic axiom known as the Gibbs relation [14, p. 58], which in the case of a perfect gas can be written as

$$\begin{aligned} \vartheta \,\text {d}\eta = \text {d}E - c_{\textrm{v}} (\gamma -1)\vartheta \rho ^{-1}\text {d}\rho \qquad (\text {perfect gases}), \end{aligned}$$

(4)

where $\eta$ is the specific entropy and E is the specific internal energy. Here, we note for later reference the relations

$$\begin{aligned} E = c_{\textrm{v}}\vartheta =H/\gamma \qquad (\text {perfect gases}), \end{aligned}$$

(5)

where H is the specific enthalpy.

2.2 Navier–Stokes–Fourier system in 1D

For the 1D flow of a perfect gas along the x-axis of a Cartesian coordinate system, the Navier–Stokes–Fourier (NSF) system [9, p. 513] can, assuming the absence of all body forces, be written in the following form:

$$\begin{aligned} \frac{\partial \rho }{\partial t}+u\frac{\partial \rho }{\partial x} + \rho \frac{\partial u}{\partial x}&=0, \end{aligned}$$

(6a)

$$\begin{aligned} \rho \left( \frac{\partial u}{\partial t}+ u\frac{\partial u}{\partial x}\right) + \rho c_{\textrm{p}}\frac{\partial \vartheta }{\partial x}&= \rho \vartheta \frac{\partial \eta }{\partial x} \nonumber \\&\!\!\!\!+ \frac{\partial }{\partial x}\!\left( \mu {\upsilon }\frac{\partial u}{\partial x}\right),\end{aligned}$$

(6b)

$$\begin{aligned} \rho \vartheta \left( \frac{\partial \eta }{\partial t} +u\frac{\partial \eta }{\partial x} \right) - \varPhi&=\rho r - \frac{\partial q}{\partial x},\end{aligned}$$

(6c)

$$\begin{aligned} q&=-K\frac{\partial \vartheta }{\partial x},\end{aligned}$$

(6d)

$$\begin{aligned} c_{\textrm{v}}\ln (\vartheta /\vartheta _0) -c_{\textrm{v}}(\gamma -1)\ln (\rho /\rho _0)&=\eta -\eta _{0}, \end{aligned}$$

(6e)

where $p=p(x,t)$, $\rho = \rho (x,t)$, $\vartheta = \vartheta (x,t)$, and $\eta =\eta (x,t)$ under this flow geometry. In Sys. (6), $\textbf{u}=(u(x,t),0,0)$ and $\textbf{q}=(q(x,t),0,0)$ are, respectively, the velocity and heat flux vectors; $\mu (> 0)$ is the shear viscosity; ${\upsilon }= \tfrac{4}{3} +\mu _{\textrm{b}}/\mu$ is the viscosity number, where $\mu _{\textrm{b}}(\ge 0)$ is the bulk viscosity; $K(>0)$ is the thermal conductivity; r, which carries units of W/kg, represents the external rate of supply of heat per unit mass; $\varPhi$, the dissipation function [9, 14], here takes the form

$$\begin{aligned} \varPhi = \mu {\upsilon }\left( \partial u/\partial x\right) ^{2}; \end{aligned}$$

(7)

and Eq. (6e) follows from integrating Eq. (4) after substituting in E from Eq. (5).

In what follows we consider the compressive version of the classic (1D) piston problem. That is, the piston, whose face we take to be thermally insulated, is located at $x=-\infty$ and moving to the right with constant speed $u_{\textrm{p}}(> 0)$ while the gas at $x=+\infty$ is in its equilibrium state. In this regard, considering the piston’s motion is strictly compressive, and assuming the field variables are free of perturbation(s)², it follows that $u \in [0, u_{\textrm{p}}]$ and $\partial u/\partial x \le 0$ will always hold under the assumed flow geometry.

Additionally, we will invoke the assumption

$$\begin{aligned} \mu _{\textrm{b}} = 0, \end{aligned}$$

(8)

which of course is Stokes’ hypothesis [9, 14]. Here, we stress that Eq. (8), which in the case of air, e.g., is only an approximation [14, Table 1.1], will not be a limitation on our analysis. This is because our numerical results will focus exclusively on the (monatomic) gas Ar—one for which Eq. (8) has been shown, by both theory and experiment, to hold exactly; see, e.g., Refs. [16, 17].

Remark 1

The pressure gradient term that would normally have appeared in Eq. (6b) was eliminated using the relevant 1D special case of the thermodynamic relation [14, p. 71]

$$\begin{aligned} \rho ^{-1}\nabla p = \nabla H - \vartheta \nabla \eta , \end{aligned}$$

(9)

i.e., our momentum equation is expressed in “Friedmann form”.

2.3 Isothermal piston problem

Assuming hereafter that the flow is isothermal, i.e., $\vartheta \equiv \vartheta _{0}$, we find that Eq. (1) (i.e., our EoS) and the constitutive relations given in Eqs. (6d) and (6e) reduce, respectively, to

$$\begin{aligned} p = b_{0}^{2} \rho = p_{0}\rho /\rho _{0}, \end{aligned}$$

(10)

which is simply Boyle’s law [3];

$$\begin{aligned} q=0, \end{aligned}$$

(11)

since $\partial \vartheta _{0}/\partial x =0$; and

$$\begin{aligned} \eta -\eta _{0} =-c_{\text {v}}(\gamma - 1)\ln (\rho /\rho _{0}), \end{aligned}$$

(12)

which is the isothermal special case of Eq. (6e).

On carrying out these substitutions, followed by the use of Eqs. (6a), (7), and (8), Sys. (6) is reduced to

$$\begin{aligned} \frac{\partial \rho }{\partial t}+u\frac{\partial \rho }{\partial x} + \rho \frac{\partial u}{\partial x}&=0, \end{aligned}$$

(13a)

$$\begin{aligned} \rho \left( \frac{\partial u}{\partial t}+ u\frac{\partial u}{\partial x}\right) + b_{0}^{2} \frac{\partial \rho }{\partial x} - \frac{4}{3}\frac{\partial }{\partial x}\!\left( \mu \frac{\partial u}{\partial x}\right)&=0,\end{aligned}$$

(13b)

$$\begin{aligned} \vartheta _{0}+\frac{b_{0}^{2}}{c_{\textrm{v}} \varkappa _{0}}\frac{\partial u}{\partial x} - \frac{(4/3)}{c_{\textrm{v}} \varkappa _{0}} \left( \frac{\mu }{\rho }\right) \!\left( \frac{\partial u}{\partial x}\right) ^{2}&= \vartheta _{\textrm{e}}, \end{aligned}$$

(13c)

where our adoption of Stokes’ hypothesis yields ${\upsilon }= 4/3$. In Eq. (13c), we have taken r to be given by the isothermal special case of Newton’s law of cooling, viz.,

$$\begin{aligned} r=- c_{\textrm{v}} \varkappa _{0} (\vartheta _{0} - \vartheta _{\textrm{e}}), \end{aligned}$$

(14)

where $\vartheta _{\textrm{e}}=\vartheta _{\textrm{e}}(x,t)$ is the temperature of the surrounding environment and $\varkappa _{0} (> 0)$, the “velocity of cooling” [2, p. 307], carries units of 1/s; see also Refs. [5, pp. 651, 687] and [6, p. 1023]. [Note that Sys. (13) is the 1D version of the special case of Hunt’s [6] system corresponding to isothermal propagation in a monatomic perfect gas.]

Under Sys. (13), $\vartheta _{\textrm{e}}$ is an additional dependent variable that is controllable by the experimenter based on “output” from Eq. (13c). That is, under the isothermal assumption, the role of our energy equation has changed; indeed, it has ceased to serve as the evolution equation for the temperature field and is now a control function. This of course is necessary because the gas must be able to radiate away the resulting heat of its compression, at a rate that cannot be assumed constant, if our assumption of isothermal flow is to be everywhere satisfied³. (Note that the ability of the gas to conduct heat plays no role under the isothermal assumption.) In this regard, we have adopted the assumptions stated by Rayleigh [8, p. 28] regarding the physical and thermal characteristics of the enclosing cylinder.

2.4 Viscosity laws: classical and artificial

In this subsection we give the precise statement of the four viscosity laws mentioned in Sect. 1. Note that the first two stem from classical continuum theory while the latter two are of the artificial type.

• (i) Constant shear viscosity:

  $$\begin{aligned} \mu =\mu _{0}; \end{aligned}$$

  (15)

  recall this is the case considered in Ref. [3, pp. 270–271]; it is also the exact form of $\mu$ for the current (i.e., isothermal) problem under the kinetic theory of gases.

• (ii) Shear viscosity proportional to mass density:

  $$\begin{aligned} \mu =\nu _{0} \rho ; \end{aligned}$$

  (16)

  see Refs. [16, § 12.11] and [18].

• (iii) von Neumann–Richtmyer⁴ (vNR) artificial viscosity:

  $$\begin{aligned} \mu = -{\mathfrak {b}}_{\textrm{iii}}^{2} \lambda _{0}^{2} \rho \left( \frac{\partial u}{\partial x}\right); \end{aligned}$$

  (17)

  see Refs. [20] and [21, § V-D-1].

• (iv) Evans–Harlow–Longley (EHL) artificial viscosity:

  $$\begin{aligned} \mu = \tfrac{1}{2}{\mathfrak {b}}_{\textrm{iv}} \lambda _{0} \rho u; \end{aligned}$$

  (18)

  see Refs. [21, § V-D-2], [22, p. 16], and [23, p. 11].

Here, $\mu _{0}$ and $\nu _{0}=\mu _{0}/\rho _{0}$ represent, respectively, the (constant) equilibrium state values of the shear and kinematic viscosity coefficients; in the case of hard-sphere molecules we have, according to the kinetic theory of gases [14, § 2.7],

$$\begin{aligned} \mu _{0}=\tfrac{5}{32}\pi \rho _{0}{\bar{c}}_{0}\lambda _{0}, \end{aligned}$$

(19)

an expression which also follows on setting “$\delta$” in Ref. [24, Eq. (9b)] equal to $5\pi /32 \approx 0.491$; we let $\lambda _{0}(>0)$ denote the equilibrium state value of the molecular mean-free-path (see, e.g., Refs. [24, p. 680] and [14, pp. 95–97]); the equilibrium state value of the mean molecular speed is given by [14, p. 108]

$$\begin{aligned} {\bar{c}}_{0}=c_{0}\sqrt{8/(\gamma \pi )} = b_{0}\sqrt{8/\pi }; \end{aligned}$$

(20)

and ${\mathfrak {b}}_{\textrm{iii}}(>0)$ and ${\mathfrak {b}}_{\textrm{iv}}(>0)$ are adjustable dimensionless parameters [21, § V-D-1].

Lastly, since our investigation is to be carried out primarily by analytical methodologies, and we seek an approach that would allow us to compare/contrast these four cases in a consistent manner, we have taken $\varDelta x = \lambda _{0}$, where $\varDelta x$ is the spatial mesh increment used in the usual statements of both the vNR and EHL laws. And with regard to $\lambda _{0}$ we record here, for later reference, the following result from kinetic theory:

$$\begin{aligned} \lambda _{0} =\frac{16\nu _{0}}{b_{0}\sqrt{50\pi }}, \end{aligned}$$

(21)

which is easily obtained after eliminating ${\bar{c}}_{0}$ between Eqs. (19) and (20), and we note that $16/\sqrt{50\pi } \approx 1.277$.

3 Traveling wave reduction

3.1 Ansatzs and wave variable

Invoking the traveling wave assumption, we set

$$\begin{aligned} u(x,t) =f(\zeta ), \quad \rho (x,t)=g(\zeta ), \quad \vartheta _{\textrm{e}}(x,t)=\varTheta _{\textrm{e}}(\zeta ), \end{aligned}$$

(22)

where $\zeta := x - vt$ is the wave (i.e., similarity) variable, and where the parameter $v(>0)$ will be seen to represent the speed of the resulting shocks. On substituting the above ansatzs into Sys. (13), the latter is reduced to the following system of ODEs:

$$\begin{aligned}{} & {} \frac{\text {d}}{\text {d}\zeta } \left( -vg + fg\right) = 0, \end{aligned}$$

(23a)

$$\begin{aligned}{} & {} g(-v+f)f^{\prime } +b_{0}^{2}g^{\prime }-\frac{4}{3}\frac{\text {d}}{\text {d}\zeta }\left( \mu f^{\prime }\right) = 0, \end{aligned}$$

(23b)

$$\begin{aligned}{} & {} \vartheta _{0}+\left( \frac{b_{0}^{2}}{c_{\textrm{v}} \varkappa _{0}}\right) f^{\prime } - \frac{(4/3)}{c_{\textrm{v}} \varkappa _{0}} \left( \frac{\mu }{g}\right) \!\left( f^{\prime }\right) ^{2} = \varTheta _{\textrm{e}}, \end{aligned}$$

(23c)

where a prime denotes $\text {d}/\text {d}\zeta$.

This system is to be integrated subject to the asymptotic conditions

$$\begin{aligned}&f \rightarrow u_{\textrm{p}}, \quad f^{\prime } \rightarrow 0 \qquad (\zeta \rightarrow -\infty ),\nonumber \\&\quad g \rightarrow \rho _{0}, \quad f, f^{\prime } \rightarrow 0 \qquad (\zeta \rightarrow +\infty ), \end{aligned}$$

(24)

which of course correspond to a shock moving to the right; recall that $v >0$.

3.2 Shock speed and associated ODE

Using the fact that Eq. (23a) integrates to

$$\begin{aligned} g = \frac{\rho _{0} v}{v - f}, \end{aligned}$$

(25)

allows us to, in turn, integrate Eq. (23b):

$$\begin{aligned} -\rho _{0} vf +b_{0}^{2}g- (4\mu /3) f^{\prime } = b_{0}^{2}\rho _{0}, \end{aligned}$$

(26)

where the resulting constants of integration were found to be ${\mathcal {K}}_{1}=-\rho _{0}v$ and ${\mathcal {K}}_{2}=\rho _{0}b_{0}^{2}$, respectively. Now eliminating g between the former and latter equations yields

$$\begin{aligned} (4\mu /3)(v - f) f^{\prime }=\rho _{0}[(b_{0}^{2}-v^{2})f+vf^2], \end{aligned}$$

(27)

i.e., a Riccati type equation. Employing the asymptotic conditions once again leads us to consider

$$\begin{aligned} v^{2} -b_{0}^{2}=u_{\textrm{p}}v, \end{aligned}$$

(28)

a quadratic whose only positive root is

$$\begin{aligned} v=\frac{u_{\textrm{p}} +\sqrt{u_{\textrm{p}}^2+4b_{0}^{2}}}{2} = \tfrac{1}{2}u_{\textrm{p}}\left( 1+\sqrt{1+4 \text {Ma}^{-2}}\,\right), \end{aligned}$$

(29)

where $\text {Ma} = u_{\textrm{p}}/b_{0}$ is the piston Mach number.

With these results in-hand, we can reduce Sys. (23) to the two-equation system

$$\begin{aligned}{} & {} (4\mu /3)(v - f) f^{\prime }+\rho _{0}vu_{\textrm{p}}(1 - f/u_{\textrm{p}})f =0, \end{aligned}$$

(30a)

$$\begin{aligned}{} & {} \vartheta _{0}-\left( \frac{b_{0}^{2}}{c_{\textrm{v}} \varkappa _{0}}\right) |f^{\prime }| - \frac{(4\mu /3)}{c_{\textrm{v}} \varkappa _{0}} \left( \frac{v - f}{\rho _{0} v}\right) \left| f^{\prime }\right| ^{2} = \varTheta _{\textrm{e}}. \end{aligned}$$

(30b)

Eq. (30a) is the associated ODE of our traveling wave analysis; in the next four sections, we shall integrate it, under each of the aforementioned cases of $\mu$, subject to the wave-front condition $f(0)=\tfrac{1}{2}u_{\textrm{p}}$.

3.3 Definitions of shock thicknesses, Q-metric, and jump amplitude

Employing the notation

$$\begin{aligned} f(\pm \infty ):=\lim _{\zeta \rightarrow \pm \infty }f(\zeta ), \qquad g(\pm \infty ):=\lim _{\zeta \rightarrow \pm \infty }g(\zeta ), \end{aligned}$$

(31)

we define the thickness (or width) of the shock exhibited by the velocity profile as

$$\begin{aligned} \ell _{j} :=\frac{f(-\infty ) - f(+\infty )}{\max \big | f^{\prime }(\zeta )\,\big |}= \frac{u_{\textrm{p}}}{|f^{\prime }(\zeta _{j}^{\bullet })|}, \end{aligned}$$

(32)

a definition which Morduchow and Libby [24, p. 680] attribute to Prandtl, and that exhibited by the density profile as

$$\begin{aligned}&l_{j} :=\frac{g(-\infty ) - g(+\infty )}{\max \big | g^{\prime }(\zeta )\,\big |}\nonumber \\&\quad = \left( \frac{2}{-1+\sqrt{1+4 \text {Ma}^{-2}}}\right) \frac{\rho _{0}}{|g^{\prime }(\zeta _{j}^{*})|}. \end{aligned}$$

(33)

Here, $\zeta =\zeta _{j}^{\bullet }$ and $\zeta =\zeta _{j}^{*}$ denote the relevant critical points of $f^{\prime }$ and $g^{\prime }$, respectively, i.e., $f^{\prime \prime }(\zeta _{j}^{\bullet })=0$ and $g^{\prime \prime }(\zeta _{j}^{*})=0$; the subscript j represents the number [i.e., (i)–(iv)] of the case under consideration; and with regard to Eq. (33) we note the following:

$$\begin{aligned} g^{\prime }(\zeta ) = \frac{\rho _{0} vf^{\prime }}{(v - f)^{2}}= - \frac{3\rho _{0}^{2} v^{2}(u_{\textrm{p}}-f)f}{4\mu (v - f)^{3}} \end{aligned}$$

(34)

and

$$\begin{aligned} g(-\infty )&=\frac{\rho _{0}v}{v-u_{\textrm{p}}} = \rho _{0}\left( \frac{1+\sqrt{1+4 \text {Ma}^{-2}}}{-1+\sqrt{1+4 \text {Ma}^{-2}}}\right) \nonumber \\&> g(+\infty ) = \rho _{0}. \end{aligned}$$

(35)

We also define the Q- (or asymmetry) metric

$$\begin{aligned} Q(\text {Ma})=\frac{\int _{-\infty }^{0}[1-R(\zeta )]\,\text {d}\zeta }{\int _{0}^{+\infty } R(\zeta )\,\text {d}\zeta }, \end{aligned}$$

(36)

where

$$\begin{aligned} R(\zeta ) =\frac{g(\zeta )-\rho _{0}}{g(-\infty )-\rho _{0}} \implies \lim _{\zeta \rightarrow \mp \infty }R(\zeta )=1,0, \end{aligned}$$

(37)

respectively. As Schmidt [25, p. 369]⁵ points out, not only is Q a “sensitive measure of asymmetry”, but it also complements the shock thickness as a characterizing metric since the latter “fails to give sufficiently detailed information about [shock] structure; . . .” [25, p. 361]. In Sect. 8.3 (below), we use Q to quantify the degree of asymmetry exhibited by each of the four g vs. $\zeta$ profiles studied below.

And lastly, we define, following Morro [26] and Straughan [27], the amplitude of the jump in a function ${\mathfrak {F}}={\mathfrak {F}}(\zeta )$ across the plane $\zeta =\zeta _{\textrm{d}}$ as

$$\begin{aligned}{}[\![{\mathfrak {F}}]\!]\Big |_{\zeta _{\textrm{d}}} =\lim _{\zeta \rightarrow \zeta _{\textrm{d}}^-} {\mathfrak {F}}(\zeta ) - \lim _{\zeta \rightarrow \zeta _{\textrm{d}}^+} {\mathfrak {F}}(\zeta ), \end{aligned}$$

(38)

where it is assumed that both limits exist and that they are different. Here, we call attention to the fact that $[\![{\mathfrak {F}}]\!]$ is positive (resp. negative) when the jump in ${\mathfrak {F}}$ is from higher (resp. lower) to lower (resp. higher) values.

4 Constant shear viscosity case

Recall that under Case (i), $\mu =\mu _{0}$; consequently, Eq. (30a) becomes

$$\begin{aligned} (4\nu _{0}/3)(v - f) f^{\prime }+ vu_{\textrm{p}}(1 - f/u_{\textrm{p}})f =0, \end{aligned}$$

(39)

which on setting ${\mathcal {F}}(\zeta ) = -1+(2/u_{\textrm{p}})f(\zeta )$ is reduced to

$$\begin{aligned} (k + {\mathcal {F}}) {\mathcal {F}}^{\prime } = \frac{3v}{4\nu _{0}}(1 - {\mathcal {F}}^{2}). \end{aligned}$$

(40)

This ODE, like the former, is a particularly simple special case of Abel’s equation [28, p. 74]; as such, it is easily integrated and yields the exact, but generally implicit⁶, TWS:

$$\begin{aligned}&\left( \frac{3v}{4\nu _{0}}\right) \zeta \nonumber \\&\quad = k \tanh ^{-1}({\mathcal {F}})-\frac{1}{2}\ln (1-{\mathcal {F}}^{2}) \qquad ( |{\mathcal {F}}| <1). \end{aligned}$$

(41)

Here, the constant of integration is zero, by way of the fact that $f(0)=u_{\textrm{p}}/2$ implies ${\mathcal {F}}(0) =0$; we have set

$$\begin{aligned} k = 1 - 2v/u_{\textrm{p}} = -\sqrt{1+4 \text {Ma}^{-2}}\,; \end{aligned}$$

(42)

and we note for later reference (in Appendix B) that Eq. (41) can also be expressed as

$$\begin{aligned}&\left( \frac{3v}{2\nu _{0}}\right) \zeta =(k-1)\ln (1+{\mathcal {F}}) \nonumber \\&\quad - (k+1)\ln (1-{\mathcal {F}}) \qquad ( |{\mathcal {F}}| <1). \end{aligned}$$

(43)

Because $k <-1$, the integral curves described by Eq. (41) can only take the form of fully dispersed shocks, also referred to by some as kinks; see, e.g., Ref. [29, § 5.2.2]. For this velocity traveling wave profile, therefore, we can show that the shock thickness is given by

$$\begin{aligned} \ell _{\textrm{i}}=\frac{8(\nu _{0}/b_{0})\text {Ma}}{3\!\left( \text {Ma}+\sqrt{4+\text {Ma}^{2}}\,\right) \left( - 2 +\sqrt{4+\text {Ma}^{2}}\,\right) }, \end{aligned}$$

(44)

to which corresponds the critical point

$$\begin{aligned} \zeta _{\textrm{i}}^{\bullet }&=-\left( \frac{4\nu _{0}}{3v}\right) \Bigg [\sqrt{1+4\text {Ma}^{-2}}\nonumber \\&\times \tanh ^{-1}\left( \frac{-2+\sqrt{4+\text {Ma}^{2}}}{\text {Ma}}\,\right) \nonumber \\&+\frac{1}{2}\ln \left( \frac{-8+4\sqrt{4+\text {Ma}^{2}}}{\text {Ma}^{2}}\,\right) \Bigg ]; \end{aligned}$$

(45)

here, we observe that

$$\begin{aligned} {\mathcal {F}}(\zeta _{\textrm{i}}^{\bullet })= {\mathcal {F}}_{\textrm{i}}^{\bullet } :=|k|-\sqrt{k^{2} - 1}=|k|-2/\text {Ma}, \end{aligned}$$

(46)

which when related back to f yields

$$\begin{aligned} f(\zeta _{\textrm{i}}^{\bullet }) = f_{\textrm{i}}^{\bullet } := \tfrac{1}{2}u_{\textrm{p}}\left( 1+|k|-2/\text {Ma}\right) . \end{aligned}$$

(47)

In order to determine $l_{\textrm{i}}$, we must first determine the (only) positive root of $\varPi (Y)=0$, where

$$\begin{aligned} \varPi (Y)=Y^{2} + 2|k|Y - 3. \end{aligned}$$

(48)

This quadratic arises when we attempt to solve $g^{\prime \prime }(\zeta ) =0$ after expressing it in terms of ${\mathcal {F}}$ and simplifying, i.e., when seeking the solution of

$$\begin{aligned}{}[3(1 - {\mathcal {F}}^{2}) +2{\mathcal {F}}(k + {\mathcal {F}})]{\mathcal {F}}^{\prime }=0, \end{aligned}$$

(49)

which we do subject to the constraint $|{\mathcal {F}}|\in (0,1)$. Denoting the aforementioned root by $Y={\mathcal {F}}_{\textrm{i}}^{*}$, it is not difficult to establish that

$$\begin{aligned} {\mathcal {F}}(\zeta _{\textrm{i}}^{*})={\mathcal {F}}_{\textrm{i}}^{*} := - |k| +\sqrt{k^{2} + 3}\,, \end{aligned}$$

(50)

which when related back to f yields

$$\begin{aligned} f(\zeta _{\textrm{i}}^{*}) = f_{\textrm{i}}^{*} := \tfrac{1}{2}u_{\textrm{p}}\left( 1- |k| +\sqrt{k^{2} + 3}\,\right), \end{aligned}$$

(51)

where the critical point of the corresponding $g^{\prime }$ vs. $\zeta$ profile is given by

$$\begin{aligned} \zeta _{\textrm{i}}^{*} = \left[ \frac{8\nu _{0}}{3u_{\textrm{p}}(|k|+1)}\right] \! \left\{ k \tanh ^{-1}({\mathcal {F}}_{\textrm{i}}^{*})-\tfrac{1}{2}\ln \left[ 1-({\mathcal {F}}_{\textrm{i}}^{*})^{2}\right] \right\} \!. \end{aligned}$$

(52)

With Eq. (50) in hand and observing that, under Case (i), Eq. (34) becomes

$$\begin{aligned} g^{\prime }(\zeta ) = -\frac{3\rho _{0} v^2(u_{\textrm{p}}f-f^2)}{4\nu _{0}(v - f)^{3}} =\left( \frac{3v^{2}\rho _{0}}{2u_{\textrm{p}}\nu _{0}}\right) \!\frac{(1 - {\mathcal {F}}^{2})}{(k + {\mathcal {F}})^{3}}, \end{aligned}$$

(53)

the density profile is seen to admit the shock thickness

$$\begin{aligned} l_{\textrm{i}}= \frac{16(\nu _{0}/b_{0})}{3\text {Ma}(|k|-1)(|k|+1)^2} \left\{ \frac{|k + {\mathcal {F}}_{\textrm{i}}^{*}|^{3}}{1-({\mathcal {F}}_{\textrm{i}}^{*})^{2}}\right\}. \end{aligned}$$

(54)

Remark 2

Small-$|\zeta |$ and large-$|\zeta |$ approximations to ${\mathcal {F}}$ can easily be determined from the corresponding expressions for “${\mathcal {U}}$” given in Ref. [29, Remark 9], wherein “$\xi$” plays the role of $\zeta$. Mention should also be made of the explicit, but approximate, result [29, Remark 10]

$$\begin{aligned} f(\zeta ) \approx \tfrac{1}{2}u_{\textrm{p}}\left[ 1-\tanh \left( 2\zeta /{\hat{\ell }}_{\textrm{i}} \right) \right] \qquad (\text {Ma} \ll 1), \end{aligned}$$

(55)

for which the shock thickness is ${\hat{\ell }}_{\textrm{i}}= 16\nu _{0}/(3b_{0}\text {Ma})$, and we note that $\text {Ma} \ll 1$ implies $|k|\gg 1$.

5 The case $\mu \propto \rho$

Under Case (ii), $\mu =\nu _{0}\times \,$ Eq. (25); as such, Eq. (30a) is reduced to the following Bernoulli-type equation:

$$\begin{aligned} (4\nu _{0}/3) f^{\prime }+ u_{\textrm{p}}(1 - f/u_{\textrm{p}})f =0, \end{aligned}$$

(56)

which is easily integrated and yields the exact (Taylor shock) TWS

$$\begin{aligned} f(\zeta )=\frac{u_{\textrm{p}}}{1+\exp \left( 4\zeta /\ell _{\textrm{ii}}\right) }, \end{aligned}$$

(57)

where the shock thickness for this case of f is given by

$$\begin{aligned} \ell _{\textrm{ii}}=\frac{16(\nu _{0}/b_{0})}{3\,\text {Ma}} \qquad \qquad \qquad (\zeta _{\textrm{ii}}^{\bullet }=0). \end{aligned}$$

(58)

With the aid of Eq. (57), the density profile for this case is found to be

$$\begin{aligned} g(\zeta )&= \rho _{0}\left( 1+\sqrt{1+4 \text {Ma}^{-2}}\,\right) \nonumber \\&\times \!\left[ 1+\sqrt{1+4 \text {Ma}^{-2}}-\frac{2}{1+\exp \left( 4\zeta /\ell _{\textrm{ii}}\right) }\right] ^{-1}\!; \end{aligned}$$

(59)

and this profile admits the shock thickness

$$\begin{aligned} l_{\textrm{ii}}=\ell _{\textrm{ii}}, \end{aligned}$$

(60)

with corresponding critical point

$$\begin{aligned} \zeta _{\textrm{ii}}^{*} =\left( \frac{\ell _{\textrm{ii}}}{4}\right) \ln \left( \frac{-1+\sqrt{1+4 \text {Ma}^{-2}}\,}{1+\sqrt{1+4 \text {Ma}^{-2}}}\,\right). \end{aligned}$$

(61)

From the latter it is readily established that $\zeta _{\textrm{ii}}^{*} < 0$, which follows from the fact that $\text {Ma} >0$, and, moreover, that

$$\begin{aligned} \zeta _{\textrm{ii}}^{*} \approx -\left( \frac{\ell _{\textrm{ii}}\text {Ma}}{4}\right) \left( 1-\frac{\text {Ma}^{2}}{24} \right) \qquad (\text {Ma} \ll 1), \end{aligned}$$

(62)

which follows from the Taylor expansion of the $\ln$-term about $\text {Ma} = 0$.

6 von Neumann–Richtmyer artificial viscosity

Under this formulation [i.e., Case (iii)], $\mu$ is given by Eq. (17); Eq. (30a), therefore, becomes

$$\begin{aligned} \left( \frac{4{\mathfrak {b}}_{\textrm{iii}}^{2}\lambda _{0}^{2}}{3}\right) (f^{\prime })^{2} - u_{\textrm{p}}(1 - f/u_{\textrm{p}})f =0, \end{aligned}$$

(63)

or the equivalent

$$\begin{aligned} \frac{\text {d}f}{\text {d}\zeta } = \mp \left( \frac{\sqrt{3}}{2{\mathfrak {b}}_{\textrm{iii}}\lambda _{0}}\right) \! \sqrt{f \left( u_{\textrm{p}}- f \right) }\,. \end{aligned}$$

(64)

A phase plane analysis of Eq. (64) reveals that its equilibrium solutions ${\bar{f}}=\{0, u_{\textrm{p}}\}$ are rendered (one-sided) stable and (one-sided) unstable, respectively, and thus consistent with the compressive version of the piston problem, only when the “−” sign case is selected. Regardless of the sign selected, however, it should be noted that uniqueness is not assured because the right-hand side of Eq. (64) does not satisfy a Lipschitz condition [28, § 4.3] at either of the equilibria; i.e., the tangents to the phase portrait at ${\bar{f}}=\{0, u_{\textrm{p}}\}$ are vertical lines.

On rejecting the “$+$” sign case, it is a straightforward matter to integrate Eq. (64) (see, e.g., Refs. [18, 20]) and show that the velocity TWS under the vNR case is given by the following semi-compact⁷, composite integral curve:

$$\begin{aligned} f(\zeta )={\left\{ \begin{array}{ll} u_{\textrm{p}}, &{} \zeta \le - \tfrac{\pi }{4}\ell _{\textrm{iii}},\\ \displaystyle {\tfrac{u_{\textrm{p}}}{2}\left[ 1-\sin (2\zeta /\ell _{\textrm{iii}})\right] ,} &{} -\tfrac{\pi }{4}\ell _{\textrm{iii}}< \zeta < \tfrac{\pi }{4}\ell _{\textrm{iii}},\\ 0, &{} \zeta \ge \tfrac{\pi }{4}\ell _{\textrm{iii}}, \end{array}\right. } \end{aligned}$$

(65)

the shock thickness of which is [recall Eq. (32)]

$$\begin{aligned} \ell _{\textrm{iii}}= \frac{4\lambda _{0}{\mathfrak {b}}_{\textrm{iii}}}{\sqrt{3}} \qquad \qquad (\zeta _{\textrm{iii}}^{\bullet }=0). \end{aligned}$$

(66)

We also find, on substituting Eq. (65) into Eq. (26) and making use of Eq. (29), that the density TWS for this case is given by

$$\begin{aligned} g(\zeta )&= \rho _{0}\nonumber \\&\times \!{\left\{ \begin{array}{ll} \frac{1+\sqrt{1+4 \text {Ma}^{-2}}}{-1+\sqrt{1+4 \text {Ma}^{-2}}}, &{} \zeta \le - \tfrac{\pi }{4}\ell _{\textrm{iii}},\\ \frac{1+\sqrt{1+4\text {Ma}^{-2}}}{\sin (2\zeta /\ell _{\textrm{iii}}) + \sqrt{1+4\text {Ma}^{-2}}}, &{} -\tfrac{\pi }{4}\ell _{\textrm{iii}}< \zeta < \tfrac{\pi }{4}\ell _{\textrm{iii}},\\ 1, &{} \zeta \ge \tfrac{\pi }{4}\ell _{\textrm{iii}}, \end{array}\right. } \end{aligned}$$

(67)

to which corresponds the (density) shock thickness [recall Eq. (33)]

$$\begin{aligned} l_{\textrm{iii}}&=\ell _{\textrm{iii}}\!\left( \frac{\text {Ma}}{4\sqrt{2}}\right) \nonumber \\&\times \!\left[ \frac{20+9\text {Ma}^{2}-3\sqrt{(4+\text {Ma}^{2})(4+9\text {Ma}^{2})}}{\sqrt{-4-3\text {Ma}^{2}+\sqrt{(4+\text {Ma}^{2})(4+9\text {Ma}^{2})}}}\right]. \end{aligned}$$

(68)

The critical point corresponding to $l_{\textrm{iii}}$ is given by

$$\begin{aligned} \zeta _{\textrm{iii}}^{*} = \tfrac{1}{2}\ell _{\textrm{iii}}\,\sin ^{-1} \!\left( \!\frac{ \sqrt{1+4\text {Ma}^{-2}}-\sqrt{9+4\text {Ma}^{-2}}}{2}\,\right), \end{aligned}$$

(69)

which we note can also be expressed as

$$\begin{aligned} \zeta _{\textrm{iii}}^{*}&=-\tfrac{1}{2}\ell _{\textrm{iii}}\nonumber \\&\times\cos ^{-1} \!\left( \!\sqrt{\frac{-3-4\text {Ma}^{-2}+\sqrt{16\text {Ma}^{-4}+40\text {Ma}^{-2}+9}}{2}}\,\right), \end{aligned}$$

(70)

where we observe that $-\tfrac{\pi }{4}\ell _{\textrm{iii}}< \zeta _{\textrm{iii}}^{*} < 0$.

Remark 3

The f vs. $\zeta$ profile admits a pair of weak discontinuities⁸, both of second order; i.e., the $f^{\prime \prime }$ vs. $\zeta$ profile exhibits two jumps, the amplitudes and locations of which are:

$$\begin{aligned}{}[\![f^{\prime \prime }\,]\!]\Big |_{-\tfrac{\pi }{4}\ell _{\textrm{iii}}} = \quad [\![f^{\prime \prime }\,]\!]\Big |_{+ \tfrac{\pi }{4}\ell _{\textrm{iii}}} = \quad 2u_{\textrm{p}}/\ell _{\textrm{iii}}^{2}. \end{aligned}$$

(71)

Likewise, the present g vs. $\zeta$ profile also exhibits (two) weak discontinuities of order two; in the case of these jumps we have

$$\begin{aligned}&[\![g^{\prime \prime }\,]\!]\Big |_{\mp \tfrac{\pi }{4}\ell _{\textrm{iii}}} = \frac{4\rho _{0}\left( 1+\sqrt{1+4 \text {Ma}^{-2}}\right) }{\ell _{\textrm{iii}}^{2}\left( 1-\sqrt{1+4 \text {Ma}^{-2}}\right) ^{2}}, \nonumber \\&\quad \frac{4\rho _{0}}{\ell _{\textrm{iii}}^{2}\left( 1+\sqrt{1+4 \text {Ma}^{-2}}\right) }, \end{aligned}$$

(72)

respectively.

Remark 4

The composite nature of the TWS under this case and the associated discontinuities signals the fact that the nonlinearity exhibited by the vNR law has turned the normally parabolic momentum equation into one that exhibits a distinctive degeneracy. Specifically, while the vNR-based momentum equation exhibits a parabolic character within the shock transition layer, where $|\partial u/\partial x |$ is close/equal to its maximum value, it assumes the character of the Euler (i.e., lossless) momentum equation outside this layer, i.e., as $\partial u/\partial x \rightarrow 0$; see, e.g., Refs. [20, § III] and [21, V-D-1].

7 Evans–Harlow–Longley artificial viscosity

Under this formulation [i.e., Case (iv)], for which $\mu$ is given by Eq. (18), Eq. (30a) reduces to

$$\begin{aligned} f\left[ \left( \frac{2{\mathfrak {b}}_{\textrm{iv}}\lambda _{0}}{3}\right) f^{\prime } + u_{\textrm{p}}(1 - f/u_{\textrm{p}})\right] =0. \end{aligned}$$

(73)

Performing a phase plane inspection of this ODE, after expressing it in standard form, reveals that its phase portrait exhibits a removable-type discontinuity at $f=0$ while the equilibrium solution ${\bar{f}}=u_{\textrm{p}}$ is unstable. Nevertheless, the integration of Eq. (73) is not difficult; omitting the details, we find that

$$\begin{aligned} f(\zeta ) = {\left\{ \begin{array}{ll} u_{\textrm{p}}\left[ 1-(1/2)\exp (\zeta /\ell _{\textrm{iv}})\right] \!, &{} \zeta < \ell _{\textrm{iv}}\ln (2),\\ 0, &{} \zeta \ge \ell _{\textrm{iv}}\ln (2),\\ \end{array}\right. } \end{aligned}$$

(74)

which like its Case (iii) counterpart is a semi-compact, composite integral curve of its “parent” ODE. The shock thickness of this profile is given by

$$\begin{aligned} \ell _{\textrm{iv}} =(2/3)\lambda _{0}{\mathfrak {b}}_{\textrm{iv}}, \end{aligned}$$

(75)

which we computed by evaluating the limit⁹

$$\begin{aligned} \lim _{\zeta \rightarrow (\zeta _{\textrm{iv}}^{\bullet })^{-}}\frac{u_{\textrm{p}}}{|f^{\prime }(\zeta )|} \quad \qquad \qquad (\zeta _{\textrm{iv}}^{\bullet } =\ell _{\textrm{iv}}\ln 2). \end{aligned}$$

(76)

Similarly, we have for the density profile

$$\begin{aligned} g(\zeta )=\rho _{0}{\left\{ \begin{array}{ll} \frac{1+\sqrt{1+4 \text {Ma}^{-2}}}{\exp (\zeta /\ell _{\textrm{iv}})-1+\sqrt{1+4 \text {Ma}^{-2}}}, &{} \zeta < \ell _{\textrm{iv}}\ln (2),\\ 1, &{} \zeta \ge \ell _{\textrm{iv}}\ln (2),\\ \end{array}\right. } \end{aligned}$$

(77)

which admits the shock thickness

$$\begin{aligned} l_{\textrm{iv}}= \frac{8\ell _{\textrm{iv}}}{1+\sqrt{1+4 \text {Ma}^{-2}}} = \frac{16{\mathfrak {b}}_{\textrm{iv}}\lambda _{0}}{3\left( 1+\sqrt{1+4 \text {Ma}^{-2}}\right) }, \end{aligned}$$

(78)

with

$$\begin{aligned} \zeta _{\textrm{iv}}^{*}=\ell _{\textrm{iv}}\ln \left( -1+\sqrt{1+4 \text {Ma}^{-2}}\,\right). \end{aligned}$$

(79)

Remark 5

With regard to the present TWS, the removable discontinuity noted above manifests itself as an acoustic acceleration wave¹⁰; in other words, the $f^{\prime }$ vs. $\zeta$ profile under this case suffers a jump discontinuity, the amplitude and location of which are:

$$\begin{aligned}{}[\![f^{\prime }\,]\!]\Big |_{\ell _{\textrm{iv}}\ln (2)} = - u_{\textrm{p}}/\ell _{\textrm{iv}}. \end{aligned}$$

(80)

From Eq. (77) it is clear that the g vs. $\zeta$ profile also exhibits an acceleration wave, whose amplitude and location are

$$\begin{aligned}{}[\![g^{\prime }\,]\!]\Big |_{\ell _{\textrm{iv}}\ln (2)} = \frac{-2(\rho _{0}/\ell _{\textrm{iv}})\text {Ma}}{\text {Ma}+\sqrt{4+\text {Ma}^{2}}}. \end{aligned}$$

(81)

Remark 6

The composite nature of the TWS under this case and the associated discontinuity stem from the fact that the nonlinearity exhibited by the EHL law has turned the normally parabolic momentum equation into one that is degenerate parabolic-hyperbolic; see, e.g., Ref. [32], wherein the present degeneracy corresponds to $p=2$. That is, while the EHL-based momentum equation is strictly parabolic for $u > 0$, it is degenerate on the level set $\{u=0\}$, where we have employed the terminology of Chen and Perthame [32], who state that: “Even though the nonlinear equation is parabolic, the solutions exhibit a certain hyperbolic feature, which results from the degeneracy.” The “feature” referred to by these authors, as they go on to note, is that: “The supports of these solutions propagate at finite speeds . . .”

8 Numerical results

8.1 Parameter values: Ar

In the case of Ar at $\vartheta _{0} = 300\,\text {K}$ and $p_{0}=50\,\text {mTorr}$, the gas/conditions on/under which Alsmeyer’s [34] shock experiments were performed, we have the following:

$$\begin{aligned} \rho _{0}&= 0.00010676\,\text {kg/}\hbox {m}^{3},\quad \mu _{0}=2.2656\times 10^{-5}\,\text {Pa}\cdot\hbox {s},\nonumber \\ c_{0}&= 322.59\,\text {m/s}, \quad \end{aligned}$$

(82)

from which we find that

$$\begin{aligned} b_{0}\approx 249.88\,\text {m/s}, \quad \nu _{0}\approx 0.212\,\hbox {m}^{2}\text {/s}, \quad \lambda _{0}\approx 1.084\,\text {mm}. \end{aligned}$$

(83)

We have also used the result $\gamma =5/3$, which according to kinetic theory holds not only for Ar, but also for all monatomic gases [14, 16, 17]. The values of $\rho _{0}$, $\mu _{0}$, and $c_{0}$ were obtained from the NIST Chemistry WebBook, SRD 69 (see: https://webbook.nist.gov/chemistry/form-ser/); those of $b_{0}$, $\nu _{0}$, and $\lambda _{0}$, in contrast, were computed using Eq. (3), the defining relation $\nu _{0}=\mu _{0}/\rho _{0}$, and Eq. (21), respectively.

And so as to achieve

$$\begin{aligned} \ell _{\textrm{iii}}=\ell _{\textrm{iv}}=3\lambda _{0}, \end{aligned}$$

(84)

which follows from Roache’s¹¹ recommendation after recalling our assumption $\varDelta x =\lambda _{0}$, we henceforth take ${\mathfrak {b}}_{\textrm{iii}}=\tfrac{1}{4}\sqrt{27}\,$ and ${\mathfrak {b}}_{\textrm{iv}}= 9/2$.

8.2 Shock thickness results

Figure 1 has been generated in accordance with Ref. [34, Fig. 2], which displays data for non-isothermal shock propagation in Ar. In doing so, we have introduced the dimensionless reciprocal shock thickness parameter, viz.,

$$\begin{aligned} \delta _{j}=\lambda _{0}\left( l_{j}\Big |_{\text {Ma}=(M_{\textrm{s}}^{2}-1)/M_{\textrm{s}}}\right) ^{-1} \qquad (\text {j = i, ii, iii, iv}), \end{aligned}$$

(85)

and the shock Mach number $M_{\textrm{s}} = v/b_{0}$, where we observe that $M_{\textrm{s}} > 1$.

Figure 1 reveals that, of the four curves we have plotted, only the one corresponding to Case (ii) exhibits qualitative agreement with Ref. [34, Fig. 2]. The quantitative disagreement, however, between this curve and the data in Ref. [34, Fig. 2], i.e., the fact that the former predicts a smaller shock thickness than the latter, is not unexpected. This is because under the isothermal assumption, K is absent from the NSF system [recall Sys. (13)]; i.e., the dissipation associated with the gas’s ability to conduct heat, which tends to increase the shock’s thickness, does not occur in isothermal propagation.

Fig. 1

$\delta _{j}$ vs. $M_{\textrm{s}}$, based on Ref. [34, Fig. 2], for the gas Ar. Blue: Case (i). Orange: Case (ii). Green: Case (iii). Lavender: Case (iv)

8.3 Determination of Q-metric values

In Table 1, values of Q based on the parameter values given above for Ar are presented. While those for Cases (ii)–(iv), as well as the $M_{\textrm{s}}=\sqrt{2}$ case of Case (i) (see Appendix B), were computed using expressions obtained from evaluating the integrals in Eq. (36) analytically, the entries corresponding to the remaining $M_{\textrm{s}}$ values under Case (i) were computed from the numerical solution of Eq. (39), the process of which involved both the NDSolve $\texttt {[}\,\cdot \,\texttt {]}$ and NIntegrate$\texttt {[}\,\cdot \,\texttt {]}$ commands provided in Mathematica.

Table 1 Values of Q in Ar corresponding to Cases (i)–(iv) for selected Mach number values

From Table 1 it is clear that, in all cases shown, Q is a strictly increasing function of the shock Mach number; i.e., profile asymmetry increases with $M_{\textrm{s}}$. This behavior, we observe, is in agreement with the data presented in Refs. [25, 34] for non-isothermal shock propagation in Ar. It is also clear from Table 1 that Cases (i)–(iii) all yield values of Q that are quite close to unity (i.e., quite close to being perfectly symmetric), and to each other, for $\text {Ma} = 0.01$. In this regard, we point out that $\text {Ma} \ll 1$ defines the “realm” of finite-amplitude (or weakly-nonlinear) acoustics theory, within which velocity traveling wave profiles can be expected to have the form of Eqs. (55) and (57); see, e.g., Refs. [29, 35], as well as those cited therein.

Finally, the last three entries in the first row of Table 1 highlight the following noteworthy feature associated with Case (i):

$$\begin{aligned} \int _{-\infty }^{0}[1-R(\zeta )]\,\text {d}\zeta = M_{\textrm{s}}^{2}\int _{0}^{+\infty } R(\zeta )\,\text {d}\zeta , \end{aligned}$$

(86)

for $M_{\textrm{s}}=\sqrt{2}, \sqrt{3}, 2$. Interestingly, as shown in Appendix B, these values are three of the five shock Mach number values for which Case (i) yields explicit TWSs.

8.4 Determination of $\text {Ma}_{\textrm{sup}}$ values

Because of the thermodynamic requirement $\varTheta _{\textrm{e}} >0$, the terms in Eq. (30b) must satisfy the inequality

$$\begin{aligned} c_{\textrm{v}} \varkappa _{0}\vartheta _{0} > \left\{ b_{0}^{2}|f^{\prime }| + \left[ \frac{4\mu (v - f)}{3\rho _{0} v}\right] \left| f^{\prime }\right| ^{2}\right\} . \end{aligned}$$

(87)

Ensuring that this restriction is everywhere satisfied begins with determining the $\zeta _{j}^{\textrm{e}}$, where

$$\begin{aligned} \varTheta _{\textrm{e}}^{\prime }(\zeta _{j}^{\textrm{e}}) =0\qquad (j=\,\text {i, ii, iii, iv}). \end{aligned}$$

(88)

With the $\zeta _{j}^{\textrm{e}}$ in hand, the next step is to determine the value of $\text {Ma}_{\textrm{sup}}$, where the subscript “sup” denotes supremum, for each of our four cases; doing this requires us to seek the smallest (positive) value of $\text {Ma}_{\textrm{sup}}$ that satisfies the equation $\varPi _{j}(\text {Ma}_{\textrm{sup}})= 0$, where we have set

$$\begin{aligned} \varPi _{j}(\text {Ma}_{\textrm{sup}}) := T_{\textrm{e}}(\zeta _{j}^{\textrm{e}})\Big |_{\text {Ma} := \text {Ma}_{\textrm{sup}}} \quad (j=\,\text {i, ii, iii, iv}), \end{aligned}$$

(89)

and where $T_{\textrm{e}}(\zeta )$ is the dimensionless version of $\varTheta _{\textrm{e}}(\zeta )$ most appropriate to the case under consideration. The importance of $\text {Ma}_{\textrm{sup}}$ follows from the fact that taking $\text {Ma} \ge \text {Ma}_{\textrm{sup}}$ means that isothermal propagation is not possible because the speed of the piston (i.e., $u_{\textrm{p}}$) is too great relative to $b_{0}$; in other words, taking $\text {Ma} \ge \text {Ma}_{\textrm{sup}}$ requires $\varTheta _{\textrm{e}} \le 0$, which is impossible from the standpoint of classical thermodynamics.

The values of $\text {Ma}_{\textrm{sup}}$ presented below were computed using the parameter values for Ar (see Sect. 8.1) and are based, in part, on what we term the radiative Mach number $M_{\textrm{r}}$, where we define this (dimensionless) parameter as $M_{\textrm{r}} := b_{0}^{-1}\sqrt{\varkappa _{0}\nu _{0}}$. Here, we observe that, since the gas under consideration is always the same (i.e., Ar), and the value of $\theta _{0}$ is fixed, varying $M_{\textrm{r}}$ corresponds to varying $\varkappa _{0}$.

8.4.1 Case (i)

With the aid of Eq. (39), this case of Eq. (88) can be expressed in the more explicit form

$$\begin{aligned} \left\{ \frac{\text {d}}{\text {d}\zeta }\left[ \frac{{\mathfrak {f}}(1-{\mathfrak {f}})}{v/u_{\textrm{p}} - {\mathfrak {f}}}+ \frac{\text {Ma}^{2}{\mathfrak {f}}^2(1 - {\mathfrak {f}})^2}{v/u_{\textrm{p}} - {\mathfrak {f}}}\right] \right\} \Bigg |_{\zeta = \zeta _{\textrm{i}}^{\textrm{e}}} = 0, \end{aligned}$$

(90)

where we have set ${\mathfrak {f}}(\zeta ) = f(\zeta )/u_{\textrm{p}}$. Apart from being able to show that

$$\begin{aligned} {\mathfrak {f}}(\zeta _{\textrm{i}}^{\textrm{e}})=\frac{1}{6}\left( 3+2\sqrt{1+\text {Ma}^{-2}} - \sqrt{1+4\text {Ma}^{-2}}\right), \end{aligned}$$

(91)

where we observe that $1/2< {\mathfrak {f}}(\zeta _{\textrm{i}}^{\textrm{e}}) <2/3$ for $\text {Ma}>0$, this case, unfortunately, does not readily lend itself to treatment by analytical means. Here, ${\mathfrak {f}}(\zeta _{\textrm{i}}^{\textrm{e}})$ was determined using Mathematica’s $\texttt {Solve}{} \texttt {[}\,\cdot \,\texttt {]}$ command to symbolically factor the quartic (in ${\mathfrak {f}}$) that results after performing the indicated differentiation in Eq. (90).

As such, we instead seek to determine bounds on the value of $\text {Ma}_{\textrm{sup}}$ under this case via numerical means. To this end, we return to Eq. (30b) and specialize it to Case (i), the result being:

$$\begin{aligned} 1-\frac{3v(\gamma -1)\text {Ma}}{4b_{0}M_{\textrm{r}}^{2}}\left[ \frac{{\mathfrak {f}}(1-{\mathfrak {f}})}{v/u_{\textrm{p}} - {\mathfrak {f}}}+ \frac{\text {Ma}^{2}{\mathfrak {f}}^2(1 - {\mathfrak {f}})^2}{v/u_{\textrm{p}} - {\mathfrak {f}}}\right] = T_{\textrm{e}}, \end{aligned}$$

(92)

where in the present case $T_{\textrm{e}}(\zeta ) =\varTheta _{\textrm{e}}(\zeta )/\vartheta _{0}$. If we now replace the right-hand side of Eq. (92) with zero; set $\text {Ma} := \text {Ma}_{\textrm{sup}}$, where in this regard we recall that $\text {Ma}=u_{\textrm{p}}/b_{0}$ and that v is given by Eq. (29); and replace ${\mathfrak {f}}$ with ${\mathfrak {f}}(\zeta _{\textrm{i}}^{\textrm{e}})$, then it is a straightforward matter to establish, using the Mathematica command $\texttt {NSolve}{} \texttt {[}\,\cdot \,\texttt {]}$, that under Case (i):

$$\begin{aligned} 1.64108< \text {Ma}_{\textrm{sup}} < 1.64109 \quad (M_{\textrm{r}}=1). \end{aligned}$$

(93)

In closing this subsection we observe that, because they stem from particular values of Ma, the present analysis is not applicable to the special case TWSs treated in Appendix B.

8.4.2 Case (ii)

Using Eq. (25), this case of Eq. (88) can be expressed in the more transparent form

$$\begin{aligned} \left\{ \left[ b_{0}^{2}+\left( \frac{8\nu _{0}}{3}\right) |f^{\prime }|\right] f^{\prime \prime }\right\} \Bigg |_{\zeta = \zeta _{\textrm{ii}}^{\textrm{e}}} = 0, \end{aligned}$$

(94)

where $\zeta _{\textrm{ii}}^{\textrm{e}} = \zeta _{\textrm{ii}}^{\bullet }$ is obvious on inspection. Because $\varTheta _{\textrm{e}}^{\prime }(\zeta _{\textrm{ii}}^{\bullet })=0$ and $\zeta _{\textrm{ii}}^{\bullet }=0$, we can analytically solve $\varPi _{\textrm{ii}}(\text {Ma}_{\textrm{sup}})= 0$ to obtain the exact value of $\text {Ma}_{\textrm{sup}}$ for this case; here, with $T_{\textrm{e}}(\zeta )=\varOmega _{\textrm{ii}}(M_{\textrm{r}}) \varTheta _{\textrm{e}}(\zeta )/\vartheta _{0}$, we have

$$\begin{aligned} \varPi _{\textrm{ii}}(\text {Ma}_{\textrm{sup}}) = T_{\textrm{e}}(0)\Big |_{\text {Ma} := \text {Ma}_{\textrm{sup}}}, \end{aligned}$$

(95)

where

$$\begin{aligned} \varPi _{\textrm{ii}}(\text {Ma}) = \varOmega _{\textrm{ii}}(M_{\textrm{r}}) -\text {Ma}^{2}-\tfrac{1}{4}\text {Ma}^{4}, \end{aligned}$$

(96)

from which Eq. (58) was used to eliminate $\ell _{\textrm{ii}}$, and where $\varOmega _{\textrm{ii}}(M_{\textrm{r}}) = (16/3)M_{\textrm{r}}^{2}/(\gamma -1)$.

Since Eq. (96) is a bi-quadratic, it is easily established that

$$\begin{aligned} \text {Ma}_{\textrm{sup}} =\sqrt{-2+2\sqrt{1+\varOmega _{\textrm{ii}}(M_{\textrm{r}})}}\,, \end{aligned}$$

(97)

which is the only positive root of $\varPi _{\textrm{ii}}(\text {Ma}_{\textrm{sup}})= 0$. Thus, under Case (ii):

$$\begin{aligned} \text {Ma}_{\textrm{sup}} = 2 \qquad (M_{\textrm{r}}=1). \end{aligned}$$

(98)

8.4.3 Case (iii)

Employing Eq. (25) once again, we find that this case of Eq. (88) can be expressed as

$$\begin{aligned} \left\{ \left[ b_{0}^{2}+\left( \frac{27\lambda _{0}^{2}}{4}\right) (f^{\prime })^{2}\right] f^{\prime \prime }\right\} \Bigg |_{\zeta = \zeta _{\textrm{iii}}^{\textrm{e}}} = 0, \quad |\zeta | \in [0, \tfrac{\pi }{4}\ell _{\textrm{iii}}), \end{aligned}$$

(99)

from which it is evident that $\zeta _{\textrm{iii}}^{\textrm{e}} = \zeta _{\textrm{iii}}^{\bullet }$. Because $\zeta =\zeta _{\textrm{iii}}^{\bullet }$ satisfies Eq. (99) and $\zeta _{\textrm{iii}}^{\bullet }=0$, we can analytically solve $\varPi _{\textrm{iii}}(\text {Ma}_{\textrm{sup}})= 0$ to obtain the exact value of $\text {Ma}_{\textrm{sup}}$ for this case as well; here, with $T_{\textrm{e}}(\zeta )=\varOmega _{\textrm{iii}}(M_{\textrm{r}}) \varTheta _{\textrm{e}}(\zeta )/\vartheta _{0}$, we have

$$\begin{aligned} \varPi _{\textrm{iii}}(\text {Ma}_{\textrm{sup}}) = T_{\textrm{e}}(0)\Big |_{\text {Ma} := \text {Ma}_{\textrm{sup}}}, \end{aligned}$$

(100)

where

$$\begin{aligned} \varPi _{\textrm{iii}}(\text {Ma})=\varOmega _{\textrm{iii}}(M_{\textrm{r}})-\tfrac{1}{3}\text {Ma}-\tfrac{1}{12}\text {Ma}^{3}, \end{aligned}$$

(101)

from which the ${\mathfrak {b}}_{\textrm{iii}}=\tfrac{1}{4}\sqrt{27}$ [recall Eq. (84)] special case of Eq. (66) has been used to eliminate $\ell _{\textrm{iii}}$, and where

$$\begin{aligned} \varOmega _{\textrm{iii}}(M_{\textrm{r}}) = \frac{16 M_{\textrm{r}}^{2}}{(\gamma -1)\sqrt{50\pi }}\,, \end{aligned}$$

(102)

from which we have eliminated $\lambda _{0}$ with the aid of Eq. (21).

Since $\varPi _{\textrm{iii}}(\text {Ma}_{\textrm{sup}})$ is a depressed cubic, applying Cardano’s formula is a relatively simple matter; omitting the details, we find that

$$\begin{aligned}&\text {Ma}_{\textrm{sup}} = \root 3 \of {6\varOmega _{\textrm{iii}}(M_{\textrm{r}})+2\sqrt{9\varOmega _{\textrm{iii}}^{2}(M_{\textrm{r}})+\tfrac{16}{27}}}\nonumber \\&\quad +\root 3 \of {6\varOmega _{\textrm{iii}}(M_{\textrm{r}})-2\sqrt{9\varOmega _{\textrm{iii}}^{2}(M_{\textrm{r}})+\tfrac{16}{27}}}\,, \end{aligned}$$

(103)

which is the only positive root of $\varPi _{\textrm{iii}}(\text {Ma}_{\textrm{sup}})= 0$. Thus, under Case (iii):

$$\begin{aligned} \text {Ma}_{\textrm{sup}} \approx 2.379 \qquad (M_{\textrm{r}}=1). \end{aligned}$$

(104)

Remark 7

The $\varTheta _{\textrm{e}}^{\prime }(\zeta )$ vs. $\zeta$ profile exhibits two jumps under Case (iii), the amplitudes and locations of which are:

$$\begin{aligned}{}[\![\varTheta _{\textrm{e}}^{\prime }\,]\!]\Big |_{- \tfrac{\pi }{4}\ell _{\textrm{iii}}} = [\![\varTheta _{\textrm{e}}^{\prime }\,]\!]\Big |_{+ \tfrac{\pi }{4}\ell _{\textrm{iii}}}= \frac{2b_{0}^{2}u_{\textrm{p}}}{9c_{\textrm{v}}\varkappa _{0}\lambda _{0}^{2}}. \end{aligned}$$

(105)

8.4.4 Case (iv)

Using Eq. (74), this case of Eq. (88) can be expressed in the (simplified) explicit form

$$\begin{aligned}&\Big [3\text {Ma}^{2} \exp (2\zeta /\ell _{\textrm{iv}})\nonumber \\&\quad - 4 \text {Ma}^{2} \exp (\zeta /\ell _{\textrm{iv}})-4 \Big ]\Big |_{\zeta =\zeta _{\textrm{iv}}^{\textrm{e}}} =0, \quad \zeta < \zeta _{\textrm{iv}}^{\bullet }, \end{aligned}$$

(106)

where we have again made use of Eq. (25). Although doing so is not simply a matter of solving Eq. (106), due in part to the fact that $\zeta _{\textrm{iv}}^{\textrm{e}}$ varies with Ma, it can be shown that $\zeta _{\textrm{iv}}^{\textrm{c}}$, the critical point of $\varTheta _{\textrm{e}}(\zeta )$ under the present case, is exactly given by

$$\begin{aligned} \zeta _{\textrm{iv}}^{\textrm{c}}= {\left\{ \begin{array}{ll} \zeta _{\textrm{iv}}^{\textrm{e}}, &{} \text {Ma} > 1,\\ \zeta _{\textrm{iv}}^{\bullet }, &{}\text {Ma} \le 1, \end{array}\right. } \end{aligned}$$

(107)

where $\zeta _{\textrm{iv}}^{\textrm{e}} = \ell _{\textrm{iv}}\ln [Y_{\textrm{iv}}(\text {Ma})]$, and where

$$\begin{aligned} Y_{\textrm{iv}}(\text {Ma})= \frac{2\text {Ma}+2\sqrt{3+\text {Ma}^{2}}}{3\text {Ma}} \qquad (\text {Ma} > 1). \end{aligned}$$

(108)

Here, we observe that $\zeta =\zeta _{\textrm{iv}}^{\textrm{c}}$ satisfies Eq. (106) only for $\text {Ma} > 1$, in which case $0< \zeta _{\textrm{iv}}^{\textrm{e}} < \zeta _{\textrm{iv}}^{\bullet }$, where we also observe that $\zeta _{\textrm{iv}}^{\textrm{e}} \rightarrow (\zeta _{\textrm{iv}}^{\bullet })^{-}$ as $\text {Ma} \rightarrow 1^{+}$.

Using Eqs. (74) and (75), the latter with ${\mathfrak {b}}_{\textrm{iv}}= 9/2$ [recall Eq. (84)], we now specialize Eq. (30b) to Case (iv); doing so yields, after expressing the result in terms of $T_{\textrm{e}}(\zeta )$ and simplifying,

$$\begin{aligned} T_{\textrm{e}}(\zeta )&= \varOmega _{\textrm{iv}}(M_{\textrm{r}}) \nonumber \\&- {\left\{ \begin{array}{ll} \tfrac{1}{6} \text {Ma} \exp (\zeta /\ell _{\textrm{iv}})\\ \qquad + \tfrac{1}{12} \text {Ma}^{3} \exp (2\zeta /\ell _{\textrm{iv}}) \\ \qquad \qquad - \tfrac{1}{24} \text {Ma}^{3} \exp (3\zeta /\ell _{\textrm{iv}}) &{} \zeta < \zeta _{\textrm{iv}}^{\bullet }, \\ 0, &{} \zeta \ge \zeta _{\textrm{iv}}^{\bullet }, \end{array}\right. } \end{aligned}$$

(109)

where $\varOmega _{\textrm{iv}}(M_{\textrm{r}}) =\varOmega _{\textrm{iii}}(M_{\textrm{r}})$ and, in this subsection, $T_{\textrm{e}}(\zeta )=\varOmega _{\textrm{iv}}(M_{\textrm{r}}) \varTheta _{\textrm{e}}(\zeta )/\vartheta _{0}$.

We are now led to consider the algebraic equation $\varPi _{\textrm{iv}}(\text {Ma}_{\textrm{sup}})= 0$, which can be solved analytically to obtain the exact value of $\text {Ma}_{\textrm{sup}}$ for this case; thus, utilizing only the $\zeta < \zeta _{\textrm{iv}}^{\bullet }$ branch of Eq. (109), we have

$$\begin{aligned}&\varPi _{\textrm{iv}}(\text {Ma}_{\textrm{sup}})\nonumber \\&\quad = {\left\{ \begin{array}{ll} T_{\textrm{e}}(\zeta _{\textrm{iv}}^{\textrm{e}})\Big |_{\text {Ma} := \text {Ma}_{\textrm{sup}}}, &{} M_{\textrm{r}} > M_{\textrm{r}}^{\star },\\ \lim _{\zeta \rightarrow (\zeta _{\textrm{iv}}^{\bullet })^{-}}T_{\textrm{e}}(\zeta )\Big |_{\text {Ma} := \text {Ma}_{\textrm{sup}}}, &{} M_{\textrm{r}} \le M_{\textrm{r}}^{\star }, \end{array}\right. } \quad \zeta < \zeta _{\textrm{iv}}^{\bullet }, \end{aligned}$$

(110)

which after simplifying can be expressed as

$$\begin{aligned}&\varPi _{\textrm{iv}}(\text {Ma})=\varOmega _{\textrm{iv}}(M_{\textrm{r}}) \nonumber \\&\quad - {\left\{ \begin{array}{ll} \tfrac{1}{6} \text {Ma} Y_{\textrm{iv}} + \tfrac{1}{12} \text {Ma}^{3} Y_{\textrm{iv}}^{2} - \tfrac{1}{24} \text {Ma}^{3} Y_{\textrm{iv}}^{3}, &{} M_{\textrm{r}} > M_{\textrm{r}}^{\star },\\ \\\tfrac{1}{3} \text {Ma}, &{} M_{\textrm{r}} \le M_{\textrm{r}}^{\star }. \end{array}\right. } \end{aligned}$$

(111)

Here, we call attention to the critical value

$$\begin{aligned} M_{\textrm{r}}^{\star } :=\frac{1}{2}\sqrt{\frac{5(\gamma -1)}{3}\sqrt{\frac{\pi }{8}}} \qquad (0< M_{\textrm{r}}^{\star } <0.42), \end{aligned}$$

(112)

where we observe that $\varOmega _{\textrm{iv}}(M_{\textrm{r}}^{\star })=1/3$, and we recall that $Y_{\textrm{iv}}$ is a function of only Ma.

While it is a trivial matter to establish that

$$\begin{aligned} \text {Ma}_{\textrm{sup}} = 3\varOmega _{\textrm{iv}}(M_{\textrm{r}}) \qquad (M_{\textrm{r}} \le M_{\textrm{r}}^{\star }), \end{aligned}$$

(113)

suffice it to say that the process of determining $\text {Ma}_{\textrm{sup}}$ for the cubic case of Eq. (111) is algebraically intensive—so much so that we now set our analytical efforts aside and return to our numerical tools. Hence, following an approach similar to that used in Sect. 8.4.1, we find that under Case (iv):

$$\begin{aligned} 2.92641< \text {Ma}_{\textrm{sup}} < 2.92642 \quad (M_{\textrm{r}}=1). \end{aligned}$$

(114)

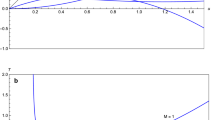
To help clarify the forgoing analysis, we have plotted $T_{\textrm{e}}(\zeta )$ vs. $\zeta$ in Fig. 2(a, b), where the former and latter correspond to $M_{\textrm{r}} > M_{\textrm{r}}^{\star }$ and $M_{\textrm{r}} < M_{\textrm{r}}^{\star }$, respectively. From these plots it is clear that the $T_{\textrm{e}}(\zeta )$ vs. $\zeta$ profile admits a stationary point only for $M_{\textrm{r}} > M_{\textrm{r}}^{\star }$; see Fig. 2a. Because this (i.e., blue) profile is based on $\text {Ma}_{\textrm{sup}}$, however, the stationary point is, from the physical standpoint, not its absolute minimum, but rather its infimum, i.e., $\inf [T_{\textrm{e}}(\zeta )]$, whose value is of course zero. The $T_{\textrm{e}}(\zeta )$ vs. $\zeta$ profile depicted in Fig. 2b, in contrast, does not admit a stationary point, only an infimum, where $\inf [T_{\textrm{e}}(\zeta )]$ for this (i.e., red) profile is also zero.

Remark 8

The temperature of the surrounding environment must exhibit a jump discontinuity across $\zeta =\zeta _{\textrm{iv}}^{\bullet }$ under the present case; specifically [recall Eq. (38)]

$$\begin{aligned}{}[\![T_{\textrm{e}} ]\!]\big |_{\zeta _{\textrm{iv}}^{\bullet }} = (\varOmega _{\textrm{iv}}(M_{\textrm{r}}) - \tfrac{1}{3}\text {Ma}) - \varOmega _{\textrm{iv}}(M_{\textrm{r}}) = - \tfrac{1}{3}\text {Ma}, \end{aligned}$$

(115)

for all $\text {Ma}>0$. The plots in Fig. 2(a, b) also serve to illustrate this phenomenon. Evaluating numerically, we find that $[\![T_{\textrm{e}} ]\!]\big |_{\zeta _{\textrm{iv}}^{\bullet }} \approx - 0.9755$ and $[\![T_{\textrm{e}} ]\!]\big |_{\zeta _{\textrm{iv}}^{\bullet }} \approx -0.0833$, respectively, in Fig. 2(a, b).

Fig. 2

$T_{\textrm{e}}(\zeta )$ vs. $\zeta$ generated from Eq. (109) with $\text {Ma}$ replaced by $\text {Ma}_{\textrm{sup}}$ and using the parameter values for Ar given in Sect. 8.1; here, $M_{\textrm{r}}^{\star }=\tfrac{1}{6}\sqrt{5}(\pi /2)^{1/4} \approx 0.4172$, and we recall that ${\mathfrak {b}}_{\textrm{iv}}=9/2 \implies \ell _{\textrm{iv}}=3\lambda _{0}$. Blue curve: $M_{\textrm{r}} = 1 \implies \text {Ma}_{\textrm{sup}}$ given by Eq. (114). Red curve: $M_{\textrm{r}}= \tfrac{1}{2}M_{\textrm{r}}^{\star }\implies \text {Ma}_{\textrm{sup}} = 1/4$ [see Eq. (113)]. Magenta-broken line: $\zeta =\zeta _{\textrm{iv}}^{\textrm{e}} \approx 0.0012$. Black-broken line: $\zeta = \zeta _{\textrm{iv}}^{\bullet }\approx 0.0023$

9 Closing remarks and observations

◆ While $f, g \in {\mathcal {C}}^{\infty }(\mathbb {R})$ under both Cases (i) and (ii), the same is not true under Cases (iii) and (iv); specifically, $f, g \in {\mathcal {C}}^{1}(\mathbb {R})$ and $f, g \in {\mathcal {C}}^{0}(\mathbb {R})$, respectively, under the former and latter. Exemplar velocity field plots illustrating these differences in smoothness between the classical and artificial viscosity cases are presented in Figs. 3 and 4 .

◆ By averaging the (1D) Euler system under finite-scale theory (FST), one obtains a system containing an “effective viscosity” that is given by Eq. (17) with ${\mathfrak {b}}_{\textrm{iii}} =1/\sqrt{12}$ and $\lambda _{0}$ replaced by L, where $L(>0)$ is the length scale that appears in the averaging transform of FST; see Refs. [18, 36] and those cited therein.

◆ The $\varTheta _{\textrm{e}}(\zeta )$ vs. $\zeta$ profile under Case (iii) admits a pair of temperature-rate waves (see Refs. [26, 37, 38]), i.e., jumps in $\varTheta _{\textrm{e}}^{\prime }(\zeta )$, across $\zeta =\mp \pi \ell _{\textrm{iii}}/4$; see Remark 7.

◆ A thermal shock (see, e.g., Refs. [37, 38]), i.e., a jump in $T_{\textrm{e}}(\zeta )$, must occur under Case (iv); see Remark 7.

◆ While they are quite distinct from those presented for Ar in Refs. [25, 34], the TWS profiles generated under Case (iv), an example of which is the blue curve in Fig. 3, are very similar to those given in Ref. [39, Fig. 2], which depict non-isothermal shocks in $\hbox {CO}_{{2}}$; see also Ref. [40].

◆ While they are so under Cases (i)–(iii), under Case (iv), Eqs. (13b) and (13c) are not invariant with respect to Galilean transformations [14, § 1.5]. (We thank Reviewer 2 for bringing this fact to our attention.)

Fig. 3

Both plots depicted here were generated using $\text {Ma}=0.25$ and the parameter values for Ar given in Sect. 8.1. Red curve: Plotted from Eq. (43) after making use of the relation ${\mathcal {F}}(\zeta ) = -1+(2/u_{\textrm{p}})f(\zeta )$. Blue curve: Plotted from Eq. (74), with $\ell _{\textrm{iv}}$ given by Eq. (84)

Fig. 4

Both plots depicted here were generated using $\text {Ma}=0.25$ and the parameter values for Ar given in Sect.n 8.1. Red curve: Plotted from Eq. (57). Blue curve: Plotted from Eq. (65), with $\ell _{\textrm{iii}}$ given by Eq. (84)

Appendices

Appendix A: Comparison with Stokes (1851)

In this appendix the EoM derived by Stokes in Ref. [2], which describes non-isothermal propagation with radiation under the linear approximation, is re-derived. We also give the isothermal version of Stokes’ model and the linearized, reduced, version of the present (i.e., isothermal) governing system. Key aspects of all three models are noted and briefly discussed.

In terms of the present notation, the governing system of equations considered by Stokes [2], and later Rayleigh [8, § 247]¹², can be expressed as

$$\begin{aligned} s_{t}&= - u_{x}, \end{aligned}$$

(A.1a)

$$\begin{aligned} \rho _{0}u_{t}&=-p_{x},\end{aligned}$$

(A.1b)

$$\begin{aligned} \theta _{t}-(\gamma -1)s_{t}&= - \varkappa _{0}\theta ,\end{aligned}$$

(A.1c)

$$\begin{aligned} p&= p_{0}(1+s+\theta ). \end{aligned}$$

(A.1d)

In Sys. (A.1), $s=(\rho -\rho _0)/\rho _{0}$ is known as the condensation; we have set $\theta =(\vartheta -\vartheta _0)/\vartheta _{0}$; the term on the right-hand side of Eq. (A.1c) follows from taking, prior to cancellation of the product $c_{\textrm{v}} \rho _{0}\vartheta _{0}$,

$$\begin{aligned} r=- c_{\textrm{v}} \varkappa _{0}\vartheta _{0}\theta , \end{aligned}$$

(A.2)

i.e., r to be given by the general (i.e., non-isothermal) form of Newton’s law of cooling; and $\mu$, $\mu _{\textrm{b}}$, and K have all been set equal to zero. (Unless stated herein, the definitions of all quantities, terms, etc., appearing in this appendix can be found in Section 2.)

Now using Eqs. (A.1a) and (A.1d) to eliminate u and p, respectively, from Eq. (A.1b) reduces Sys. (A.1) to

$$\begin{aligned} s_{tt}&= b_{0}^{2}s_{xx}+b_{0}^{2}\theta _{xx},\end{aligned}$$

(A.3a)

$$\begin{aligned} (\varkappa _{0} + \partial _{t})\theta&= (\gamma -1)s_{t}, \end{aligned}$$

(A.3b)

where we have re-written Eq. (A.1c) in operator form.

At this point it is instructive to introduce the isothermal counterpart of Sys. (A.3):

$$\begin{aligned} s_{tt} - b_{0}^{2}s_{xx}&=0,\end{aligned}$$

(A.4a)

$$\begin{aligned} \vartheta _{\textrm{e}}&=\vartheta _{0}[1- \varkappa _{0}^{-1}(\gamma -1)s_{t}], \end{aligned}$$

(A.4b)

where, as in Sect. 2.3, $\vartheta _{\textrm{e}}=\vartheta _{\textrm{e}}(x,t)$ is controllable by the experimenter, and

$$\begin{aligned} s_{tt} - b_{0}^{2}s_{xx}&=\tfrac{4}{3}\nu _{0}s_{txx},\end{aligned}$$

(A.5a)

$$\begin{aligned} \vartheta _{\textrm{e}}&=\vartheta _{0}[1- \varkappa _{0}^{-1}(\gamma -1)s_{t}], \end{aligned}$$

(A.5b)

which is easily obtained from the linearized version of Sys. (13). Here, in parallel with the analyses carried out in Sect. 8.4, we stress the fact that if $s_{t} >0$ (i.e., compression) is a possibility, then suitable additional restrictions must be placed on the boundary and/or initial data for Eqs. (A.4a) and (A.5a) to ensure that Eqs. (A.4b) and (A.5b) are consistent with $\vartheta _{\textrm{e}} > 0$. If, however, $\max |s_{t}| \ll \varkappa _{0}$, then $\vartheta _{\textrm{e}} \approx \vartheta _{0}$; recall the long-period piston example cited in Refs. [2] and [8, p. 26].

As we conclude this appendix, we return to Sys. (A.3) and, on eliminating $\theta$ between its two PDEs, obtain the modern form of the EoM first derived by Stokes in 1851, viz.,

$$\begin{aligned} s_{ttt}-c_{0}^{2}s_{txx} + \varkappa _{0}(s_{tt} - b_{0}^{2}s_{xx}) = 0; \end{aligned}$$

(A.6)

see Refs. [2, Eq. (7)] and [8, § 247(6)]. (See also Truesdell’s [5, § 4] critiques of the analyses performed in Refs. [2] and [8, § 247].) In recent years, many authors have begun referring to PDEs of this type as (Stokes–)Moore–Gibson–Thompson equations; see, e.g., Ref. [41, p. 3], wherein an interesting stability condition for Eq. (A.6) and its multi-D extensions is presented and discussed. With regard to modeling experiments involving both radiation and non-isothermal conditions, however, we observe that Sys. (A.1) is preferred to Eq. (A.6) in terms of initial data requirements; i.e., while both formulations require knowledge of s(x, 0), it appears to be much easier, from the standpoint of performing the experiment, for one to accurately specify $\theta (x,0)$, u(x, 0) than $s_{t}(x,0)$, $s_{tt}(x,0)$.

Appendix B: Explicit TWSs under Case (i)

We begin with the observation that Eq. (43) can also be written as

$$\begin{aligned}&\frac{3v\zeta }{2\nu _{0}(|k|-1)} = \ln (1-{\mathcal {F}}) \nonumber \\&\quad -\left( \frac{|k|+1}{|k|-1}\right) \ln (1+{\mathcal {F}}) \qquad ( |{\mathcal {F}}| <1), \end{aligned}$$

(B.1)

where we recall that $k <-1$. Prompted by the derivation of the special case TWS presented in Ref. [35, § 4], wherein Becker’s assumption (see also Ref. [24]) was adopted, we find that setting $\text {Ma}=1/\sqrt{2}$ ($\implies k=-3$, $M_{\textrm{s}}=\sqrt{2}$) reduces Eq. (B.1) to

$$\begin{aligned} \left( \frac{3b_{0}\sqrt{2}}{4\nu _{0}}\right) \zeta =\ln \left[ \frac{1-{\mathcal {F}}}{(1+{\mathcal {F}})^2} \right], \end{aligned}$$

(B.2)

which is readily solved to yield the explicit expression

$$\begin{aligned} f(\zeta )&=\frac{1}{4}u_{\textrm{p}}\exp \left[ - (3+2\sqrt{2}\,)\zeta /\ell _{\textrm{i}}\right] \nonumber \\&\times \left\{ -1+\sqrt{1+8\exp \left[ (3+2\sqrt{2}\,)\zeta /\ell _{\textrm{i}}\right] }\,\right\}, \end{aligned}$$

(B.3)

where we recall our use of the relation ${\mathcal {F}}(\zeta ) = -1+(2/u_{\textrm{p}})f(\zeta )$. In the case of Eq. (B.3), the shock thickness and corresponding critical point are given by

$$\begin{aligned} \ell _{\textrm{i}} = \frac{\nu _{0}(3+2\sqrt{2})\sqrt{8}}{3b_{0}}, \,\,\,\, \zeta _{\textrm{i}}^{\bullet }= \left( \frac{4\nu _{0}}{b_{0}\sqrt{18}}\right) \ln \!\left[ \tfrac{1}{4}(1+\sqrt{2}\,)\right], \end{aligned}$$

(B.4)

respectively.

The corresponding density TWS is easily found to be

$$\begin{aligned} g(\zeta )&=\rho _{0}\Bigg (1-\tfrac{1}{8}\exp \left[ - (3+2\sqrt{2}\,)\zeta /\ell _{\textrm{i}}\right] \nonumber \\&\times \left\{ -1+\sqrt{1+8\exp \left[ (3+2\sqrt{2}\,)\zeta /\ell _{\textrm{i}}\right] }\,\right\} \Bigg )^{-1}, \end{aligned}$$

(B.5)

a profile that admits the shock thickness

$$\begin{aligned} l_{\textrm{i}} = 2(\nu _{0}/b_{0})\sqrt{6}, \end{aligned}$$

(B.6)

with corresponding critical point $\zeta _{\textrm{i}}^{*}= - l_{\textrm{i}} \ln \left( 2\right)$.

We close by pointing out that four other explicit TWSs are possible under Case (i). Apart from noting that their derivation requires one to solve the cubic and quartic equations

$$\begin{aligned} (1-{\mathcal {F}})\exp \left[ -\,\frac{3b_{0}\zeta \sqrt{m}}{2\nu _{0} (|k|-1)}\right] = (1+{\mathcal {F}})^{m}, \end{aligned}$$

(B.7)

however, we leave this task to the reader; here,

$$\begin{aligned} m={\left\{ \begin{array}{ll} 4/3 (\implies k=-7), &{} \text {Ma}=1/\sqrt{12},\\ 3/2 (\implies k=-5), &{} \text {Ma}=1/\sqrt{6},\\ 3 (\implies k=-2), &{} \text {Ma}=2/\sqrt{3},\\ 4 (\implies k=-5/3), &{} \text {Ma}=3/2, \end{array}\right. } \end{aligned}$$

(B.8)

where $m(>1)$ is given by $m= (|k|+1)(|k|-1)^{-1}=M_{\textrm{s}}^{2}$.