Skip to main content
SpringerLink
Log in

Dynamic analysis of moving beams featuring time-varying velocity under self-excited force moving along with the end

  • Published:
Meccanica Aims and scope Submit manuscript

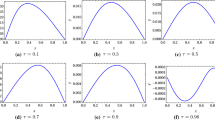
Abstract

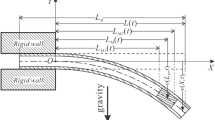
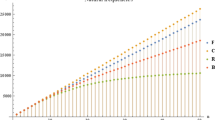
Moving beam is a typical continuous system model. This paper studies the dynamics of moving beams featuring time-varying velocity subjected to a self-excited force moving along with the end, subject to general initial conditions. Based on the D'Alembert principle, the partial differential equation of motion with time-varying parameters for governing transverse vibration of the beam is derived. The equation is discretized by the Galerkin truncation method. A set of ordinary differential equations with transient coefficients is obtained by the Galerkin method. The effects of deployment time and self-excited force on the dynamic response of the beam are investigated by solving the ordinary differential equations. The natural frequencies are obtained by the eigenvalue method. The numerical simulation is employed to analyze the dynamic characteristics of axially moving beams. Furthermore, the effects of parameters such as motion acceleration, excitation, and initial length are discussed theoretically. The numerical results obtained are compared with the results of previous investigations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Gaiko NV, Horssen WTV (2018) Resonances and vibrations in an elevator cable system due to boundary sway. J Sound Vib 424:272–292

    Article  Google Scholar 

  2. Ma X, Pan G, Zhang P, Xu Q, Shi X, Xiao Z, Han Y (2021) Experimental evaluation of braking pad materials used for high-speed elevator. Wear 477:203872

    Article  Google Scholar 

  3. Qiu L, Wang Z, Zhang S, Zhang L, Chen J, Wang C (2020) A vibration-related design parameter optimization method for high-speed elevator horizontal vibration reduction. Shock Vib 2020:1269170

    Google Scholar 

  4. Nguyen TX, Miura N, Sone A (2019) Analysis and control of vibration of ropes in a high-rise elevator under earthquake excitation. Earthq Eng Eng Vib 18(2):447–460

    Article  Google Scholar 

  5. Gao X, Jin D, Chen T (2018) Analytical and experimental investigations of a space antenna system of four DOFs with internal resonances. Commun Nonlinear Sci Numer Simul 63:380–403

    Article  MathSciNet  MATH  Google Scholar 

  6. Gao X, Jin D, Chen T (2018) Nonlinear analysis and experimental investigation of a rigid-flexible antenna system. Meccanica 53(1):33–48

    Article  MathSciNet  MATH  Google Scholar 

  7. Hr ÖZ (2002) Current research on the vibration and stability of axially moving materials. J Sound Vib 259(2):445–456

    Google Scholar 

  8. Alexander H, Ivo S, Loc V (2020) General sliding-beam formulation: a non-material description for analysis of sliding structures and axially moving beams. J Sound Vib 480:115341

    Article  Google Scholar 

  9. Marynowski K (2018) Vibration analysis of an axially moving sandwich beam with multiscale composite facings in thermal environment. Int J Mech Sci 146:116–124

    Article  Google Scholar 

  10. Zhang Y, Hou S, Xu K, Yang T, Chen L (2017) Forced vibration control of an axially moving beam with an attached nonlinear energy sink. Acta Mech Solida Sin 30(6):674–682

    Article  Google Scholar 

  11. Ali EM, Hoda S, Masoud R (2020) On the vibrations of axially graded Rayleigh beams under a moving load. Appl Math Model 84:554–570

    Article  MathSciNet  MATH  Google Scholar 

  12. Tang Y, Zhang Y, Yang X (2018) On parametric instability boundaries of axially moving beams with internal resonance. Acta Mech Solida Sin 31(4):470–483

    Article  Google Scholar 

  13. Wang Y, Ding H, Chen L (2017) Asymptotic solutions of coupled equations of supercritically axially moving beam. Nonlinear Dyn 87(1):25–26

    Article  MathSciNet  MATH  Google Scholar 

  14. Tang Y, Ma Z (2019) Nonlinear vibration of axially moving beams with internal resonance, speed-dependent tension, and tension-dependent speed. Nonlinear Dyn 98(1):2475–2490

    Article  MATH  Google Scholar 

  15. Vetyukov Y (2018) Non-material finite element modelling of large vibrations of axially moving strings and beams. J Sound Vib 414:299–317

    Article  Google Scholar 

  16. Park S, Yoo HH, Chung J (2013) Vibrations of an axially moving beam with deployment or retraction. AIAA J 51(3):686–696

    Article  Google Scholar 

  17. Yang X, Zhang W, Melnik RVN (2016) Energetics and invariants of axially deploying beam with uniform velocity. AIAA J 54(7):2183–2189

    Article  Google Scholar 

  18. Rong CL Jr, Jung H, Tong C (2010) Vibration and stability of an axially moving Rayleigh beam. Appl Math Model 34:1482–1497

    Article  MathSciNet  MATH  Google Scholar 

  19. Ding H, Lim C, Chen L (2018) Nonlinear vibration of a traveling belt with non-homogeneous boundaries. J Sound Vib 424:78–93

    Article  Google Scholar 

  20. Zhang Y, Yuan B, Fang B, Chen L (2017) Reducing thermal shock-induced vibration of an axially moving beam via a nonlinear energy sink. Nonlinear Dyn 87(2):1159–1167

    Article  Google Scholar 

  21. Yang T, Fang B, Yang X, Li Y (2013) Closed-form approximate solution for natural frequency of axially moving beams. Int J Mech Sci 74:154–160

    Article  Google Scholar 

  22. Ma G, Xu M, Chen L, An Z, Burdzik R (2015) Transverse free vibration of axially moving stepped beam with different length and tip mass. Shock Vib 2015:507581

    Google Scholar 

  23. Farokhi H, Ghayesh MH, Amabili M (2013) In-plane and out-of-plane nonlinear dynamics of an axially moving beam. Chaos Solitons Fractals 54:101–121

    Article  MATH  Google Scholar 

  24. Zhang W, Sun L, Yang X, Jia P (2013) Nonlinear dynamic behaviors of a deploying-and-retreating wing with varying velocity. J Sound Vib 332:6785–6797

    Article  Google Scholar 

  25. Yang X, Wang S, Zhang W, Qin Z, Yang T (2017) Dynamic analysis of a rotating tapered cantilever Timoshenko beam based on the power series method. Appl Math Mech 38(10):1425–1438

    Article  MathSciNet  MATH  Google Scholar 

  26. Tang J, Ren G, Zhu W, Ren H (2010) Dynamics of variable-length tethers with application to tethered satellite deployment. Commun Nonlinear Sci Numer Simul 16(8):3411–3424

    Article  MathSciNet  MATH  Google Scholar 

  27. Tang Y, Chen L (2010) Nonlinear free transverse vibrations of in-plane moving plates: Without and with internal resonances. J Sound Vib 330(1):110–126

    Article  Google Scholar 

  28. Yang X, Ming L, Zhang W, Melnik RVN (2016) Invariant and energy analysis of an axially retracting beam. Chinese J Aeronaut 29(4):952–961

    Article  Google Scholar 

  29. Yan T, Yang T, Chen L (2020) Direct multiscale analysis of stability of an axially moving functionally graded beam with time-dependent velocity. Acta Mech Solida Sin 33(2):150–163

    Article  Google Scholar 

  30. Ghaleh PB, Malaek SM (2015) On dynamic stiffness of spacecraft flexible appendages in deployment phase. Aerosp Sci Technol 47:1–9

    Article  Google Scholar 

  31. Deng L, Zhang Y (2020) A consistent corotational formulation for the nonlinear dynamic analysis of sliding beams. J Sound Vib 476:115298

    Article  Google Scholar 

  32. Zhu K, Chung J (2015) Nonlinear lateral vibrations of a deploying Euler-Bernoulli beam with a spinning motion. Int J Mech Sci 90:200–212

    Article  Google Scholar 

  33. Zhu K, Chung J (2016) Dynamic modeling and analysis of a spinning Rayleigh beam under deployment. Int J Mech Sci 115:392–405

    Article  Google Scholar 

  34. Özkaya E, Pakdemirli M (2000) Vibrations of an axially accelerating beam with small flexural stiffness. J Sound Vib 234:521–535

    Article  Google Scholar 

  35. Özkaya E, Pakdemirli M (1999) Vibrations of an axially moving beam with time-dependent velocity. J Sound Vib 227:239–257

    Article  Google Scholar 

  36. Zhang D, Tang Y, Chen L (2017) Irregular instability boundaries of axially accelerating viscoelastic beams with 1:3 internal resonance. Int J Mech Sci 133:535–543

    Article  Google Scholar 

  37. Zhu B, Dong Y, Li Y (2018) Nonlinear dynamics of a viscoelastic sandwich beam with parametric excitations and internal resonance. Nonlinear Dyn 94(4):2575–2612

    Article  Google Scholar 

  38. Wang L, Xu M, Li Y (2018) Vibration analysis of deploying laminated beams with generalized boundary conditions in hygrothermal environment. Compos Struct 207:665–676

    Article  Google Scholar 

  39. Bigoni D, Bosi F, Dal Corso F, Misseroni D (2014) Instability of a penetrating blade. J Mech Phys Solids 64:411–425

    Article  MathSciNet  Google Scholar 

  40. Bosi F, Misseroni D, Dal Corso F, Bigoni D (2015) Self-encapsulation, or the ‘dripping’ of an elastic rod. P Roy Soc A-Math Phy 471(2179):20150195

    Google Scholar 

  41. Dal Corso F, Misseroni D, Pugno NM, Movchan AB, Movchan NV, Bigoni D (2017) Serpentine locomotion through elastic energy release. R Soc Interface 14(130):20170055

    Article  Google Scholar 

  42. Dal Corso F, Tallarico D, Movchan NV, Movchan AB, Bigoni D (2019) Nested Bloch waves in elastic structures with configurational forces. P Roy Soc A-Math Phy 377(2156):20190101

    MathSciNet  MATH  Google Scholar 

  43. Bosi F, Misseroni D, Dal Corso F, Bigoni D (2014) An elastica arm scale. P Roy Soc A-Math Phy 470(2169):20140232

    MathSciNet  MATH  Google Scholar 

  44. Armanini C, Dal Corso F, Misseroni D, Bigoni D (2019) Configurational forces and nonlinear structural dynamics. J Mech Phys Solids 130:82–100

    Article  MathSciNet  Google Scholar 

  45. Bigoni D, Dal Corso F, Bosi F, Misseroni D (2015) Eshelby-like forces acting on elastic structures: theoretical and experimental proof. Mech Mater 80:368–374

    Article  Google Scholar 

  46. Bosi F, Misseroni D, Dal Corso F, Bigoni D (2015) Development of configurational forces during the injection of an elastic rod. Extreme Mech Lett 4:83–88

    Article  Google Scholar 

  47. Singh N, Sharma I, Gupta SS (2020) Dynamics of variable length geometrically exact beams in three-dimensions. Int J Solids Struct 191:614–627

    Article  Google Scholar 

  48. Han S (2022) Configurational forces and geometrically exact formulation of sliding beams in non-material domains. Comput Method Appl M 395:115063

    Article  MathSciNet  MATH  Google Scholar 

  49. Boyer F, Lebastard V, Candelier F, Renda F (2022) Extended Hamilton’s principle applied to geometrically exact Kirchhoff sliding rods. J Sound Vib 516:116511

    Article  Google Scholar 

  50. Zhang C, Li C, Xu M, Yao G, Liu Z, Dai W (2022) Cutting force and nonlinear chatter stability of ball-end milling cutter. Int J Adv Manuf Tech 120(9):5885–5908

    Google Scholar 

  51. Molnar TG, Berezvai S, Kiss AK, Bachrathy D, Stepan G (2019) Experimental investigation of dynamic chip formation in orthogonal cutting. Int J Mach Tools Manuf 145:103429

    Article  Google Scholar 

  52. Miao H, Wang C, Li C, Yao G, Zhang X, Liu Z, Xu M (2022) Dynamic modeling and nonlinear vibration analysis of spindle system during ball end milling process. Int J Adv Manuf Tech 121(11):7867–7889

    Article  Google Scholar 

  53. Wang C, Miao H, Li C, Li J, Xu M, Liu Z (2022) Effect of cutting vibration on the surface quality of commercially pure titanium (TA2) based on rotor dynamics model analysis. Int J Mech Mater Des 112:1–20

    Google Scholar 

  54. Gibbons TJ, Ozturk E, Xu L, Sims ND (2020) Chatter avoidance via structural modification of tool-holder geometry. Int J Mach-Tools Manuf 150:103514

    Article  Google Scholar 

  55. Xu C, Dou J, Chai Y, Li H, Shi Z, Xu J (2018) The relationships between cutting parameters, tool wear, cutting force and vibration. Adv Mech Eng 10(1):1–14

    Google Scholar 

  56. Wang H, Pei Z, Cong W (2020) A feeding-directional cutting force model for end surface grinding of CFRP composites using rotary ultrasonic machining with elliptical ultrasonic vibration. Int J Mach Tools Manuf 152:103540

    Article  Google Scholar 

  57. Miao H, Wang C, Hao J, Li C, Xu M, Liu Z (2022) Dynamic analysis of the column-spindle system considering the nonlinear characteristics of kinematic joints. Mech Mach Theory 174:104922

    Article  Google Scholar 

  58. Rubio L, Loya JA, Miguélez MH, Fernández-Sáez J (2013) Optimization of passive vibration absorbers to reduce chatter in boring. Mech Syst Signal Pr 41:691–704

    Article  Google Scholar 

  59. Hao J, Yao Z, Li C, Song W, Miao H, Xu M, Liu Z (2023) Dynamic characteristics analysis of asynchronous motorized spindle considering combined unbalanced magnetic pull and nonlinear bearing restoring force effects. Mech Syst Signal Pr 185:109807

    Article  Google Scholar 

  60. Al-Bedoor BO, Khulief YA (1996) An approximate analytical solution of beam vibrations during axial motion. J Sound Vib 192:159–171

    Article  Google Scholar 

  61. Bedford A, Liechti KM (2020) Mechanics of materials. Springer Nature, Switzerland.

Download references

Acknowledgements

The work is supported by the National Natural Science Foundation of China (Grant No. 52075087), the Fundamental Research Funds for the Central Universities (Grant No. N2003006 and N2103003), and the National Natural Science Foundation of China (Grant No. U1708254).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

    Jin Hao, Changyou Li, Tianzhi Yang & Jiancheng Yang

  2. School of Energy and Power Engineering, Shenyang University of Chemical Technology, Shenyang, 110142, China

    Yimin Zhang

Authors
  1. Jin Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Changyou Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tianzhi Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jiancheng Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yimin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

JH: Methodology, Conceptualization, Data curation, Formal analysis, Investigation, Writing—original draft, Writing—review & editing. CL: Conceptualization, Formal analysis, Project administration, Resources, Funding acquisition, Methodology, Supervision, Writing—review & editing. TY: Investigation, Methodology, Funding acquisition, Writing—review & editing. JY: Investigation, Methodology, Writing—review & editing. YZ: Investigation, Methodology, Writing—review & editing.

Corresponding author

Correspondence to Changyou Li.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hao, J., Li, C., Yang, T. et al. Dynamic analysis of moving beams featuring time-varying velocity under self-excited force moving along with the end. Meccanica 57, 2905–2927 (2022). https://doi.org/10.1007/s11012-022-01604-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-022-01604-7

Keywords

Search

Navigation