1 Introduction

The modern industry is developing rapidly in the field of nanotechnology. This fact leads to the need for new studies of the nanostructures (nanobeams, nanoplates, nanoshells) used in the design of sensors, resonators, nanoelectromechanical systems (NEMS), nanooptomechanical structures, energy storage systems, DNA detectors, drug delivery [1,2,3,4,5,6]. One of the important objects of analysis is graphene structures because this nanomaterial has excellent mechanical, electrical, and thermal characteristics [7,8,9]. By the experimental and theoretical studies [10, 11] of nanoobjects, it was also observed that the appearance of size-effect and influence of atomic forces cannot be detected by the classical (local) theory. In order to obtain accurate outcomes, nonclassical continuum theories have been developed. Here it is pertinent to mention the theory of micropolar elasticity [12], the couple stress theory [13,14,15], the nonlocal elasticity theory [16], the strain gradient theory [17]. In the present work, we employed the nonlocal elasticity theory, which is based on the fact that the stress at a given point depends on strains at all other points of structure. This theory was successfully used in various linear problems of single-layer plates [18,19,20,21,22,23] and multi-layer plate system. Pradhan and Phadikar in [24] applied the Navier method for linear vibration problems of single and double-layer plates based on the classical plate theory and first-order shear deformation theory. Bonded linear vibrations of double nanoplate systems are investigated by Murmu and Adhikari [25]. Double orthotropic nanoplates embedded in an elastic medium are investigated by Pouresmaeeli et al. [26].

Nonlinear vibrations of single-layer nano/microplates are studied by Ajri et al. [27] with the help of both the Bubnov–Galerkin and the Runge–Kutta methods. The paper of Ebrahimy and Hosseini [28] is devoted to investigation of nonlinear electroelastic vibration behaviour of double viscoelastic nanoplates by the generalized differential quadrature method. Nonlinear free vibrations of double-layer graphene sheet system located in a polymer matrix aroused by the nonlinear van der Waals interactions are analyzed by Mahdavi et al. [29] via the harmonic balance method. Whereas the differential quadrature method was used for nonlinear vibration analysis of a double-layer graphene sheet by Ravandi et al. [30]. The publication of Jomehzadeh and Saidi [31] is aimed at the nonlinear vibrations of orthotropic multi-layer plates. Mahmoudpour et al. [32] considered FG double-layer plates based on nonlocal strain gradient theory. The Galerkin method in combination with the harmonic balance method are employed in [31, 32]. The nonlocal viscoelastic double-layer nanoplates were studied on the basis of the Galerkin method and the multiple scale method by Wang et al. [33, 34].

Despite notable studies in the considered field, there are still many questions requiring additional research. In the mentioned works [31,32,33,34] related to geometrically nonlinear vibrations of multi-layer nanoplate system, where the authors use a mixed form of governing equations and introduce the Airy function, it is used the compatibility equation in classical form (without taking into account the nonlocal parameter). Note, that a similar approach was applied to single-layer magneto-electro-elastic nanoplates by Farajpour et al. [35], where the influence of the nonlocal parameter in the compatibility equation was indicated. Thus, in contrast to the listed works for multi-layer systems, we propose employing the size-dependent compatibility equation, where the nonlocal parameter is introduced based on the nonlocal constitutive relation.

Also, an obviously important issue is the study of the behaviour of the system under the influence of additional factors, in particular, affected by a magnetic field. Vibrations of single-layer graphene sheets in the uniaxial magnetic field are investigated by Murmu et al. [36] and Kiani [37], where the Navier method is applied. Ritz method for vibration analysis of embedded single-layer graphene sheets in a magnetic field is employed by Mazur and Awrejcewicz [38]. In addition, Zhang et al. [39] analysed vibrations of quadrilateral graphene sheets subjected to an in-plane magnetic field by the element-free kp-Ritz method. Stamenkovíc Atanasov et al. [40] devoted their work to the analysis of double-layer nanoplates under the influence of the magnetic field within the nonlocal plate theory, and the study was carried out on the basis of linear relations. Based on the nonlocal theory, the influence of in-plane magnetic field on the viscoelastic orthotropic multi-nanoplate system embedded in a viscoelastic medium is analysed by Karličić et al. [41]. Vibrations of double bonded orthotropic graphene sheets in 2D-magnetic field and subjected to biaxial in-plane forces are considered by Ghorbanpour Arani [42]. Sobhy and Radwan [43] studied hygrothermal bending of sandwich CNTs-reinforced microplates with viscoelastic core embedded in a viscoelastic medium in 2D magnetic filed based on application of the Navier method. In reviewed works, the study of double- and multi-layer systems in a magnetic field is performed employing the mathematical model based on linear plate theory. It should be emphasized that in the case of single-layer nanoplates, new publications, where the mathematical model is based on nonlinear von Kármán plate theory, have recently appeared. Ghadiri and Hosseini [44] investigated nonlinear vibration and dynamic instability of single-layer graphene sheet under parametric excitation, magnetic field action with help of the Bubnov–Galerkin approach combined with multiple time scales method. Nonlinear vibrations of single-layer graphene sheet in a magnetic field are investigated by Bubnov–Galerkin method in the work [45]. Therefore, the problem of geometrically nonlinear vibration of double-layer nanoplate system in a magnetic field is challenging and still open.

Summing up, the novelty of the work is an investigation of geometrically nonlinear vibration of a double-layer graphene sheet system in a uniaxial magnetic field, whereas the mathematical model contains size-dependent equations including compatibility equation. The main objectives are to determine whether the contribution of the nonlocal compatibility equation is significant, and also to analyze the influence of the Lorentz force caused by the magnetic field on the response curve for both in-phase and anti-phase vibration modes.

2 Mathematical formulation

2.1 Single-layer nanoplate

For the small-scale study of the single-layer graphene sheet (SLGS) the nonlocal elasticity theory is used. According to that theory the stress at a point is a function of strains at all points in the body, and the constitutive relation for the nonlocal stress tensor in an integral form takes the following form [16, 46]

$$\begin{aligned} \sigma = \int _V K \left( |{X} ^ {'} -X|,\tau \right) \sigma '(X')dX', \end{aligned}$$
(1)

where \(\sigma\), \(\sigma '\) are nonlocal and local stress tensors, \(K \left( |{X} ^ {'} -X|,\tau \right)\) is the nonlocal modulus, \(\tau =e_0\alpha /l\), \(\alpha\) is the internal characteristic length, \(e_0\) stands for a constant appreciate to material, whereas l is external characteristics length. Due to complexity of the integral form, Eq. (1), it is transformed [46] to the differential form:

$$\begin{aligned} \left( 1-\mu \nabla ^2 \right) \sigma =\sigma ', \end{aligned}$$
(2)

where \(\mu =(e_0 \alpha )^2\) stands for the nonlocal parameter and \(\nabla ^2=\frac{\partial ^2}{\partial x^2} +\frac{\partial ^2}{\partial y^2}\) is the Laplacian operator.

In the case of isotropic Kirchhoff’s plate, the constitutive relation with regard to Eq. (2) are presented in the following form

$$\begin{aligned} \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy} \end{bmatrix}= \begin{bmatrix} \frac{E}{1-\nu ^2 }&{} \quad \frac{\nu E}{1-\nu ^2 }&{} 0\\ \frac{\nu E}{1-\nu ^2 }&{} \quad \frac{E}{1-\nu ^2}&{} 0\\ 0&{} 0&{}\frac{E}{2(1+\nu )}\\ \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{xy} \end{bmatrix}, \end{aligned}$$
(3)

where E is Young’s modulus, \(\nu\) is Poisson’s ratio and \(\sigma _{xx}, \sigma _{yy}\), \(\sigma _{xy}\) are components of stress tensor \(\sigma\), whereas \(\varepsilon _{xx}, \varepsilon _{yy}, \varepsilon _{xy}\) are components of strain tensor.

According to the von Kármán nonlinear theory the components of strain tensor have the following form [47]

$$\begin{aligned} \begin{aligned} \varepsilon _{ xx }&=\varepsilon _{ xx }^0+z k_{xx}, \varepsilon _{ yy }=\varepsilon _{ yy }^0+z k_{yy}, \varepsilon _{ xy }=\varepsilon _{ xy }^0+z k_{xy},\\ \varepsilon _{ xx }^0&=\frac{{\partial }u}{{\partial }x}+\frac{1}{2}\left( \frac{{\partial }w}{{\partial }x}\right) ^2,k_{xx}=-\frac{{\partial }^2w}{{\partial }x^2},\\ \varepsilon _{ yy }^0&=\frac{{\partial }v}{{\partial }y}+\frac{1}{2}\left( \frac{{\partial }w}{{\partial }y}\right) ^2, k_{yy}=-\frac{{\partial }^2w}{{\partial }y^2},\\ \varepsilon _{ xy }^0&=\frac{{\partial }u}{{\partial }y}+\frac{{\partial }v}{{\partial }x}+\frac{{\partial }w}{{\partial }x}\frac{{\partial }w}{{\partial }y}, k_{xy}=-2\frac{{\partial }^2w}{{\partial }x{\partial }y}, \end{aligned} \end{aligned}$$
(4)

where u, v, w are displacements in x, y and z directions, respectively. The simple transformation of the relations (4) gives the compatibility equation for strains in the nanoplate middle surface:

$$\begin{aligned} \frac{\partial ^2 \varepsilon _{xx}^0}{\partial y^2 } +\frac{\partial ^2 \varepsilon _{yy}^0}{\partial x^2 }-\frac{\partial ^2 \varepsilon _{xy}^0}{\partial x \partial y }=\left( \frac{{\partial }^2w}{{\partial }x{\partial }y}\right) ^2-\frac{{\partial }^2w}{{\partial }x^2}\frac{{\partial }^2w}{{\partial }y^2}. \end{aligned}$$
(5)

The system of the governing equations for nonlinear vibrations of isotropic plate is yielded by application of the the Hamilton’s principle as follows [47]:

$$\begin{aligned} \begin{aligned}&\frac{{\partial }N_x}{{\partial }x}+\frac{{\partial }N_{ xy }}{{\partial }y}=m_0\frac{{\partial }^2u}{{\partial }t^2},\\&\frac{{\partial }N_{ xy }}{{\partial }x}+\frac{{\partial }N_y}{{\partial }y}=m_0\frac{{\partial }^2v}{{\partial }t^2}, \end{aligned} \end{aligned}$$
(6)
$$\begin{aligned} \begin{aligned}&\frac{{\partial }^2M_x}{{\partial }x^2}+2\frac{{\partial }^2M_{ xy }}{{\partial }x{\partial }y}+\frac{{\partial }^2M_y}{{\partial }y^2}= -\frac{{\partial }}{{\partial }x}\left( N_x\frac{{\partial }w}{{\partial }x}+N_{ xy }\frac{{\partial }w}{{\partial }y}\right) -\\&-\frac{{\partial }}{{\partial }y}\left( N_{ xy }\frac{{\partial }w}{{\partial }x}+N_y\frac{{\partial }w}{{\partial }y}\right) +m_0\frac{{\partial }^2w}{{\partial }t^2}, \end{aligned} \end{aligned}$$
(7)

with

$$\begin{aligned} m_0=\int _{-h/2}^{h/2} \rho dz . \end{aligned}$$
(8)

In Eqs. (6), (7) h stands for thickness and \(\rho\) is the density of the plate. The resultant in-plane forces and moments are as follows [47]:

$$\begin{aligned} \begin{aligned} N_x=&\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{xx}dz, N_y=\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{yy}dz,\\ N_{xy}=&\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{xy}dz, \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned} \begin{aligned} M_x=&\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{xx}zdz, M_y=\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{yy}zdz,\\ M_{xy}=&\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{xy}zdz. \end{aligned} \end{aligned}$$
(10)

In view of Eqs. (3), (9), (10), the next relations can be formulated as [48]

$$\begin{aligned} \begin{bmatrix} &{}&{}N_{x}\\ N_{y}\\ N_{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} N_{x}\\ N_{y}\\ N_{xy} \end{bmatrix}= h\begin{bmatrix} \frac{E}{1-\nu ^2 }&{} \quad \frac{\nu E}{1-\nu ^2}&{} \quad 0\\ \frac{\nu E}{1-\nu ^2}&{} \quad \frac{E}{1-\nu ^2}&{} \quad 0\\ 0&{} \quad 0&{} \quad \frac{E}{2(1+\nu )}\\ \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}^0\\ \varepsilon _{yy}^0\\ \varepsilon _{xy}^0 \end{bmatrix}, \end{aligned}$$
(11)
$$\begin{aligned} \begin{bmatrix} M_{x}\\ M_{y}\\ M_{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} M_{x}\\ M_{y}\\ M_{xy} \end{bmatrix}= \frac{h^3}{12}\begin{bmatrix} \frac{E}{1-\nu ^2 }&{} \quad \frac{\nu E}{1-\nu ^2}&{} \quad 0\\ \frac{\nu E}{1-\nu ^2}&{} \quad \frac{E}{1-\nu ^2}&{} \quad 0\\ 0&{} 0&{}\frac{E}{2(1+\nu )}\\ \end{bmatrix} \begin{bmatrix} k_{xx}\\ k_{yy}\\ k_{xy} \end{bmatrix}. \end{aligned}$$
(12)

Taking into account Eq.(4), the relations (12) are written explicitly

$$\begin{aligned} \begin{aligned} M_{x} -\mu \nabla ^2 M_{x}=-D(\frac{\partial ^2 w}{\partial x^2}+\nu \frac{\partial ^2 w}{\partial y^2}),\\ M_{y} -\mu \nabla ^2 M_{y}=-D(\nu \frac{ \partial ^2 w}{\partial x^2}+\frac{\partial ^2 w}{\partial y^2}),\\ M_{xy} -\mu \nabla ^2 M_{xy}=-D(1-\nu )\frac{\partial ^2 w}{\partial x \partial y}, \end{aligned} \end{aligned}$$
(13)

where \(D=\frac{Eh^3}{12(1-\nu ^2)}\) represents flexural nanoplate rigidity. In current investigation we use the mixed form of the governing equations, so the stress Airy function is introduced by the following relations:

$$\begin{aligned} N_x=\frac{\partial ^2F}{\partial y^2}, N_y=\frac{\partial ^2F}{\partial x^2}, N_{ xy }=-\frac{\partial ^2F}{\partial x\partial y}, \end{aligned}$$
(14)

and propagation of waves in longitudinal equations is neglected. The Eq. (7) in terms of deflection w and stress Airy function F, considering (13) and (14), can be presented in the following counterpart form

$$\begin{aligned} \begin{aligned} D\varDelta ^2 w=\left( 1-\mu {\nabla }^2\right) \left(L\left( w,F\right) -m_0\frac{\partial ^{2,}w}{\partial t^2}\right), \end{aligned} \end{aligned}$$
(15)

where \(\varDelta ^2=\left(\frac{\partial ^2}{\partial x^2} +\frac{\partial ^2}{\partial y^2}\right)^2\). Expressing the strains \(\varepsilon _{xx}^0, \varepsilon _{yy}^0, \varepsilon _{xy}^0\) from Eq. (11) and substituting them into the the compatibility Eq. (5), the second equation connecting the stress function F and deflection w is obtained

$$\left( {1 - \mu \nabla ^{2} } \right)\frac{1}{E}\Delta ^{2} F = - \frac{h}{2}L\left( {w,w} \right).{\text{ }}$$
(16)

The differential operators L(w, F), L(w, w) in (15), (16) are defined below

$$\begin{aligned} \begin{aligned} L\left( w,F\right)&=\frac{{\partial }^2w}{{\partial }x^2}\frac{{\partial }^2F}{{\partial }y^2}+\frac{{\partial }^2F}{{\partial }x^2}\frac{{\partial }^2w}{{\partial }y^2}-2\frac{{\partial }^2w}{{\partial }x{\partial }y}\frac{{\partial }^2F}{{\partial }x{\partial }y}, \\ L\left( w,w\right)&=2\left( \frac{{\partial }^2w}{{\partial }x^2}\frac{{\partial }^2w}{{\partial }y^2}-\left( \frac{{\partial }^2w}{{\partial }x{\partial }y}\right) ^2\right) . \end{aligned} \end{aligned}$$
(17)

2.2 Double-layer nanoplate system

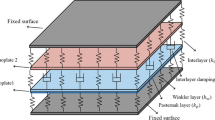
Now we consider the double-layer graphene sheet system (DLGSs). Interaction between two layers regards the action of van der Waals force (vdW) [49, 50]. This interaction is often modeled as the Winkler foundation [33], (Fig. 1). We assume that both nanoplates have the same mechanical properties. Taking into account the equations (15) and (16) the governing equations for each layer are taken as:

Fig. 1
figure 1

Diagram of double-layer graphene sheet system

Full size image

1-st nanoplate:

$$\begin{aligned} \begin{aligned} D\varDelta ^2 w_1&=\left( 1-\mu {\nabla }^2\right) (L\left( w_1,F_1\right) \\&\quad -c(w_1-w_2)-m_0\frac{\partial ^{2,}w_1}{\partial t^2} ), \\&\quad \left( 1-\mu {\nabla }^2\right) \frac{1}{E}\varDelta ^2F_1=-\frac{h}{2}L\left( w_1,w_1\right) , \end{aligned} \end{aligned}$$
(18)

where c stands for interaction coefficient. System of of the governing equations for the 1-st nanoplate is supplemented with the boundary conditions:

  1. (1)

    simply supported movable edges

    $$\begin{aligned} \begin{aligned} w_1=0,\frac{{\partial }^2w_1}{{\partial }x^2}+\nu \frac{{\partial }^2w_1}{{\partial }y^2}=0, \frac{{\partial }^2F_1}{{\partial }x{\partial }y}=0,\\ \int _0^b\frac{{\partial }^2F_1}{{\partial }y^2}dy=0,x=0,a, \\ w_1=0,\frac{\partial ^2w_1}{\partial y^2}+\nu \frac{{\partial }^2w_1}{{\partial }x^2}=0, \frac{{\partial }^2F_1}{{\partial }x{\partial }y}=0,\\ \int _0^a\frac{{\partial }^2F_1}{{\partial }x^2}dx=0,y=0,b; \end{aligned} \end{aligned}$$
    (19)
  2. (2)

    simply supported immovable edges:

    $$\begin{aligned} \begin{aligned} w_1=0,\frac{{\partial }^2w_1}{{\partial }x^2}+\nu \frac{{\partial }^2w_1}{{\partial }y^2}=0, \frac{{\partial }^2F_1}{{\partial }x{\partial }y}=0,u_1=0,x=0,a, \\ w_1=0,\frac{{\partial }^2w_1}{{\partial }y^2}+\nu \frac{{\partial }^2w_1}{{\partial }x^2}=0, \frac{{\partial }^2F_1}{{\partial }x{\partial }y}=0,v_1=0, y=0,b,\\ u_1=\int _0^x((1-\mu \nabla ^2 )\frac{1}{Eh}\left(\frac{\partial ^2F_1}{\partial y^2}-\nu \frac{\partial ^2F_1}{\partial x^2}\right)-\frac{1}{2}\left(\frac{\partial w_1}{\partial x})^2\right) dx ,\\ v_1=\int _0^y((1-\mu \nabla ^2 )\frac{1}{Eh}\left(\frac{\partial ^2F_1}{\partial x^2}-\nu \frac{\partial ^2F_1)}{\partial y^2}\right)-\frac{1}{2}\left(\frac{\partial w_1}{\partial y})^2\right) dy ; \end{aligned} \end{aligned}$$
    (20)

2-nd nanoplate:

$$\begin{aligned} \begin{aligned} D\varDelta ^2 w_2&=\left( 1-\mu {\nabla }^2\right) (L\left( w_2,F_2\right) -c(w_2-w_1)-m_0\frac{\partial ^{2,}w_2}{\partial t^2}, \\&\left( 1-\mu {\nabla }^2\right) \frac{1}{E}\varDelta ^2F_2=-\frac{h}{2}L\left( w_2,w_2\right) ; \end{aligned} \end{aligned}$$
(21)

the following boundary conditions for \(w_2\) and \(F_2\) are taken:

  1. (1)

    simply supported movable edges

    $$\begin{aligned} \begin{aligned} w_2=0,\frac{{\partial }^2w_2}{{\partial }x^2}+\nu \frac{{\partial }^2w_2}{{\partial }y^2}=0, \frac{{\partial }^2F_2}{{\partial }x{\partial }y}=0,\\ \int _0^b\frac{{\partial }^2F_2}{{\partial }y^2}dy=0,x=0,a, \\ w_2=0,\frac{\partial ^2w_2}{\partial y^2}+\nu \frac{{\partial }^2w_2}{{\partial }x^2}=0, \frac{{\partial }^2F_2}{{\partial }x{\partial }y}=0,\\\int _0^a\frac{{\partial }^2F_2}{{\partial }x^2}dx=0,y=0,b; \end{aligned} \end{aligned}$$
    (22)
  2. (2)

    simply supported immovable edges

    $$\begin{aligned} \begin{aligned} w_2=0,\frac{{\partial }^2w_2}{{\partial }x^2}+\nu \frac{{\partial }^2w_2}{{\partial }y^2}=0, \frac{{\partial }^2F_2}{{\partial }x{\partial }y}=0,u_2=0,x=0,a, \\ w_2=0,\frac{{\partial }^2w_2}{{\partial }y^2}+\nu \frac{{\partial }^2w_2}{{\partial }x^2}=0, \frac{{\partial }^2F_2}{{\partial }x{\partial }y}=0,v_2=0, y=0,b,\\ u_2=\int _0^x((1-\mu \nabla ^2 )\frac{1}{Eh}(\frac{\partial ^2F_2}{\partial y^2}-\nu \frac{\partial ^2F_2}{\partial x^2})-\frac{1}{2}(\frac{\partial w_2}{\partial x})^2) dx ,\\ v_2=\int _0^y((1-\mu \nabla ^2 )\frac{1}{Eh}(\frac{\partial ^2F_2}{\partial x^2}-\nu \frac{\partial ^2F_2)}{\partial y^2})-\frac{1}{2}(\frac{\partial w_2}{\partial y})^2) dy . \end{aligned} \end{aligned}$$
    (23)

3 Vibrations of double-layer nanoplate system in the magnetic field

The considered DLGSs is supposed to be under the in-plane uniaxial magnetic field, that can influence significantly on its behaviour [36, 37, 40]. The vector of magnetic field strength is defined as

$$\begin{aligned} \overrightarrow{H}=(H_x,0,0). \end{aligned}$$
(24)

Following [37, 45] and taking into account Maxwell’s relations one can get the Lorentz force for Kirchhoff–Love plate in the form

$$\begin{aligned} q_l=\int _{-h/2}^{h/2}f_z dz =\eta hH _x^2\left( \frac{{\partial }^2w}{{\partial }x^2}-\frac{{\partial }^2w}{{\partial }y^2}\right) , \end{aligned}$$
(25)

where \(\eta\) is the magnetic permeability. Thus, the governing system for DLGSs subjected to in-plane uniaxial magnetic field takes the form

$$\begin{aligned} \begin{aligned} D\varDelta ^2 w_1&=\left( 1-\mu {\nabla }^2\right) (L\left( w_1,F_1\right) -c(w_1-w_2)\\&+\eta hH _x^2\left( \frac{{\partial }^2w_1}{{\partial }x^2}-\frac{{\partial }^2w_1}{{\partial }y^2})-m_0\frac{\partial ^{2,}w_1}{\partial t^2}\right) , \\&\left( 1-\mu {\nabla }^2\right) \frac{1}{E}\varDelta ^2F_1=-\frac{h}{2}L\left( w_1,w_1\right) ,\\ D\varDelta ^2 w_2&=\left( 1-\mu {\nabla }^2\right) (L\left( w_2,F_2\right) -c(w_2-w_1)\\&+\eta hH _x^2\left( \frac{{\partial }^2w_2}{{\partial }x^2}-\frac{{\partial }^2w_2}{{\partial }y^2}\right) -m_0\frac{\partial ^{2,}w_2}{\partial t^2}, \\&\left( 1-\mu {\nabla }^2\right) \frac{1}{E}\varDelta ^2F_2=-\frac{h}{2}L\left( w_2,w_2\right) . \end{aligned} \end{aligned}$$
(26)

4 Nonlinear vibrations of double-layer nanoplate system

We present the deflections \(w_i(x,y,t), i=1,2\) of each nanoplate as

$$\begin{aligned} w_i\left( x,y,t\right) = y_i\left( t\right) W(x,y), i=1,2, \end{aligned}$$
(27)

where W(x, y) is shape function and \(y_i(t)\) is generalized coordinate for i-th layer. The shape function depends on the shape of the plate and boundary conditions, and in the considered case of rectangular simply supported nanoplate with sides a and b it has the form

$$\begin{aligned} W(x,y)=\sin \frac{ \pi x }{a}\sin \frac{ \pi y }{b}. \end{aligned}$$
(28)

Moreover, substitution (27) into the second and fourth equations of the governing system (26) yields the expressions for stress functions respectively:

$$\begin{aligned} F_i\left( x,y,t\right) =f_1\cos \frac{2\pi x}{a}+f_2\cos \frac{2\pi y}{b}+p_1 x^2+p_2y^2, \end{aligned}$$
(29)

where

$$\begin{aligned} f_1= & {} \frac{y_i^2 h Ea^4}{32b^2(a^2+4\mu \pi ^2)}, \nonumber \\ f_2= & {} \frac{y_i^2 h Eb^4}{32a^2 (b^2+4\mu \pi ^2)}, i=1,2, \end{aligned}$$
(30)

and \(p_1,p_2\) are defined from the boundary conditions. Thus, for movable boundary conditions (19), (22) \(p_1=0, p_2=0\), while for immovable boundary conditions (20), (23) these coefficients are determined by the following formulas

$$\begin{aligned} p_1=\frac{\pi ^2E y_i^2h(a^2+\nu b^2)}{16a^2b^2(1-\nu ^2)}, p_2=\frac{\pi ^2Ey_i^2h(\nu a^2+b^2)}{16a^2b^2(1-\nu ^ 2)}. \end{aligned}$$
(31)

Further, we replace the deflections and stress functions by their expressions (27), (29) in (18), (21) and apply the Bubnov–Galerkin approach that yields the following system of the coupled second order ordinary differential equations (ODEs)

$$\begin{aligned} \begin{aligned} y_1^{''}+ \alpha y_1+\beta (y_1- y_2)+\gamma y_1^3=0, \\ y_2^{''}+ \alpha y_2+\beta ( y_2-y_1)+\gamma y_2^3=0. \end{aligned} \end{aligned}$$
(32)

The coefficients of this system are determined in the following way

$$\begin{aligned} \alpha =\frac{\pi ^4{D}({a^2}+ {b^2})^2}{m_0a^2b^2(a^2b^2+\mu \pi ^2({a^2}+{b^2}))}\nonumber \\ +\frac{\pi ^2\eta h H_x^2}{m_0a^2b^2}(b^2-a^2), \beta =\frac{c}{m_0}, \end{aligned}$$
(33)

whereas the coefficient near the cubed terms is dependent on the boundary conditions type:

  1. (1)

    for movable plate we have

    $$\begin{aligned} \gamma =\frac{E\pi ^4h^3( a^2b^2(a^4+b^4)+4\mu \pi ^2(a^6+b^6))}{16m_0a^4b^4(a^2+4\mu \pi ^2 )(b^2+4\mu \pi ^2 )}, \end{aligned}$$
    (34)
  2. (2)

    for immovable plate one gets

    $$\begin{aligned} \begin{aligned} \gamma&=\frac{E\pi ^4h^3( a^2b^2(a^4+b^4)+4\mu \pi ^2(a^6+b^6))}{16m_0a^4b^4(a^2+4\mu \pi ^2 )(b^2+4\mu \pi ^2 )}+\\&\quad +\frac{E\pi ^4h^3(a^4+b^4+2\nu a^2b^2)}{8a^4b^4m_0(1-\nu ^2)}. \end{aligned} \end{aligned}$$
    (35)

    Solving the system (32) is performed by the method of harmonic balance. Presenting the solution as

    $$\begin{aligned} y_i=A_i \cos {\omega t}, i=1,2, \end{aligned}$$
    (36)

    where \(A_i, \omega\) are amplitude and frequency of vibrations, respectively, and expanding the equation coefficients by cosines, the following system is obtained

    $$\begin{aligned} \omega ^2 A_1=\alpha A_1+\beta (A_1-A_2)+\frac{3}{4}\gamma A_1^3, \end{aligned}$$
    (37)
    $$\begin{aligned} \omega ^2 A_2=\alpha A_2+\beta (A_2-A_1)+\frac{3}{4}\gamma A_2^3. \end{aligned}$$
    (38)

Further, we consider two cases:

  1. (1)

    in-phase vibration (IPV) mode, that means \(A_1 = A_2 = A\), and nonlinear frequency is defined as follows

    $$\begin{aligned} \omega _{1N}^2 =\omega _{1L}^2 +\frac{3}{4}\gamma A^2, \omega _{1L}^2 =\alpha , \omega _{1N}=\omega ; \end{aligned}$$
    (39)
  2. (2)

    anti-phase vibration (APV) mode, in this case \(A_1 =-A_2 = A\), thus, from (37) and (38) the nonlinear resonant frequency is derived as

    $$\begin{aligned} \omega _{2N}^2 =\omega _{2L}^2 +\frac{3}{4}\gamma A^2, \omega _{2L}^2 =\alpha +2\beta , \omega _{2N}=\omega . \end{aligned}$$
    (40)

It should be noted that \(\omega _{1L}, \omega _{2L}\) stand for linear frequencies of in-phase and anti-phase vibrations, respectively. Also it is shown that in case of in-phase vibrations frequency-amplitude ratio (39) does not depend on vdW interaction coefficient c and DLGSs behaves as single-layer nanoplate (Fig. 2).

Fig. 2
figure 2

Schematic diagrams of IPV (a) and APV (b) modes

Full size image

5 Numerical results

In order to validate the proposed algorithm we consider several problems. Presented formulas for linear frequencies (39), (40) [regarding (33)] in both cases coincide with reported in reference [25] after small transformation. It is worthy to mention that in case of IPV mode the linear frequency of DLGSs is the same as the linear corresponding frequency of SLGS, whereas in APV mode case the frequencies are higher due to vdW interaction. We calculated the natural frequencies of the double-layer isotropic simply supported square plate with side \(a=10nm\). The thickness of each layer is \(h=0.34nm\) and material properties are taken as follows [32, 49]

$$\begin{aligned} E=1.02\,\text {TPa}, \nu =0.16, \rho =2250\;\text {kg/m}^3. \end{aligned}$$
(41)

The vdW interaction is governed by the following fixed parameter \(c=108\) GPa/nm. In the work [32] the nonlocal parameter is neglected (\(\mu =0\)) and authors reported the following values of linear frequencies \(\omega _{1\,L}=0.0663\;\text {THz}, \omega _{2\,L}=2.6726\;\text {THz}\). At same time presented calculation gives \(\omega _{1L}=0.0665\;\text {THz}, \omega _{2L}=2.6752\;\text {THz}\).

The next test problem is aimed at nonlinear vibrations of single-layer plate in framework classical plate theory (\(\mu =0\)). The results are obtained for Poisson’s ratio \(\nu =0.3\) and simply supported boundary conditions (immovable case). Our results are compared with those published in [51,52,53] ones, see Table 1.

Table 1 Nonlinear frequency ratio \(\omega _N/ \omega _L\) of the isotropic simply supported immovable square plate (\(\nu =0.3\))
Full size table

As a test study case, the problem of the influence of a unidirectional magnetic field on vibrations of a single-layer graphene sheet is considered. We compared the results with ones presented in [37], where the properties of the plate are taken as follows: \(E=1.06\;\text {TPa}, \nu =0.25, \rho =2300\,\;\text {kg/m}^3, h=0.34\;\text {nm}\). The dimensionless frequency parameter \(\varOmega _{1L}=\omega _{1L}a^2 \sqrt{\frac{\rho h}{D}}\) [37] is calculated for various values of magnetic parameter MP, defined by the formula

$$\begin{aligned} MP=\frac{\eta hH_x^2 a^2}{D}, \end{aligned}$$
(42)

and for nonlocal ratio \(\sqrt{\mu }/a\). These results are calculated for square nanoplate \(a/b=1\) (a) as well as nanoribbon \(a/b=10^{-5}\) (b) and presented in Fig. 3. Comparing the results one can conclude that the values of frequency parameters are very close to those obtained by Kiani [37]. We have to mention that in the publication [37] the bending moments are taken into account, but its influence is negligible [41].

Fig. 3
figure 3

Dimensionless frequency parameter \(\varOmega _{1L}\) for various values of magnetic and nonlocal parameters

Full size image

The objective of the current study is focused on the analysis of the influence of the nonlocal parameter that occurred in the compatibility equation. Some researchers used the compatibility equation [see Eqs. (18), (21)] in the classical form (\(\mu =0\)). On the contrary, in this work, we considered three options for the derivation of the governing equations: the classical plate theory (CPT), the nonlocal plate theory with the classical compatibility equation (CCE) and the nonlocal compatibility equation (NCE). The numerical results are presented for DLGSs with the material properties presented in Eq. (41), the geometrical parameters \(a=10\;\text {nm}, h = 0.34 \;\text {nm}\) and interaction coefficient is \(c = 108 \;\text {GPa/nm}\). The nonlocal parameter is taken as \(\mu =2\;\text {nm}^2\) for the nonlocal elasticity theory (NCE, CCE). The nonlinear frequency ratios \(\omega _{1N}/ \omega _{1L}\) and \(\omega _{2N}/ \omega _{2L}\) are calculated for two cases of boundary conditions and presented in Fig. 4 (movable boundary conditions), Fig. 5 (immovable boundary conditions). It can be seen a difference in the results of the nonlocal theory with CCE and NCE for all considered cases. Moreover, for the simply supported immovable DLGSs, IPV mode, see Fig. 5a, the values of the nonlinear ratio \(\omega _{1N}/ \omega _{1L}\) found by the nonlocal theory are higher than the ones obtained by the classical plate theory. While for the simply supported movable plate the values of nonlinear ratio obtained by nonlocal theory with NCE are lower than the results of the classical theory, see Fig. 4a. It should be emphasized, that despite a negligible change in the nonlinear frequency ratio \(\omega _{2N}/ \omega _{2L}\) depending on the amplitude in the case of anti-phase vibration mode, the results of the nonlocal theory with NCE differ from the results of the nonlocal theory with CCE and classical plate theory (\(\mu =0\)). The values of the \(\omega _{2N}/ \omega _{2L}\) obtained by the nonlocal theory with NCE are lower than the corresponded ones by using classical plate theory as well as the nonlocal theory with CCE for movable and immovable boundary conditions.

Fig. 4
figure 4

Nonlinear frequency ratio for simply supported movable DLGSs for CPT, nonlocal theory with CCE, NCE

Full size image
Fig. 5
figure 5

Nonlinear frequency ratio for simply supported immovable DLGSs for CPT, nonlocal theory with CCE, NCE

Full size image

The influence of the magnetic field is investigated for a rectangular DLGSs with an aspect ratio \(b/a=2\), side size \(a=10\;\text {nm}\), and layer thickness \(h=0.34\;\text {nm}\), whereas material properties (41), and interaction parameter \(c=108\;\text {GPa/nm}\). In Table 2 one can find the values of dimensionless frequencies

$$\begin{aligned} \varOmega _{1L}= \omega _{1L} a^2\sqrt{\frac{\rho h}{D}}, \varOmega _{2L}=\omega _{2L} a^2\sqrt{\frac{\rho h}{D}} \end{aligned}$$

for several values of nonlocal parameter \(\mu\) and magnetic parameter MP, introduced by the formula (42)

Table 2 Dimensionless linear frequencies \(\varOmega _{1L}\), \(\varOmega _{2L}\) for rectangular DLGSs, \(b/a=2\), subjected to magnetic field with magnetic parameter MP
Full size table

Analyzing data in Table 2, it can be noted that an increase in the magnetic parameter MP brings an increase in the values of the frequency parameters, while with an increase in the small-scale parameter \(\mu\), the values of the frequency parameters decrease. Also, it is worth noting that in the case of anti-phase vibration mode the influence of the considered magnetic field is insignificant, as well as the effect of the change in the nonlocal parameter \(\mu\). The Figs. 6 and 7 show the amplitude-frequency dependencies for various values of the magnetic parameter MP. It can be mentioned the significant influence of the magnetic field on the considering characteristics for in-phase mode, including the more pronounced one for the immovable simply supported boundary conditions. An increase in the value of the magnetic parameter contributes to a decrease in the value of the frequency ratio. In the case of anti-phase mode vibrations of DLGSs, the effect of the magnetic field is negligible.

Fig. 6
figure 6

Nonlinear frequency ratio for movable simply supported DLGSs for \(MP=0,10,20,30,40,50, \mu =2\)

Full size image
Fig. 7
figure 7

Nonlinear frequency ratio for immovable simply supported DLGSs for \(MP=0,10,20,30,40,50, \mu =2\)

Full size image

6 Concluding remarks

The nonlinear vibrations of double-layer graphene sheet systems are studied. The governing equations of the problem are based on the nonlocal elasticity theory, Kirchhoff hypothesis, the von Kármán equations and are presented in the mixed form with the Airy function. Two graphene sheets are bonded by van der Waals force. Considered DLGSs is subjected to an in-plane uniaxial magnetic field, and the Lorentz force is included in the governing system.

The investigation of the influence of the nonlocal parameter in the compatibility equation is performed. It is concluded that the nonlocal parameter in the compatibility equation can significantly change the results and should be taken into account in order to achieve reliable results. It is shown that for all considered cases (movable and immovable boundary conditions, in-phase and anti-phase vibration modes) the values of the nonlinear frequency ratio obtained by the nonlocal theory are lower with NCE than with CCE. If in the case of anti-phase vibration mode, due to a very small difference in results, accounting for the nonlocal parameter may be omitted, then in the case of in-phase vibration mode this parameter in the compatibility equation plays an important role. The influence of the magnetic field is significant in the case of IPV mode, with an increase in the magnetic parameter MP, the value of the linear frequency parameter increases. It should be noted the effect of MP on the nonlinear amplitude-frequency characteristics as well.