Skip to main content
SpringerLink
Log in

An investigation of fluid-structure interaction in pipe conveying flow using reduced-order models

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

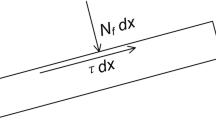
Fluid-structure interactions are essential to be evaluated in pipelines where the fluid dynamics induces structural vibrations that need to be properly investigated for engineering design. The flow of internal fluids can be laminar or turbulent, which makes such analysis a complex task. This paper investigates the analysis of Fluid-structure interaction from reduced-order models where a Bernoulli–Euler beam is employed to represent the pipe while fluid dynamics is represented by nonlinear oscillators. Structural analysis employs the Galerkin method for spatial discretization. Fluid dynamics is described by considering van der Pol oscillator together with the Langevin equation. In this regard, laminar and turbulent responses are described. Results show that the reduced-order model allows one to replicate the frequency spectrum of the pipeline response considering the parametric variation of the flow velocity and stochastic fluctuations. Nonlinear dynamics perspective shows to be interesting representing instabilities and some complex responses as limit cycle behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Aranha JAP (2004) Weak three dimensionality of a flow around a slender cylinder: the ginzburg-landau equation. J Braz Soc Mech Sci Eng 26(4):355–367. https://doi.org/10.1590/S1678-58782004000400002

    Article  Google Scholar 

  2. Bai Y, Xie W, Gao X, Xu W (2018) Dynamic analysis of a cantilevered pipe conveying fluid with density variation. J Fluids Struct 81:638–655. https://doi.org/10.1016/j.jfluidstructs.2018.06.005

    Article  Google Scholar 

  3. Czerwi A (2018) Non-planar vibrations of slightly curved pipes conveying fluid in simple and combination parametric resonances. J Sound Vib 413:270–290. https://doi.org/10.1016/j.jsv.2017.10.026

    Article  Google Scholar 

  4. El-Sayed TA, El-Mongy HH (2019) Free vibration and stability analysis of a multi-span pipe conveying fluid using exact and variational iteration methods combined with transfer matrix method. Appl Math Model 71:173–193. https://doi.org/10.1016/j.apm.2019.02.006

    Article  MathSciNet  MATH  Google Scholar 

  5. Franzini GR, Bunzel LO (2018) A numerical investigation on piezoelectric energy harvesting from vortex-induced vibrations with one and two degrees of freedom. J Fluids Struct 77:196–212. https://doi.org/10.1016/j.jfluidstructs.2017.12.007

    Article  Google Scholar 

  6. Gonçalves RT, Franzini GR, Rosetti GF, Fujarra ALC, Nishimoto K (2012) Analysis methodology for vortex-induced motion (VIM) of a monocolumn platform applying the Hilbert-Huang transform. Offshore Mech Artic Eng. https://doi.org/10.1115/1.4003493

    Article  Google Scholar 

  7. Gu J, Ma T, Duan M (2016) Effect of aspect ratio on the dynamic response of a fluid-conveying pipe using the Timoshenko beam model. Ocean Eng 114:185–191. https://doi.org/10.1016/j.oceaneng.2016.01.021

    Article  Google Scholar 

  8. Korkischko IÃ, Meneghini JR (2010) Experimental investigation of flow-induced vibration on isolated and tandem circular cylinders fitted with strakes. J Fluids Struct 26(4):611–625. https://doi.org/10.1016/j.jfluidstructs.2010.03.001

    Article  Google Scholar 

  9. Kurushina V, Pavlovskaia E, Postnikov A, Wiercigroch M (2018) Calibration and comparison of VIV wake oscillator models for low mass ratio structures. Int J Mech Sci 142–143:547–560. https://doi.org/10.1016/j.ijmecsci.2018.04.027

    Article  Google Scholar 

  10. Loiseau J-C, Noack BR, Brunton SL (2018) Sparse reduced-order modelling: sensor-based dynamics to full-state estimation. J Fluid Mech 844:459–490

    Article  MATH  Google Scholar 

  11. Lü L, Hu Y, Wang X, Ling L (2015) Dynamical bifurcation and synchronization of two nonlinearly coupled fluid-conveying pipes. Nonlinear Dyn 79:2715–2734. https://doi.org/10.1007/s11071-014-1842-y

    Article  MathSciNet  MATH  Google Scholar 

  12. Meng S, Kajiwara H, Zhang W (2017) Internal flow effect on the cross-flow vortex-induced vibration of a cantilevered pipe discharging fluid. Ocean Eng 137:120–128. https://doi.org/10.1016/j.oceaneng.2017.03.055

    Article  Google Scholar 

  13. Ni Q, Wang Y, Tang M, Luo Y, Yan H, Wang L (2015) Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints. Nonlinear Dyn 81:893–906. https://doi.org/10.1007/s11071-015-2038-9

    Article  Google Scholar 

  14. Ni Q, Luo Y, Li M, Yan H (2017) Natural frequency and stability analysis of a pipe conveying fluid with axially moving supports immersed in fluid. J Sound Vib 403:173–189. https://doi.org/10.1016/j.jsv.2017.05.023

    Article  Google Scholar 

  15. Ogink RHM, Metrikine A (2010) A wake oscillator with frequency dependent coupling for the modeling of vortex-induced vibration. J Sound Vib 329(26):5452–5473. https://doi.org/10.1016/j.jsv.2010.07.008

    Article  Google Scholar 

  16. Orsino RMM, Pesce CP, Franzini GR (2018) Cantilevered pipe ejecting fluid under VIV : an investigation based on a planar nonlinear reduced-order model. J Braz Soc Mech Sci Eng. https://doi.org/10.1007/s40430-018-1467-z

    Article  Google Scholar 

  17. Païdoussis MP, Luu TP, Prabhakar S (2008) Dynamics of a long tubular cantilever conveying fluid downwards, which then flows upwards around the cantilever as a confined annular flow. J Fluids Struct 24(1):111–128. https://doi.org/10.1016/j.jfluidstructs.2007.07.004

    Article  Google Scholar 

  18. Païdoussis MP (2013) Fluid-structure interactions. Academic Press

    Google Scholar 

  19. Pavlovskaia E, Keber M, Postnikov A, Reddington K, Wiercigroch M (2016) Multi-modes approach to modelling of vortex-induced vibration. Int J Non-Linear Mech 80:40–51. https://doi.org/10.1016/j.ijnonlinmec.2015.11.008

    Article  Google Scholar 

  20. Pope SB (1994) Lagrangian PDF methods for turbulent flows. Annu Rev Fluid Mech 26:23–63. https://doi.org/10.1146/annurev.fluid.26.1.23

    Article  MathSciNet  MATH  Google Scholar 

  21. Postnikov A, Pavlovskaia E, Wiercigroch M (2017) 2DOF CFD calibrated wake oscillator model to investigate vortex-induced vibrations. Int J Mech Sci 127:176–190. https://doi.org/10.1016/j.ijmecsci.2016.05.019

    Article  Google Scholar 

  22. Ritto TG, Soize C, Rochinha FA, Sampaio R (2014) Dynamic stability of a pipe conveying fluid with an uncertain computational model. J Fluids Struct 49:412–426. https://doi.org/10.1016/j.jfluidstructs.2014.05.003

    Article  Google Scholar 

  23. Sazesh S, Shams S (2019) Vibration analysis of cantilever pipe conveying fluid under distributed random excitation. J Fluids Struct 87:84–101. https://doi.org/10.1016/j.jfluidstructs.2019.03.018

    Article  Google Scholar 

  24. Tang Y, Zhen Y, Fang B (2018) Nonlinear vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid. Appl Math Model 56:123–136. https://doi.org/10.1016/j.apm.2017.11.022

    Article  MathSciNet  MATH  Google Scholar 

  25. Ueno T (2019) Numerical investigations on passive supression of vortex-induced vibrations using non-linear vibration absorber: a wake-oscillator approach, MSc Dissertation, USP

Download references

Acknowledgements

The authors would like to acknowledge the support of the Brazilian Research Agencies CNPq, CAPES and FAPERJ.

Author information

Authors and Affiliations

  1. COPPE - Department of Mechanical Engineering, Center for Nonlinear Mechanics, Universidade Federal Do Rio de Janeiro, P.O. Box – 68.503, Rio de Janeiro, RJ, 21941-972, Brazil

    João D. B. dos Santos, Gustavo R. Anjos & Marcelo A. Savi

Authors
  1. João D. B. dos Santos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gustavo R. Anjos
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marcelo A. Savi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcelo A. Savi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

dos Santos, J.D.B., Anjos, G.R. & Savi, M.A. An investigation of fluid-structure interaction in pipe conveying flow using reduced-order models. Meccanica 57, 2473–2491 (2022). https://doi.org/10.1007/s11012-022-01586-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-022-01586-6

Keywords

Search

Navigation