Skip to main content
SpringerLink
Log in

Theoretical analysis of non-linear dynamic response of a bridge pier under two-phase flow excitation

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

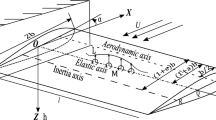
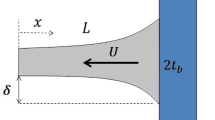
In this paper, analytical and numerical approaches are used to investigate the vibration and non-linear dynamic responses of a bridge pier under two harmonic excitations, caused by aero- and hydro-flows, acting on different portions of the beam. The mechanical system is reduced using the Galerkin method to an ordinary differential equation, and the multiple scale method (MSM) is employed to analyse sub- and super-harmonic resonances. The variation of beam amplitude of vibration caused by a significant effect due to axial force, and two-frequency excitations due to flows are captured. These conduct to the evaluation of nonlinear dynamic behaviour through some frequency-response curves, time history curves of amplitudes vibrations, and phase diagrams presented. In order to gain more features of this system, the discrete general equation is treated numerically. The results show a good accordance between the analytical and numerical solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. Simui and R. H. Scanlan, Wind Effects on Structures: Fundamentals and Applications to Design, 3rd Ed., John Wiley and Sons (1996).

  2. S. Di Nino and A. Luongo, Nonlinear aeroelastic behavior of a base-isolated beam under steady wind flow, International Journal of Non-Linear Mechanics, 119 (2020) 103340.

    Article  Google Scholar 

  3. Luongo and D. Zulli, Parametric, external and self-excitation of a tower under turbulent wind flow, J. Sound and Vib., 330 (13) (2011) 3057–3069.

    Article  Google Scholar 

  4. T. Rabczuk, E. Samaniego and T. Belytschko, Simplified model for predicting impulsive loads on submerged structures to account for fluid-structure interaction, Int. J. Impact Eng., 34 (2007) 163–177.

    Article  Google Scholar 

  5. L. M. Anague Tabejieu, B. R. Nana Nbendjo and G. Filatrella, Vibrations of an elastic beam subjected by two kinds of moving loads and positioned on a foundation having fractional order viscoelastic physical properties, Advances in Dyn. Sys. Theory, Models, Algorithms and Applications, IntechOpen (2021).

  6. A. M. Ngounou, S. C. Mba Feulefack, L. M. Anague Tabejieu and B. R. Nana Nbenjo, Design, aanalysis and horseshoes chaos control on tension leg platform system with fractional nonlinear viscoelastic tendon force under regular sea wave excitation, Chaos, Solitons and Fractals, 157 (2022) 111952.

    Article  Google Scholar 

  7. C. Xu, Z. Wang and B. Li, Dynamic stability of simply supported beams with multi-harmonic parametric excitation, Int. J. Struct. Stab. Dyn. (2021) 250027.

  8. H. Ilgin and M. Gunel, The role of aerodynamic modifications in the form of tall buildings against wind excitation, Metu Jfa (2011) (24) 2 (2007).

    Google Scholar 

  9. H. Moeenfard and S. Awtar, Modeling geometric nonlinearity in the free vibration of a planar beam flexure with a tip mass, Journal of Mechanical Design, 136 (2014) 044502–1.

    Article  Google Scholar 

  10. W. Su and C. Cesnik, Strain-baised geometrically nonlinear beam formulation ofr modelling very flexible aircraft, Int. J. Solids Struct., 48 (2011) 2349–2360.

    Article  Google Scholar 

  11. A. Mamandi and H. Mohammad, Dynamic analysis of inclined Timoshenko beam travaled by successive moving masses forces with inclusion of geometric nonlinearities, Acta Mech., 218 (2011) 9–29.

    Article  MATH  Google Scholar 

  12. I. Kovacic and M. J. Brennan, The Duffing Equation: Nonlinear Oscillators and Their Behaviour, John Wiley and Sons, UK (2011).

    Book  MATH  Google Scholar 

  13. L. N. Virgin, Introduction to Experimental Nonlinear Dynamics: A Case Study in Mechanical Vibration, Cambridge University Press, Cambridge (2000).

    Book  MATH  Google Scholar 

  14. J. Peng, G. Zhang, M. Xiang, H. Sun, X. Wang and X. Xie, Vibration control for the nonlinear resonant response of piezoelectric elastic beam via time-delayed feedback, Smart Mater. Struct., 28 (9) (2019) 095010.

    Article  Google Scholar 

  15. A. M. Ngounou, B. R. N. Nbendjo and U. Dorka, Effect of the delay between the direction of vibration and the action of tendons on the dynamics response of tension leg platform (TLP) under sea waves excitations, Journal of Applied Nonlinear Dynamics, 10 (4) (2021) 643–659.

    Article  Google Scholar 

  16. A. Sofroniou and S. Bishop, Dynamics of a parametrically excited system with two forcing terms, Mathematics, 2 (3) (2014) 172–195.

    Article  MATH  Google Scholar 

  17. H. Kang, Y. Cong and G. Yan, Theoretical analysis of dynamic behaviors of cable-stayed bridges excited by two harmonic forces, Nonlinear Dyn., 102 (2020) 965–992.

    Article  Google Scholar 

  18. Y. Cong, H. Kang and G. Yan, Investigation of dynamic behavior of a cable-stayed cantilever beam under two-frequency excitations, International Journal of Non-Linear Mechanics, 129 (2021) 103670.

    Article  Google Scholar 

  19. Y. Zhao, Z. Guo, C. Huang, L. Chen and S. Li, Analytical solutions for planar simultaneous resonances of suspended cables involving two external periodic excitations, Acta Mech., 229 (2018) 4393–4411.

    Article  MathSciNet  MATH  Google Scholar 

  20. C. Sun, X. Zhou and S. Zhou, Nonlinear responses of suspended cable under phase-differed multiple support excitations, Nonlinear Dyn., 104 (2021) 1097–1116.

    Article  Google Scholar 

  21. B. Sahoo, L. N. Panda and G. Pohit, Combination, principal parametric and internal resonances of an accelerating beam under two frequency parametric excitation, International Journal of Non-Linear Mechanics, 78 (2016) 35–44.

    Article  Google Scholar 

  22. Y. Zhao, C. Huang, L. Chen and J. Peng, Nonlinear vibration behaviors of suspended cables under two-frequency excitation with temperature effects, Journal of Sound and Vibration, 416 (2018) 279–294.

    Article  Google Scholar 

  23. J. D. Bricker, K. Kawashima and A. Nakayama, CFD analysis of bridge deck failure due to tsunami, Proceeding of Int. Symposium on Eng. Lessons Learned from the 2011 Great East Japan Earthquake, Japan (2012).

  24. S. Kaneko, T. Nakamura, F. Inada and M. Kato, Flow Induced Vibrations: Classifications and Lessons from Practical Experiences, Japan Society of Mechanical Engineers, Elsevier Ltd. (2014).

  25. I. D. R. Grant, Flow and pressure drop single-phase and two-phase flow on the shell side of segmentally baffled shell-and-tube exchangers, Advances in Thermal and Mechanical Design of Shelland-Tube Heat Exchangers, Report of a Meeting at NEL (1975) Report No. 590.

  26. F. K. Alfosail and M. I. Younis, Multi-frequency excitation of an inclined marine riser under internal resonances, Nonlinear Dynamics, 99 (2020) 149–171.

    Article  MATH  Google Scholar 

  27. S. P. Timoshenko and J. M. Gere, Theory of Elastic Stability, 2nd Ed., McGraw-Hill (1961).

  28. I. A. Karnovsky and O. I. Lebed, Formulas for Structural Dynamics: Tables, Graphs and Solutions, McGraw Hill (2004).

  29. S. Di Nino and A. Luongo, Nonlinear dynamics of a baseisolated beam under turbulent wind flow, Nonlinear Dyn., 107 (2022) 1529–1544.

    Article  Google Scholar 

  30. S. Di Nino and A. Luongo, Nonlinear interaction between self-and parametrically excited wind-induced vibrations, Nonlinear Dyn., 103 (2021) 79–101.

    Article  Google Scholar 

  31. W. Yang and Q. Li, The expanded Morison equation considering inner and outer water hydrodynamic pressure of hollow piers, Ocean Engineering, 69 (2013) 79–87.

    Article  Google Scholar 

  32. R. H. Plaut, N. Haquang and D. T. Mook, Simultaneous resonances in non-linear structural vibrations under two-frequency excitation, J. Sound. Vib., 106 (3) (1986) 361–376.

    Article  MATH  Google Scholar 

  33. J. R. Morison, M. P. O’Brien, J. W. Johnson and S. A. Schaaf, The force exerted by surface waves on piles, Petroleum Transactions, AIME, 189 (1950) 2846.

    Google Scholar 

  34. Z. G. Ying, Y. Q. Ni and L. Fan, Parametrically excited stability of periodically supported beams under longitudinal harmonic excitations, International Journal of Structural Stability and Dynamics, 19 (9) (2019) 1950095.

    Article  MathSciNet  Google Scholar 

  35. A. M. Elshurafa, K. Khirallah, H. H. Tawifk, A. Emira, A. K. S. Abdel Aziz and S. M. Sedky, Nonlinear dynamics of spring softening and hardening in folded-MEMS comb drive resonators, Journal of Microelectromechanical Systems, 20 (4) (2011) 943–958.

    Article  Google Scholar 

  36. A. H. Nayfeh and P. F. Pai, Linear and Nonlinear Structural Mechanics, Wiley-VCH, Germany (2004).

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Applied Mechanics, Department of Physics, University of Yaounde 1, P.O. BOX 812, Yaounde, Cameroon

    Loic Z. Ngou, Hyacinthe K. Simo, Benjamin K. Lekama & Yves C. Mbono Samba

  2. Laboratory of Fundamental Mechanics and Complex Systems, Department of Physics, University of Yaounde 1, P.O. BOX 812, Yaounde, Cameroon

    Serge I. Fewo

Authors
  1. Loic Z. Ngou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hyacinthe K. Simo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Benjamin K. Lekama
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Serge I. Fewo
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yves C. Mbono Samba
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yves C. Mbono Samba.

Additional information

Pr Mbono Samba Yves C. is an Associate Professor of University of Yaoundé 1. He received his Ph.D. in University of Paris 6 in 1995. His research interests include fluid-structure interactions, fluid mechanics, multibody dynamics, structural dynamics, multiphase flow and turbulent flow.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ngou, L.Z., Simo, H.K., Lekama, B.K. et al. Theoretical analysis of non-linear dynamic response of a bridge pier under two-phase flow excitation. J Mech Sci Technol 37, 5683–5693 (2023). https://doi.org/10.1007/s12206-023-1009-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-023-1009-1

Keywords

Search

Navigation