A hysteretic model of localized frictional contacts with instrumental stiffness

Abstract

The steady-state dynamic response of a single-degree-of-freedom system comprising both a hysteretic element and a spring is considered. The Hertz–Cattaneo–Mindlin theoretical framework for modeling of local tangential contact with friction is applied in conjunction with the Masing model of hysteresis to describe the hysteretic behavior of the multiple localized frictional contact interface. The steady-state tangential displacement amplitude of a rigid body under harmonic tangential force excitation is approximately determined by means of the equivalent linearization technique, based on the harmonic balance principle. A special attention is paid to the evaluation of the frictional damping and the determination of the backbone curve of the Masing model from the dissipation-amplitude relation.

1 Introduction

Systems with localized frictional contacts, which can be found in various engineering applications [1, 2], exhibit both hysteretic dissipative behavior and elastic nonlinearity (due to variable contact area). The recent interest to such systems was inspired by studies of relaxation damping [3]. Therefore, modeling of the hysteretic-type nonlinear effect in mechanical oscillations is an important issue [4].

Several models of hysteresis are available in the literature [5,6,7]. In particular, the bilinear model of hysteresis was used in a number of papers [8,9,10]. The steady-state dynamic response of a single-degree-of-freedom (SDoF) system with a histeretic element of a Preisach type [6, 11] was studied analytically by Spanos et al. [12], using the equivalent linearization technique. Very recently, Casini and Vestroni [13] applied the Bouc–Wen model [14] for describing the hysteretic behavior of SDoF mechanical systems.

The properties of rate-independent hysteresis were considered by Al-Bender et al. [15], who showed that the regime of free oscillations of a SDoF hysteretic system is amendable to an exact solution. They also examined the case of forced oscillations by an approximate treatment using the Masing model of hysteresis [16]. An overview of approximate analytical tools applicable for the analysis of nonlinear steady-state dynamic response of hysteretic oscillators was given by Wong et al. [17].

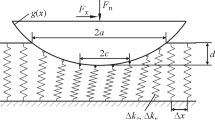
In the present paper, we apply the Cattaneo–Mindlin theory [18, 19] to model the tangential reaction force at the localized frictional contact interface (see Fig. 1a). An analogous modeling framework has been previously used in a number of papers [20,21,22,23]. Experimentally, this approach was verified by Koh et al. [20]. A novel feature of our study is that one of the hysteretic elements of Masing type is assumed to be connected in series to a spring element (see Fig. 1b).

Fig. 1

Hysteretic models: a Cattaneo–Mindlin model; b Series connection of a linear spring element with a Cattaneo–Mindlin element

In what follows, we utilize the Masing modeling framework to describe the frictional contact force, which assumes that the unloading and reloading force–displacement relations in a cyclic tangential loading are geometrically similar to the initial-loading curve, called the backbone relation. A state-of-the-art literature survey on the application of Masing’s hypothesis in the analysis of frictional interface was given by Huang et al. [24] and Mathis et al. [25]. At the same time, there is another equivalent analytical description of frictional interfaces [26, 27], which is associated with the so-called Iwan’s models. The latter mechanistic models are composed of spring/frictional damper elements and are regarded as appropriate in the development of physically based models for the incorporation of interfaced-induced dissipation in larger structural models [28].

As it was shown by Segalman and Starr [16], any Masing model has an equivalent Iwan model [29]. In particular, the Cattaneo–Mindlin type backbone curve

$$\begin{aligned} F(x)=F_{\max }\left\{ \begin{array}{ll} \displaystyle 1-\Bigl (1-\frac{x}{x_{*}}\Bigr )^{\beta }, &{}\quad x\in (0,x_{*}), \\ 1, &{} \quad x\ge x_{*} \end{array} \right. \end{aligned}$$

(1)

can be represented in the form of the Iwan parallel-series model (see Fig. 2) in simple loading by the force–displacement relation

$$\begin{aligned} F(x)=\int \limits _{0}^{x} \xi \varrho (\xi )\,d\xi +x\int \limits _{x}^{\infty }\varrho (\xi )\,d\xi \end{aligned}$$

(2)

with the density

$$\begin{aligned} \varrho (x)=F_{\max }\left\{ \begin{array}{ll} \displaystyle \frac{\beta (1-\beta )}{x_{*}^{2}} \Bigl (1-\frac{x}{x_{*}}\Bigr )^{\beta -2}, &{}\quad x\in (0,x_{*}), \\ 0, &{}\quad x\ge x_{*}. \end{array} \right. \end{aligned}$$

It should be underlined that both the Masing modeling framework and the Iwan models are phenomenological approaches—in the sense that either the backbone curve of Masing model or the Iwan density function should be identified via fitting the model response to experimental data on the reaction of a frictional interface to tangential loading. On the other hand, the Cattaneo–Mindlin theory can be regarded as a predictive model, since it readily provides the form of tangential force–displacement relation for a specified Hertzian contact geometry. That is why, while the analysis developed below is fairly general (i.e., applicable for a wide class of Masing models), we utilize the Cattaneo–Mindlin theory in order to be as much specific as possible. The latter theory was recently extended to the case of elastically similar, transversely isotropic elastic materials [30] and generalized [31] by introducing an ‘adhesive’ model for friction in the Hertzian spherical contact.

Fig. 2

a Iwan parallel-series model; b A series connection of the Iwan element with a linear spring element

For our purposes, we would need to consider a series connection of the Iwan element (2) with a linear spring element of stiffness k, which is called the instrumental stiffness (see Fig. 2b). The problem is not as simple as it would appear at first sight. Interestingly, though the parallel-series and series-parallel Iwan models have similar features (see Figs. 2a and 3), a series connection of a linear spring element with a parallel-series Iwan element (compare Figs. 1b and 2b) is not reduced to known modeling schemes [16, 29, 32]. Since this conclusion is not evident, it is explained briefly in the next two paragraphs.

Fig. 3

Iwan series–parallel model

It is clear that in the range of displacement $x\in (0,x_{*})$, the response of the Iwan element is equivalent to that of a non-linear spring element with the force–displacement relation $F={\mathcal{F}}(x)$, where the function ${\mathcal{F}}(x)$ is given by the first line on the right-hand side of Eq. (1). Therefore, by denoting its inverse function as $x={\mathcal{F}}^{-1}(F)$, the mentioned series connection (see Fig. 2b) will be characterized by the displacement–force relation

$$\begin{aligned} x=\frac{F}{k}+{\mathcal{F}}^{-1}(F). \end{aligned}$$

(3)

A general theory for analytical evaluating the inverse constitutive relations in the Iwan models was developed by Segalman and Starr [16]. However, it should be underlined that the method of inversion of Masing models via continuous Iwan systems suggested in [16] is not applicable if $x\ge x_{*}$, when the density $\varrho (x)$ is identically equal to zero and, therefore, the incremental stiffness vanishes. That is why, the specific hysteretic frictional system under consideration is not covered by the general theory [16]. Moreover, for the purpose of dynamic analysis, generally speaking, one needs to invert Eq. (3) to express the friction reaction F in terms of the displacement x. In the case (1), when $\beta =3/2$, this can be done by reducing Eq. (3) to a cubic equation. In our method of evaluating the evaluation of the frictional damping, presented below, we avoid this tedious approach and consider the general case $\beta \in [1,2]$, as it is suggested by the generalized Cattaneo–Mindlin theory [33, 34] (see also, [35], Chapter 6).

The aim of the present study is to account for the so-called instrumental stiffness effect in a mechanically motivated hysteretic modeling of localized frictional contacts.

2 A single-degree-of-freedom oscillating system with a Masing-type hysteresis

Consider a parallelepiped block of mass m resting on three hemispherical support pads of radius $R_{3}$, which are fixed on a rigid base (see Fig. 4). The block is loaded in the vertical direction by a constant normal load, $F_{N}^{0}$, applied on the fourth hemispherical pad of radius $R_{1}$, which is in contact with the upper surface of the block and is assumed to be elastically fixed in the tangential direction by means of a linear spring of finite stiffness $k_{2}$ (or, equivalently, by two springs of stiffness $k_{2}/2$ connected in parallel). The block is supposed to be excited by a tangential force of amplitude $F_{T}^{0}$ and angular frequency $\omega$. The stiffness $k_{2}$ is termed as the instrumental stiffness, as its purpose is to characterize the tangential fixation of the load element.

Fig. 4

A single-degree-of-freedom system with a Masing-type hysteresis

We assume that the parallelepiped block, the three lower and one upper hemispherical pads are made of different linearly-elastic materials with the Young’s moduli and Poisson’s ratios $E_{0}$, $\nu _{0}$, $E_{3}$, $\nu _{3}$, and $E_{1}$, $\nu _{1}$, respectively. Thus, the upper and lower local contacts will be characterized by the following reduced elastic and shear moduli [36]:

$$\begin{aligned} E_{01}^{*}&=\Bigl (\frac{1-\nu _{0}^{2}}{E_{0}}+\frac{1-\nu _{1}^{2}}{E_{1}}\Bigr )^{-1},\nonumber \\ G_{01}^{*}&=\biggl (\frac{(2-\nu _{0})(1+\nu _{0})}{2E_{0}}+ \frac{(2-\nu _{1})(1+\nu _{1})}{2E_{1}}\biggr )^{-1}, \end{aligned}$$

(4)

$$\begin{aligned} E_{03}^{*}&=\Bigl (\frac{1-\nu _{0}^{2}}{E_{0}}+\frac{1-\nu _{3}^{2}}{E_{3}}\Bigr )^{-1},\nonumber \\ G_{03}^{*}&=\biggl (\frac{(2-\nu _{0})(1+\nu _{0})}{2E_{0}}+ \frac{(2-\nu _{3})(1+\nu _{3})}{2E_{3}}\biggr )^{-1}. \end{aligned}$$

(5)

By neglecting the elastic wave phenomena in the block, we may assume that the contact reactions at the support pads can be determined from the static equilibrium equations. The analysis can be simplified further by neglecting the effect of tangential displacement of the upper contact pad on the distribution of the support normal reactions, so that each of them will be equal to $(1/3)F_{N}^{0}$. Finally, by neglecting the tangential global deformation of the block, we assume that the three tangential support reactions, which arise due to friction, will also be equal each other.

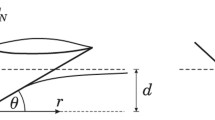
The local normal and tangential contacts will be modeled according to the Hertz theory [37] and the Cattaneo–Mindlin theory [18, 19], respectively. So, in view of the axisymmetry of local contact geometry, under the action of a normal force, $F_{N}$, a circular area of local contact is established at each of the four contact patches and its radius is given by the Hertzian formula

$$\begin{aligned} a=\Bigl (\frac{3}{4}\frac{F_{N} R}{E^{*}}\Bigr )^{1/3}. \end{aligned}$$

(6)

We note that the upper and lower contact radii can be obtained from Eq. (6) by substituting $F_{N}^{0}$, $R_{1}$, $E_{01}^{*}$ and $(1/3)F_{N}^{0}$, $R_{3}$, $E_{03}^{*}$, respectively.

Let $\xi _{03}$ and $\xi _{01}$ denote the relative displacements between the block and the lower and upper pads, respectively. If $\xi$ denotes the absolute displacement of the block, then, evidently, $\xi _{03}=\xi$, since the lower contact pads have been fixed. If $\xi _{2}$ denotes the absolute displacement of the upper contact pad, then $\xi _{01}=\xi -\xi _{2}$.

The presence of friction forces at the contact interface leads to a hysteretic-type tangential force–displacement relation, which can be characterized using Masing’s hypothesis as follows:

$$\begin{aligned}&\overleftarrow{F}(x)=F_{A}-2F\Bigl (\frac{A-x}{2}\Bigr ),\quad x\in (-A,A), \end{aligned}$$

(7)

$$\begin{aligned}&\overrightarrow{F}(x)=-\overleftarrow{F}(-x),\quad x\in (-A,A). \end{aligned}$$

(8)

Here, F(x) is the so-called backbone force–displacement curve, which is defined for $x\in [0,A]$, A is the amplitude of displacement x, and $F_{A}$ is the corresponding force amplitude, that is

$$\begin{aligned} F_{A}=F(A). \end{aligned}$$

(9)

Equations (7) and (8) create a symmetric loop of hysteresis (see Fig. 5), namely, the function $\overrightarrow{F}(x)$ describes the forward movement when the displacement coordinate x increases from $-A$ to A, whereas the function $\overleftarrow{F}(x)$ is responsible for the backward movement in the opposite direction, when the displacement coordinate x decreases from A to $-A$. By construction, the functions $\overrightarrow{F}(x)$ and $\overleftarrow{F}(x)$, which represent respectively the ascending and descending parts of the hysteresis loop, are obtained from the backbone function F(x) by means of an affine transformation without shearing. From mechanical reasons, we may assume that the function F(x) is positive (to be more precise, $F(x)>0$ for $x\in (0,A]$ and $F(0)=0$) and monotonic for $x\le A<u_{c}$, where $u_{c}$ is some critical value of the tangential displacement, i.e., its derivative $F^{\prime }(x)$ is positive as well. Moreover, in regard to frictional interfaces, the backbone curve may be assumed to be concave, that is, its second derivative $F^{\prime \prime }(x)$ is negative for $x\in (0,A)$.

Fig. 5

Masing’s model for the hysteresis loop

Thus, for any value of the displacement $x\in (-A,A)$, according to Eqs. (7) and (8), there exist two points on the hysteresis loop with the coordinates $(x,\overrightarrow{F}(x))$ and $(x,\overleftarrow{F}(x))$. In particular, for $x=0$, we will have $\overleftarrow{F}(0)=F(A)-2F(A/2)$ and $\overrightarrow{F}(0)=2F(A/2)-F(A)$. By using Jensen’s inequality for convex functions (see, e.g., [38]), it can be proved that $\overleftarrow{F}(0)<0<\overrightarrow{F}(0)$. It is also to note that the points $(0,\overrightarrow{F}(0))$ and $(0,\overleftarrow{F}(0))$ originate from the middle point of the backbone curve, since the domain (0, A) of the backbone function F(x) is mapped onto the symmetric interval $(-A,A)$.

In what follows, the backbone curve is modeled using the Cattaneo–Mindlin theory as

$$\begin{aligned} F(x)=F_{\max }\left\{ \begin{array}{ll} 1-(1-x/u_{c})^{\beta },&{}\quad x\in (0,u_{c}), \\ 1,&{} \quad x\ge u_{c}, \end{array} \right. \end{aligned}$$

(10)

where $F_{\max }=\mu F_{N}$, $\mu$ is the coefficient of friction, $\beta =3/2$ for the Hertzian contact geometry, and $u_{c}$ is the maximum (critical) tangential displacement achieved when the tangential load F(x) reaches its maximum, that is $F(u_{c})=F_{\max}$.

According to the Cattaneo–Mindlin theory, we have

$$\begin{aligned} u_{c}=\frac{\mu E^{*}}{G^{*} R}a^{2}, \end{aligned}$$

(11)

where the contact radius a is given by the Hertzian formula (6).

The substitution of (6) into Eq. (11) yields

$$\begin{aligned} u_{c}=\frac{\mu (E^{*})^{1/3}}{G^{*} R^{1/3}} \Bigl (\frac{3}{4}F_{N}\Bigr )^{2/3}. \end{aligned}$$

(12)

As it can be seen from Eqs. (10) and (12), the maximum tangential load $F_{\max }$ and the critical tangential displacement $u_{c}$ both depend on the normal load $F_{N}$.

Let A be the amplitude of the block displacement, so that $\vert x(t)\vert \le A$ at any time moment t. Moreover, let $\mu _{03}$ denote the coefficient of friction at the lower contact interface. Then, the total tangential reaction force produced at the three lower contact pads will be described by the equations

$$\begin{aligned} \overleftarrow{F}^{03}(\xi )=F_{A}(A)-2F\bigl ((A-\xi )/2\bigr ),\quad \overrightarrow{F}^{03}(\xi )=-\overleftarrow{F}^{03}(-\xi ), \end{aligned}$$

(13)

where F(x) is provided by formula (10) with $F_{N}$ and $u_{c}$ being replaced respectively by $F_{N}^{0}$ and $u_{c}^{03}$ given by Eq. (12) for $(1/3)F_{N}^{0}\mu _{03}$, $E^{*}_{03}$, $G^{*}_{03}$, and $R_{3}$, i.e.,

$$\begin{aligned} u_{c}^{03}=\Bigl (\frac{1}{4}F_{N}^{0}\Bigr )^{2/3}\frac{\mu _{03} (E^{*}_{03})^{1/3}}{G^{*}_{03} R_{3}^{1/3}} , \quad F_{\max }^{03}=\mu _{03}F_{N}^{0}. \end{aligned}$$

(14)

We would like to emphasize that $u_{c}^{03}$ is smaller than the critical tangential displacement in the case of only one lower support of the same radius and material parameters (for the same total normal load $F_{N}$).

Further, by taking into account Eq. (10), we can rewrite Eqs. (7) and (8) as follows [23]:

$$\begin{aligned}&\frac{\overleftarrow{F}(x)}{F_{\max }}=\frac{F_{A}}{F_{\max }}-2 +2\biggl \{1+\frac{1}{2}\biggl [ \frac{x}{u_{c}}-1+\Bigl (1-\frac{F_{A}}{F_{\max }} \Bigr )^{1/\beta } \biggr ]\biggr \}^{\beta }, \end{aligned}$$

(15)

$$\begin{aligned}&\frac{\overrightarrow{F}(x)}{F_{\max }}=-\frac{F_{A}}{F_{\max }}+2 -2\biggl \{1-\frac{1}{2}\biggl [ \frac{x}{u_{c}}+1-\Bigl (1-\frac{F_{A}}{F_{\max }} \Bigr )^{1/\beta } \biggr ]\biggr \}^{\beta }. \end{aligned}$$

(16)

Considering the case of partial slip, when $\vert x\vert <u_{c}$, Eqs. (15) and (16) can be inverted as

$$\begin{aligned}&\frac{\overleftarrow{x}(F)}{u_{c}}=2\biggl (1+\frac{F-F_{A}}{2F_{\max }} \biggr )^{1/\beta }-1-\Bigl (1-\frac{F_{A}}{F_{\max }} \Bigr )^{1/\beta }, \end{aligned}$$

(17)

$$\begin{aligned}&\frac{\overrightarrow{x}(F)}{u_{c}}=1+\Bigl (1-\frac{F_{A}}{F_{\max }} \Bigr )^{1/\beta }-2\biggl (1-\frac{F+F_{A}}{2F_{\max }} \biggr )^{1/\beta }. \end{aligned}$$

(18)

By introducing the displacement–force back bone curve

$$\begin{aligned} x(F)=u_{c}\biggl \{ 1-\Bigl (1-\frac{F}{F_{\max }} \Bigr )^{1/\beta } \biggr \}, \end{aligned}$$

(19)

where $F\in (0,F_{\max })$, Eqs. (17) and (18) can be represented in the form

$$\begin{aligned} \overleftarrow{x}(F)=A-2x\Bigl (\frac{F_{A}-F}{2}\Bigr ),\quad \overrightarrow{x}(F)=-\overleftarrow{x}(-F), \end{aligned}$$

(20)

where $A=x(F_{A})$.

Let $\overrightarrow{\overleftarrow{F}}^{01}$ and $F_{A}^{01}$ denote the tangential reaction force at the upper contact pad and its amplitude. First, we assume that $F_{A}^{01}<\mu _{01}F_{N}^{0}$, where $\mu _{01}$ is the coefficient of friction at the upper contact interface. Therefore, according to Eqs. (19) and (20), the displacement–force relation at the upper contact pad will be

$$\begin{aligned} \overleftarrow{\xi }(F^{01})=\overleftarrow{x}_{\!2}(F^{01}),\quad \overrightarrow{\xi }(F^{01})=-\overleftarrow{\xi }(-F^{01}), \end{aligned}$$

(21)

where $\overleftarrow{x}_{\!2}(F)$ is given by the first Eq. (20) with $F_{A}=F_{A}^{01}$ and $A=x(F_{A}^{01})$ for x(F) defined as for the modified backbone curve

$$\begin{aligned} x_{2}(F^{01})=\frac{F^{01}}{k_{2}}+u_{c}^{01}\biggl \{ 1-\Bigl (1-\frac{F^{01}}{F_{\max }^{01}} \Bigr )^{1/\beta } \biggr \} \end{aligned}$$

(22)

with $F_{\max }^{01}=\mu _{01}F_{N}^{0}$ and $u_{c}^{01}$ given by Eq. (12) for $F_{N}^{0}$, $\mu _{01}$, $E^{*}_{01}$, $G^{*}_{01}$, and $R_{1}$. We note that formula (22) reflects a series connection of a Cattaneo–Mindlin element with a linear spring (see Fig. 1b).

Thus, the equation of motion for the system under consideration can be written as

$$\begin{aligned} m\ddot{\xi }+\overrightarrow{\overleftarrow{F}}^{03}(\xi ) +\overrightarrow{\overleftarrow{F}}^{01}(\xi )=F_{T}^{0}\cos \omega t, \end{aligned}$$

(23)

where $\overrightarrow{\overleftarrow{F}}^{01}(\xi )$ is determined by the inverse equations to Eq. (21).

Remark 1

The substitution of $F_{\max }^{01}$ for $F^{01}$ into Eq. (22) yields $x_{2}(F_{\max}^{01})=u_{c}^{01}+F_{\max }^{01}/k_{2}$. Hence, we will have $\overrightarrow{\overleftarrow{F}}^{01}(\xi )=\pm F_{\max }^{01}$ for $\vert \xi \vert \ge x_{2}(F_{\max }^{01})$.

3 Equivalent linearization of the hysteretic restoring force model

In this section, following Krylov and Bogoliubov [39], we apply the method of equivalent linearization (based on the harmonic balance principle) to approximate the non-linear reaction force

$$\begin{aligned} \overrightarrow{\overleftarrow{F}}(\xi )= \overrightarrow{\overleftarrow{F}}^{03}(\xi ) +\overrightarrow{\overleftarrow{F}}^{01}(\xi ) \end{aligned}$$

(24)

by the linear spring dash-pot model $b_{\mathrm{eq}}{{\dot{\xi }}}+k_\mathrm{eq}\xi$ with the coefficients

$$\begin{aligned}&k_{\mathrm{eq}}=\frac{1}{\pi A}\int \limits _{0}^{2\pi } \overrightarrow{\overleftarrow{F}}(A\cos \theta )\cos \theta \,d\theta , \end{aligned}$$

(25)

$$\begin{aligned}&b_{\mathrm{eq}}=-\frac{1}{\pi A\omega }\int \limits _{0}^{2\pi } \overrightarrow{\overleftarrow{F}}(A\cos \theta )\sin \theta \,d\theta , \end{aligned}$$

(26)

where $\omega$ is the angular frequency of oscillation.

Remark 2

As it was first observed by Krylov and Bogoliubov [39], there is no reason whatever to derive the differential equation for the oscillations before linearizing the system, provided we are dealing with systems which do not differ too much from harmonic systems. Indeed, the equivalent linear force $b_{\mathrm{eq}}^{03}{\dot{\xi }}+k_{\mathrm{eq}}^{03}\xi$ for the hysteretic force response $\overrightarrow{\overleftarrow{F}}^{03}(\xi )$ to the harmonic displacement oscillation $\xi =A\cos (\omega t+\varphi )$ will be likewise harmonic with the same angular frequency $\omega$. At the same time, the non-linear force $\overrightarrow{\overleftarrow{F}}^{03}(\xi )$ will be periodic but with various harmonics whose angular frequencies will be multiples of $\omega$, and there is no difficulty in showing that the equivalent linear force $b_{\mathrm{eq}}^{03}{\dot{\xi }}+k_\mathrm{eq}^{03}\xi$ with the coefficients defined according to Eqs. (25) and (26) provides the fundamental harmonic of the nonlinear force $\overrightarrow{\overleftarrow{F}}^{03}(\xi )$ subjected to the given harmonic excitation. The process of obtaining $k_\mathrm{eq}^{03}$ and $b_{\mathrm{eq}}^{03}$ directly from the fundamental harmonic of the non-linear force $\overrightarrow{\overleftarrow{F}}^{03}(\xi )$ is referred to as the principle of harmonic balance [39].

It follows by the definition of $\overrightarrow{\overleftarrow{F}}^{03}(\xi )$ (see Eq. [13)] that

$$\begin{aligned} \pi A k_{\mathrm{eq}}^{03}=\int \limits _{0}^{\pi } \overleftarrow{F}^{03}(A\cos \theta )\cos \theta \,d\theta +\int \limits _\pi ^{2\pi } \overrightarrow{F}^{03}(A\cos \theta )\cos \theta \,d\theta . \end{aligned}$$

(27)

Using the change of integration variable $\xi =A\cos \theta$, Eq. (26) can be reduced to

$$\begin{aligned} \pi A^{2}\omega b_{\mathrm{eq}}=\int \limits _{-A}^{A} \bigl (\overrightarrow{F}(\xi ) -\overleftarrow{F}(\xi )\bigr )\,d\xi , \end{aligned}$$

(28)

from where, in particular, it follows that

$$\begin{aligned} \pi A^{2}\omega b_{\mathrm{eq}}^{03}=\int \limits _{-A}^{A} \bigl (\overrightarrow{F}^{03}(\xi ) -\overleftarrow{F}^{03}(\xi )\bigr )\,d\xi . \end{aligned}$$

(29)

Fig. 6

Equivalent stiffness (a) and damping (b) coefficients as functions of amplitude of oscillation for the hysteretic restoring force at the lower contact interface

The variations of $k_{\mathrm{eq}}^{03}$ and $b_{\mathrm{eq}}^{03}$ as functions of the relative amplitude $A/u_{c}^{03}$ are shown in Fig. 6. It is interesting to observe that the damping coefficient $b_{\mathrm{eq}}^{03}$ possesses maximum at an amplitude larger than the critical tangential displacement $u_{c}^{03}$.

The straightforward application of Eqs. (25) and (26) for $\overrightarrow{\overleftarrow{F}}^{01}(\xi )$ seems to be not possible, since the inverse function to $\overrightarrow{\overleftarrow{\xi }}(F^{01})$ is not readily available, though Eq. (22) can be reduced to a cubic equation for $\beta =3/2$. Hence, the equivalent linearization of the tangential reaction force at the upper contact pad requires a special consideration.

Let $u_{c}^{12}$ denote a critical displacement, when $F^{01}$ reaches its maximum value $F_{\max }^{01}$. According to Eq. (22), we have

$$\begin{aligned} u_{c}^{12}=\frac{F_{\max }^{01}}{k_{2}}+u_{c}^{01}. \end{aligned}$$

(30)

First, we consider the case when $A<u_{c}^{12}$. Then, Eq. (25) can be rewritten in the form

$$\begin{aligned} \pi A^{2} k_{\mathrm{eq}}=\int \limits _{-A}^{A} \overleftarrow{F}(\xi )\frac{\xi \,d\xi }{\sqrt{A^{2}-\xi ^{2}}} +\int \limits _{-A}^{A} \overrightarrow{F}(\xi )\frac{\xi \,d\xi }{\sqrt{A^{2}-\xi ^{2}}}. \end{aligned}$$

(31)

Now, by introducing the left-forward and right-forward compliances

$$\begin{aligned} \overleftarrow{C}(F)=\frac{d\overleftarrow{\xi }(F)}{dF},\quad \overrightarrow{C}(F)=\frac{d\overrightarrow{\xi }(F)}{dF} \end{aligned}$$

(32)

and the reaction force amplitude $F_{A}$ as a root of the equation

$$\begin{aligned} A=\frac{F}{k_{2}}+u_{c}^{01}\biggl \{ 1-\Bigl (1-\frac{F}{F_{\max }^{01}} \Bigr )^{1/\beta } \biggr \}, \end{aligned}$$

(33)

we can transform Eq. (31) by the change of the integration variable as follows:

$$\begin{aligned} \pi A^{2} k_{\mathrm{eq}}=\int \limits _{-F_{A}}^{F_{A}} \frac{\overleftarrow{\xi }(F)\overleftarrow{C}(F)F}{\sqrt{A^{2}-\overleftarrow{\xi }(F)^{2}}}\,dF +\int \limits _{-F_{A}}^{F_{A}} \frac{\overrightarrow{\xi }(F)\overrightarrow{C}(F)F}{\sqrt{A^{2}-\overrightarrow{\xi }(F)^{2}}}\,dF. \end{aligned}$$

(34)

Here, in view of Eqs. (20)–(22) and (32), we have

$$\begin{aligned}&\overleftarrow{C}(F)=\frac{1}{k_{2}} +\frac{u_{c}^{01}}{\beta F_{\max }^{01}} \biggl ( 1-\frac{F_{A}-F}{2 F_{\max }^{01}} \biggr )^{(1-\beta )/\beta }, \end{aligned}$$

(35)

$$\begin{aligned}&\overrightarrow{C}(F)=\frac{1}{k_{2}} +\frac{u_{c}^{01}}{\beta F_{\max }^{01}} \biggl ( 1-\frac{F_{A}+F}{2 F_{\max }^{01}} \biggr )^{(1-\beta )/\beta }. \end{aligned}$$

(36)

At the same time, from Eq. (28), it follows that

$$\begin{aligned} \pi A^{2}\omega b_{\mathrm{eq}}=\int \limits _{-F_{A}}^{F_{A}} \overleftarrow{\xi }(F)\,dF -\int \limits _{-F_{A}}^{F_{A}}\overrightarrow{\xi }(F)\,dF. \end{aligned}$$

(37)

The substitution of (21) into Eq. (37) yields

$$\begin{aligned} \pi A^{2}\omega b_{\mathrm{eq}}^{01}= & {} 4AF_{A}-8u_{c}^{01}F_{A}-\frac{4}{k_{2}}F_{A}^{2} \nonumber \\ {}{} & {} {}+\frac{8u_{c}^{01}F_{\max }^{01}\beta }{1+\beta } \biggl \{ 1-\Bigl (1-\frac{F_{A}}{F_{\max }^{01}} \Bigr )^{(1+\beta )/\beta } \biggr \}, \end{aligned}$$

(38)

where $F_{A}<F_{\max }^{01}$, and $F_{A}$ is related to A by Eq. (33), provided $A<u_{c}^{12}$ with $u_{c}^{12}$ being given by Eq. (30).

Second, we consider the case when $A>u_{c}^{12}$, so that $\overrightarrow{F}^{01}(\xi )=F_{\max }^{01}$ for $\xi \in (2u_{c}^{12}-A,A)$ and $\overleftarrow{F}^{01}(\xi )=-F_{\max}^{01}$ for $\xi \in (-A,A-2u_{c}^{12})$. Correspondingly, Eq. (31) can be rewritten as

$$\begin{aligned} \pi A^{2} k_{\mathrm{eq}}= & {} -F_{\max }^{01}\int \limits _{-A}^{A-2u_{c}^{12}} \frac{\xi \,d\xi }{\sqrt{A^{2}-\xi ^{2}}} +\int \limits _{A-2u_{c}^{12}}^{A} \frac{\overleftarrow{F}(\xi )\xi \,d\xi }{\sqrt{A^{2}-\xi ^{2}}} \nonumber \\ {}{} & {} {}+ \int \limits _{-A}^{2u_{c}^{12}-A} \frac{\overrightarrow{F}(\xi )\xi \,d\xi }{\sqrt{A^{2}-\xi ^{2}}} +F_{\max }^{01}\int \limits _{2u_{c}^{12}-A}^{A} \frac{\xi \,d\xi }{\sqrt{A^{2}-\xi ^{2}}}. \end{aligned}$$

(39)

It can be easily verified that the first and fourth terms on the right-hand side of Eq. (39) are equal to $F_{\max}^{01}\sqrt{A^{2}-(A-2u_{c}^{12})^{2}}$. Thus, evaluating the second and third integrals in (39) by the change of integration variable, we obtain

$$\begin{aligned} \pi A^{2} k_{\mathrm{eq}}^{01}= & {} 2F_{\max }^{01}\sqrt{A^{2}-(A-2u_{c}^{12})^{2}} \nonumber \\&+\int \limits _{-F_{\max }^{01}}^{F_{\max }^{01}} \frac{\overleftarrow{\xi }_{\!*}(F)\overleftarrow{C}_{\!*}(F)F}{\sqrt{A^{2}-\overleftarrow{\xi }_{\!*}(F)^{2}}}\,dF\nonumber \\&+\int \limits _{-F_{\max }^{01}}^{F_{\max }^{01}} \frac{\overrightarrow{\xi }_{\!*}(F)\overrightarrow{C}_{\!*}(F)F}{\sqrt{A^{2}-\overrightarrow{\xi }_{\!*}(F)^{2}}}\,dF, \end{aligned}$$

(40)

where $\overleftarrow{\xi }_{\!*}(F)$, $\overrightarrow{\xi }_{\!*}(F)$ and $\overleftarrow{C}_{\!*}(F)$, $\overrightarrow{C}_{\!*}(F)$ are given by (21), (22) and (35), (36), respectively, for $A=u_{c}^{01}$ and $F_{A}=F_{\max }^{01}$.

On the other hand, when $A>u_{c}^{12}$, we will have

$$\begin{aligned} \pi A^{2}\omega b_{\mathrm{eq}}^{01}=4F_{\max }^{01}(A-u_{c}^{12}) +\int \limits _{-F_{\max }^{01}}^{F_{\max }^{01}} \bigl (\overleftarrow{\xi }_{\!*}(F)-\overrightarrow{\xi }_{\!*}(F) \bigr )\,dF, \end{aligned}$$

(41)

where the last integral can be evaluated by means of Eqs. (37), (38), and (33) as

$$\begin{aligned} \int \limits _{-F_{\max }^{01}}^{F_{\max }^{01}} \bigl (\overleftarrow{\xi }_{\!*}(F)-\overrightarrow{\xi }_{\!*}(F) \bigr )\,dF =\frac{4(\beta -1)}{1+\beta }u_{c}^{01}F_{\max }^{01}. \end{aligned}$$

(42)

Fig. 7

The effect of instrumental compliance on the equivalent stiffness (a) and damping (b) coefficients as functions of amplitude of oscillation for the hysteretic restoring force at the upper contact interface

Thus, the hysteretic restoring force $\overrightarrow{\overleftarrow{F}}^{01}(\xi )$ can be linearized by the spring dash-pot model $b_{\mathrm{eq}}^{01}{\dot{\xi }}+k_\mathrm{eq}^{01}\xi$ with the coefficients $k_{\mathrm{eq}}^{01}$ and $b_\mathrm{eq}^{01}$ being given by formulas (34)–(36), (38) and (40)–(42) in the cases $A\le u_{c}^{12}$ and $A\ge u_{c}^{12}$, respectively.

Fig. 8

The effect of the parameter $\beta$ on the equivalent stiffness (a) and damping (b) coefficients $k_\mathrm{eq}^{01}$ and $b_{\mathrm{eq}}^{01}$ as functions of amplitude of oscillation for the hysteretic restoring force at the upper contact interface

The effect of the parameters $\gamma$ and $\beta$ on the equivalent characteristics $k_{\mathrm{eq}}^{01}$ and $b_{\mathrm{eq}}^{01}$ is illustrated in Figs. 7 and 8. According to the known solution of the normal contact problem for a monomial indenter [35, 40, 41], the value of $\beta$ is allowed to vary between 1 and 2. We note that the different characteristic lengths $u_{c}^{01}$ and $u_{c}^{12}$ are used for normalization in Figs. 7 and 8, respectively.

Remark 3

In the limit as $\beta$ tends to 1, the modified backbone curve (22) reduces to

$$\begin{aligned} x_{2}(F^{01})=\biggl (\frac{1}{k_{2}} +\frac{u_{c}^{01}}{F_{\max }^{01}}\biggr )F^{01}, \end{aligned}$$

which, in view of (30), can be represented as

$$\begin{aligned} x_{2}(F^{01})=\frac{u_{c}^{12}}{F_{\max }^{01}}F^{01}, \end{aligned}$$

(43)

where it is assumed that $0\le ^{01}<F_{\max }^{01}$.

Fig. 9

A spring/frictional damper element: a A schematic; b A dissipative hysteresis loop for the Coulomb force in a series connection with an elastic spring

The limit backbone relation (43) is linear (up to the inception of slip) and models the spring/frictional damper element shown in Fig. 9a. The spring-damper model, which produces a parallelogram-type hysteresis loop (see Fig. 9b), was considered in detail in [20, 42], where the following simple formulas have been derived:

$$\begin{aligned} \left. k_{\mathrm{eq}}^{01}\right| _{\beta =1}= & {} \frac{u_{c}^{12}}{\pi F_{\max }^{01}} \biggl [\arccos \Bigl (1-\frac{2 u_{c}^{12}}{A}\Bigr ) \nonumber \\ {}{} & {} {}-\frac{1}{2}\sin \biggl (2\arccos \Bigl (1-\frac{2 u_{c}^{12}}{A}\Bigr )\biggr ) \biggr ], \end{aligned}$$

(44)

$$\begin{aligned} \left. b_{\mathrm{eq}}^{01}\right| _{\beta =1}= & {} \frac{4\bigl (u_{c}^{12}\bigr )^{2}}{\pi \omega F_{\max }^{01}} \frac{1}{A}\Bigl (1-\frac{u_{c}^{12}}{A}\Bigr ). \end{aligned}$$

(45)

So, namely formulas (44) and (45) yield the solid red lines ($\beta =1$) in Fig. 8.

4 Dissipation at the discrete frictional contact interface

In the steady-state oscillation with a period $T=2\pi /\omega$, the energy dissipation at the lower contact interface is

$$\begin{aligned} D_{03}= & {} \int \limits _{0}^T \overrightarrow{\overleftarrow{F}}^{03}(\xi (t)) {\dot{\xi }}(t)\,dt \nonumber \\ {}= & {} \int \limits _{-A}^{A}\overrightarrow{F}^{03}(\xi )\,d\xi -\int \limits _{-A}^{A}\overleftarrow{F}^{03}(\xi )\,d\xi , \end{aligned}$$

(46)

where A is the corresponding amplitude of vibration.

Fig. 10

Dissipation at the frictional contact discrete interface as a function of the normal contact load: a The case of one pad contact at different values of the relative oscillation amplitude A/R, which is consequently equal to $1.3\times 10^{-5}$, $1.5\times 10^{-5}$, $1.7\times 10^{-5}$, $1.9\times 10^{-5}$, and $2.1\times 10^{-5}$; b The case of n equally loaded identical contact pads at a constant oscillation amplitude

By comparing the right-hand sides of Eqs. (46) and (29), we find that

$$\begin{aligned} D_{03}=\pi A\omega b_{\mathrm{eq}}^{03}. \end{aligned}$$

(47)

Therefore, Fig. 6b presents the variation of $u_{c}^{03}D_{03}/ (\pi A F_{\max }^{03})$ as a function of the oscillation amplitude.

Further, recall that the amplitude of the reaction force $\overrightarrow{\overleftarrow{F}}^{03}(\xi )$ depends on the normal contact load [see Eqs. (10), (12), and (13)]. This dependence is illustrated in Fig. 10 for $\mu _{03}=0{.}2$ and $E_{03}^{*}/G_{03}^{*}=1{.}25$. It is interesting that with increasing the number of contact pads n, which are supposed to equally share the normal contact load, the maximum dissipated energy increases as well (see Fig. 10b).

Let us introduce the notation

$$\begin{aligned} \gamma =\frac{F_{\max }^{01}}{k_{2} u_{c}^{01}},\quad \alpha =\frac{A}{u_{c}^{01}},\quad f_{A}=\frac{F_{A}}{F_{\max }^{01}}. \end{aligned}$$

(48)

Then, the dissipation produced by the reaction force $\overrightarrow{\overleftarrow{F}}^{01}(\xi )$, according to Eqs. (38), (41), (42) is given by

$$\begin{aligned} \frac{D^{01}}{F_{\max }^{01}u_{c}^{01}}= 4f_{A}(\alpha -2-\gamma f_{A})+\frac{8\beta }{1+\beta } \bigl \{ 1-(1-f_{A})^{(1+\beta )/\beta } \bigr \} \end{aligned}$$

(49)

for $\alpha <\gamma +1$, and

$$\begin{aligned} \frac{D^{01}}{F_{\max }^{01}u_{c}^{01}}= 4(\alpha -1-\gamma )+\frac{4(\beta -1)}{1+\beta } \end{aligned}$$

(50)

for $\alpha \ge \gamma +1$.

Recall that, in light of Eq. (33), the relative force amplitude $f_{A}$ is defined as a root of the equation

$$\begin{aligned} \gamma f+1-(1-f)^{1/\beta }=\alpha . \end{aligned}$$

(51)

We note that according to Eq. (51), we have $\alpha =\gamma f_{A}+1-(1-f_{A})^{1/\beta }$, and the substitution of this value for $\alpha$ in formula (49) yields

$$\begin{aligned} \frac{D^{01}}{F_{\max }^{01}u_{c}^{01}}=-4f_{A}\bigl [ 1+(1-f_{A})^{1/\beta }\bigr ] +\frac{8\beta }{1+\beta } \bigl \{ 1-(1-f_{A})^{(1+\beta )/\beta } \bigr \}, \end{aligned}$$

(52)

where it is assumed that $f_{A}\in (0,1)$. It is readily seen that the limit value of $D^{01}$ as $f_{A}$ tends to 1 is equal to $4(\beta -1)(\beta +1)^{-1}F_{\max }^{01}u_{c}^{01}$.

It is to emphasize that the right-hand side of Eq. (52) does not depend on the parameter $\gamma$, that is the energy dissipation $D^{01}$ as a function of the force amplitude $F_{A}$ is independent of the instrumental stiffness $k_{2}$. This is simply explained by the fact that the spring element is dissipationless.

Remark 4

For the spring/frictional damper model [see Fig. 9a and Eqs. (43)–(45)], when $\beta =1$, Eqs. (49) and (50) yield

$$\begin{aligned} \left. D^{01}\right| _{\beta =1}= \left\{ \begin{array}{ll} 0, &{}\quad A<u_{c}^{12}, \\ 4F_{\max }^{01}(A-u_{c}^{12}), &{}\quad A\ge u_{c}^{12}. \end{array} \right. \end{aligned}$$

(53)

We note that formula (53) is in complete agreement with Eq. (45).

Fig. 11

Dissipation at the upper frictional contact interface a as a function of the oscillation amplitude for different values of the relative compliance of the fixation device for the upper contact pad and b as a function of the tangential load amplitude

Figure 11a shows the variation of $D^{01}$ as a function of $\alpha$ for different values of $\gamma$. We note that, in view of the first equation (48), $\gamma$ has the meaning of relative instrumental compliance $(1/k_{2})/(u_{c}^{01}/F_{\max}^{01})$. Also, Fig. 11 demonstrates that the frictional damping at the upper contact patch decreases as the spring stiffness $k_{2}$ decreases, since the contribution of the elastic spring to the displacement amplitude increases. Figure 11b shows the variation of the relative dissipation as a function of the relative tangential load amplitude. The solid red line corresponds to the leading asymptotic term.

It is of interest to note that energy dissipation in spherical contacts subject to an oscillating tangential force was studied experimentally by Johnson [43], who also applied the Cattaneo–Mindlin theory for evaluating the energy loss per cycle as a function of the tangential force amplitude. For the generalized Cattaneo–Mindlin theory [33, 34] (where the axisymmetric contact geometry differs from the Hertzian geometry of contact, described by paraboloids) it was shown [23] that irrespectively of the value of the dimensionless parameter $\beta$, the dependence of the energy dissipation on the force amplitude at its relatively small values (see the initial parts of the curves in Fig. 11) is predicted to be cubic, that is exactly the same as for the Hertzian case, when $\beta =3/2$. As one of possible sources for discrepancy of the theoretical predictions with the experimental results, Johnson [43] has pointed out at a variation in the effective coefficient of friction throughout the contact circle.

Remark 5

Let us return to the general Masing model (7)–(9) and evaluate the energy dissipation, D, in one cycle. In view of (46), (8), and (9), we have

$$\begin{aligned} D=-2\int \limits _{-A}^{A}\overleftarrow{F}(x)\,dx =-4F(A)A+8\int \limits _{0}^{A} F(x)\,dx, \end{aligned}$$

(54)

where F(x) is the backbone force–displacement relation.

For a given backbone curve, Eq. (54) defines the energy dissipation D as a function of the displacement amplitude A. Now, let us consider the inverse problem: namely, given the dissipation function D(A), find the corresponding backbone function F(x).

By differentiating both sides of Eq. (54) with respect to the variable A, we arrive at the equation

$$\begin{aligned} D^{\prime }(A)=4F(A)-4A F^{\prime }(A), \end{aligned}$$

(55)

which can be regarded as a linear first-order differential equation for the function F(A).

In this way, after the integration of Eq. (55), we arrive at the following result:

$$\begin{aligned} F(A)=CA-\frac{A}{4}\int \limits _{0}^{A} \frac{D^{\prime }(x)}{x^{2}}\,dx. \end{aligned}$$

(56)

Here, $D^{\prime }(x)$ is the derivative of the function D(x), which is obtained from D(A) by replacing A with x, and C is an integration constant (which from a physical point of view may be assumed to be positive). To the best of the authors’ knowledge, formula (56) has been reported in the literature for the first time.

Observe that the first term on the right-hand side of Eq. (56), represents the linearly elastic response, which is dissipationless. In other words, the function F(A) can be determined from the function D(A) only up to a linear term CA (i.e., up to one integration constant).

Further, by assuming that $D(A)\simeq \mathrm{const} A^{\sigma }$, as suggested by experimental observations, formula (56) yields

$$\begin{aligned} F(A)\simeq CA-\mathrm{const} A^{\sigma -1}, \end{aligned}$$

(57)

if $\sigma >2$ in order to allow integration in (56).

In the presence of the linear term in Eqs. (56), (57) implies that $D(A)\simeq \mathrm{const} F_{A}^{\sigma }$, provided the value of the exponent $\sigma$ is greater than two. Thus, in principle, the Masing modelling framework allows the dependence of dissipation D on tangential load amplitude $F_{A}$ to be less than cubic and even approach quadratic.

5 Steady-state harmonic response

Let us assume that the system is subjected to a harmonic excitation force of the form $F_{T}(t)=F_{T}^{0}\cos \omega t$. By making use of the equivalent linearization [see Eqs. (25) and (26)], we approximate the hysteretic restoring force as

$$\begin{aligned} \overrightarrow{\overleftarrow{F}}(\xi )=b_{\mathrm{eq}}{\dot{\xi }}+k_{\mathrm{eq}}\xi , \end{aligned}$$

(58)

so that the steady-state solution of Eq. (23) can be sought in the form

$$\begin{aligned} \xi (t)=A\cos (\omega t+\phi ), \end{aligned}$$

(59)

where A and $\phi$ are the amplitude and phase of the displacement response.

The substitution of (58) and (59) into Eq. (23) yields

$$\begin{aligned} A=\frac{F_{T}^{0}}{\sqrt{ b_{\mathrm{eq}}^{2}\omega ^{2}+(k_{\mathrm{eq}}-m\omega ^{2})^{2}}}. \end{aligned}$$

(60)

Moreover, the phase shift is negative and can be written as

$$\begin{aligned} \phi =\left\{ \begin{array}{ll} \displaystyle -\arctan \frac{b_{\mathrm{eq}}(A)\omega }{k_{\mathrm{eq}}(A)-m\omega ^{2}},&{}\quad \omega <\sqrt{\frac{k_{\mathrm{eq}}(A)}{m}},\\ \displaystyle -\pi +\arctan \frac{b_{\mathrm{eq}}(A)\omega }{m\omega ^{2}-k_{\mathrm{eq}}(A)},&{}\quad \omega >\sqrt{\frac{k_{\mathrm{eq}}(A)}{m}}. \end{array} \right. \end{aligned}$$

(61)

It should be emphasized that the equivalent damping and stiffness coefficients, $b_{\mathrm{eq}}$ and $k_{\mathrm{eq}}$, are functions of the amplitude A, so that Eq. (60) implicitly determines the dependence of A on $F_{T}^{0}$.

Let us first focus on the small amplitude vibrations. In this case, according to Eqs. (27) and (34), we obtain that

$$\begin{aligned} k_{\mathrm{eq}}^{03}\simeq \frac{\beta F_{\max }^{03}}{u_{c}^{03}},\quad k_{\mathrm{eq}}^{01}\simeq \biggl ( \frac{1}{k_{2}}+\frac{u_{c}^{01}}{\beta F_{\max }^{01}} \biggr )^{-1},\quad A\rightarrow 0. \end{aligned}$$

(62)

At the same time, as it was shown in [23], the equivalent damping coefficients vanish in the limit as A tends to zero.

Thus, the resonance angular frequency at small amplitudes is given by

$$\begin{aligned} \omega _{0}\simeq \sqrt{\frac{\beta }{m}\biggl [ \frac{F_{\max }^{01}}{u_{c}^{01}}(1+\beta \gamma )^{-1} +\frac{F_{\max }^{03}}{u_{c}^{03}} \biggr ]}, \end{aligned}$$

(63)

where $\gamma$ is defined by the first formula (48). It should be emphasized that the simple asymptotic formula (63) overestimates the resonance frequency, as the equivalent tangential stiffness in the limit of small amplitudes is maximal.

Observe [see, in particular, Eqs. (10) and (12)] that the ratio $F_{\max }/u_{c}$ is proportional to $F_{N}^{1/3}$. Therefore, from formula (63), it follows that the resonance frequency increases with the normal force, evidently, since the tangential contact stiffness increases.

Fig. 12

Relative displacement amplitude (a) and phase shift (b) as functions of the relative angular frequency of the external excitation force for different values of the relative force amplitude $f=F_{T}^{0}/F_{\max }^{01}$

When the simplifying assumption of small oscillations should be abandoned, Fig. 12a shows the variation of the displacement amplitude versus the excitation angular frequency of the external tangential force. The illustrative example is given for the case when $\mu _{03}=\mu _{01}$, $F_{\max }^{03}=F_{\max}^{01}$, $R_{3}=R_{1}$, $E^{*}_{03}=E^{*}_{01}$, and $G^{*}_{03}=G^{*}_{01}$, so that $u_{c}^{03}/u_{c}^{01}=3^{-2/3}$.

6 Discussion and conclusion

First, it is necessary to emphasize that the equivalent linearization formulas (25) and (26) are in complete agreement with those obtained in [20] using the harmonic balance method, where they were applied for the analysis of hysteresis produced by the Coulomb force. Generally speaking, while the method of equivalent linearization was applied in the present study (using the readily available formulas first given by Krylov and Bogoliubov [39]), the harmonic balance method [44, 45] leads to the same results on equivalent linearization as well as the first approximation in the Krylov–Bogoliubov– Mitropolsky asymptotic method of slowly varying amplitude and phase [46] or the method of statistical harmonic linearization [47].

It is to note that some of the simplifying assumptions made in the derivation of the presented model can be easily relaxed. For instance, the effect of body weight has been neglected in the evaluation of the support reactions. Otherwise, the model parameters $u_{c}^{03}$ and $F_{\max }^{03}$ should be determined by formulas (14) with $F_{N}^{0}$ being replaced by $F_{N}^{0}+mg$, where g is the gravitational acceleration.

Further, in the analysis of the single-degree-of-freedom model shown in Fig. 4, it was assumed that the lower support reactions are equal due to the symmetry of the support configuration. Generally speaking, when the parallelepiped block moves, the reaction forces change as the center of gravity of the block shifts. However, when the characteristic distance between the supports is in the range of millimetres or even centimetres and the amplitude of displacements of the block’s center of mass in the range of micrometres, the effect of variation of support reactions is about a fraction of a percent. It is also to note that contact problems of multiple contact, which arise in connection with elastic interaction between the contact spots, have been studied in [48, 49].

Observe that the frequency-response curves presented in Fig. 12 for a range of excitation force amplitudes are described by single-valued functions. This implies that the steady-state solutions are stable [13]. As it can be seen from Fig. 12, the hysteretic SDoF system under consideration exhibits a soft-type resonance [8], since the resonance peak shifts to a lower frequency if the excitation force amplitude increases.

It is of interest to note that the energy dissipated per cycle [see Eq. (46)] can be calculated as the area enclosed by the hysteresis loop in the $\xi$–F plane. Though, the first integral in (46) involves the velocity ${\dot{\xi }}$, the result is independent of the velocity and depends only on the displacement amplitude [see Eq. (47)]. It is pertinent to recall here [15] that this type of damping is called the hysteretic energy dissipation.

Fig. 13

a Experimental amplitude-frequency diagrams for different values of the normal force $F_{N}^{0}=1,2,3,4,5$; b Theoretical predictions [based on formula (60)] superimposed onto the experimental data: The effect of the instrumental stiffness

An interesting finding of the present study is that the frictional damping at the discrete contact interface increases with increasing the number of contact patches (see Fig. 10b).

It is noteworthy that the simple introduction of a spring fixation element into the SDoF hysteretic system involves a nontrivial analysis of the reaction force–displacement relationship. At the same time, the effect of instrumental stiffness does not introduce new qualitative features in the system behavior. Figure 13a shows typical amplitude-frequency diagrams obtained experimentally for a range of the normal forces for the following set of the model parameters: $\mu _{01}=\mu _{03}=0.3$, $E_{0}=70$ GPa, $\nu _{0}=0.35$, $E_{1}=210$ GPa, $\nu _{1}=0.28$, $E_{3}=200$ GPa, $\nu _{3}=0.3$, $R_{1}=56.148$ mm, $R_{3}=6.245$ mm, and $m=0.2$ kg. We note that the corresponding experimental setup, which is signified by the schematic shown in Fig. 4, was designed for studies of frictional dissipation under varying normal load, and as such, the value of instrumental stiffness $k_{2}$ has been designed to be small, in order to not interfere with the tangential movement while modulating the normal load.

Observe that in view of formula (26), which defines the equivalent damping coefficient, the quantity $b_{\mathrm{eq}}\omega$ is independent of the angular frequency $\omega$, and therefore, the dependence of the denominator in formula (60) for the displacement amplitude on $\omega$ is fully determined by the second term, that is $(k_{\mathrm{eq}}-m\omega ^{2})^{2}$. Hence, the linearized model predicts the following value for the resonance angular frequency $\omega _{0}=\sqrt{k_{\mathrm{eq}}/m}$, which, in view of (25), depends on displacement amplitude. Further, as it seen from Fig. 6a, the equivalent stiffness coefficient $k_{\mathrm{eq}}$ is a decreasing function of the displacement amplitude, and therefore, the asymptotic formula (63), indeed, essentially (depending on the relative displacement amplitude) overestimates the resonance angular frequency $\omega _{0}$.

When applying formula (60) for finite amplitudes, we make use of the fact that the resonant amplitude equals $A_{0}=F_{T}^{0}/(b_{\mathrm{eq}}\omega _{0})$. In case when the force amplitude $F_{T}^{0}$ is employed as an input, the latter equation is used for determining the value of the displacement amplitude $A_{0}$ (we recall that $b_{\mathrm{eq}}$ depends on the displacement amplitude as well, and thus the application of a numerical method is needed to relate $A_{0}$ to $F_{T}^{0}$). For illustrative purposes, the theoretical predictions are superimposed onto the experimental results in Fig. 13b. The relative amplitude of the tangential force is defined as $f_{T}^{0}=F_{T}^{0}/F_{\max }^{03*}$, where $F_{\max}^{03*}$ is evaluated for the body weight only. It can be seen that the effect of the instrumental stiffness variation strongly influences the value of the resonance frequency, as it controls the stiffness of the connection at the upper contact patch.

Observe that in contrast to the derived analytical model, the experimental data shows a somewhat weaker dependence of the resonance frequency $f_{0}=\omega _{0}/(2\pi )$ on the normal load (see Fig. 13b). This can be explained by the effect of wear that results in changes of the local contact geometries, which gradually deviate from the Hertzian profile $\varPhi (r)=r^{2}/(2R)$, where r is the radial coordinate. Using the generalized Cattaneo–Mindlin theory for the monomial profile $\varPhi (r)=\varLambda r^{\lambda }$ (see, e.g., [36]), the developed model can be extended to a broader class of local contact configurations. In particular, it can be shown that $\beta =(\lambda +1)/\lambda$, with $\beta \in (1,2]$ for $\lambda \in [1,+\infty )$, and the ratio $F_{\max }/u_{c}$ is proportional to the $1/(\lambda +1)$ exponent of the normal load $F_{N}^{0}$, so that the resonance frequency is found to be proportional to the $1/[2(\lambda +1)]$ exponent of the normal load. Therefore, the flatter the slope of the dependence of $f_{0}$ on $F_{N}^{0}$, the larger should be the value the shape parameter $\lambda$.

Apparently, the most important factor that is missed in the outlined analysis of the experimental data presented in Fig. 13a is that they are taken from a two-degrees-of-freedom system (see Fig. 4). However, the extension of the model for the case of many degrees of freedom lies outside the scope of the present study. The explanation for this effect, which is observed under constant normal loading as well as constant tangential displacement amplitude, is that the critical displacement that determines the inception of slip at a particular contact spot is sensitive to the partial normal load that is transferred by this contact spot. Indeed, if the number of localized contacts, n, increases for the same total normal load applied to the multiple contact system, then a share of the load that is carried by each particular localized contact will proportionally decrease, and therefore, for a given tangential displacement amplitude, the stage of partial slip shortens, while the contribution from the full slip stage becomes more dominated as $n\rightarrow \infty$.

There is no question that the theoretical and practical value of the developed analytical framework for modeling the effect of instrumental stiffness is by far not limited to macro tribological systems, since localized frictional contacts are encountered in diverse engineering applications. For instance, the schematic of a Cattaneo–Mindlin type contact element with a linear spring in series connection as shown in Fig. 2 naturally appears [50] in a combination of AFM-based nanoindentation with a spherical probe (normal loading) and quartz crystal microbalance (tangential loading), when the AFM cantilever stiffness plays a role assigned to the instrumental stiffness $k_{2}$.

To conclude, the steady-state dynamic response of a SDoF system containing both a spring and hysteretic elements has been analyzed. By utilizing the equivalent linearization technique, the steady-state response amplitude under harmonic excitation is approximately determined, and the frictional damping per cycle is evaluated.