Abstract
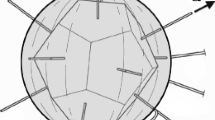
The proposed embedded strain sensor consists of six elastic rings, placed in an icosahedral symmetry, whose measured elongations give access to the complete 3D strain tensor in the surrounding matrix. The linear relationship between the ring elongations and the strain tensor in the matrix is given. From this relation it is deduced that the tensor is isotropic, i.e. its sensitivity is independent of the rotation of the strain tensor and that the sensor is more sensitive to hydrostatic strains than to deviatoric strains. The additional perturbation of the strain field in the matrix, induced by the presence of the sensor, is studied by means of a numerical integration of the Kelvin solution and the use two dimensionless factors relating to geometry and elasticity. From this study we obtain, in a generic way, an evaluation of the intensity of this additional strain field and the value of the measurement bias due to the elasticity of the ring, which allows in practice to reduce this bias. A draft of the realisation is proposed, for which it is verified that the disturbance of the strain field in the matrix as well as the bias to be corrected are small.







Similar content being viewed by others
References
Bourquin F, Godard B (2014) SHM trends and opportunities for the civil engineering sector. In: EWSHM—7th Eur. Workshop on Structural Health Monitoring, vol. 1, p. 121. Nantes, France
Buljac A, Jailin C, Mendoza A, Neggers J, Taillandier-Thomas T, Bouterf A, Smaniotto B, Hild F, Roux S (2018) Digital volume correlation: review of progress and challenges. Exp Mech 58(5):661–708. https://doi.org/10.1007/s11340-018-0390-7
François MLM, Lecieux Y, Leduc D, Lupi C (2014) Dispositif de mesure de contraintes. Patent PCT/FR2014/050585 and WO/2014/140496
François MLM, Lecieux Y, Leduc D, Lupi C, Rozière E (2017) An embedded 3D strain tensor based on the eshelbys inclusion. Exp Mech 57(5):801–811. https://doi.org/10.1007/s11340-017-0266-2
Lecieux Y, Roziere E, Lupi C, Leduc D, François MLM (2018) Towards a 3D shrinkage measurement in concrete using an embedded strain sensor. Smart Mater Struct 27(10):105032. https://doi.org/10.1088/1361-665x/aadbd5
Guigot C, Lecieux Y, Lupi C, Leduc D, François MLM (2021) Dispositif tridimensionnel de mesurer localement les déformations. Patent examination BNT229835
Lecieux Y, Leduc D, Guigot C, François M, Lupi C (2022) Whispering gallery modes for 3d strain measurement. Opt Laser Technol 149, 107862 . https://doi.org/10.1016/j.optlastec.2022.107862.https://www.sciencedirect.com/science/article/pii/S0030399222000196
Bechterew P (1926) Analytical study of the generalized hookes law. Application of the method of coordinate transformation. Zh. Fiz. Khim. Obshch 58(3):415–446
Dieulesaint E, Royer D (1974) Ondes élastiques dans les solides: application au traitement du signal. Masson
Forte S, Vianello M (1996) Symmetry classes for elasticity tensors. J Elast 43:81–108
Auffray N, Kolev B, Petitot M (2014) On anisotropic polynomial relations for the elasticity tensor. J Elast 115(1):77–103. https://doi.org/10.1007/s10659-013-9448-z
Kelvin Thomson W (1856) Elements of mathematical theory of elasticity. Phil. Trans. R. Soc. 146:481–498
Annin BD, Ostrosablin NI (2008) Anisotropy of elastic properties of materials. J Appl Mech Tech Phys 49:998–1014
Rychlewski JJ (1984) On Hookes law. Prikladnaya Matematika i Mekhanika 48:303–314
Kelvin Thomson W (1882) Note on integration of the equations of equilibrium of an elastic solid. Math. Phys. Pap. 1:97
Love AEH (1927) A treatise on the mathematical theory of elasticity, 4th edn. Cambridge University Press, Cambridge
Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond Ser A 241(1226):376–396. https://doi.org/10.1098/rspa.1957.0133
Kachanov M, Shafiro B, Igor T (2003) Handbook of elasticity solutions. Springer, New York. https://doi.org/10.1007/978-94-017-0169-3
Andrianov IV, Kalamkarov AL, Weichert D (2012) Buckling of fibers in fiber-reinforced composites. Comp B Eng 43(4):2058–2062
Acknowledgements
This work has been supported by a grant from the Région Pays de la Loire within the SMOG project and by a grant from the Agence Nationale de la Recherche within the MOMAP project (Grant Number ANR-19-CEl0-0005-01).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.