Skip to main content
SpringerLink
Log in

Investigation on dynamic characteristics of herringbone planetarygear system considering tooth surface friction

  • Published:
Meccanica Aims and scope Submit manuscript

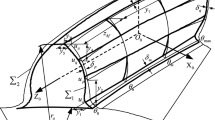
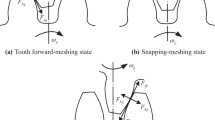
Abstract

The sliding friction on the tooth surface is an important factor affecting the dynamic characteristics of herringbone planetary gear system (HPGS) which is a complex high power density system. A novel coupling dynamic model of HPGS with friction effect is proposed through an iterative numerical scheme under the tribo-dynamic condition, and the dynamic characteristics are discussed considering tooth surface friction. The results show that the dynamic meshing force amplitude increases obviously after considering friction, and rises slowly with the increase of roughness. When the load increases gradually, the main peak of dynamic meshing force response increases obviously, but the frequency of the main resonance peak remains unchanged. With the increase of input torque, the main peak of meshing force increases because the input torque, as the input of the transmission system, is positively correlated with the dynamic characteristics of herringbone planetary gear transmission system. The influence of friction excitation on dynamic characteristics gradually decreases with the increase of input speed. As the internal excitation of the system, the friction excitation will also affect the dynamic characteristics. The main peak of dynamic mesh force increases significantly compared with that without considering friction, and increases slowly with the increase of roughness. With the increase of roughness, the dynamic characteristics of the transmission system increase slightly after friction excitation, so the amplitude of dynamic meshing force increases. However, as the roughness continues to increase, the lubrication state changes from full film lubrication to partial elastohydrodynamic lubrication. When the \({S}_{avg}\) of the tooth surface exceeds 1.2 μm, that is, the rough peak contacts, the friction excitation has little effect on the dynamic characteristics, so the amplitude of the main peak of dynamic meshing remains almost unchanged.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Abbreviations

HPGS:

Herringbone planetary gear system

EHL:

Elastohydrodynamic lubrication

TVMS:

Time-varying mesh stiffness

\(A\) :

The rough surface area

\({\mathbf{C}}_{b}\) :

The support damping matrix

\({\mathbf{C}}_{m}(t)\) :

The meshing damping matrix

\({c}_{sni}^{\theta }(t)\) :

Time-varying mesh damping of the right and left-side ith sun-planet mesh (\(\theta =l,r\))

\({c}_{rni}^{\theta }(t)\) :

Time-varying mesh damping of the right and left-side ith ring-planet mesh (\(\theta =l,r\))

\(E,v\) :

Yang’s modulus and Poisson ratio

\({E}^{^{\prime}}\) :

Equivalent elastic modulus of gear pair

\({e}_{sni}^{\theta }\) :

Transmission error of sun-planetary gear meshing pair (\(\theta =l,r\))

\({e}_{rni}^{\theta }\) :

Transmission error of ring-planetary gear meshing pair (\(\theta =l,r\))

\(\mathbf{F}(t)\) :

Excitation force caused by transmission error excitation and time-varying stiffness excitation

\({F}_{f}(t)\) :

The total friction force expression in a meshing period

\({F}_{fij}(t)\) :

Tooth surface friction force on the jth contact line on the ith slice at the time of \(t\)

\({F}_{ij}(t)\) :

Contact line load on the jth contact line on the ith slice at the time of \(t\)

\({F}_{fs}^{\theta }(t)\) :

Sliding friction forces exerted by the sun gears on the ith planet gear (\(\theta =l,r\))

\({F}_{sni}^{\theta }(t)\) :

Dynamic mesh forces of the ith sun -planet gear pair (\(\theta =l,r\))

\({F}_{rni}^{\theta }(t)\) :

Dynamic mesh forces of the ith ring-planet gear pair (\(\theta =l,r\))

\({f}_{\Lambda (t)}\) :

Percentage of point contact load distribution in mixed state

\(\mathbf{G}\) :

Gyroscopic matrix

\(L(t)\) :

Length of integrated meshing line

\({L}_{i}^{\theta }(t)\) :

The length of the contact line on the left and right side of the pitch points (\(\theta =l,r\))

\({L}_{ij}(t)\) :

Time-varying contact line length

\({l}_{m},{l}_{n}\) :

Actual meshing line length and theoretical meshing line length

\({l}_{p}^{l}\) :

Left length Left length of single gear pitch

\(\mathbf{M}\) :

Matrix of mass

\({\mathbf{M}}_{\Omega e}\) :

Beam element mass submatrix (\(\Omega =s,r,n\))

\({h}_{c}(t)\) :

Central film thickness

\({H}_{pi}^{\theta }\left(t\right),{H}_{gi}^{\theta }(t)\) :

Torque arms of the contact line on left and right side of the driving gear and the passive gear (\(\theta =l,r\))

\({I}_{\Omega }\) :

The rotational inertia of the component (\(\Omega =s,r,n\))

\({\mathbf{K}}_{b}\) :

The matrix of support stiffness

\({\mathbf{K}}_{m}(t)\) :

The meshing stiffness matrix

\({\mathbf{K}}_{\omega }\) :

The centripetal stiffness matrix

\({\mathbf{K}}_{\Omega e}\) :

Submatrix of beam element stiffness (\(\Omega =s,r,n\))

\({k}_{s\zeta }^{\theta }\) :

The support stiffness of left and right sun gear (\(\zeta =x,y,z\), \(\theta =l,r\))

\({k}_{as\zeta }\) :

Bending stiffness in x, y direction and axial tension stiffness of sun gear retreating groove (\(\zeta =x,y,z\))

\({k}_{asu}\) :

Torsion stiffness of sun gear retreat groove

\(k_{{sni}}^{\theta } \left( t \right)\) :

Time-varying mesh stiffness of the right and left-side ith sun-planet mesh (θ = l, r)

\(k_{{rni}}^{\theta } \left( t \right)\) :

Time-varying mesh stiffness of the right and left-side ith ring-planet mesh (θ = l, r)

\(k_{b} ,k_{s} ,k_{a} ,k_{h} ,k_{f}\) :

Bending, shear and axial compressive, Hertzian and fillet-foundation and elastic stiffness of the gear tooth

\({p}_{t}\) :

The tooth pitch of the end face

\({P}_{hij}(t)\) :

Hertz pressure of tooth contact point on the jth contact line on the ith slice at the time of t

\({R}_{ij}(t)\) :

Meshing comprehensive radius of curvature on the jth contact line on the ith slice at the time of t

\({r}_{\Omega }\) :

Pitch circle of the component (\(\Omega =s,r,n\))

\({r}_{a\Omega }\) :

Addendum circle of the component (\(\Omega =s,r,n\))

\({r}_{b\Omega }\) :

The base pitch of the component (\(\Omega =s,r,n\))

\(S{R}_{ij}(t)\) :

Slip ratio of tooth surface velocity on the jth contact line on the ith slice at the time of \(t\)

\({S}_{avg}\) :

The root mean square value of the roughness

\({t}_{c}\) :

Time of one mesh circle.

\({T}_{s}\) :

The external load on the sun gear

\({T}_{fpij}(t),{T}_{fgij}(t)\) :

The friction torque of driving gear and passive gear on the jth contact line on the ith slice at the time of \(t\)

\({T}_{fp}(t),{T}_{fg}(t)\) :

The total tooth friction torque of driving gear and passive gear

\({T}_{fs}^{\theta }(t)\) :

Sliding friction torques exerted by the nth planet gear on the sun gears (\(\theta =l,r\))

\(\mathbf{T}\) :

External torque vector

\(z(x,y)\) :

The rough surface height

\({\alpha }_{1}\) :

Viscosity–pressure coefficient of the lubricant

\({{\mu }_{m}}_{ij}(t)\) :

The time-varying friction coefficient in mixed state on the jth contact line on the ith slice at the time of \(t\)

\({{\mu }_{e}}_{ij}(t)\) :

The time-varying friction coefficient of elastohydrodynamic lubrication contact on the jth contact line on the ith slice at the time of \(t\)

\({\mu }_{b}\) :

The average friction coefficient of rough contact

\({{u}_{s}}_{ij}(t),{{u}_{r}}_{ij}(t)\) :

Sliding velocity and entrainment velocity on the jth contact line on the ith slice at the time of \(t\)

\({\eta }_{0}\) :

Ambient viscosity of the lubricant

\({\omega }_{c}\) :

Planet carrier angular rate

\(\Lambda (t)\) :

Film thickness ratios

\({\psi }_{sni},{\psi }_{rni}\) :

Angle made by the plane of action with the vertical y-axis

\({\psi }_{ni}\) :

The relative angle of ith planet gear on the right rotates to the position of the first planet gear

\({\varepsilon}_{p}, {\varepsilon }_{g}\) :

The rough peak height of two contact rough surfaces.

\(\lambda\) :

Constants related to helical gear overlap ratio

\({\xi }_{g}\) :

Gear meshing damping ratio

\(c\) :

Planet carrier

\(n\) :

Planet gear

\(r\) :

Ring gear

\(s\) :

Sun gear

l :

Left side

\(r\) :

Right side

References

  1. Hou S, Wei J, Zhang A, Lim TC, Zhang C (2018) Study of dynamic model of helical/herringbone planetary gear system with friction excitation. J Comput Nonlin Dyn, 13. https://doi.org/10.1115/1.4041774.

  2. Han L, Xu L, Qi H (2017) Influences of friction and mesh misalignment on time-varying mesh stiffness of helical gears. J Mech Sci Technol 31:3121–3130. https://doi.org/10.1007/s12206-017-0602-6

    Article  Google Scholar 

  3. Han L, Qi H (2019) Dynamic response analysis of helical gear pair considering the interaction between friction and mesh stiffness. Meccanica 54:2325–2337. https://doi.org/10.1007/s11012-019-01088-y

    Article  MathSciNet  Google Scholar 

  4. Guerine A, El Hami A, Walha L, Fakhfakh T, Haddar M (2015) Dynamic response of a Spur gear system with uncertain friction coefficient. Adv Eng Softw 120:45–54. https://doi.org/10.1016/j.advengsoft.2016.05.009.

  5. Park CI (2019) Tooth friction force and transmission error of spur gears due to sliding friction. J Mech Sci Technol 33:1311–1319. https://doi.org/10.1007/s12206-019-0232-2

    Article  Google Scholar 

  6. Miler D, Hoić M, Domitran Z, Žeželj D (2019) Prediction of friction coefficient in dry-lubricated polyoxymethylene spur gear pairs. Mech Mach Theory 138:205–222. https://doi.org/10.1016/j.mechmachtheory.2019.03.040

    Article  Google Scholar 

  7. Wang J, Zheng J, Yang A (2011) An analytical study of bifurcation and chaos in a spur gear pair with sliding friction. Pro Eng 31:563–570. https://doi.org/10.1016/j.proeng.2012.01.1068

    Article  Google Scholar 

  8. Ouyang T, Huang G, Chen J, Gao B, Chen N (2019) Investigation of lubricating and dynamic performances for high-speed spur gear based on tribo-dynamic theory. Tribol Int 136:421–431. https://doi.org/10.1016/j.triboint.2019.03.009

    Article  Google Scholar 

  9. Ma H, Feng M, Li Z, Feng R, Wen B (2017) Time-varying mesh characteristics of a spur gear pair considering the tip-fillet and friction. Meccanica 52:1695–1709. https://doi.org/10.1007/s11012-016-0502-3

    Article  MathSciNet  Google Scholar 

  10. Bobach L, Beilicke R, Bartel D (2020) Transient thermal elastohydrodynamic simulation of a spiral bevel gear pair with an octoidal tooth profile under mixed friction conditions. Tribol Int 143:106020. https://doi.org/10.1016/j.triboint.2019.106020

    Article  Google Scholar 

  11. Liu W, Shuai Z, Guo Y, Wang D (2019) Modal properties of a two-stage planetary gear system with sliding friction and elastic continuum ring gear. Mech Mach Theory 135:251–270. https://doi.org/10.1016/j.mechmachtheory.2019.01.026

    Article  Google Scholar 

  12. Parker RG, Lin J (2004) Mesh phasing relationships in planetary and epicyclic gears. J Mech Design 126:365–370. https://doi.org/10.1115/1.1667892

    Article  Google Scholar 

  13. Sondkar P, Kahraman A (2013) A dynamic model of a double-helical planetary gear set. Mech Mach Theory 70:157–174. https://doi.org/10.1016/j.mechmachtheory.2013.07.005

    Article  Google Scholar 

  14. Wang C, Wei J, Wu Z, Lu L, Gao H (2019) Load sharing performance of herringbone planetary gear system with flexible pin. Int J Pr Eng Man 20:2155–2169. https://doi.org/10.1007/s12541-019-00236-4

    Article  Google Scholar 

  15. Ren F, Li A, Shi G, Wu X, Wang N (2020) The effects of the planet–gear manufacturing eccentric errors on the dynamic properties for herringbone planetary gears. Appl Sci 10:1060–1079. https://doi.org/10.3390/app10031060

    Article  Google Scholar 

  16. Ren F, Qin D, Lim TC, Lyu S (2014) Study on dynamic characteristics and load sharing of a herringbone planetary gear with manufacturing errors. Int J Pr Eng Man 15:1925–1934. https://doi.org/10.1007/s12541-014-0547-y

    Article  Google Scholar 

  17. Ren F, Luo G, Shi G, Wu X, Wang N (2018) Influence of manufacturing errors on dynamic floating characteristics for herringbone planetary gears. Nonlinear Dyn 93:361–372. https://doi.org/10.1007/s11071-018-4197-y

    Article  Google Scholar 

  18. Zhang L, Wang Y, Wu K, Sheng R, Huang Q (2016) Dynamic modeling and vibration characteristics of a two-stage closed-form planetary gear train. Mech Mach Theory 97:12–28. https://doi.org/10.1016/j.mechmachtheory.2015.10.006

    Article  Google Scholar 

  19. Xiang L, Gao N, Hu A (2018) Dynamic analysis of a planetary gear system with multiple nonlinear parameters. J Comput Appl Math 327:325–340. https://doi.org/10.1016/j.cam.2017.06.021

    Article  MathSciNet  MATH  Google Scholar 

  20. Chen R, Zhou J, Sun W (2018) Dynamic characteristics of a planetary gear system based on contact status of the tooth surface. J Mech Sci Technol 32:69–80. https://doi.org/10.1007/s12206-017-1208-8

    Article  Google Scholar 

  21. Wei J, Zhang A, Qin D, Lim TC, Shu R, Lin X, Meng F (2017) A coupling dynamics analysis method for a multistage planetary gear system. Mech Mach Theory 110:27–49. https://doi.org/10.1016/j.mechmachtheory.2016.12.007

    Article  Google Scholar 

  22. Parker RG (2000) A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration. J Sound Vib 236:561–573. https://doi.org/10.1006/jsvi.1999.2859

    Article  Google Scholar 

  23. Guo Y, Keller J, Parker RG (2014) Nonlinear dynamics and stability of wind turbine planetary gear sets under gravity effects. Eur J Mech A Solids 47:45–57. https://doi.org/10.1016/j.euromechsol.2014.02.013

    Article  Google Scholar 

  24. Ambarisha VK, Parker RG (2007) Nonlinear dynamics of planetary gears using analytical and finite element models. J Sound Vib 302:577–595. https://doi.org/10.1016/j.jsv.2006.11.028

    Article  Google Scholar 

  25. Kar C, Mohanty AR (2007) An algorithm for determination of time-varying frictional force and torque in a helical gear system. Mech Mach Theory 42:482–496. https://doi.org/10.1016/j.mechmachtheory.2006.04.007

    Article  MATH  Google Scholar 

  26. Yang Y, Li W, Wang J, Zhou Q (2019) On the mixed EHL characteristics, friction and flash temperature in helical gears with consideration of 3D surface roughness. Industrial Lubrication Tribol 71(1):10–21. https://doi.org/10.1108/ILT-04-2017-0113.

  27. Castro J, Seabra J (2007) Coefficient of friction in mixed film lubrication: gears versus twin-discs. P I Mech Eng J-J Eng 208:399–411. https://doi.org/10.1243/13506501JET257

    Article  Google Scholar 

  28. Hu Y, Zhu D (2000) A full numerical solution to the mixed lubrication in point contacts. J Tribol 122:1–9. https://doi.org/10.1115/1.555322

    Article  Google Scholar 

  29. Dowson D, Higginson GR (2006) A numerical solution to the elastohydrodynamic problem. J Mech Eng Sci 1(1):6–15. https://doi.org/10.1243/JMES_JOUR_1959_001_004_02

    Article  MATH  Google Scholar 

  30. Xu H, Kahraman A (2007) Prediction of friction-related power losses of hypoid gear pairs. P I Mech Eng K-J Mul 221:387–400. https://doi.org/10.1243/14644193JMBD48

    Article  Google Scholar 

  31. Wan Z, Cao H, Zi Y, He W, Chen Y (2015) Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears. Mech Mach Theory 92:447–463. https://doi.org/10.1016/j.mechmachtheory.2015.06.011

    Article  Google Scholar 

  32. Lin HH, Huston RL, Coy JJ (1988) On dynamic loads in parallel shaft transmissions: Part I-Modelling and Analysis. J Mech Design 110:221–225. https://doi.org/10.1115/1.3258929

    Article  Google Scholar 

  33. Zhang S, Wang W, Zhao Z (2014) The effect of surface roughness characteristics on the elastic–plastic contact performance. Tribol Int 79:59–73

    Article  Google Scholar 

Download references

Acknowledgements

This research is supported by the Foundation of the National Key Research and Development Plan of China (No. 2018YFB2001300), the Foundation of National Natural Science of China (No. 51975078), the Chongqing Science Fund for Distinguished Young Scholars (cstc2021jcyj-jqX0010).

Author information

Authors and Affiliations

  1. School of Mechatronics and Vehicle Engineering, Chongqing Jiaotong University, ChongQing, 400074, China

    Xiangyang Xu, Guosong Jiang, Han Wang & Xihui Liang

  2. Department of Mechanical Engineering, University of Manitoba, Winnipeg, MB, Canada

    Xihui Liang

Authors
  1. Xiangyang Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guosong Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Han Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xihui Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiangyang Xu.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, X., Jiang, G., Wang, H. et al. Investigation on dynamic characteristics of herringbone planetarygear system considering tooth surface friction. Meccanica 57, 1677–1699 (2022). https://doi.org/10.1007/s11012-022-01526-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-022-01526-4

Keywords

Search

Navigation