Contact behavior between rail and elastic foundation

Abstract

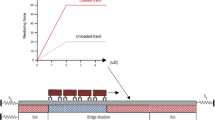
This paper made a revisit on the contact behavior and application of a beam (rail) on a half-plane/half-space. It is found that when the beam is subjected to a concentrated force, the shear deformation of the beam must always be considered, because the deformation only occurs within a limited length of the beam. The second finding of this paper is that the reactions and the surface settlements of the half-plane/half-space are significantly affected by the load position on the cross-section of the beam (on the top of rail in the concerned areas of application) and must be considered in practice. The Flamant/Boussinesq solutions are used to establish integral equations for the surface settlement of the half-plane/half-space below the beam. The Fourier Transform is applied to the first derivative of these integral equations and to the differential equations of the Timoshenko beam. Solving these two equations and employing the inverse Fourier Transform, the deflection and the reaction can be obtained in a compact format. After dispersing the wheel pressure on top of the rail to the centroid, the deflection and reaction are in agreement with the finite element analysis. Finally, simplified equations for equivalent bearing lengths are proposed. Nonuniform distribution of the reactions along the width of the beam is treated by using an equivalent uniform width. If the shear deformation is ignored, the problem becomes the classic one solved by Biot (J Appl Mech 4:A1–A7, 1937). Compared with Biot solution, the current way of solution is compact, their minor differences are the characteristic length. The current solution is a fourth root while the Biot solution is a cube root.

Appendix: Comparisons between the present paper and the Biot solution

• 1. In [1], the load of (48) ($n(y) = 1.0$) was expanded in the full range of $- \infty \le y \le \infty$, so the Biot solution required the following integration (keeping Biot’s notation)

  $$\int\limits_{0}^{\infty } {\frac{{\sin \left( {y/b + 1} \right)\alpha }}{{\alpha \sqrt {\alpha^{2} + \beta^{2} } }}} d\alpha \;{\text{and}}\;\int\limits_{0}^{\infty } {\frac{{\sin \left( {y/b - 1} \right)\alpha }}{{\alpha \sqrt {\alpha^{2} + \beta^{2} } }}} d\alpha$$

  (60)

  Such integrals do not appear in the paper.

• 2. The characteristic length defined by [1] was

  $$L^{\prime } = \left[ {C(1 - \nu^{2} )\frac{{E_{b} I_{b} }}{Eb}} \right]^{1/3}$$

  (61)

  while in the paper the characteristic length is given by (38), which is a fourth root and has no relation with the beam half-width $b$.

• 3. If shear deformation is neglected, $\alpha_{s} = 0$, Eqs. (42) and (43) become

  $$w(x) = \frac{{2(1 - \nu^{2} )Pc}}{{\pi^{2} EL}} \cdot \int\limits_{0}^{\infty } {\frac{\Omega (\beta )\cos (\beta c\xi )}{{1 + c^{4} \beta^{4} \Omega (\beta )}}d\beta }$$

  (62)
  $$M(x) = \frac{PL}{\pi }c^{3} \int_{0}^{ + \infty } {\frac{{\beta^{2} \Omega (\beta )\cos (\beta c\xi )}}{{1 + c^{4} \beta^{4} \Omega (\beta )}}d\beta }$$

  (63)

In [1]

$$w(x) = \frac{P}{{\pi E_{b} I_{b} }}\int_{0}^{\infty } {\frac{\cos (\lambda x)}{{\lambda^{4} + \frac{E}{{C(1 - \nu^{2} )E_{b} I_{b} }}\beta \Psi (\beta )}}} d\lambda = \frac{{2(1 - \nu^{2} )Pc}}{{\pi^{2} EL}}\int_{0}^{\infty } {\frac{{\frac{\pi }{2\beta \Psi (\beta )}\cos (\lambda x)}}{{\beta^{4} c^{4} \frac{\pi }{2\beta \Psi (\beta )} + 1}}} d\beta$$

(64)

$$M(x) = \frac{P}{\pi }\int_{0}^{\infty } {\frac{\lambda \cos \lambda xd\lambda }{{\lambda^{3} + \frac{1}{{C(1 - \nu^{2} )}}\frac{E}{{E_{b} }}\frac{b}{{I_{b} }}\Psi (\beta )}}} = \frac{PL}{\pi }c^{3} \int_{0}^{\infty } {\frac{{\beta^{2} \frac{\pi }{2\beta \Psi (\beta )}\cos \lambda xd\beta }}{{1 + \beta^{4} c^{4} \frac{\pi }{2\beta \Psi (\beta )}}}}$$

(65)

(62) and (63) are found to be the same as (64) and (65) respectively, if the following equation is valid:

$$\Omega (\beta ) = \frac{\pi }{2\beta \Psi (\beta )}$$

(66)

The development of the function $\Psi (\beta )$ in [1] was as follows:

$$\int_{0}^{\infty } {\frac{d\alpha }{\alpha }\frac{\sin \gamma \alpha }{{\sqrt {\alpha^{2} + \beta^{2} } }}} = I$$

$$\frac{dI}{{d\gamma }} = \int_{0}^{\infty } {\frac{\cos \gamma \alpha }{{\sqrt {\alpha^{2} + \beta^{2} } }}d\alpha } = K_{0} (\gamma \beta )$$

$$I = \frac{1}{\beta }\int_{0}^{\gamma \beta } {K_{0} (u)du}$$

$$\varphi (\zeta ) = \int_{0}^{\zeta } {K_{0} (u)du}$$

$$\Psi (\beta ) = \frac{2}{{\int_{ - 1}^{ + 1} {\left\{ {\varphi \left[ {(1 + y/b)\beta } \right] - \varphi \left[ {(y/b - 1)\beta } \right]} \right\}d(y/b)} }}$$

$$\zeta \le 0.1:\varphi (\zeta ) = \zeta (1.116 - \log \zeta )$$

$$\beta \le 0.1:\Psi (\beta ) = \frac{2}{\pi \beta }\left[ {0.923 - \ln \beta } \right]^{ - 1}$$

(67)

When $\zeta > 0.1$ and $\beta \ge 0.1$, values of the functions $\varphi (\zeta )$ and $\Psi (\beta )$ are tabulated in Table

Table 5 values of functions $\varphi (\zeta )$ and $\Psi (\beta )$

5.

Comparison of $\frac{\pi }{2\beta \Psi (\beta )}$ in [1] with $\Omega (\beta )$ of this paper is illustrated in Fig. 

Fig. 15

Comparison of Biot’s numerical approximation

15, some differences are obvious. It seems that [1] has a misprint in (67). If it has the following form, the agreement between both is achieved although (33) has a better accuracy:

$$\beta \le 0.1:\Psi (\beta ) = \frac{\pi }{2\beta }\left[ {0.923 - \ln \beta } \right]^{ - 1}$$

(68)