Numerical and experimental evaluation of the magnetic interaction for frequency up-conversion in piezoelectric vibration energy harvesters

Abstract

The purpose of this work is to improve the modelling process for the application of permanent magnets in a frequency up-conversion (FuC) mechanism for piezoelectric energy harvesters. More specifically, the aim is to avoid the burdensome finite element analyses (FEA) in the framework of electromechanical devices design. The analytical calculations are compared with experimental tests conducted by an ad-hoc set up and with FEA. After investigations on the interaction, an application of FuC mechanism is proposed on a meso-scale case study in which a low frequency seismic mass (LFM) interacts non-linearly, due to magnetic field, with an high frequency piezoelectric vibration energy harvester (PVEH). Numerical simulations have been carried out in the time domain (step-by-step analysis) under a harmonic low-frequency input acceleration signal. The peculiar behavior, due to non-linear dynamics, is investigated in both the repulsive and the attractive configurations of the magnets. The results confirm the effectiveness of magnetic FuC and show that the repulsive case allows the device to recover a larger amount of energy than the attractive configuration.

1 Introduction

The development of energetically autonomous Micro-Electro-Mechanical Systems (MEMS) sensors paves the way for the creation of large networks of devices, with no need for wires or batteries. To this purpose, the available kinetic energy in the environment could be transformed into electrical energy, through suitable energy harvesting systems, e.g. by means of piezoelectric transduction [1,2,3]. Unfortunately, the energy content of the environment, in which MEMS operate, is distributed over a low-frequency spectrum (e.g. 0–100 Hz [4, 5]) and the piezoelectric vibration energy harvesters (PVEHs in the following) are characterized by high natural frequency of vibrations. Such a mismatch implies that the dynamics of the harvester is pratically not activated and the scavenged energy is negligible. In the last decades, researchers have investigated the resonant behaviour [5,6,7]; at present, the attention is focussed on the so called frequency up-conversion techniques (FuC, see e.g. [8, 9]). Many scientists have considered the adoption of multi-stable systems. Cottone et al. [10] proposed a piezoelectric buckled beam that can operate for a random input vibration, with huge gain in terms of power generation with respect to the unbuckled device. Recently, Speciale et al. [11] proposed a snap-through buckling mechanism that can activate the natural vibration of a transducer attached to the bistable structure. Xu et al. [12] realized a piezoelectric MEMS buckled beam that operates below 100 Hz. Another possible approach for frequency conversion is based on impacts. Umeda et al. [13] investigated the efficiency of energy transfer by impacts using piezoelectric oscillators. Halim et al. [14] used transverse impacts induced by a low frequency motion of 5.2 Hz to drive a piezo-magnetic energy harvester. However, a privileged position in FuC techniques is occupied by the magnetic interaction via permanent magnets. The high non-linearity of the magnetic field can be exploited for creating impulsive phenomena on the piezoelectric transducer without any contact. Many works have been done in recent years with application on rotor mechanisms. Pillatsch et al. [15] realized a prototype of energy harvester with rotating proof mass as in mechanical watches [16]. Other works in rotor mechanisms have been proposed by Xue and Roundy [17, 18] and by Fu and Yeatman [19]. A proof of concept of the rotational device with an imposed motion has been proposed by Pozzi [20] and also by Kuang and Yang [21] for the implementation of a knee-joint energy harvester. Regarding translational mechanisms, Li et al. [22] investigated the effect of the bistable magnetic FuC if the movable magnet is connected to a mechanical spring. Kim et al. [23] introduced another improvement in the operational bandwidth for the case of two oscillators. In the mentioned works, the magnetic forces are computed via analytical approaches (or, rarely, via FEA [20]), but the comparison between numerical results and experiments is only presented for the complete harvesting system. The main objective of this paper is the experimental verification of the approximated formulas for the magnetic force simulation in the framework of PVEH design. To that purpose, an ad-hoc experimental setup is introduced and the magnetic forces are measured in different configurations. The experimental data are used to validate different analytical approaches, that could be used instead of the expensive FEA especially in the preliminary design of the devices. The accuracy should be checked not only with reference to the peak force, but most importantly on the whole force-displacement curve: as a matter of fact, such a curve plays a paramount role in case of application to PVEH. The paper is organized as follows. Section 2 contains an in-depth investigation of the force between permanent magnets computed with different analytical formulas. Section 3shows the results of the experimental campaign and the comparison with analytical predictions and finite element analysis. Then, in Sect. 4, magnetic FuC is applied on a possible harvesting system composed of two magnetically coupled oscillators (a LFM and a high frequency PVEH). In that section, also the mathematical model is proposed on the basis of classical Euler-Lagrangian equations. In Sect. 5, numerical simulations of the harvesting system are presented on a realistic meso-scale case study with the permanent magnets of the FuC core both in repulsive and in attractive configurations under harmonic acceleration of the device. The dynamics of the coupled system of oscillators is then discussed pointing out the linking of the output results with the nature of magnetic coupling, respectively repulsive or attractive. Closing remarks are proposed in Sect. 6.

2 Magnetic interaction: analytical formulas

The interaction force between two permanent magnets is here evaluated theoretically and experimentally. The theoretical evaluation of the force is a complex operation due to the fact that it depends non-linearly from many variables, (e.g. shape of the magnets, entity of magnetization vector, spatial orientation of the magnets). Due to this complexity, the interaction is typically modelled by means of numerical techniques (e.g. Finite Element Analyses, FEA) through commercial computer codes. However, from a computational point of view, an accurate solution requires 3D simulations with many degrees of freedom and, consequently, high computing time. For this reason, it is useful to have an analytical fast prediction of the magnetic force. Akoun and Yonnet presented in [24] an analytical approach for the calculation of the magnetic force exerted between two cuboidal magnets with uniform, rigid and parallel magnetization vectors. Their approach is pratically an integral version of the multi-dipole technique. This theory was expanded by Yonnet and Allag in [25] by taking into account the torque between magnets and the interaction in case of orthogonal magnetization vectors. By combining [24, 25], it is possible to compute every force component for a general orientation of magnetization vectors. Rakotoarison et al. in [26] found semi-analytical expressions for the scalar potential and magnetic field produced by a radially polarized permanent magnet through the Coulombian approach. Rubeck et al. in [27] presented an analytical method for the calculation of magnetic field created by a polyhedron-shaped permanent magnet. Another approach was presented by Santra et al. in [28], with reference to the passive magnetic force in a radial magnetic bearing. Given the analogy between the magnetic and the electrostatic problems, Pillatsch et al. in [16] introduced an additional semplification and assumed an inverse square relationship between the magnetic force and the relative distance between the magnets. Similarly, Schomburg et al. in [29] assumed a sort of inverse square relationship but with two fitting parameters instead of the single parameter of the classical inverse square.

In this work, we compute first the magnetic force by following the Yonnet approach [24]. The formulation is based on the computation of the interaction energy between two cuboidal magnets, with parallel magnetization vectors, then the force is derived through the gradient operator. The generic component of the force in 3D space is obtained in the following:

$$\begin{aligned} \begin{aligned}&F_i=\frac{\mathbf {J} \cdot \mathbf {J'}}{4\cdot \pi \cdot \mu _0}\cdot \sum _{m,n,p,q,r,s=0}^1 \left( -1\right) ^{m+n+p+q+r+s} \cdot \\&\phi _i( U_{mn},V_{pq},W_{rs},R) \end{aligned} \end{aligned}$$

(1)

J and J′ are the magnetization vectors expressed in Tesla, $\mu _0$ is the magnetic permeability of vacuum equal to $4\pi \cdot 10^{-7}$ H/m. The parameters m, n, p, q, r, s are related to the corners of the two magnets. They can be equal to 0 or 1. The combinations of m, p, r identifies the corner of one magnet and q, r, s of the other. The coefficients $\phi _i$ that appear in (1) are:

$$\begin{aligned} \begin{aligned}&\phi _x(U_{mn},V_{pq},W_{rs},R)\\&=\frac{V_{pq^2}-W_{rs}^2}{2}\cdot ln(R-U_{mn})+U_{mn}\cdot V_{pq}\cdot ln(R-V_{pq})\\&+V_{pq}\cdot {W_{rs}}\cdot \arctan \left( \frac{U_{mn}\cdot V_{pq}}{W_{rs}\cdot R}\right) +\frac{1}{2}\cdot U_{mn}\cdot R \end{aligned} \end{aligned}$$

(2)

$$\begin{aligned} \begin{aligned}&\phi _y(U_{mn},V_{pq},W_{rs},R)\\&=\frac{U_{mn^2}-W_{rs}^2}{2}\cdot ln(R-V_{pq})+U_{mn}\cdot V_{pq}\cdot ln(R-U_{mn})\\&+U_{mn}\cdot {W_{rs}}\cdot \arctan \left( \frac{U_{mn}\cdot V_{pq}}{W_{rs}\cdot R}\right) +\frac{1}{2}\cdot V_{pq}\cdot R \end{aligned} \end{aligned}$$

(3)

$$\begin{aligned} \begin{aligned}&\phi _z(U_{mn},V_{pq},W_{rs},R)=\\&-U_{mn}\cdot W_{rs}\cdot ln(R-U_{mn})-V_{pq}\cdot W_{rs}\cdot ln(R-V_{pq})\\&+U_{mn}\cdot {W_{rs}}\cdot \arctan \left( \frac{U_{mn}\cdot V_{pq}}{W_{rs}\cdot R}\right) -W_{rs}\cdot R \end{aligned} \end{aligned}$$

(4)

Fig. 1

Schematization of interacting magnets in the Yonnet analysis

By considering the Fig. 1, two Cartesian reference systems are located in the centroids of the two magnets; $\alpha$, $\beta$ and $\gamma$ are the vector components of the distance between the centers O and O’ of the reference systems, and a, b, c, A, B, C are the half-lengths of the magnets sides. The coefficients $U_{mn}$, $V_{pq}$, $W_{rs}$, R are defined as:

$$\begin{aligned}&U_{mn}=\alpha +A(-1)^m-a(-1)^n \end{aligned}$$

(5)

$$\begin{aligned}&V_{pq}=\beta +B(-1)^q-b(-1)^p \end{aligned}$$

(6)

$$\begin{aligned}&W_{rs}=\gamma +C(-1)^s-c(-1)^r \end{aligned}$$

(7)

$$\begin{aligned}&R=\sqrt{U_{mn}^2+V_{pq}^2+W_{rs}^2} \end{aligned}$$

(8)

As an alternative, one can assume an inverse square approximation for the magnetic force between two magnets. With reference to Fig. 2 one can write:

$$\begin{aligned} F_{mag}=\frac{F_0\,h^2}{r_{mag}^2} \end{aligned}$$

(9)

In Eq. 9, $F_{mag}$ is the magnetic force module, $F_0$ is the peak of magnetic force that is exerted when the magnets are separated by the so called gap distance h; $r_{mag}$ is their relative distance. In view of the specific examples considered in this paper, the in-plane behavior is of interest. By simple trigonometric manipulations it is possible to obtain the $F_z$ and $F_y$ force components of $F_{mag}$:

$$\begin{aligned}&F_{z}=F_0\,h^2\frac{z_2-z_1}{\left( {h^2+(z_2-z_1)^2}\right) ^{3/2}} \end{aligned}$$

(10)

$$\begin{aligned}&F_{y}=F_0\,h^3\frac{1}{\left( {h^2+(z_2-z_1)^2}\right) ^{3/2}} \end{aligned}$$

(11)

Fig. 2

Illustration of the interaction layout between two permanent magnets

It is important at this stage to highlight that, if one want to use inverse square approach, the peak force must be known. In the Yonnet approach case, the only parameter is the magnetization J of the magnets, that is a physical property and is independent from the relative distance between magnets. Conversely, the inverse square approach needs a fitting procedure with reference to the peak force. Both approaches are insensitive to an inversion in sign of the interaction nature. In other words, the attractive interaction between magnets is simply the repulsive one changed in sign.

As an example, Fig. 3 shows the forces computed via the Yonnet approach for two cuibic magnets, $2A=2B=2C=2a=2b=2c=3.0$ mm, with equal magnetization $J=J'=1.32$ T. The gap in y direction is $h=1$ mm, the relative distance is given by $z_2-z_1$ and ranges between $-20$ mm and $+20$ mm. The $F_y$ component is an even function while $F_z$ is an odd function. The absolute peak values of the components are 1.574 N for $F_y$ and 0.744 N for $F_z$. By using the peak of $F_y$ as $F_0$ in the Eqs. 10 and 11, it is possible to set up the inverse square model. The comparison between Yonnet model and inverse square relation is summarized in Fig. 4a for the y-component and in Fig. 4b for the z-component. A first observation is that, in case of Yonnet approach, both $F_y$ and $F_z$ have an inversion in sign for increasing relative distance. This feature is not present in the inverse square model. In the inverse square model, the interaction is more concentrated around the zero relative-position between magnets. This aspect has important consequences on the physics of the system because strong variations in forces mean strong variations in magnetic potential. Third and fundamental observation is that if the inverse square is tuned on the peak y-component, then an important mismatch is present for the z-component: in this specific example there is a difference of $18.01\%$ between the peak force along z. Obviously, one could tune the inverse square parameter to match the peak of the z-component, but in that case the agreement on the y-component is missed. As expected, the agreement between the two considered models is improved if the gap h increases.

Fig. 3

Magnetic force components through Yonnet formula

Moreover, the y-component can be computed with the following expression [29] (under the assumption that $A\ge a$):

$$\begin{aligned} F_{y}=\left\{ \begin{array}{l} F_0\frac{d_e^2}{(h+d_e)^2} \quad \text {if} \quad |z_2-z_1| \le A-a\\ \frac{F_0 d_e^2}{(h+d_e)^2}\left[ \frac{A+a}{2a}- \frac{z_2-z_1}{2a}\right] \, \text {if} \, A-a \le |z_2-z_1| \le A+a\\ 0 \quad \text {if} \quad |z_2-z_1| \ge A+a \end{array}\right. \end{aligned}$$

(12)

where $F_0$ is the force that is exerted with magnets put in contact and $d_e$ is the gap distance at which the maximun force with aligned magnets ($z_2-z_1=0$) reduces to 1/4 of $F_0$. Both $F_0$ and $d_e$ are unknown, so a best-fit procedure should be implemented. The z-component is calculated as:

$$\begin{aligned} F_{z}=F_{z,m}\,\left[ \frac{a^4}{a^4+\left( z_2-z_1-A\right) ^4}-\frac{a^4}{a^4+\left( z_2-z_1+A\right) ^4}\right] \end{aligned}$$

(13)

A and a are the half-lengths of the two magnets facing to the direct interaction expressed in accordance to the Fig. 1; $F_{z,m}$ contains the parameters $F_0$ and $d_e$ and depends on the gap h. This approach can be used after the experimental characterization.

Fig. 4

Comparison of a $F_y$ and b $F_z$ component

3 Magnetic interaction: experimental and numerical validation

Fig. 5

Experimental set up and zoom on a single magnet

At this stage an experimental investigation is presented. The involved magnets have been provided by “Supermagnete” dealer [30]. Their physical and geometrical features are the same as in the previous analysis. A cubic magnet (3 × 3 × 3 $\hbox {mm}^3$) of this type is represented in Fig. 5. These magnets are composed of a Neodymium-Iron-Boron alloy (NdFeB). They have much higher coercive force and remanence with respect to the classical ferrite magnets. For this reason they are largely used in advanced industrial applications (e.g. eolian generators, electrical motors in aerospace, automotive). The conducted tests have the scope to ascertain the real force interaction between magnets as simulated through analytical formulas. The experimental set up is shown in Fig. 5, it is composed of an electrical integrated servo-positioner (SMART Automation, SM2316D, max 48vdc rated velocity 66 rpm), an handcrafted actuator, a load cell S2 Tech 514QD (full scale FS 30 N, repeatability error: $\le \pm 0.033\%$ FS, total error: $\le \pm 0.023\%$ FS, sensitivity: 2 mV/V/FS ) and a displacement sensor. The data acquisition device (DAQ) is a $\hbox {DAQCard}^{\scriptscriptstyle \mathrm {TM}}$-6062E by National Instruments (12 bit resolution, maximum sampling rate of 500 kHz). In order to set the gap distance between magnets, a simple mechanical gauge has been used. In the experiment, one magnet has been connected on the motion axis of the actuator and the other one on the load cell. The last one plays the role of “fixed at ground” magnet as indicated in Fig. 2. However, the magnets are not directly fixed on the cell and on the axis but they have been glued with cyanoacrylate on two Aluminium rods machined with a numerical control lathe. This last operation has been done in order to prevent the interaction of the magnetic field with the supporting system. The experiment provides the magnetic force evaluation exerted between magnets for different values of gap distance h, equal to 0.5 mm, 1 mm, 2.0 mm. For each gap distance two configurations have been tested: attractive and repulsive. The velocity of the motion axis of the actuator has been fixed to 0.5 mm/s. All experimental curves have been independently fitted with a Gaussian model:

$$\begin{aligned} F_i=\sum _{k=1}^n a_k e^{-\left( \frac{z-b_k}{c_k}\right) ^2} \end{aligned}$$

(14)

where the index i is the spatial direction y or z and $a_k$, $b_k$, $c_k$ are fitting parameters. The variable z at exponent is the relative distance between magnets on the z-axis with reference to the Fig. 2. In all cases, three terms in the summation of Eq. 14 provides a good estimate of the curve (nine coefficients with 95% confidence bounds). In order to have also a comparison with a numerical solution, 3D finite element simulations have been performed with the software COMSOL Multiphysics^® by using quadratic tetrahedral finite elements. In Figs. 6, 7 and 8, the results are summarized in case of attractive configurations and it is shown the comparison of experimental tests with Yonnet prediction, the inverse square assumption, the numerical models (FEM) and also the Gaussian fit.

Fig. 6

a $F_y$ an b $F_z$ comparisons for $h=0.5$ mm

Fig. 7

a $F_y$ an b $F_z$ comparisons for $h=1.0$ mm

Fig. 8

a $F_y$ an b $F_z$ comparisons for $h=2.0$ mm

It is important to highlight that, since the real magnetization of the magnets is not exactly as assumed in the simulations of the previous paragraph, to have more realistic results, the Yonnet algorithm has been fitted by matching the peak force of y-component in case of gap equal to 2.0 mm and the same value has been used in the finite element models. The inverse square instead, because of its rude grade of approximation, must be set case-by-case on the $F_y$ experimental component. For the sake of completeness, we add in Fig. 8 the force components estimated through the Eq. 13, but it is not a reasonable approximation with respect to the other approaches, especially for the $F_y$ component.

Tests have also been conducted for the repulsive case, the results are qualitatively similar to the attractive ones though with the opposite sign. As declared a priori by the supplier, there is a slight difference in absolute force value for the two configurations. More in detail, it can be noticed in Fig. 9a that for the $F_y$ component, the attractive values are greater than the repulsive ones. The opposite holds for the $F_z$ component when the gap h is very small (Fig. 9b). The difference is due to micro-structure reasons: when the magnets are in repulsive configuration, each magnet disturbs the parallel orientation of the dipole in the other magnet. This means that the force is lower in y direction but higher in z because the missed parallelization increases the z-component. In any case, when the magnets are sufficiently distant, the repulsive curves tend in absolute value to the attractive ones. For all analyzed cases the effect is less than $10\%$ at peaks. The Fig. 10a, b, related to attractive configuration, highlight the non-linear nature of the peak forces for varying gap distance h. In Fig. 10a the inverse square coincides with the experimental one for initial assumptions of its calibration.

Fig. 9

Experimental a $F_y$ and b $F_z$ comparison for attractive and repulsive configuration, in the case $h=0.5$ mm

From the above results, it appears that the peak force of interest can be represented with each of theoretical presented approach. However, a good matching in terms of peak force is not a sufficient condition for a good representation of reality. In fact, the shape of the force-displacement law is directly representative of the involved interaction energy. The inverse square approximation is good to capture the physical evidence, as reported in Fig. 6b, but fails in the representation of the whole force-displacement curve, that is strictly connected to the global magnetic energy. In terms of shape of the force-displacement curve, Yonnet approach and finite element analysis are in good agreement with the experiment. However, the computations with the Yonnet approach (as well as the other analytical formulations) are carried out instantaneously by a computer. Conversely, the presented finite element models required more or less 2 h 10 min of computing time. This is due to the high number of degrees of freedom typical of such a technique. For more refined energetic representation of the phenomenon the Yonnet approach appears the best choice if opportunely set. Such a conclusion is corroborated by the evaluation of the overall error on the force-distance curve. A dimensionless $L^2$ norm of the discrepancy is applied, as follows:

$$\begin{aligned} \text {error}=\frac{\int _{-20 \text {mm}}^{+20 \text {mm}} (F_i-F_{exp})^2 \, dz}{\int _{-20 \text {mm}}^{+20 \text {mm}} (F_{exp})^2 \, dz} \end{aligned}$$

(15)

where $F_i$ is referred to the various simulations. Table 1 summarizes the errors for each case of interaction and gaps. In general, the Yonnet approach provides good results: the overall error is by far less than the case of inverse square and it is well aligned with FEA. The inverse square approximation is reasonable for large gaps only: as a matter of fact, the error is decreased when the gap between the magnets is increased. The Gaussian fit provides excellent approximation with three terms only, but it cannot be used as a predictive tool since it is just a fit of experimental data.

Fig. 10

a $F_y$ and b $F_z$ peaks for different gap distances

Table 1 Dimensionless $L^2$ discrepancy with respect to the experimental results

4 FuC via magnetic plucking: problem formulation

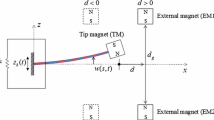
Concept of the application In this section, the work focuses on the application of the magnetic interaction in piezoelectric vibration energy harvesters (PVEH) from the theoretical modelling point of view. As specified in the introduction, we use the magnetic interaction as a frequency up-conversion mechanism for activating a train of free-vibrations on the piezoelectric structural element.We consider a mechanism composed of a low frequency spring-mass (LFM) system equipped with a magnet and a PVEH in the typical form of cantilever beam or plate, also equipped with a magnet on the tip as in Fig. 11.

Fig. 11

a Lateral and b top view of the device proposed in [31]

The functionality of the mechanism is completely general with respect to the scale. In the presented mechanism, the piezoelectric beam can be seen as a MEMS device with high natural frequency. The LFM can vibrate for very low-frequency input acceleration. The magnetic interaction is used to implement the frequency up-conversion by means of contactless plucking.

Mathematical modelling In order to model the entire mechanism, LFM and PVEH are treated separately and then put in a global model through the magnetic interaction. A lumped-parameter approach is adopted, which belongs to the framework of discretization methods. The simplest mechanical model of the seismic mass is the one-degree-of-freedom oscillator with a proper damper. The modelling of piezolaminated beam has been carried out in previous works (see Ardito et al. [32] and Gafforelli et al. [33]). In particular, Rayleigh-Ritz method has been used for each involved physics. The displacement field w(x) of the transducer has been modeled with a single time-dependent degree of freedom W(t) and a classical polynomial shape function ${\psi} _w$ (see [32, 34]).

$$\begin{aligned}w(x,t)={\psi}_w(x)W(t) \end{aligned}$$

(16)

$$\begin{aligned}{\psi} _w(x)=\frac{3}{2}\left( \frac{x}{L}\right) ^2-\frac{1}{2}\left( \frac{x}{L}\right) ^3 \end{aligned}$$

(17)

The piezoelectric coupling is in the so-called 31-mode, that means that the longitudinal strain is coupled to the transverse electric field $E_3$. The electric potential is assumed to be linear in the thickness $t_p$ and constant along the longitudinal axis of the beam. This is due respectively to the very small thickness of the layer and to the extension of the electrodes along the entire length of the transducer. For the mentioned reasons, the electric field is constant. In this case the time-dependent degree of freedom is the voltage at the free electrode V(t).

$$\begin{aligned} E_3=-\frac{V(t)}{t_p} \end{aligned}$$

(18)

In the framework of small strains and displacements, the discretized governing equations read:

$$\begin{aligned} {\left\{ \begin{array}{ll} m \ddot{W}(t)+c_m \dot{W}(t)+k_l W(t) - \Theta V(t)=f_{ext} \\ C_e V(t)+\Theta W(t) = q(t) \end{array}\right. } \end{aligned}$$

(19)

The involved coefficients are computed as integral over the volume of the structure. m is the total inertia term, $c_m$ is the linear mechanical damping coefficient, $k_l$ is the linear elastic stiffness, $C_e$ is the capacitance associated to the piezoelectric layer. $\Theta$ is the coupling coefficient and represents the multiphysics nature of the system. If the piezoelectric element is connected to a simple resistive circuit, the Kirchhoff’s law establishes that:

$$\begin{aligned} \dot{q}=-\frac{V(t)}{R} \end{aligned}$$

(20)

Therefore the differential system (19) becomes:

$$\begin{aligned} {\left\{ \begin{array}{ll} m \ddot{W}(t)+c_m \dot{W}(t)+k_l W(t) - \Theta V(t)=f_{ext} \\ C_e \dot{V}(t)+\Theta \dot{W}(t) +V(t)/R=0 \end{array}\right. } \end{aligned}$$

(21)

The external force $f_{ext}$ in this case is the sum of the vibrational input on the harvester and the magnetic interaction since the frequency up-conversion technique is employed. By combining the piezoelectric transducer with the LFM system, both equipped of a magnet as in Fig. 12 one obtains the following dynamic equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} m \ddot{W}+c_m \dot{W}+k_l W - \Theta V=-m_z\ddot{Z}+F_z(W,W_s) \\ C_e \dot{V}+\Theta \dot{W} +V/R=0 \\ m_s \ddot{W_s}+c_m \dot{W_s}+k_s W_s =-m_s\ddot{Z}-F_z(W,W_s) \\ \end{array}\right. } \end{aligned}$$

(22)

Fig. 12

Mechanical 1-D schematization of the system

The differential system (22) becomes highly non-linear for the presence of the magnetic interaction ($F_z$). The y-component of the magnetic force ($F_y$) does not appear in the model because it would induce an axial force in the cantilever, with no effect on the bending deformation (the maximum displacements is small enough to justify the hypothesis of linearized kinematics). The experimentally measured magnetic force is used in the following simulations.

5 Numerical simulations and results

The differential system (22) has been implemented in a MATLAB© software [35]. For the simulations we consider a mesoscale case study. The magnets are the same of the sections 2 and 3. Then, a unimorph piezoelectric cantilever is considered with 13 mm length and a width of 2 mm. The laminate section is composed of $200 \, {\upmu }$m thickness of silicon layer under a lead zirconate titanate (PZT) film $100 \, {\upmu }$m thick. The materials properties are summarized in Table 2 together with all simulation data. Note that $\varepsilon _{33}^S$ is expressed in terms of dielectric constant in vacuum, $\varepsilon _0=8.854\times 10^{-12}$ F/m.

Table 2 Parameters for the simulations

The mechanical quality factor $Q_m$ is assumed to be equal to 250. So, it is possible to compute the damping ratio by definition:

$$\begin{aligned} \zeta _m=\frac{1}{2Q_m}=0.002 \end{aligned}$$

(23)

The damping ratio is related to the damping coefficient through the following equation:

$$\begin{aligned} c_m=2 m \omega _r \zeta _m \end{aligned}$$

(24)

Fig. 13

Displacement $W_s$ of LFM in repulsive magnetic interaction. The displacement of the tip beam W is pratically inappreciable

Fig. 14

Detail on the free vibration state of PVEH

Fig. 15

Displacement of the LFM over 60 s, in the repulsive case

Fig. 16

Power of PVEH in repulsive magnetic interaction

The seismic mass has been conceived from a simple consideration: its oscillation must be as much as possible large when excited at the frequency content of the human motion. Environmental vibrations and also human movement have significant energy in the frequency band $0.5{-}{10}$ Hz (see e.g. Keli et al. [36]). The mass has been chosen of 0.05 kg and connected to a stiffness of 60 N/m with resultant resonance frequency of about 5.5 Hz. Clearly, the combination of mass and stiffness that provide a specific frequency are infinite but consider, in this context, that small mass implies small device. For the LFM a mechanical quality factor $Q_M$ of 40 has been adopted, this means a damping ratio of 0.0125. The analysis has been carried out with a harmonic monochromatic acceleration input on the entire device, amplitude 2g and frequency 3 Hz. This frequency has been choosen in order to represent realistic circumstances in which the natural frequency of the LFM is not exactly the frequency of the input signal. A resistive load of 100 k${\Omega }$ has been used. Note that the natural frequency of the piezoelectric beam is 507.29 Hz. Computational analysis are presented both in repulsive and in attractive configurations in order to compare them by assuming the experimental interaction ($F_z$) with 1 mm gap distance. Figures 13, 14, 15 and 16 show displacements and power for the repulsive case. Figure 14 put in evidence the effect of the magnetic interaction on the vibration of the transducer: the two elements initially mode together, but at a certain point the beam is suddenly released because the elastic restoring force of the PVEH is higher than the magnetic force. Then, the LFM continues its motion far from the PVEH that enters in a free vibration phase at a frequency of 507.29 Hz. This behaviour is repeated at each cycle.

Fig. 17

Displacement $W_s$ of LFM in attractive magnetic interaction. The displacement of the tip beam W is pratically inappreciable

Fig. 18

Detail on the free vibration state of PVEH in case of attractive interaction

Fig. 19

LFM displacement over 60 s, in the attractive case

Fig. 20

Power of PVEH in attractive magnetic interaction

From the results, the oscillation of the seismic mass is strongly disturbed by the magnetic interaction and does not seem to get the regime situation. This is evidenced by the time history of LFM displacement over 60 s, see Fig. 15. This aspect is easily interpreted: in the presence of repulsive force, at each cycle the LFM is subjected to an impulsive load due to the unstable behaviour when the two magnets are aligned. The non-linear effects are such that the system does not reach the orbit of oscillation which would be imposed by the simple harmonic forcing function.

Other simulations have been conducted with attractive configuration, see Figs. 17, 18, 19 and 20. It is interesting to notice that in this case, opposite to the repulsive one, the system reaches a real regime vibration after the effect of the initial condition. In fact, in attractive scheme, the interaction is such that the motion is accelerated, before the critical phase of energy exchange. After the plucking the attraction tends to reclaim the mass, so pratically there is a sort of affinity with the motion. In other words, the attractive interaction consolidates the trend of the uncoupled harmonically forced oscillator. It is an important result because it highlights the non-holonomic nature of this kind of coupling in mechanical systems.

A quantitative comparison is now introduced in terms of harvested power. In the repulsive configuration, peaks of power of the order of 3.9 mW are obtained; in the attractive configuration, the initial peak is 1.8 mW, then in the regime situation the power is 0.7 mW. This is an important result in both conditions if one consider that without the frequency up-conversion the transducer does not vibrate at 3 Hz with consequent zero energy harvested. For what concerns the integral terms, Table 3 summarizes the overall harvested energy and the RMS (Root-Mean-Square) voltage on a period of 60 s; in order to compute the mean power, the Joule’s law is employed:

$$\begin{aligned} P_{mean}=\frac{V_{RMS}^2}{R} \end{aligned}$$

(25)

Table 3 contains also the results which are obtained if the experimental force is replaced by the Yonnet approximation via Eq. (1). The RMS voltage obtained in this case shows differences of 18% and 9% with respect the use of experimental data, for the case of attractive and repulsive configuration, respectively. Another interesting aspect is that if the Yonnet interaction is used, the attractive case corresponds to a larger amount of RMS voltage than the repulsive one. This is due to the shape of the Yonnet force-distance curve, that is lower than the real one for high relative distance. The particular non-linear behavior of Figs. 13 and 15 is then pratically lost. In fact, in this case the behavior of the oscillator is similar to the classical one as in Figs. 17 and 19. Additional simulations, here not reported extensively for the sake of brevity, confirm that, by increasing the gap distance, the relative difference of RMS voltage in case of using Yonnet or experimental data tends to vanish.

Table 3 Synopsis of the results: RMS Voltage, Power and energy harvested over 60 s. E: experimental and Y: Yonnet interaction

6 Conclusions

The present paper is focused on the investigation of magnetic interaction for frequency up-conversion in piezoelectric energy harvesters. The main contributions are provided in sections 2 and 3, in which different analytical approaches have been presented and compared to experimental results and finite element analysis to model the interactions forces between permanent magnets. The purpose is to provide a fast computational approach to designers for a good representation of the physical phenomena. The conclusions of the investigations can be summarized as follows. The inverse square approach can represent the peak forces in a rigorous way but it provides bad estimate in energy terms. The interaction is too much concentrated around the zero-relative position between magnets and it is not in agreement with the experimental evidence. Better approximation is achieved in case of large distance between the magnets. A possible improvement, from an energetic point of view, is the approach of Schomburg et al [29] in which the interaction is more spread in the space domain with respect to the inverse square formula. However, this formula is quite poor in the representation of the $F_y$ component and it requires two fitting parameters ($F_{0}$ and $d_e$) making necessary experimental data or finite element simulations. A predominant position, both in terms of peak forces and magnetic energy, is provided by the Yonnet algorithm which is based on the multi-dipole approach with the magnetization value as fitting parameter. This approach shows also a good agreement with the presented finite element results. In section 3, the mathematical model of the piezoelectric harvesters has been proposed on the basis of previous works ([32, 33]). In section 4, the application of the model has been implemented on a unimorph cantilever beam with a length of 13 mm interacts, through the magnetic FuC, with a low frequency oscillating mass tuned at a resonant frequency of about 5.5 Hz. A harmonic, monocromatic acceleration has been imposed on the entire device with 2g of amplitude and 3 Hz of frequency. Numerical simulations have been carried out in the time domain (step-by-step analysis) both in repulsive and in attractive configuration of the magnets. The results, in terms of scavenged energy, are more promising when the FuC works in repulsive configuration, but interesting values for consumer applications emerge from both configurations. Over a working period of 60 s, with a resistive load of 100 k${\Omega }$, the harvester can recover 1.96 mJ of energy for the repulsive configuration and 1.26 mJ for the attractive one. Interesting non-linear effects emerge from the analysis that lead to different behaviors of the oscillators depending from the magnets configuration. The results of this work increment our emphasis on magnetic FuC solution for low frequency piezoelectric energy harvesters. It guarantees a contactless frequency conversion avoiding the detrimental effects of impacts on piezoelectric materials. As reported in [37], the reliability of piezoelectric beams is an important issue, even in the absence of impacts: the degradation of piezoelectric bending beams impairs drastically the power output and the natural frequency. Further analyses are needed for assessing time-dependent effects on the harvester. Other possible developments regard the prototyping of the presented FuC mechanism. Moreover, it would be interesting to develop a non-linear model in order to study the effects of moderately large rotations on the performance of PVEH. Also other types of electric circuit can be brought in consideration for realistic techological applications (e.g. RLC circuits, electrical non-linearities, see [38]). Nowadays, geometrical and physical non-linearities appear the only way to move the energy content in frequency spectrum and this opens new fascinating challenges for future works.