Skip to main content
SpringerLink
Log in

A numerical study of instability transition of a beam-like plate with imperfections loaded by a steady axial airflow

  • Brief Notes and Discussions
  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

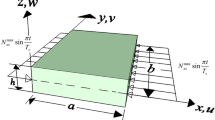
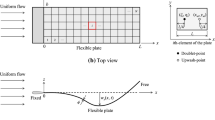
The actual plate structures are not as ideal as the general theoretical analysis. They are potentially subjected to imperfections, significantly influencing their instability behaviors when they vibrate in fluids. On the one hand, the possible imperfections come from the structure itself, and on the other hand, they come from the mismatch between theoretical and experimental modelings. The lack of influence analysis of imperfections will lead to many deviations in our understanding of the structure’s mechanical properties and the experimental results. This brief note presents a numerical study on the instability of a plate with two types of imperfections: the crack defect and imperfect edge-support, and reveals the influence of these imperfections on the plate instability behaviors when the plate is subjected to a steady axial airflow. The crack defect is modeled as an all-over part-through crack in the plate and the imperfect edge-support as elastic end support with transversal and rotational springs. For the uncracked plate, the elastic end support allows the coexistence of the flutter and divergence instability. The rotational spring plays a vital role in the distributions of instability regions and the transition of two instability types. The plate exhibits more complicated instability behaviors with the effect of both crack and elastic end support. There will be transitions between instability regions, and the instability transition processes between different instability types are more diversified.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Raghunathan RS, Kim HD, Setoguchi T (2002) Aerodynamics of high-speed railway trains. Prog. Aerosp. Sci. 38:469–514

    Article  Google Scholar 

  2. Li P, Yang YR, Xu W, Chen G (2020) Imperfect bifurcations in an initially curved plate loaded by incompressibale axial flow. Nonlinear Dyn. 99:1379–1402

    Article  Google Scholar 

  3. Li P, Wang ZX, Zhang DC, Yang YR (2021) On bifurcations and chaos of a focred rectangular plate with large deflection loaded by subsonic airflow. Thin-walled Struct 161:107421. https://doi.org/10.1016/j.tws.2020.107421

    Article  Google Scholar 

  4. Dowell EH (1975) Aeroelasticity of plates and shells. Noordhoff International Publishing, Leyden

    MATH  Google Scholar 

  5. Dowell EHA (2015) modern course in aeroelasticity, fifth revised and, enlarged. Springer Cham Heidelberg New York Dordrecht London

  6. Païdoussis MP (2004) Fluid-structure interactions. Slender structures and axial flow, vol 2, 1st edn. Elsevier Academic Press, London

  7. Watanabe Y, Suzuki S, Sugihara M, Sueoka Y (2002) A experimental study of paper flutter. J Fluids Struct 16:529–542

    Article  Google Scholar 

  8. Watanabe Y, Isogai K, Suzuki S, Sugihara M (2002) A theoretical study of paper flutter. J Fluids Struct 16:543–560

    Article  Google Scholar 

  9. Allen JJ, Smits AJ (2001) Energy harvesting eel. J Fluids Struct 15:629–640

    Article  Google Scholar 

  10. de Breuker R, Abdalla MM, Gürdal Z (2008) Flutter of partially rigid cantilevered plates in axial flow. AIAA J 46:936–946

    Article  Google Scholar 

  11. Dugundji J, Dowell EH, Perkin B (1963) Subsonic flutter of panels on continuous elastic foundations. AIAA J 5:1146–1154

    Article  Google Scholar 

  12. Ishii T (1965) Aeroelastic instabilities of simply supported panels in subsonic flow. Los Angeles, AIAA Paper, Meeting of the AIAA, pp. 765–772

  13. Shahrokh A, Ellen CH (1979) The stability of partially rigid two-dimensional surfaces in uniform incompressible flow. J Sound Vib 65:339–351

    Article  Google Scholar 

  14. Kornecki A, Dowell EH, O‘Brien J (1974) On the aeroelastic instability of two-dimensional panels in uniform incompressible flow. J Sound Vib 47:163–178

    Article  Google Scholar 

  15. Wang Q, Koh CG (2003) Regions of flutter and bucking instability for a cracked beam. AIAA J 41:2302–2304

    Article  Google Scholar 

  16. Beloiu DM, Ibrahim RA, Pettit CL (2005) Influence of boundary conditions relaxation on panle flutter with compressive in-plane loads. J Fluids Struct 21:743–767

    Article  Google Scholar 

  17. Li P, Yang YR (2014) On the stability and chaos of a plate with motion constraints in subsonic flow. Int J Non-Linear Mech 59:28–36

    Article  Google Scholar 

  18. Li P, Li ZW, Dai CD, Yang YR (2018) On the non-linear dynamics of a forced plate with boundary conditions correction in subsonic flow. J Appl Model 64:15–46

    Article  MathSciNet  Google Scholar 

  19. Li P, Li ZW, Dai CD, Yang YR (2018) Non-linear limit cycle flutter of a plate with Hertzian contact in axial flow. J Fluids Struct 81:131–160

    Article  Google Scholar 

  20. Li P, Liang S, Zhang DC, Zhu YZ, Yang YR (2019) The instability of a plate fixed at both ends in an axial flow revisited: an application of the DQ-BE method. J Eng Math 118:43–61

    Article  MathSciNet  Google Scholar 

  21. Caddemi S, Caliò I (2009) Exact closed-form solution for the vibration modes of the Euler-Bernoulli beam with multiple open cracks. J Sound Vib 327:473–489

    Article  Google Scholar 

  22. Caddemi S, Caliò I (2012) The influence of the axial force on the vibration of the Euler-Bernoulli beam with an arbitrary number of cracks. Arch Appl Mech 82:827–839

    Article  Google Scholar 

  23. Yang ZC, Xia W (2010) Analytical models, numerical solutions and advances in the study of panel flutter. Adv Mech 40(1):81–97 (in Chinese)

    MathSciNet  Google Scholar 

  24. Kornecki A (1973) On the character of instability of certain aeroelastic systems. AIAA J 40:616–617

    MATH  Google Scholar 

  25. Sundararajan C (1976) Influence of an elastic end support on the vibration and stability of Beck‘s column. Int J Mech Sci 18:239–241

    Article  Google Scholar 

  26. Simitses GJ, Hodges DW (2006) Fundamentals of structureal stability. Elsevier Academic Press, London

    MATH  Google Scholar 

  27. Shih YS, Wu GY (2002) Effect of vibration on fatigue crack growth of an edge crack for a rectangular plate. Int J Fatigue 24:557–566

    Article  Google Scholar 

  28. Paulus M, Dasgupta A (2012) Semi-empirical life model of a cantilevered beam subjected to random vibration. Int J Fatigue 45:82–90

    Article  Google Scholar 

  29. Strganac TW, Kim YI (1996) Aeroelastic behavior of composite plates subject to damage growth. J Aircraft 33:638–73

    Article  Google Scholar 

  30. Wang K, Inman DJ (2007) Crack-induced effects on aeroelasticity of an unswept composite wing. AIAA J 45:542–551

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos: 12072298; 11772273). The authors are grateful to the anonymous reviewers whose comments helped immensely in writing this paper.

Author information

Authors and Affiliations

  1. School of Mechanics and Engineering, Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, Southwest Jiaotong University, Chengdu, 610031, People’s Republic of China

    Peng Li, Yizhang Zhu, Dechun Zhang & Yiren Yang

Authors
  1. Peng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yizhang Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dechun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yiren Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peng Li.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, P., Zhu, Y., Zhang, D. et al. A numerical study of instability transition of a beam-like plate with imperfections loaded by a steady axial airflow. Meccanica 57, 507–521 (2022). https://doi.org/10.1007/s11012-021-01455-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-021-01455-8

Keywords

Search

Navigation