The instability of a plate fixed at both ends in an axial flow revisited: an application of the DQ–BE method

Abstract

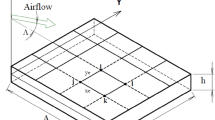
This work revisits the aero-elastic instability of a plate subjected to an axial subsonic flow and reports a refined numerical solution. The plate is fixed at its both ends, and the fluid computational region is decomposed into two subregions belonging to the plate area and the downstream outside area of the plate. Compared with the previous studies, the present numerical method is simple and straightforward, and is successfully extended to include the effect of the downstream outside area. By considering the downstream outside area, this problem is formulated as a boundary integral equation and three partial differential equations. Then the boundary integral equation is solved by the boundary element (BE) method, and the differential quadrature (DQ) method is applied for the partial differential equations. A wind tunnel experiment is completed for validations of the present fluid solution. Three cases of outside-area boundary conditions and four cases of plate boundary conditions are considered, and their influences on the plate instability behavior are studied. Results show that the present formulation is workable and is in good agreement with the existing theories. The effects of the outside area on the plate instability behavior, which have escaped the attention of the previous studies, are clearly observed. The present study can serve as references for other relative studies on plate instability.

Appendix

The matrixes in Eq. (21) are:

$$\begin{aligned} {\mathbf{C}}_{lr}^{{\mathrm{bb}}}&= {\left[ {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad {C_{2,2}^l}&{}\quad {C_{2,N + 3}^l}&{}\quad 0\\ 0&{}\quad {C_{N + 3,2}^r}&{}\quad {C_{N + 3,N + 3}^r}&{}\quad 0 \end{array}} \right] _{4 \times 4}}, \end{aligned}$$

(A.1a)

$$\begin{aligned} {\mathbf{C}}_{lr}^{{\mathrm{bp}}}&= {\left[ {\begin{array}{*{20}{c}} 0&{}\quad 0&{}\quad \cdots &{}\quad 0\\ 0&{}\quad 0&{}\quad \cdots &{}\quad 0\\ {C_{2,3}^l}&{}\quad {C_{2,4}^l}&{}\quad \cdots &{}\quad {C_{2,N + 2}^l}\\ {C_{N + 3,3}^r}&{}\quad {C_{N + 3,4}^r}&{}\quad \cdots &{}\quad {C_{N + 3,N + 2}^r} \end{array}} \right] _{4 \times N}}. \end{aligned}$$

(A.1b)

The matrices in Eq. (22a,b) are:

$$\begin{aligned} {\mathbf{C}}_4^{{\mathrm{pp}}}&= {\left[ {\begin{array}{*{20}{c}} {C_{3,3}^4}&{}\quad {C_{3,4}^4}&{}\quad \cdots &{}\quad {C_{3,N + 2}^4}\\ {C_{4,3}^4}&{}\quad {C_{4,4}^4}&{}\quad \cdots &{}\quad {C_{4,N + 2}^4}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{} \quad \vdots \\ {C_{N + 2,3}^4}&{}\quad {C_{N + 2,4}^4}&{}\quad \cdots &{}\quad {C_{N + 2,N + 2}^4} \end{array}} \right] _{N \times N}},\end{aligned}$$

(A.2a)

$$\begin{aligned} {\mathbf{C}}_4^{{\mathrm{pb}}}&= {\left[ {\begin{array}{*{20}{c}} {C_{3,1}^4}&{}\quad {C_{1,2}^4}&{}\quad {C_{1,N + 3}^4}&{}\quad {C_{1,N + 4}^4}\\ {C_{3,1}^4}&{}\quad {C_{2,2}^4}&{}\quad {C_{2,N + 3}^4}&{}\quad {C_{2,N + 4}^4}\\ \vdots &{}\quad \vdots &{} \quad \vdots &{} \quad \vdots \\ {C_{N + 2,1}^4}&{}\quad {C_{N + 2,2}^4}&{}\quad {C_{N + 2,N + 3}^4}&{}\quad {C_{N + 2,N + 4}^4} \end{array}} \right] _{N \times 4}},\end{aligned}$$

(A.2b)

$$\begin{aligned} {\mathbf{C}}_1^{{\mathrm{pp}}}&= {\left[ {\begin{array}{*{20}{c}} {C_{3,3}^1}&{}\quad {C_{3,4}^1}&{}\quad \cdots &{}\quad {C_{3,N + 2}^1}\\ {C_{4,3}^1}&{}\quad {C_{4,4}^1}&{}\quad \cdots &{}\quad {C_{4,N + 2}^1}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {C_{N + 2,3}^1}&{}\quad {C_{N + 2,4}^1}&{}\quad \cdots &{}\quad {C_{N + 2,N + 2}^1} \end{array}} \right] _{N \times N}},\end{aligned}$$

(A.2c)

$$\begin{aligned} {\mathbf{C}}_1^{{\mathrm{pb}}}&= {\left[ {\begin{array}{*{20}{c}} {C_{3,1}^1}&{}\quad {C_{1,2}^1}&{}\quad {C_{1,N + 3}^1}&{}\quad {C_{1,N + 4}^1}\\ {C_{3,1}^1}&{}\quad {C_{2,2}^1}&{}\quad {C_{2,N + 3}^1}&{}\quad {C_{2,N + 4}^1}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{} \quad \vdots \\ {C_{N + 2,1}^1}&{}\quad {C_{N + 2,2}^1}&{}\quad {C_{N + 2,N + 3}^1}&{}\quad {C_{N + 2,N + 4}^1} \end{array}} \right] _{N \times 4}}. \end{aligned}$$

(A.2d)