Analytical results in transient brush tyre models: theory for large camber angles and classic solutions with limited friction

Abstract

This paper establishes new analytical results in the mathematical theory of brush tyre models. In the first part, the exact problem which considers large camber angles is analysed from the perspective of linear dynamical systems. Under the assumption of vanishing sliding, the most salient properties of the model are discussed with some insights on concepts as existence and uniqueness of the solution. A comparison against the classic steady-state theory suggests that the latter represents a very good approximation even in case of large camber angles. Furthermore, in respect to the classic theory, the more general situation of limited friction is explored. It is demonstrated that, in transient conditions, exact sliding solutions can be determined for all the one-dimensional problems. For the case of pure lateral slip, the investigation is conducted under the assumption of a strictly concave pressure distribution in the rolling direction.

1 Introduction

The mechanics of pneumatic tyres is an ubiquitous topic in vehicle dynamics. Indeed, tyres almost represent the unique interface which allows ground vehicles to exchange traction forces with the external environment. These forces result from friction-related phenomena occurring in a relatively small region, customarily called contact patch, in which the tyre-road contact takes place. The size and the shape of the contact patch are determined by a wide set of parameters, including vertical load, inflation pressure and viscoelastic properties of the rubber compound which the tyre is made of. Clearly, the optimisation of the tyre operating conditions is crucial when it comes to enhance the vehicle’s performance and has been object of several studies which led, in the last decades, to the offspread of a large number of ad hoc developed models.

On the other hand, despite their simplistic nature, the so called brush models [1,2,3,4,5,6] represent a solid basis for a basilar understanding of the tyre dynamics, being only grounded on physical assumptions which allow for a straightforward interpretation of the tyre-road interaction. In the brush theory, the tyre, modelled as a rigid body, is equipped with bristles which deform in longitudinal and lateral direction inside the contact patch. The kinematic relationships ruling the brush models are linear transport equations expressed according to the Eulerian approach. Apart for its intrinsic pedagogical value, the success of the brush theory may be also explained considering the ubiquitous presence of brush-like contact models in every tyre formulation, however complex. In fact, according to Pacejka [2, 7], the brush models were firstly introduced by Fromm, as reported in [8], and derived starting from the more sophisticated formulation presented in [9]. It seems, however, that their origin may be traced back to the studies pioneered by Kalker few years later¹ on the simplified theory of rolling contact [10,11,12,13,14,15,16,17].²

In any case, they were soon integrated into enhanced hybrid formulations [18]. For example, Higuchi [19, 20] combined the classic brush theory with the stretched string model camber angles to derived an alternative version of the tyre-road kinematic equations in presence of large camber angles. In Higuchi’s footsteps, Pauwelussen [21] proposed an alternative analysis of the brush-string model for combined slip by using the singular integral method. Hybrid formulations between brush and string-like tyre models have been also introduced more recently by Takacs [22, 23], who enthusiastically continued the tradition of studies about shimmy and micro-shimmy related phenomena [24,25,26,27,28]. Svendenius et al. [29,30,31] and Albinsson et al. [32,33,34] investigated the possibility of employing the brush models for the purpose of real time friction estimation. Guiggiani [1] recently revisited the brush theory with a very methodical and fresh touch, introducing new perspectives and concepts. His emphasis on the rigorous mathematical aspects of the brush models should be regarded as a starting point for a modern analysis.

Even the most advanced tyre models requiring computer simulations, e.g. FTire^® [35,36,37] and CDTire [38], take advantage of the brush theory to provide a more realistic description of the local contact phenomena occurring between the tyre tread and the road. In particular, the FTire^® represents the most sophisticated model based on a nonlinear beam formulation and incorporates additional features such as belt compliance and distributed spring-like elements to properly capture the tread deformation. CDTire is based instead on a 3D shell description of both the sidewall and the belt, but also includes a dedicated brush type contact model. Currently, their are both extensively used in the context of advanced driving simulations or for comfort applications requiring real-time performance.

A major limitation of the brush models is that they are usually used to only describe the steady-state characteristics of tyres. Indeed, the solution of the PDEs governing the tyre-road interaction requires analytical and computational efforts which do not always fit the need for real-time performance. A customary approach is to introduce an additional structural element, the tyre carcass, which is modelled as a linear spring and is held accountable for the transient phenomena. This approach was introduced in [19, 20] as an approximation of the stretched-string tyre model and then extended towards more complex applications to include camber-related effects. Analogous pragmatic formulations may be also found in [39,40,41,42]. The effectiveness of this approach has also motivated its integration with the LuGre formulation in [43, 44].

Recently, Romano et al. have independently developed an exhaustive theory which captures the dynamics of the bristles in the contact patch [45]. The analysis has been further extended in [46] to investigate the salient phenomena connected with the presence of large turning speeds and camber angles. The formulation proposed by the authors, in particular, allows to circumvent the well-known limitations of the classic brush theory, which is only valid for values of the camber angle limited within few degrees.³

In opposition to the classic approach used in brush tyre modelling, the results derived in [45, 46] relied on analytical tools and general concepts which are most of the time extraneous to the traditional treatments, whose limitations emerged especially in [46]. For example, it seems to the authors that the classic notions of leading and trailing edges are often vague and circumstantial, whilst a correct definition should be instead grounded on precise mathematical conditions. This has been addressed partially in [46] with reference to a very specific problem, whereas the authors feel the urgency of extending the notion to a wider class of solutions. Also, the reasoning behind the derivation of the sliding solution for the bristle deflection is rather obscure in may reference texts, and often based on arguments which are not corroborated by a strong analytical counterpart. The authors do believe, instead, that it would be beneficial to approach the treatment from an alternative, more mathematically rigorous viewpoint, especially in conjunction with the transient problem.

Thus, the scope of this paper is to place the transient brush theory into a more comprehensive, mathematical framework. The manuscript is organised as follows: Sect. 2 introduces the tyre-road contact equations in their most general form, states the main assumption of the model, including the boundary (BCs) and initial conditions (ICs), and defines the slip parameters.

In Sect. 3, a broader treatment of the general theory introduced in [45] is given which frames the governing equations of the tyre-rolling contact into the wider context of the linear system theory. It is shown, in particular, that the PDEs ruling the dynamics of the brush models may be reinterpreted as a system of simpler ODEs, to which the classic results of existence and uniqueness borrowed from the well-established theory for ordinary differential equations (ODEs) fairly apply. In the case of constant slip inputs, some explicit solutions to the problem are then provided for a rectangular and elliptical contact patch. A comparison is also performed against the classic theory, showing a good agreement between the two formulations. This analysis is restricted to the stationary problem, owing to the complexity of the exact theory.

Section 4 returns to the classic theory, which approximates the two-dimensional velocity field inside the contact patch with the scalar rolling speed. All the one-dimensional transient problems are investigated analytically. The formal results advocated in this paper establish that, under the assumption of concave pressure distributions in the rolling direction, the adhesion and sliding zone originating from the boundary prescription are always unique.

The main conclusions are finally drawn in Sect. 5.

2 Tyre-road contact mechanics equations

This paper assumes that the contact between the tyre and the road takes place on the plane $\varPi = \{{\varvec{x}}\in {\mathbb {R}}^3 \mathrel {|} z =0\}$ inside the contact patch, defined mathematically as a compact set ${\mathscr{P}}$, with interior and boundary denoted by $\mathring{{\mathscr{P}}}$ and $\partial {\mathscr{P}}$, respectively. Additionally, the road surface is assumed to be homogeneous and isotropic.

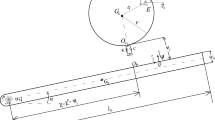
A reference frame (O; x, y, z) with unit vectors $(\hat{\varvec{e}}_x, \hat{\varvec{e}}_y, \hat{\varvec{e}}_z)$ is introduced whose origin O is contact-fixed, that is attached to the contact patch ${\mathscr{P}}$. In nominal operating conditions, it coincides with the actual contact point or contact centre C, which lies in the road plane laterally to the wheel hub centre [1, 2]⁴. In pure rolling conditions, C moves with the rolling velocity of the tyre $\varvec{V}_{\rm r} = V_{\rm r}\hat{\varvec{e}}_x \triangleq \varOmega R_{\rm r}\hat{\varvec{e}}_x$, where $\varOmega$ is the angular speed of the rim around its axis and $R_{\rm r}$ the rolling radius [1]. The coordinate system is oriented according to the SAE convention: the x axis is directed towards the longitudinal direction of motion, the z axis points downward and the y axis lies in on the road surface and is oriented so that the coordinate system is right-handed. In the formulation presented in this paper, the time variable t is replaced by the travelled distance $s \triangleq \int _{0}^{t} V_{\rm r}\bigl (t^\prime \bigr ) {\hbox {d}}t^\prime$.⁵

The part of the tyre making contact with the road is equipped with bristles which undergo a deformation described by the vector displacement ${\varvec{u}}({\varvec{x}},s) = u_x({\varvec{x}},s)\hat{\varvec{e}}_x + u_y({\varvec{x}},s)\hat{\varvec{e}}_y + u_z({\varvec{x}},s)\hat{\varvec{e}}_z$. The bristles travel inside ${\mathscr{P}}$ with nondimensional velocity given by the vector field ${\hbox {d}}{{\varvec{x}}}/{\hbox {d}}s = \bar{\varvec{v}}({\varvec{x}},s) = \bar{v}_x({\varvec{x}},s)\hat{\varvec{e}}_x + \bar{v}_y({\varvec{x}},s)\hat{\varvec{e}}_y + \bar{v}_z({\varvec{x}},s)\hat{\varvec{e}}_z$ and are subjected to a force per unit of area ${\varvec{q}}({\varvec{x}},s) = q_x({\varvec{x}},s)\hat{\varvec{e}}_x + q_y({\varvec{x}},s)\hat{\varvec{e}}_y + q_z({\varvec{x}},s)\hat{\varvec{e}}_z$.

Since only the planar problem is considered, it may be beneficial to define the tangential (or planar) nondimensional velocity field, displacement and stress as $\bar{\varvec{v}}_{\varvec{t}}({\varvec{x}},s) = \bar{v}_x({\varvec{x}},s)\hat{\varvec{e}}_x + \bar{v}_y({\varvec{x}},s)\hat{\varvec{e}}_y$, ${\varvec{u}}_{\varvec{t}}({\varvec{x}},s) =u_x({\varvec{x}},s)\hat{\varvec{e}}_x +u_y({\varvec{x}},s)\hat{\varvec{e}}_y$ and ${\varvec{q}}_{\varvec{t}}({\varvec{x}},s) =q_x({\varvec{x}},s)\hat{\varvec{e}}_x +q_y({\varvec{x}},s)\hat{\varvec{e}}_y$, so that $\bar{\varvec{v}}({\varvec{x}},s) = \bar{\varvec{v}}_{\varvec{t}}({\varvec{x}},s) + \bar{v}_z({\varvec{x}},s)\hat{\varvec{e}}_z$, ${\varvec{u}}({\varvec{x}},s) ={\varvec{u}}_{\varvec{t}}({\varvec{x}},s) + u_z({\varvec{x}},s) \hat{\varvec{e}}_z$. The quantity ${\varvec{q}}_{\varvec{t}}({\varvec{x}},s)$ is also called shear stress vector.

As customary, it is assumed that the planar problem may be decoupled from the vertical one. More specifically, the pressure distribution $q_z({\varvec{x}},s)$ is supposed not to be influenced by friction-related phenomena.⁶ To simplify the analysis, with some abuse of notation, the vectors in the reduced Euclidean space ${\mathbb {R}}^2$ are considered in the following, since the contact between the tyre and the road always takes place on the plane $\varPi$.

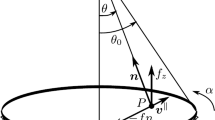
Owing to the premises above, the nondimensional relative speed between the bristles and the road, called nondimensional tangential micro-sliding speed and indicated with $\bar{\varvec{v}}_{\rm s}({\varvec{x}},s) = \bar{v}_{\mathrm {s}x}({\varvec{x}},s)\hat{\varvec{e}}_x + \bar{v}_{\mathrm {s}y}({\varvec{x}},s) \hat{\varvec{e}}_y$,⁷ may be derived as in [1, 2, 4, 6, 17, 45]:

$$\bar{\varvec{v}}_{\rm s}({\varvec{x}},s)= -{\varvec{\sigma}}(s)-{{\mathbf {A}}}_\varphi (s) \bigl ({\varvec{x}} + \chi _{\psi } (s) {\varvec{u}}_{\varvec{t}}({\varvec{x}},s)\bigr )+ \frac{\partial {\varvec{u}}_{\varvec{t}}({\varvec{x}},s)}{\partial s}+ \bigl ( \bar{\varvec{v}}_{\varvec{t}}({\varvec{x}},s) \cdot \nabla _{\varvec{t}}\bigr ){\varvec{u}}_{\varvec{t}}({\varvec{x}},s),({\varvec{x}},s) \in \mathring{{\mathscr{P}}}\times {\mathbb {R}}_{>0},$$

(1)

where the tangential gradient is given by $\nabla _{\varvec{t}}\triangleq \begin{bmatrix}\partial /\partial x&\partial /\partial y\end{bmatrix}^{\rm T}$. In Eq. (1), the following quantities have been defined:

$$\begin{aligned} \bar{\varvec{v}}_{\varvec{t}}({\varvec{x}},s)&= -\begin{bmatrix} 1 \\ 0 \end{bmatrix}+{{\mathbf {A}}}_{\varphi _\gamma } (s) {\varvec{x}}, \end{aligned}$$

(2a)

$$\begin{aligned} {{\mathbf {A}}}_\varphi (s)&\triangleq \begin{bmatrix} 0 & -\varphi (s)\\ \varphi (s) & 0 \end{bmatrix}, \end{aligned}$$

(2b)

$$\begin{aligned} {\mathbf {A}}_{\varphi _\gamma } (s)&\triangleq \begin{bmatrix} 0 & \varphi _\gamma (s)\\ -\varphi _\gamma (s)& 0 \end{bmatrix}. \end{aligned}$$

(2c)

The tensors ${\mathbf {A}}_\varphi (s)$ and ${\mathbf {A}}_{\varphi _\gamma } (s)$ are called spin and camber tensors, respectively, whilst ${\varvec{\sigma}}(s) = \begin{bmatrix} \sigma _x(s)&\sigma _y(s) \end{bmatrix}^{\mathrm {T}}$ and $\varphi (s)$ are the so-called theoretical slip variables. In particular, the quantities $\sigma _x(s)$ and $\sigma _y(s)$ are referred to as longitudinal and lateral slip, respectively, and represent the normalised difference between the longitudinal and lateral speeds of the actual contact point and the rolling velocity. The spin $\varphi (s)$ may further be decomposed in the two following contributions:

$$\begin{aligned} \varphi _{\gamma }(s)&= \dfrac{1 }{R_{\rm r}} \bigl (1-\varepsilon _{\gamma } \bigr )\sin \gamma (s), \end{aligned}$$

(3a)

$$\begin{aligned} \varphi _{\psi } (s)&= -\dfrac{\dot{\psi } (s)}{V_{\rm r} (s)}, \end{aligned}$$

(3b)

where $\gamma (s)$ is the camber angle, $\dot{\psi }(s)$ is the turning speed [2]. Finally, the quantity $\varepsilon _{\gamma }$ is known as camber reduction factor, and represents an additional parameter introduced to account for the elastic phenomena previously mentioned. It is said that motorcycle tyres have almost constant camber reduction factor $\varepsilon _{\gamma } \simeq 0$, whilst for car and truck tyres this parameter ranges between 0.4 and 0.7 [1, 2, 4, 55]. The camber reduction factor $\varepsilon _{\gamma }$ cannot be deduced directly from geometric considerations, and must be determined experimentally [55].

The quantities $\varphi _{\gamma }(s)$ and $\varphi _{\psi } (s)$ are called camber and turn spin, respectively. They may be interpreted as two different signed curvatures $\varphi _\gamma = 1/R_\gamma$ and $\varphi _\psi = -1/R_\psi$; the actual curvature of the contact patch centre is thus given by the difference $\varphi = 1/R_\gamma -1/R_\psi$. For what follows, it may be convenient to express them as a ratio of the total spin, that is $\varphi _{\gamma } = \chi _\gamma \varphi$ and $\varphi _{\psi } = \chi _{\psi } \varphi$, with $\chi _\gamma + \chi _{\psi } = 1$. The coefficients $\chi _\gamma$ and $\chi _{\psi }$ have been introduced by Romano et al. [46] and are called camber and turn ratio, respectively.

Equation (1) is complemented by the two following conditions:

$$\begin{aligned} \bar{\varvec{v}}_{\rm s}({\varvec{x}},s)&= \mathbf{0} \implies q_{\varvec{t}}({\varvec{x}},s) \le \mu q_z({\varvec{x}}), \end{aligned}$$

(4a)

$$\begin{aligned} \bar{\varvec{v}}_{\rm s}({\varvec{x}},s)&\not = \mathbf{0} \iff {{\varvec{q}}_{\varvec{t}}({\varvec{x}},s)} = \mu q_z({\varvec{x}})\hat{\varvec{s}}_{\varvec{t}}({\varvec{x}},s), \end{aligned}$$

(4b)

where the sliding direction $\hat{\varvec{s}}_{\varvec{t}}({\varvec{x}},s)$ is defined as

$$\begin{aligned} \hat{\varvec{s}}_{\varvec{t}}({\varvec{x}},s) \triangleq - \frac{\bar{\varvec{v}}_{\rm s}({\varvec{x}},s)}{\bar{v}_{\rm s}({\varvec{x}},s)}. \end{aligned}$$

(5)

In Eqs. (4a, 4b), $q_{\varvec{t}}({\varvec{x}},s) = \Vert {{\varvec{q}}_{\varvec{t}}({\varvec{x}},s)}\Vert$ and $\mu$ is the friction coefficient. Analogously, $\bar{v}_{\rm s}({\varvec{x}},s) = \Vert \bar{\varvec{v}}_{\rm s}({\varvec{x}},s)\Vert$. In general, both quantitites may be made dependent explicitly on the vector position ${\varvec{x}}$ or on the nondimensional sliding speed $\bar{\varvec{v}}_{\rm s}({\varvec{x}},s)$; however, to keep the complexity of the analysis within acceptable levels, this paper only uses a constant values for $\mu$,⁸ under the assumption of Amontons-Coulomb friction. For more sophisticated formulations the reader may instead refer to [49,50,51,52,53,54].

Equation (4a) basically states that a bristle manages to stick to the ground only if the magnitude of the shear stress acting upon it is lower than the available friction. When the shear stress exceeds the available friction, the bristle starts sliding and the nondimensional tangential sliding speed assumes nonzero values, that is $\bar{\varvec{v}}_{\rm s}({\varvec{x}},s)\not = \mathbf{0}$. In view of these considerations, the contact patch may be partitioned into an adhesion region ${\mathscr{P}}^{\rm (a)}$ and a sliding one ${\mathscr{P}}^{\rm (s)}$ defined by

$$\begin{aligned} {\mathscr{P}}^{\rm (a)}&\triangleq \bigl \{{\varvec{x}}\in {\mathscr{P}}\mathrel {\big |} {\text {Eq. (4a) holds}} \bigr \}, \end{aligned}$$

(6a)

$$\begin{aligned} {\mathscr{P}}^{\rm (s)}&\triangleq \bigl \{{\varvec{x}}\in {\mathscr{P}}\mathrel {\big |} {\text {Eq. (4b) holds}} \bigr \}. \end{aligned}$$

(6b)

Accordingly, a generic quantity is denoted by $(\cdot )^{\rm (a)}({\varvec{x}})$ if ${\varvec{x}}\in {\mathscr{P}}^{\rm (a)}$, and by $(\cdot )^{\rm (s)}({\varvec{x}})$ if ${\varvec{x}}\in {\mathscr{P}}^{\rm (s)}$.

To solve Eqs. (4a, 4b), it is necessary to assume a constitutive relationship between ${\varvec{u}}_{\varvec{t}}({\varvec{x}},s)$ and ${\varvec{q}}_{\varvec{t}}({\varvec{x}},s)$. In the brush theory, the relationship between the bristle deflection and the shear stress is often postulated in the form

$$\begin{aligned} {\varvec{q}}_{\varvec{t}}({\varvec{x}},s) = \mathbf {K}_{\varvec{t}} {\varvec{u}}_{\varvec{t}}({\varvec{x}},s), \end{aligned}$$

(7)

where the tangential stiffness matrix

$$\begin{aligned} \mathbf {K}_{\varvec{t}} = \begin{bmatrix} k_{xx} & k_{xy} \\ k_{yx} & k_{yy} \end{bmatrix} \end{aligned}$$

(8)

may be generally assumed to be positive definite [1].

2.1 Boundary and initial conditions

Equations (1) are two coupled PDEs – more specifically, linear transport equations – defined on a finite open domain $\mathring{{\mathscr{P}}}$. Thus, to guarantee the uniqueness of the solution, a BC and an initial condition (IC) need to be prescribed. To formalise the BC correctly, it is firstly necessary to define the leading edge ${\mathscr {L}}$, the neutral edge ${\mathscr {N}}$ and the trailing edge ${\mathscr {T}}$. These may be defined mathematically as in the following Definition 2.1.

Definition 2.1

(Leading edge, neutral edge and trailing edge) The leading, neutral and trailing edges ${\mathscr {L}}$, ${\mathscr {N}}$ and ${\mathscr {T}}$ are defined respectively by

$$\begin{aligned} {\mathscr {L}}\;\triangleq\; \biggl \{ {\varvec{x}} \in \partial {\mathscr{P}} \mathrel {\bigg |} \bigl [\bar{\varvec{v}}_{\varvec{t}}({{\varvec{x}}},s)-\bar{\varvec{v}}_{\partial {\mathscr{P}}}({\varvec{x}},s) \bigr ]\cdot \hat{\varvec{\nu }}_{\partial {\mathscr{P}}}({\varvec{x}},s) < 0\biggr \}, \end{aligned}$$

(9a)

$$\begin{aligned} {\mathscr {N}}\;\triangleq\; \biggl \{ {\varvec{x}} \in \partial {\mathscr{P}} \mathrel {\bigg |} \bigl [\bar{\varvec{v}}_{\varvec{t}}({{\varvec{x}}},s)-\bar{\varvec{v}}_{\partial {\mathscr{P}}}({\varvec{x}},s) \bigr ]\cdot \hat{\varvec{\nu }}_{\partial {\mathscr{P}}}({\varvec{x}},s) = 0\biggr \}, \end{aligned}$$

(9b)

$$\begin{aligned} {\mathscr {T}}\;\triangleq\; \biggl \{ {\varvec{x}} \in \partial {\mathscr{P}} \mathrel {\bigg |} \bigl [\bar{\varvec{v}}_{\varvec{t}}({{\varvec{x}}},s)-\bar{\varvec{v}}_{\partial {\mathscr{P}}}({\varvec{x}},s) \bigr ]\cdot \hat{\varvec{\nu }}_{\partial {\mathscr{P}}}({\varvec{x}},s) > 0\biggr \}. \end{aligned}$$

(9c)

where $\hat{\varvec{\nu }}_{\partial {\mathscr{P}}}({\varvec{x}},s)$ is the outer-pointing unit normal to $\partial {\mathscr{P}}$ and $\bar{\varvec{v}}_{\partial {\mathscr{P}}}({\varvec{x}},s)$ is the velocity of the boundary of the contact patch $\partial {\mathscr{P}}$. The scalar product $[\bar{\varvec{v}}_{\varvec{t}}({{\varvec{x}}},s)-\bar{\varvec{v}}_{\partial {\mathscr{P}}}({\varvec{x}},s)]\cdot \hat{\varvec{\nu }}_{\partial {\mathscr{P}}}({\varvec{x}},s)$ represents the flow of the bristles through the boundary $\partial {\mathscr{P}}$ of the contact patch. When the contact patch is fixed in time, that is $\bar{\varvec{v}}_{\partial {\mathscr{P}}}({\varvec{x}},s) = \mathbf{0}$, the previous Definition 2.1 reduces to that given in Romano et al. [46].

It is worth emphasising that Eqs. (9a–9c) presume the existence of the unit normal. If $\partial {\mathscr{P}}$ is $C^1$, the unit normal can always be defined and the above Definition 2.1 coincides with the less formal one by Kalker [56]. On the other hand, if $\partial {\mathscr{P}}$ is only $C^0$, the solution to the PDEs (1) may be not uniquely defined on the corners.⁹

Owing to Definition 2.1, the BC may be restated in mathematical terms as

$$\begin{array}{*{20}c} {\text {BC:}}&{\varvec{q}}_{\varvec{t}} ({\varvec{x}},s) = \mathbf {K}_{\varvec{t}} {\varvec{u}}_{\varvec{t}} ({\varvec{x}},s) = \mathbf{0} \iff {\varvec{u}}_{\varvec{t}} ({\varvec{x}},s) = \mathbf{0},&({\varvec{x}},s) \in {\mathscr {L}}\times {\mathbb {R}}_{>0}. \\ \end{array}$$

(10)

Basically, the previous relation imposes that the bristles must enter the contact patch undeformed, since the points ${\varvec{x}} \in {\mathscr {L}}$ are the points inflowing into the contact patch ${\mathscr{P}}$. This is a direct consequence of the pure elastic constitutive relationship assumed.

On the other hand, the IC may formulated mathematically as

$$ {\text {IC:}}\quad {\varvec{u}}_{\varvec{t}}({\varvec{x}},0) = {\varvec{u}}_{\varvec{t}0}({\varvec{x}}),\quad {\varvec{x}} \in \mathring{{\mathscr{P}}},$$

(11)

for some ${\varvec{u}}_{\varvec{t}0}({\varvec{x}}) \in C^{1}(\mathring{{\mathscr{P}}}; {\mathbb {R}}^2)$ with ${\varvec{u}}_{\varvec{t}0}({\varvec{x}})=\mathbf{0}$ on ${\mathscr {L}}$.¹⁰ The assumption of vanishing sliding will be used consistently through Sect. 3 and then eventually removed in Sect. 4. It is however important to clarify that, even in Sect. 4, the transient problem will be solved by imposing the above BCs. Basically, this means that some kind of priority will be bestowed on the adhesion solution.

Finally, the last BCs concern the transition from adhesion to sliding. These BCs may be formulated properly by defining

$$\begin{aligned} \gamma _{\mathscr {S}}({\varvec{x}},s) \triangleq \Vert \mathbf {K}_{\varvec{t}} {\varvec{u}}_{\varvec{t}}^{\rm (a)}({\varvec{x}},s)\Vert -\mu q_{z}({\varvec{x}},s), \end{aligned}$$

(12)

where ${\varvec{u}}_{\varvec{t}}^{\rm (a)}({\varvec{x}},s)$ is a known function which does not coincide locally with the friction bound $\mu q_z({\varvec{x}},s)$. Therefore, the sliding edge may be stated mathematically as

$$\begin{aligned} {\mathscr {S}} \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}} \mathrel {\big |} \gamma _{\mathscr {S}}({\varvec{x}},s)= 0 \bigr \}. \end{aligned}$$

(13)

It may be understood that a sliding edge ${\mathscr {S}}$ separates two regions ${\mathscr{P}}^{\rm (a)}$ and ${\mathscr{P}}^{\rm (s)}$, marking the transition from Eqs. (4a) to (4b). The corresponding BCs from adhesion to sliding read

$$\begin{array}{*{20}c}{\text {BC:}}&{\varvec{u}}_{\varvec{t}}^{\rm (s)}({\varvec{x}}, s) = \mathbf {K}_{\varvec{t}}^{-1} \mu q_z({\varvec{x}},s) \hat{\varvec{s}}_{\varvec{t}}({\varvec{x}},s) ={\varvec{u}}_{\varvec{t}}^{\rm (a)}({\varvec{x}}, s) ,&({\varvec{x}}, s) \in {\mathscr {S}}\times {\mathbb {R}}_{>0}. \\ \end{array}$$

(14)

In particular, the first BC (14) states that, in the transition from adhesion to sliding, both the magnitude and the direction of the displacement are preserved. The analysis in presence of finite friction is much more involving and is only conducted in respect to the classic theory.

3 Exact theory

This section is dedicated to the most general theory which considers the presence of the exact¹¹ two-dimensional velocity field inside the contact patch, as well as the coupling between the bristle displacements due to the turn spin. The problem is firstly detailed in its general formulation and then some explicit solutions for simple contact geometries are provided. The only (very strong) assumption introduced in the authors’ mathematical treatment is the one of vanishing sliding.

Assumption 3.1

(Vanishing sliding) Adhesion conditions take place in the whole contact patch, that is Eq. (4a) holds for all ${\varvec{x}} \in {\mathscr{P}}$.

Assumption 3.1 holds approximately true when the friction available inside the contact patch is virtually infinite [2], which may be mathematically translated into $\mu \rightarrow \infty$. By virtue of Assumption 3.1, the PDEs governing the brush theory may be solved on the whole interior $\mathring{{\mathscr{P}}}$ of the domain ${\mathscr{P}}$. It should be noticed that this is not a real limitation, since the assumption can be removed once the solution has been derived. With the premises above, the tyre-road contact equations may be recast in vector-form as follows:

$$ \frac{\partial {\varvec{u}}_{\varvec{t}}({\varvec{x}},s)}{\partial s}+\bigl ( \bar{\varvec{v}}_{\varvec{t}}({\varvec{x}},s) \cdot \nabla _{\varvec{t}}\bigr ){\varvec{u}}_{\varvec{t}}({\varvec{x}},s)={\varvec{\sigma}}(s) + {\mathbf {A}}_\varphi (s)\bigl ({\varvec{x}}+\chi _{\psi } (s) {\varvec{u}}_{\varvec{t}}({\varvec{x}},s)\bigr ),\quad ({\varvec{x}},s) \in \mathring{{\mathscr{P}}}\times {\mathbb {R}}_{>0}. $$

(15)

The above Eq. (15) comes equipped with BC (10) and IC given by Eq. (11) and may be solved resorting to the results from the classic theory for first-order systems of PDEs [57, 58].¹² In reality, because the coupling between the longitudinal and lateral deflection of the bristle does not involve any partial derivative, the problem further simplifies. Assuming a parametrisation ${\varvec{x}} = {\varvec{x}}({{\varvec{\rho }}},\varsigma )$, $s = s({{\varvec{\rho }}},\varsigma )$, ${\varvec{u}}_{\varvec{t}}({\varvec{x}},s) = {\varvec{u}}_{\varvec{t}}({\varvec{x}}({{\varvec{\rho }}},\varsigma ),s({{\varvec{\rho }}},\varsigma )) = \varvec{\zeta }({{\varvec{\rho }}},\varsigma )$, Eq. (15) may be restated equivalently as

$$\begin{aligned} \frac{{\hbox {d}}s({\varvec{\rho }},\varsigma )}{{\hbox {d}}\varsigma }&= 1, \end{aligned}$$

(16a)

$$\begin{aligned} \frac{{\hbox {d}}{\varvec{x}}({\varvec{\rho }},\varsigma )}{{\hbox {d}}\varsigma }&= -\begin{bmatrix} 1 \\ 0 \end{bmatrix} +{\mathbf {A}}_{\varphi _\gamma } (s) {\varvec{x}}({\varvec{\rho }},\varsigma ), \end{aligned}$$

(16b)

$$\begin{aligned} \frac{{\hbox {d}}\varvec{\zeta }({\varvec{\rho }},\varsigma )}{{\hbox {d}}\varsigma }&= {\mathbf {A}}_{\varphi _\psi } (s) \varvec{\zeta }({\varvec{\rho }},\varsigma ) + {\varvec{\sigma}}(s) +{\mathbf {A}}_\varphi (s) {\varvec{x}}({\varvec{\rho }},\varsigma ), \end{aligned}$$

(16c)

in which the turning tensor reads ${\mathbf {A}}_{\varphi _\psi } (s) = \chi _{\psi } (s) {\mathbf {A}}_\varphi (s)$. The integral solution of the system above is obviously

$$\begin{aligned} s({\varvec{\rho }},\varsigma )&= \varsigma +s_0({\varvec{\rho }}), \end{aligned}$$

(17a)

$$\begin{aligned} {\varvec{x}}({{\varvec{\rho }}},\varsigma )&= {\varvec{\Phi }}_{\varphi _\gamma }(\varsigma ,0) {\varvec{x}}_0({{\varvec{\rho }}}) - \int _0^\varsigma {\varvec {\Phi }}_{\varphi _\gamma } \bigl (\varsigma ,\varsigma ^\prime \bigr ) \begin{bmatrix} 1 \\ 0 \end{bmatrix} {\hbox {d}}\varsigma ^\prime , \end{aligned}$$

(17b)

$$\begin{aligned} {\varvec{\zeta }}({{\varvec{\rho }}},\varsigma )= {\varvec{\Phi }}_{\varphi _\psi }(\varsigma ,0) {\varvec{\zeta }}_0({{\varvec{\rho }}}) + \int _0^\varsigma {\varvec {\Phi }}_{\varphi _\psi } \bigl (\varsigma ,\varsigma ^\prime \bigr ) \Bigl [ {{\varvec{\sigma}}}\bigl (\varsigma ^\prime + {s}_{0}({{\varvec{\rho }}})\bigr ) + {\mathbf {A}}_\varphi \bigl (\varsigma ^\prime + s_0({{\varvec{\rho }}})\bigr ) {\varvec{x}}\bigl ({{\varvec{\rho }}},\varsigma ^\prime \bigr )\Bigr ] {\hbox {d}}\varsigma ^\prime , \end{aligned}$$

(17c)

where the generic transition matrices ${\varvec {\Phi }}_{\varphi _\gamma }(\varsigma , {\tilde{\varsigma }})$ and ${\varvec {\Phi }}_{\varphi _\psi }(\varsigma , {\tilde{\varsigma }})$ for the camber and turn spin read [60]:

$$\begin{aligned} {\varvec {\Phi }}_{\varphi _\gamma } (\varsigma , {\tilde{\varsigma }})&=\mathrm {e}^{\int _{\tilde{\varsigma }}^{\varsigma }{\mathbf {A}}_{\varphi _\gamma } (\varsigma ^\prime + s_0({{\varvec{\rho }}})){\hbox {d}}\varsigma ^\prime } = \begin{bmatrix} \cos \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\gamma \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) & \sin \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\gamma \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) \\ -\sin \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\gamma \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) & \cos \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\gamma \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) \end{bmatrix}, \end{aligned}$$

(18a)

$$\begin{aligned} {\varvec {\Phi} }_{\varphi _\psi } (\varsigma , {\tilde{\varsigma} })&= \mathrm {e}^{\int _{\tilde{\varsigma }}^{\varsigma }{{\mathbf {A}}}_{\varphi _\psi } (\varsigma ^\prime + s_0({\varvec{\rho }})){\hbox {d}}\varsigma ^\prime } = \begin{bmatrix} \cos \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\psi \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) & -\sin \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\psi \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) \\ \sin \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\psi \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) & \cos \Bigl (\int _{\tilde{\varsigma }}^\varsigma \varphi _\psi \bigl (\varsigma ^\prime + s_0({\varvec{\rho }})\bigr ) {\hbox {d}}\varsigma ^\prime \Bigr ) \end{bmatrix}. \end{aligned}$$

(18b)

The well-posedness of the linear systems in Eqs. (17a–17c) depends on the regularity of their right-hand sides, which, for the case under consideration, are clearly globally Lipschitz-continuous in the independent variables. Existence and uniqueness of the solution, as well as continuous dependency on the initial data, are thus implied by the classic Cauchy–Picard theory. To uniquely solve the original PDE (15), however, an additional requirement is that the boundary and initial conditions must be noncharacteristic. Indeed, according to the Inverse Function Theorem, it is always possible to locally solve for ${\varvec{\rho }}({\varvec{x}},s)$, $\varsigma ({\varvec{x}},s)$ and transform back the variables $\varvec{\zeta }({\varvec{\rho }}({\varvec{x}},s), \varsigma ({\varvec{x}},s)) = {\varvec{u}}_{\varvec{t}}({\varvec{x}},s)$ if the following condition is satisfied:

$$\det {\mathbf{J}}({\varvec{\rho }},0) = \left| {\begin{array}{*{20}c} {\frac{{\partial x({\varvec{\rho }},0)}}{{\partial \rho _{1} }}} & {\frac{{\partial x({\varvec{\rho}} ,0)}}{{\partial \rho _{2} }}} & {\frac{{\partial x({\varvec{\rho }},0)}}{{\partial \varsigma }}} \\ {\frac{{\partial y({\varvec{\rho }},0)}}{{\partial \rho _{1} }}} & {\frac{{\partial y({\varvec{\rho }},0)}}{{\partial \rho _{2} }}} & {\frac{{\partial y({\varvec{\rho }},0)}}{{\partial \varsigma }}} \\ {\frac{{\partial s({\varvec{\rho }},0)}}{{\partial \rho _{1} }}} & {\frac{{\partial s({\varvec{\rho }},0)}}{{\partial \rho _{2} }}} & {\frac{{\partial s({\varvec{\rho }},0)}}{{\partial \varsigma }}} \end{array} } \right|\neq 0,\infty .$$

(19)

If (19) holds, then the boundaries are said to be noncharacteristic and it is possible to find a $C^2$ function solving the PDE (15) in the proximity of the boundary (or initial) curve [57]. This argument also constitutes the basis for the Cauchy–Kovalevskaya existence and uniqueness theorem. For the case under consideration, it may be proved (Proposition B.1) that the BC (10) and IC (11) are noncharacteristic (inflow boundaries and initial conditions are, to some extent, the natural boundaries for transport equations [57, 58]). In the transient brush theory, however, functions solving (15) are usually only $C^0$ due to the possible non-analiticity of the initial conditions (for example when ${\varvec{u}}_{\varvec{t}0}({\varvec{x}})$ is only $C^0({\mathscr{P}})$). In these cases, only weak solutions may be found even under vanishing sliding conditions.

3.1 Steady-state solution

When looking for the stationary deflection of the bristle, the BC (10) needs to be applied. In the general case of time-varying slips and contact patch, a closed form solution cannot be obtained. However, restricting the attention to the case of constant slips and fixed contact shape, the integral solution (17a–17c) simplifies to

$$\begin{aligned} s({{\varvec{\rho }}},\varsigma )&= \varsigma +s_0({{\varvec{\rho }}}), \end{aligned}$$

(20a)

$$\begin{aligned} {\varvec{x}}({{\varvec{\rho }}},\varsigma )&= {{\mathbf {R}}}_{\varphi _\gamma }(\varsigma )\bigl ( {\varvec{x}}_0({{\varvec{\rho }}})-{\varvec{x}}_{C_\gamma } \bigr ) +{\varvec{x}}_{C_\gamma }, \end{aligned}$$

(20b)

$$\begin{aligned} {\varvec{\zeta }}({{\varvec{\rho }}},\varsigma )&= {{\mathbf {R}}}_{\varphi _\psi }(\varsigma )\Bigl ({\varvec{\zeta} }_0({\varvec{\rho} })-{\tilde{{\varvec{\zeta }}}}_0({\varvec{\rho }}) \Bigr )+{\tilde{{\varvec{\zeta}}}}({{\varvec{\rho }}},\varsigma ) , \end{aligned}$$

(20c)

where the camber and turning rotation matrices ${\mathbf {R}}_{\varphi _\gamma } (\varsigma )$ and ${\mathbf {R}}_{\varphi _\psi } (\varsigma )$ are defined respectively as

$$\begin{aligned} {\mathbf {R}}_{\varphi _\gamma } (\varsigma )&\triangleq \mathrm {e}^{{\mathbf {A}}_{\varphi _\gamma } \varsigma } = \begin{bmatrix} \cos \bigl (\varphi _\gamma \varsigma \bigr ) & \sin \bigl (\varphi _\gamma \varsigma \bigr ) \\ -\sin \bigl (\varphi _\gamma \varsigma \bigr ) & \cos \bigl (\varphi _\gamma \varsigma \bigr ) \end{bmatrix}, \end{aligned}$$

(21a)

$$\begin{aligned} {\mathbf {R}}_{\varphi _\psi } (\varsigma )&\triangleq \mathrm {e}^{{\mathbf {A}}_{\varphi _\psi } \varsigma } = \begin{bmatrix} \cos \bigl (\varphi _\psi \varsigma \bigr ) & -\sin \bigl (\varphi _\psi \varsigma \bigr ) \\ \sin \bigl (\varphi _\psi \varsigma \bigr ) & \cos \bigl (\varphi _\psi \varsigma \bigr ) \end{bmatrix}, \end{aligned}$$

(21b)

and the coordinate vector

$$ {\varvec{x}}_{C_\gamma } = [ 0\quad y_{C_\gamma }]^{{\text{T}}}\triangleq [0\quad R_\gamma ]^{{\text{T}}} =[0\quad 1/\varphi _\gamma ]^{{\text{T}}} $$

(22)

denotes the position of the cambering centre $C_\gamma$ seen from the contact point. The function $\tilde{\varvec{\zeta }}(\cdot ,\cdot )$ is as follows:

$$\begin{aligned} {\tilde{\varvec{\zeta }}}({\varvec{\rho }},\varsigma ) = -{{\mathbf {A}}}_{\varphi _\psi }^{-1}{{\varvec{\sigma}}}-{\varvec{x}}({{\varvec{\rho }}},\varsigma ) + {\varvec{x}}_{C_\psi }, \end{aligned}$$

(23)

with the coordinate vector ${\varvec{x}}_{C_\psi }$ reading

$$\begin{aligned} {\varvec{x}}_{C_\psi } =\begin{bmatrix} 0&y_{C_\psi }\end{bmatrix}^{\rm T} \triangleq \begin{bmatrix} 0&R_\psi \end{bmatrix}^{\rm T} = \begin{bmatrix} 0&-1/\varphi _\psi \end{bmatrix}^{\rm T} \end{aligned}$$

(24)

and $\tilde{\varvec{\zeta }}_0({\varvec{\rho }}) \triangleq \tilde{\varvec{\zeta }}({\varvec{\rho }},0)$.

At this point, a map should be found such that ${\varvec{u}}_{\varvec{t}}^{-}({\varvec{x}},s) = \varvec{\zeta }({\varvec{\rho }}({\varvec{x}},s),\varsigma ({\varvec{x}},s))$. Specifically, it is necessary to find an inversion formula between the coordinates $({\varvec{\rho }}, \varsigma )$ and $({\varvec{x}},s)$. To this end, it may be noticed that the BC (10) prescribes $\varvec{\zeta }_0({\varvec{\rho }}) = \mathbf{0}$ on the leading edge. Moreover, $\tilde{\varvec{\zeta }}({\varvec{\rho }},\varsigma )$ in Eqs. (21a, 21b) may be restated as $\tilde{\varvec{\zeta }}({\varvec{\rho }}({\varvec{x}},s),\varsigma ({\varvec{x}},s)) = \tilde{{\varvec{u}}}_{\varvec{t}}({\varvec{x}})$, with

$$\begin{aligned} {\tilde{{\varvec{u}}}}_{\varvec{t}}({\varvec{x}}) \triangleq - {{\mathbf {A}}}_{\varphi _\psi }^{-1}{{\varvec{\sigma}}}-{\varvec{x}}+ {\varvec{x}}_{C_\psi }. \end{aligned}$$

(25)

Finally, Eq. (20a) together with (20b) yields

$$\begin{aligned}&x^2 + \bigl (y-1/\varphi _\gamma \bigr )^2 = \bigl (x_0({\varvec{\rho }})\bigr )^2 + \bigl (y_0({\varvec{\rho }})-1/\varphi _\gamma \bigr )^2, \end{aligned}$$

(26a)

$$\begin{aligned}&\varsigma = \dfrac{1}{\varphi _\gamma }\left[ \arctan \Biggl (\frac{x}{y-1/\varphi _\gamma }\Biggr )-\arctan \Biggl (\frac{x_0({\varvec{\rho }})}{y_0({\varvec{\rho }})-1/\varphi _\gamma } \Biggr ) \right] , \end{aligned}$$

(26b)

$$\begin{aligned}&s_0({\varvec{\rho }}) = s-\varsigma . \end{aligned}$$

(26c)

Equation (26a) is very illustrative, since it states that the characteristic projections are circles of arbitrary radius centred in the cambering centre ${\varvec{x}}_{C_\gamma }$.¹³ Equation (26a) also represents the phase portrait of the system depicted in Eq. (16b), which results in a conservative limit cycle [60, 61]. Since the radius $R_\gamma$ is the radius of curvature of the path of a bristle, it becomes clear that, the closer $\varepsilon _{\gamma }$ is to the unity, the more straightened are the trajectories of the material points inside the contact patch.

The previous relationships must be inverted locally to provide an explicit solution for ${\varvec{u}}_{\varvec{t}}^{-}({\varvec{x}},s)$ in the steady state region of the contact patch ${\mathscr{P}}^-$. When ${\mathscr{P}}$ is fixed, this may always be done by choosing a parametrisation of the type $s_0({\varvec{\rho }}) = \rho _1$ and ${\varvec{x}}_0({\varvec{\rho }}) = {\varvec{x}}_0(\rho _2)$. This leads to the final solution for the steady-state deflection of the bristle in a region ${\mathscr{P}}^{-}$ of the contact patch:

$$\begin{aligned} {\varvec{u}}_{\varvec{t}}^{-}({\varvec{x}}) = {{\mathbf {R}}}_{\varphi _\psi } \bigl (\varSigma ({\varvec{x}})\bigr ) {\varvec{\varPsi }}({\varvec{x}}) + {\tilde{{\varvec{u}}}}_{\varvec{t}}({\varvec{x}}),&({\varvec{x}},s) \in {\mathscr{P}}^{-}\times {\mathbb {R}}_{\ge 0}, \end{aligned}$$

(27)

where the functions $\varSigma (\cdot )$ and $\varvec{\varPsi }(\cdot )$ have been introduced as

$$\varSigma ({\varvec{x}}) \triangleq \dfrac{1}{\varphi _\gamma } \left[ \arctan \left(\frac{x}{y-1/\varphi _\gamma } \right)-\arctan \left(\frac{x_0(\rho _2({\varvec{x}}))}{y_0(\rho _2({\varvec{x}}))-1/\varphi _\gamma } \right) \right] ,$$

(28a)

$$\begin{aligned} {\varvec{\varPsi }}({\varvec{x}})&= \begin{bmatrix} \varPsi _x({\varvec{x}})&\varPsi _y({\varvec{x}}) \end{bmatrix}^{{\rm T}} \triangleq -\tilde{{\varvec{u}}}_{\varvec{t}}\Bigl ({\varvec{x}}_0\bigl (\rho _2({\varvec{x}})\bigr )\Bigr ). \end{aligned}$$

(28b)

As expected, it may be observed that ${\varvec{u}}_{\varvec{t}}^-({\varvec{x}})$ in Eq. (27) does not depend on the variable s, and therefore is actually steady-state. On the other hand, when the slip inputs are not constant, the solution is only stationary, because it persists after the initial transient phase, but still depends on the travelled distance.

In Eq. (27), the domain ${\mathscr{P}}^{-}$ may be defined from the condition $s_0(\rho _1({\varvec{x}},s))= \rho _1({\varvec{x}},s) > 0$ in Eq. (26c), which, combined with (26b), implies $s > \varSigma ({\varvec{x}})$. Thus, introducing

$$\begin{aligned} \gamma _{\varSigma }({\varvec{x}},s) \triangleq \varSigma ({\varvec{x}})-s, \end{aligned}$$

(29)

it is possible to define ${\mathscr{P}}^{-}$ mathematically as follows:

$$\begin{aligned} {\mathscr{P}}^- \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}} \mathrel {\big |} \gamma _{\varSigma }({\varvec{x}},s) < 0 \bigr \}, \end{aligned}$$

(30)

since the implicit curve $\gamma _{\varSigma }({\varvec{x}},s) = 0$ separates the steady-state domain from the transient one. Therefore, the curve described by $\gamma _{\varSigma }({\varvec{x}},s) = 0$ is referred to as transient or travelling edge.

3.2 Transient solution

The transient solution ${\varvec{u}}_{\varvec{t}}^+({\varvec{x}},s)$ may be obtained by parametrising ${\varvec{x}}_0({\varvec{\rho }}) = {\varvec{\rho }}$ for $s_0({\varvec{\rho }}) = 0$. It follows from compatibility that $\varvec{\zeta }_0({\varvec{\rho }}({\varvec{x}},s)) = {\varvec{u}}_{\varvec{t}0}({\varvec{x}}_0({\varvec{x}},s))$, and therefore the transient solution is given by

$$\begin{aligned} {\varvec{u}}_{\varvec{t}}^{+}({\varvec{x}},s) = {\varvec {\Phi}}_{\varphi_\psi }(s,0) {\varvec{u}}_{{\varvec{t}}0}\bigl ({\varvec{x}}_0({\varvec{x}},s)\bigr ) + \int _0^s {\varvec {\Phi }}_{\varphi _\psi } \bigl (s,s^\prime \bigr ) \Bigl [{ {\varvec{\sigma}}}\bigl (s^\prime \bigr ) + {{\mathbf {A}}}_{\varphi} \bigl (s^\prime \bigr ) {\varvec{x}}\bigl ({\varvec{\rho} },s^\prime \bigr )\Bigr ] {\hbox {d}}s^\prime , \end{aligned}$$

(31)

where ${\varvec{x}}_0({\varvec{x}},s)$ reads

$$\begin{aligned} {\varvec{x}}_0({\varvec{x}},s) = {\varvec {\Phi}}_{\varphi _\gamma }(0,s)\Biggl [ {\varvec{x}} + \int _0^s {\varvec {\Phi} }_{\varphi _\gamma } \bigl (s,s^\prime \bigr ) \begin{bmatrix} 1 \\ 0 \end{bmatrix} {\hbox {d}}s^\prime \Biggr ]. \end{aligned}$$

(32)

Equations (31) and (32) provide the most general, closed-form expression for the transient solution under vanishing sliding conditions. When the slip quantities are constant, the above relationships further simplify to

$$\begin{aligned} {\varvec{u}}_{\varvec{t}}^{+}({\varvec{x}},s) = {\mathbf {R}}_{\varphi _\psi }(s) \Bigl [{\varvec{u}}_{\varvec{t}0}\bigl ({\varvec{x}}_0({\varvec{x}},s)\bigr )- \tilde{{\varvec{u}}}_{\varvec{t}0}({\varvec{x}},s)\Bigr ] + \tilde{{\varvec{u}}}_{\varvec{t}}({\varvec{x}}),&({\varvec{x}},s) \in {\mathscr{P}}^{+}\times {\mathbb {R}}_{\ge 0}, \end{aligned}$$

(33)

where $\tilde{{\varvec{u}}}_{\varvec{t}0}({\varvec{x}},s) \triangleq \tilde{{\varvec{u}}}_{\varvec{t}}({\varvec{x}}_0({\varvec{x}},s))$ and

$$\begin{aligned} {\varvec{x}}_0({\varvec{x}},s)&= {{\varvec{\rho }}}({\varvec{x}},s) = {{\mathbf {R}}}_{\varphi _\gamma }^{-1}(s)\bigl ({\varvec{x}}-{\varvec{x}}_{C_\gamma } \bigr )+{\varvec{x}}_{C_\gamma }. \end{aligned}$$

(34)

In this case, the transient solution applies in the transient region of the contact patch defined by

$$\begin{aligned} {\mathscr{P}}^+ \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}} \mathrel {\big |} \gamma _{\varSigma }({\varvec{x}},s) \ge 0 \bigr \}, \end{aligned}$$

(35)

and is clearly continuous on the travelling edge, that is ${\varvec{u}}_{\varvec{t}}^+({\varvec{x}},\varSigma ({\varvec{x}})) = {\varvec{u}}_{\varvec{t}}^-({\varvec{x}})$. The global solution over the contact patch ${\mathscr{P}} = {\mathscr{P}}^{-} \cup {\mathscr{P}}^{+}$ may be then formally constructed as

$$\begin{aligned} {\varvec{u}}_{\varvec{t}}({\varvec{x}},s) = {\left\{ \begin{array}{ll} {\varvec{u}}_{\varvec{t}}^{-}({\varvec{x}}), & ({\varvec{x}},s) \in {\mathscr{P}}^{-}\times {\mathbb {R}}_{\ge 0}, \\ {\varvec{u}}_{\varvec{t}}^{+}({\varvec{x}},s), & ({\varvec{x}},s) \in {\mathscr{P}}^{+}\times {\mathbb {R}}_{\ge 0}. \end{array}\right. } \end{aligned}$$

(36)

Accordingly, the shear stress may also be split into a steady-state ${\varvec{q}}_{\varvec{t}}^{-}({\varvec{x}}) \triangleq \mathbf {K}_{\varvec{t}} {\varvec{u}}_{\varvec{t}}^{-}({\varvec{x}})$ and transient ${\varvec{q}}_{\varvec{t}}^{+}({\varvec{x}},s) \triangleq \mathbf {K}_{\varvec{t}} {\varvec{u}}_{\varvec{t}}^{+}({\varvec{x}},s)$ part in ${\mathscr{P}}^{-}$ and ${\mathscr{P}}^{+}$, respectively.

Finally, it should be emphasised that the expression for the transient deformations of the bristles are formally independent of the contact shape. Indeed, the inversion formula given by Eq. (33) is independent of the specific geometry. The analytical expressions for the steady-state deflection ${\varvec{u}}_{\varvec{t}}^{-}({\varvec{x}})$ depend instead on the shape of the leading edge, as discussed in next Subsect. 3.3.

3.3 Explicit solutions for some contact shapes

Analytical solutions for the steady-state deflection of the bristle may be provided for simple contact geometries, for example rectangular and elliptical. For both, the semilength and semiwidth are denoted by a and b, respectively.

Albeit not a very realistic shape for cambered tyres, the rectangular shape may still highlight some important aspects which seem to find confirmation in the shear stress distributions found in [62,63,64]. The boundary of the domain, in this case, cannot be described by a continuous smooth function, and three BCs must be prescribed on the straight edges depending on the sign of the camber angle $\gamma$, and hence of $\varphi _\gamma$. As a result, three different analytical expressions are obtained, namely ${\varvec{u}}_{1\varvec{t}}^{-}({\varvec{x}})$, ${\varvec{u}}_{2\varvec{t}}^{-}({\varvec{x}})$ and ${\varvec{u}}_{3\varvec{t}}^{-}({\varvec{x}})$, depending on the specific BC applied in turn. Even in the steady-state case, the global solution is not $C^0({\mathscr{P}})$. Starting from the known distribution of the deformation, the tangential forces and self-aligning moment may be obtained by integration over the contact patch. In presence of dry friction, Eq. (15) is complemented by Eqs. (4a, 4b) in the sliding zone, where the bristle displacements (or, equivalently, the shear stresses) need to be computed numerically, for example assuming a parabolic pressure distribution (similar to Eq. (49) in Sect. 4).

Figure 1 compares the Gough plots for the exact and classic brush theory presented in the next Sect. 4. In both cases, the value of the spin is $\varphi = 3.33$, with $\chi _\gamma = 0.9$, and the total vertical force acting on the tyre amounts to $F_z = 3000$ N. The bristle is assumed to be isotropic with $k_{xx} = k_{yy} = 4.52\cdot 10^7$ and $k_{xy}=k_{yx} = 0$. More specifically, the solid lines refer to the characteristics predicted by the classic theory, whilst the dashed ones to the forces and moment obtained from the exact theory. It may be observed that the curvature due to camber plays an important role in the determination of the tyre characteristics, especially at low value of the total translational slip (blue lines). Also, it is interesting to notice that the value considered for the spin is quite smaller than the critical spin $\varphi ^{\rm cr} = 4.00$ from the classic brush theory.

Fig. 1

Steady-state characteristics predicted by the classic (solid lines) and exact (dashed-lines) theories for different values of the lateral slip $\sigma _y$ for a rectangular contact patch. Tyre parameters: $\varphi = 3.33$, $\chi _\gamma = 0.9$, $F_z = 3000$ N, $a=0.075$ m, $b = 0.05$ m, $\mu = 1$

An elliptical contact patch is typical of motorcycle tyres or railway wheels. In this case, a unique solution $C^1({\mathscr{P}}^{-}\times {\mathbb {R}}_{\ge 0};{\mathbb {R}}^2)$ may always be found if the condition $a^2 \le b(b+1/|\varphi _\gamma |)$ is verified.

The comparison between the classic theory and the exact one for an elliptical contact patch is shown in Fig. 2, again with $\varphi = 3.33$, $\chi _\gamma = 0.9$. In this case, the discrepancy between the two formulations is less evident, due to the fact that a single steady-state solution applies to the overall contact patch.

Fig. 2

Steady-state characteristics predicted by the classic (solid lines) and exact (dashed-lines) theories for different values of the lateral slip $\sigma _y$ for an elliptical contact patch. Tyre parameters: $\varphi = 3.33$, $\chi _\gamma = 0.9$, $F_z = 3000$ N, $a=0.075$ m, $b = 0.05$ m, $\mu = 1$

For both contact geometries, further details about the analytical espressions for the steady-state deflection of the bristles are given in Appendix A. In any case, the transient extinguishes after a travelled distance $s \simeq 2a$, as also predicted by the classic theory. In general, it may be argued that the classic theory represents already a very good approximation to the exact one, with the advantage of being much simpler and allowing analytical results even for a few cases where limited friction is considered, as discussed extensively in the following Sect. 4. On the other hand, the complexity of the exact theory makes the transient analysis prohibitive, whereas numerical techniques need to be employed.

However, it is worth observing that some results from the exact formulation may be essential to gain some intuition about the main phenomena determining not only the generation process of tyre forces and moment, but also the geometry of the contact patch. In particular, the knowledge gained about the shape of the trajectories of the bristle (the characteristic projections) may corroborate analytically the hypothesis of a curved contact shape in case of large camber angles [2, 65]. This would further legitimate the introduction of the camber reduction factor $\varepsilon _{\gamma }$ to accomodate camber-induced distortions of the tyre carcass [2, 55].

4 The classic brush theory

In this section, some formal results for the classic brush theory are established. The analysis is conducted with reference to the cases of pure lateral slip, pure spin and combined lateral slip and spin. Through all the exposition, an isotropic tyre is considered, that is $k_{xx} = k_{yy} = k$ and $k_{xy} = k_{yx} = 0$.¹⁴ For the case of pure lateral slip, a strictly concave pressure distribution in the rolling direction is assumed; to account for the presence of (small) camber angles, the vertical pressure distribution is modelled explicitly by means of a parabolic trend. Finally, the slip variables, the contact shape and the vertical pressure distribution are assumed to be constant over time.

Apart from Lemmata B.1 and B.2, all the findings presented in Sect. 4.2 are, to the autors’ best knowledge, completely novel.

The analysis presented in this paper is grounded on the two following Assumptions 4.1 and 4.2.

Assumption 4.1

The contact patch ${\mathscr{P}}$ is a compact, D-convex¹⁵ set along the direction $\hat{\varvec{e}}_x$.

Assumption 4.1 is customary [1] and ensures the existence of a continuous leading edge. Clearly, both the ’classic’ rectangular and elliptical contact shapes satisfy Assumption 4.1.

To proceed with the analysis, it may also be useful to introduce a proper change of coordinates.¹⁶ If the leading and trailing edges are parametrised by $x=x_{\mathscr {L}}(y)$ and $x=x_{\mathscr {T}}(y)$, respectively, it is possible to define

$$\begin{aligned} \varvec{\xi } = \begin{bmatrix} \xi \\ \eta \\ \zeta \end{bmatrix}&\triangleq \begin{bmatrix} x_{\mathscr {L}}(y)-x \\ y \\ z \end{bmatrix}. \end{aligned}$$

(37)

It should be noticed that $(\varvec{\xi })$ is a local reference frame, where $\xi$ represents the distance from the leading edge (parametrised explicitly by $\xi = \xi _{\mathscr {L}} =0$) for a fixed $\eta$, and it is often referred to as distance from the entrance. The transformation (37) may be used when the contact patch is fixed, whilst in the more general case of time-varying shape a similar procedure to that presented in Sect. 3 should be employed. Using the coordinates $(\varvec{\xi })$, the trailing edge may be parametrised explicitly as $\xi = \xi _{\mathscr {T}}(\eta )$. Clearly, the variable $\zeta$ has a different meaning than that used in Sect. 3.

Assumption 4.2

For every $\varvec{\xi }\in {\mathscr{P}}$, consider the restrictions of the contact patch and vertical pressure distribution obtained for $\eta$ fixed, i.e. ${\mathscr{P}}^{(\eta )}\triangleq {\mathscr{P}}\upharpoonright _{\eta }$ and $q_z^{(\eta )}(\xi ) \triangleq q_z(\varvec{\xi })\upharpoonright _{\eta }$. It is assumed that $q_z^{(\eta )} \in C^1({\mathscr{P}}^{(\eta )};{\mathbb {R}})$, with $q_z^{(\eta )}(\xi ) = 0$ on $\partial {\mathscr{P}}^{(\eta )}$ and $q_z^{(\eta )}(\cdot)$ strictly concave (i.e. $q_z(\cdot)$ strictly D-concave in direction $\hat{\varvec{e}}_x$).

4.1 Vanishing sliding

When the camber angle and the spin angular speed are sufficiently small to be neglected, the exact theory presented in the previous Sect. 3 is equivalent to the classic one. The latter, in fact, approximates the tangential velocity field inside the contact patch neglecting the camber spin, that is $\bar{\varvec{v}}_{\varvec{t}}({\varvec{x}}, s) \simeq - \hat{\varvec{e}}_x$, and also neglects the turn spin ($\chi _{\psi } \rightarrow 0$). Accordingly, the characteristics projections are straightened over the contact patch. Of course, these simplifications are always reasonable for car and truck tyres, where the camber angles are limited within few degrees and the turning speed is negligible. Owing to the premises above, Eq. (1) becomes

$$\begin{aligned} {\bar{{\varvec{v}}}}_{\rm s}({\varvec{\xi }}, s) &= -{{\varvec{\sigma}}}( s) - {{\mathbf {A}}}_\varphi ( s) \begin{bmatrix}x_{\mathscr {L}}(\eta )-\xi \\ \eta \end{bmatrix} \\ & \quad +\frac{\partial {\varvec{u}}_{\varvec{t}}({\varvec{\xi }}, s)}{\partial s} + \frac{\partial {\varvec{u}}_{\varvec{t}}({\varvec{\xi} }, s)}{\partial \xi }, \quad ({\varvec{\xi }}, s) \in \mathring{{\mathscr{P}}}\times {\mathbb {R}}_{> 0}, \end{aligned}$$

(38)

which, under vanishing sliding assumptions, simplifies further to

$$\begin{aligned} \frac{\partial {\varvec{u}}_{\varvec{t}}({\varvec{\xi }}, s)}{\partial s} + \frac{\partial {\varvec{u}}_{\varvec{t}}({\varvec{\xi} }, s)}{\partial \xi } & = {\varvec{\sigma} }( s)+ {{\mathbf {A}}}_\varphi ( s)\begin{bmatrix}x_{\mathscr {L}}(\eta )-\xi \\ \eta \end{bmatrix},\\ \quad &({\varvec{\xi} }, s) \in \mathring{{\mathscr{P}}}\times {\mathbb {R}}_{> 0}. \end{aligned}$$

(39)

The above Eq. (39) comes equipped with the following BC and IC:

$$\begin{array}{*{20}c}{\text {BC:}}&{\varvec{u}}_{\varvec{t}}(0,\eta , s) = \mathbf{0},&s \in {\mathbb {R}}_{>0}, \\ \end{array}$$

(40)

$$\begin{array}{*{20}c}{\text {IC:}}&{\varvec{u}}_{\varvec{t}}(\varvec{\xi },0) = {\varvec{u}}_{\varvec{t}0}(\varvec{\xi }),&\varvec{\xi } \in \mathring{{\mathscr{P}}}. \\ \end{array}$$

(41)

If constant slip inputs¹⁷ are assumed, the steady-state and transient solutions to Eq. (39) are given by

$$\begin{array}{*{20}l} {\varvec{u}}_{\varvec{t}}^-({\varvec{\xi }})= {\varvec{\sigma}}\xi + {{\mathbf {A}}}_{\varphi} \xi \left[{\begin{array}{*{20}c} x_{\mathscr {L}}(\eta )-\xi /2 \\ \eta \\ \end{array}} \right], \hfill&({\varvec{\xi }}, s) \in {\mathscr{P}}^{-}\times {\mathbb {R}}_{\ge 0}, \hfill \\ \end{array}$$

(42a)

$$\begin{aligned} {\varvec{u}}_{\varvec{t}}^+({\varvec{\xi }}, s)&= {\varvec{\sigma}} s + {{\mathbf {A}}}_{\varphi} s\begin{bmatrix} x_{\mathscr {L}}(\eta )-\xi + s/2 \\ \eta \end{bmatrix}+ {\varvec{u}}_{\varvec{t}0}(\xi - s,\eta ) ,&({\varvec{\xi }}, s) \in {\mathscr{P}}^{+}\times {\mathbb {R}}_{\ge 0}, \end{aligned}$$

(42b)

with ${\mathscr{P}}^{-}$ and ${\mathscr{P}}^{+}$ reading as in Eqs. (30), (35), respectively, and the travelling edge described implicitly by $\gamma _{\varSigma }(\varvec{\xi }, s) \triangleq \xi - s=0$. Accordingly, the global solution over the contact patch ${\mathscr{P}}$ may be formally constructed similarly as in Eq. (36) and is $C^0({\mathscr{P}}\times {\mathbb {R}}_{\ge 0})$. Moreover, the steady-state and transient solutions are also uniquely defined on ${\mathscr{P}}$ owing to Assumption 4.1.

From Eqs. (42a, 42b), it may be deduced that the transient extinguishes after a value of the travelled distance equal to $s=2a$, where a is again the semilength of the contact patch. The same result has been obtained empirically and also by applying other theories [66].

When the slip values are relatively high or the available friction is limited, the assumption of vanishing sliding does not hold anymore. For the case under consideration, Eq. (4b) in the sliding zone may be restated as follows:

$$\begin{aligned} {\varvec{u}}_{\varvec{t}}^{\rm (s)}(\varvec{\xi }, s) = \dfrac{\mu }{k}q_z(\varvec{\xi }) \hat{\varvec{s}}_{\varvec{t}}(\varvec{\xi }, s), \end{aligned}$$

(43)

where the sliding direction $\hat{\varvec{s}}_{\varvec{t}}(\varvec{\xi }, s)$ is defined as in Eq. (5) and the nondimensional micro-sliding velocity reads as in Eq. (38).

4.2 Transient sliding solutions

In this section, the presence of limited friction is considered. Closed-form solutions are derived for vertical pressure distributions satisfying Assumption 4.2.¹⁸ For the case of pure translational slips, the shape of this concave function may be arbitrary; for the case of pure spin slip (camber), it is modelled explicitly using a parabolic trend. For the problems at hand, well-posed solutions are considered functions at least $C^0({\mathscr{P}}\times {\mathbb {R}}_{\ge 0};{\mathbb {R}}^2)$ solving Eq. (39) weakly in the adhesion zone ${\mathscr{P}}^{\rm (a)}$, satisfying the BC and IC given respectively by Eqs. (40), (41) and of the form (43) in ${\mathscr{P}}^{\rm (s)}$.

The analysis is notheworthy since, in spite of Kalkers’s claims [17, 68], some authors [68,69,70] have highlighted that it is possible to explain nonstationary phenomena within the theoretical framework of the brush models. Opposed to [45], where the sliding directions were assumed to be oriented as the slips, the sliding solutions derived in this paper also consider the deformation of the bristle in the computation of the micro-sliding velocity.

4.2.1 Pure lateral slip

The pure translational slips conditions are perfectly analogous. Therefore, the present discussion is limited to the case of $\sigma _x = \varphi = 0$, $\sigma _y \not = 0$; it is also assumed that $u_{x0}(\varvec{\xi }) = 0$ for all $\varvec{\xi }\in {\mathscr{P}}$. The analysis is based on the (almost complete) solution proposed by Kalker for the pure longitudinal problem. The main intuition is that, even in presence of limited friction, the complete transient solution may be constructed combining the full-adhesion expressions in Eqs. (42a, 42b) with stationary sliding solutions (these may be found, for example, in Pacejka [2]). In this case, however, it is necessary to allow for solutions which have opposite sign to the one of the lateral slip input $\sigma _y$, depending on the initial conditions. Indeed, since it is identically $u_x(\varvec{\xi },s) = 0$, when $\sigma _y \not = 0$, the sliding solution ${\varvec{u}}_{\varvec{t}}^{\rm (s)}(\varvec{\xi },s) = u_y^{\rm (s)}(\varvec{\xi },s)\hat{\varvec{e}}_y$ may be sought by assuming

$$\begin{array}{*{20}l} u_{y}^{\rm (s)}(\varvec{\xi })= \frac{\mu }{k}{q_z(\varvec{\xi })}{{\,{{\mathrm{sgn}}}\,}}\sigma _y&\mathrm {if}&\sigma _y u_y^{\rm (a)}\bigl (\xi _{\mathscr {S}}(\eta ,s),\eta ,s\bigr ) \ge 0,&k|\sigma _y| > \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }, \\ \end{array}$$

(44a)

$$\begin{array}{*{20}l} u_y^{\rm (s)}(\varvec{\xi })= -\frac{\mu }{k}{q_z(\varvec{\xi })}{{\,{\mathrm{sgn}}\,}}\sigma _y&\mathrm {if}&\sigma _y u_y^{\rm (a)}\bigl (\xi _{\mathscr {S}}(\eta ,s),\eta ,s\bigr )< 0,&k|\sigma _y| <- \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }, \\ \end{array}$$

(44b)

where $\xi = \xi _{\mathscr {S}}(\eta ,s)$ is an explicit representation of a generic sliding edge ${\mathscr {S}}$. The sliding solutions provided by Eqs. (44a) and (44b) correspond to the cases for which the lateral component of the adhesion shear stress $q_y^{\rm (a)}(\varvec{\xi },s) = k u_y^{\rm (a)}(\varvec{\xi },s)$ calculated from Eqs. (42a, 42b) exceeds the friction bound which is, in turn, concordant or discordant with the sign of the slip $\sigma _y$, and are characterised by constant sliding directions given by $\hat{\varvec{s}}_{\varvec{t}} = \pm {{\,{\mathrm{sgn}}\,}}\sigma _y \hat{\varvec{e}}_y$. It is possible to observe that Eqs. (44a) and (44b) preserve the continuity of the sign in the transition between adhesion and sliding, and therefore satisfy the BC (14). On the other hand, the case $\sigma _y = 0$ is trivial: the sliding solution must have direction $\hat{\varvec{s}}_{\varvec{t}}(s) = {{\,{\mathrm{sgn}}\,}}(u_y^{\rm (a)}(\xi _{\mathscr {S}}(\eta ,s),\eta ,s))\hat{\varvec{e}}_y$.

In light of the above considerations, the global solution over ${\mathscr{P}}$ may be constructed as

$${\varvec{u}}_{\varvec{t}}(\varvec{\xi },s) = {\left\{ \begin{array}{ll}{\varvec{u}}_{\varvec{t}}^{\rm (a)}(\varvec{\xi },s) = u_y^{\rm (a)}(\varvec{\xi },s)\hat{\varvec{e}}_y, & (\varvec{\xi },s) \in {\mathscr{P}}^{\rm (a)} \times {\mathbb {R}}_{\ge 0}, \\ {\varvec{u}}_{\varvec{t}}^{\rm (s)}(\varvec{\xi }) = u_{y}^{\rm (s)}(\varvec{\xi })\hat{\varvec{e}}_y, & (\varvec{\xi },s) \in {\mathscr{P}}^{\rm (s)}\times {\mathbb {R}}_{\ge 0},\end{array}\right. } $$

(45)

where, from Eqs. (42a, 42b), $u_y^{\rm (a)}(\varvec{\xi },s)$ reads

$$u_y^{\rm (a)}(\varvec{\xi },s) = {\left\{ \begin{array}{ll} u_y^{-}(\xi ) = \sigma _y \xi , & (\varvec{\xi },s) \in {\mathscr{P}}^{-}\times {\mathbb {R}}_{\ge 0}, \\ u_y^{+}(\varvec{\xi },s) = \sigma _y s + u_{y0}(\xi -s, \eta ), & (\varvec{\xi },s) \in {\mathscr{P}}^{+}\times {\mathbb {R}}_{\ge 0}, \end{array}\right. } $$

(46)

the lateral displacement $u_y^{\rm (s)}(\varvec{\xi })$ in the sliding zone is given by Eqs. (44a, 44b), and this time ${\mathscr{P}}^{\rm (a)}$ and ${\mathscr{P}}^{\rm (s)}$ may be defined more conveniently as

$$\begin{aligned} {\mathscr{P}}^{\rm (a)}&\triangleq \biggl \{\varvec{\xi } \in {\mathscr{P}} \mathrel {\bigg |} k |u_y^{\rm (a)}(\varvec{\xi },s)| \le \mu q_z(\varvec{\xi }) \biggr \}, \end{aligned}$$

(47a)

$$\begin{aligned} {\mathscr{P}}^{\rm (s)}&\triangleq \biggl \{\varvec{\xi } \in {\mathscr{P}} \mathrel {\bigg |} k |u_y^{\rm (a)}(\varvec{\xi },s)| > \mu q_z(\varvec{\xi }) \biggr \}. \end{aligned}$$

(47b)

Indeed, it is possible to show that, owing to the condition

$$\begin{aligned} |q_{y0}(\varvec{\xi })| = k|u_{y0}(\varvec{\xi })| \le \mu q_z(\varvec{\xi }),&\mathrel {\forall } \varvec{\xi } \in {\mathscr{P}}, \end{aligned}$$

(48)

and the concavity of $q_z(\varvec{\xi })$ in the rolling direction, the alternative definitions (47a, 47b) are equivalent to the original ones given by Eqs. (6a, 6b) (Lemma B.1). Clearly, the constraint imposed by Eq. (48) must necessarily be fulfilled in presence of limited friction, and thus the solution ${\varvec{u}}_{\varvec{t}}(\varvec{\xi },s)$ constructed according to Eq. (45) is $C^0({\mathscr{P}}\times {\mathbb {R}}_{\ge 0}; \{0\}\times {\mathbb {R}})$ and always well-defined. In particular, Lemma B.1 states that, independently of the initial conditions $u_{y0}(\varvec{\xi })$, the lateral shear stress $q_y^{\rm (a)}(\varvec{\xi },s)$ can exceed the friction bounds which are concordant and discordant with the slip sign, in turn, only when the conditions on the right-hand sides of Eqs. (44a, 44b) are satisfied, that is only for values of $\varvec{\xi }\in {\mathscr{P}}$ such that $k|\sigma _y| > \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$ and $k|\sigma _y| <- \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$, respectively. This is equivalent to have $\bar{\varvec{v}}_{\rm s}(\varvec{\xi },s) \not = \mathbf{0}$ when $|q_y^{\rm (a)}(\varvec{\xi },s)| > \mu q_z(\varvec{\xi })$. It should be noticed that the solutions of $k|\sigma _y| = \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$ and $k|\sigma _y| =- \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$ are the points where the slope of the lateral shear stress equals that of the friction bound.

A graphical interpretation of Lemma B.1 is shown in Fig. 3, where the transient solution is plotted for a value of the nondimensional travelled distance $\bar{s} \triangleq s/(2a) = 1/3$ against the nondimensional coordinate $\bar{\xi } \triangleq \xi /(2a)$ starting from initial conditions ${\varvec{u}}_{\varvec{t}0}(\varvec{\xi }) = u_{y0}(\varvec{\xi })\hat{\varvec{e}}_y$ which have opposite sign to the new slip value $\sigma _y > 0$. In Fig. 3, the pressure distribution is parabolic as in Eq. (49). It may be observed that there are two interesting points, namely B and C, for which the partial derivatives with respect to $\xi$ of the positive and negative traction bounds equal the slope of the lateral shear stress $k\sigma _y$. For the case under consideration, Lemma B.1 asserts that the transient solution is only allowed to exceed the positive (negative) friction parabola on the right of B (C). This always ensures nonzero values of the micro-sliding speed in the sliding regions, implying the well-posedness of the solution constructed as in Eq. (45). For negative slip inputs, the situation is perfectly mirrored.

Fig. 3

Transient solution for $s = 1/3$ starting from lateral initial conditions $u_{y0}(\varvec{\xi })$ which have opposite sign to the new slip value

Another interesting aspect to investigate concerns the dynamics of a bristle which travels from the leading to the trailing edge. It is found that, once a bristle starts sliding at some longitudinal coordinate $\xi$, it keeps sliding until it relinquishes the contact patch. The argument is as follows: for some value of the travelled distance s, a bristle travelling inside the contact patch occupies the position $\xi$; after a small increment of travelled distance $\delta s$, the same bristle will be located at $\xi +\delta s$. To show that the bristle keeps sliding until it leaves the contact patch, it should be demonstrated that, if the absolute value of the lateral shear stress $|q_y^{\rm (a)}(\varvec{\xi },s)|$ exceeded the friction bound at the previous time step, it would automatically be greater than the friction bound also for $s+\delta s$, when the bristle is located at $\xi + \delta s$. This result is advocated in Lemma B.2. These translate the previous considerations into mathematical terms for the cases of strictly concave and simply concave pressure distributions in the rolling direction. This does not mean, however, that, for a fixed coordinate $\xi$, the adhesion shear stress will always exceed the friction bound if it did at a previous time step; instead, the result should be interpreted from a Lagrangian viewpoint, by following the moving bristle. Indeed, in the Eulerian approach, different bristles will occupy the position $\xi$ for different values of s.

A possible transient evolution for the lateral shear stress is shown in Fig. 4, where an initial deformation is considered similar to the so-called Cattaneo’s distribution [71]. For the problem at hand, this trend usually originates from a previous transient distribution for values of the slip equal or higher than the critical one, that is $|\sigma _y| \ge \sigma ^{\rm cr}$ (see, for example, [45]). When the new manoeuvre starts, the initial shear stress distribution is progressively shoved out by the transient solution until steady-state conditions take place again. The solution is similar to the one found numerically in [72].

Fig. 4

Transient evolution of the lateral shear stress due to a lateral slip input starting from Cattaneo’s initial conditions. a $\bar{ s}=0$; b $\bar{ s}=1/3$; c $\bar{ s}=2/3$; d $\bar{ s}=1$

In general, depending on the value of the lateral slip, different adhesion and sliding areas arise inside the contact patch. Some analytical results are available in [45] for zero initial conditions.

It is finally worth noticing that the trainsient analysis for the case of combined translational slips is analogous to the case of pure lateral slip if the initial conditions are oriented as the new slip ${\varvec{\sigma}}$.

4.2.2 Pure spin slip

The transient dynamics in case of pure spin may be investigated under the hypothesis of a thin tyre ($b \ll a$) [2, 4], which allows to approximate the problem by only considering the middle plane of the tyre. Therefore, the contact patch may assumed to be one-dimensional and described by ${\mathscr{P}} = \{\xi \in {\mathbb {R}} \mathrel {|} 0 \le \xi \le 2a\}$ or equivalently by ${\mathscr{P}} = \{x \in {\mathbb {R}} \mathrel {|} -a \le x \le a\}$ in the original variable x (the dependency on y or $\eta$ is hereafter omitted for the sake of notation). Furthermore, a parabolic pressure distribution is considered as follows:

$$\begin{aligned} q_z(\xi ) = \dfrac{q_z^*}{a^2}\xi (2a-\xi ), \end{aligned}$$

(49)

where $q_z^*$ is the maximum pressure in the contact patch. Clearly, the function $q_z(\cdot ) \equiv q_z^{(\eta )}(\cdot )$ in Eq. (49) satisfies Assumption 4.2, with the trailing edge parametrised by $\xi =\xi _{\mathscr {T}} =2a$ and the leading edge by $x = x_{\mathscr {L}} = a$ in the original variable x.

Since non-negligible spin values are mainly due to high camber levels, the investigation is restricted to the case of non-supercritical spin, that is $|\varphi | \le \varphi ^{\rm cr} \triangleq 2 \mu \dfrac{ q_z^{*} }{k a^2}$. With a parabolic pressure distribution as in Eq. (49), supercritical spin values $|\varphi | > \varphi ^{\rm cr}$ cause the first half of the contact patch to slide in steady-state. In contrast, the condition $|\varphi | \le \varphi ^{\rm cr}$ ensures full adhesion. Again, it is assumed that $u_{x0}(\xi ) = 0$. Owing to these premises, the analysis is similar to that conducted for the case of pure lateral slip. Indeed, the general sliding solution may still be sought in the same form of Eq. (45). In this case, however, for $\varphi \not = 0$, the lateral component of the sliding displacement is assumed to be of the form

$$u_{y}^{\rm (s)}(\xi )= \frac{\mu }{k}{q_z(\xi )}{{\,{\mathrm{sgn}}\,}}\varphi \quad \rm {if}\quad \varphi u_y^{\rm (a)}\bigl (\xi _{\mathscr {S}}(s),s\bigr ) \ge 0, \quad (|\varphi |-\varphi ^{\rm cr})(a-\xi ) > 0, $$

(50a)

$$u_{y}^{\rm (s)}(\xi )= -\frac{\mu }{k}{q_z(\xi )}{{\,\rm{sgn}}}\varphi\quad \mathrm {if} \quad \varphi u_y^{\rm (a)}\bigl (\xi _{\mathscr {S}}(s),s\bigr )< 0,\quad\bigl (|\varphi | + \varphi ^{\rm cr}\bigr )(a-\xi ) < 0.$$

(50b)

The corresponding sliding directions are therefore given by $\hat{\varvec{s}}_{\varvec{t}} = \pm {{\,{\mathrm{sgn}}\,}}\varphi \hat{\varvec{e}}_y$. Noticing that, in the present case ${\mathscr{P}}^{-} = \{ \xi \in {\mathscr{P}} \mathrel {|} 0\le \xi <s\}$ and ${\mathscr{P}}^{+} = \{ \xi \in {\mathscr{P}} \mathrel {|} s \le \xi \le 2a\}$, a global solution ${\varvec{u}}_{\varvec{t}}(\xi ,s) \in C^0({\mathscr{P}}\times {\mathbb {R}}_{\ge 0}; \{0\}\times {\mathbb {R}})$ may be tentatively constructed in the spirit of Eq. (45) with

$$\begin{aligned} u_y^{\rm (a)}(\xi ,s) = {\left\{ \begin{array}{ll} u_y^{-}(\xi ) = \dfrac{1}{2}\varphi \xi (2a-\xi ), & (\xi ,s) \in {\mathscr{P}}^{-} \times {\mathbb {R}}_{\ge 0}, \\ u_y^{+}(\xi ,s) = \dfrac{1}{2}\varphi s(2a-2\xi + s)+ u_{y0}(\xi -s), & (\xi ,s) \in {\mathscr{P}}^{+} \times {\mathbb {R}}_{\ge 0}, \end{array}\right. } \end{aligned}$$

(51)

the lateral component of the sliding deflection $u_y^{\rm (s)}(\xi )$ given by Eqs. (50a, 50b), and ${\mathscr{P}}^{\rm (a)}$, ${\mathscr{P}}^{\rm (s)}$ defined similarly as in Eqs. (47a, 47b).

The global solution ${\varvec{u}}_{\varvec{t}}(\xi ,s)$ constructed by in this way must satisfy the two criteria on the right-hand side of (50a, 50b). In this context, it is worth observing that Eqs. (50a, 50b) allow nonzero values of the micro-sliding speed are only in the right-half of the contact patch, that is for $\xi \in (a, 2a]$. Under the assumption $|q_{y0}(\xi )| \le \mu q_z(\xi )$, Lemma B.3 demonstrates that, in the region $\xi \in [0, a]$, sliding never occurs and thus the lateral shear force can only exceed the friction parabola in the right-half of the contact patch. In subcritical spin slips conditions, that is $|\varphi | < \varphi ^{\rm cr}$, this is sufficient to establish the correctness of the proposed solution, since both solutions (50a, 50b) are meaningful. On the other hand, when $|\varphi | = \varphi ^{\rm cr}$, the only possible sliding solution to the transient problem is provided by Eq. (50b), implying that the lateral shear stress due to pure critical spin slip may only exceed the friction parabola which is discordant with the spin itself. This additional result is asserted in Lemma B.4, implying the well-posedness of the proposed solution.

The transient evolution of the lateral shear stress due to pure spin is illustrated in Fig. 5 starting from an initial distribution corresponding to the steady-state solution for a small spin $\varphi < 0$.

Fig. 5

Transient evolution of the lateral shear stress due to pure rotational slip is shown considering an initial distribution resulting from an opposite value of the spin parameter. a $\bar{ s}=0$; b $\bar{ s}=1/3$; c $\bar{ s}=2/3$; d $\bar{ s}=1$

Analogous to what already discussed to for the case of pure lateral slip, it is again possible to show that a britsle which starts siding at some coordinate $\xi$ and travelled distance s keeps sliding until it relinquishes the contact patch (Lemma B.5).

4.2.3 Lateral slip and spin

The transient problem for the case combined lateral and spin slips may be addresses in a similar way as done before. The main assumptions are those of subcritical spin slip, that is $|\varphi |<\varphi ^{\rm cr}$, thin tyre ($b \ll a$), parabolic pressure distribution as in Eq. (49), and $u_{x0}(\xi ) = 0$.

In this case, the fundamental intuition behind the proposed solution resides in the fact that, in steady-state conditions, the sliding solution is always concordant with the sign of the lateral slip $\sigma _y \not = 0$. Therefore, the lateral deflection in the sliding zone is sought in the following form:

$$u_{y}^{\rm (s)}(\xi )= \frac{\mu }{k}{q_z(\xi )}{{\,{\mathrm{sgn}}\,}}\sigma _y\quad \mathrm {if}\quad \sigma _y u_y^{\rm (a)}\bigl (\xi _{\mathscr {S}}(s),s\bigr ) \ge 0,\quad |\sigma _y| > \Bigl (\varphi ^{\rm cr}-|\varphi |{{\,{\mathrm{sgn}}\,}}\bigl (\sigma _y\varphi \bigr ) \Bigr )(a-\xi ), $$

(52a)

$$u_{y}^{\rm (s)}(\xi )= -\frac{\mu }{k}{q_z(\xi )}{{\,{\mathrm{sgn}}\,}}\sigma _y\quad \mathrm {if}\quad \sigma _y u_y^{\rm (a)}\bigl (\xi _{\mathscr {S}}(s),s\bigr )< 0, \quad |\sigma _y| <\Bigl (\varphi ^{\rm cr}+|\varphi |{{\,{\mathrm{sgn}}\,}}\bigl (\sigma _y \varphi \bigr ) \Bigr )(\xi -a), $$

(52b)

with the sliding direction reading $\hat{\varvec{s}}_{\varvec{t}} = \pm {{\,{\mathrm{sgn}}\,}}\sigma _y \hat{\varvec{e}}_y$. A global solution ${\varvec{u}}_{\varvec{t}}(\xi ,s)\in C^0({\mathscr{P}}\times {\mathbb {R}}_{\ge 0}; \{0\}\times {\mathbb {R}})$ is again constructed using a similar relationship to (45) together with (52a, 52b), but this time with the lateral adhesion solution clearly reading

$$\begin{aligned} u_y^{\rm (a)}(\xi ,s) = {\left\{ \begin{array}{ll} u_y^{-}(\xi ) = \sigma _y \xi + \dfrac{1}{2}\varphi \xi (2a-\xi ), & (\xi ,s) \in {\mathscr{P}}^{-} \times {\mathbb {R}}_{\ge 0}, \\ u_y^{+}(\xi ,s) = \sigma _y s + \dfrac{1}{2}\varphi s(2a-2\xi + s)+ u_{y0}(\xi -s), & (\xi ,s) \in {\mathscr{P}}^{+} \times {\mathbb {R}}_{\ge 0}. \end{array}\right. } \end{aligned}$$

(53)

The remaining part of the analysis is identical to what discussed for the cases of pure lateral slip and spin, respectively. Specifically, Lemma B.6 ensures that the shear stress never exceeds the friction parabolae which are concordant and discordant with the slip sign for values of $\xi$ such that $|\sigma _y| \le (\varphi ^{\rm cr}-|\varphi | {{\,{\mathrm{sgn}}\,}}(\sigma _y \varphi ))(a-\xi )$ and $|\sigma _y| \ge (\varphi ^{\rm cr}+|\varphi | {{\,{\mathrm{sgn}}\,}}(\sigma _y \varphi ))(\xi -a)$, respectively. This result itself sufficies to demonstrate the well-posedness of the solution. Finally, from the perspective of a physical interpretation, Lemmata B.7 represents the counterpart of Lemmas B.2 and B.5. It asserts that, once a bristle starts sliding at position $\xi$ and travelled distance s, it continues sliding until it leaves the contact patch.

5 Conclusions

This paper brings new analytical results in the transient theory of brush tyre models. The first part of the present work is aimed at framing the theory into a more general context. The authors have commented extensively on the implications of considering a two-dimensional vector field inside the contact area. This is actually the case for motorcycle tyres, often subjected to high camber angles. The main source of inspiration for this analysis is clearly the recent paper by some of the authors [46]. In this paper, some previous results have been reformulated and a new interpretation of the tyre dynamics has been given. More specifically, it has been shown that it is possible to describe the dynamics of the bristles inside the contact patch by means of a simplified linear system, to which the well-known theorems about existence and uniqueness of the solution from the ODE theory apply. The general analysis has been conducted in respect to time-varying slip inputs and contact shape, for which the boundary conditions have been properly formulated. Analytical expressions for the steady-state deflection of the bristle have been provided for the cases of rectangular and elliptical contact shape, and a qualitative comparison has been performed against the classic theory, which appears to represent a sufficient accurate approximation to the exact formulation.

Compared to some previous results advocated by Romano et al. [45], the treatment has been further enriched by taking into consideration additional terms, such as the camber reduction factor.

The second part of the paper is then dedicated to the classic transient theory. In terms of pure tyre-related literature, the primary sources of inspiration for the present work were Pacejka’s book [2] and the authoritative survey coauthored by Sharp [67]. From a methodological perspective, on the other hand, the fundamental reference for this second part is represented by the excellent survey authored by Kalker [10]. Some important results about the correctness of the non-stationary solution have been established by means of several proofs, all aimed at demonstrating that, owing to certain assumptions, the governing PDEs of the system may always be solved by enforcing a general initial condition to the whole domain. To this extent, all the one dimensional problems (pure lateral, spin and combined lateral and spin) have been covered. The authors’ findings generalise the ones by Kalker [10].

It appears that the theoretical treatment of the brush models is almost complete, covering all relevant cases for which closed-form solutions are admitted. However, whilst the classic theory rests on a long tradition of empirical evidence, experimental validation might still be needed to confirm some of the results advocated in this paper, particularly with reference to the ones presented in Sect. 3. Apart from an agreement between the predicted tyre forces and the measured one, it would be very interesting to trace the trajectories of the material points inside the contact patch, to investigate accurately the presence of a two-dimensional velocity field. Such an experimental campaign is not simple to set up, but it would be definitely strengthen the significance of the present analytical study.

Appendices

Appendix A: Analytical solutions for rectangular and elliptical contact patches

This Appendix derives the analytical expressions for the steady-state deflection of the bristle for a rectangular and elliptical contact patch. The analytical solutions may be derived from the conditions:

$$ y< R_\gamma = \dfrac{1}{|\varphi _\gamma |},\quad\varphi _\gamma > 0,\quad{\varvec{x}} \in {\mathscr{P}}, $$

(54a)

$$y> R_\gamma = -\dfrac{1}{|\varphi _\gamma |},\quad\varphi _\gamma < 0,\quad{\varvec{x}} \in {\mathscr{P}}. $$

(54b)

1.1 A. 1: Rectangular contact patch

The contact patch is defined mathematically as

$$\begin{aligned} {\mathscr{P}} \triangleq \bigl \{{\varvec{x}} \in \varPi \mathrel {\big |} - a \le x \le a, \, -b\le y \le b \bigr \}. \end{aligned}$$

(55)

The three leading edges are described by the following functions

$$x= x_{{\mathscr {L}}_1}(y) =a, \quad y\in (-b,b),$$

(56a)

$$ y= y_{{\mathscr {L}}_2}(x)= b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma, \quad x\in (0,a),$$

(56b)

$$y= y_{{\mathscr {L}}_3}(x)= -b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma, \quad x\in (-a,0).$$

(56c)

Accordingly, it is possible to identify three different subdomains of the contact patch which the solutions refer to:

$$\begin{aligned} {\mathscr{P}}_1&\triangleq \bigl \{ {\mathscr{P}} \setminus ( {\mathscr{P}}_2 \cup {\mathscr{P}}_3) \bigr \}, \end{aligned}$$

(57a)

$$\begin{aligned} {\mathscr{P}}_2&\triangleq \Bigl \{{\varvec{x}} \in {\mathscr{P}} \mathrel {\Big |} R_1^2< \varGamma ({\varvec{x}}) < R_2^2 \Bigr \}, \end{aligned}$$

(57b)

$$\begin{aligned} {\mathscr{P}}_3&\triangleq \Bigl \{{\varvec{x}} \in {\mathscr{P}} \mathrel {\Big |} R_3^2< \varGamma ({\varvec{x}})< R_4^2,\,x <0\Bigr \}, \end{aligned}$$

(57c)

where $\varGamma ({\varvec{x}})$ reads

$$\begin{aligned} \varGamma ({\varvec{x}}) \triangleq x^2 + \bigl (y-1/\varphi _\gamma \bigr )^2, \end{aligned}$$

(58)

and the radii $R_0$, $R_1$, $R_2$, $R_3$ and $R_4$ are given by

$$\begin{aligned} &R_0\triangleq a,\\&R_1 \triangleq b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma -1/\varphi _\gamma ,\\&R_2 \triangleq \sqrt{{R}_1^2+R_0^2}, \\ &R_3\triangleq b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma +1/\varphi _\gamma ,\\&R_4 \triangleq \sqrt{{R}_3^2+R_0^2}. \end{aligned}$$

(59)

The following circumferences may also be defined:

$$\begin{aligned} \mathcal {C}_0({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_0^2\Bigr \}, \end{aligned}$$

(60a)

$$\begin{aligned} \mathcal {C}_1({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_1^2 \Bigr \}, \end{aligned}$$

(60b)

$$\begin{aligned} \mathcal {C}_2({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_2^2 \Bigr \}, \end{aligned}$$

(60c)

$$\begin{aligned} \mathcal {C}_3({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_3^2\Bigr \}, \end{aligned}$$

(60d)

$$\begin{aligned} \mathcal {C}_4({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_4^2\Bigr \}. \end{aligned}$$

(60e)

Each of this subdomains is in turn partitioned in a region ${\mathscr{P}}_i^{-}$ where steady-state conditions reign and a second one ${\mathscr{P}}_i^{+}$ where the transient takes place. In formulae, the following sets may be introduced:

$$\begin{aligned} {\mathscr{P}}_1^- \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}}_1 \mathrel {\big |} \gamma _{\varSigma _1}({\varvec{x}},s) < 0 \bigr \},&{\mathscr{P}}_1^+ \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}}_1 \mathrel {\big |} \gamma _{\varSigma _1}({\varvec{x}},s) \ge 0 \bigr \}, \end{aligned}$$

(61a)

$$\begin{aligned} {\mathscr{P}}_2^- \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}}_2 \mathrel {\big |} \gamma _{\varSigma _2}({\varvec{x}},s) < 0 \bigr \},&{\mathscr{P}}_2^+ \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}}_2 \mathrel {\big |} \gamma _{\varSigma _2}({\varvec{x}},s) \ge 0 \bigr \}, \end{aligned}$$

(61b)

$$\begin{aligned} {\mathscr{P}}_3^- \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}}_3 \mathrel {\big |} \gamma _{\varSigma _3}({\varvec{x}},s) < 0 \bigr \},&{\mathscr{P}}_3^+ \triangleq \bigl \{ {\varvec{x}} \in {\mathscr{P}}_3 \mathrel {\big |} \gamma _{\varSigma _3}({\varvec{x}},s) \ge 0 \bigr \}. \end{aligned}$$

(61c)

Therefore, the three different steady-state solutions may be finally constructed as follows:

$${\varvec{u}}_{1\varvec{t}}^{-}({\varvec{x}})= {\mathbf {R}}_{\varphi_\psi} \bigl (\varSigma _1({\varvec{x}})\bigr ) \varvec{\varPsi }_1({\varvec{x}}) + \tilde{{\varvec{u}}}_{\varvec{t}}({\varvec{x}}),\quad ({\varvec{x}},s) \in {\mathscr{P}}_1^{-}\times {\mathbb {R}}_{\ge 0}, $$

(62a)

$$ {\varvec{u}}_{2\varvec{t}}^{-}({\varvec{x}})= {\mathbf {R}}_{\varphi_\psi} \bigl (\varSigma _2({\varvec{x}})\bigr ) \varvec{\varPsi }_2({\varvec{x}}) + \tilde{{\varvec{u}}}_{\varvec{t}}({\varvec{x}}) ,\quad ({\varvec{x}},s) \in {\mathscr{P}}_2^{-}\times {\mathbb {R}}_{\ge 0}, $$

(62b)

$${\varvec{u}}_{3\varvec{t}}^{-}({\varvec{x}})= {\mathbf {R}}_{\varphi_\psi} \bigl (\varSigma _3({\varvec{x}})\bigr ) \varvec{\varPsi }_3({\varvec{x}}) + \tilde{{\varvec{u}}}_{\varvec{t}}({\varvec{x}}), \quad ({\varvec{x}},s) \in {\mathscr{P}}_3^{-}\times {\mathbb {R}}_{\ge 0}, $$

(62c)

with

$$\begin{aligned} \varSigma _{1}({\varvec{x}})&\triangleq \frac{1}{\varphi _\gamma }\left[ \arctan \Biggl (\frac{x}{y-1/\varphi _\gamma } \Biggr )+\arctan \Biggl (\frac{R_0}{ \sqrt{\varGamma ({\varvec{x}})-R_0^2}} \Biggr ){{\,{\mathrm{sgn}}\,}}\varphi _\gamma \right] , \end{aligned}$$

(63a)

$$\begin{aligned} \varSigma _{2} ({\varvec{x}})&\triangleq \frac{1}{\varphi _\gamma }\left[ \arctan \Biggl (\frac{x}{y-1/\varphi _\gamma } \Biggr )-\arctan \Biggl (\frac{\sqrt{\varGamma ({\varvec{x}})-R_1^2}}{R_1} \Biggr )\right] , \end{aligned}$$

(63b)

$$\begin{aligned} \varSigma _{3} ({\varvec{x}})&\triangleq \frac{1}{\varphi _\gamma }\left[ \arctan \Biggl (\frac{x}{y-1/\varphi _\gamma } \Biggr )-\arctan \Biggl (\frac{\sqrt{\varGamma ({\varvec{x}})-R_3^2}}{R_3} \Biggr )\right] . \end{aligned}$$

(63c)

The components of the vector functions $\varvec{\varPsi }_1(\cdot )$, $\varvec{\varPsi }_2(\cdot )$, $\varvec{\varPsi }_3(\cdot )$ read as follows:

$$\begin{aligned} \varPsi _{1x}({\varvec{x}})&\triangleq \frac{\sigma _y }{\varphi _\psi } + a, \end{aligned}$$

(64a)

$$\begin{aligned} \varPsi _{2x}({\varvec{x}})&\triangleq \frac{\sigma _y}{\varphi _\psi } + \sqrt{\varGamma ({\varvec{x}})-R_1^2}, \end{aligned}$$

(64b)

$$\begin{aligned} \varPsi_{3x}({\varvec{x}})&\triangleq \frac{\sigma _y }{ \varphi _\psi } - \sqrt{\varGamma ({\varvec{x}})-R_3^2}, \end{aligned}$$

(64c)

$$\begin{aligned} \varPsi _{1y}({\varvec{x}})&\triangleq \frac{1}{\varphi _\psi }(1-\sigma _x) - \sqrt{\varGamma ({\varvec{x}})-R_0^2}{{\,{\mathrm{sgn}}\,}}\varphi _\gamma +\frac{1}{\varphi _\gamma },\end{aligned}$$

(64d)

$$\begin{aligned} \varPsi _{2y}({\varvec{x}})&\triangleq \frac{1}{\varphi _\psi }(1-\sigma _x) +b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma , \end{aligned}$$

(64e)

$$\begin{aligned} \varPsi _{3y}({\varvec{x}})&\triangleq \frac{1}{\varphi _\psi }(1-\sigma _x)- b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma . \end{aligned}$$

(64f)

Both in transient and steady-state conditions, the complete solution over the whole contact patch is not $C^1({\mathscr{P}}\times {\mathbb {R}}_{\ge 0};{\mathbb {R}}^2)$ nor $C^0({\mathscr{P}}\times {\mathbb {R}}_{\ge 0};{\mathbb {R}}^2)$. Indeed, the continuity between the regions ${\mathscr{P}}_1$ and ${\mathscr{P}}_2$ stems directly from the fact that the value assumed by the bristle deflection at $x=x_{{\mathscr {L}}_1}(y) = a$ is the same for both Eqs. (62a) and (62b). In contrast, the continuity of the solution is not preserved on $\mathcal {C}_3({\varvec{x}})$.

1.2 A. 2: Elliptical contact patch

The contact patch may be represented mathematically as

$$\begin{aligned} {\mathscr{P}} \triangleq \Biggl \{{\varvec{x}} \in \varPi \mathrel {\Bigg |} \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} \le 1\Biggr \}, \end{aligned}$$

(65)

with the leading and trailing edges in explicit form as follows:

$$x= x_{\mathscr {L}}(y ) = a\sqrt{1-\dfrac{y^2}{b^2}},\quad y \in (-b,b), $$

(66a)

$$ x = x_{\mathscr {T}}(y ) =-a\sqrt{1-\dfrac{y^2}{b^2}},\quad y \in (-b,b).$$

(66b)

The following radii are defined:

$$\begin{aligned} R_1 \triangleq b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma -1/\varphi _\gamma ,\,&R_2 \triangleq b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma +1/\varphi _\gamma , \end{aligned}$$

(67)

and subsequently the two circles:

$$\begin{aligned} \mathcal {C}_1({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_1^2 \Bigr \}, \end{aligned}$$

(68a)

$$\begin{aligned} \mathcal {C}_2({\varvec{x}})&\triangleq \Bigl \{{\varvec{x}} \in \varPi \mathrel {\Big |}\varGamma ({\varvec{x}}) = R_2^2 \Bigr \}, \end{aligned}$$

(68b)

which are tangent to ${\mathscr{P}}$ at the neutral points ${\varvec{x}}_{\mathscr {N}_1} = (0, b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma )$ and ${\varvec{x}}_{\mathscr {N}_2} = (0, -b{{\,{\mathrm{sgn}}\,}}\varphi _\gamma )$, respectively. The function $\varGamma (\cdot )$ appearing in Eqs. (68a, 68b) reads exactly as in Eq. (58).

The global solution may be constructed combining Eqs. (26a–26c). In particular, for the steady-state deflection in ${\mathscr{P}}^{-}$, the following expression may be derived for $y_0({\varvec{\rho }}({\varvec{x}}))$:

$$\begin{aligned} y_0\bigl ({\varvec{\rho }}({\varvec{x}})\bigr ) = \dfrac{\dfrac{1}{\varphi _\gamma } - \sqrt{\dfrac{1}{\varphi _\gamma ^2}-\Biggl ( 1-\dfrac{a^2}{b^2}\Biggr )\Biggl (\dfrac{1}{\varphi _\gamma ^2}+a^2-\varGamma ({\varvec{x}}) \Biggr )}{{\,{\mathrm{sgn}}\,}}\varphi _\gamma }{\Biggl ( 1-\dfrac{a^2}{b^2}\Biggr )}, \end{aligned}$$

(69)

and $x_0({\varvec{\rho }}({\varvec{x}})) = x_{\mathscr {L}} \circ y_0({\varvec{\rho }}({\varvec{x}}))$ with $x_{\mathscr {L}}(\cdot )$ as in Eq. (66a).

Appendix B: Propositions and Lemmata with proofs

1.1 B. 1: Noncharacteristic BC and IC

Proposition B.1

The BC (10) and IC (11) are noncharacteristic for the PDEs (15).

Proof

According to what asserted in Sect. 3, the BC and IC are said to be noncharacteristic if $\det \mathbf {J}({\varvec{\rho }},0) \not = 0, \infty$. Thus, it should be proved that the determinant of the Jacobian matrix in Eq. (19) evaluated at $\varsigma = 0$ never vanishes nor diverges when imposing the BC (10) and IC (11). The result is firstly derived when imposing the BC. In this case, on the boundary curve $\varsigma = 0$, the initial coordinates are given by ${\varvec{x}}_0({\varvec{\rho }}) = {\varvec{x}}_{\mathscr {L}}({\varvec{\rho }})$, where ${\varvec{x}}_{\mathscr {L}}({\varvec{\rho }})$ is a local parametrisation of the leading edge. On the other hand, the initial conditions for the travelled distance may be chosen, without loss of generality, as $s_0({\varvec{\rho }}) = \rho _1$. Renaming $\mathbf {J}_0({\varvec{\rho }}) \triangleq \mathbf {J}({\varvec{\rho }},0)$, the determinant in Eq. (19) becomes

$$\det {\mathbf{J}}_{0} ({\varvec{\rho }}) = \left| {\begin{array}{*{20}l} {\frac{{\partial x_{0} ({\varvec{\rho }})}}{{\partial \rho _{1} }}} \hfill & {\frac{{\partial x_{0} ({\varvec{\rho }})}}{{\partial \rho _{2} }}} \hfill & {\bar{v}_{x} (y_{0} ({\varvec{\rho }}),\rho _{1} )} \hfill \\ {\frac{{\partial y_{0} ({\varvec{\rho }})}}{{\partial \rho _{1} }}} \hfill & {\frac{{\partial y_{0} ({\varvec{\rho }})}}{{\partial \rho _{2} }}} \hfill & {\bar{v}_{y} (x_{0} ({\varvec{\rho }}),\rho _{1} )} \hfill \\ 1 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right|,$$

(70)

which may be restated as

$$\begin{aligned} \det \mathbf {J}_0({\varvec{\rho }}) = \Bigl [ \bar{\varvec{v}}_{\varvec{t}}\bigl ({\varvec{x}}_0({\varvec{\rho }}),\rho _1\bigr )-\bar{\varvec{v}}_{ \mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )\Bigr ] \cdot \varvec{\nu }_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr ), \end{aligned}$$

(71)

being

$$\begin{array}{*{20}l} \varvec{\nu }_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )\,\triangleq \left[ {\begin{array}{*{20}l}-\frac{\partial y_0({\varvec{\rho }})}{\partial \rho _2}&\frac{\partial x_0({\varvec{\rho }})}{\partial \rho _2}\end{array}}\right]^\mathrm {T}\, &{\text{and}} &\bar{\varvec{\nu }}_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr ) \triangleq \left[{\begin{array}{*{20}l} \frac{\partial x_0({\varvec{\rho }})}{\partial \rho _1}&\frac{\partial y_0({\varvec{\rho }})}{\partial \rho _1}\end{array}}\right]^\mathrm {T}. \\ \end{array}$$

(72)

The above result may be better interpreted by recalling that, at $\varsigma = 0$, $s \equiv s_0({\varvec{\rho }}) =\rho _1$, and therefore the vector $\bar{\varvec{v}}_{\mathscr {L}}({\varvec{x}}_0({\varvec{\rho }}))$ actually represents the velocity of leading edge. Equations (71) and (72) basically state that the bristles entering the contact patch cannot have the same velocity of the leading edge. The unit normal $\hat{\varvec{\nu }}_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )$ at ${\varvec{x}}_0({\varvec{\rho }})$, if existing, is given by

$$\begin{aligned} \hat{\varvec{\nu }}_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr ) = \pm \dfrac{\varvec{\nu }_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )}{\Vert \varvec{\nu }_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )\Vert } = \pm \dfrac{\varvec{\nu }_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )}{\sqrt{\left( \frac{\partial x_0({\varvec{\rho }})}{\partial \rho _2} \right) ^2 + \left( \frac{\partial y_0({\varvec{\rho }})}{\partial \rho _2}\right) ^2}}. \end{aligned}$$

(73)

Since $\bar{\varvec{v}}_{\varvec{t}}({\varvec{x}},s)$ is Lipschitz and thus bounded in ${\mathscr{P}}$, combining Eqs. (71) and (73) yields

$$\det \mathbf {J}_0({\varvec{\rho }}) =\pm \Bigl [ \bar{\varvec{v}}_{\varvec{t}}\bigl ({\varvec{x}}_0({\varvec{\rho }}),\rho _1\bigr )-\bar{\varvec{v}}_{ \mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )\Bigr ]\cdot \hat{\varvec{\nu }}_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr ) \Vert \varvec{\nu }_{\mathscr {L}}\bigl ({\varvec{x}}_0({\varvec{\rho }})\bigr )\Vert \not = 0, \infty ,\quad \mathrel {\forall } {\varvec{\rho }} \mathrel {|} {\varvec{x}}_0({\varvec{\rho }}) \in {\mathscr {L}}, $$

(74)

provided that the velocity of the boundary is also bounded. The above relationship implies that the BC is never characteristic. Actually, it may be deduced that the determinant of the Jacobian matrix only vanishes if ${\varvec{x}}_0({\varvec{\rho }}) \in \mathscr {N}$.

On the other hand, imposing the IC (11), which corresponds to $s_0({\varvec{\rho }}) = 0$, $x_0({\varvec{\rho }})= \rho _1$, $y_0({\varvec{\rho }}) = \rho _2$, yields

$$\det {\mathbf{J}}_{0} (\rho ) = \left| {\begin{array}{*{20}l} 1 & 0 & {\bar{v}_{x} (y_{0} (\rho _{2} ))} \\ 0 & 1 & {\bar{v}_{y} (x_{0} (\rho _{1} ))} \\ 0 & 0 & 1 \\ \end{array} } \right| = 1 \ne 0,\infty .$$

(75)

1.2 B.2: Lemmata for pure lateral slip

The results advocated in the following are based on Assumption 4.2 and $u_{x0}(\varvec{\xi }) = 0$.

Lemma B.1

Consider pure lateral slip conditions, i.e. $\sigma _x = 0$, $\sigma _y \not = 0$, $\varphi = 0$. Then, if $q_z(\varvec{\xi })$ satisfies Assumption 4.2 and $|q_{y0}(\varvec{\xi })| = k|u_{y0}(\varvec{\xi })| \le \mu q_z(\varvec{\xi })$ for all $\varvec{\xi } \in {\mathscr{P}}$, the following implications hold for all $(\varvec{\xi },s) \in {\mathscr{P}} \times {\mathbb {R}}_{>0}$ such that $\xi \in (0,\xi _{\mathscr {T}}(\eta )]$:

$$\begin{aligned}&\sigma _y \ge 0&\implies&q_y^{\rm (a)}(\varvec{\xi },s) < \mu q_z(\varvec{\xi }),&k|\sigma _y| \le \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }, \end{aligned}$$

(76a)

$$\begin{aligned}&\sigma _y \ge 0&\implies&q_y^{\rm (a)}(\varvec{\xi },s) >- \mu q_z(\varvec{\xi }),&k|\sigma _y| \ge -\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }, \end{aligned}$$

(76b)

$$\begin{aligned}&\sigma _y < 0&\implies&q_y^{\rm (a)}(\varvec{\xi },s) >- \mu q_z(\varvec{\xi }),&k|\sigma _y| \le \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi },\end{aligned}$$

(76c)

$$\begin{aligned}&\sigma _y< 0&\implies&q_y^{\rm (a)} (\varvec{\xi },s)< \mu q_z(\varvec{\xi }),&k|\sigma _y| \ge - \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }. \end{aligned}$$

(76d)

Proof

The proofs for $\sigma _y \ge 0$ and $\sigma _y < 0$ are mirrored, and thus only the analysis for $\sigma _y \ge 0$ is conducted.

• 1. Consider the case $\sigma _y \ge 0 , k|\sigma _y| \le \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$. For $\xi \in (0, s)$, Eq. (46) gives

  $$\begin{aligned} q_y^{\rm (a)}(\varvec{\xi },s)= q_y^{-}(\varvec{\xi })= k|\sigma _y|\xi \le \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }\xi < \mu q_z(\varvec{\xi }), \end{aligned}$$

  (77)

  where the last inequality follows from Assumption 4.2. For $\xi \in [s,\xi _{\mathscr {T}}(\eta )]$, again from Eq. (46):

  $$\begin{aligned} q_y^{\rm (a)}(\varvec{\xi },s) = q_y^{+}(\varvec{\xi },s) = k|\sigma _y|s + ku_{y0}(\xi -s,\eta ) \le \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }s + \mu q_z(\xi -s, \eta ) < \mu q_z(\varvec{\xi }), \end{aligned}$$

  (78)

  the last inequality following from Assumption 4.2. Combining (77) and (78), (76a) is deduced.

• 2. Consider the case $\sigma _y \ge 0 , k|\sigma _y| \ge -\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$. For $\xi \in (0, s)$, Eq. (46) gives

  $$\begin{aligned} q_y^{\rm (a)}(\varvec{\xi },s)= q_y^{-}(\varvec{\xi }) = k|\sigma _y|\xi \ge -\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }\xi >- \mu q_z(\varvec{\xi }). \end{aligned}$$

  (79)

  For $\xi \in [s, \xi _{\mathscr {T}}(\eta )]$, again from Eq. (46):

  $$\begin{aligned} q_y^{\rm (a)}(\varvec{\xi },s)= q_y^{+}(\varvec{\xi },s) = k|\sigma _y|s + ku_{y0}(\xi -s,\eta ) \ge -\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }s - \mu q_z(\xi -s, \eta ) >- \mu q_z(\varvec{\xi }), \end{aligned}$$

  (80)

  the last inequality following from Assumption 4.2. Combining (79) and (80), (76b) is deduced.

Lemma B.2

Consider pure lateral slip conditions, i.e. $\sigma _x = 0$, $\sigma _y \not = 0$, $\varphi = 0$, and a vertical pressure distribution $q_z(\varvec{\xi })$ satisfying Assumption 4.2. Then, the following implications hold for all $(\varvec{\xi },s) \in {\mathscr{P}}\times {\mathbb {R}}_{>0}$ such that $(\xi + \delta s, \delta s) \in (0, \xi _{\mathscr {T}}(\eta )] \times {\mathbb {R}}_{>0}$:

$$\begin{array}{*{20}l}\sigma _y \ge 0 , \, q_y^{\rm (a)}(\varvec{\xi },s) \ge \mu q_z(\varvec{\xi })&\implies&q_y^{\rm (a)}(\xi +\delta s, \eta , s+\delta s) > \mu q_z(\xi +\delta s, \eta ), \\\end{array}$$

(81a)

$$\begin{array}{*{20}l}\sigma _y \ge 0 , \, q_y^{\rm (a)}(\varvec{\xi },s) \le -\mu q_z(\varvec{\xi })&\implies&q_y^{\rm (a)}(\xi +\delta s, \eta , s+\delta s) < -\mu q_z(\xi +\delta s, \eta ), \\ \end{array}$$

(81b)

$$\begin{array}{*{20}l}\sigma _y < 0, \, q_y^{\rm (a)}(\varvec{\xi },s) \ge \mu q_z(\varvec{\xi })&\implies&q_y^{\rm (a)}(\xi +\delta s, \eta , s+\delta s) > \mu q_z(\xi +\delta s, \eta ), \\ \end{array}$$

(81c)

$$\begin{array}{*{20}l}\sigma _y< 0, \, q_y^{\rm (a)}(\varvec{\xi },s) \le -\mu q_z(\varvec{\xi })&\implies&q_y^{\rm (a)}(\xi +\delta s, \eta , s+\delta s)< - \mu q_z(\xi +\delta s, \eta ) . \\ \end{array}$$

(81d)

Proof

Again, the Lemma is only proved for ${\sigma}_{y} < 0$; the cases for $\sigma _y$ are specular.

• 1. Consider the case $\sigma _y \ge 0, q_y^{\rm (a)}(\varvec{\xi },s) \ge \mu q_z(\varvec{\xi })$. First it is observed that, owing to (76a), it must necessarily be $k|\sigma _y| >\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$ to have $q_y^{\rm (a)}(\varvec{\xi },s) \ge \mu q_z(\varvec{\xi })$. Thus, recalling Assumption 4.2 and Eq. (46), it holds that

  $$\begin{aligned} q_y^{\rm (a)}(\xi +\delta s, \eta , s+\delta s) = k|\sigma _y|\delta s + q_y^{\rm (a)}(\varvec{\xi },s)> \mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }\delta s + \mu q_z(\varvec{\xi }) > \mu q_z(\xi +\delta s, \eta ). \end{aligned}$$

  (82)

• 2. Consider the case $\sigma _y \ge 0, q_y^{\rm (a)}(\varvec{\xi },s) \le -\mu q_z(\varvec{\xi })$. First it is observed that, owing to (76b), it must necessarily be $k|\sigma _y| <-\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }$ to have $q_y^{\rm (a)}(\varvec{\xi },s) \le - \mu q_z(\varvec{\xi })$. Thus, recalling Assumption 4.2 and Eq. (46), it holds that

  $$\begin{aligned} q_y^{\rm (a)}(\xi +\delta s, \eta , s+\delta s) = k|\sigma _y|\delta s + q_y^{\rm (a)}(\varvec{\xi },s)< -\mu \frac{\partial q_z(\varvec{\xi })}{\partial \xi }\delta s - \mu q_z(\varvec{\xi }) <- \mu q_z(\xi +\delta s, \eta ). \end{aligned}$$

  (83)

Remark B.1

If Assumption 4.2 is only satisfied with $q_z^{(\eta )}(\cdot )$ concave but not strictly concave, the right-hand sides of implications (76a–76d) hold non-strictly for all $(\varvec{\xi },s) \in {\mathscr{P}}\times {\mathbb {R}}_{>0}$. Also, the right-hand sides of implications (81a–81d) hold non-strictly.

Remark B.2

If Assumption 4.2 is only satisfied with $q_z^{(\eta )} \in C^1(\mathring{{\mathscr{P}}}^{(\eta )};{\mathbb {R}})$ for some or every fixed $\eta$, then, for those fixed $\eta$, the results advocated in Lemma B.1 are only valid for $(\xi ,s) \in \mathring{{\mathscr{P}}}^{(\eta )}\times {\mathbb {R}}_{>0}$. The same holds if $q_z^{(\eta )}(\cdot )$ in Assumption 4.2 is concave but not strictly concave.

1.3 B.3: Lemmata for pure spin conditions

The results advocated in the following assume a parabolic pressure distribution as in Eq. (49) and $u_{x0}(\xi ) = 0$.

Lemma B.3

Consider non-supercritical pure spin slip conditions, i.e. ${\varvec{\sigma}}=\mathbf{0}$, $|\varphi |\le \varphi ^{\rm cr}$. Then, if $|q_{y0}(\xi )| = k|u_{y0}(\xi )| \le \mu q_z(\xi )$ for all $\xi \in [0,2a]$, it holds that $|q_y^{\rm (a)}(\xi ,s)| \le \mu q_z(\xi )$ for all $(\xi , s)\in (0,a] \times {\mathbb {R}}_{>0}$. Additionally, if $|\varphi | < \varphi ^{\rm cr}$, then $|q_y^{\rm (a)}(\xi ,s)| < \mu q_z(\xi )$ for all $(\xi , s)\in (0,a] \times {\mathbb {R}}_{>0}$.

Proof

The case for $\xi \in [0,s)$ is trivial and follows directly by the assumption $|\varphi | \le \varphi ^{\rm cr}$. Instead, when $\xi \in [s, a]$, from Eq. (53):

$$\begin{aligned} {\begin{matrix} |q_{y}^{\rm (a)}(\xi ,s)| & = k|\dfrac{1}{2}\varphi s (2a-2\xi +s) + u_{y0}(\xi -s)| \le \dfrac{1}{2}k|\varphi |s (2a-2\xi +s) + k|u_{y0}(\xi -s)|\\ & =\dfrac{1}{2}k|\varphi |s (2a-2\xi +s)+ |q_{y0}(\xi -s)| \le \mu \frac{q_z^{*}}{a^2} s(2a-2\xi +s) +\mu q_z(\xi -s) = \mu q_z(\xi ). \end{matrix}} \end{aligned}$$

(84)

The case for $|\varphi | < \varphi ^{\rm cr}$ may be proved similarly.

Lemma B.4

Consider pure critical spin slip conditions, i.e. ${\varvec{\sigma}} = \mathbf{0}$, $|\varphi | = \varphi ^{\rm cr}$. Then, if $|q_{y0}(\xi )| = k|u_{y0}(\xi )| \le \mu q_z(\xi )$ for all $\xi \in [0,2a]$, the following implications hold for all $(\xi ,s) \in [s, 2a] \times {\mathbb {R}}_{>0}$:

$$ {\varphi}={ \varphi}^{\rm cr}{\implies}q_{y}^{\rm (a)}(\xi ,s) \le \mu q_{z}(\xi ),$$

(85a)

$$ {\varphi}=- {\varphi} ^{\rm cr}{\implies}q_{y}^{\rm (a)}(\xi ,s) \ge - \mu q_{z}(\xi ). $$

(85b)

Proof

The proof is omitted for brevity.

Lemma B.5

Consider non-supercritical pure spin slip conditions, i.e. ${\varvec{\sigma}} = \mathbf{0}$, $|\varphi | \le \varphi ^{\rm cr}$. Then, if $|q_{y}^{\rm (a)}(\xi ,s)| \ge \mu q_z(\xi )$ for some $\xi \in [a,2a]$, it holds that $|q_y^{\rm (a)}(\xi +\delta s,s+\delta s)| \ge \mu q_z(\xi +\delta s)$ for all $(\xi ,s) \in (a,2a] \times {\mathbb {R}}_{>0}$ such that $(\xi + \delta s, \delta s) \in (a, 2a]\times {\mathbb {R}}_{>0}$. Additionally, if $|\varphi | < \varphi ^{\rm cr}$, then $|q_y^{\rm (a)}(\xi +\delta s,s+\delta s)| > \mu q_z(\xi +\delta s)$ for all $(\xi ,s) \in (a,2a] \times {\mathbb {R}}_{>0}$ such that $(\xi + \delta s, \delta s) \in (a, 2a)\times {\mathbb {R}}_{>0}$.

Proof

The proof may be worked out similarly as in Lemma B.2 and is omitted for brevity.

1.4 B.4: Lemmata for combined lateral slip and subcritical spin

The results advocated in the following assume a parabolic pressure distribution as in Eq. (49) and $u_{x0}(\xi ) = 0$.

Lemma B.6

Consider combined lateral and spin slips conditions with subcritical spin, i.e. $\sigma _x = 0$, $\sigma _y \not = 0$, $|\varphi | < \varphi ^{\rm cr}$. Then, if $|q_{y0}(\xi )| = k|u_{y0}(\xi )| \le \mu q_z(\xi )$ for all $\xi \in [0,2a]$, the following implications hold for every $(\xi , s) \in (0,2a]\times {\mathbb {R}}_{>0}$:

$$\begin{array}{*{20}l}\sigma _y > 0&\implies&q_y^{\rm (a)}(\xi ,s) < \mu q_z(\xi ),&|\sigma _y|\le \Bigl (\varphi ^{\rm cr}-|\varphi |{{\,{\mathrm{sgn}}\,}}\bigl (\sigma _y\varphi \bigr ) \Bigr )(a-\xi ), \end{array}$$

(86a)

$$\begin{array}{*{20}l}\sigma _y> 0&\implies&q_y^{\rm (a)}(\xi ,s) >- \mu q_z(\xi ),&|\sigma _y|\ge \Bigl (\varphi ^{\rm cr}+|\varphi |{{\,{\mathrm{sgn}}\,}}\bigl (\sigma _y \varphi \bigr ) \Bigr )(\xi -a), \end{array}$$

(86b)

$$\begin{array}{*{20}l}\sigma _y < 0&\implies&q_y^{\rm (a)}(\xi ,s) >- \mu q_z(\xi ),&|\sigma _y|\le \Bigl (\varphi ^{\rm cr}-|\varphi |{{\,{\mathrm{sgn}}\,}}\bigl (\sigma _y\varphi \bigr ) \Bigr )(a-\xi ), \\ \end{array}$$

(86c)

$$\begin{array}{*{20}l}\sigma _y< 0&\implies&q_y^{\rm (a)}(\xi ,s) < \mu q_z(\xi ),&|\sigma _y|\ge \Bigl (\varphi ^{\rm cr}+|\varphi |{{\,{\mathrm{sgn}}\,}}\bigl (\sigma _y \varphi \bigr ) \Bigr )(\xi -a). \end{array}$$

(86d)

Proof

The proof may be worked out similarly as in Lemma B.1 and is omitted for brevity.

Lemma B.7

Consider combined lateral and spin slips conditions with subcritical spin, i.e. $\sigma _x = 0$, $\sigma _y \not = 0$, $|\varphi | < \varphi ^{\rm cr}$. Then, for every $(\xi ,s) \in (0,2a] \times {\mathbb {R}}_{>0}$ such that $(\xi + \delta s, \delta s) \in (0,2a] \times {\mathbb {R}}_{>0}$, the following implications hold:

$$\begin{array}{*{20}l}\sigma _y> 0 , \, q_y^{\rm (a)}(\xi ,s) \ge \mu q_z(\xi )&\implies&q_y^{\rm (a)}(\xi +\delta s, s+\delta s) > \mu q_z(\xi +\delta s), \\ \end{array}$$

(87a)

$$\begin{array}{*{20}l}\sigma _y > 0 , \, q_y^{\rm (a)}(\xi ,s) \le -\mu q_z(\xi )&\implies&q_y^{\rm (a)}(\xi +\delta s, s+\delta s) < -\mu q_z(\xi +\delta s), \\ \end{array}$$

(87b)

$$\begin{array}{*{20}l}\sigma _y < 0, \, q_y^{\rm (a)}(\xi ,s) \ge \mu q_z(\xi )&\implies&q_y^{\rm (a)}(\xi +\delta s, s+\delta s) > \mu q_z(\xi +\delta s), \\ \end{array}$$

(87c)

$$\begin{array}{*{20}l}\sigma _y< 0, \, q_y^{\rm (a)}(\xi ,s) \le -\mu q_z(\xi )&\implies&q_y^{\rm (a)}(\xi +\delta s, s+\delta s)< - \mu q_z(\xi +\delta s) . \\ \end{array}$$

(87d)

Proof

The proof may be worked out similarly as in Lemma B.2 and is omitted for brevity.