Frictional moving contact problem between a conducting rigid cylindrical punch and a functionally graded piezoelectric layered half plane

Abstract

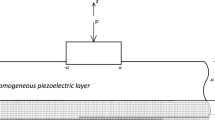
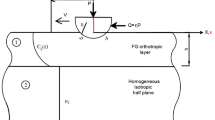
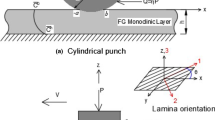
In this study, a frictional moving contact problem between an electrically conducting rigid cylindrical punch and a functionally graded piezoelectric material (FGPM) layer bonded to a piezoelectric homogeneous half plane is considered. The punch moves on the layer in the lateral direction at a subsonic constant velocity V and transmits the normal and the tangential loads. The mechanical and the electrical material properties of the layer are assumed to vary exponentially along the thickness direction. Using Fourier integral transform technique and Galilean transformation, the mixed boundary value problem is reduced to the singular integral equations in which the unknowns are the contact stress, the contact width, and the electric charge distribution. The singular integral equations are solved numerically applying the appropriate Gauss-Jacobi integration formulas. Numerical results for the contact width, the contact stress and the electric charge distribution are given as a solution. This work is the first study that investigates the moving contact problem of a graded piezoelectric materials.

Appendices

Appendix 1

Expressions of $L_{1j}$ and $L_{2j}$ $(j = 1,2,...6)$ appearing in (10) and (16) are given as follows.

$$L_{11} = 3\gamma /\xi$$

(42)

$$\begin{aligned} L_{12} & = (e_{330} ((2c_{440} e_{310} + 2c_{130} (e_{150} + e_{310} ) - c_{110} e_{330} + e_{330} V^{2} \rho_{0} )\xi^{2} + 3c_{440} e_{330} \gamma^{2} ) \\ & \quad - c_{330} \xi^{2} ((e_{150} + e_{310} )^{2} + c_{440} \in_{110} ) + (c_{130}^{2} + 2c_{130} c_{440} + c_{440} V^{2} \rho_{0} )\xi^{2} \in_{330} \\ & \quad + c_{330} \xi^{2} ( - c_{110} \xi^{2} + V^{2} \rho_{0} \xi^{2} + 3c_{440} \gamma^{2} ) \in_{330} )/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} )) \\ \end{aligned}$$

(43)

$$\begin{aligned} L_{13} & = (e_{330} (2(2c_{440} e_{310} + 2c_{130} (e_{150} + e_{310} ) - c_{110} e_{330} + e_{330} V^{2} \rho_{0} )\xi^{2} + 3c_{440} e_{330} \gamma^{2} ) \\ & \quad - 2c_{330} \xi^{2} ((e_{150} + e_{310} )^{2} + c_{440} \in_{110} ) + 2(c_{130}^{2} + 2c_{130} c_{440} + c_{440} V^{2} \rho_{0} )\xi^{2} \in_{330} \\ & \quad + c_{330} \xi^{2} ( - 2c_{110} \xi^{2} + 2V^{2} \rho_{0} \xi^{2} + c_{440} \gamma^{2} ) \in_{330} )/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} )) \\ \end{aligned}$$

(44)

$$\begin{aligned} L_{14} & = - (\xi^{2} (c_{130}^{2} {\kern 1pt} \in_{110} {\kern 1pt} - c_{110} (2e_{150} e_{330} + c_{330} \in_{110} ) + 2c_{130} (e_{150} (e_{150} + e_{310} ) + c_{440} \in_{110} ) - c_{440} (c_{310}^{2} {\kern 1pt} + c_{110} \in_{330} )) \\ & \quad + V^{2} \rho_{0} \xi^{2} ((e_{150} + e_{310} )^{2} + 2e_{150} e_{330} + (c_{330} + c_{440} ) \in_{110} + {\kern 1pt} \,(c_{110} + c_{440} - V^{2} \rho_{0} ) \in_{330} ) \\ & \quad + \gamma^{2} ( - e_{330} (3c_{130} e_{150} + 2c_{130} e_{310} + 3c_{440} e_{310} - c_{110} e_{330} + e_{330} V^{2} \rho_{0} ) - (c_{130}^{2} + 3c_{130} c_{440} + c_{440} V^{2} \rho_{0} ) \in_{330} \\ & \quad + c_{330} (e_{150}^{2} + 3e_{150} e_{310} + e_{310}^{2} + c_{440} \in_{110} + c_{110} \in_{330} - V^{2} \rho_{0} \in_{330} ))/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} )) \\ \end{aligned}$$

(45)

$$\begin{aligned} L_{15} & = - \gamma (\xi^{2} (c_{130}^{2} {\kern 1pt} \in_{110} {\kern 1pt} - c_{110} (2e_{150} e_{330} + c_{330} \in_{110} ) + 2c_{130} (e_{150} (e_{150} + e_{310} ) + c_{440} \in_{110} ) \\ & \quad - c_{440} (e_{310}^{2} + c_{110} \in_{330} )) + V^{2} \rho_{0} \xi^{2} (e_{150}^{2} + e_{310}^{2} + 2e_{150} (e_{310} + e_{330} ) + (c_{330} + c_{440} ) \in_{110} \\ & \quad + (c_{110} + c_{440} - V^{2} \rho_{0} ){\kern 1pt} \in_{330} ) + \gamma^{2} (c_{330} e_{310} e_{150} - c_{440} e_{310} e_{330} - c_{130} (e_{150} e_{330} + c_{440} \in_{330} )))/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} )) \\ \end{aligned}$$

(46)

$$L_{16} = - c_{110} \xi^{2} (e_{150}^{2} {\kern 1pt} + c_{440} \in_{110} ) + V^{2} \rho_{0} \xi^{2} (e_{150}^{2} {\kern 1pt} + (c_{110} + c_{440} - V^{2} \rho_{0} ) \in_{110} ) - \gamma^{2} (e_{150} e_{310} V^{2} \rho_{0} + c_{130} (e_{150}^{2} {\kern 1pt} + c_{440} \in_{110} )))/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} ))$$

(47)

$$\begin{aligned} L_{22} & = (e_{330} ((2c_{440} e_{310} + 2c_{130} (e_{150} + e_{310} ) - c_{110} e_{330} + e_{330} V^{2} \rho_{0} )\xi^{2} ) \\ & \quad - c_{330} \xi^{2} ((e_{150} + e_{310} )^{2} + c_{440} \in_{110} ) + (c_{130}^{2} + 2c_{130} c_{440} + c_{440} V^{2} \rho_{0} )\xi^{2} \in_{330} \\ & \quad + c_{330} \xi^{2} ( - c_{110} \xi^{2} + V^{2} \rho_{0} \xi^{2} ) \in_{330} )/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} )) \\ \end{aligned}$$

(48)

$$\begin{aligned} L_{24} & = - (\xi^{2} (c_{130}^{2} {\kern 1pt} \in_{110} {\kern 1pt} - c_{110} (2e_{150} e_{330} + c_{330} \in_{110} ) + 2c_{130} (e_{150} (e_{150} + e_{310} ) + c_{440} \in_{110} ) - c_{440} (c_{310}^{2} {\kern 1pt} + c_{110} \in_{330} )) \\ & \quad + V^{2} \rho_{0} \xi^{2} ((e_{150} + e_{310} )^{2} + 2e_{150} e_{330} + (c_{330} + c_{440} ) \in_{110} + {\kern 1pt} \,(c_{110} + c_{440} - V^{2} \rho_{0} ) \in_{330} ) \\ & \quad + c_{330} (e_{150}^{2} + 3e_{150} e_{310} + e_{310}^{2} + c_{440} \in_{110} + c_{110} \in_{330} - V^{2} \rho_{0} \in_{330} ))/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} )) \\ \end{aligned}$$

(49)

$$L_{26} = - c_{110} \xi^{2} (e_{150}^{2} {\kern 1pt} + c_{440} \in_{110} ) + V^{2} \rho_{0} \xi^{2} (e_{150}^{2} {\kern 1pt} + (c_{110} + c_{440} - V^{2} \rho_{0} ) \in_{110} ))/(c_{440} \xi^{2} (e_{330}^{2} + c_{330} \in_{330} ))$$

(50)

Appendix 2

Expressions of $k_{ij} (x,\omega )$ and $\beta_{ij}$ appearing in (15) are given as follows.

$$k_{11} (x,\omega ) = \int\limits_{0}^{\infty } {(\;M_{11} } (\xi ) - \beta_{11} )\sin \xi (\omega - x)d\xi$$

(51)

$$k_{12} (x,\omega ) = \int\limits_{0}^{\infty } {(\;M_{12} } (\xi ) - \beta_{12} )\cos \xi (\omega - x)d\xi$$

(52)

$$k_{13} (x,\omega ) = \int\limits_{0}^{\infty } {(\;M_{13} } (\xi ) - \beta_{13} )\sin \xi (\omega - x)d\xi$$

(53)

$$k_{21} (x,\omega ) = \int\limits_{0}^{\infty } {(\;M_{21} } (\xi ) - \beta_{21} )\sin \xi (\omega - x)d\xi$$

(54)

$$k_{22} (x,\omega ) = \int\limits_{0}^{\infty } {(\;M_{22} } (\xi ) - \beta_{22} )\cos \xi (\omega - x)d\xi$$

(53)

$$k_{23} (x,\omega ) = \int\limits_{0}^{\infty } {(\;M_{23} } (\xi ) - \beta_{23} )\sin \xi (\omega - x)d\xi$$

(54)

where

$$M_{11} (\xi ) = \xi \sum\limits_{j = 1}^{6} {A_{j}^{p} } k_{j} ,\quad M_{12} (\xi ) = \xi \sum\limits_{j = 1}^{6} {A_{j}^{\eta } } k_{j} ,\quad M_{13} (\xi ) = \xi \sum\limits_{j = 1}^{6} {A_{j}^{q} } k_{j}$$

(55)

$$M_{21} (\xi ) = \xi \sum\limits_{j = 1}^{6} {A_{j}^{p} } \lambda_{j} ,\quad M_{22} (\xi ) = \xi \sum\limits_{j = 1}^{6} {A_{j}^{\eta } } \lambda_{j} ,\quad M_{23} (\xi ) = \xi \sum\limits_{j = 1}^{6} {A_{j}^{q} } \lambda_{j}$$

(56)

$$\beta_{11} = \mathop {\lim }\limits_{\xi \to \infty } \;M_{11} (\xi ),\quad \beta_{12} = \mathop {\lim }\limits_{\xi \to \infty } \;M_{12} (\xi ),\quad \beta_{13} = \mathop {\lim }\limits_{\xi \to \infty } \;M_{13} (\xi )$$

(57)

$$\beta_{21} = \mathop {\lim }\limits_{\xi \to \infty } \;M_{21} (\xi ),\quad \beta_{22} = \mathop {\lim }\limits_{\xi \to \infty } \;M_{22} (\xi ),\quad \beta_{23} = \mathop {\lim }\limits_{\xi \to \infty } \;M_{23} (\xi )$$

(58)