1 Introduction

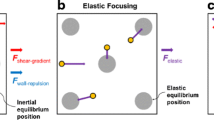
We study particle focusing in strongly inertial and weakly elastic flows, whose importance is defined by two critical dimensionless numbers: the Reynolds and Weissenberg numbers. The Reynolds number, quantifying the importance of inertia over viscous effects, is defined as \(Re = \rho UcH/\mu\), where \(\rho\) is the fluid density, \(Uc\) is the centreline flow velocity, H is the characteristic length across the microfluidic channel cross-section, and μ is the shear viscosity of the fluid. The Weissenberg number is defined as \(Wi = \lambda Uc/H\), where λ is the relaxation time of the polymer additives. The ratio between these two parameters gives the elasticity number \(El = Wi/Re\). In Newtonian fluids, it has been well recognized that in the laminar flows typical of microfluidic channels (\(Re>1\) and \(Re<2300\)) [1], inertia does play a role and particles tend to migrate to equilibrium positions at distances of order \(0.6\) of the channel hydraulic diameter, \(R\), from the center, closer to channel centerlines, as initially predicted by Segré and Silberberg [2]. Numerous studies exploited this effect in microfluidic applications, frequently referred to as “inertial focusing” of particles [3,4,5,6,7]. The equilibrium position in inertial microfluidic flows result from the balance of two opposing forces: (1) the wall-induced lift force arising out of the interaction between the particle and the adjacent wall, which directs the particle away from the wall and (2) the shear-gradient force, induced by the velocity profile curvature, pushing the particle away from the flow channel centreline and towards the wall [1, 8, 9].

Particle migration and focusing have also been extensively investigated for viscoelastic fluids in microfluidic channels [10,11,12,13]. It has been observed that in purely viscoelastic flows, the particles tend to flow through a narrower focused beam close to the centreline of the channel [14,15,16,17]. The phenomenon of single line focusing of particles has been observed in a wide range of microfluidic channel geometries that include circular, [18,19,20] and square channels [15, 16, 21] typically at low Reynolds numbers (\(Re<1\)) elastic flows. The added effect of inertia coupled with the viscoelastic effect leads to particle migration to the channel centreline and has been utilized in numerous applications for selective separation of particles based on physical parameters such as size and shape. As an example, under constant viscoelasticity but comparatively higher inertia for a bigger sized particle, the larger particle moves first towards the channel centreline and can thus be separated from smaller sized particles in sample. Various applications have been developed on the phenomenon of viscoelastic focusing such as microflow cytometry, [22, 23] cell and particle focusing, [24] as well as droplet [25] and bubble [5] manipulation. A recent review by Stoecklein and Di Carlo [26] covers the underlying physics as well as an exhaustive set of applications related to elasto-inertial microfluidics.

A clear observation from all the studies involving the combined effect of inertia and elasticity, clearly points towards a bistability scenario, i.e. the particles either focus at the Segre-Silberberg annulus when inertia dominates or at the channel centreline when elastic effects gain an upper hand [27]. In this study, we explored a weak elasto-inertial regime experimentally, by diluting PBS solution with PEO concentrations ranging from \(1 \mathrm{ppm}\) till \(50 \mathrm{ppm}\) (El = 0.001–0.5). We found that particle focusing in elasto-inertial microfluidics is tuneable at this regime, and the particle focusing bandwidth is not restricted to the bistability scenario, but rather can be engineered to any analogue value that lies between the centreline focusing and the Segre-Silberberg annulus positions. The phenomenon has been reported in the past in spiral microchannels, where the presence of Dean forces is exploited for particle manipulation [28]. However, the same particle focussing behaviour has not been observed in straight channels (e.g. rectangular and circular cross-section straight channels) in the weak elasto-inertial fluid regime (El ~ 0.1 or less). This regime of viscoelasticity is clearly not very well understood as previous reports on viscoelastic fluids have focussed on elasticity numbers 1 or higher [29, 30], which means the elasticity component was not negligible. Hence, particle tuneability in straight channels in the weak elasticity regime can lead to new insights on the focussing mechanisms for elasto-inertial microfluidics in a straight circular geometry.

We support our hypothesis with both experimental observations as well as numerical simulations. For the numerical simulations, an Immersed Boundary method is used to predict particle velocities and trajectories [31], whereas the elastic component of the stress, due to the presence of the polymers in the fluid, is modelled by the Finite Element Non-Linear Extensibility Peterlin model (FENE-P) [32]. One of the reasons for choosing the FENE-P model over the popular Oldroyd-B and Giesekus models [33,34,35], which also have been used for studying viscoelastic flows, is the robustness of the FENE-P model at finite inertia even for Weissenberg numbers greater than 1. The three-dimensional fully resolved direct numerical simulations provide access to viscous and elastic stresses in the flow, which enable us to explain the entire dynamics of particle migration, particle stability and equilibrium for low elasticity flows in a circular pipe, in the intermediate Reynolds number regime. We believe our current study addresses a crucial aspect in the understanding of weakly viscoelastic flows in elasto-inertial microfluidics, and more importantly demonstrates the possibility to tune the particle position in microchannels by to addition of minute amounts of elasticity.

2 Methods

2.1 Experimental setup

The experiments were carried out in a single-inlet and single outlet silicon capillary tube with a diameter of \(56 \,\upmu {\text{m}}\). A solution containing \(10\,\upmu {\text{m}}\) fluorescent particles is pumped through the silicon capillary tube by a syringe pump (Nemesys, Centoi Gmbh). The applied flow rates reach up to \(240 \,\upmu {\text{l}}/{\text{min}}\). Fluorescent polystyrene particles, 10 \(\,\upmu {\text{m}}\) diameter (Fluoro-Max, Thermo Scientific) at a volume fraction of 0.1% were suspended in Newtonian and viscoelastic fluids. The Newtonian fluid comprised of Phosphate Buffer Saline (PBS 1x) aqueous solution containing 0.1% Tween20. The viscoelastic fluid is prepared by mixing a range of different concentrations (from \(0.0001\) to \(0.05 \,{\text{wt}}\%\)) of Polyethylene Oxide (PEO) (with an average molecular weight equal to \(1 \times 10^{6} \,{\text{Da}}\)) in a Phosphate Buffered solution (PBS). A homogenization process for up to 2 h follows the preparation of the solution, after which the experiments were carried out immediately. All the experiments are done at room temperature, i.e., 25 degree centigrade.

In the present work, a systematic parametric study is performed by varying the Reynolds and Weissenberg numbers. To this end, we need to introduce several parameters, e.g., the zero shear viscosity (\(\eta_{0}\)), the infinite shear viscosity (\(\eta_{\infty }\)), the shear-rate (\(\dot{\gamma }\)) and the relaxation time (\(\lambda\)) of the resulting PEO solution, as well as the channel dimensions and volumetric flow rates. The Bird–Carreau model [36, 37] is used to calculate the effective viscosity \(\eta_{eff}\) of the PEO solution at different shear-rates \(\dot{\gamma }\), which is given by

$$\eta_{eff} = \eta_{\infty } + \left( {\eta_{0} - \eta_{\infty } } \right) \times \left[ {1 + \left( {\lambda \dot{\gamma }} \right)^{2} } \right]^{{\frac{{\left( {n - 1} \right)}}{2}}} .$$
(1)

In a previous study, Ebagninin et al. [38] reported that, in dilute regimes of PEO concentrations, the zero shear viscosity \(\eta_{0}\) varies as \(\eta_{0} \sim c^{2.17}\) for concentrations \(c\) less than \(0.1 \,{\text{wt}}\%\). Also, based on other results from the same study, it can be deduced that the zero to infinite viscosity ratio, \(\frac{{\eta_{0} }}{{\eta_{\infty } }}\), is approximately equal to \(2\) for PEO concentrations up to \(0.1\,{\text{ wt}}\%\) and \(\frac{{\eta_{0} }}{{\eta_{\infty } }} \approx 3.33\) for PEO concentrations between \(0.2\) and \(1\,{\text{ wt}}\%\). Finally, the flow index \(n\) in the Bird-Carreau model is found by comparing viscosities at two different shear-rates. The relaxation time \(\lambda\) was computed based on a recent study [39] on weakly viscoelastic flows, which gave an empirical law:

$$\lambda \left( {{\text{ms}}} \right) = 0.045\left[ {c\left( {{\text{ppm}}} \right)} \right]^{1.14} .$$
(2)

2.2 Imaging technique

For imaging the particle flow in the circular capillary, we used an inverted microscope (Nikon Eclipse TI, USA) with a CMOS camera (Andoe Zyla,USA) and a LED lighting system (Lumenor Spectra X LED,USA). To capture the images and control the microscope movements, the Micro-Manager Open Source Microscopy Software was used, while the image processing was performed with the MATLAB software (R2018a, Mathworks, USA). In particular, we measured from the images the particle focusing bandwidth \(F\) (see Fig. 1), which is the difference between the width of the streaks of particles captured in the images and their diameter, normalized by the entire cross section of the channel. For example, say a spherical particle of dimension 0.18 times the diameter of the circular cross section focusses at the equilibrium position in a channel inertial flow, i.e. at a focusing position that is 0.3 times the diameter. In this case the center of this particle will be at 0.2D, and if viewed from the top the particle streak will appear across 0.11D to 0.29D. As the equilibrium position of particle inertial focusing is symmetrical about the centre in a circular cross section, so there should be a particle streak with its center at 0.8D as well, that stretches from 0.71D till 0.89D. Thus, the value of \(F\) (center to center distance) in this case will be 0.8D-0.18D = 0.62D. F will be \(0\) when the particle is focused at the center and have a maximum value of \(0.82\) if the particle sticks by the wall.

Fig. 1
figure 1

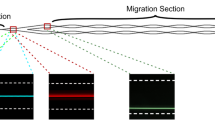
Fluid flow setup for the experimental and numerical simulations in a circular microcapillary (drawn to scale). The ratio of the particle to pipe diameters is approximately \(1:5\) for both the experimental and numerical cases. The cross-sectional view shows the existence of possible multiple particle equilibrium states in very dilute pressure driven flows in a circular microchannel. The top view defines F, the focusing bandwidth

Full size image

2.3 Numerical setup

We study the motion of rigid neutrally buoyant spherical particles in a straight pipe with a circular cross section. The fluid is incompressible and Non-Newtonian, and its motion is governed by the Navier–Stokes equations

$$\partial_{t} u_{i} + \partial_{j} u_{i} u_{j} = - \partial_{i} p + \frac{P}{Re}\partial_{j} \partial_{j} u_{i} + \frac{1 - P}{{Re}}\partial_{j} \tau_{ij} + f_{i}$$
(3)
$$\partial_{i} u_{i} = 0,$$
(4)

where \(u_{i}\) is the velocity vector field, \(p\) denotes the hydrodynamic pressure, \(\tau_{ij}\) the polymer stress tensor, \(f_{i}\) the immersed boundary force to account for the presence of the suspended particles, \(P\) is the ratio of the solvent viscosity to the total viscosity (function of the concentration of polymers), and \(Re\) is the Reynolds number as introduced above.

The additional stress tensor \(\tau_{ij}\) describes the Non-Newtonian behavior of the carrier fluid, modeled with the Finite Element Non Linear Extensibility Peterlin model (FENE-P) as commonly done in numerical simulations of polymeric fluids [40].. In the FENE-P model, \(\tau_{ij}\) is written as a function of the configuration tensor \(C_{ij}\) defined as

$$\tau_{ij} = \frac{1}{Wi}\left( {\frac{{C_{ij} }}{{1 - \frac{{C_{kk} }}{{L^{2} }}}} - \partial_{ij} } \right),$$
(5)

where \(L\) is the dumbbell extensibility, \(\partial_{ij}\) the Kroeneker delta and \(Wi\) the Weissenberg number. The configuration tensor is a symmetric second-order tensor, solution of the following dynamic equation for its 6 independent components

$$\partial_{t} C_{ij} + u_{k} \partial_{k} C_{ij} = C_{kj} \partial_{k} u_{i} + C_{ik} \partial_{k} u_{j} - \tau_{ij} .$$
(6)

The previous equation represents a balance between the advection of the configuration tensor on the left-hand side, and the stretching and relaxation of the polymer, represented by the first two terms and the last one on the right-hand side, respectively.

The motion of a neutrally buoyant rigid spherical particle is dictated by the Newton–Euler equations [31] given as:

$$m^{p} \frac{{dU_{c}^{p} }}{dt} = \oint\limits_{\partial Vp} {\left[ { - pI + \mu \left( {\nabla u + \nabla u^{T} } \right)} \right] \cdot n dS} ,$$
(7)
$$I^{p} \frac{{d\Omega_{c}^{p} }}{dt} = \oint\limits_{\partial Vp} {r \times \left\{ {\left[ { - pI + \mu \left( {\nabla u + \nabla u^{T} } \right)} \right] \cdot n} \right\}}$$
(8)

where \(m^{p}\) and \(I^{p}\) are the mass and moment of inertia of the particle, and \(U_{c}^{p}\) and \(\Omega_{c}^{p}\) its center velocity and rotation vectors. The integrals are performed over the surface of the particles \(\partial Vp\) with unit normal vector \(n\); \(r\) is the vector connecting the particle center to its surface. The no-slip and no-penetration boundary conditions on the suspended particle are enforced through the body force \(f_{i}\) found by a direct forcing Immersed Boundary Method [41, 42].

The boundary conditions on the curved pipe surface are enforced by a volume penalization method [43], while periodic boundary conditions are imposed in the streamwise direction. The numerical domain size is \(15D \times 5D \times 5D\), \(D being\) the particle diameter, and is discretized with \(480 \times 164 \times 164\) grid points in the streamwise and crossflow directions, respectively. The equations of motion are solved with a fractional-step method with the low-storage third-order Runge–Kutta scheme for time integration and the second-order finite difference scheme for the spatial derivatives. Note that, the fifth-order Weighted Essentially Non-Oscillatory scheme [44] is used for the advection terms in the evolution equation for the conformation tensor. This numerical method has been used in the past for several applications with appropriate modifications, which include simulating spherical and oblate particle trajectory in a Newtonian fluid in microchannels [31], as well as elastic particles [45, 46] and cell membranes in shear flows [47]. The interested reader is referred to the work by Izbassarov et al. [48] and Rosti and Brandt [49] for a detailed description of the numerical methods used to simulate multiphase flows in various Non-Newtonian fluids. Finally, we perform box-size and resolution studies to ensure that our results are not affected by any numerical artefact in a previous study [31].

3 Results and discussion

3.1 Experimental analysis

The particle behaviour in circular capillaries is studied by examining the amount of focusing obtained in a Newtonian and Non-Newtonian flow, covering a wide range of flow-rates and ppm concentrations. Past studies have reported in detail that due to symmetric cross sectional stresses in a circular geometry, the particles settle on a symmetric annular radius, both in Newtonian [2] and viscoelastic flows [23]. As it can be seen in Fig. 2, we measured the area occupied by the particles in the channel and found that it corresponds to \(78\%\) of the entire channel. The maximum particle streak centre to centre distance is denoted by \(F\) and is called the focussing bandwidth, as mentioned earlier. \(F\) is computed as the distance between the particle streaks, minus the particle diameter, normalised by the channel size. Since the ratio of the particle to channel dimension (\(10\,\upmu {\text{m}}\) and \(56 \,\upmu {\text{m}}\), respectively) is \(18\%\), this implies that the maximum particles centre to centre distance is \(F = 60\%\) (\(78 - 18\%\)) for the Newtonian case. \(F = 0.6D\) corresponds well to the theoretical predictions and to the previous experimental observations reported in the.

Fig. 2
figure 2

Different particle focusing equilibrium positions for concentrations of PEO solution ranging from 0 to \(500 {\text{ppm}}\) and for flow rates in the range from 5 till \(180 \,\upmu {\text{l}}/{\text{min}}\). a Top view of capillary for Newtonian case, the particles reach equilibrium position at \(0.6R\) from the center at \(F = 0.6D\). Scalebar:50 \(\upmu {\text{m}}\) b \(F = 0.5D\), Non-Newtonian fluid at \(10 \,{\text{ppm}}\): the behavior is similar to the one reported for a Newtonian fluid, except that the particles never reach a \(0.6R\) distance but focus on a narrower bandwidth (\(F = 0.5D\) vs. \(0.6D\) at \(180 \,\upmu {\text{l}}/{\text{min}}\)). c \(F = 0.4D\), Non-Newtonian fluid at \(50 \,{\text{ppm}}\): the particles move even closer to the center than for \(5\,{\text{ ppm}}\) (\(F = 0.4D\) vs \(0.6D\) at \(180 \,\upmu {\text{l}}/{\text{min}}\)). d \(F = 0\) case for Non-Newtonian fluid at \(500 \,{\text{ppm}}\), where particles achieve centerline focusing at low Reynolds number (\(Re < 1\), \(Wi = 0.1\) at \(20 \,\upmu {\text{l}}/{\text{min}}\))). e Cross sectional view of the four cases a–d

Full size image

literature for the equilibrium position of a particle in a Newtonian inertial flow [2].\(F = 0.6D\) translates to an equilibrium position at \(0.6R\) with \(R = \frac{D}{2}\) being the radius of the channel. Further, we observe that the focussing bandwidth of a particle shrinks (shrinking focusing bandwidth) towards the center due to the combined effect of Reynolds and Weissenberg number. In the Non-Newtonian case with very low PEO concentration.

(\(5 \,{\text{ppm}}\)) reported in Fig. 2b, we observe that the particle focussing bandwidth is \(0.5F\) instead of \(0.6F\) for the same flow rate of \(180 \,\upmu {\text{l}}/{\text{min}}\). Thus, the elastic effects of Non-Newtonian fluids are visible even with a slight increase in the elasticity of the fluid at high Reynolds number. This is because with an increasing Reynolds number, the Weissenberg number also becomes significantly prominent due to an increasing shear rate. A similar trend is observed for even larger elasticity concentrations, where at \(50 \,{\text{ppm}}\) a more compressed particle focusing bandwidth (Fig. 2c) is found at \(0.4D\) for the same flow rate as the Newtonian case (\(180\,\upmu {\text{l}}/{\text{min}},{ }50\,{\text{ppm}}\)). Finally, Fig. 2d shows a centreline focussing scenario where the Reynolds number and Weissenberg number are comparable, but both are very low (\(< 1\)), which results in the dominance of elastic effects. Similar results on centreline particle focussing have also been reported in previous studies related to elasto-inertial fluids [10, 50].

We tested the particle behaviour for various concentrations of PEO in PBS and for different flow rates in order to study the dual effects of the Reynolds and Weissenberg numbers on the particle focusing. It has previously been reported that in Newtonian fluids for circular cross sections, the particles achieve a focused state at a Reynolds number of 25 onwards [51]. We varied the concentration of PEO from 1 to \(50\,{\text{ ppm}}\) and the flow rate from 5 to \(240 \,\upmu {\text{l}}/{\text{min}}\) (Re = 1–100). In Fig. 3 we report the focusing bandwidth \(F\) as a function of the Weissenberg number, at four different Reynolds numbers (\(Re = 25\), \(50\), \(75\) and \(93\)).

Fig. 3
figure 3

Effect of the Reynolds and Weissenberg numbers on the particle focusing. Particle focusing as a function of \(Wi\) at four different\(Re\). In all cases, the particle moves closer to the center as \(Wi\) increases

Full size image

We observe that the focusing bandwidth reduces as the Weissenberg number increases, i.e. particles tend to approach the microcapillary center, for all the Reynolds numbers. On the other hand, at a fixed Weissenberg number, the particles move away from the center with increasing Reynolds number for all the cases considered. While imaging the cross sectional distribution of the particle is out of the scope of this work, a previous report has demonstrated the distribution of particles to be symmetric about the channel cross-section for all Reynolds number [51] in viscoelastic fluids.

3.2 Numerical simulations

In order to gain more physical insight on our experimental observations, we performed three-dimensional direct numerical simulations of a rigid spherical particle in a polymeric flow modelled by the FENE-P model. This model allows to reach higher \(Wi\) in dilute polymer flows than other viscoelastic models such as the Oldroyd-B [52] and better prediction of shear viscosity at high shear rates than Giesekus fluids [53] and Phan–Tien Thanner models [54].

The simulations consider a single particle, in both the Newtonian and Non-Newtonian case, and are started from a fully developed single-phase flow obtained at the selected \(Re\) and \(Wi\). In our simulations, a dilute particle suspension is therefore studied, with a single rigid spherical particle with diameter to channel size ratio equal to \(1{:}5\), similar to the experimental conditions. Also, in the viscoelastic cases, the dumbbell extensibility \(L\) is fixed equal to \(60\) and \(P\) to \(0.9\).

The Reynolds number is varied between \(35\) and \(600\), and the Weissenberg number between \(0\) and \(3\). In the Newtonian case, we found that the particle equilibrium position stabilizes at \(0.6R\) for a Reynolds number of about \(100\), as shown in Fig. 4. This is consistent with the experimental measurements and the Segre-Silberberg theory which predicts that in an inertial laminar flow and in the absence of elasticity, the particles focus at a distance \(0.6R\) from the center of the channel. From our results we can observe slight variations of the particle focusing position as \(Re\) increases, with the equilibrium position approaching more towards the wall at moderate \(Re \left( {Re = 10 - 150} \right)\) and then reducing again for \(Re > 150\). Note that, the particle focuses at approximately \(0.53R\) at \(Re = 35\), which is in very good agreement with the theoretical prediction by Asmolov et al. [55], who reported the same equilibrium position for a finite size neutrally buoyant particle of the same size at the same Reynolds number, and also agrees with the experimental results shown in Fig. 3. In a Non-Newtonian solution, an inverse Segre-Silberberg scenario has been proposed in the past to explain particle migration towards the walls, as well as channel centreline, at low \(Re\) and \(Wi{ }\) [14]. This is due to the distribution of first normal stress difference which is minimum at the channel centre in case of circular cross section channels and minimum at the centre and walls in case of square and rectangular cross sections[50]. In an elasto-inertial regime with appreciable elasticity and inertia, the corner positions disappear and only centerline focusing is observed. However, we observe that under appreciable inertia and weak elasticity, the elastic effects no longer exert complete dominance on inertia..

Fig. 4
figure 4

Results of the numerical simulations showing the particle equilibrium position as a function of \(Re\) for four Weissenberg numbers, \(Wi\) (\(0\), \(1\), \(2\) and \(3\))

Full size image

Instead, multiple equilibrium positions exist that depends on competitive domination of inertia and elasticity of the carrier fluid.

The simulation results (Fig. 4) are in good agreement with our experimental measurements (Fig. 3). The particles move away from the center until a critical Reynolds number of about \(200\) for the Newtonian cases as well as for \(Wi = 1\), with a resulting particle focusing position close to \(0.6R\). With increasing Weissenberg numbers (Wi = 0, 1, 2, 3), the particles move closer to the center at all Reynolds number which matches with the experimental observations in Fig. 3. While at \(Wi = 0\) and \(1\) inertial effects dominate over elasticity and the particle settles close to \(0.6R\), above \(Wi = 2\) elasticity effects start dominating displacing the particle consistently closer to the center as \(Re\) Increases (see the Supplementary movies S1 and S2). Note that, for each \(Wi\) there is a critical Reynolds number \(Re_{M}\) where the particle has a maximum distance from the center, i.e., the. particle is closer to the walls, and that \(Re_{M}\) is smaller for higher Weissenberg numbers. This is not so visible till \(Re = 100\) which is our experimental observation range, but the trend is clearly seen in the simulation results. Beyond this critical Reynolds number \(Re_{M}\), the particles start moving closer to the center with increasing effect of inertia, and the probable cause of this discrepancy beyond the critical Reynolds number \((Re_{M} )\) can be due to dominance of particle size effect as well as the curvature of the pipe [56].

Figure 5 shows the first normal stress difference as a function of the Weissenberg number, and also the interaction of the particle and the polymeric component of the fluid to generate a distorted and non-symmetric field. A stretching similar to that of a rubber band is observed due to the first normal stress difference around the particle, which causes the particle to move closer to the center in an oscillatory fashion with increasing elastic effects. The first normal stress difference increases with the Weissenberg number, i.e., with the fluid elasticity, thus inducing larger particle displacements. Next, we study the entire particles trajectory, from their initial position (\(0.3R\)) to their final equilibrium positions, for a fixed Reynolds number \(Re 300\) and different Wi (Fig. 6a). For all the Weissenberg numbers, the particles right upon introduction have a short transient motion towards the center of the channel. The short transient motion can be attributed to the stress build-up around the particle right upon introduction in a fully developed baseflow, as well as to inertial effects.

Fig. 5
figure 5

First normal stress difference in the polymeric fluid flow for \(Re 300\) and a \(Wi=1\), b \(Wi=2\), c \(Wi=3\). The presence of the particle generates a distortion of the first normal stress difference field which is responsible for pushing the particle towards the center of the channel. The amplitude of the first normal stress difference increases with \(Wi\)

Full size image
Fig. 6
figure 6

a Particle trajectories at \(Re 300\) for different Weissenberg numbers. The particles progressively focus closer to the centre as \(Wi\) increases. b Particles introduced from different starting positions converge to the same final equilibrium position for both the Newtonian (\(Wi=0\)) and Non-Newtonian fluid (\(Wi=1\)); the two different starting position are 0.3 \(R \mathrm{and} 0.7R\)

Full size image

Interestingly, while the particle moves smoothly in the Newtonian fluid, in the polymeric flow, the final equilibrium position is reached through oscillations which slightly increase in amplitude with \(Wi\) and \(Re\), and are in the order of \(R/10\). Note that, the particle in the Non-Newtonian fluid oscillates also when its final equilibrium position is reached (Fig. 6a, Wi = 1,2,3). This is due to the distorted first normal stress difference that builds up around the particle leading to an oscillatory stretching around the particle as shown in Fig. 5c, see also [57]. The final equilibrium position of the particle is also shown to be independent of its initial condition for both the Newtonian and the Non-Newtonian fluid, as shown in Fig. 6b, where the results obtained from two different initial conditions for the particle are compared (\(0.3R\) and \(0.7R\)).

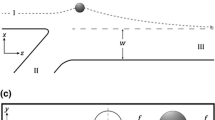
Finally, we also performed preliminary numerical simulations at fixed finite Reynolds and Weissenberg numbers, \(Re 300\) and \(Wi = 2\), in a channel with square cross section, in order to compare the results with those in a circular pipe. In the square channel, different equilibrium positions are reached when the particle is initialized at two different azimuthal positions (vertical axis and diagonal), even if they are at the same distance from the center. This is due to the loss of periodicity in the azimuthal direction induced by the presence of the four corners.

In Newtonian fluids, particles tend to settle in one of the four positions that are at right angle from the centre, i.e., along the horizontal and vertical lines passing through the centre, even at non-zero and finite Reynolds numbers.

On the other hand, it has been previously shown that in viscoelastic fluids with no inertia, particles tend to focus in the centre of the channel and also in one of the four corners [50]. The differences between the two geometries can be explained by considering the first normal stress difference, reported in Fig. 7a and Fig. 7b. While in the circular cross section (Fig. 7a) case, the first normal stress difference is uniform in the azimuthal direction, this is not the case in the square cross section (Fig. 7b) case, where it shows a strongly non uniform distribution. In particular, it is maximum at the wall in the intersection with the horizontal and vertical lines passing through the center, while it is minimum in the channel center and in the four corners. Figure 7c shows a comparison of the final equilibrium positions in the cases of square and circular cross sections in presence of both finite inertia and elasticity. In both the geometries and for all the initial positions considered, the particle first moves towards the center of the channel and then towards the walls, eventually reaching the equilibrium positions.

Fig. 7
figure 7

First normal stress difference in the polymeric fluid flow for \(Re 300\) and \(Wi=2\) in a channel with a circular and b square cross section. c Sketch of the comparison of the final equilibrium positions at \(Re 300\) and \(Wi=2\) in a circular and square channel. The initial and final positions of the particles are marked with the open rectangles and the solid circles, respectively; blue denotes the results for the circular cross section while magenta denotes those of the square cross section with three different starting positions

Full size image

The initial motion towards the center can be explained due to stress build-up around the particle upon introduction as well as the effect of inertia, as in the circular capillary.

Note, in the square duct (Fig. 7c) two different equilibrium positions are found: one on the horizontal and vertical lines at right angle from the center, similarly to Newtonian fluids, and the other one on the main diagonals, similar to viscoelastic fluids. The latter case is really interesting as in a similar case for a Newtonian fluid it was earlier observed that the particle first reaches an equilibrium manifold and then undergoes slow lateral migration to the vertical or horizontal axis [9, 31]. However, due to the finite inertia considered in our simulations, the particle does not reach the corner, but settles at a certain distance from it, and the symmetrical first normal stress difference about the diagonal axis prevents the slow migration of the particle along the equilibrium manifold [31]. This result is similar to what observed in the case of deformable capsules in a Newtonian fluid [52]. The interested reader is referred to the work by Trofa et al. [58] and Lashgari et al. [31] for further analysis on the different migration dynamics of particles in square channels.

4 Conclusions

We have reported results of a combined experimental and numerical effort to characterize the dynamics of very dilute suspensions of particles in a circular micro-capillary for both Newtonian and Non-Newtonian fluids. In particular, we study the phenomenon of particle elasto-inertial focusing in presence of moderate inertia and weak fluid elasticity and found a general tendency of the particle to assume multiple equilibrium positions based on competitive effects of inertia and elasticity. The results demonstrate for the first time, the possibility of analog tuning of the particle focusing positions in elasto-inertial flows.

By introducing in the carrier fluid a small amount of viscoelasticity of the order of a few ppm of PEO solution, it is possible to tune the position of the particle at any desired position in the microcapillary that lies between \(F = 0.6R\) and \(F = 0\).

The experimental evidence is supported by well-resolved three-dimensional numerical simulations, where the FENE-P model is used to account for the viscoelastic behavior of the flow. From the numerical simulations, we show the entire particle migration process and extend the predictions to moderate viscoelastic regimes where the inertial effect is predominant (\(Re > 100)\). We believe the possibility of particle tuning in weakly elasto-inertial regimes will greatly aid in a better fundamental understanding of elasto-inertial focusing in microfluidic channels in a new perspective.