Abstract
As proven in a recently published paper [Messa GV, Matoušek V (2020) Analysis and discussion of two fluid modelling of pipe flow of fully suspended slurry. Powder Technol 30:747\(-\)768.], the \(\beta\)-\(\sigma\) two-fluid model is capable of accurately reproducing the main features of turbulent, fully-suspended slurry flows in horizontal pipes provided that suitable values of the two parameters \(\beta\) and \(\sigma\) are chosen. At present, the case-specific nature of \(\beta\) and \(\sigma\) and their lack of a clear physical meaning are the main obstacles that must be overcome to give the \(\beta\)-\(\sigma\) two-fluid model value not only as interpretative tool, but also as a predictive one. An important preliminary step to achieve this goal is to disclose the mathematical essence of the \(\beta\)-\(\sigma\) two-fluid model, namely, to interpret the fluid-dynamic solution on the grounds of the structure of the differential and discretized equations. Such a methodological approach is applied here to the benchmark case of turbulent slurry flow between two infinite, horizontal, parallel plates, focusing, in particular, on the influence of the bulk-mean velocity of the slurry and the volumetric concentration of the solids in the flow. The study provides not only deeper insight into the \(\beta\)-\(\sigma\) model, but also indicates important implications for alternative two-fluid models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Computational Fluid Dynamics (CFD) exhibits great potential in the application to slurry flows in pipeline systems for a number of inter-related reasons, including the relatively low cost compared to experimental testing, the growing capability of computer technology and CFD codes, the detailed information on the flow that can be obtained from a CFD simulation, and the absence of constraints on the size and the geometrical complexity of the system under investigation. CFD appears to be a powerful tool not only for engineers, but also for academic researchers dealing with slurry pipe flows. On one hand, it allows prototype testing of large-scale slurry systems and components, such as fittings or hydraulic devices and machinery, which are difficult to test in laboratory experiments. On the other hand, it allows gaining deep insight into the fluid dynamic behaviour of slurry flows, providing a better understanding of the physical processes underlying slurry pipe transport and helping to justify the experimental findings.
For about ten years, research has been carried out at Politecnico di Milano on the development of mathematical models for the CFD simulation of slurry flows, with significant contributions from Concentration, Heat And Momentum Limited and Institute of Hydrodynamics of the Czech Academy of Sciences. The main achievement obtained so far is the \(\beta\)-\(\sigma\) two-fluid model, whose most comprehensive formulation has been reported in Messa and Matoušek [1]. When compared with alternative models, the \(\beta\)-\(\sigma\) model demonstrated potential interest for engineering design owing to its formal simplicity, good numerical stability, effective convergence, and satisfactory accuracy of the solution. At the same time, it suffers from two main flaws. First, it is subjected to three applicability conditions, the most critical being that the flow must be fully suspended, in the sense that the particle transport must be driven by the interactions between the particles and the turbulent liquid, whilst particle-particle interactions play a minor role. Second, it includes two empirical parameters, \(\beta\) and \(\sigma\), which, although being broadly associated with specific physical mechanisms, need to be calibrated with experimental data. Particularly, the \(\sigma\) parameter is related to the turbulent dispersion of particles, and \(\beta\) is associated with the increased flow resistance encountered by a particle in the slurry due to the presence of surrounding particles. Owing to the case-specific nature of \(\beta\) and \(\sigma\), the \(\beta\)-\(\sigma\) model might have interpretative value, in the sense that it can serve to complement experiments to determine difficult-to-measure quantities, or gain further insight into the characteristics of the flow. However, the predictive value of the \(\beta\)-\(\sigma\) model, namely, its capacity to procure reliable predictions outside the calibration range, has not been adequately proven yet, although some pipe size-up scaling tests have been performed successfully.
The mid- and long-term research goals are to overcome the two flaws of the \(\beta\)-\(\sigma\) two-fluid model. Firstly, efforts will be devoted to validating the extrapolation of the calibrated model to different flow conditions, providing guidelines and recommendations for the determination of suitable values of \(\beta\) and \(\sigma\). Then, an attempt will be made to provide a physical characterization for \(\beta\) and \(\sigma\), giving them a more solid foundation. Finally, research will be aimed at broadening the applicability of the model by making it capable of simulating slurry flows dominated by inter-particle collisions and contacts. In order to achieve these goals, it is of utmost importance to understand deeply the principles of the \(\beta\)-\(\sigma\) model, going beyond its function of being a tool to predict engineering-relevant features of slurry flows. This requires going back to the fundamental conservation equations, trying to understand how the interplay of their different terms affect the fluid dynamic solution provided to the user. The present paper deals with a methodological approach to CFD modelling, here applied to the \(\beta\)-\(\sigma\) two-fluid model for fully-suspended slurry flows. The core of this work is to disclose the mathematical essence of the model, that is, to start from its mathematical structure and try to answer questions like: Why is the solution as it is and not something else? Why does a change in the inflow conditions produce the observed variation in the solution? Why does a change in the value of an empirical parameter affect certain features of the solution and not others? Note that here the aim is to provide mathematical justifications, and not (necessarily) physical justifications, which will be required at a more advanced stage of model development. According to the authors’ understanding, gaining insight into the mathematical characteristics of a model is an essential prerequisite to evaluating properly its capabilities, since any physical or engineering interpretation of a CFD solution cannot ignore the mathematical structure of the model which produced that solution. Therefore, assessing the mathematical meaning of a CFD model is needed to fully establish its physical and engineering impact, in its current form, or in view of improvements.
This is certainly true for the \(\beta\)-\(\sigma\) model because of its clearly empirical nature, arising from the presence of the parameters \(\beta\) and \(\sigma\). However, it is noted that the interest in the investigative approach presented here goes beyond a specific CFD model; in fact, the physical phenomena governing fluid-dynamic processes and, in particular, slurry transport, are so complex to describe that, in the end, all CFD models for engineering use show a certain degree of empiricism. A detailed overview of the models employed to simulate turbulent slurry flows in pipeline systems has been presented in Messa and Matoušek [1]. The Eulerian-Eulerian, two-fluid approach appears to be the preferred one, because models relying on the Lagrangian tracking of the solid particle trajectories require much higher computational capacity, especially when particle-particle interactions need to be accounted for in the model. This explains why the number of studies in which slurry pipe flows were simulated using Eulerian-Lagrangian models is still rather limited [2,3,4], whereas there are a lot of published literature concerning the Eulerian-Eulerian modelling of these flows. Apart from few exceptions [5,6,7], most two-fluid models employed by other researchers rely on constitutive equations for the solid phase derived from the Kinetic Theory of Granular Flows (KTGF), which develops around the concept of granular temperature of the solid phase, \(\varTheta _{\mathrm {s}}\), defined as proportional to the kinetic energy of the random motion of the particles [8,9,10,11,12,13,14,15,16]. It is certainly true that, compared with the \(\beta\)-\(\sigma\) two-fluid model, KTGF-based models have the advantage of a stronger physical basis, since the stresses within the solid phase have been derived from basic physical principles and attributed a precise physical meaning. At the same time, the turbulent slurry transport in pipeline systems is much more complicated compared to the framework in which the KTGF was developed. As a result, KTGF-based models are not fully theoretically based, but depend of a number of parameters whose values are difficult to decide in practice.
Most published studies using KTGF-based models included comparison against experimental data in terms of the quantities that are practically feasible to measure in laboratory setups, namely, hydraulic gradient (that is, the pressure gradient in meters of water per unit channel length), solids concentration profile along the vertical diameter, and, rarely, also the vertical profile of the streamwise velocity of the mixture. Generally, limited or no information was provided regarding the criteria adopted to select all the many sub-models and parameters of the two-fluid model, nor it was explicitly declared whether some kind of tuning of the model constants has been made. Therefore, it was not clear whether the good agreement with experimental data, as often observed, was the result of a calibration or, rather, of a successful validation. In Ekambara et al. [9], the experimental database used for comparison with the CFD simulations was large enough to assess the robustness of the numerical estimates. However, this study appears an exception, since, in most cases, reference was made to a limited number of experimental conditions. Therefore, there is currently little evidence that KTGF-based models can be regarded as “predictive” tools in the sense previously given.
It is worth mentioning that, in addition to being the only practically measurable quantities, the hydraulic gradient, concentration, and velocity are of considerable importance for engineering design. This might explain why some of the numerical investigations reported in the literature were focused only on these parameters [8,9,10, 12]. Instead, others discussed also difficult-to-measure features of the CFD solutions, such as the granular temperature of the solid phase and its related variables within the framework of the KTGF, and the turbulence characteristics of the carrier liquid [11, 13,14,15,16]. The authors commented on the numerical results on the grounds of the underlying physical processes.
Analyzing the CFD solution on the grounds of the mathematical structure of the two-fluid model would provide beneficial insight regardless of the specific two-fluid model used. If the aim were to develop a predictive model, it would help to shed light on the role played by the most uncertain model parameters. If the scope of the model were the interpretative one, such an analysis would help to clarify whether any comment on the behaviour of the solution is merely speculative or coherent with the model.
The remainder of this paper is divided into three sections, followed by conclusions and future perspectives. The \(\beta\)-\(\sigma\) two-fluid model is briefly illustrated in Sect. 2 whereas, in Sect. 3, the mass and momentum conservation equations in differential and Finite Volume forms are presented for the benchmark case of fully-developed turbulent flow between horizontal plates, and their implementation in the PHOENICS code is explained. Section 4 summarizes and discusses the results obtained from the simulations. After providing a summary of the case studies (Sect. 4.1), in Sect. 4.2 the focus is on the effect of the computational mesh. Then, the presentation of the fluid dynamic solution (Sect. 4.3) is followed by its in-depth analysis based on the inspection of the fundamental conservation equations (Sect. 4.4), with particular focus on the influence of the bulk slurry velocity and solid concentration imposed at the inlet boundary (Sects. 4.5 and 4.6). Finally, in Sect. 4.7, some discussion around the impact of the results for the more engineering relevant case of slurry flows in circular pipes and for other two-fluid models are made.
2 The \(\beta\)-\(\sigma\) two-fluid model
The reader is referred to Messa and Matoušek [1] for a complete description of the \(\beta\)-\(\sigma\) two-fluid model, which has been implemented in the PHOENICS code version 2018, and arises as an extension to slurry flows of the built-in Inter Phase Slip Algorithm of Spalding [17]. The \(\beta\)-\(\sigma\) model, based on the Eulerian–Eulerian approach, solves for the locally averaged conservation equations of the liquid (\(k={\mathrm {l}}\)) and solid (\(k={\mathrm {s}}\)) phases, which are treated as interpenetrating continua. The mass and momentum conservation equations for phase \(k=\mathrm {l,s}\) read as follows
where \(\alpha\), \({\mathbf {U}}\), P are the volume fraction, velocity vector, and pressure, respectively, \(\rho\) and \(\mu\) are density and dynamic viscosity, respectively, \(\mu ^{\mathrm {t}}\) is the eddy viscosity, \({\mathbf {g}}\) is the gravitational acceleration vector, \({\mathbf {M}}_{k' \rightarrow k}\) is the interfacial momentum transfer term exerted on phase k from the other phase \(k'\), and \(\sigma\) is the turbulent Schmidt number for volume fractions.
As discussed in Messa and Matoušek [1] on the grounds of the framework described by Burns et al. [18], Eqs. 1 and 2 might be interpreted as the result of a double-averaging process, which considers time-averaging of the local instantaneous mass and momentum conservation equations after the volume average operator is applied. Under this perspective, \(\alpha _k\) can be interpreted as the time-average value of the proportion of local volumetric space occupied by a phase, and, similarly, \({\mathbf {U}}_k\), and P are the time-average of the locally-averaged phase velocity vector and pressure. Double-averaging of the mass and momentum conservation equations of phase k yields terms depending on the correlations between the time-fluctuating locally-averaged volume fraction, \(\alpha _k'\), and the time-fluctuating locally-averaged velocity vector, \({\mathbf {u}}_k'\). Following a well known approach in the literature, which is based on an analogy between the turbulent transport of inertial particles and that of a passive scalar, the double correlations \(\overline{\alpha _k'{\mathbf {u}}_k'}\), are modeled by means of the gradient diffusion approximation, as follows:
where, as already said, \(\mu _{\mathrm {l}}^{\mathrm {t}}\) is the eddy viscosity of the liquid and \(\sigma\) is the turbulent Schmidt number for volume fractions. Previous research indicated that there is no single constant value of \(\sigma\) which can be used to accurately reproduce the various sets of experimental data concerning liquid-solid slurry flows in pipes, and this is the reason why \(\sigma\) is one of the two main empirical parameters of the \(\beta\)-\(\sigma\) two-fluid model. The values of \(\sigma\) considered so far were in the range 0.5 to 1.5 [1, 19]. The correlations \(\overline{\alpha _k'{\mathbf {u}}_k'}\), modeled through Eq. 3, appear in the last two terms of Eqs. 1 and 2, which are called phase diffusion terms and will play a significant role in the present study.
The eddy viscosities of the two phases, \(\mu _{\mathrm {l}}^{\mathrm {t}}\) and \(\mu _{\mathrm {s}}^{\mathrm {t}}\), are related to each other by an algebraic correlation, and the following two-phase extension of the k-\(\varepsilon\) standard turbulence model, available as option in PHOENICS, was employed to calculate \(\mu _{\mathrm {l}}^{\mathrm {t}}\):
In the equation above, \(P_k\) is the volumetric production rate of k by shearing stresses, calculated as in [20], and the empirical constants are \(C_\mu =0.09\), \(\sigma _k=1.0\), \(\sigma _\varepsilon =1.314\), \(C_{1\varepsilon }=1.44\), and \(C_{2\varepsilon }=1.92\). Note that, for consistency with the mass and momentum conservation equations, the phase diffusion terms appear also in the transport equations for k and \(\varepsilon\).
Unlike \(\mu _{\mathrm {l}}\), which is a physical property of the carrier liquid, the viscosity of the solid phase, \(\mu _{\mathrm {s}}\), is a function of the local flow conditions and it is calculated as:
where \(\mu _{\mathrm {m}}\) is a friction parameter, which will be discussed later.
The interfacial momentum transfer term, \({\mathbf {M}}_{k' \rightarrow k}\), accounts for the transfer of momentum from phase \(k'\) to phase k. Under the assumption that such transfer is uniquely due to the drag force, and considering that \({\mathbf {M}}_{{\mathrm {l}} \rightarrow {\mathrm {s}}}=-{\mathbf {M}}_{{\mathrm {s}} \rightarrow {\mathrm {l}}}\) owing to the action-reaction principle, the following formula is obtained:
where \(d_{\mathrm {p}}\) is the volume-equivalent particle diameter, \(U_{\mathrm {rel}}\) is the modulus of the relative velocity between liquid and solid phase (that is, \(U_{\mathrm {rel}}=\left| {\mathbf {U}}_{\mathrm {l}}-{\mathbf {U}}_{\mathrm {s}}\right|\)), and \(C_{\mathrm {d}}\) is the drag coefficient, calculated according to the following expression:
Note that Eq. 9 is an analogue of the formula of Schiller and Naumann for the drag coefficient of a single spherical particle [21]. The only difference is that, in Eq. 9, the particle Reynolds number is not calculated with respect to the viscosity of the liquid but, rather, to the friction parameter \(\mu _{\mathrm {m}}\). This is a distinctive character of the \(\beta\)-\(\sigma\) two-fluid model, the rationale being to account in a simple and effective way for the increased flow resistance experienced by a particle in a slurry mixture compared to the single-particle case. The friction parameter, in turn, is calculated as
based on a purely formal analogy with the formula of Cheng and Law for the viscosity of a mixture [22].
The last unusual feature of the \(\beta\)-\(\sigma\) two-fluid model resides in the evaluation of the wall shear stress of the solid phase, \({\tau }_{\mathrm {s}}^{\mathrm {w}}\), through the following formula:
which is based on an analogy with the equilibrium wall function of Launder and Spalding for smooth walls. The symbols in Eq. 12 are as follows, namely, \(s_{\mathrm {s}}\) is the friction factor of the solid phase, \({\mathbf {U}}_{\mathrm {s}}^\parallel\) is the resultant velocity of the solid phase parallel to the wall at the first grid nodes, \(\kappa =0.41\) is von Karman’s constant, \(E=8.6\) is a roughness parameter, \(Re_{\mathrm {s}}^{\mathrm {w}}\) is a wall Reynolds number of the solid phase, and \(\delta\) is the normal distance of the first grid point to the wall.
The applicability of the \(\beta\)-\(\sigma\) two-fluid model is subjected to the fulfilment of three constraints, well discussed in [1] for slurry flows in horizontal pipes. The first is \(d_{\mathrm {p}}^+<30\) for the validity of Eq. 12, where \(d_{\mathrm {p}}^+\) is a dimensionless particle diameter, namely, some sort of near-wall Reynolds number based on \(d_{\mathrm {p}}\), \(\rho _{\mathrm {l}}\), \(\mu _{\mathrm {l}}\), and the friction velocity of the liquid phase, \(\sqrt{\tau _{\mathrm {l}}^{\mathrm {w}}/\rho _{\mathrm {l}}}\), as follows:
The wall shear stress of the liquid phase, \(\tau _{\mathrm {l}}^{\mathrm {w}}\), is an output of the numerical simulation. However, for slurry flows in horizontal pipes, a reasonable estimation of this parameter could be obtained by applying the Blasius correlation for the friction factor of turbulent single-phase flows in smooth pipes [23]. Therefore, a more practical constraint is
where \(d_{\mathrm {p}}^{+\mathrm {B}}\) is the estimate of \(d_{\mathrm {p}}^+\) using Blasius’ law, D is the pipe diameter and \(V_{\mathrm {m}}\) is the slurry bulk-mean velocity, that is, the ratio between the volumetric flow rate of the mixture and the area of the pipe cross-section. The two other applicability constraints both relate to the fully suspended nature of the slurry flow. These are \(V_{\mathrm {m}}>1.5V_{\mathrm {dl}}^{\mathrm {T}}\), where \(V_{\mathrm {dl}}^{\mathrm {T}}\) is the estimate of the deposition limit velocity proposed by Thomas [24], and \(\alpha _{\mathrm {s}}<0.45\), on the grounds of the experimental findings by Korving [25].
3 Mass and momentum conservation equations for turbulent, fully-developed slurry flow between horizontal plates and implementation of the benchmark case in the PHOENICS code
The scope of a slurry flow simulation is usually to gather information about macroscopic quantities, either concentrated or distributed, such as the energy losses or the preferential location of the solids in the domain. Conversely, this study analyses the \(\beta\)-\(\sigma\) two-fluid model at a deeper level, by interpreting the fluid dynamic solution in the light of the mathematical structure of the fundamental conservation equations. Reference was made to the benchmark case of fully developed slurry flow between two infinite, horizontal, parallel plates which, in addition to the similarities with the more engineering-relevant case of horizontal pipe flow, allows for an easier interpretation of the results owing to the one-dimensional nature of the flow.
Let z and y be the horizontal and the vertical coordinates, respectively, and \(U_{k,z}\) and \(U_{k,y}\) the corresponding velocity components of phase \(k=\mathrm {l,s}\). The two plates are located at \(y=0\) and \(y=H\) (Fig. 1). For this specific type of flow, the mass and momentum conservation equations for phase \(k=\mathrm {l,s}\) are as follows:
where g is the modulus of the gravitational acceleration vector, which points along direction \(-y\), and \(M_{k'\rightarrow k, y}\) and \(M_{k'\rightarrow k, z}\) are the components of the interfacial momentum transfer term (Eq. 8) along directions y and z, respectively.
Although the fully developed flow between two parallel plates is one-dimensional in the y-direction, the simulations were run in a two-dimensional domain 200H long along the z-direction. The boundary conditions were: inlet with uniform distributions of \(U_{{\mathrm {s}},z}=U_{{\mathrm {l}},z}=V_{\mathrm {m}}\), \(U_{{\mathrm {s}},y}=U_{{\mathrm {l}},y}=0\), \(\alpha _{\mathrm {s}}=1-\alpha _{\mathrm {l}}\), k, and \(\varepsilon\) at \(z=0\); solid walls at \(y=0\) and \(y=H\); outlet with zero pressure at \(z=200H\) (Fig. 2). At the solid walls, the wall shear stress of the solid phase \({\tau }_{\mathrm {s}}^{\mathrm {w}}\) was imposed according to Eq. 12, whereas the wall shear stress of the liquid phase and the values of k and \(\varepsilon\) in the near-wall cells were obtained from the equilibrium log-law wall function option of PHOENICS. The fully-developed state was reached at about \(z=130H\) downstream of the inlet. Such estimate was obtained by inspecting the streamwise profiles, at three different elevations above the bottom wall, of all elementary terms in the FV formulation of the two z-momentum equations, which will be listed in the following. Such analysis revealed that, for \(z \ge 130H\), all curves deviate less than 1% from the values at \(z=170H\), which is the slab used to extract the transversal profiles subject of discussion in this study.
The domain was discretized using a cartesian mesh with rectangular, “brick” elements, and the influence of the computational mesh on the numerical solution will be subject of discussion in Sect. 4.2. The solution of the FV equations was performed following the elliptic staggered formulation, in which the scalar variables are stored at the cell centres, and the velocity components at the cell faces. Hereafter, in order to denote the different mesh elements, reference will be made to the notation employed by Versteeg and Malalasekera [26], namely \(\ldots I-1, I, I+1\ldots\) for the cell centres in direction z, \(\ldots J-1, J, J+1\ldots\) for the cell centres in direction y, \(\ldots i-1, i, i+1\ldots\) for the cell faces in direction z, and \(\ldots j-1, j, j+1\ldots\) for the cell faces in direction y (Fig. 3a). Due to the staggered formulation, the control volumes for the continuity equations and the transport equations for scalar quantities k and \(\varepsilon\) (Fig. 3b) are different from those of the \(U_{k,y}\) momentum equations (Fig. 3c) and from those of the \(U_{k,z}\) momentum equations (Fig. 3d).
Since, as already mentioned, PHOENICS uses the Finite Volume method, the derivation of the FV analogue of Eqs. 15–17 is now presented. As it is well known, the FV formuation of the differential problem is obtained by integrating the equations over the generic cell in the computational domain and evaluating approximately the different terms from the values in the storage locations of the fluid dynamic variables.
The FV formulation of the mass conservation equations at cell (I, J) and those of the momentum equations for the generic velocity components \(U_{k,y}^{I,j}\) and \(U_{k,y}^{i,J}\) can be written as:
where the reason for the use of the symbol “1” in Eq. 18 is that this is the actual transported variable in the continuity equations. The parameters in the three equations above are as follows:
-
1.
\({\mathcal {C}}^{\mathrm {n}}\) and \({\mathcal {C}}^{\mathrm {s}}\) are the convection terms through the “north” and “south” faces of the control volumes of each equation, labelled as “n” and “s” in Fig. 3b–d. These quantities are present in all conservation equations. The \({\mathcal {C}}^{\mathrm {n}}\) terms were estimated as:
$$\begin{aligned} {\mathcal {C}}^{\mathrm {n}} (1_k^{I,J})= & {} - {\mathcal {F}}^{\mathrm {n}} (1_k^{I,J}) \end{aligned}$$(21a)$$\begin{aligned} {\mathcal {C}}^{\mathrm {n}} (U_{k,y}^{I,j})\,=\, & {} \mathrm {max}\left[ -{\mathcal {F}}^{\mathrm {n}}(U_{k,y}^{I,j}),0\right] U_{k,y}^{I,j+1} \nonumber \\&-\mathrm {max}\left[ {\mathcal {F}}^{\mathrm {n}}(U_{k,y}^{I,j}),0\right] U_{k,y}^{I,j} \end{aligned}$$(21b)$$\begin{aligned} {\mathcal {C}}^{\mathrm {n}} (U_{k,z}^{i,J})\,=\, & {} \mathrm {max}\left[ -{\mathcal {F}}^{\mathrm {n}}(U_{k,z}^{i,J}),0\right] U_{k,z}^{i,J+1} \nonumber \\&-\mathrm {max}\left[ {\mathcal {F}}^{\mathrm {n}}(U_{k,z}^{i,J}),0\right] U_{k,z}^{i,J} \end{aligned}$$(21c)where the \({\mathcal {F}}^{\mathrm {n}}\)-terms are the y-directed convection fluxes through the north face of the control volumes, calculated as:
$$\begin{aligned} {\mathcal {F}}^{\mathrm {n}}(1_k^{I,J})\,= \,& {} A^{\mathrm {n}}\rho _k \cdot {U_{k,y} \alpha _k}\vert ^{I,j+1} \end{aligned}$$(22a)$$\begin{aligned} {\mathcal {F}}^{\mathrm {n}}(U_{k,y}^{I,j})\,= \,& {} A^{\mathrm {n}}\rho _k \cdot {U_{k,y} \alpha _k}\vert ^{I,J} \end{aligned}$$(22b)$$\begin{aligned} {\mathcal {F}}^{\mathrm {n}}(U_{k,z}^{i,J})= & {} A^{\mathrm {n}}\rho _k \cdot {U_{k,y} \alpha _k}\vert ^{i,j+1} \end{aligned}$$(22c)In Eqs. 22a–22c, \(A^{\mathrm {n}}\) is the north cell-face area, and the vertical bar indicates that the product between the y-velocities \(U_{k,y}\) and the volume fractions \(\alpha _k\) have been evaluated at the center of the north cell-face area of the control volumes, that is, at \((I,j+1)\), (I, J), and \((i,j+1)\) for Eqs. 18–20, respectively. The whole-field values of the \({\mathcal {F}}^{\mathrm {n}}\)-terms were automatically calculated and provided as output by PHOENICS.
-
2.
\({\mathcal {D}}^{\mathrm {n}}\) and \({\mathcal {D}}^{\mathrm {s}}\) are the diffusion terms through the north and south faces. These terms are present only in the momentum conservation equations. Using the central differencing scheme, they were estimated as:
$$\begin{aligned} {\mathcal {D}}^{\mathrm {n}}(U_{k,y}^{I,j})= & {} \varGamma ^{\mathrm {n}}(U_{k,y}^{I,j}) A^{\mathrm {n}} \dfrac{U_{k,y}^{I,j+1}-U_{k,z}^{I,j}}{y^{I,j+1}-y^{I,j}} \end{aligned}$$(23a)$$\begin{aligned} {\mathcal {D}}^{\mathrm {n}}(U_{k,z}^{i,J})= & {} \varGamma ^{\mathrm {n}}(U_{k,z}^{i,J}) A^{\mathrm {n}} \dfrac{U_{k,z}^{i,J+1}-U_{k,z}^{i,J}}{y^{i,J+1}-y^{i,J}} \end{aligned}$$(23b)where \(\varGamma ^{\mathrm {n}}(U_{k,y}^{I,j})\) and \(\varGamma ^{\mathrm {n}}(U_{k,z}^{i,J})\) are the exchange coefficient of \(U_{k,y}^{I,j}\) and \(U_{k,z}^{i,J}\) over the north faces of the control volumes associated with these velocity components. They were given by:
$$\begin{aligned} \varGamma ^{\mathrm {n}}(U_{k,y}^{I,j})= & {} \left. \alpha _k\left( \mu _k+\mu _k^{\mathrm {t}}\right) \right| ^{I,J} \end{aligned}$$(24a)$$\begin{aligned} \varGamma ^{\mathrm {n}}(U_{k,z}^{i,J})= & {} \left. \alpha _k\left( \mu _k+\mu _k^{\mathrm {t}}\right) \right| ^{i,j+1} \end{aligned}$$(24b)Since \(\alpha _k\), \(\mu _k\), and \(\mu _k^{\mathrm {t}}\) are scalar quantities and, therefore, are stored in the cell centres, they had to be interpolated to the centres of the north cell-face areas of the control volumes for \(U_{k,y}^{I,j}\) and \(U_{k,z}^{i,J}\). This was achieved by applying a harmonic mean.
-
3.
\(\mathcal {PD}^{\mathrm {n}}\) and \(\mathcal {PD}^{\mathrm {s}}\) are the phase-diffusion terms through the north and south faces, and they are present in all conservation equations. In the mass and momentum ones, the \(\mathcal {PD}^{\mathrm {n}}\)-terms were estimated as:
$$\begin{aligned} \mathcal {PD}^{\mathrm {n}} (1_k^{I,J})= & {} \varPhi ^{\mathrm {n}} (1_k^{I,J}) \end{aligned}$$(25a)$$\begin{aligned} \mathcal {PD}^{\mathrm {n}}(U_{k,y}^{I,j})= & {} \mathrm {max}\left[ \varPhi ^{\mathrm {n}}(U_{k,y}^{I,j}),0\right] U_{k,y}^{I,j+1} \nonumber \\&-\mathrm {max}\left[ -\varPhi ^{\mathrm {n}}(U_{k,y}^{I,j}),0\right] U_{k,y}^{I,j} \end{aligned}$$(25b)$$\begin{aligned} \mathcal {PD}^{\mathrm {n}}(U_{k,z}^{i,J})= & {} \mathrm {max}\left[ \varPhi ^{\mathrm {n}}(U_{k,z}^{i,J}),0\right] U_{k,z}^{i,J+1} \nonumber \\&-\mathrm {max}\left[ -\varPhi ^{\mathrm {n}}(U_{k,z}^{i,J}),0\right] U_{k,z}^{i,J} \end{aligned}$$(25c)where the \(\varPhi ^{\mathrm {n}}\)-terms are the y-directed phase diffusion fluxes through the north cell-face areas of the control volumes, and they are equal to:
$$\begin{aligned} \varPhi ^{\mathrm {n}}(1_k^{I,J})= & {} A^{\mathrm {n}}\dfrac{\rho _k}{\rho _{\mathrm {l}} \sigma } \cdot \mu _{\mathrm {l}}^{\mathrm {t}} \left. \dfrac{\partial \alpha _k}{\partial y}\right| ^{I,j+1} \end{aligned}$$(26a)$$\begin{aligned} \varPhi ^{\mathrm {n}}(1_k^{I,J})= & {} A^{\mathrm {n}}\dfrac{\rho _k}{\rho _{\mathrm {l}} \sigma } \cdot \mu _{\mathrm {l}}^{\mathrm {t}} \left. \dfrac{\partial \alpha _k}{\partial y}\right| ^{I,J} \end{aligned}$$(26b)$$\begin{aligned} \varPhi ^{\mathrm {n}}(1_k^{I,J})= & {} A^{\mathrm {n}}\dfrac{\rho _k}{\rho _{\mathrm {l}} \sigma } \cdot \mu _{\mathrm {l}}^{\mathrm {t}} \left. \dfrac{\partial \alpha _k}{\partial y}\right| ^{i,j+1} \end{aligned}$$(26c)where the products \(\mu _{\mathrm {l}}^{\mathrm {t}} \cdot \partial \alpha _k/\partial y\) were evaluated by PHOENICS at the centres of the north cell-face areas of the control volumes. The whole-field values of the \(\varPhi ^{\mathrm {n}}\)-terms were provided as output by the code.
-
4.
\(\varPi ^{\mathrm {n}}(U_{k,y}^{I,j})\) and \(\varPi ^{\mathrm {s}}(U_{k,y}^{I,j})\) are the pressure-force terms through the “north” and “south” faces of the \(U_{k,y}^{I,j}\) control volume. Similarly, \(\varPi ^{\mathrm {t}}(U_{k,z}^{i,J})\) and \(\varPi ^{\mathrm {b}}(U_{k,z}^{i,J})\) are the corresponding pressure-force terms through the “top” and “bottom” faces of the \(U_{k,z}\) control volume, labelled as “t” and “b” in Fig. 3d. These terms were calculated as:
$$\begin{aligned} \varPi ^{\mathrm {n}}(U_{k,y}^{I,j})= & {} - \alpha _k^{I,J}P^{I,J}A^{\mathrm {n}} \end{aligned}$$(27a)$$\begin{aligned} \varPi ^{\mathrm {s}}(U_{k,y}^{I,J})= & {} \alpha _k^{I,J-1}P^{I,J-1}A^{\mathrm {s}} \end{aligned}$$(27b)$$\begin{aligned} \varPi ^{\mathrm {t}}(U_{k,z}^{i,J})= & {} - \alpha _k^{I,J}P^{I,J}A^{\mathrm {t}} \end{aligned}$$(27c)$$\begin{aligned} \varPi ^{\mathrm {b}}(U_{k,z}^{i,J})= & {} \alpha _k^{I-1,J}P^{I-1,J}A^{\mathrm {b}} \end{aligned}$$(27d)where \(A^{\mathrm {b}}=A^{\mathrm {t}}\) are the top and bottom cell-face areas, respectively.
-
5.
\({\mathcal {G}}(U_{k,y}^{I,j})\) represents the y-component of the gravitational force acting of phase k over the control volume of \(U_{k,y}^{I,j}\). This term, appearing only in the momentum equations along direction y, is equal to:
$$\begin{aligned} {\mathcal {G}}(U_{k,y}^{I,j})=-W {\widetilde{\alpha }}_k^{I,j} \rho _k g \end{aligned}$$(28)where W is the cell volume, and the tilde symbol “\(\sim\)” indicates that the solid volume fraction \(\alpha _k\) was interpolated to the location of \(U_{k,y}^{I,j}\).
-
6.
\({\mathcal {M}}(U_{k,y}^{I,j})\) and \({\mathcal {M}}(U_{k,z}^{i,J})\) are the interphase friction force terms representing the y- and z-components of the total force exerted on phase k by the other phase, \(k'\), and acting on the control volumes of \(U_{k,y}^{I,j}\) and \(U_{k,z}^{i,J}\), respectively. These terms, appearing in the momentum equations along directions y and z, were estimated as:
$$\begin{aligned} {\mathcal {M}}(U_{{\mathrm {s}},y}^{I,j})&=-{\mathcal {M}}(U_{{\mathrm {l}},y}^{I,j})= \nonumber \\&= W\frac{{{\widetilde{\alpha }}}_{\mathrm {s}}^{I,j}}{\dfrac{4}{3}\pi \left( \dfrac{d_{\mathrm {p}}}{2}\right) ^3}\cdot \frac{1}{2}\rho _{\mathrm {l}}{{\widetilde{C}}}_{\mathrm {d}}^{I,j}\left( \pi \frac{d_{\mathrm {p}}^2}{4}\right) {{\widetilde{U}}}_{\mathrm {rel}}^{I,j}\cdot \left( U_{{\mathrm {l}},y}^{I,j}-U_{{\mathrm {s}},y}^{I,j}\right) \end{aligned}$$(29a)$$\begin{aligned} {\mathcal {M}}(U_{{\mathrm {s}},z}^{i,J})&=-{\mathcal {M}}(U_{{\mathrm {l}},z}^{i,J})= \nonumber \\&= W\frac{{{\widetilde{\alpha }}}_{\mathrm {s}}^{i,J}}{\dfrac{4}{3}\pi \left( \dfrac{d_{\mathrm {p}}}{2}\right) ^3}\cdot \frac{1}{2}\rho _{\mathrm {l}}{{\widetilde{C}}}_{\mathrm {d}}^{i,J}\left( \pi \frac{d_{\mathrm {p}}^2}{4}\right) {{\widetilde{U}}}_{\mathrm {rel}}^{i,J}\cdot \left( U_{{\mathrm {l}},z}^{i,J}-U_{{\mathrm {s}},z}^{i,J}\right) \end{aligned}$$(29b)where once again, the tilde symbol “\(\sim\)” indicates that the solid volume fraction \(\alpha _{\mathrm {s}}\), the drag coefficient \(C_{\mathrm {d}}\), and the modulus of the relative velocity \(U_{\mathrm {rel}}\) have been interpolated to locations (I, j) and (i, J).
The equations from 21a to 29b have been employed for all computational cells except for those adjacent to the solid walls, noting that, for a given cell, \({\mathcal {C}}^{\mathrm {s}}\), \({\mathcal {D}}^{\mathrm {s}}\), and \(\mathcal {PD}^{\mathrm {s}}\) are equal to minus \({\mathcal {C}}^{\mathrm {n}}\), \({\mathcal {D}}^{\mathrm {n}}\), and \(\mathcal {PD}^{\mathrm {n}}\) of the neighbouring cell along direction \(-y\). A different calculation method was employed for the wall-boundary cells. In the lower near-wall cells
whereas, in the upper near-wall cells
where \(N_y\) is the number of cells along the y-direction. In Eqs. 30c and 31c, the friction factors of the liquid and solid phases were obtained from the equilibrium log-law wall function applied to the fluid and from the user-defined wall boundary condition of the solid phase (Eq. 12), respectively. As far as the y-momentum equations are concerned, the no-slip conditions impose that \(U_{k,y}^{I,j=1}\)=0 and \(U_{k,y}^{I,j=N_y+1}\)=0.
The system of the algebraic, FV equations for the mass conservation of the two phases, the momentum conservation of the two phases, and the transport of the turbulent variables k and \(\varepsilon\) in the 2D domain was solved iteratively by means of the SIMPLEST [27] and IPSA [17] algorithms of Spalding, using the PHOENICS code version 2018. In PHOENICS, the calculation procedure is organized in a slab-by-slab manner, in which the equation-solving operation moves through the grid in the z-direction, and all the dependent variables are solved at the current slab before the solver routine moves to the next slab. The PHOENICS solver was run until the sum of the absolute residual errors over the whole solution domain is less than 1% of reference quantities based on the total inflow of the variable in question. Appropriate under-relaxation of the field variables was required to achieve convergence. Inertial relaxation is applied to the momentum equations with a false-time step of 0.1 s. A linear relaxation factor of 0.5 is applied to all other flow variables. In order to reduce the considerable computational demand of output generation, each simulation consisted of two subsequent runs. No user-defined variable was stored until a converged steady-state solution was reached, which required approximately 4000 iterations based on a standard initialization from the inlet conditions. Afterwards, storage and print out of the terms in the streamwise momentum equations was activated, and the simulation was restarted from its previous state for further 50 iterations. The simulations were run on a desktop computer with Intel Core i7\(-\)4790 CPU @ 3.60 GHz 3.60 GHz and 8.00 GB RAM using a single processor. The overall simulation time was about 90 minutes, about half of which was needed for the 50 iterations restart only. Finally, the PHOENICS output was imported into MATLAB and post-processed using dedicated in-house subroutines.
4 Results and discussion
4.1 Case studies
The case studies considered in the present work can be interpreted as the “channel-flow” analogous of the fine glass-bead slurry pipe flow experiments of Matoušek et al. [28], in the sense that the distance between the parallel plates, H, was equal to the pipe diameter in [28] and the other features of the flow (characteristics of the solid particles, bulk-mean velocity of the mixture and area-averaged concentration) were the same. Particularly, H was 0.10 m, and the particles were glass beads with mean diameter 0.18 mm and density 2450 kg/\(\hbox {m}^3\). Twelve different flow conditions were simulated, combining three bulk-mean velocities (\(V_{\mathrm {m}}\)=2.25, 3.0, and 4.0 m/s), and four area-averaged volumetric concentrations (\(C_A\)=0.11, 0.18, 0.25, 0.38).
At the inlet section, the streamwise velocity of both phases and the solid volume fraction were imposed as uniformly distributed, their values being equal to \(V_{\mathrm {m}}\) and \(C_A\), respectively. The values of k and \(\varepsilon\) at the same boundary were set based on an inlet turbulent intensity \(TI_{\mathrm {inlet}}\)=0.05 and a length scale equal to 0.07H, as these are the default settings in PHOENICS. In this paper, no sensitivity analysis will be presented regarding the effect of varying \(TI_{\mathrm {inlet}}\), since this parameter was found to have practically no influence on the numerical solution in the fully-developed region. In fact, numerical tests on case \(V_{\mathrm {m}}\)=4.0 m/s and \(C_A\)=0.38, in which \(TI_{\mathrm {inlet}}\) was 0.0, 0.05, and 0.10, showed that production and dissipation of turbulence are mainly associated with the effect of the solid walls, and that the level of turbulence in the unform flow at the inlet affects only the very first development of the boundary layer, but not the fully-developed flow field.
In this study, \(\beta\) and \(\sigma\) were set as 1.0 and 0.7, respectively, since previous research indicated that such combination of values procured a reasonably accurate prediction of the experimental findings [28] for the circular pipe counterpart of the channel-flow cases discussed hereafter. Note that, provided that a plausible set of constants was used, the specific values of \(\beta\) and \(\sigma\) are not relevant to the purpose of this study, which focuses on ideal numerical benchmark cases without an experimental validation. The analysis of the influence of \(\beta\) and \(\sigma\) is shelved for future research work.
4.2 Effect of the computational mesh
Preliminary analyses were made to assess the influence of the computational mesh on the numerical results for the reference case of \(V_{\mathrm {m}}\)=4.0 m/s and \(C_A\)=0.38. As already mentioned, the grid consisted of rectangular elements with uniform spacing along the z-direction and the fully-developed profiles were extracted from section \(z=170H\). After verifying the minor influence of the number of subdivisions in z direction, this parameter was set constant and equal to \(N_z=1000\). Initially, the mesh spacing in direction y was kept uniform and the corresponding number of cells was progressively doubled, as follows: \(N_y=25\), \(N_y=50\), and \(N_y=100\). These meshes were referred to as Grid 1, Grid 2, and Grid 3, respectively, and they are shown in Fig. 4. At first, the mesh sensitivity analysis was made by referring to basic fluid dynamic variables such as the vertical profiles of \(\alpha _{\mathrm {s}}\), \(U_{{\mathrm {l}},z}\), and \(U_{{\mathrm {s}},z}\), which were found to be essentially grid-independent. Later, it was extended to the single terms in the FV equations and, particularly, the y-profiles of the different terms in the streamwise momentum equation for the solid phase (Eq. 20 with \(k={\mathrm {s}}\)). Since these terms arise from an integration of the momentum equation over each computational cells, clearly they do depend on the size of the mesh. Therefore, the comparison was possible only after “restricting” all solutions back to the coarsest mesh level, which is Grid 1. The followed procedure is partially exemplified in Fig. 5. The terms representing the fluxes through the north and south faces, which are \({\mathcal {C}}^{\mathrm {n}}(U_{k,z}^{i,J})\), \({\mathcal {C}}^{\mathrm {s}}(U_{k,z}^{i,J})\), \({\mathcal {D}}^{\mathrm {n}}(U_{k,z}^{i,J})\), \({\mathcal {D}}^{\mathrm {s}}(U_{k,z}^{i,J})\), \(\mathcal {PD}^{\mathrm {n}}(U_{k,z}^{i,J})\), \(\mathcal {PD}^{\mathrm {s}}(U_{k,z}^{i,J})\), were picked up every two cells (for Grid 2) and every four cells (for Grid 3). Conversely, the terms proportional to the cell volumes or to the top and bottom cell-face areas, which are \(\varPi ^{\mathrm {t}}(U_{k,z}^{i,J})\), \(\varPi ^{\mathrm {b}}(U_{k,z}^{i,J})\), and \({\mathcal {M}}(U_{k,z}^{i,J})\), were summed up in groups of two (for Grid 2) and four (for Grid 3).
As shown in Fig. 6, the numerical results indicated a significant effect of the mesh resolution, especially in the upper half of the domain. For most terms in Eq. 20, slow grid convergence was observed, whereas the total pressure-force term, \(\varPi (U_{{\mathrm {s}},z})=\varPi ^{\mathrm {t}}(U_{{\mathrm {s}},z})+\varPi ^{\mathrm {b}}(U_{{\mathrm {s}},z})\), was even found to diverge (Fig. 6d). In order to gather further insight into the influence of the spatial discretization, two additional meshes were defined, referred to as Grid 1A and Grid 2A. These two meshes are the analog of Grid 1 and 2 in the bulk region, but the cell spacing along the y-direction was progressively reduced close to the plates in such as a way that the height of the near-wall cells became equal to 0.01H, as in Grid 3 (Fig. 4). Figure 7 clearly shows that the influence of the mesh is highly reduced if the height of the first rows of cells is kept constant and, particularly, the solutions computed on Grids 2A and 3 are nearly indistinguishable from each other.
Exemplary results of the mesh sensitivity analysis based on Grids 1, 2, and 3. In order to better interpret the results in these plots, as in similar ones hereafter, the reader should bear in mind that gravity acts along direction \(-y\), as shown in Fig. 1
the same as Fig. 6 for Grids 1A, 2A, and 3
The curves in Fig. 7 suggested that the grid discretization error might be mostly related to the size of the near wall cells, which is particularly relevant as the wall boundary conditions of the two phases are applied to those elements. In order to verify such interpretation, the wall shear stresses of the two phases were plotted as a function of the corresponding dimensionless wall distances of the first grid nodes, \(y^+\). On the grounds of what was previously discussed, the absolute values of the wall shear stresses of the two phases \(k=\mathrm {l,s}\) on the lower “south” and upper “north” plates were calculated as:
where the meaning of all symbols have already been explained in Sect. 3. The dimensionless wall distance \(y^+\) was calculated with respect to the properties of the liquid phase, that is
Note that, since the solution of the two-fluid model is not symmetrical with respect to the mid plane of the channel, the values of \(y^+\) are different for the cells adjacent to the upper and lower plates. The results in Fig. 8 confirm that the influence of the wall distance of the first grid points on the wall shear stress is not negligible. In particular, whereas \(\tau _{\mathrm {l}}^{\mathrm {w,s}}\) and \(\tau _{\mathrm {s}}^{\mathrm {w,n}}\) increase with increasing \(y^+\), an opposite behaviour is observed for \(\tau _{\mathrm {l}}^{\mathrm {w,n}}\) and \(\tau _{\mathrm {s}}^{\mathrm {w,s}}\). The total wall shear stress, \(\tau ^{\mathrm {w,tot}}\), obtained by summing up the four contributions, decreases with increasing \(y^+\). The percentage deviation between the calculated \(\tau ^{\mathrm {w,tot}}\) at \(y^+=37\) and the estimated value at \(y^+= 130\) (obtained by linear interpolation from the two adjacent points) was found to be about 7.1%.
Effect of \(y^+\) on the total wall shear stress and each component. For each series, the percentage deviations are calculated between the first point and the value corresponding to \(y^+=130\), estimated by linear interpolation from the two nearest points. The values of \(y^+\) of the total wall shear stress data are the average over the upper and lower near-wall cells
The significant influence of the near-wall cell spacing upon \(\tau ^{\mathrm {w,tot}}\) might have important practical implications, since this parameter is related with the already mentioned hydraulic gradient, \(i_{\mathrm {m}}\), which is one of the key parameters in slurry pipeline design. From the momentum equation of the two phases, it can be easily demonstrated that, for the slurry flow between two parallel plates,
and, therefore, \(i_{\mathrm {m}}\) and \(\tau ^{\mathrm {w,tot}}\) have the same percentage deviation ( \(\approx 7.1\%\)). This finding was surprising since, when investigating the turbulent slurry flow in a horizontal pipe in [1], the influence of \(y^+\) upon \(i_{\mathrm {m}}\) was found to be practically negligible (\(<1\%\)) for \(y^+\) ranging from 20 to 90. In order to verify whether the different geometry was the reason for this unexpected difference, the circular-pipe analog of the present channel flow case was investigated. Thus, computational simulations were run for a horizontal pipe flow with diameter D=H=0.10 m, inlet bulk-mean velocity \(V_{\mathrm {m}}\)=4.0 m/s and area-averaged concentration \(C_A\)=0.38. The computational domain, the boundary conditions, and all other numerical settings were as reported in [1]. Particularly, the structured mesh used to discretize the 120D long pipe was defined in cylindrical-polar coordinates, and it consisted of 30, 30, and 200 subdivisions along the azimuthal, radial, and axial direction, respectively. The radial subdivisions were densified close to the pipe wall, and the thickness of the near-wall cells was adjusted to obtain the desired value of \(y^+\). As it will be shown later in Sect. 4.7, the hydraulic gradient (and, thus, the total wall shear stress) is not the same for the channel flow and circular pipe analog. Therefore, in order to make the results comparable, \(\tau ^{\mathrm {w,tot}}\) was normalized by dividing for the estimated value at \(y^+=130\), once again obtained by linear interpolation from the two adjacent points. Figure 9 revealed the existence of a geometry effect, in the sense that the increase in \(\tau ^{\mathrm {w,tot}}\) at low \(y^+\) is steeper for the circular pipe and more gradual for the channel. Note that, in the channel flow, \(y^+\) is the average over the values in the upper and lower cells, whereas in the circular pipe flow, this parameter is the average over the entire pipe wall circumference (30 cells). This might partially explain the results, since the average over a higher number of data points is expected to be a more robust measure. Repetition of the analysis for a different test case, namely, \(V_{\mathrm {m}}\) = 3.0 m/s and \(C_A\) = 0.11, confirmed the same geometry effect, but it also highlighted an influence of the flow conditions, primarily the concentration. As Fig. 9 suggests, the influence of \(y^+\) is enhanced at higher concentration. This behaviour is not fully surprising since, as the concentration decreases, the contribution of the liquid phase to the frictional losses becomes increasingly important and, as shown in Fig. 8, it is \(\tau _{\mathrm {s}}^{\mathrm {w}}\) rather than \(\tau _{\mathrm {l}}^{\mathrm {w}}\) that is mostly affected by \(y^+\).
Effect of \(y^+\) on the ratio between \(\tau ^{{\mathrm {w,tot}}}\) and the estimated value at \(y^+=130\), \(\tau ^{\mathrm {ref}}\): comparison between two channel flow cases and the corresponding circular pipe analogues. For the channel flow cases, \(y^+\) is the mean between the values of the upper and lower near-wall cells. For the pipe flow cases, \(y^+\) is the average over the entire pipe circumference
Based on the mesh sensitivity study described above, it was decided to run the reminder of the channel flow simulations using the \(100\times 1000\) cells mesh (Grid 3). Such level of discretization, in fact, is sufficiently fine to accurately predict the y-profiles of the terms in the momentum equation in the bulk region of the flow (Fig. 9). At the same time, is corresponds to values of \(y^+\) around 75, 60, and 45 for \(V_{\mathrm {m}}\) equal to 4.0, 3.0, and 2.25 m/s, respectively. According to Fig. 9, such values of \(y^+\) are expected to produce consistent estimates of the total wall shear stress.
4.3 Flow characterization
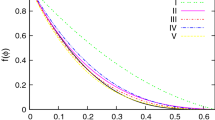
As it will be further discussed in Sect. 4.7, from a purely qualitative point of view, and if the attention is restricted to the vertical plane, the CFD solutions obtained in this work were similar to those previously obtained when simulating the slurry flow in circular pipes. The pressure decreases along the flow direction owing to the frictional losses, and the concentration increases towards the lower plate owing to the effect of gravity. As for the circular pipe case, the concentration profile tends to be uniform as either the concentration or the velocity increase (Fig. 10a, b).
For the flow conditions under investigation, the mean streamwise velocities of the two phases are almost indistinguishable to each other and, not surprisingly, the maximum \(U_{k,z}\) is shifted towards the upper plate. As shown in Fig. 11a, the degree of asymmetry of the \(U_{k,z}\) profiles increases with increasing concentration. The asymmetrical shape of the velocity profiles is a well-known feature of slurry pipe flows, which was explained by Ling et al. [29] by considering that, due to the effect of gravity, the density of the mixture is higher in the lower part of the pipe. Starting from the definition of the density of the mixture, \(\rho _{\mathrm {m}}=\rho _{\mathrm {l}}(1-\alpha _{\mathrm {s}})+\rho _{\mathrm {s}}\alpha _{\mathrm {s}}\), the gradient of \(\rho _{\mathrm {m}}\) along the y-direction is
Figure 10c shows that, in absolute terms, \(d\alpha _{\mathrm {s}}/dy\) increases with increasing \(C_{\mathrm {A}}\), especially in the upper part of the channel. According to Eq. 36, a similar influence will be exerted by \(C_{\mathrm {A}}\) on \(\rho _{\mathrm {m}}\), and this might provide a justification to the increase in the elevation of the point of maximum streamwise velocity. In interpreting the results in Fig. 11a, it must be noted that the \(\beta\)-\(\sigma\) two-fluid model applies to fully-suspended flows and, therefore, it ignores the effects of inter-particle collisions. Particle-particle interactions might become important for slurry flows at high concentration and, therefore, they could produce an effect on the velocity field that the \(\beta\)-\(\sigma\) model is not able to capture. In Fig. 11b, it is highlighted that the degree of asymmetry of the \(U_{k,z}\) profiles decreases with increasing flow velocity. This is not surprising since at high \(V_{\mathrm {m}}\), the fluid turbulence become more and more effective in keeping the solid suspended, and the flow tends to become homogeneous, with uniform distribution of the solids and axisymmetric velocity profiles. Further confirmation of this behavior can be found in Fig. 10d, which shows that, in absolute terms, \(d\alpha _{\mathrm {s}}/dy\) decreases with increasing flow velocity.
In the fully developed region, there exist also two transversal velocity components, which undergo smooth variations throughout the vertical plane. Both \(U_{{\mathrm {l}},y}\) and \(U_{{\mathrm {s}},y}\) are of the order of a few per thousands of the bulk-mean velocity but, whereas \(U_{{\mathrm {l}},y}\) is directed upwards, \(U_{{\mathrm {s}},y}\) is directed downwards (Fig. 11c, d).
This unusual feature of the \(\beta\)-\(\sigma\) two-fluid model arises from the presence of phase diffusion fluxes in the mass conservation equations. In fact, integration of Eq. 15 from \(y=0\) up to the generic y yields, after some algebraic manipulation
Due to the effect of gravity, the solid concentration \(\alpha _{\mathrm {s}}\) decreases with increasing y (\(\partial \alpha _{\mathrm {s}}/\partial y<0\)), as already observed in Fig. 10a, b. Therefore, on the grounds of Eq. 37, \(U_{{\mathrm {s}},y}<0\), confirming the findings in Fig. 11c, d. Similarly, since \(\alpha _{\mathrm {l}}=1-\alpha _{\mathrm {s}}\), then \(\partial \alpha _{\mathrm {l}}/\partial y>0\) and, therefore, \(U_{{\mathrm {l}},y}>0\).
Figure 11c, d also indicate that the crosswise velocities are affected by the solid concentration, \(C_A\), and the mixture velocity, \(V_{\mathrm {m}}\). The effect of these variables can be explained, once again, from Eq. 37. Later in this section it will be shown that the eddy viscosity of the liquid, \(\mu _{\mathrm {l}}^{\mathrm {t}}\), increases as either \(C_A\) or \(V_{\mathrm {m}}\) increase. Since also \(|\partial \alpha _{\mathrm {s}}/\partial y|\) becomes larger as \(C_A\) spans from 0.11 to 0.38 (Fig. 10c), then the product \(\mu _{\mathrm {l}}^{\mathrm {t}} \cdot |\partial \alpha _{\mathrm {s}}/\partial y|\) increases with increasing concentration. At the same time, \(1/\alpha _{\mathrm {s}}\) becomes smaller, resulting in an overall decrease of \(|U_{{\mathrm {s}},y}|\) with increasing concentration, as indicated by the red curves in Fig. 11c. An opposite situation occurs for the liquid phase. In this case, \(\mu _{\mathrm {l}}^{\mathrm {t}}\), \(|\partial \alpha _{\mathrm {l}}/\partial y|\), and \(1/\alpha _{\mathrm {l}}\) all increase with increasing \(C_A\). The product of these terms produces a larger \(U_{{\mathrm {l}},y}\) at higher concentration, as confirmed by the blue series in Fig. 11c.
An analogous argument can be made to explain the effect of \(V_{\mathrm {m}}\) upon \(U_{k,y}\) for the same \(C_A\), highlighted in Fig. 11d. When increasing \(V_{\mathrm {m}}\), \(\mu _{\mathrm {l}}^{\mathrm {t}}\) becomes larger and \(|\partial \alpha _k/\partial y|\) becomes smaller (Fig. 10d). Since \(1/\alpha _k\) is broadly the same for all simulations with the same \(C_A\), the opposite trends of \(\mu _{\mathrm {l}}^{\mathrm {t}}\) and \(|\partial \alpha _k/\partial y|\) with \(V_{\mathrm {m}}\) combine to yield almost stable values of \(U_{k,y}\). As a result, \(U_{k,y}\) becomes a progressively smaller fraction of \(V_{\mathrm {m}}\) as this variable increases, providing some justification to the results in Fig. 11d.
Profiles of mean streamwise velocity of the liquid phase and of the transversal velocity of both phases for different combinations of \(C_A\) and \(V_{\mathrm {m}}\). In plots c and d, the blu and red series represent the liquid and solid phase, respectively. In plots a and c, results are also reported for the single-phase case with \(V_{\mathrm {m}}=4\hbox { m/s}\)
The viscosities of the solid phase, \(\mu _{\mathrm {s}}\), and the eddy viscosities of both phases, \(\mu _{\mathrm {l}}^{\mathrm {t}}\) and \(\mu _{\mathrm {s}}^{\mathrm {t}}\), are important parameters in the \(\beta\)-\(\sigma\) two-fluid model, as they have a direct influence on diffusion and phase diffusion. Figure 12a, b show the ratio of the solid to liquid viscosities for different combinations of \(C_A\) and \(V_{\mathrm {m}}\). Taking Eqs. 7 and 11 into account, it is not surprising to see that \(\mu _{\mathrm {s}}\) increases with the local solid volume fraction and, consequently, with the area-averaged concentration, \(C_A\). Conversely, \(\mu _{\mathrm {s}}\) is only minorly affected by \(V_{\mathrm {m}}\). In this study, the maximum solid viscosity occurred in the lower near-wall cell for case \(C_A=0.38\) and \(V_{\mathrm {m}}=2.25\) m/s, and it was around \(50 \cdot \mu _{\mathrm {l}}\).
Figure 12c, d show the vertical profile of the total viscosity of the liquid phase, \(\mu _{\mathrm {l}} + \mu _{\mathrm {l}}^{\mathrm {t}}\), normalized by its laminar component \(\mu _{\mathrm {l}}\), for the same combinations of \(C_A\) and \(V_{\mathrm {m}}\). As typical of highly turbulent flows, the eddy viscosity \(\mu _{\mathrm {l}}^{\mathrm {t}}\) is much larger than the laminar component \(\mu _{\mathrm {l}}\), and, particularly, it was found to be about three orders of magnitude higher. This implies that \(\mu _{\mathrm {l}}\) is substantially negligible compared to \(\mu _{\mathrm {l}}^{\mathrm {t}}\). Similar considerations can be done for the viscosities of the solid phase. In fact, starting from Fig. 12c, d and considering that \(\mu _{\mathrm {s}}^{\mathrm {t}}=\mu _{\mathrm {l}}^{\mathrm {t}} \cdot \rho _{\mathrm {s}} / \rho _{\mathrm {l}} \approx 2.5 \cdot \mu _{\mathrm {l}}^{\mathrm {t}}\) (Eq. 4) and \(\mu _{\mathrm {s}}<50 \cdot \mu _{\mathrm {l}}\), it is clear that \(\mu _{\mathrm {s}}\) is negligible compared to \(\mu _{\mathrm {s}}^{\mathrm {t}}\).
Based on the above, neglecting \(\mu _{\mathrm {l}}\) and \(\mu _{\mathrm {s}}\) in the diffusive terms of the momentum equations (Eqs. 23a and 23b) is not likely to produce any change to the numerical solution. Conversely, \(\mu _{\mathrm {s}}\) plays a significant role in the evaluation of the interfacial momentum transfer terms (Eqs. 29a and 29b), and of the wall shear forces of the solid phase (Eqs. 30c and 31c). In fact, on one hand, \(\mu _{\mathrm {s}}\) directly appears in the wall Reynolds number of the solid phase \(Re^{\mathrm {w}}_{\mathrm {s}}\), used to calculate the friction factor \(s_{\mathrm {s}}\) (Eq. 12). On the other, \(\mu _{\mathrm {s}}\) affects the Reynolds number \(Re_{\mathrm {m}}\) used to calculate the drag coefficient (Eqs. 9 and 10) because \(\mu _{\mathrm {m}}\) is related to \(\mu _{\mathrm {s}}\) through Eq. 7. Starting from the vertical profiles of \(\mu _{\mathrm {s}}/\mu _{\mathrm {l}}\) (such as those exemplified in Fig. 12a, b), it is possible to find out the corresponding profiles of \(\mu _{\mathrm {m}}/\mu _{\mathrm {l}}\). \(\mu _{\mathrm {m}}\) is approximately equal to \(1.4\cdot \mu _{\mathrm {l}}\), 1.7\(\cdot \mu _{\mathrm {l}}\), \(2.3\cdot \mu _{\mathrm {l}}\), and 4.6\(\cdot \mu _{\mathrm {l}}\) for \(C_A=0.11, 0.17, 0.25, 0.38\) in the bulk-region of the domain, whereas it reaches peaks around 30\(\cdot \mu _{\mathrm {l}}\) close to the lower plate for \(C_A=0.38\). As a result, the drag coefficient evaluated with respect to \(\mu _{\mathrm {m}}\) is much higher than that obtained using the classical particle Reynolds number \(\rho _{\mathrm {l}}d_{\mathrm {p}}U_{\mathrm {rel}}/\mu _{\mathrm {l}}\).
Ratio of solid to liquid viscosities (a, b) and of total viscosity of liquid divided by laminar component (c, d) for different combinations of \(C_A\) and \(V_{\mathrm {m}}\). Note that the profiles of \(1+\mu _{\mathrm {s}}^{\mathrm {t}}/\mu _{\mathrm {s}}\) are approximately equal to those of \(1+\mu _{\mathrm {l}}^{\mathrm {t}}/\mu _{\mathrm {l}}\) multiplied by the density ratio \(\rho _{\mathrm {s}}/\rho _{\mathrm {l}} \approx 2.5\)
Finally, for the same of completeness, the characterization of the flow has been extended to the hydraulic gradient, \(i_{\mathrm {m}}\), depicted in Fig. 13 as a function of the bulk-mean velocity and the area-averaged concentration for all the case studies. Not surprisingly, the \(i_{\mathrm {m}}\) was found to increase with either \(C_A\) and \(V_{\mathrm {m}}\).
4.4 Vertical profiles of the terms in the streamwise momentum equations
After focusing on the fluid dynamic variables produced as output by the \(\beta\)-\(\sigma\) two-fluid model, the analysis was extended at the deeper level of the single terms in the FV equations, in order to gather further understanding of the model from the point of view of its mathematical structure. Referring, once again, to the case \(C_A=0.11\) and \(V_{\mathrm {m}}\)=4 m/s, the profiles along direction y of all terms in the \(U_{k,z}\)-momentum equations (Eq. 20) are reported in Fig. 14a,b for the liquid phase and the solid one, respectively. Although complexity of the two-fluid model makes the interpretation of the plots a challenging task, the following considerations help to correlate the curves in Fig. 14a, b with the fluid dynamic solution presented in Sect. 4.3.
a, b Profiles of each term in Eq. 20 and c, d net balances for case \(C_A=0.11\) and \(V_{\mathrm {m}}\)=4 m/s. The two \(\varPi\)-terms are out of scale in plot (a)
Firstly, the \({\mathcal {D}}^{\mathrm {n}} (U_{k,z})\)-distributions can be correlated with the corresponding \(U_{k,z}\) profiles, shown in Fig. 11a. Eq. 23b indicates that \({\mathcal {D}}^{\mathrm {n}} (U_{k,z})\) is positive in the lower branch of the \(U_{k,z}\) profile, where \(\partial U_{k,z} / \partial y >0\), and negative in the upper branch, where \(\partial U_{k,z} / \partial y <0\). A zero \({\mathcal {D}}^{\mathrm {n}} (U_{k,z})\) corresponds to the maximum mean axial velocity and, not surprisingly, it occurs in the upper half of the channel.
Another interesting finding is that, for both phases, \({\mathcal {C}}^{\mathrm {n}} (U_{k,z})\) (Eq. 21c) and \(\mathcal {PD}^{\mathrm {n}} (U_{k,z})\) (Eq. 25c) are opposite in sign and broadly equal to each other. For the liquid phase, \({\mathcal {C}}^{\mathrm {n}} (U_{{\mathrm {l}},z})\) is negative since \(U_{{\mathrm {l}},y}>0\) (Fig. 11c, d), whereas \(\mathcal {PD}^{\mathrm {n}} (U_{{\mathrm {l}},z})\) is positive since \(\partial \alpha _{{\mathrm {l}},z} / \partial y >0\). In the same way, for the solid phase, \({\mathcal {C}}^{\mathrm {n}} (U_{{\mathrm {s}},z})\) is positive since \(U_{{\mathrm {s}},y}<0\) (Fig. 11c, d), whereas \(\mathcal {PD}^{\mathrm {n}} (U_{{\mathrm {s}},z})\) is negative since \(\partial \alpha _{{\mathrm {s}},z} / \partial y <0\) (Fig. 10c, d). A justification of the fact that \({\mathcal {C}}^{\mathrm {n}} (U_{k,z}) \approx -\mathcal {PD}^{\mathrm {n}} (U_{k,z})\) can be obtained by combining the expressions of these terms (Eqs. 21c and 25c) with the mass conservation equations (Eq. 18). Since, for the liquid phase, \(U_{{\mathrm {l}},y}>0\) and \(\partial \alpha _{{\mathrm {l}},z} / \partial y >0\), then Eqs. 21c and 25c become:
Since the flow is fully-developed and the grid spacing is uniform along direction z, the fluxes \({\mathcal {F}}^{\mathrm {n}}\) and \(\varPhi ^{\mathrm {n}}\) of the control volume of \(U_{{\mathrm {l}},z}^{i,J}\) (Fig. 3d) will be the same as those of the control volume of the mass conservation equation \(1_{\mathrm {l}}^{i,J}\) (Fig. 3b). Therefore, Eq. 38 can be rewritten as:
By summing up the mass conservation equation of the liquid phase (Eq. 18 with \(k={\mathrm {l}}\)) for J ranging from 1 to the generic J, and considering that \({\mathcal {C}}^{\mathrm {s}}(1_{\mathrm {l}}^{I,J=1})=0\) (Eq. 30a) and \(\mathcal {PD}_{\mathrm {l}}^{\mathrm {s}}(1^{I,J=1})=0\) (Eq. 30b), the following constraint is obtained:
Taking into account the formulas for \({\mathcal {C}}^{\mathrm {n}} (1_{\mathrm {l}}^{I,J})\) (Eq. 21a) and \(\mathcal {PD}^{\mathrm {n}} (1_{\mathrm {l}}^{I,J})\) (Eq. 25a), the above equation becomes:
Comparing Eqs. 39 and 41, it follows that \({\mathcal {C}}^{\mathrm {n}}(U_{{\mathrm {l}},z}^{i,J}) + \mathcal {PD}^{\mathrm {n}}(U_{{\mathrm {l}},z}^{i,J}) \approx 0\) if \(U_{{\mathrm {l}},z}^{i,J} \approx U_{{\mathrm {l}},z}^{i,J+1}\), which appears to be the case if the grid is sufficiently fine. A similar argument can be applied to the solid phase.
As far as the pressure force terms are concerned, it can be noted that, since \(U_{k,y}\) is very small, the y-momentum equations (Eq. 19) reduce to:
and, therefore:
where \(P^{\mathrm {w,n}}\) is the pressure in correspondence to the upper wall at a certain distance z from the inlet section. Comparison of Eq. 43 and the formula for the \(\varPi (U_{k,z})\)-terms (Eq. 27d) helps to understand why the vertical profiles of \(\varPi ^{\mathrm {t}}(U_{{\mathrm {l}},z})\) and \(\varPi ^{\mathrm {b}}(U_{{\mathrm {l}},z})\) are as shown in Fig. 14b (the corresponding profiles for the liquid phase are out of scale in Fig. 14a).
Finally, Fig. 14a, b also indicate that, for both phases, the interphase friction force \({\mathcal {M}}(U_{k,z})\) is generally much smaller than the other terms of the \(U_{k,z}\)-momentum equations. This is not surprising since, as already mentioned, the difference between the mean streamwise velocities of the two phases is very small for the fully-suspended slurry flows considered in this study.
Some considerations around the main physical mechanisms driving the slurry transport can be made by grouping the \({\mathcal {C}}\)-, \({\mathcal {D}}\)-, \(\mathcal {PD}\)-, and \(\varPi\)-terms together, thereby referring to the net convection, \({\mathcal {C}}(U_{k,z}^{i,J})={\mathcal {C}}^{\mathrm {n}}(U_{k,z}^{i,J})+{\mathcal {C}}^{\mathrm {s}}(U_{k,z}^{i,J})\), the net diffusion, \({\mathcal {D}}(U_{k,z}^{i,J})={\mathcal {D}}^{\mathrm {n}}(U_{k,z}^{i,J})+{\mathcal {D}}^{\mathrm {s}}(U_{k,z}^{i,J})\), the net phase diffusion, \(\mathcal {PD}(U_{k,z}^{i,J})=\mathcal {PD}^{\mathrm {n}}(U_{k,z}^{i,J})+\mathcal {PD}^{\mathrm {s}}(U_{k,z}^{i,J})\), and the net pressure force, \(\varPi (U_{k,z}^{i,J})=\varPi ^{\mathrm {t}}(U_{k,z}^{i,J})+\varPi ^{\mathrm {b}}(U_{k,z}^{i,J})\). As shown in Fig. 14c, d, the “net” profiles in the bulk region are about an order of magnitude smaller compared to those of the single terms. On the grounds of the previous discussion, the net convection and the net phase diffusion broadly cancel out, and, therefore, the slurry transport appears mainly governed by inter-phase friction, pressure gradient, and within-phase diffusion. Whereas, for both phases, pressure gradient acts as driving force and within-phase diffusion acts as resistance force, the role played by inter-phase friction is different for solids and liquid. On one hand, the interaction with the liquid accelerates the particles, and therefore, inter-phase friction is a driving force for the solid phase. On the other hand, the particles slow down the liquid, and, therefore, \({\mathcal {M}}\) represents a resistance force in the \(U_{{\mathrm {l}},z}\)-momentum equation.
In order to make the interpretation of the slurry flow results in Fig. 14 easier, they were compared with those of pure water flow at the same bulk-mean velocity, \(V_{\mathrm {m}}\)=4 m/s. The single-phase flow simulations were performed using the same domain, computational mesh, differencing schemes, convergence criteria, and under-relaxation factors of the slurry flow ones. The FV formulation of the streamwise momentum equation for the single phase case (identified by subscript “sp”) is
and the \({\mathcal {C}}\)-, \({\mathcal {D}}\)-, and \(\varPi\)-terms are calculated by using the same formulas illustrated in Sect. 3 after setting the volume fraction to a unit value. From the mass conservation principle (Eq. 15) and the no-slip condition at the walls, it immediately follows that no y-velocity exists if only one phase is present, as it is also confirmed in Fig. 11c. Therefore, \({\mathcal {C}}^{\mathrm {n}} (U_{\mathrm {sp},z}^{i,J})={\mathcal {C}}^{\mathrm {s}} (U_{\mathrm {sp},z}^{i,J})=0\), and the mass transport is governed by a balance between pressure gradient, which acts as driving force, and viscous and turbulent diffusion, which act as resistance force. The profiles of the individual terms in Eq. 44 are their net effects are shown in Fig. 15a, b, respectively. As it is well known from fundamental fluid mechanics [23], the total shear stress varies linearly along the y-direction, and it becomes zero at half of the channel height where the streamwise velocity has the maximum value (Fig. 11a). The net \({\mathcal {D}}\)-, and \(\varPi\)-terms are uniform throughout the channel, and they balance each other.
a Profiles of each term in Eq. 44 and b net balances for pure water flow with \(V_{\mathrm {m}}=4\hbox { m/s}\)
In the simulation of slurry transport processes, the near-wall cells are a very relevant region of the flow domain, since the wall shear stresses dictating the energy consumption are applied at these locations. Figure 16a, b highlight, in the form of vertical bars, the values of the different terms of the streamwise momentum equations in the lower and upper near\(-\)wall cells for the case under investigation, namely, \(C_A=0.11\) and \(V_{\mathrm {m}}\)=4 m/s. On the grounds of Eqs. 30a and 30b, in the cells adjacent to the lower plate, \({\mathcal {C}}^{\mathrm {s}} (U_{k,z}^{i,J=1})\)=0 and \(\mathcal {PD}^{\mathrm {s}} (U_{k,z}^{i,J=1})\)=0. Similarly, on the grounds of Eqs. 31a and 31b, in the cells adjacent to the upper plate, \({\mathcal {C}}^{\mathrm {n}} (U_{k,z}^{i,J=N_Y})\)=0 and \(\mathcal {PD}^{\mathrm {n}} (U_{k,z}^{i,N_Y})\)=0. The \({\mathcal {D}}^{\mathrm {s}} (U_{k,z}^{i,J=1})\) and the \({\mathcal {D}}^{\mathrm {n}} (U_{k,z}^{i,J=N_Y})\) terms represent the wall shear forces acting on the two plates, and they were calculated from Eqs. 30c and 31c, respectively. Not surprisingly, the net \({\mathcal {D}}\)-terms (\(={\mathcal {D}}^{\mathrm {n}}+{\mathcal {D}}^{\mathrm {s}}\)) are negative in the near-wall cells, since within phase diffusion provides resistance to the flow. In a similar way, the driving, pressure terms are positive. It is interesting to comment about the sign of the interphase friction force, \({\mathcal {M}}(U_{k,z}^{i,J})\). Owing to their higher density, in a horizontal slurry flow the particles are transported at lower velocity compared to the carrier fluid, and therefore, as already mentioned, the friction between the two phases acts as driving force for the solid phase and as resistance force for the liquid phase. The predictions of the \(\beta\)-\(\sigma\) two-fluid model confirm this behaviour over most of the channel height, where \({\mathcal {M}}(U_{{\mathrm {l}},z}^{i,J})<0\) and \({\mathcal {M}}(U_{{\mathrm {s}},z}^{i,J})>0\). However, these terms change their signs near the upper wall, indicating that the particles move faster than the fluid in that region. This might be interpreted as a consequence of the fact that the particle concentration has the lowest value in the upper near-wall cells and, therefore, the solid wall shear stress is relatively small there. As a result, in order to balance the pressure driving force, interphase friction must act as an additional resistance force slowing down the particles.
4.5 Effect of inlet concentration on the streamwise momentum balances
Parametric analyses were carried out to obtain insight into the influence of the area-averaged solid volume fraction, \(C_A\), and the slurry bulk-mean velocity, \(V_{\mathrm {m}}\), on the solution of the \(\beta\)-\(\sigma\) model. Particularly, the attempt was to analyze the fluid dynamic solution, illustrated in Sect. 4.3, on the grounds of the behavior of the terms in the FV equations. The study was performed for all combinations of \(C_A\) and \(V_{\mathrm {m}}\) summarized in Sect. 4.1, but the results will be reported and discussed only for the scenarios already seen in Sect. 4.3, namely, increasing \(C_A\) from 0.11 to 0.38 at costant \(V_{\mathrm {m}}\)=4 m/s, and increasing \(V_{\mathrm {m}}\) from 2.25 to 4 m/s at constant \(C_A\)=0.11. The present section is dedicated to the effect of \(C_A\).
Vertical profiles of some terms in Eq. 20 for \(V_{\mathrm {m}}=4\hbox { m/s}\) and \(C_A\) increasing from 0.11 to 0.38
The vertical profiles of \({\mathcal {D}}^{\mathrm {n}}(U_{k,z})\), \(\mathcal {PD}^{\mathrm {n}}(U_{k,z})\), \(\varPi (U_{k,z})\), and \({\mathcal {M}}(U_{k,z})\) are compared in Fig. 17 for different concentrations at \(V_{\mathrm {m}}\)=4 m/s. Note that all other terms can be immediately obtained from the constraints \({\mathcal {C}}^{\mathrm {s}}(U_{k,z})^{i,J}=-{\mathcal {C}}^{\mathrm {n}}(U_{k,z})^{i,J-1}\), \({\mathcal {D}}^{\mathrm {s}}(U_{k,z})^{i,J}=-{\mathcal {D}}^{\mathrm {n}}(U_{k,z})^{i,J-1}\), \(\mathcal {PD}^{\mathrm {s}}(U_{k,z})^{i,J}=-\mathcal {PD}^{\mathrm {n}}(U_{k,z})^{i,J-1}\), and by considering that \({\mathcal {C}}^{\mathrm {n}}(U_{k,z})^{i,J}+\mathcal {PD}^{\mathrm {n}}(U_{k,z})^{i,J} \approx 0\).
As already noticed, a zero value of \({\mathcal {D}}^{\mathrm {n}}(U_{k,z})\) corresponds to a local maximum in the \(U_{k,z}\)-profile. Therefore, Fig. 17a indicates that the elevation at which the mean axial velocity is larger increases with increasing \(C_A\), in agreement with Fig. 11a. Figure 17a also indicates that, whereas \(C_A\) has a clear effect on the \({\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {s}},z})\) (red curves of solid phase), it has minor influence on \({\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {l}},z})\) (blue curves of liquid phase). An explanation of this behaviour could be found by considering that \({\mathcal {D}}^{\mathrm {n}}(U_{k,z})\) is directly proportional to the product of the volume fraction \(\alpha _k\), the total viscosity \(\mu _k + \mu _k^{\mathrm {t}} \approx \mu _k^{\mathrm {t}}\), and the gradient of the streamwise velocity \(U_{k,z}\) along direction y (Eqs. 23b and 24b). Unlike those of \(U_{k,z}\), and, therefore, those of \(dU_{k,z}/dy\), the y-profiles of \(\alpha _k\) and \(\mu _k^{\mathrm {t}}\) are significantly affected by \(C_A\) (Figs. 10a, 11a, and 12c). Looking at the fluid dynamic results in Sect. 4.3, is it not surprising to see that the \({\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {s}},z})\)-profile strongly increases with increasing \(C_A\), especially in the lower half of the channel (red curves of solid phase in Fig. 17a). A different situation is found for the liquid, since, for that phase, increasing \(C_A\) causes \(\mu _{\mathrm {l}}^{\mathrm {t}}\) to increase and \(\alpha _{\mathrm {l}}\) to decrease. The two effects broadly cancel out, resulting in \({\mathcal {D}}^{\mathrm {s}}(U_{{\mathrm {l}},z})\) profiles which are rather insensitive to the inlet concentration (blue curves of liquid phase in Fig. 17a).
The effect of \(C_A\) on the phase diffusion term is shown in Fig. 17b. Clearly, in absolute terms, both \(\mathcal {PD}^{\mathrm {n}}(U_{{\mathrm {l}},z})\) and \(\mathcal {PD}^{\mathrm {n}}(U_{{\mathrm {s}},z})\) increase with the inlet concentration. Starting from the formula for evaluating \(\mathcal {PD}^{\mathrm {n}}(U_{k,z})\) (Eq. 25c), this behavior is in clear correspondence with the fact that both \(\mu _{\mathrm {l}}^{\mathrm {t}}\) and \(|\partial \alpha _k/\partial y|\) increase with increasing \(C_A\) (Figs. 10c and 12c).
As far as the net pressure force is concerned, both \(\varPi (U_{{\mathrm {l}},z})\) and \(\varPi (U_{{\mathrm {s}},z})\) increase with increasing \(C_A\) (Fig. 17c). Summing up Eq. 20 for both phases and for all cells in the y direction yields:
The FV equation above clearly highlights that the increase in pressure force with inlet concentration is associated with the wall shear stresses and, at the macroscopic level, it results in a higher hydraulic gradient, as already seen in Fig. 13. The profiles of \(\varPi (U_{{\mathrm {l}},z})\) and \(\varPi (U_{{\mathrm {s}},z})\) are directly proportional to the corresponding volume fractions. This is immediately evident by combining the FV analogue of Eq. 43 with the definition of \(\varPi (U_{k,z})\) (Eq. 27d). In fact, considering that, for fully developed flow, \(\alpha _k^{I,J}=\alpha _k^{I-1,J}\), and that \(A^{\mathrm {t}}=A^{\mathrm {b}}\):
From Eq. 46, it is also clear that \(\varPi (U_{{\mathrm {l}},z}^{i,J})+\varPi (U_{{\mathrm {s}},z}^{i,J})\) is independent of y.
Finally, Fig. 17d indicates that the interphase friction force of the solid phase, \({\mathcal {M}}(U_{{\mathrm {s}},z})\) slightly increases with \(C_A\) (in absolute terms). Starting from Eq. 29b, such behaviour was interpreted as a consequence of two aspects, namely, the increase in \(\alpha _{\mathrm {s}}\), and the increase in \(C_d\), which, in turn, is produced by the increase in the viscosity of the solid phase, \(\mu _{\mathrm {s}}\) (Fig 12a). It is interesting to note that the amount of negative slip close to the upper plate, that is, the (negative) difference between the fluid and solid streamwise velocities, increases with increasing \(C_A\). The trend of \({\mathcal {M}}(U_{{\mathrm {l}},z})\) can be derived immediately from that of \({\mathcal {M}}(U_{{\mathrm {s}},z})\) since \({\mathcal {M}}(U_{{\mathrm {l}},z})=-{\mathcal {M}}(U_{{\mathrm {s}},z})\).
4.6 Effect of inlet velocity on the streamwise momentum balances
The parametric analysis was then extended to the influence of \(V_{\mathrm {m}}\). Figure 18 is the analogous of Fig. 17 for \(C_A\)=0.11 and different values of \(V_{\mathrm {m}}\).
The same as Fig. 17 for \(C_A=0.11\) and \(V_{\mathrm {m}}\) equal to 2.25, 3.0, and 4.0 m/s
The \({\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {l}},z})\) profiles corresponding to the three values of \(V_{\mathrm {m}}\) are very different from each other, whereas the \({\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {s}},z})\) profiles undergo mild variations (Fig. 18a); however, for both phases, the effect of increasing \(V_{\mathrm {m}}\) is to enhance \({\mathcal {D}}^{\mathrm {n}}(U_{k,z})\). Starting from the definition of \({\mathcal {D}}^{\mathrm {n}}(U_{k,z})\) (Eqs. 23b and 24b), this behaviour can be correlated to the fact that increasing \(V_{\mathrm {m}}\) causes an increase in both \(|\partial U_{k,z}/\partial y|\) and \(\mu _k^{\mathrm {t}}\), whereas \(\alpha _k\) keeps almost the same for the three velocities (Figs. 10b, 11b, and 12d). Furthermore, at a given \(V_{\mathrm {m}}\), \(|\partial U_{k,z}/\partial y|\) is substantially the same for both phases, \(\mu _{\mathrm {s}}^{\mathrm {t}}\) is higher than \(\mu _{\mathrm {l}}^{\mathrm {t}}\) (since \(\mu _{\mathrm {s}}^{\mathrm {t}} = \rho _{\mathrm {s}}/\rho _{\mathrm {l}} \cdot \mu _{\mathrm {l}}^{\mathrm {t}} \approx 2.5\mu _{\mathrm {l}}^{\mathrm {t}}\)), and \(\alpha _{\mathrm {s}} \ll \alpha _{\mathrm {l}}\) for \(C_A\)=0.11. The combination of these effects makes \(|{\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {s}},z})|<|{\mathcal {D}}^{\mathrm {n}}(U_{{\mathrm {l}},z})|\), as observed in Fig. 18a.
The results in Figs. 18b and 18c, concerning the influence of \(V_{\mathrm {m}}\) on the \(\mathcal {PD}^{\mathrm {n}}(U_{k,z})\) and \(\varPi (U_{k,z})\) profiles, appear easier to interpret. As far as the phase diffusion terms are concerned, it might be simply noted that, whereas \(|\partial \alpha _{k,z}/\partial y|\) is rather minorly affected by \(V_{\mathrm {m}}\), \(\mu _{\mathrm {l}}^{\mathrm {t}}\) strongly increases with \(V_{\mathrm {m}}\) (Figs. 10d and 12d). At the same time, the pressure force needed to convey a slurry flow is obviously an increasing function of velocity, making the behaviour of the curves in Fig. 18c not surprising at all. Note that, due to the relatively low particle concentration (\(C_A\)=0.11), most of the driving pressure is spent to convey the carrier liquid.
Comparison of Figs. 17d and 18d might suggest that the interphase friction force is mostly affected by changes in concentration rather than by changes in velocity. The red curves in Fig. 18d indicate that, in absolute terms, \({\mathcal {M}}(U_{{\mathrm {s}},z})\) increases with increasing \(V_{\mathrm {m}}\), and this might be interpreted as a consequence of the finding that, in the bulk region of the flow, the (small) streamwise slip velocity, \(U_{{\mathrm {l}},z}-U_{{\mathrm {s}},z}\) scales almost linearly with \(V_{\mathrm {m}}\). Finally, as already noted, the behaviour of \({\mathcal {M}}(U_{{\mathrm {l}},z})\) can be immediately derived from that of \({\mathcal {M}}(U_{{\mathrm {s}},z})\) considering that \({\mathcal {M}}(U_{{\mathrm {l}},z})=-{\mathcal {M}}(U_{{\mathrm {s}},z})\).
4.7 Impact of this study for circular pipe flows and other two\(-\)fluid models
This work exemplifies, for a specific benchmark case, how the fluid dynamic solution of a CFD model could be correlated to and interpreted in the light of its mathematical structure. The choice of the benchmark case (that is, the fully developed turbulent slurry flow between two parallel horizontal plates, here referred to as “channel flow”) was guided by the need to keep the mathematical treatment sufficiently simple to make the derivation of the equations and the interpretation of the results as easy as possible. The circular pipe geometry is definitely more relevant for the applications, but analyzing the fully-developed flow in a horizontal pipe would have required dealing with three velocity components in a two-dimensional space. Furthermore, a circular pipe cannot be discretized using a cartesian grid of “brick” elements, thereby making it necessary to derive the finite volume formulation for either a cylindrical-polar or an unstructured mesh. At the same time, the channel flow and the circular pipe flow appear rather similar in nature, at least from a qualitative point of view. In order to provide further evidence of this similarity, each channel flow solution was compared with the circular pipe counterpart.
Obviously, the solid volume fraction decreases with increasing elevation above the pipe bottom also in the circular pipe. The isolines of constant solid volume fractions are nearly straight, horizontal lines in the pipe cross section and, therefore, the profile of \(\alpha _{\mathrm {s}}\) along the vertical diameter is fully representative of the concentration distribution. Figure 19 indicates that the concentration profiles of a channel flow and of a circular pipe flow are similar with each other at low \(C_A\), but they tend to deviate at high \(C_A\). This was interpreted as a consequence of the stronger coupling between the phases occurring in dense flows, which makes the lateral confinement of the pipe walls more effective and, therefore, tends to produce a more uniform distribution of the solids.
As far as the velocity field is concerned, Fig. 20a shows that, for a given \(V_{\mathrm {m}}\), the streamwise velocity distributions are different for channel flow and circular pipe flows, once again owing to the lateral confinement of the pipe walls. Careful inspection of the profiles reveals that an increase in the elevation of the point of maximum velocity with increasing \(C_A\) occurs also for circular pipe flows, but this effect is definitely less pronounced than in the channel flow case. In circular pipe flows, two crosswise velocity components exist, giving rise to in-plane vectors. The magnitude of the in-plane vectors is higher for the solid phase than for the liquid one, but, for both phases, it is only a relatively small fraction of \(V_{\mathrm {m}}\). The in-plane vectors of the liquid phase exhibit complex patterns, as exemplified in Fig. 20b for the specific case \(V_{\mathrm {m}}\)=4 m/s and \(C_A\)=0.11, which appear to be dependent upon the flow conditions. Conversely, the in-plane vectors of the solid phase tend to be directed downwards (Fig. 20c), as for the channel flow case. In the channel flow, the direction of the crosswise velocities was inferred from the mass conservation equations, taking the shape of the volume fraction profiles into account (Sect. 4.3). Similar considerations could not be made \(-\)at least not so easily \(-\)for the pipe flow case, due to the two-dimensional nature of the secondary flows. Finally, as exemplified in Fig. 20d, the difference between the streamwise velocities of the liquid and solid phase is only a few per thousands of the velocity of the mixture \(V_{\mathrm {m}}\). Close to the pipe crown, the particles move faster than the fluid, as already observed in the channel flow simulations.
a Profiles of mean streamwise fluid velocity profiles for channel flow and circular pipe flows for \(V_{\mathrm {m}}=4\hbox { m/s}\) and two values of \(C_A\); b, c, d pipe flow solution for \(V_{\mathrm {m}}=4\hbox { m/s}\) and \(C_A=0.11\) in terms of b in-plane vectors of liquid phase, c in-plane vectors of solid phase, d difference of streamwise velocities
The last point of comparison was the hydraulic gradient. As shown in Fig. 21, for a given flow velocity and area-averaged solid concentration, the hydraulic gradient of the pipe flow simulations is higher than that of the channel flow counterpart. This result is not surprising since, for the same flow area, the wetted perimeter is larger for pipe flows, thereby requiring more energy to convey the slurry.
The results in Figs. 19, 20 and 21 indicate that, from a quantitative point of view, the channel flow solution is not equal to the circular pipe flow counterpart along the vertical diameter. Nevertheless, similarities exist from a qualitative point of view, especially in relation with the influence exerted by \(V_{\mathrm {m}}\) and \(C_A\) on the volume fraction profiles, the streamwise velocities, the hydraulic gradient, and the eddy viscosity. The more significant qualitative differences between the two geometries are observed in terms of the secondary flow pattern, which is much more complicated in the circular pipe owing to the two-dimensional nature of the cross-wise velocity distributions. Therefore, the interpretative efforts done for the channel flow might help to explain some features of the circular pipe flow solution, whereas others require dealing with the higher complexity of the actual finite volume formulations.
The CFD model used in this study was the \(\beta\)-\(\sigma\) two\(-\)fluid model, as this was developed by the authors and it is currently the subject of their research. Anyway, as already discussed in the introduction, alternative two\(-\)fluid models exist in the literature for the simulation of slurry flows, and, therefore, it is useful to understand whether the present work might have sufficiently broad implications. Obviously, the importance of interpreting a fluid dynamic solution in the light of the mathematical structure of a CFD model abstracts from the specific model employed. Conversely, the derivations outlined in Sect. 3 are not only specific to the \(\beta\)-\(\sigma\) two\(-\)fluid model, but they also require the use of the finite volume method based on the staggered grid arrangement. Even leaving aside the last two aspects, the point about the specific two-fluid model formulation employed deserves attention.
Most two\(-\)fluid models used for the simulation of slurry flows in pipeline systems employ closures based on the Kinetic Theory of Granular Flows (KTGF). Compared to the \(\beta\)-\(\sigma\) model, the KTGF-based models used by [8,9,10,11,12,13,14,15,16] have the following differences: no phase-diffusion terms are included in any conservation equations, a solid pressure term \(-\nabla P_{\mathrm {s}}\) is added to the momentum equations of the solid phase, and no eddy viscosity of the solid phase is present. The solid pressure, \(P_{\mathrm {s}}\), and the solid viscosity, \(\mu _{\mathrm {s}}\), are both expressed as a function of the granular temperature of the solid phase, \(\varTheta _{\mathrm {s}}\), which is obtained from the solution of its own conservation equation and appears also in the formula for the wall shear stress of the solid phase. If such KTGF-based models were used to simulate the fully-developed channel flow, the FV formulation of the streamwise momentum equations would be different from Eq. 20, since: \(\mathcal {PD}^{\mathrm {n}}(U_{k,z})=\mathcal {PD}^{\mathrm {s}}(U_{k,z})=0\), due to the absence of the phase diffusion terms; for the solid phase, Eqs. 24a and 24b would not include \(\mu _{\mathrm {s}}^{\mathrm {t}}\); for the solid phase, two additional terms would be associated with the solid pressure, their sum being \(P_{\mathrm {s}}\left( \varTheta _{\mathrm {s}}\right) ^{I-1,J} A^{\mathrm {b}}-P_{\mathrm {s}}\left( \varTheta _{\mathrm {s}}\right) ^{I,J}A^{\mathrm {t}}\).
The absence of phase diffusion terms would have a direct effect on the fluid dynamic solution. Focusing on the fully-developed channel flow, Eq. 40 would reduce to \({\mathcal {C}}^{\mathrm {n}}(1_k^{I,J})=0\) if \(\mathcal {PD}^{\mathrm {n}}(1_k^{I,J})=0\). As a result, no transversal velocity components would be present (\(U_{k,y}=0\)). As already mentioned in [1], this would not be the case for circular pipe flows, where in-plane vectors have two components. Integration of the mass conservation equations up to a certain elevation y above the pipe bottom would yield, after some manipulation:
which implies that \(U_{k,y}\) must change its sign along each horizontal chord, \(\gamma\), for both k=l and k=s (Fig. 20c). A distribution of in-plane vectors all directed downwards, as in Fig. 20c, would not be consistent with the absence of phase diffusion terms. Note that, although the commonly-used KTGF-based models do not have phase-diffusion terms, the absence of these terms is not necessarily related to the use of KTGF closures. As it was well discussed by Burns et al. [18], the presence or the absence of phase diffusion terms arise from the type of averaging operator applied to the instantaneous flow equations.
As a final note, it is remarked that, sometimes, the momentum equations in two\(-\)fluid models are written in terms of the averaged stresses tensors. Although there is some variation among the different papers, the following formulation of the momentum equation for the liquid phase is one of the possible alternatives to Eq. 2:
where \({\mathbf {T}}_{\mathrm {l}}\) and \({\mathbf {T}}_{\mathrm {l}}^{Re}\) are the viscous and Reynolds stresses tensors of the liquid phase. Similarly to other authors, Jiang and Zhang [12] calculated the sum of the two tensors as:
where “+” indicates that the transpose of the dyadic \(\nabla {\mathbf {U}}_{\mathrm {l}}\) is taken, and \({\mathbf {I}}\) is the identity tensor. From the equation above, it immediately follows that:
After replacing Eq. 50 into Eq. 48 and comparing with Eq. 2, it is clear that the second and the third terms of Eq. 50 are neglected in the \(\beta\)-\(\sigma\) model. If accounted for, these terms would not produce significant changes to the solution of the fully-developed channel flow. In fact, for this particular flow, the last two terms are zero in the \(U_{{\mathrm {l}},z}\)-momentum equation, and provide only little contribution to the \(U_{{\mathrm {l}},y}\)-momentum one.
5 Conclusion
This article focuses on the numerical simulation of turbulent slurry flow between two horizontal plates in the fully-suspended regime, performed using the \(\beta\)-\(\sigma\) two-fluid model described in a previous publication [1]. However, the main added value of the contribution does not reside in the simulation results themselves but, rather, in the effort paid to correlate the fluid dynamic solution with the mathematical structure of the two\(-\)fluid model. Achieving this goal required gaining insight into the partial differential equations governing the flow, as well as their finite volume formulations, whose derivation is shown in Sect. 3 for the specific benchmark case.
Firstly, an extensive mesh sensitivity study was carried out, coming to the conclusion that the whole-field values of the elementary terms in the streamwise momentum equations are only minorly influenced by the overall mesh size, but they are strongly affected by the thickness of the cells adiacent to the solid walls. The macroscopic implication of this finding is that the predicted hydraulic gradient, or equivalently, the total wall shear stess, is subject to non-negligible changes when \(y^+\) of the near-wall cells varies in the range 30 to 150. The effect of \(y^+\) on the total shear stress is more gradual for the two-dimensional channel flow compared to the circular pipe flow, and it appears enhanced for high slurry velocity and solid concentration.
Disclosing the mathematical essence of the \(\beta\)-\(\sigma\) two-fluid model allowed providing an interpretation to the calculated volume fraction, velocity, and pressure fields for different combinations of bulk-mean velocity of the slurry and volume fraction of solids in the flow. Particularly, the degree of asymmetry of the axial velocity profiles of the two phases was correlated with the crosswise gradient of their volume fractions. As already noticed in [1], non-zero crosswise velocity components arise as a consequence of the presence of phase diffusion fluxes in the phasic continuity equations. In this study, a deeper insight was gained by relating the crosswise velocity components with the eddy viscosities, the volume fractions, and their crosswise gradients. Some discussion was also made around the relative importance of the laminar and eddy viscosities of the two phases.
Additionally, the single terms in the streamwise momentum equations, namely, convection, within-phase diffusion, phase diffusion, pressure-force, and inter-phase friction force, were investigated. The crosswise profiles of each elementary term were presented and correlated to those of the basic fluid dynamic output variables, such as velocity, volume fraction, and eddy viscosity. Clear relations were demonstrated between the convection and phase diffusion terms by exploiting the mass conservation principle. It was noticed that, even if the streamwise velocity difference between the two phases is small for the simulated cases, the inter-phase friction term is of the same order of magnitude of the net convection and of the net diffusion ones. This allowed identifying pressure force, within-phase diffusion, and inter-phase friction as the main driving and resistance forces governing slurry transport, opening the way to establishing their roles for different slurry velocities and concentrations.
In summary, the present work addresses the challenge of achieving the mathematical interpretation of the results in addition to and before providing physical justification. Its scope is to propose a methodological guidance for the development of CFD models for engineering use, which typically contain several sub-models, coefficients, and parameters of uncertain nature or difficult to be defined. The most important ones in the \(\beta\)-\(\sigma\) two-fluid model are the coefficients \(\beta\) and \(\sigma\). Without a deep insight into the mathematical features of the models, it would not be possible to shed light into the role played by such uncertain actors, thereby turning the models into real predictive tools and opening the way for further improvement. In this perspective, the last part of the article is devoted to underlining the impact of this study outside the specific benchmark case and two\(-\)fluid model used. Particularly, comparisons were presented between a plane channel flow and a circular pipe flow with the same bulk mean velocity and solid concentration. Finally, the methodological approach was expanded to alternative two\(-\)fluid models for slurry pipe flows, such as models not including phase diffusion terms or models employing different formulations of the viscous and Reynolds stresses tensor.
Abbreviations
- A :
-
Surface area of volume W (\(\hbox {L}^2\))
- \(C_A\) :
-
Area–averaged volume fraction (−)
- \(C_{1\varepsilon }\) :
-
Constant in Eq. 6 (−)
- \(C_{2\varepsilon }\) :
-
Constant in Eq. 6 (−)
- \(C_{\mu }\) :
-
Constant in Eq. 4 (−)
- \(C_{\mathrm {d}}\) :
-
Drag coefficient (−)
- \({\mathcal {C}}\) :
-
Convection term in FV equations
- D :
-
Pipe diameter (L)
- \({\mathcal {D}}\) :
-
Diffusion term in FV momentum equations (\(\hbox {MLT}^{-2}\))
- \(d_{\mathrm {p}}\) :
-
Volume-equivalent particle diameter (L)
- \(d_{\mathrm {p}}^{+}\) :
-
Dimensionless particle diameter, Eq. 13 (−)
- \(d_{\mathrm {p}}^{+\mathrm {B}}\) :
-
Estimate of \(d_{\mathrm {p}}^{+}\) using Eq. 14 (−)
- E :
-
Roughness parameter (−)
- \({\mathcal {F}}\) :
-
Outward convection flux through cell face (\(\hbox {MT}^{-1}\))
- \({\mathcal {G}}\) :
-
Gravitational force in FV y-momentum equations (\(\hbox {MLT}^{-2}\))
- g :
-
Modulus of the gravitational acceleration vector (\(\hbox {LT}^{-2}\))
- H :
-
Distance between the two plates (L)
- \(i_{\mathrm {m}}\) :
-
Hydraulic gradient (−)
- k :
-
Turbulent kinetic energy of the liquid phase (\(\hbox {L}^2\hbox {T}^{-2}\))
- M :
-
Component of \({\mathbf {M}}\) (\(\hbox {ML}^{-2}\hbox {T}^{-2}\))
- \({\mathcal {M}}\) :
-
Interphase friction force term in FV momentum equations (\(\hbox {MLT}^{-2}\))
- N :
-
Number of cells along a given direction (−)
- n :
-
Scalar coordinate corresponding to vector \({\mathbf {n}}\) (L)
- P :
-
Local double-averaged pressure (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \(P_k\) :
-
Volumetric production rate of k (\(\hbox {L}^2\hbox {T}^{-3}\))
- \(\mathcal {PD}\) :
-
Phase-diffusion term in FV equations (\(\hbox {MLT}^{-2}\))
- \(Re_{\mathrm {m}}\) :
-
Modified particle Reynolds number, Eq. 10 (−)
- \(Re^{\mathrm {w}}\) :
-
Wall Reynolds number (−)
- s :
-
Friction factor (−)
- \(TI_{\mathrm {inlet}}\) :
-
Turbulent intensity at inlet section (−)
- U :
-
Component of \({\mathbf {U}}\) (\(\hbox {LT}^{-1}\))
- \(U_{\mathrm {rel}}\) :
-
Modulus of the relative velocity between the phases (\(\hbox {LT}^{-1}\))
- \(V_{\mathrm {dl}}^{\mathrm {T}}\) :
-
Deposition-limit velocity estimated form Thomas’ correlation [24]
- \(V_{\mathrm {m}}\) :
-
Slurry bulk-mean velocity (\(\hbox {LT}^{-1}\))
- W :
-
Integration volume (\(\hbox {L}^3\))
- x :
-
Horizontal coordinate in pipe flow (L)
- y :
-
Horizontal coordinate (L)
- z :
-
Vertical coordinate (L)
- \(\alpha\) :
-
Local time-averaged volume fraction (−)
- \(\alpha '\) :
-
Fluctuating component of the local volume fraction (−)
- \(\beta\) :
-
Parameter of the two-fluid model (−)
- \(\varGamma _k\) :
-
Exchange coefficient (\(\hbox {ML}^{-1}\hbox {T}^{-1}\))
- \(\gamma\) :
-
Length of the horizontal chord of a circular pipe section (L)
- \(\delta\) :
-
Normal distance of the first grid point to the wall (L)
- \(\varepsilon\) :
-
Turbulence dissipation rate of the liquid phase (\(\hbox {L}^2\hbox {T}^{-3}\))
- \(\varTheta _{\mathrm {s}}\) :
-
Granular temperature (\(\hbox {L}^2\hbox {T}^{-2}\))
- \(\kappa\) :
-
von Karman constant (−)
- \(\mu\) :
-
Dynamic viscosity (\(\hbox {ML}^{-1}\hbox {T}^{-1}\))
- \(\mu _{\mathrm {m}}\) :
-
Friction, mixture-viscosity related parameter (\(\hbox {ML}^{-1}\hbox {T}^{-1}\))
- \(\mu ^{\mathrm {t}}\) :
-
Eddy viscosity (\(\hbox {ML}^{-1}\hbox {T}^{-1}\))
- \(\varPi\) :
-
Pressure-force term in FV momentum equations (\(\hbox {MLT}^{-2}\))
- \(\rho\) :
-
Density (\(\hbox {ML}^{-3}\))
- \(\sigma\) :
-
Turbulent Schmidt number for volume fractions (−)
- \(\sigma _k\) :
-
Constant in Eq. 5 (−)
- \(\sigma _\varepsilon\) :
-
Constant in Eq. 6 (−)
- \(\tau ^{\mathrm {ref}}\) :
-
Reference wall shear stress (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \(\tau ^{\mathrm {w}}\) :
-
Modulus of the wall shear stress (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \(\tau ^{\mathrm {w,tot}}\) :
-
Modulus of the total wall shear stress (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \(\varPhi\) :
-
Phase-diffusion flux (\(\hbox {MT}^{-1}\))
- \({\mathbf {g}}\) :
-
Gravitational acceleration vector (\(\hbox {LT}^{-2}\))
- \({\mathbf {M}}\) :
-
Interfacial momentum transfer term (\(\hbox {ML}^{-2}\hbox {T}^{-2}\))
- \({\mathbf {n}}\) :
-
Inward-directed unit normal vector to A (−)
- \({\mathbf {U}}\) :
-
Local double-averaged velocity vector (\(\hbox {LT}^{-1}\))
- \({\mathbf {U}}^\parallel\) :
-
Component of \({\mathbf {U}}\) parallel to the wall at the near-wall nodes (\(\hbox {LT}^{-1}\))
- \({\mathbf {u}}'\) :
-
Time fluctuating component of the locally-averaged velocity vector (\(\hbox {LT}^{-1}\))
- \({\tau }^{\mathrm {w}}\) :
-
Shear stress vector at the wall (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \({\mathbf {I}}\) :
-
Identity tensor (−)
- \({\mathbf {T}}\) :
-
Viscous stresses tensor (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \({\mathbf {T}}^{Re}\) :
-
Reynolds stresses tensor (\(\hbox {ML}^{-1}\hbox {T}^{-2}\))
- \(k'\) :
-
Phase indicator
- k :
-
Phase indicator
- \({\mathrm {l}}\) :
-
Liquid phase
- \({\mathrm {s}}\) :
-
Solid phase
- \(\mathrm {sp}\) :
-
Single-phase case
- y,z :
-
Along direction y,z
- \({\mathrm {b}}\) :
-
Bottom face
- I :
-
Index of cell centre along direction z
- i :
-
Index of “top” cell face along direction z
- J :
-
Index of cell centre along direction y
- j :
-
Index of “north” cell face along direction y
- \({\mathrm {n}}\) :
-
North face/upper “north” plate
- \({\mathrm {s}}\) :
-
South face/lower “south” plate
- \({\mathrm {t}}\) :
-
Top face
- \({\mathrm {w}}\) :
-
At the wall / in the near-wall cells
- CFD:
-
Computational fluid dynamics
- FV:
-
Finite volume
- KTGF:
-
Kinetic theory of granular flow
References
Messa GV, Matoušek V (2020) Analysis and discussion of two fluid modelling of pipe flow of fully suspended slurry. Powder Technol 30:747–768
Capecelatro J, Desjardins O (2013) Eulerian–Lagrangian modeling of turbulent liquid-solid slurries in horizontal pipes. Int J Multiph Flow 55:64–79
Arolla SK, Desjardins O (2015) Transport modeling of sedimenting particles in a turbulent pipe flow using Euler–Lagrange large eddy simulation. Int J Multiph Flow 75:1–11
Uzi A, Levy A (2018) Flow characteristics of coarse particles in horizontal hydraulic conveying. Powder Technol 326:302–321
Roco MC, Shook CA (1983) Modeling of slurry flow: the effect of particle size. Can J Chem Eng 61:494–503
Roco MC, Balakrishnam N (1985) Multi-dimensional flow analysis of liquid-solid mixtures. J Rheol 29:431–456
Chen RC (1994) Analysis of homogeneous slurry pipe flow. J Mar Sci Technol 2(1):37–45
Hernández FH, Blanco AJ, Rojas-Solórzano L (2008) CFD modeling of slurry flows in horizontal pipes. In: Proceedings of ASME 2008 fluids engineering summer meeting FEDSM2008, Paper No. 55103
Ekambara K, Sanders RS, Nandakumar K, Masliyah JH (2009) Hydrodynamic simulation of horizontal slurry pipeline flow using ANSYS-CFX. Ind Eng Chem Res 48:8159–8171
Antaya CL, Freeman K, Adane K, Sanders RS (2012) Modelling concentrated slurry pipeline flows. In: Proceedings of ASME 2012 fluids engineering summer meeting FEDSM2012, Paper No. 72379
Kaushal DR, Thinglas T, Tomita Y, Kuchii S, Tsukamoto H (2012) CFD modeling for pipeline flow of fine particles at high concentration. Int J Multiph Flow 43:85–100
Jiang YY, Zhang P (2013) Pressure drop and flow pattern of slush nitrogen in a horizontal pipe. AIChE J 59:1762–1773
Gopaliya MK, Kaushal DR (2015) Analysis of effect of grain size on various parameters of slurry flow through pipeline using CFD. Part Sci Technol 33:369–384
Gopaliya MK, Kaushal DR (2016) Modeling of sand-water slurry flow through horizontal pipe using CFD. J Hydrol Hydromech 64:261–272
Kumar N, Gopaliya MK, Kaushal DR (2019) Experimental investigations and CFD modeling for flow of highly concentrated iron ore slurry through horizontal pipeline. Part Sci Technol 37:232–250
Singh MK, Kumar S, Ratha D (2020) Computational analysis on disposal of coal slurry at high solid concentrations through slurry pipeline. Int J Coal Prep Util 40:116–130
Spalding DB (1980) Numerical computation of multi-phase fluid flow and heat transfer. In: Taylor C, Morgan K (eds) Prineridge Press Limited. Swansea, UK, pp 139–168
Burns AD, Frank T, Hamill I, Shi JM (2004) The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows. In: Proceedings of \(5^{{\rm th}}\) international conference on multiphase flow ICMF2004, Paper No. 392
Messa GV, Malavasi S (2014) Numerical prediction of dispersed turbulent liquid–solid flows in vertical pipes. J Hydraul Res 52:684–692
Launder BE, Spalding DB (1974) The numerical computation of turbulent flows. Comput Meth Appl Mech Eng 3:269–289
Schiller L, Naumann A (1935) A drag coefficient correlation. Z Ver Dtsch Ing 77:318–320
Cheng NS, Law AWK (2003) Exponential formula for computing effective viscosity. Powder Technol 129(1–3):150–160
Munson BR, Okiishi TH, Huebsch WW, Rothmayer AP (2013) Fluid mechanics, 7th edn. Wiley, Singapore
Thomas A (2015) A modification of the Wilson & Judge deposit velocity equation, extending its applicability to finer particles and larger pipe sizes. In: Proceedings of \(17^{{\rm th}}\) Int Conf Transport and Sedimentation of Solid Particles
Korving AC (2002) High concentrated fine-sand slurry flow in pipelines: experimental study. In: Proceedings of \(15^{{\rm th}}\) Int Conf Hydrotransport
Versteeg HK, Malalasekera W (2007) An introduction to computational fluid dynamics. The Finite Volume Method. Pearson Prentice Hall, Harlow UK
Spalding DB (1980) Mathematical modelling of fluid-mechanics, heat-transfer and chemical-reaction processes: a lecture course, CFDU Report HTS/80/1. Imperial College, London
Matoušek V, Krupička J, Konfršt J, Pěník V (2013) Internal structure of settling-slurry flows: solids distribution and friction in horizontal pipe. In: Proceedings of \(16^{{\rm th}}\) Int Conf Transport and Sedimentation of Solid Particles
Ling J, Skudarnov PV, Lin CX, Ebadian MA (2003) Numerical investigations of liquid-solid slurry flows in a fully developed turbulent flow region. Int J Heat Fluid Flow 24:389–398
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.. The research at the Institute of Hydrodynamics in Prague was supported by the Czech Academy of Sciences (project RVO 67985874).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Messa, G.V., Malin, M. & Matoušek, V. Parametric study of the \({\beta }\)-\({\sigma }\) two-fluid model for simulating fully suspended slurry flow: effect of flow conditions. Meccanica 56, 1047–1077 (2021). https://doi.org/10.1007/s11012-021-01314-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-021-01314-6