1 Introduction

It is not justified to categorize the fractional calculus theory as a young science. The origin of fractional calculus is as old as classical calculus itself. During the past few decades it has become the focus of interest of many disciplines of science and technology which provides an excellent and efficient tool for modeling and describing various scientific and complex engineering phenomena such as aerodynamics, polymer rheology, electrodynamics of complex medium, fluid-dynamic traffic model [23, 33, 34, 44, 56] etc. In the last few decades there have been a lot of research on the applications of fractional calculus theory to various scientific fields ranging from the physics of diffusion and advection phenomena to control system of finance and economics. Fractional differentiation has a lot of advantages on the simulation of dynamical systems and physical phenomena as compared to integer order differentiation, due to its non-Markovian and non-local behaviors. In many cases it is not possible to model the known equations in fractional order forms. For this some basic physical postulates are to be satisfied before giving its shape into fractional order system. Therefore every equation can not be generalised simply by replacing the integer order derivative by fractional order derivative.

From literature survey, it is seen that the fundamental ideas of the algorithms correlated to the ideas proposed by authors of [3, 57] and Bhrawy [6] have been used to develop the efficient and accurate algorithms for the purpose of solving partial differential equations [32]. Additionally, for finding the numerical solutions of linear fractional differential equations (FDEs), Bhrawy et al. [7] have developed an operational matrix with the popular Laguerre polynomials for the fractional order integration and have revised the generalized Laguerre polynomials on the semi-infinite intervals. In [1], the authors have introduced an operational matrix for the fractional order derivative for solving the linear and non-linear FDEs with given initial conditions.

A significant portion of fractional calculus theory is the two-dimensional fractional differential equations and integral equations which have further been studied in the articles [43, 45,46,47,48]. In [12], the authors have solved the two-dimensional fractional percolation equation in a non-homogeneous porous med- ium. In the present article, an accurate and efficient numerical technique has been proposed to solve two-dimensional fractional order reaction-diffusion equation arising in porous media.

Several kinds of flow problems like percolation flow problems, seepage flow problems have been examined and discussed in many aspects of research fields including groundwater hydraulics, seepage hydraulics, fluid dynamics and groundwater dynamics in the porous media [13, 26]. The two-dimensional flow of the solute in the porous medium is governed under the hypothesis of continuity and Darcy’s law is given by J. Bear and A. Verruijt [4] in the equation

$$\begin{aligned} \frac{\partial }{\partial x}(k_{x} \frac{\partial P}{\partial x}) + \frac{\partial }{\partial y}(k_{y} \frac{\partial P}{\partial y}) =A_{0}\frac{\partial P}{\partial t}, (x,y) \in \varOmega , \end{aligned}$$
(1)

where \(A_{0}\) denotes the specific storativity, which is approximated by the effective porosity or specific yield; P denotes the pressure head, the intrinsic permeability of the medium is given by \(K= \frac{k \rho g}{\mu }\), which is the hydraulic conductivity having the components in the x, y directions as \(k_{x}\) and \(k_{y}\); \( \rho \) denotes the water density ; \(\mu \) be the viscosity; and g the gravitational acceleration; \(\varOmega \) is the percolation domain.

Since there is a large digression from the ordinary Gaussian diffusion, therefore the underlying superposition is not appropriate in tracing the movement of the solute concentration in a porous medium which is non-homogeneous. Additionally, a supplementary realistic model can be obtained by the consideration of the application of fractional order density gradient to recapture the non-homogeneity of the porous medium. The Modified Darcy law was proposed by the authors of [22] with Riemann-Liouville fractional order derivative. Under the assumption of the continuity of seepage flow and the Darcy law, the percolation equation (1) is deduced into the the following forms as these assumptions are not valid for real seepage flow. The differential system with ordinary derivative does not quantify the flow of fluid with spatial path dependency and/or time memory. This limitation in the application of ordinary differential system has motivated the authors of [22] to model the fractional Darcy law.

$$\begin{aligned} q_{x}= & {} k_{x}\frac{\partial ^{\alpha _{1}} P}{\partial x^{\alpha _{1}}}, \quad 0<\alpha _{1}<1, \end{aligned}$$
(2)
$$\begin{aligned} q_{y}= & {} k_{y}\frac{\partial ^{\alpha _{2}} P}{\partial y^{\alpha _{2}}}, \quad 0<\alpha _{2}<1. \end{aligned}$$
(3)

In the special case, the usual Darcy law can be obtained by putting \(\alpha _{1}=\alpha _{2}=1.\)

Einstein’s theory of Brownian motion reveals that the mean square displacement (MSD) of a particle moving randomly is proportional to time, which also can be justified for the case of a simple integer order linear diffusion equation. But as the research on fractional calculus progresses, it is found that the MSD for the anomalous case i.e., for time fractional diffusion equation, increases slowly with time. For the linear time fractional diffusion equation \(\frac{\partial ^\alpha u}{\partial t^\alpha }=\frac{\partial ^2 u}{\partial x^2},\) the MSD is \(\langle X^2(t) \rangle \sim t^\alpha ,\) where \(0<\alpha <1\) is the anomalous diffusion exponent. The equation represents an evolution equation which generates the fractional Brownian motion, a generalization of Brownian motion. Thus it is seen that for the diffusion model, if the integer order time derivative is replaced by the fractional order time derivative, it changes the fundamental concept of evolution of foundation of physics. The physical meaning of the fractional order time derivative related to the statistics is the waiting time in accordance with the Montroll-Weiss theory. Hilfer and Anton [25] have showed that Montroll-Weiss continuous time random walk (CTRW) with a Mittag-Leffler waiting time density is equivalent to a fractional order master equation. Later, Hilfer [24] explained that this underlying CTRW of the model is connected to the time fractional diffusion equation in the asymptotic sense of long time and large distance. Thus random walk approach is needed to simulate diffusive phenomena of a fractional order equation. Gorenflo et al. [18] stated that the time fractional order diffusion equation generates a class of symmetric densities whose moments of order 2m are proportional to the \(m\alpha \) power of time. Thus classes of non-Markovian stochastic processes can be obtained, which exhibit slow anomalous diffusions. By using fractional order Fokker-Plank equation approach, Metzler et al. [35] have shown that anomalous diffusion is based upon Boltzman statistics. Many researchers have used fractional equations during description of Levy flights or diverging diffusion. The tool is very powerful in modeling multi scale problems, characterized by wide time or length scale. The fractional order differential operator has the characteristic of non-local property, which states that the future state not only depends upon the present state but also upon all of the history of its previous states. Due to the greater flexibilities, the fractional order models have gained popularity to investigate the dynamical system.

The anomalous diffusion process seeks the attention of many researchers [5, 8, 14]. Anomalous diffusion can be easily seen within complex systems like diffusion process in porous media. The fluid particles undergoes in sub-diffusion process if \(\alpha <1\). A subclass of anomalous diffusive system is the fractional sub-diffusion equation (FSDE), which can be illustrated from the standard parabolic PDE by replacing the first-order time derivative with a fractional derivative of order \(\alpha , 0< \alpha < 1\) (Moodie and Tait [37]).

In the real world problems, the FSDE has been widely applied in several fields of research [11, 20, 30]. So finding the solutions of these equations have become increasingly interesting and popular. The authors of [17, 36, 39] have provided a typical explanation of the anomalous diffusion process based on the continuous time random walk. The process of anomalous diffusion for real complex physical systems can be well explained by fractional order diffusion models.

The variations of the solute concentration with respect to the column length and time depend upon the several species and factors in fluid. It is very hard to find the overshoots of probability density function for the several cases like conservative and non-conservative systems. In addition to this, interactions of the solutes with medium or other species play a significant role in the flow of the fluid through porous media. In order to analyze the diffusion of the solute in porous media in two-dimension, an attempt has taken in the present article to develop a two-dimensional sub-diffusion physical model (4) with the prescribed initial and boundary conditions (5–9), where the fractional derivative is taken in Caputo sense. The fractional time derivative corresponds to long-time heavy tail decay.

$$\begin{aligned} \begin{aligned} \frac{\partial ^\alpha u}{\partial t^\alpha}\,=\,\frac{\partial }{\partial x}\left(u \frac{\partial u}{\partial x}\right) + \frac{\partial }{\partial y}\left(u \frac{\partial u}{\partial y}\right)+&k u(1-u) ; 0<\alpha <1, \\&0\le x\le 1,0\le y\le 1, \\&\end{aligned} \end{aligned}$$
(4)

with

$$\begin{aligned} u(x,y,0)\,=\,0, \end{aligned}$$
(5)
$$\begin{aligned} u(0,y,t)\,=\,c_{0}, \end{aligned}$$
(6)
$$\begin{aligned} u_{x}(1,y,t)\,=\,0, \end{aligned}$$
(7)
$$\begin{aligned} u_{y}(x,0,t)\,=\, 0, \end{aligned}$$
(8)
$$\begin{aligned} u_{y}(x,1,t)\,=\, 0, \end{aligned}$$
(9)

where \( \alpha \) is an arbitrary fractional order, k denotes the reaction coefficient and \( c_{0}\) be a constant. For the approximation of solute concentration we have used Kronecker product which is discussed later.

When the ground water is mostly adulterate, then the resuscitate is considered to be very difficult and more expensive. A very careful approach and attention is very much necessary for describing the boundary conditions, problem domain and model parameters for using the numerical approach of groundwater model of the field problems. Hydrology is an interdisciplinary part of science and engineering, in which the topic of solute transport through the groundwater is included.

The generalized solute transport model in the porous media is the well known reaction-advection-dispersion equation (RADE) [15, 27]. This equation has the combined effects of advection, reaction and dispersion process due to which the concentration of the solute is dispersed while transported down along the stream and sometimes it reacts with the medium through which it moves. From the mass balance principles, the advection-dispersion equation can be easily derived. The modeling of solute transport is very helpful for the prediction of solute concentration in rivers, streams, aquifers and lakes, which can be represented mathematically as

$$\begin{aligned} \frac{\partial u}{\partial t}= \nabla \cdot (d \nabla u)- \nabla (\nu u)+R, \end{aligned}$$
(10)

where R denotes the reaction term of the species u, and the symbol \(\nabla \) is defined in \(R^{n}\) in terms of partial derivative operators as \(\nabla =(\frac{\partial }{\partial x_{1}},\dots ,\frac{\partial }{\partial x_{n}})\).

In the right-hand side of the equation (10), the first term describes the dispersion phenomena, the second term represents the advection process and the last term is for the reaction kinetics. If there is no reaction between the solute and the medium through which the solute moves, and also there is no kind of radioactive decay then this type of system is called as conservative system, otherwise it is non-conservative. In the case of non-conservative system, the last term of the equation (10) is encountered. If there is only diffusion process which is responsible for the movement of the solute concentration, then the above equation is known as diffusion equation.

In this article a drive has been taken to develop the operational matrix with Laguerre polynomials to use in collocation method to find the numerical solution of two-dimensional fractional order non-linear reaction-diffusion equation. We have introduced an efficient way to approximate the non-linear multiple-order fractional boundary value problem with the help of Laguerre spectral collocation method to obtain the numerical solution with the use of Laguerre operational matrix.

The article is organized in following ways. Section 2 contains some important properties and definitions of fractional calculus. A brief overview of the conservation principle is given in Sect. 3. In Sect. 4, some outlines of Laguerre polynomials are given. In Sect. 5, an overview of Kronecker product and its properties are given. In Sects. 6 and 7, the Laguerre operational matrix for fractional order derivative in Caputo sense is given to solve our proposed model. The detail of convergence analysis of the proposed numerical scheme is given in Sect. 8. In Sect. 9, few examples to illustrate the accuracy and applicability of the proposed method are considered and comparisons between the numerical results obtained by our proposed method with the existing analytical solutions are shown through the graphs and tables. Numerical results and discussion of the considered two-dimensional nonlinear model are given in Sect. 10, which is followed by the outcomes of the overall research work given in the section Conclusion.

2 Preliminaries

In this section of the manuscript, the basic definitions and properties of variable order derivatives are given. The Riemann-Liouville’s derivative has some drawbacks in the modeling the mathematical modeling for some real and physical phenomena. Fractional order derivative operator \(D^\eta \) of the given order \( \eta >0 \) of a function f(t) in the Caputo sense is given by [29, 41]

$$\begin{aligned} (D^\eta f)(t)= {\left\{ \begin{array}{ll} \frac{d^r f(t)}{dt^r}, &{}\text{ if } \eta = r \in {N}, \\ \frac{1}{\varGamma (r-\eta )}\int _{0}^{t} (t-\rho )^{r-\eta -1}f^{(r)}(\rho ) d\rho , &{} \text{ if } r-1<\eta <r. \end{array}\right. } \end{aligned}$$
(11)

In the above expression r is the integer number. Few properties of Caputo fractional derivatives are:

$$\begin{aligned} D^\eta C=0, \end{aligned}$$
(12)

where C is an arbitrary constant.

$$\begin{aligned} D^\eta t^{\varepsilon }= {\left\{ \begin{array}{ll} 0, \quad&{}\text{ if } \varepsilon \in {N}\cup \{0\} ,\varepsilon <\lceil \eta \rceil , \\ \frac{\varGamma (\varepsilon +1)}{\varGamma (\varepsilon -\eta +1)} t^{\varepsilon -\eta }, \quad&{} \text{ if } \varepsilon \in {N}\cup \{0\} , \varepsilon \ge \lceil \eta \rceil or \varepsilon \notin {N} ,\varepsilon >\lfloor \eta \rfloor , \end{array}\right. } \end{aligned}$$
(13)

where \( \lceil \eta \rceil \) be the ceiling function and \(\lfloor \eta \rfloor \) be the floor function.

3 The general conservation principle

In this section of the article, a fluid continuum in flowing state is considered. In general a multicomponent fluid has been considered in such a way that it follows the continuum approach and each component in itself is a continuum filling of the entire space, as in Fig. 1. Let \(H_{a}\) be the initial amount of the the extensive fluid property (e.g., mass) is contained in a volume V within a portion of space at time t and enclosed by a surface S. Consider the position of the system at time \(t+\bigtriangleup t\), in the time interval \(\bigtriangleup t\), the system moves and gets deformed. At time t, the system is of surface area S and volume V, whereas the system at time \( t + \bigtriangleup t \) is of volume \( V' \) and surface \( S' \). These are composed of the regions: \( V = V_{1} + V_{2}, V' = V_{2} + V_{3}. \) The region \( V_{2} \) is common to V and \( V' \).

Fig. 1
figure 1

Fluid continuum in the flowing process

Full size image

In Lagrange point of view, the temporal rate of change \((D/Dt)H_{a}\) of \(H_{a}\) for the moving system is given by

$$\begin{aligned}&\frac{DH_{a}}{Dt}\vert _{system}\nonumber \\&\quad =\lim _{\bigtriangleup t\rightarrow \infty }\{\frac{[(H_{a})_{2}+(H_{a})_{3}]_{t+\bigtriangleup t}-[(H_{a})_{1}+(H_{a})_{2}]_{t}}{\bigtriangleup t}\}, \end{aligned}$$
(14)

where

$$\begin{aligned}&(H_{a})_{i}=\int _{(V_{i})}\rho _{a}\gamma _{a} dV=\int _{(V_{i})}h_{a} dV, \nonumber \\&\quad i=1,2,3; H_{a}/\delta V=h_{a}. \end{aligned}$$
(15)

The general conservation principle of a property for the species \('a'\) is given by

$$\begin{aligned} \partial h_{a}/\partial t+\text{ div }(h_{a}V_{H_{a}})=I_{a}, \end{aligned}$$
(16)

where \( I_{a} \) is the temporal rate per unit volume and \(V_{H_{a}}\) is the velocity field.

3.1 Mass conservation of species

Mass conservation of the fluid across a porous material involves the fundamental principle that total mass flux entered minus total mass flux out equals to the increase in mass amount stored by the medium. This means that the total mass of fluid is conserved. For a system of multicomponent fluid of a species \('a'\), substituting \( h_{a}=\rho _{a} \) and \( V_{H_{a}}=V_{a} \) in above equation, we get

$$\begin{aligned} \partial \rho _{a}/\partial t+\text{ div }(\rho _{a}V_{a})=I_{a}, \end{aligned}$$
(17)

where \(I_{a}\) is the rate at which mass of the species \( 'a' \) produced per unit volume during the chemical reaction in the system. From the Eulerian point of view, above equation is the equation of continuity (or equation of mass conservation) [21].

If we assume the case of stationary fluid and \( I_{a}=0 \) then from above, we deduce the Fick’s second law for diffusion for binary fluid as

$$\begin{aligned} \partial \rho _{a}/\partial t=\text{ div }(D_{ab}\text{ grad } \rho _{a}), \end{aligned}$$
(18)

where \(D_{ab}\) is the diffusion coefficient.

4 Laguerre polynomials and its some properties

The involvement of Laguerre polynomial in several aspects of engineering and applied mathematics seeks the attention of many researchers and establishes it as a strong tool for finding the numerical solution of integer as well as fractional order partial differential equations (PDEs). The \(l^{th}\) degree Laguerre polynomial is defined as [40]

$$\begin{aligned} L_{l}(t)=\frac{1}{l!}e^{t}{\partial _{t}^{l}(t^{l}e^{-t})},\quad l=0,1,...; \end{aligned}$$
(19)

The Laguerre polynomial of degree l on the interval I is simplified from above as

$$\begin{aligned} L_{l}(t)=\sum _{k=0}^{l}\dfrac{l!(-1)^{k}}{(-k+l)!(k!)^{2}}x^{k},\quad k=0,1,...; \end{aligned}$$
(20)

The following recurrence relations are satisfied by Laguerre polynomial

$$\begin{aligned} \begin{aligned} {\partial _{t}(te^{-t}\partial _{t}L_{l}(t))}+le^{-t}L_{l}(t)&=0,\quad t\in I,\\ L_{l}(t)&=\partial _{t}L_{l}(t)-\partial _{t}L_{l+1}(t), \quad l\ge 0,\\ L_{l+1}(t)&=\frac{(2l+1-t)L_{l}(t)-lL_{l-1}(t)}{l+1}, \\&\quad \forall l \ge 1. \end{aligned} \end{aligned}$$
(21)

The set of all Laguerre polynomials form an orthogonal system in \(L_{r}^{2}(I)\) i.e.,

$$\begin{aligned} \int _{I}L_{a}(t)L_{b}(t)r(t) dt=\delta _{lm}, \forall a,b \ge 0, \end{aligned}$$
(22)

where \(r(t)=e^{-t}\) is weight function and \(\delta _{lm}\) is the Kronecker delta function.

5 Kronecker Product and its some properties

In this section some basic and fundamental properties of the well known Kronecker product are defined [9, 19]. Furthermore, we try to give some overview of the applications and properties of the Kronecker Product, which is an operation between two arbitrary size matrices represented by the symbol \( \otimes \).

Definition

The Kronecker product of the matrix A of order \( p\times q \) and B of order \( m\times n \) is again \( pm\times qn \) order block matrix, which is denoted by \( A\otimes B \) and is defined by

$$\begin{aligned} A\otimes B=\begin{bmatrix} a_{11}B &{}a_{12}B &{}\dots &{}a_{1q}B \\ a_{21}B &{}a_{22}B &{}\dots &{}a_{21}B \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \\ a_{p1}B &{}a_{p2}B &{}\dots &{}a_{pq}B \\ \end{bmatrix}. \end{aligned}$$
(23)

Moreover, If A and B represent some linear transformations on vector spaces i.e., \( W_{1}\, \rightarrow \,V_{1} \) and \( W_{2}\, \rightarrow \,V_{2} \) respectively, then \( A\otimes B \) represents the tensor product of these two maps, \( W_{1}\otimes W_{2}\, \rightarrow \,V_{1}\otimes V_{2}\).

5.1 Basic properties

Since Kronecker product is a special case of tensor product, therefore it can satisfy the property like associativity and bi-linearity. Also, it has a lot of interesting and effective properties, few are stated below:

$$\begin{aligned} I\otimes (J+K)= & {} I\otimes J+I\otimes K, \end{aligned}$$
(24)
$$\begin{aligned} (I+J)\otimes K= & {} I\otimes K+J\otimes K, \end{aligned}$$
(25)
$$\begin{aligned} (kI\otimes J)= & {} (I\otimes kJ)=k(I\otimes J), \end{aligned}$$
(26)
$$\begin{aligned} (I\otimes J)\otimes K= & {} I\otimes (J\otimes K), \end{aligned}$$
(27)

where I, J and K are arbitrary matrices and k is a scalar.

6 Laguerre operational matrix for fractional order differentiation

The collection of Laguerre polynomials form a basis set for \(L_{r}^{2}(I).\) So any function \(\zeta (t)\in L_{r}^{2}(I)\) can be expanded as

$$\begin{aligned} \zeta (t)=\sum _{g=0}^{\infty }b_{g}L_{g}(t), m=0,1,2,...; \end{aligned}$$
(28)

where the unknown constants \(b_{g}\) can be calculated as

$$\begin{aligned} b_{g}=\int _{0}^{\infty }\zeta (t)L_{b}(t)r(t)dt. \end{aligned}$$
(29)

In the terms of first \((r+1)\) Laguerre polynomials the above approximation is reduced to

$$\begin{aligned} \zeta _{r}(t)=\sum _{g=0}^{r}b_{g}L_{g}(t)=B^{T}\cdot\sigma (t), \end{aligned}$$
(30)

where \( B^{T}=[b_{0},b_{1},\ldots,b_{r}]\) is the matrix of unknown constants and \(\sigma (t)=[L_{0}(t),L_{1}(t),\ldots,L_{r}(t)]^{T}\) is the Laguerre vector. Again a function of two variables \( \zeta (x,t)\in L^2[0,1] \) can be expressed in terms of Laguerre polynomials as

$$\begin{aligned} \zeta (x,t)\simeq \zeta _{r}(x,t)\,=\,& {} \sum _{g\,=\,0}^{r} \sum _{h\,=\,0}^{r}b_{g,h}L_{g}(x)L_{h}(t)\,=\,\sigma (x)^T. B. \sigma (t), \end{aligned}$$
(31)

where the unknown constant matrix \(B\,=\,[b_{g,h}]\) is known as Laguerre coefficient.

In similar manner, we can approximate an arbitrary two-dimensional function \( \zeta (x,y,t)\in L^2[0,1] \) in terms of Laguerre polynomial as

$$\begin{aligned} \zeta (x,y,t)\simeq \zeta _{r}(x,y,t)\,& {}=\, \sum _{g\,=\,0}^{r}\sum _{h\,=\,0}^{r}\sum _{i\,=\,0}^{r}b_{g,h,i} \varOmega _{g}(x)L_{h}(y)L_{i}(t)\nonumber \\&\,=\,\sigma (t)^{T}\cdot B \cdot \sigma (x)\otimes \sigma (y), \end{aligned}$$
(32)

where the unknown constant matrix \(B=[b_{g,h,i}]\) is the Laguerre coefficient. These coefficients can be determine by using the initial and boundary conditions. In order to derive the novel operational matrix we have provided the following lemma.

Lemma 1

Consider the fractional derivative operator \(D^{\mu }\) of fractional order \(\mu \) in Caputo sense. Let \(\sigma (t)\) be the Laguerre vector defined as in equation (30), then we have following results:

$$\begin{aligned} { ^{C}_{0} }{D}_{t}^{\mu }L_{r}(t)=0, \quad r=0,1,\ldots ,\lceil \mu \rceil -1, \quad 0<\mu \le 1. \end{aligned}$$
(33)

Proof

This result can be easily proved by using the basic properties of fractional Caputo derivative given in the equation (13). \(\square \)

We are going to derive the operational matrix of orthogonal Laguerre polynomials [40]. On solving the equations (28)–(29) and equation (20), we get the following expression as

$$\begin{aligned} { ^{C} _{0}}{D}_{t}^{\mu } L_{l}(t)= \sum _{g=0}^{l}\nonumber \\&\frac{(-1)^{g} l! D^\mu t^g}{ (l-g)! (g!)^2}= \sum _{g=\lceil \mu \rceil }^{l}\frac{(-1)^{g} l! t^{g-\mu }}{ (l-g)!\varGamma (g-\mu +1) g!},\quad l=\lceil \mu \rceil ,...,r. \end{aligned}$$
(34)

As set of Laguerre polynomials is a basis so we can write the term \(t^{g-\mu }\) as

$$\begin{aligned} t^{g-\mu }=\sum _{h=0}^{r}b_{h}L_{h}(t), \end{aligned}$$
(35)

where the constant coefficient \(b_{h}\) is given by

$$\begin{aligned} b_{h}=\sum _{a=0}^{h}\frac{(-1)^{a} h! \varGamma (g-\mu +a+1)}{ (h-a)! (a!)^2}. \end{aligned}$$
(36)

Using the equations (35)–(36) into the equation (34), we have

$$\begin{aligned} { ^{C}_{0} }{D}_{t}^{\mu }L_{l}(x)=\sum _{h=0}^{r}P_{\mu }(l,h)L_{h}(t), \quad l=\lceil \mu \rceil ,...,r; \end{aligned}$$
(37)

In the above equation the term \(P_{\mu }(l,h)\) is given by the following equation

$$\begin{aligned} P_{\mu }(l,h)=\sum _{g=\lceil \mu \rceil }^{l}\sum _{a=0}^{h}\frac{(-1)^{g+a} l! h! \varGamma (g-\nu +a+1)}{ (l-g)! \varGamma (g-\mu +1)g!(h-a)! (a!)^2}. \end{aligned}$$
(38)

The vector form of the equation (37) is written as

$$\begin{aligned} { ^{C}_{0} }{D}_{t}^{\mu } L_{l}(t)=[P_{\mu }(l,0),P_{\mu }(l,1),\ldots ,P_{\mu }(l,r)]\sigma (t),\quad l=\lceil \mu \rceil ,\ldots ,r. \end{aligned}$$
(39)

In the view of lemma 1, we have

$$\begin{aligned} { ^{C}_{0} }{D}_{t}^{\mu } L_{l}(t)=[0,0,\ldots ,0]\sigma (x), \quad l=0,1,\ldots ,\lceil \mu \rceil -1. \end{aligned}$$
(40)

Using the equations (39)–(40), we can write the equation (40) in matrix form as

$$\begin{aligned} { ^{C}_{0} }{D}_{t}^{\mu }\sigma (t)=H^{(\mu )}\sigma (t), \end{aligned}$$
(41)

where \(H^{\mu }\) is an operational matrix with fractional derivatives of \(r+1 \times r+1\) order and is given as

$$\begin{aligned} H^{(\mu )}=\begin{bmatrix} 0 &{} 0 &{}0 &{}\dots &{}0 \\ \vdots &{} \vdots &{} \vdots &{} \dots &{} \vdots \\ 0 &{} 0 &{}0 &{}\dots &{} 0 \\ P_{\mu } (\lceil \mu \rceil ,0) &{} S_{\mu } (\lceil \mu \rceil ,1) &{}P_{\mu } (\lceil \mu \rceil ,2) &{}\dots &{}P_{\mu } (\lceil \mu \rceil ,r) \\ \vdots &{} \vdots &{} \vdots &{} \dots &{} \vdots \\ P_{\mu } (i,0) &{} P_{\mu } (i,1) &{}P_{\mu } (i,2) &{}\dots &{}P_{\mu } (i,r) \\ \vdots &{} \vdots &{} \vdots &{} \dots &{} \vdots \\ P_{\mu } (r,0) &{} P_{\mu } (r,1) &{}P_{\mu } (r,2) &{}\dots &{}P_{\mu } (r,r) \\ \end{bmatrix}, \end{aligned}$$
(42)

7 Implementation of Laguerre operational matrix

Here we are going to apply the fractional operational matrix on concerned two-dimensional mathematical model using Laguerre collocation method.

Now, in view of the equation (32), we shall approximate the solute concentration u(x, y, t) in form of Laguerre polynomials in the following manner as

$$\begin{aligned} u(x,y,t)=\mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{f}(x)L_{g}(y)L_{h}(t), \end{aligned}$$
(43)

where \(c_{ghi}\) is the Laguerre coefficients, where \( g=1,2,3,\ldots ; h=1,2,3,\ldots ; i=1,2,3,\ldots ; \) The equation (43) can be represented in vector form as

$$\begin{aligned} u(x,y,t)=\sigma (t)^{T}\cdot B\cdot \sigma (x)\otimes \sigma (y), \end{aligned}$$
(44)

where \(B= [c_{fgh}]\) is a matrix of order \((r+1)\times (r+1)^2\) of constant Laguerre coefficients and \(\sigma (t)=[L_0(t),L_1(t) \ldots L_r(t)]^T\) is a column vector. Applying the fractional derivative of order \(\alpha \) with respect to time variable variable t on equation (44) and using the equation (41), we get

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}=H^{\alpha } u(x,y,t)=[H^{\beta }\cdot \sigma ^{T}(t)]\cdot B\cdot \sigma (x)\otimes \sigma (y). \end{aligned}$$
(45)

Similarly,

$$\begin{aligned} \frac{\partial u}{\partial x}=H u(x,y,t)= \sigma ^{T}(t)\cdot B\cdot (H^{1} \times I)\cdot \sigma (x)\otimes \sigma (y), \end{aligned}$$
(46)
$$\begin{aligned} \frac{\partial u}{\partial y}= H u(x,y,t)=\sigma ^{T}(t)\cdot B\cdot (I \times H^{1} )\cdot \sigma (x)\otimes \sigma (y). \end{aligned}$$
(47)

In above equations I be the \((r+1)\times (r+1)\) identity matrix. Now from prescribed initial and boundary conditions (5)-(9) with the aid of equation (44), we get

$$\begin{aligned} \sigma ^{T}(0)\cdot B\cdot \sigma (x)\otimes \sigma (y)= & {} 0, \end{aligned}$$
(48)
$$\begin{aligned} \sigma ^{T}(t)\cdot B\cdot \sigma (0)\otimes \sigma (y)= & {} c_{0}, \end{aligned}$$
(49)
$$\begin{aligned} \sigma ^{T}(t)\cdot B\cdot (H^{1}\times I)\cdot \sigma (1)\otimes \sigma (y)= & {} 0, \end{aligned}$$
(50)
$$\begin{aligned} \sigma ^{T}(t)\cdot B\cdot (I\times H^{1})\cdot \sigma (x)\otimes \sigma (0)= & {} 0, \end{aligned}$$
(51)
$$\begin{aligned} \sigma ^{T}(t)\cdot B\cdot (I\times H^{1})\cdot \sigma (x)\otimes \sigma (1)\,=\, 0. \end{aligned}$$
(52)

Now, we collocate Eq. (4) with the help of equations (48–52) at points \(x_{b}\)=\(\frac{b}{r}\) for \(b=0,1,2,\ldots ,r\), \(y_{r}\)=\(\frac{b}{r}\) for \(b\,=\,0,1,2,\ldots ,r\) and \(t_{r}\)=\(\frac{b}{r}\) for \(b\,=\,0,1,2,\ldots ,r\). Using these collocation points and fractional operational matrix, a nonlinear system of algebraic equations are found. On simplifying this system we can calculate the Laguerre coefficients matrix B which can further be used in Eq. (44) to find the approximate numerical solution.

8 Error bound of the approximation

In this section the upper bound of the error of proposed numerical approximation is estimated.

Theorem 1

For the generalized Laguerre polynomial \( L_{l}^{(\theta )}(x), \) the global uniform bounds can be given by

$$\begin{aligned} \mid L_{l}^{(\theta )}(x)\mid \le {\left\{ \begin{array}{ll} \frac{(\theta +1)_{l}}{l!} e^\frac{x}{2}, &{}\text{ if } \theta \ge 0, x\ge 0, l=0,1,2,...; \\ (2-\frac{(\theta +1)_{l}}{l!}) e^\frac{x}{2}, &{}\text{ if } -1<\theta \le 0, x\ge 0, l=0,1,2,... \end{array}\right. } \end{aligned}$$
(53)

where \( (b)_{l}= b(b+1)(b+2)\ldots (b+l-1), l = 1,2,3,\ldots ; \)

Proof

M. Abramowitz and I. A. Stegun have proved the global uniform bounds in [2]. The estimates are also been discussed in [28]. \(\square \)

Remark

The global uniform bound (53) for the usual Laguerre polynomial is given as

$$\begin{aligned} \mid L_{r}(x)\mid \le \frac{1}{r!} e^\frac{x}{2},\quad x\ge 0,\quad x=0,1,2,\ldots . \end{aligned}$$
(54)

Theorem 2

Suppose u(x, y, t) be the sufficiently smooth function on the region A and \( (\frac{\partial ^{\alpha }u}{\partial t^{\alpha }})_{r} \) be the approximation of \( (\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}) \) . Then the approximated error \( (\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}) \) by \( (\frac{\partial ^{\alpha }u}{\partial t^{\alpha }})_{r} \) is bounded by

$$\begin{aligned} \mid E(r) \mid \le&\mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} \frac{c_{fgh}}{f!.g!.m!}. \chi _{mhr}. e^{\frac{x+y+t}{2}},\nonumber \\&\quad x,y,t \ge 0,\quad f,g,m=0,1,2,\ldots ; \end{aligned}$$
(55)

where \(\chi _{mbr}= \sum _{m=0}^{r}S_{\alpha }(b,m).\)

Proof

In view of equation (43), we have

$$\begin{aligned} u(x,y,t)=\mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{f}(x)L_{g}(y)L_{h}(t), \end{aligned}$$
(56)

truncating it upto \( r+1 \) terms, we have

$$\begin{aligned} u_{r}(x,y,t)=\mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{f}(x)L_{g}(y)L_{h}(t). \end{aligned}$$
(57)

We can write \(\alpha \) order partial derivative of u(x, y, t) and \(u_{r}(x,y,t) \) w.r.to t as

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}= & {} \mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{f}(x)L_{g}(y) \frac{\partial ^{\alpha }L_{h}(t)}{\partial t^{\alpha }}, \end{aligned}$$
(58)
$$\begin{aligned} \left(\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}\right)_{r}= & {} \mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{f}(x)L_{g}(y) \frac{\partial ^{\alpha }L_{h}(t)}{\partial t^{\alpha }}. \end{aligned}$$
(59)

From the above equations, we can write

$$\begin{aligned} E(r)& {}= \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}\nonumber \\&-\left(\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}\right)_{r} \nonumber \\&= \mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{f}(x)L_{g}(y) \frac{\partial ^{\alpha }L_{h}(t)}{\partial t^{\alpha }}. \end{aligned}$$
(60)

Using (37), the above equation reduces to

$$ \left| {E(r)} \right| = {\text{ }}\left| {\sum\limits_{{f = 0}}^{r} {\sum\limits_{{g = 0}}^{r} {\mathop \sum \limits_{{h = 0}}^{r} } } c_{{fgh}} L_{f} (x)L_{g} (y)\left( {\sum\limits_{{m = 0}}^{r} {S_{\alpha } } (b,m)L_{m} (t)} \right)} \right| $$
(61)

or,

$$\begin{aligned} \mid E(r) \mid= & {} \mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} c_{fgh} L_{g}(y) \nonumber \\& \cdot \chi _{mhr} \mid L_{f}(x) \mid .\mid L_{g}(y) \mid \cdot \mid L_{m}(t) \mid . \end{aligned}$$
(62)

Applying equation (54), we get

$$\begin{aligned}&\mid E(r) \mid \le \mathop {\sum _{f=0}^{r}\sum _{g=0}^{r} \sum _{h=0}^{r}} c_{fgh}.\nonumber \\&\quad \chi _{mhr}.\frac{1}{m!} e^\frac{t}{2}.\frac{1}{f!} e^\frac{x}{2}.\frac{1}{g!} e^\frac{y}{2}. \end{aligned}$$
(63)

Using the formulae S1 and S2 given in [31] and subtracting the truncated series from the infinite series, bounding each term in the difference, and summing the bounds complete the proof of the theorem.

$$\begin{aligned}&\mid E(r) \mid \le \mathop {\sum _{f=0}^{r}\sum _{g=0}^{r}\sum _{h=0}^{r}} \frac{c_{fgh}}{f!.g!.m!} \nonumber \\&\quad \cdot \chi _{mhr}. e^{\frac{x+y+t}{2}}, \quad x,y,t \ge 0,\quad f,g,m=0,1,2,\cdot \cdot \cdot . \end{aligned}$$
(64)

\(\square \)

9 Numerical simulations and error analysis

Laguerre fractional operational matrix has been applied on some existing fractional order problems to find their approximate numerical solutions. The obtained numerical results have been compared with the existing analytical solutions through finding the absolute error for approximation to illustrate the capability and validity of the proposed numerical scheme. All the numerical calculations are carried out by using the software MATHEMATICA 11.3.

The absolute error is defined by [16] as

$$\begin{aligned} E_{abs}(x,y,t)=\mid u_{exact}-u_{num}(x,y,t)\mid . \end{aligned}$$
(65)

Maximum error for the problem in x for fixed y and t is defined as

$$\begin{aligned} \text{ Max } E_{abs}(x,0.5,0.5)=\underset{0 \le x \le 1}{\text{ max }}\mid E_{abs}(x,0.5,0.5) \mid . \end{aligned}$$
(66)

The absolute for the concerned test examples with a fix value of t and x is given by

$$\begin{aligned} \text{ Max } E_{abs}(0.5,y,0.5)=\underset{0 \le y \le 1}{\text{ max }}\mid E_{abs}(0.5,y,0.5) \mid . \end{aligned}$$
(67)

The order of convergence for two successive approximation \( N_{1} \)and \( N_{2} \) is also calculated to validate the higher order accuracy of the numerical scheme which is given as

$$\begin{aligned} Order=\dfrac{\text{ log } \left(\dfrac{\text{ Max } E_{abs}(N_{1})}{\text{ Max } E_{abs}(N_{2})}\right)}{\text{ log } \left(\dfrac{N_{2}}{N_{1}}\right)}, \end{aligned}$$
(68)

where \( \text{ Max } E_{abs}(N)\) is the maximum absolute error during the approximation of degree N.

Example 1

Let us consider a two-dimensional non-linear non-homogeneous fractional order advection-diffusion equation as

$$\begin{aligned} \frac{\partial ^\alpha u}{\partial t^\alpha }=\frac{\partial ^2 u}{\partial x^{2}}+\frac{\partial ^2 u}{\partial y^{2}}+\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}+\frac{u^2}{3}+f(x,y,t), \end{aligned}$$
(69)

with \(f(x,y,t)=-x\sqrt{t}-y\sqrt{t}-\frac{x^2y^2t}{3}-\frac{0.682734xy}{t^{0.3}}\) and boundary conditions

$$\begin{aligned} \begin{aligned} u(x,y,0)&=0,\\ u(0,y,t)&=0,\\ u(x,0,t)&=0,\\ u(1,y,t)&=y\sqrt{t},\\ u(x,1,t)&=x\sqrt{t}. \end{aligned} \end{aligned}$$
(70)

For the above example, the exact solution is \( u(x,y,t)=xy\sqrt{t} \) for the fractional order parameters \(\alpha =0.8\). The absolute errors between the results obtained by our proposed numerical scheme and the exact solutions are exhibited through Tables 1 and 2 for \(y=0.5,0 \le x \le 1 \) and \(x=0.5,0 \le y \le 1 \) respectively for the order of approximation \(N=5,7,9\) at \(t=1\). The tables clearly confirm that the order of convergence for our proposed method increases as the degree of Laguerre polynomials in x and y increases. Again absolute error decreases with the increase of the order of approximation of the polynomial N, which clearly shows the effectiveness of our proposed numerical method. Again the data of CPU time shows that it takes minimum time to obtain accurate result showing that the method is computationally effective to solve the two-dimensional fractional order PDEs.

Table 1 Efficiency of the numerical method for Example 1 at \( y=t=0.5 \)
Full size table
Table 2 Efficiency of the numerical method for Example 1 at \( x=t=0.5 \)
Full size table

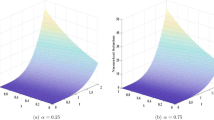
The absolute error is graphycally shown through Fig. 2 for various values of y and t for a fixed value of \( x=0.5 \). Figure 2 shows that the numerical solution is approximately accurate to the exact solution even for small value \(N=5\), the better convergence can be achieved increasing N. Thus comparing the numerical solution with the exact solution, we can say that the proposed method is very much efficient.

Fig. 2
figure 2

Plot of the absolute error between the exact and numerical solutions vs. y and t at \( x=0.5 \)

Full size image

Example 2

We consider time-fractional non-linear Fisher’s equation as

$$\begin{aligned} \frac{\partial ^\alpha u}{\partial t^\alpha }= \frac{1}{2}\nabla ^{2}u(x,y,t)+u^2(1-u)+f(x,y,t), \end{aligned}$$
(71)

where \(f(x,y,t)=e^{xy}(1.91116 t^{1.1}+e^{xy}t^4(-1+e^{xy}t^2)-0.5t^2(x^2+t^2))\) with the following initial and boundary conditions as

$$\begin{aligned} \begin{aligned} u(x,y,0)&=0,\\ u(0,y,t)&=t^2,\\ u(x,0,t)&=t^2,\\ u(1,y,t)&=e^yt^2,\\ u(x,1,t)&=e^xt^2. \end{aligned} \end{aligned}$$
(72)

The exact solution of this time-fractional Fisher’s equation is \(u(x,y,t)=e^{xy}t^2\) for the fractional order time parameter \(\alpha =0.9.\) The absolute errors, order of convergence and the CPU time required for the PDE with our proposed method are given in Tables 3 and 4 for \(y=0.5,{0 \le x \le 1} \) and \(x=0.5,{0 \le y \le 1} \) respectively for the order of approximation \(N=3,5,7\) at \(t=1\). The tables clearly exhibit that our proposed scheme is computationally effective even for less CPU time.

Table 3 Efficiency of the numerical method for Example 2 at \( y=t=0.5 \)
Full size table
Table 4 Efficiency of the numerical method for Example 2 at \( x=t=0.5 \)
Full size table

The absolute error between the numerical solution and the exact solution is depicted through Fig. 3 at \( t=1 \) for various values of x and y.

Fig. 3
figure 3

Plot of the absolute error between the exact and numerical solutions vs. x and y at \( t=1. \)

Full size image

Figure 3 shows that the numerical solution is approximately accurate to the exact solution even for \(N=5\). The better convergence can be achieved with increase in N.

Example 3

Consider following two-dimensional non-linear non-homogeneous fractional order advection-reaction-diffusion equation as

$$\begin{aligned} \frac{\partial ^\alpha u}{\partial t^\alpha }=\frac{\partial ^2 u}{\partial x^{2}}+\frac{\partial ^2 u}{\partial y^{2}}+\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}+u(1-u)+f(x,y,t), \end{aligned}$$
(73)

where \(f(x,y,t)=1.91116 t^{1.1} x^2 y^2 + t^4 x^4 y^4 + t^2 (-2 xy^2 - 2 y^2 + x^2 (-2 - y^2)) - 2 x^2 yt^2\) with the following initial and boundary conditions

$$\begin{aligned} \begin{aligned} u(x,y,0)=&0,\\ u(0,y,t)\,=\,0,\\ u(x,0,t)=&0,\\ u(1,y,t)=&y^2t^2,\\ u(x,1,t)=&x^2t^2. \end{aligned} \end{aligned}$$
(74)

The exact solution for this concerned example is \( u(x,y,t)\,=\,x^2 y^2t^2 \) for fractional order time parameter \(\alpha \,=\,0.9\). The absolute errors, order of convergence and the CPU time required for the PDE with our proposed method are given in Tables 5 and 6 for \(y\,=\,0.5,0 \le x \le 1 \) and \(x\,=\,0.5,0 \le y \le 1 \) respectively for the order of approximation \(N\,=\,5,7,9\) at \(t\,=\,1\). It is clear from the tables that our proposed scheme is computationally effective even for less CPU time.

Table 5 Efficiency of the numerical method for Example 3 at \( y\,=\,t\,=\,0.5 \)
Full size table
Table 6 Efficiency of the numerical method for Example 3 at \( x\,=\,t\,=\,0.5 \)
Full size table

The absolute error between the numerical solution and the exact solution is depicted through Fig. 4 at \( t\,=\,1 \) for various values of x and y.

Fig. 4
figure 4

Plot of the absolute error between the exact and numerical solutions vs. x and t at \( y\,=\,0.5. \)

Full size image

Figure 4 shows that the numerical solution is approximately accurate to the exact solution even for \(N\,=\,5\). The better convergence can be achieved with increase in N.

10 Results and discussion for proposed model

After being a justification of the accuracy and effectiveness of the method, the authors have been motivated to apply their proposed numerical scheme to solve the concerned two-dimensional nonlinear time fractional order reaction-diffusion model (4) under the prescribed initial and boundary conditions (5)–(9). The variations of the solute concentration u(x, y, t) vs. the column length x and y at \(t\,=\,0.5\) for various values of the fractional order time parameter \( \alpha \) for conservative case \((k\,=\,0)\) and non-conservative case (\(k\ne 0\)) are calculated numerically and are displayed graphically through Figs. 5, 6, and 7.

Fig. 5
figure 5

Plots of the field variable u(x, y, t) vs. x and y at \( t\,=\,0.5 \) for \( k\,=\,-1 \) for different values of \(\alpha \)

Full size image
Fig. 6
figure 6

Plots of the field variable u(x, y, t) vs. x and y at \( t\,=\,0.5 \) for \( k\,=\,0 \) for different values of \(\alpha \)

Full size image
Fig. 7
figure 7

Plots of field variable u(x, y, t) vs. x and y at \( t\,=\,0.5 \) for \(\alpha\,=\,0.7\) for different values of k

Full size image

The effects of reaction term on the solution profile for various values of the fractional order time derivative are found for \(k\,=\,-1\) and \(k\,=\,0,\) which are shown through Figs. 5 and 6 respectively. It is seen that the overshoots of sub-diffusion are decreased as the system advances towards fractional order from standard order. It is also seen from the figures that dampings are found due the presence of sink term (\( k\,=\,-1 \)). Figure 7 reveals that it consumes less time to stabilize the probability density function u(x, y, t) at \( t\,=\,0.5 \) for the case \( \alpha \,=\, 0.7 \) due to the effect of sink term \(k\,=\,-1\) as compared to the case of \( k\,=\,0 \) and also the presence of source term \( k\,=\,1 \), which clearly shows that physical importance of the presence of sink term in the system to enhance the stability region.

11 Conclusions

Four objectives have been accomplished through the present scientific contribution. First one is finding the solute concentration u(x, y, t) for two-dimensional non-linear fractional order reaction-diffusion equation employing the powerful and efficient technique Laguerre operational matrix. Second one is the pictorial presentations of the nature of overshoots in the form of sub-diffusion due to presence of reaction terms for different particular cases. The third one is the graphical presentations of the damping nature of the solute concentration when the system advances towards fractional order from standard order in the presence of sink term. The most important part of the present study is the exhibition of the order of convergence during validation of the proposed method while applying on the existing problems having analytical solutions. The FDE model has already been applied to describe heat transfer in ceramic polycrystalline composite materials made of two phases [49, 51, 38], in metal matrix composites [42, 50, 10, 54, 55] or in ceramic porous materials [52, 53]. The authors are optimist that the numerical solution by the proposed algorithm can be extended to a wide range i.e., for solving 3D nonlinear time-space fractional order diffusion equations which will be the topic of our future research.