Abstract
Dynamics of a rotor composed of a flexible beam attached to a slewing rigid hub is presented in the paper. Dynamics of the structure is studied for a slender beam model, based on extended Bernoulli–Euler theory, which takes into account a nonlinear curvature, coupled transversal and longitudinal oscillations and non-constant angular velocity of the hub. Moreover, to demonstrate a general case for dynamical boundary conditions, lumped mass fixed at the beam tip is added. The partial differential equations (PDEs) are derived from Hamilton principle of the least action. The analytical solutions of the PDEs are obtained by the multiple time scale method applied directly to PDEs. Forced vibrations around selected resonance zones are studied and the influence of beam rotation, preset angle, hub radius, tip mass is presented. Hardening and softening phenomena, respectively for the first and the second mode, are obtained for various angular velocity values.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction and motivation
Rotating structures play an important role in mechanical or aerospace engineering, wind turbines or helicopter blades may serve as classical examples. Linear models of such structures are very useful in a case of relatively stiff systems, performing small oscillations. The development of composite materials technology gives a new possibility to create rotating blades having new properties and enable to perform large deformations. The methodology of determining equations of motion of composite beams or blades considered as a thin-walled structures was presented in books [13, 20, 22]. The rotating thin-walled composite blades model which takes into account composite beam layout and also hub dynamics was derived on the basis of Hamilton principle in [15]. The model enabled to study complex \(3-D\) deformations of the blade, including warping effect, for various configurations of placement of the reinforcing fibres. The elaborated model took into account varied angular speed, coupled hub and beam dynamics and complex deformations of the thin-walled beam. But the proposed model gave reliable results for relatively small deformations of the beam.
For flexible systems large deformations may occur. Therefore, nonlinear models have to be developed to predict properly dynamics of such flexible cases. The nonlinear beam model for flexural and torsional beam dynamics was proposed in pioneer works by Crespo da Silva and Glynn in [4, 5]. However, the main assumption in that model was that the beam was inextensible. Then, in papers [6, 7] the inextensible beam model was extended to nonlinear flexural-torsional vibrations of rotating beam applied to helicopter blades. The complete analysis of the \(3-D\) rotating helicopter blade was published in [8] where the full nonlinear partial differential equations governing the motion of the blade were derived. The blade model was based on extended Bernoulli–Euler theory and took into account the geometrical nonlinearities due to large deformations. However, again the axial strain was assumed as a very small quantity and equaled to zero what corresponded to the inextensible beam model. Nonlinear free vibration of a rotating beam was presented in [10]. The hub–beam model was formulated on the basis of Bernoulli–Euler beam theory with an assumption of inextensibility of the beam, and next reduced by the mode projection to a nonlinear one degree of freedom oscillator with geometrical and inertia nonlinearities. The effect of the hub radius, preset angle and angular speed on natural frequencies and softening/hardenning effect has been analytically obtained by the time transformation method and demonstrated for the first three natural modes. The effect of a flexible supported hub as well as the preset angle of the beam on rotor dynamics was presented in [11]. The nonlinear Bernoulli–Euler hub–beam model was reduced to three nonlinear ordinary differential equation of motions. Response of the system driven by prescribed torque was studied numerically and it was shown that for a soft base and a low preset angle unstable vibrations of the rotor might occur. The proposed model took into account hub dynamics, the beam nonlinear curvature and axial inertia arose from large flexural deformations. Nevertheless, the inextensibility condition was applied in the mathematical model formulation. An interesting study of outward and inward oriented beam clamped outside or inside of a rigid ring was presented in [25]. The PDEs nonlinear beam model was derived from extended Bernoulli–Euler theory and then reduced to ODEs by Galerkin procedure taking linear modes of a non-rotating cantilever beam for projection. Free and forced vibrations were determined on the basis of Lindstedt–Poinceré method and solved numerically. A change from hardening to softening behaviour due to change of rotational speed was demonstrated. The jump phenomena in a case of the main and subharmonic resonances was detected. The influence of the energy source i.e. DC motor supplied torque to the hub–beam rotor was investigated in [9] for a few selected resonance conditions. The derived partial differential equations have been reduced to ordinary differential equations and then solved by the multiple scale method. The solutions have been determined for primary and secondary resonances assuming small angular speed of the structure (slewing motion) and different perturbation orders for excitation amplitude and frequency.
Recently, the importance of the nonlinear effects for rotating inextensible beams which may lead to strong nonlinear phenomena, has been presented in [23]. The model demonstrated both softening or hardening resonance characteristics in spite of the rotation stiffening effect. The Coriolis as well as nonlinear effects due to the coupling of bending–stretching, bending–twist and twist–stretching were studied in [24]. To accurately predict vibration characteristics of the rotating beam, the model was divided on segments into axial direction. The numerical solutions demonstrated that Coriolis effect could essentially change dynamics of the hub–beam system in a case of small hub radius, large beam slenderness and high angular velocity. Furthermore, a coupling among axial, torsional and flexural oscillations was observed.
Analysis of free vibrations of rotating thick plates presented in [12]. The Mindlin plate theory combined with a second order strain displacement has been applied in the finite element formulation for the rotating plate. The formulation included Coriolis effect, centrifugal force and coupling between in-plane and out-of-plane vibrations. The formulated problem was solved numerically and on this basis the importance of in-plane vibrations of rotating structures for high speed values was demonstrated.
Parametric vibrations of a nonlinear beam model induced by periodic modulation of angular velocity were studied in [1]. The coupling of lagging and axial motion due to Coriolis force was taken into account. The zones of parametric resonances were determined analytically by the multiple tome scales method. Authors introduced so called the effective nonlinearity coefficient to determine the parametric resonances and to demonstrate importance of exact geometrical formulation of the studied problem.
The recent studies on a non-rotating nonlinear beam model with an attached axial spring, represented imperfect boundary conditions, were published in [2, 3, 16, 19]. The model took into account geometrical nonlinearities, the shear effect and coupling between flexural and longitudinal vibrations. The importance of the definition of geometric curvature was discussed in [18]. The strict nonlinear shearable beam model was solved analytically by a direct attack of the nonlinear partial differential equations and the results were verified by a finite element method by means of the commercial Abaqus_CAE© software [14]. The results showed softening versus hardening dichotomy in the resonance curves and also strong interactions between flexural and longitudinal (axial) vibrations, leading to internal resonances occurring for specific stiffness of the axial spring. Those new results obtained for nonlinear beams (considered as fixed structures), the observed interactions between transversal and longitudinal vibrations and the dichotomy of the softening and hardening effect [14] motivated authors to equivalent studies of rotating structures. The nonlinear phenomena observed for the rotating inextensible beams [23, 24] suggested to analyse a more general case of the extensional beam. The effect of longitudinal vibrations can be more important if the rotating beam carries a heavy tip mass which generates additional forces due to rotation and oscillations.
A preliminary study of a rotating extensional beam model which takes into account transversal and also longitudinal vibrations was presented in [26]. In the present work the configuration of the system for an arbitrary preset angle of the beam and added tip mass is considered. We also modify definition of the beam curvature taken in the model, according to the comments presented in [17]. On the basis of the complete beam model approximate solutions are determined on the basis of the multiple time scales method applied directly to the partial differential equations and associated dynamic boundary conditions. Then, the influence of the most important parameters is shown.
2 Model of extensional rotating beam
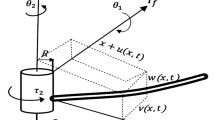
A model of the considered rotating structure is composed of a rigid hub and a flexible blade oscillating in one plane. We assume that out-of-plane bending, torsion and warping are negligible. However, the oscillations and rotation planes may have different orientations, defined by a preset angle \(\theta\) measured from the rotating horizontal plane (Fig. 1).
Lumped mass is added to the beam tip which allows to study a more general case with dynamic boundary conditions and furthermore, the mass can be used to tune the structure to the specific resonance conditions. The beam with a rectangular cross-section is made of isotropic material with linear material properties and assumed to be thin, thus, the model is based on Bernoulli–Euler beam theory. Nevertheless, due to possible large oscillations, the theory is extended and it takes into account geometrical nonlinear terms and also both flexural and longitudinal beam deformations. It means that the beam is extensible. The rotation and oscillations of the system arise from the external torque \(T_{ext}\) imposed on the hub or periodic force applied directly to the beam. The torque is assumed to be composed of constant and periodic parts, thus, the structure may rotate and oscillate. Depending on amplitude and frequency of excitation as well as structural parameters, dynamics of the studied extensional beam differs from its inextensible counterpart, e.g. [23].
2.1 Model formulation
To describe motion of the structure we introduce a fixed coordinates set \((X_0,Y_0,Z_0)\) located at the hub centre C, a set of coordinates (X, Y, Z) rotating with the hub and with the same origin located at C point, and a set of rotating coordinates (x, y, z) oriented according to the symmetry axes of the undeformed beam and with the origin located at point 0—the clamping beam point, as shown in Fig. 1. The preset angle of the beam \(\theta\) is presented on a side view in Fig. 1b. For any arbitrary preset angle the beam oscillates in the plane different than the plane of rotation. For \(\theta =0\) the oscillations and rotation planes overlap.
The longitudinal and transversal displacements u(x, t) and v(x, t) of an elementary segment located in point A, and next moved to \(A'\) position are defined in the rotating coordinate frame, as presented in Fig. 1c. The displacement of both ends of the elementary segment from initial position A and B to the final position \(A'\) and \(B'\) is shown in Fig. 1d where dx denotes the undeformed beam element while ds is the deformed segment at any arbitrary time instant. A hub position is defined by angle of rotation \(\psi (t)\). We assume that beam is deformed only in (x, y) plane because of its high stiffness in z direction. Twist and warping of the beam is neglected in this study as well.
Taking into account Fig. 1d we find
where \(\phi\) is angle of rotation of the elementary segment which also defines angle of rotation of the cross-section as in Bernoulli–Euler beam model shear deformation is neglected. Primes denote partial derivative with respect to x coordinate. Considering that
and then applying Eq. (1), we find the definition for \(\phi '\)
The strain e of the elementary segment is determined as
The beam curvature based on geometric definition has the form [2, 17, 18]
thus, taking into account that \(\displaystyle {\frac{\partial s }{\partial x} = \sqrt{\left( 1+u'\right) ^2 + v'^2}}\), the geometric beam curvature is defined as:
If we assume that \(u'=0\) and \(u''=0\) we obtain the classical definition of a geometrical curvature for a line given by analytical function y(x). On the other hand the mechanical curvature [18] is defined as \(\displaystyle \kappa _m=\frac{\partial \phi }{\partial x}\) which is equivalent to the formula (3).
For inextensible beams the geometrical \(\kappa _g\) or mechanical \(\kappa _m\) curvatures can be obtained assuming \(e=0\) which results in \(u' = \sqrt{1-v'^2} -1\). Computing second derivative \(\displaystyle {u''=\frac{-v'v''}{\sqrt{1-v'^2}}}\) and then substituting mentioned formulae into mechanical and geometrical curvatures we get
This means that for an inextensible beam both definitions give the same result.
In this paper, for the extensible beam model, according to [18] we apply the mechanical curvature definition.
Equations of motion of the rotating structure are derived on the basis of Hamilton principle of the least action
where T and V are kinetic and potential energies and \(\delta W_{nc}\) is virtual work of nonconservative forces. In our case we can consider work of viscous damping forces acting in longitudinal and transversal directions, work of external torque \(T_{ext}\) supplied to the hub and forces acting directly on the beam in axial and transversal directions representing aerodynamic forces for example.
The potential energy V takes the form
Bending moment M is defined by the mechanical curvature
while normal force N by strain
where E is Young modulus, A, I the area of the beam cross-section and its geometrical moment of inertia with respect to neutral axis of bending. Thus, potential energy has the form
Substituting Eqs. (3) and (4) into potential energy (9) we get
where the function under integral is defined as
Kinetic energy of the hub, beam and tip mass takes the form
where \({\mathbf {R}}\) is a radius vector of an arbitrary beam point and \({\mathbf {R}}_t\) is a radius vector of the beam tip point. A dot means time derivative, \(J_h\) is mass moment of hub inertia, \(m_t\) is lumped tip mass and \(\rho _1\) beam mass per unit length.
To obtain motion of the beam in the absolute coordinate frame we transform the rotating coordinates (x, y, z) to the coordinates frame \((X_0, Y_0, Z_0)\) taking into account transformation matrixes \(\mathbf{A }_{\theta }\), \(\mathbf{A }_{\psi }\), which include the rotation and preset angle, respectively [11, 15]
where
Thus, the velocity vector is defined as
From the above equation we get the components of the velocity vector
Substituting (19) into (15) we obtain kinetic energy of the system
where
and subscript t denotes the beam tip point at \(x=L\).
To use Hamilton principle of the least action (8) variations of kinetic and potential energies are expressed as
Substituting Eq. (20) and Eq. (13) into Eq. (8) then applying Eq. (23), after integration by parts and grouping terms for variations \(\delta u\), \(\delta v\), \(\delta \psi\), we obtain differential equations of motions and terms which correspond to boundary conditions for the rotating hub–beam structure with tip mass. The equations of motion obtained for particular variations take the form
-
variation \(\delta u\)
$$\begin{aligned}&\rho _1 \left[ \ddot{u} - \left( R_h + x +u \right) {\dot{\psi }}^2 \nonumber \right. \\&\left. \quad -\, 2\dot{v} {\dot{\psi }} \cos \theta \nonumber \right. \\&\quad \left. - v \ddot{\psi }\cos \theta \right] + c_u {\dot{u}}\nonumber \\&\quad +\, \left[ \frac{\partial F_V}{\partial u'} - \left( \frac{\partial F_V}{\partial u''} \right) ' \right] ' = f_u \end{aligned}$$(24)where \(f_u\) is generalised force and \(c_u\) the damping coefficient corresponding to u coordinate, and
$$\begin{aligned} \frac{\partial F_V}{\partial u'}&= E I \left\{ \frac{ v'' \left[ \left( 1 + u' \right) v'' - v' u'' \right] }{\left[ \left( 1 + u' \right) ^2 + v'^2 \right] ^2} \nonumber \right. \\&\quad\left. - \frac{ 2 \left( 1 + u' \right) \left[ \left( 1 + u' \right) v'' - v' u'' \right] ^2}{\left[ \left( 1 + u' \right) ^2 + v'^2 \right] ^3} \right\} \nonumber \\&\quad+ EA \frac{\left( 1 + u' \right) \left( \sqrt{\left( 1 + u' \right) ^2 + v'^2} - 1 \right) }{\sqrt{\left( 1 + u' \right) ^2 + v'^2}} \end{aligned}$$(25)$$\begin{aligned} \frac{\partial F_V}{\partial u''}&= E I \frac{v' \left[ \left( 1 + u' \right) v'' - v' u'' \right] }{\left[ \left( 1 + u' \right) ^2 + v'^2 \right] ^2} \end{aligned}$$(26) -
variation \(\delta v\)
$$\begin{aligned}&\rho _1 \left[ \ddot{v} + \left( R_h + x +u \right) \ddot{\psi }\cos \theta \nonumber \right. \\&\left. \quad +\, 2{\dot{u}} {\dot{\psi }} \cos \theta - v {\dot{\psi }}^2 \cos ^2 \theta \right] \nonumber \\&\quad +\, c_v \dot{v} + \left[ \frac{\partial F_V}{\partial v'} - \left( \frac{\partial F_V}{\partial v''} \right) ' \right] ' = f_{v} \end{aligned}$$(27)where \(f_v\) is generalised force and \(c_v\) the damping coefficient corresponding to v coordinate, and
$$\begin{aligned} \frac{\partial F_V}{\partial v'}&= -E I \left\{ \frac{u'' \left[ \left( 1+u'\right) v'' - v' u'' \right] }{\left[ \left( 1 + u' \right) ^2 + v'^2 \right] ^2} \right. \nonumber \\&\left. \quad+ \frac{2 v' \left[ \left( 1 + u' \right) v'' - v' u'' \right] ^2}{\left[ \left( 1 + u' \right) ^2 + v'^2 \right] ^3} \right\} \nonumber \\&\quad+ EA \frac{v' \left( \sqrt{\left( 1 + u' \right) ^2 + v'^2} - 1 \right) }{\sqrt{\left( 1 + u' \right) ^2 + v'^2}} \end{aligned}$$(28)$$\begin{aligned} \frac{\partial F_V}{\partial v''}&= E I \frac{\left( 1 + u' \right) \left[ \left( 1 + u' \right) v'' - v' u'' \right] }{\left[ \left( 1 + u' \right) ^2 + v'^2 \right] ^2} \end{aligned}$$(29) -
variation \(\delta \psi\)
$$\begin{aligned}&J_h \ddot{\psi }+ c_\psi {\dot{\psi }} + \int _{0}^{L} \rho _1 \left\{ \left[ \left( R_h + x + u \right) ^2 \nonumber \right. \right. \\&\quad \left. \left. + v^2 \cos ^2 \theta \right] \ddot{\psi }\right. \nonumber \\&\quad + \,\left. \left[ \left( R_h + x + u \right) \ddot{v} - v \ddot{u} \right] \cos \theta + 2 \nonumber \right. \\&\left. \qquad \left[ \left( R_h + x + u \right) {\dot{u}} + v \dot{v} \cos ^2 \theta \right] {\dot{\psi }} \right\} dx \nonumber \\&\quad +\, m_t \left\{ \left[ \left( R_h + L + u_t \right) ^2 + v_t^2 \cos ^2 \theta \right] \ddot{\psi }\nonumber \right. \\&\quad \left. + \left[ \left( R_h + L + u_t \right) \ddot{v}_t - v_t \ddot{u}_t \right] \cos \theta \right. \nonumber \\&\quad +\, \, \left. 2 \left[ \left( R_h + L + u_t \right) {\dot{u}}_t + v_t \dot{v}_t \cos ^2 \theta \right] {\dot{\psi }} \right\} = T_{ext} \end{aligned}$$(30)where \(T_{ext}\) is external torque supplied to the hub and \(c_{\psi }\) the related damping coefficient.
The boundary terms obtained after integrations, which must vanish, take the form
For the considered case of the rotating cantilever beam we have
for \(x =0\),
and from (26) we get \(\displaystyle \left( \frac{\partial F_V}{\partial u''} \right) _{x=0} = 0\).
For \(x=L\) we get dynamical boundary conditions. The lumped mass at the tip generates inertia forces in axial and transversal directions with bending moment equal to zero. Dynamical (natural) BC require vanishing terms collected for proper variations for \(x=L\)
The derived above partial differential equations and associated boundary conditions describe nonlinear dynamics of the rotating multibody system with the flexible extensional beam.
2.2 Third order approximation model
The equations presented in Sect. 2.1 are derived on the basis of the nonlinear model of the rotating hub–beam–tip mass system without any additional simplifications. However, to determine analytical solutions we introduce formal small parameter \(\epsilon\), and express displacements u, v as
and then the nonlinear functions are expanded in Taylor series. Therefore, Eqs. (24), (27) and (30) take the form
Note that tilde has been dropped out for further notation simplicity.
Considering the cantilever beam with lumped mass at the tip, the boundary conditions formulated in (32), (33) take the form
for \(x=0\)
for \(x=L\)
3 Oscillations of rotating beam with constant angular velocity
The first attempt to analyse the system response neglects dynamics of the hub and takes constant angular velocity of the system. Therefore, Eq. (37) is neglected and in equations of motion (35), (36) we assume constant angular velocity \({\dot{\psi }}(t) = \varOmega\).
In order to get approximate solutions in a proper perturbation orders we express angular speed, viscous damping and external forces with respect to the formal small parameter \(\epsilon\),
The proposed scaling takes into account not very high angular speeds, damping and external forces which guarantee moderate large oscillations. Under such assumptions coupled transversal–longitudinal vibrations of the rotating nonlinear beam with the tip mass are studied.
The scaling requires reformulation of perturbation orders in PDEs of motion
and boundary conditions for \(x=L\)
The above equations will be solved analytically by the multiple time scale method.
4 Perturbation method
The mathematical model of the beam-tip mass system rotating with constant angular speed is governed by the set of partial differential equations (43), (44) which represent coupled transversal–longitudinal beam oscillations. Furthermore, the tip mass loads the beam in both directions and creates dynamical boundary conditions (45)–(47). In contrast to standard procedure based on Galerkin orthogonalisation method and modal reduction, we apply directly the multiple time scales method to partial differential equations and associated boundary conditions [21]. The proposed method has been applied in [14] to solve coupled transversal–longitudinal oscillations of fixed simply supported beam with a spring at the end.
According to the multiple time scale method we introduce different time scales related to small parameter \(\epsilon\)
where \(t_0\) is the fast time scale, and \(t_1\) and \(t_2\) are the slow time scales (slow flow) and T is time. The time decomposition (48) generates new definitions of the first- and second-order time derivatives. Thus, the first and the second order time derivatives take the form
where operator \(D_j^k(.) = \frac{\partial ^k}{\partial {t_j}^k}(.)\) denotes the \(k^{th}\) order partial derivative with respect to the \(t_j\) time scale.
The solutions are expressed in a series of the small parameter
where \(v_j(x,t_0,t_1,t_2)\) and \(u_j(x,t_0,t_1,t_2)\) denote the solutions in the zeroth, first, and second perturbation orders \((j=0,1,2)\).
We assume that excitation force in the axial direction is neglected \(f_u=0\). The system is excited by external force \(\xi _v(x)\) distributed along the beam spam and acting in transversal direction as periodic load
where \(\sigma\) is a detuning of excitation frequency \(\omega\) with respect to natural frequency \(\omega _0\),
We note that the definition of the detuning parameter is based on the natural frequency of the not rotating beam. The effect of angular speed is taken into account in the successive perturbation orders. This differs from a standard approach which takes into account rotation in the zero order perturbation and the detuning parameter is defined around this state.
Substituting solutions (50) and their derivatives into equations of motion (43), (44) and boundary conditions (45)–(47) and considering boundary conditions (38), we get equations of motion and boundary conditions in the successive perturbation orders
First order (\(\varepsilon\))
and boundary conditions,
Second order (\(\varepsilon ^2\))
where
and boundary conditions,
Third order (\(\varepsilon ^3\))
where
and boundary conditions,
The above equations of motion together with boundary conditions will be solved successively up to the third order perturbations.
4.1 First order solution
We assume that the internal resonances are excluded in this study. The reason for this assumption is based on the results obtained from the FEM model for accepted structural parameters and angular speeds. To analyze internal resonances, special cases of the model with properly tuned parameters together with selected angular speed should be examined. Excluding internal resonances, the first order solution is sought as a product of time depended and space depended functions expressed in the general form:
where \(A(t_1,t_2)\) and \(B(t_1,t_2)\) are complex amplitudes decomposed on real and imaginary parts indicated by subscripts re and im, respectively and i is imaginary unit. The longitudinal and transversal mode shapes are defined by space functions \({{\hat{u}}}_0(x)\) and \({{\hat{v}}}_0(x)\).
The natural frequencies are given as:
and must be analysed together with \(\lambda _u\) and \(\lambda\) which are defined by transcendental equations:
We note that boundary conditions (64) lead to vanishing parameter \(c_2\).
4.2 Second order solution
Second order equations can be solved if and only if following solvability conditions are satisfied:
After some mathematical manipulations, integration left hand side by parts, together with equations (53) and boundary conditions (57)–(60) and (54), we obtain
In this step we focus only on secular generating terms determination. Equations are decomposed on harmonics, and therefore functions which contain \(e^{i \omega _{0A} t_0}\) or \(e^{-i \omega _{0A} t_0}\) in longitudinal direction and \(e^{i \omega _0 t_0}\) or \(e^{-i \omega _0 t_0}\) in transversal direction are studied in order to determine time derivatives of real and imaginary amplitudes with respect to time \(t_1\), thus, for
\(e^{i \omega _{0A} t_0}\):
\(e^{-i \omega _{0A} t_0}\):
\(e^{i \omega _0 t_0}\):
\(e^{-i \omega _0 t_0}\):
This leads us directly to \(\frac{\partial A_{re}}{\partial t_1}=\frac{\partial A_{im}}{\partial t_1}=\frac{\partial B_{re}}{\partial t_1}=\frac{\partial B_{im}}{\partial t_1}=0\), what means that derivatives of amplitudes are independent of first time scale and in the following \(D_1\) is equal to zero.
Now, ordinary differential equations (55) and associated boundary conditions (57)–(60) can be solved without any special efforts. Their mathematical expression of solutions are complex and can be reported here only with simplified notation using coefficients \(c_7\)-\(c_{18}\), that are functions of spacial coordinate x
It is worth to remark that the second order axial vibration \(u_1\) depends on the transversal vibration frequency \(\omega _0\), while the transversal vibration \(v_1\) depends on the axial frequency \(\omega _{0A}\). This highlights the nonlinear coupling between axial and transversal motions.
4.3 Third order solution
In the third order approximation only time derivatives with respect to the second slow time scale \(t_2\) are to be solved, therefore the solvability conditions are applied in the form:
which through integration by parts, substituting boundary conditions (57)–(60), (64)–(67), and then equaling to zero the secular generating terms, provides a set of the four ordinary differential equations
where the coefficients \(c_{19}-c_{26}\) are numbers (depending only on the mechanical and geometrical properties of the beam) with very long and involved expressions that cannot be reported. However, they can be detected by a symbolic software manipulator. Parameter \(\xi =\int _0^L \xi _v(x) v_0(x) dx\) is amplitude of external loading.
Next, the complex amplitudes are expressed in the polar form
and then, collecting real and imaginary parts of Eq. (81), we get modulation equations
The above equations can be investigated for specific set of parameters and corresponding vibration modes. To study influence of selected parameters and bifurcation scenarios we select a few important parameters which are taken as free bifurcation parameters. Highlighting the presence of \(\varOmega\), \(\sigma\), \(\xi\), \(C_u\), \(C_v\), \(R_h\), \(\theta\), (83) can be rewritten as
To solve above equations analytically we introduce new variable \(\gamma (t_2) = \sigma t_2 - \beta _b(t_2)\) and substitute it into (84) by replacing \(\beta _b\). In a steady state \(a'(t_2)=0\), \(\beta _a'(t_2)=0\), \(b'(t_2)=0\), \(\gamma '(t_2)=0\), thus from Eq. (84) we may determine equation which involves amplitude versus selected bifurcation parameters
The above equation allows computing resonance curves against the detuning parameter \(\sigma\) as well as bifurcation scenarios for the crucial structural parameters of the rotating system.
We note that for the transient oscillations all four modulation equations (84) are involved in the solution. While for the steady solution \(a(t_2)=0\), that means that the transversal excitation does not force the axial displacement to the first order, while excites it in the second order, due to the nonlinear coupling, see (78). This is a consequence of lack of internal resonance, and of the fact of forcing in the vicinity of transversal resonance. That is an hypothesis done for the purpose of this paper. The case of internal resonances will be demonstrated in a separate analysis.
5 Numerical analysis
Numerical computations are performed for a carbon-epoxy composite beam composed of 18 layers \([0,-60,60,0,-60,60,60,60,-60,-60,0,0,-60,0,0,60,60,-60]\) having thickness 0.00005 m of each individual layer. The assumed configuration corresponds to resultant homogenous and isotropic properties. The beam parameters takes values: length of the beam—\(L=0.35\) m, mass per length—\(\rho _1=0.04131\) kg/m, stiffness coefficients—\(EI=0.127883\) Nm\(^2\), \(EA=1.89457 \times 10^6\) N.
To validate the analytical model the structure has been modeled in a commercial finite element (FE) software Abaqus_CAE©. Then, the modal analysis of FE model is compared with the analytical results. The comparison is presented in “Appendix 1” in Tables 1 and 2 for selected transversal and longitudinal modes and different tip mass values, \({\bar{m}}_t=0\), \({\bar{m}}_t=0.05\), \({\bar{m}}_t=0.1\), \({\bar{m}}_t=1.0\), defined as the ratio to the beam mass \({\bar{m}}_t =\frac{m_t}{L*\rho _1}\). The results show a very good agreement of FE and the analytical models. The influence of the tip mass \({\bar{m}}_t\) on the modes shape is presented in Fig. 2. The change of tip mass almost does not influence the first bending mode (Fig. 2a), but the second and the third modes (Fig. 2b, c) for relatively heavy mass (\({\bar{m}}_t=1.0\)) are changed essentially, in contrast to zero or small tip mass. The influence of the tip mass on the first longitudinal mode is presented in Fig. 2d and the mode is affected by added mass changing its shape from curvilinear to almost linear if mass is heavy.
Vibration modes for selected tip mass \({\bar{m}}_t=0\) (black), \({\bar{m}}_t=0.05\) (green), \({\bar{m}}_t=0.1\) (blue), \({\bar{m}}_t=1\) (red). First flexural vibration mode (a), the second flexural mode (b), the third flexural mode (c), and the first longitudinal mode (d). (Color figure online)
On the base of the analytical approach presented in Sect. 4 we can compute the coefficients given in equation (85). They depend on the value of tip mass \({\bar{m}}_t\) and as well as on the vibration mode. For the need of our study we select the first and the second bending mode and two values of tip mass, defined with respect to beam mass, \({\bar{m}}_t=0.05\) and \({\bar{m}}_t=1.0\), which represent relatively light and heavy tip mass, \(5\%\) and \(100\%\) of the beam mass, respectively. In the analysis the radius of the hub is fixed as 0.1 of the beam length L, \(R_h=0.035\) m.
For the assumed cases the coefficients of Eq. (85) take values:
First bending mode, \({\bar{m}}_t=0.05\)
Second bending mode, \({\bar{m}}_t=0.05\)
First bending mode, \(~{\bar{m}}_t=1.0\)
Second bending mode, \({\bar{m}}_t=1.0\)
Amplitude and frequency of excitation \(\xi\), \(\omega\), angular velocity of the beam \(\varOmega\) and preset angle \(\theta\) are varied in the analysis.
The resonance curves for the first and the second vibration mode for small tip mass \({\bar{m}}_t=0.05\), preset angle \(\theta =45^{\circ }\), and selected angular speed are presented in Fig. 3. The nonlinear beam dynamics is observed for large beam deformations. The resonance curves plotted against detuning parameter \(\sigma\) (which corresponds to changing excitation frequency with respect to the natural frequency) demonstrate a small stiffening effect for the first mode, without the unstable branch. Whereas, for the second mode a very clear softening effect is demonstrated in Fig. 3b. The rotational speed does not change the nature of the curves but just increase the natural frequency and shifts the frequency-response curves toward higher frequencies. To confirm this conclusion resonance curves have been plotted for very large value of \(\varOmega =300\) rad/s for the first (Fig. 3c) and for the second (Fig. 3d) vibration mode, and the nature of the curve is still maintained, just large shift of frequency is observed. This result confirms the conclusions presented in paper [23] where softening phenomenon was observed despite enlarged angular speed.
Resonance curves for selected angular velocity and tip mass \({\bar{m}}_t=0.05\), a and c first flexural vibration mode: \(\xi =0.2\), \(C_v=0.0292\), \(\theta =45^\circ\), b and d second flexural mode: \(\xi =0.2\), \(C_v=0.0423\), \(\theta =45^\circ\). \(\varOmega =0\) rad/s—black, \(\varOmega =10\) rad/s—red, \(\varOmega =20\) rad/s—blue, \(\varOmega =300\) rad/s—green. (Color figure online)
Resonance curves for selected angular velocity and tip mass \({\bar{m}}_t=1.0\), a first flexural vibration mode: \(\xi =0.045\), \(C_v=0.0142\), \(\theta =45^\circ\), b second flexural mode: \(\xi =0.045\), \(C_v=0.0169\), \(\theta =45^\circ\). \(\varOmega =0\) rad/s (black), \(\varOmega =5\) rad/s (red), \(\varOmega =10\) rad/s (blue). (Color figure online)
The heavy tip mass, \({\bar{m}}_t=1.0\), enlarge the nonlinear effect of the rotating beam. As it is seen in Fig. 4 stiffening (Fig. 4a) and softening (Fig. 4b) are increased and the tendency is maintained for \(\varOmega =0\) rad/s, \(\varOmega =5\) rad/s, \(\varOmega =10\) rad/s. We may conclude that in fact angular velocity does not affect the nature of the resonance curves but just shifts the resonance zone into higher frequency.
Bifurcation diagrams against amplitude of excitation for selected detuning parameters a mode 1, \(\sigma =-5.0\) (black), \(\sigma =0\) (blue), \(\sigma =1.0\) (red), \(\sigma =1.5\) (green), \(\sigma =3.0\) (brown), \(C_v=0.0292\), and b mode 2, \(\sigma =-5.0\) (black), \(\sigma =-2.0\) (blue), \(\sigma =0\) (red), \(\sigma =1.0\) (green), \(\sigma =5.0\) (brown), \(C_v=0.0423\); \(\theta =45^\circ\), \(\varOmega =10\) rad/s, tip mass \({\bar{m}}_t=0.05\). (Color figure online)
The bifurcation analysis is performed also against amplitude of excitation \(\xi\) for fixed angular speed and for selected excitation frequencies (detuning parameter). For the first mode nonlinear behaviour, with saddle-node bifurcation, occurs for large and positive values of detuning \(\sigma =1.5\) (green), \(\sigma =3.0\) (brown) in Fig. 5a. For the first mode the bifurcations can be obtained for very large oscillations which for the studied structure can be difficult to be achieved in practice. In contrast, for the second mode the nonlinear effect occurs for negative values of detuning parameter \(\sigma =-5.0\) (black), \(\sigma =-2.0\) (blue) or \(\sigma =0\) (red) in Fig. 5b and moderately large amplitudes, achievable in practice.
Assuming constant angular speed \(\varOmega =10\) rad/s and fixing amplitude of external loading \({\xi =0.2}\), we check an influence of the preset angle on the system response. In Fig. 6 the preset angle \(\theta\) is varied in wide ranges from \(\theta =0^{\circ }\) up to \(\theta =90^{\circ }\). We note that in a real structure a large change of the preset angle may generate additional beam deformations which are not taken into account here as the model predicts in-plane oscillations. The change of preset angle affects the components of angular velocity vector in relation to beam’s orientation and therefore affect the beam response. For the first mode and fixed excitation amplitude the resonance curves are shifted into higher frequencies while preset angle \(\theta\) is increased (see Fig. 1). For the second mode the resonance curves are almost not affected (Fig. 6b). It means that higher modes are much less sensitive for variation of preset angle.
Resonance curves for selected preset angle \(\theta =0^{\circ }\) (black), \(\theta =15^{\circ }\) (red), \(\theta =30^{\circ }\) (blue), \(\theta =45^{\circ }\) (green), \(\theta =60^{\circ }\) (pink), \(\theta =75^{\circ }\) (orange), \(\theta =90^{\circ }\) (gray); \(\varOmega =10\) rad/s, a first flexural vibration mode: \(\xi =0.2\), \(C_v=0.0292\), \(\varOmega =10\) rad/s, \({\bar{m}}_t=0.05\) and b second flexural mode: \(\xi =0.2\), \(C_v=0.0423\), \(\varOmega =10\) rad/s, \({\bar{m}}_t=0.05\). (Color figure online)
The response of the system against angular velocity is also tested for fixed excitation amplitude and detuning parameter. The bifurcation curves for the first mode computed for data given in (86) are presented in Fig. 7. For zero or small detuning parameter \(\sigma =0\) rad/s or \(\sigma =0.2\) rad/s or if detunig parameter has negative values as presented in Fig. 7b for \(\sigma =-0.2\) rad/s till \(\sigma =-10\) rad/s, there is one maximum of the response lactated at zero angular velocity and then if we vary \(\varOmega\) in positive or negative direction amplitudes decrease, tending to zero. For large and positive values of the detuning parameter, \(\sigma =0.5\) rad/s till \(\sigma =10\) rad/s (Fig. 7a) the amplitude curves have two maxima located symmetrically with respect to zero angular velocity. As it is seen in Fig. 8 for \(\sigma =10\) rad/s and negative rotation the characteristic has an opposite slope to that obtained for positive rotation. We note that both curves are mirror symmetric being in agreement with Eq. (85) which depends on square of angular speed.
Similar analysis based on data (87) is repeated for the second vibration mode (Fig. 9). The curves are again mirror symmetric, in this case however, the slopes of the curves are opposite to those demonstrated for the first mode. Furthermore, for \(\sigma =-4\) rad/s (Fig. 9b) two separate solutions are obtained (magenta curve), the small amplitude curve with maximum located at zero and the large amplitude curve observed by the isolated “island” at the top. The above mentioned results show clearly that the beam rotation may increase vibrations and may lead to the multiple solutions.
Bifurcation diagrams against angular velocity \(\varOmega\) and for selected detuning parameters a \(\sigma =0\) rad/s (black), \(\sigma =0.2\) rad/s (red), \(\sigma =0.5\) rad/s (blue), \(\sigma =1\) rad/s (magenta), \(\sigma =4\) rad/s (green), \(\sigma =10\) rad/s (orange) and corresponding negative values b \(\sigma =-0.2\) rad/s (red), \(\sigma =-0.5\) rad/s (blue), \(\sigma =-1\) rad/s (magenta), \(\sigma =-4\) rad/s (green), \(\sigma =-10\) rad/s (orange). First flexural vibration mode; \(\theta =45\), \({\bar{m}}_t=0.05\). (Color figure online)
Bifurcation diagrams against angular velocity \(\varOmega\) and for selected detuning parameters a \(\sigma =0\) rad/s (black), \(\sigma =0.5\) rad/s (red), \(\sigma =1\) rad/s (blue), \(\sigma =4\) rad/s (magenta), \(\sigma =10\) rad/s (green) and corresponding negative values b \(\sigma =-0.5\) rad/s (red), \(\sigma =-1\) rad/s (blue), \(\sigma =-4\) rad/s (magenta), \(\sigma =-10\) rad/s (green). Second flexural vibration mode; \(\theta =45^{\circ }\), \({\bar{m}}_t=0.05\). (Color figure online)
Resonance curves a for various hub radius \(R_h=0.035\) m (black), \(R_h=5\times 0.035\) m (blue), \(R_h=20 \times 0.035\) m (red), and bifurcation diagram b of vibration amplitude against hub radius \(R_h\) for selected detuning parameters \(\sigma =-2.0\) rad/s (black), \(\sigma =0\) rad/s (blue), \(\sigma =1\) rad/s (green), \(\sigma =1.5\) rad/s (red), \(\sigma =2\) rad/s (magenta). First flexural vibration mode; \(\varOmega =10\) rad/s, \(\theta =45^{\circ }\), \({\bar{m}}_t=0.05\). (Color figure online)
Resonance curves a for various hub radius \(R_h=0.035\) m (black), \(R_h=5\times 0.035\) m (blue), \(R_h=20 \times 0.035\) m (red), and bifurcation diagram b of vibration amplitude against hub radius \(R_h\) for selected detuning parameters \(\sigma =-5.0\) rad/s (black), \(\sigma =-2.0\) rad/s (blue), \(\sigma =-1.0\) rad/s (green), \(\sigma =0.0\) rad/s (red), \(\sigma =3\) rad/s (magenta). Second flexural vibration mode; \(\varOmega =10\) rad/s, \(\theta =45^{\circ }\), \({\bar{m}}_t=0.05\). (Color figure online)
The above computations have been performed for fixed hub radius \(R_h=0.035\) m. The resonance curves computed for 5 times and 20 times larger radius for the first and the second mode are presented in Figs. 10a and 11a. As we may notice the increased hub radius shifts resonance curves into higher frequencies direction without a change of the resonance curve nature, with hardening for the first and softening for the second mode. In fact, if we increase the hub radius then the blade is shifted from the hub centre and centrifugal inertia forces increase as well. This gives an effect similar to the increased angular speed, bearing in mind all assumptions related to the model. The influence of the hub radius on natural vibrations is shown by backbone curves marked by dashed-dotted lines in Figs. 10a and 11a. The curves are shifted towards higher frequencies maintaining their hardening or softening. This result is in an agreement with result presented in [10] obtained by different approach. Bifurcation diagrams of blade response against the hub radius computed for various detuning parameters are shown in Figs. 10b and 11b, for the first and the second mode, respectively. The course of the bifurcation curves is different with the slopes opposite to the corresponding resonance curves.
6 Conclusions
The developed model of the rotating beam structure enables analysis of free and forced oscillations for a large amplitude range. The partial differential equations and associated boundary conditions are derived for constant or varied angular speed \({\dot{\psi }}=\varOmega\), arbitrary hub radius, preset angle \(\theta\), tip mass \(m_t\) attached to the beam. The beam model takes into account coupled longitudinal and transversal beam’s oscillations assuming extensionality of the beam. External and internal resonances (not presented in this paper) can be studied by the proposed model.
The mathematical model have been formulated assuming angular velocity, tip mass, preset angle, amplitude and frequency of excitation as a bifurcation parameters. Therefore, the solution has been found analytically by perturbation technique under the assumption that angular velocity is of \(\varepsilon\) order. This approach allows to construct the solution successively, starting from a non-rotating beam and then to include the influence of rotation in the successive perturbation orders. The obtained analytical solutions enable complete bifurcation analysis for the most important mentioned above structural parameters which are kept as free in the solution.
The detailed analysis is performed for selected resonance zones around the first and the second mode of transversal vibrations. The partial differential equations have been solved directly by the multiple time scales method up to the third order perturbation for the selected external resonances. The analysis exhibits hardening phenomenon for the first mode and softening for the second vibration mode. The increased angular velocity shifts the backbone curves as well as the resonance curves into the higher frequencies direction. The effect of hardening or softening however, is maintained also if angular velocity is increased. This result is due to the fact of considering angular speed as \(\varepsilon\) order. Similar effect has been observed for increased hub radius, which shifts backbone and resonance curves into higher frequencies direction without a change of the shape of the curves, maintaining hardening for the first and softening the second resonance zone. The bifurcation analysis of beam response against angular velocity shows that the response is mirror symmetric for positive and negative rotations and depending on the excitation frequency (detuning parameter) may lead to increase or decrease of vibration amplitudes and, in a case of the second mode, the existence of isolated multiple solutions. The variation of preset angle shifts the first resonance zone while for the second mode resonance the influence is very minor.
In the future research the analytical solution will be sought for coupled transversal-longitudinal oscillations due to internal resonances and for high speed rotations which requires different scaling. The model can be extended to a multi-bladed nonlinear rotor and then the effect of blades detuning on nonlinear vibration modes, resonance zones or vibration localisation can be studied for different boundary conditions, including influence of the tip mass.
References
Arvin H, Arena A, Lacarbonara W (2020) Nonlinear vibration analysis of rotating beams undergoing parametric instability: lagging-axial motion. Mech Syst Signal Process 144:106892
Babilio E, Lenci S (2017) Consequences of different definitions of bending curvature on nonlinear dynamics of beams. Proc Eng 199:1411–1416
Babilio E, Lenci S (2017) On the notion of curvature and its mechanical meaning in a geometrically exact plane beam theory. Int J Mech Sci 128–129:277–293
Crespo da Silva MRM, Glynn CC (1978) Nonlinear flexural–flexural–torsional dynamics of inextensional beams. I. Equations of motion. J Struct Mech 6 4:437–448
Crespo da Silva MRM, Glynn CC (1978) Nonlinear flexural–flexural–torsional dynamics of inextensional beams. II. Forced motions. J Struct Mech 6 4:449–461
Crespo da Silva MRM, Hodges DH (1986) Nonlinear flexure and torsion of rotating beams, with application to helicopter rotor blades-I. Formulation. Vertica 1986, 10 2:151–169
Crespo da Silva MRM, Hodges DH (1986) Nonlinear flexure and torsion of rotating beams, with application to helicopter rotor blades-II. Response and stability results. Vertica 1986, 10 2:171–186
Crespo Da Silva MRM (1998) A comprehensive analysis of the dynamics of a helicopter rotor blade. Int J Solids Struct 35(7–8):619–635
Fenili A, Balthazar JM, Brasil R (2003) Mathematical modelling of a beam-like flexible structure in slewing motion assuming non-linear curvature. J Sound Vib 268(4):825–838
Hamdan MN, AL-BEDOOR BO (2001) Non-linear free vibrations of a rotating flexible arm. J Sound Vib 242(5):839–853
Hamdan MN, El-Sinawi AH (2005) On the non-linear vibrations of an inextensible rotating arm with setting angle and flexible hub. J Sound Vib 281(1–2):375–398
Hashemi SH, Farhadi S, Carra S (2009) Free vibration analysis of rotating thick plates. J Sound Vib 323(1–2):366–384
Hodges DH (2006) Nonlinear composite beam theory. In: Progress in astronautics and aeronautics, vol 213. American Institute of Aeronautics and Astronautics, Reston
Kloda L, Lenci S, Warminski J (2018) Nonlinear dynamics of a planar beam-spring system: analytical and numerical approaches. Nonlinear Dyn 94(3):1721–1738
Latalski J, Warminski J, Rega G (2016) Bending-twisting vibrations of a rotating hub-thin-walled composite beam system. Math Mech Solids 22(6):1303–1325
Lenci S, Clementi F, Rega G (2016) A comprehensive analysis of hardening/softening behaviour of shearable planar beams with whatever axial boundary constraint. Meccanica 51(11):2589–2606
Lenci S, Clementi F, Rega G (2017) Comparing nonlinear free vibrations of Timoshenko beams with mechanical or geometric curvature definition. Procedia IUTAM 20:34–41
Lenci S, Clementi F, Rega G (2017) Reply to the discussion on ‘a comprehensive analysis of hardening/softening behavior of shearable planar beams with whatever axial boundary constraint’, by D. Genovese. Meccanica 52(11–12):3005–3008
Lenci S, Rega G (2016) Nonlinear free vibrations of planar elastic beams: a unified treatment of geometrical and mechanical effects. Proc IUTAM 19:35–42
Librescu L, Song O (2006) Thin-walled composite beams: theory and application. Springer, Dordrecht
Nayfeh AH (2000) Perturbation methods. Wiley, Hoboken
Nayfeh AH, Pai PF (2004) Linear and nonlinear structural mechanics. Wiley, Hoboken
Thomas O, Sénéchal A, Deü J-F (2016) Hardening/softening behavior and reduced order modeling of nonlinear vibrations of rotating cantilever beams. Nonlinear Dyn 86(2):1293–1318
Tian J, Su J, Zhou K, Hua H (2018) A modified variational method for nonlinear vibration analysis of rotating beams including coriolis effects. J Sound Vib 426:258–277
Turhan Ö, Bulut G (2009) On nonlinear vibrations of a rotating beam. J Sound Vib 322(1–2):314–335
Warminski J (2018) Nonlinear model of a rotating hub-beams structure: equations of motion. AIP Conf Proc 1922(100006):1–7
Acknowledgements
The work is financially supported by Grant 2016/23/B/ST8/01865 from the National Science Centre, Poland.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Comparison of finite element method and analytical model
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Warminski, J., Kloda, L. & Lenci, S. Nonlinear vibrations of an extensional beam with tip mass in slewing motion . Meccanica 55, 2311–2335 (2020). https://doi.org/10.1007/s11012-020-01236-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-020-01236-9