Abstract
In this work, planar free vibrations of a single physical pendulum are investigated both experimentally and numerically. The laboratory experiments are performed with pendula of different lengths, for a wide range of initial configurations, beyond the small angle regime. In order to approximate the air resistance, three models of damping are considered—involving the three components of the resistive force: linear (proportional to velocity), quadratic (velocity-squared) and acceleration-dependent (proportional to acceleration). A series of numerical experiments is discussed, in which the damping coefficients are estimated by means of several computational methods. Based on the observed efficiency, a gradient method for optimization is treated as the main tool for determination of a single set of damping parameters, independent of the system’s initial position. In the model of resistive force, the term proportional to acceleration, associated with the empirical Morison equation, seems to be indispensable for the successful approximation of the real pendulum motion.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The proper selection of a damping model and estimation of damping parameters is an essential problem in the area of dynamic simulation and analysis of real mechanical systems. Major difficulties result from a wide variety of energy dissipation mechanisms, their complexity and coexistence, as well as the approximate character of damping models. Typically, the inherent damping, i.e. naturally present within the system or its environment, is divided into three types: internal (material) damping, structural damping (at joints, supports or interfaces), and external damping (via fluid–structure interactions) [7].
There are several elementary models used to describe different forms of mechanical energy dissipation, such as the viscous and hysteretic damping, the Coulomb dry friction, or the velocity-squared drag model. Even if more sophisticated and physically detailed approaches to dissipation are available (e.g. within the theory of viscoelasticity or the theory of thermoelasticity for the case of internal damping), they may be too complex and therefore underused. In computational practice, relatively simple models are usually employed. The purpose is to approximately represent the overall damping in a given system, and capture only its general effects (e.g. the amplitude decay). In light of this, the basic models, especially the viscous damping or—a kind of its extension—the proportional damping, can serve as an equivalent or “resultant” representation of not only the internal, but also structural and external damping [2, 3, 7, 27].
Such an approach with the limited interest in the actual damping sources and mechanisms can be mainly justified by the fact that the amount of energy dissipated within numerous real systems is very small (heavy machines and structures, conventional materials etc.). The magnitudes of forces associated with a certain type of damping may be regarded as negligible compared to the inertial and elastic forces. However, the effect of dissipative forces can be of high importance for relatively low-mass structures undergoing large motions. Good examples are flexible slender systems like chains, cables, ropes and highly flexible beams or blades [2, 19]. Taking into account the nature of oscillations and the related geometric nonlinearity, it is quite natural to consider a pendulum to be a kind of archetype of such slender systems.
For many centuries, pendula of various types (normal/inverted, simple/physical, single/multiple, etc.) have been attractive objects of studies [1, 15, 22, 30]. It is well known that they play a vital role in the field of theoretical and experimental mechanics, and are used to demonstrate essential concepts of, among others, Newtonian and analytical mechanics, small vibration theory, nonlinear dynamics and chaos, analysis of coupled oscillators, multibody dynamics (e.g. see [28, 36, 37, 39]). Moreover, pendula became standard models and a source of test problems in other related areas such as automatic control and robotics, space technology, computational methods and algorithms, artificial intelligence, etc. When it comes to analysis and simulation of the slender systems, multiple pendula have been extensively used in investigations of chain dynamics [20, 23, 34, 38, 40], and sometimes as a basis of discrete (lumped-mass) models of elastic continua [9, 10, 32].
In the context of vibration damping, a single pendulum may also be seen as a very simple and convenient object of experimental-computational studies. Historical and mathematical background of the problem of a simple pendulum motion with air resistance was presented by Dahmen [6] and Gauld [12]. Nelson and Olsson [26] used a plane pendulum to measure the gravity acceleration, and discussed several corrections related to a rich variety of the physical features of a real pendulum, including the aerodynamic effect. The contribution from the drag on the string into the overall damping of a simple pendulum was analyzed by Mohazzabi and Shankar [24]. Ladino and Rondón [16] proposed a method to determine the damping coefficient of a simple pendulum with oscillating suspension point. The influence of both dry friction (at a support) and viscous damping on the pendulum amplitude was discussed by Zonetti et al.[42]. It should be noted that the mentioned studies are mainly focused on the case of a simple pendulum, and usually on a single damping model: the classical linear (velocity-proportional) or the quadratic (velocity-squared) damping.
In this article, planar free vibrations of a physical pendulum are investigated experimentally and numerically. The laboratory experiments are performed with pendula of different lengths, for a wide range of the initial swing angle—without the assumption of small oscillations. In a series of numerical simulations, three models of external damping with constant coefficients are used and the parameters are estimated by means of various computational methods. The aim of this study is to assess and compare the prediction accuracy of the three models, and to select the most appropriate one.
The paper is organized as follows. In order to present a gradual extension of the viscous damping model, the dynamic equations for the physical pendulum, based on the Lagrangian approach, are outlined in Sect. 2. The experimental setup and the details of the laboratory study are described in Sect. 3. Sections 4, 5 and 6 contain the results of parametric estimation for each of the three damping models, performed with the use of various numerical methods. Finally, conclusions and remarks are presented in Sect. 7.
2 Formulation of the problem
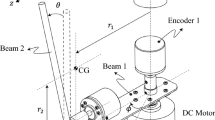
Let us consider a physical pendulum depicted schematically in Fig. 1. The system consists of a rod of length L and mass m, suspended from point O. The in-plane free oscillations of the pendulum can be described by angle \(\varphi (t)\), classically measured with respect to the vertical axis.
Neglecting any resistance forces, the equation of motion for the one-degree-of-freedom system can be easily derived using the Lagrange equation of the second kind:
where \(\varphi\) is the only generalized coordinate, \({\dot{\varphi }} = \frac{\text {d}\varphi }{\text {d}t}\) is the angular velocity, and \(L = T-V\) denotes the Lagrange function. The kinetic and potential energy of the system are given by
where \(I_O\) is the mass moment of inertia of the rod about z-axis (passing through point O). Now, applying Eq. (1) leads to
Mathematically, this idealized model is a second-order ODE with constant coefficients.
If energy dissipation in the mechanical system is taken into account, the Lagrange equation becomes
where \(Q_d\) is the generalized damping force. Classically, the quantity is assumed to be derivable from the Rayleigh dissipation function which is a quadratic form in the generalized velocity:
where \(c_1\) is a constant coefficient. Consequently, the equation of motion includes a linear dissipative (viscous) term:
The viscous damping model is the simplest one, readily used in vibration analysis, since it does not lead to any nonlinearity and computational difficulties. It is sometimes employed to approximate more complex types of internal and external damping in real systems (e.g. via the concept of equivalent viscous damping) [2, 3, 11]. However, such a linear model may be regarded as the lowest order approximation of the resistance coming from the medium surrounding a moving body. More generally, the damping force \(\mathbf {F}_d\) as a function of the oscillator velocity \(\mathbf {v}\) can be expanded in power series in the velocity [8, 17, 24, 35]:
where \(\alpha _i\) are constants (\(i = 0,\, 1,\, 2,\, \ldots\)) and \(v = |\mathbf {v}|\). Naturally, \(\alpha _0 = 0\) because there is no resistance acting on the body at rest. In most textbooks on classical mechanics the topic of resisted motion is discussed using solely the first- or second-order term of the expansion, arguably for the sake of simplicity (e.g. see [14, 36, 37]). From the viewpoint of fluid mechanics, in turn, the well-known drag model is said to be pure quadratic. However, one should notice that the non-dimensional drag coefficient involved is a function of, among others, the body Reynolds number: \(C_D = C_D(\text {Re})\). Since \(\text {Re}\) is proportional to the speed v, the final form of the resistive force may be more complicated (not necessarily purely quadratic in velocity). Particularly, at low Reynolds numbers, it may consist of the linear (or approximately linear) term [25, 41]. All in all, the dynamic Eq. (6) is extended by the second-order term:
For the purpose of the combined computational-experimental studies, the linear-quadratic model included in Eq. (8) is enriched with an acceleration-related part:
Occurance of such a term in the expression for the resistance force should not be seen as unusual. In the case of oscillatory motion of elementary bodies (sphere, infinite cylinder etc.) in a viscous fluid, purely analytical solutions (for low Reynolds numbers) lead to the drag having two parts: proportional to velocity (the dissipative part) and proportional to acceleration (the inertial part) [18, 33]. Also in the empirical Morison equation, commonly used in hydromechanics and dynamic analysis of offshore structures, the total wave force on a submerge body includes the drag and inertia forces, where the latter is related to the added-inertia concept [29, 33].
Let us introduce the dimensionless time \(\tau = \omega _0 t\), where \(\omega _0\) is the natural frequency of the undamped pendulum that undergoes small-amplitude vibrations (the linearized case):
Consequently, equations of motion (6), (8) and (9) take the following non-dimensional forms:
where now \(\varphi = \varphi (\tau )\) and an overdot denotes differentiation with respect to \(\tau\), while
are the non-dimensional damping coefficients corresponding to the three considered components of the resistive force: linear (proportional to velocity), quadratic (velocity-squared) and acceleration-dependent (proportional to acceleration).
3 Experimental studies
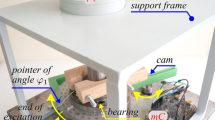
The laboratory experiments were conducted with pendula of various length: \(L \in \{100,\, 150,\, 200,\, 300\}\) mm. In each case the rod has a diameter \(d = 4\) mm and is made of an aluminium-magnesium alloy (AlMg3), which is often used for welding rods. The material density is \(\rho = 2640\) kg/m\(^3\). The ends of the rod are threaded in order to attach conical sleeves by connecting nuts (see Fig. 2a). The main purpose of the sleeves is to clamp a synthetic cord that plays a role of a connector between the rod and the support, or between two adjacent members of a multiple pendulum (in our future work, see Fig. 2b). Moreover, the nuts are a convenient location for tracking markers (see Fig. 2c). As shown in the photographs, the pendulum is mounted to the frame by the cord connection between the tip sleeve and the sleeve fixed to an auxiliary bracket. The relatively complex geometry of the pendulum link has been taken into account carefully to calculate mass and moment of inertia of the system. The inertia parameters for all the length variants are given in Table 1; additionally, the natural frequencies for the linear case are included.
Planar motion of the system was investigated by an optical measurement technique. A high speed camera was used (Photron 1024 PCI, max. resolution of \(1024 \times 1024\) pixels, max. frame rate of 10,000 fps). The experiments were performed with the frame rate of 250 fps, which allowed for recording motion lasting about 12 s. The control of the camera settings as well as the data acquisition process were done via a computer with a specialized software. The motion analysis, i.e. identification and tracking of the marker at the pendulum end, and determination of its position in particular frames, was conducted using the Photron Motion Tools application. The angle of pendulum swing was found based on the Cartesian coordinates \((x,\, y)\) of the marker and the pivot point. The experimental setup is presented schematically in Fig. 3.
The purpose of these experiments is to record behaviour of the pendula in a wide range of the swinging angle. Thus, we focused on four initial configurations of the system:
-
position in the first quarter of the coordinate system (\(\varphi _0\) at around \(60^{\circ }\))
-
nearly horizontal position (\(\varphi _0\) at around \(90^{\circ }\))
-
position in the second quarter of the coordinate system (\(\varphi _0\) at around \(135^{\circ }\))
-
nearly vertical position (\(\varphi _0\) at around \(180^{\circ }\))
Since the pendula were realeased from rest by hand, the starting angles were imposed on them only approximately. The values of \(\varphi _0\) calculated from the measured positions of the marker at the beginning of motion are given in Table 2. Here and in the further stages the initial configurations are numbered by k.
4 Numerical results for linear damping
4.1 Application of finite difference schemes
Let us start with the linear damping model included in Eq. (10). The damping coefficient will be approximated by means of the following three methods: the finite difference schemes, the bisection method and the gradient method for optimization.
The first approach is focused on the approximation of angular velocity \(\omega = {\dot{\varphi }}\) and angular acceleration \(\varepsilon = {\ddot{\varphi }}\) at a time point by the values of angle \(\varphi\) measured experimentally. Since the marker coordinates as the experimental results contain errors, and the finite-difference representation of \(\varepsilon\) may be especially sensitive to small disturbances, highly accurate (multi-point) difference schemes must be applied.
Consider a uniform grid, i.e. a sequence of equispaced time points (measurement instants). Central differece schemes are based on a stencil of \(n^{*}= (2n+1)\) nodes:
where \(h = t_{i+j} - t_{i+j-1}\) (for \(j = -n,\, -n+1,\, \ldots ,\, n\)) is the constant step size. The Taylor series expansion of a function f(t) near \(t_i\) is:
where \(f^{(j)}(t_i)\) is the jth time derivative of f, calculated at \(t_i\), whereas the remainder \(R_{p}(t,\, t_i)\) satisfies the condition:
Usually the method of undetermined coefficients is employed to derive an appropriate finite difference formula. With such an approach, expansion (14) up to term of order \(n^{*}\) is used for the \(n^{*}\)-point stencil. This leads to a \(n^{*}\times n^{*}\) Vandermonde system of linear equations that becomes poorly conditioned for large \(n^{*}\) [21]. Here we apply another technique based on symbolic computation.
We tend to use only three terms of series (14), i.e. just the derivatives that are to be determined. Thus, it is assumeed that f(t) can be represented by
where
play the role of basis functions, equivalent to the power functions from the Taylor series. Each coefficient \(d_s\), in turn, denotes the value of the derivative of order \((s-1)\) of f at \(t_i\)
which can be approximated by the central difference scheme. Namely,
where \(f_{i+j} = f(t_{i+j})\), \({\dot{f}}_i = {\dot{f}}(t_i)\), \({\ddot{f}}_i = {\ddot{f}}(t_i)\), while \(\beta ^{(s)}_{i+j}\) are the desired coefficients. Substitution of (16) and (18) into Eq. (15) produces the equation residual
As in the Galerkin method, the quantities \(d_s\) can be obtained by imposing the orthogonality conditions:
where \(\langle \bullet ,\, \bullet \rangle\) is the inner product, which we define in a discrete sense, that is
This gives a \(3\times 3\) system of algebraic equations that can be written as
where \(\mathbf {d} = [d_1,\, d_2,\, d_3]^T\), and elements of \({\mathbf {A}}\), \(\mathbf {b}\) are given by
Since the arguments and nodal values of f are kept in symbolic form (\(t_i := 0\), \(t_{i+j} := jh\), \(f_{i+j} := f[jh]\), etc.), the symbolic solution vector \(\mathbf {d}\) contains three linear combinations (18), and the desired finite difference coefficients \(\beta ^{(s)}_{i+j}\) can be easily extracted.
Generally, for these studies, the central difference schemes based on \(n^{*}= 25\) nodes (\(n = 12\)) have been constructed, i.e. the first and second derivatives of \(\varphi (t)\) are evaluated using the angle values measured at 25 time instants. In the case of first and last n time points, asymmetric schemes involving 49 nodes are used, because they are two times less accurate than the central-difference approximation.
Next, one of the simplest smoothing technique is applied to the calculated time series \(\omega _i\) and \(\varepsilon _i\), i.e. the moving average smoothing:
where the parameter q is taken equal to 10. Consequently, at our disposal we have the observed time series \(\varphi _i\) and the smoothed ones \({\hat{\omega }}_i\), \({\hat{\varepsilon }}_i\).
Finally, the damping coefficient \(c_1\) can be determined over time from Eq. (6):
Additionally, the generalized viscous force is evaluated:
The results for the case of \(L = 100\) mm are presented in Fig. 4. As can be seen, coefficient \(\alpha _1\) does not remain constant. Although very accurate finite-difference approximations have been used for the angular velocity and acceleration, the linear damping model exhibits some inadequacy. The results obtained for the other pendulum lengths and different initial angular position \(\varphi _0\) lead to scatter plots of the same character.
4.2 Bisection method
In order to determine certain values of the damping coefficient \(\alpha _1\), some optimization methods can be used. The first approach utilized in this paper is the bisection method which basically belongs to the class of bracketing root-finding techniques [5, 31].
We restrict our attention to the interval \(\Omega = \langle \alpha _L,\, \alpha _R \rangle\), where \(\alpha _L\), \(\alpha _R\) are two guesses that are supposed to bracket the optimal solution. In the first step, \(\Omega\) is divided in half, that is the midpoint \(c_{M} = (\alpha _L + \alpha _R)/2\) is calculated. Now, we deal with two subintervals, \(\Omega _{L} = \langle \alpha _L,\, \alpha _M \rangle\) and \(\Omega _{R} = \langle \alpha _M,\, \alpha _R \rangle\), having the midpoints \(\alpha _{LM} = (\alpha _L + \alpha _M)/2\) and \(\alpha _{RM} = (\alpha _M + \alpha _R)/2\). For both these values of the damping coefficient we integrate numerically the differential Eq. (10). The results are compared with the experimental time series, i.e. the total distance is calculated:
where N is the number of frames recorded, while \(\varphi _{i,\,k}^{{\text {exp}}}\) and \(\varphi _{i,\,k}^{{\text {num}}}\) denote the experimental and numerical values of the pendulum angle for the kth initial configuration. The function \(f_k\) expresses the distance in the sense of 2-norm. The minimum value of \(f_k(\alpha _{LM})\), \(f_k(\alpha _{RM})\) indicates the subinterval within which the desired solution is located. Consequently, we redefine the search interval \(\Omega\) as \(\Omega _{L}\) or \(\Omega _{R}\), and simultaneusly \(\alpha _M\) is replaced with the initial estimate of the optimum, \(\alpha _{LM}\) or \(\alpha _{RM}\). The process is repeated until a satisfactory result is achieved (the error falls below some threshold), or the difference between errors (24) in two subsequent iterations is small enough.
For the determination of \(\alpha _1\) it is reasonable to focus on the range \(\langle 0,\, 1 \rangle\), since the coefficient is a non-negative and relatively small parameter. The results obtained for all the pendulum lengths are presented in Table 3. Instead of the total distance between the numerical solutions and the experimental data, \(f_k\), the root-mean-square (RMS) error and the average (AVG) error are given:
Moreover, the total mean errors are calculated as follows:
Again, at a constant length of the pendulum the damping coefficient takes different values as the initial position is varied. The errors, in turn, reach quite high values, especially in the case of short pendula (\(L = 100\) mm and \(L = 150\) mm). For example, for \(L = 100\) and \(k = 3\) the RMS error is \(e_k^{{\text {rms}}}\approx 8.2^{\circ }\), which gives a relative error of 6% when treating the initial angle \(\varphi _0\) as the reference one (see Table 2). Simultaneously, the average distance is \(e_k^{{\text {avg}}}\approx 0.2^{\circ }\), and its relative value is less than 0.2%.
A graphical comparison between the experimental and numerical time histories of the angular position \(\varphi (t)\) is shown in Fig. 5. Slight differences in the oscillation amplitudes occur, particularly at the maxima, and a phase difference becomes more noticeable with time. However, the general character of the measured oscillations is well reflected by the numerical solution. To give a better insight into computational-experimental discrepancies, history plots focused on the first and the last 2 s of motion will be presented. As can be seen in Fig. 6, prediction quality of the model is not very poor, although the phase shift grows with time and the initial angle.
Position of the pendulum at particular time instants (the time given in seconds)—numerical solution (solid line) and experimental data (markers): a the swing of the pendulum from the initial position (top right) to the furthest top left position, b the swing of the pendulum from the furthest right to the furthest left position in the later phase of motion. Results obtained for \(L = 100\) mm, \(k = 3\) and the linear damping
Position of the pendulum at particular time instants—snapshots from the laboratory experiment and numerical results (blue line): a \(t = 0.08\) s, b \(t = 0.16\) s, c \(t = 0.2\) s, d \(t = 0.24\) s, e \(t = 0.32\) s, f \(t = 0.46\) s. Results obtained for \(L = 100\) mm, \(k = 3\) and the linear damping (compare to Fig. 7a). (Color figure online)
Figure 7 presents a simple visualization of the pendulum motion for \(L = 100\) mm and \(k = 3\). The real motion was recorded with the frame time \(\Delta t = 0.004\) s, whereas the interval between the depicted configurations is usually equal to \(10\times \Delta t\) or \(20\times \Delta t\). The increasing phase shift between the numerical and experimental results is well noticeable. The angular difference (in absolute value) between the configuration pairs shown in Fig. 7a ranges approximately from \(0.1^{\circ }\) to \(5.8^{\circ }\) whereas the difference in Fig. 7b ranges from \(0.6^{\circ }\) to \(11.3^{\circ }\). Selected frames of this motion are presented in Fig. 8 in the form of the simulation-based configurations overlaid on snapshots of the real pendulum.
4.3 Gradient method for optimization
To determine a single value of the damping coefficient for a given pendulum length, that is independent of the initial configuration, the gradient method is used. Usually the gradient-based approach is applied to multidimensional unconstrained optimization. Here we perform a one-dimensional search with the first derivative evaluation [5, 31].
We aim at minimization of the distance of type (24), but simultaneously for all the studied initial positions of the system. Thus, the objective function is constructed as follows:
where \(f_k\) has the form (24).
Firstly, we select an appropriate initial guess, \(\alpha _{1}^{(0)}\). It can be done, for example, by taking the arithmetic mean of the results given in Table 2 for particular values of L. Additionally, the initial search direction \(d^{(0)}\) and the step size \(\Delta \alpha ^{(0)}\) must be chosen. In the one-dimensional case we move along a line (\(\alpha _{1}\)-axis) by the distance \(\Delta \alpha ^{(p)}\), and the direction \(d^{(p)}\) takes the value 1 or \(-\,1\).
In the optimization procedure, equations of motion (10) are solved at the starting value \(\alpha _{1}^{(0)}\), and the error is evaluated, \(e^{(0)}\). Next, the same computation is performed for the trial point \(\alpha _{1}^{(1)} = \alpha _{1}^{(0)} + d^{(0)}\Delta \alpha ^{(0)}\), and error \(f^{(1)}\) is obtained as a result. A new direction is determined by using the approximate gradient value:
and the descent direction is
Finally, the next step size can be expressed as
where \(w_{1}\) and \(w_{2}\) are some control parameters from the interval \((0,\, 1)\). Their role is to speed up the iteration process when the consecutive steps apparently tend to the minimum, or decrease the step size after a change of direction. In further stages, Eq. (30) becomes
The process is stopped if a satisfactory error level is achieved, the difference between errors in two subsequent iterations is sufficiently small, or the maximum number of iterations is reached.
Table 4 contains the obtained results for all the pendulum lengths. Apart from the optimal values of coefficient \(\alpha _1\), the root-mean-square and average errors (25) for particular initial configurations are presented. As it is indicated by \(e_k^{{\text {rms}}}\) and \(e_k^{{\text {avg}}}\) values, if the time series for each initial angle \(\varphi _0\) is treated separately, the solutions are non-optimal, that is the bisection method leads to lower errors. The fourth initial configuration generates significantly greater errors than the others. Unlike in the latter case, the total errors are not considerably lower for the larger lengths of the pendulum. However, the main advantage of this approach is to find only one “effective” value of the damping coefficient (independent of \(\varphi _0\)), and such attempts will be continued with the more advanced models.
5 Numerical results for linear and quadratic damping
5.1 Successive search and intersection technique
The results for the linear damping suggest that this model may be insufficient. Therefore, a series of computations have been conducted for the extended, linear-quadratic model included in Eq. (11). To find coefficients \(\alpha _1\) and \(\alpha _2\), the optimization problem has been solved by means of two methods: the successive search in combination with the intersection technique, and the gradient method.
The first approach is focused on a graphical representation of the objective function \(f(\alpha _1,\, \alpha _2)\), in the identical form as (27), over a two-dimensional domain. Firstly, the search is narrowed to the region \(\Omega = \langle 0,\, a \rangle \times \langle 0,\, b \rangle\), where \(a,\, b > 0\). Next, the domain is discretized into a uniform grid of \(n_1 \times n_2\) points (see Fig. 9), characterized by the spatial step sizes in the two directions
Let \(\alpha _{1,i}\) and \(\alpha _{2,j}\) be the ith and jth values of the coordinates \(\alpha _1\) and \(\alpha _2\) on the plane, respectively (for \(i = 0,\, 1,\, 2,\, \ldots ,\, n_1\) and \(j = 0,\, 1,\, 2,\, \ldots ,\, n_2\)). For every grid point \(\{\alpha _{1,i},\, \alpha _{2,j}\}\) equation of motion (11) has been solved, and the nodal value \(f_{i,j}\) of the objective function has been evaluated. As an example, the results for \(L = 100\) mm are shown graphically in Fig. 10.
In all the studied cases, a continuous representation of the the discretized surface \(f_{i,j}(\alpha _{1,i},\, \alpha _{2,j})\) exhibits an oblong valley, and one can suppose that there exist infinitely many minima. For a better insight, the straight line (e.g. described as \(\alpha _2= A \alpha _1+ B\)) in the longitudinal direction of such a “trough” (at its bottom) has been found numerically. Then, it can be observed that the valley direction varies with the pendulum initial angle \(\varphi _0\). Finally, to determine a single representative pair of the damping coefficients for all the initial configurations, the intersection points of these lines have been analyzed within an unconstrained domain. From all the intersections, the one for which the function f takes the lowest value, is chosen as the optimal solution.
The results obtained with the intersection technique are given in Table 5. As can be seen, coefficient \(\alpha _1\) turns out to be negative in each case, but it does not have a physical meaning and indicates that the model is inappropriate.
5.2 Gradient method for optimization
The intersection technique has a relatively low accuracy, because a small disturbance of the slope coefficient of a line can lead to completely different results. Therefore, another attempt has been made to find \(\alpha _1\) and \(\alpha _2\)—by the use of the gradient method.
In the two-dimensional problem, the idea of the method is identical as in the one-dimensional case. However, the motion towards the minimum of the objective function takes place on a plane. Thus, the values of the decision variables at the pth step form a vector
and the step direction, \(\mathbf {d}^{(p)}\), is also a two-component vector. Moreover, the gradient approximation can be expressed as
and, by analogy to Eq. (29), the new direction is given by
where \(|\bullet |\) denotes the Euclidean norm. Equation (31), in turn, now takes the form
where the right-hand side includes a dot product of the previous and new direction vectors.
Table 6 contains the estimated values of the parameters and the related errors for every pendulum length. Again, the damping coefficient \(\alpha _1\) has negative values, which excludes the application of the linear-quadratic model.
In order to make full use of the two-term model, the purely quadratic damping is also examined. Thus, the gradient-based optimization outlined above has been performed for equation of motion (11) when \(\alpha _1= 0\). As shown in Table 7, coefficient \(\alpha _2\) takes smaller values now. In the case of all the pendulum lengths and initial configurations the truncated damping model, in combination with the gradient method, provides better prediction of the real motion than the linear model (see Table 4). Moreover, as our tests indicated, the same results can be obtained using relatively simple methods for the constrained optimization problem with two decision variables, \(\alpha _1\) and \(\alpha _2\) (e.g. the projected gradient method, the penalty function method or the Monte Carlo approach [4, 13]).
Figure 11 illustrates the responses of the pendulum of length \(L = 200\) mm as \(k = 1\) and \(k = 2\). Although the values of \(e_k^{{\text {rms}}}\) and \(e_k^{{\text {avg}}}\) belong to the lowest ones, significant differences in the angular displacements can be observed. Here, the phase shift is much less noticeable than the amplitude mismatch—the oscillation decay is stronger in the real mechanical system.
6 Numerical results for velocity and acceleration dependent damping
6.1 Gradient method for optimization
As could be seen in Sect. 5, the enrichment of a model by an additional term not necesserily leads to the desired results. Consequently, the three-component damping model included in Eq. (12) have been considered with the hope that it will work in the full form, i.e. simultaneously with all the (non-zero) coefficients. In other words, the third, acceleration dependent term may be the missing element, and its presence can make the other terms play their proper role in the dynamic simulation of the system under real conditions.
In this section, the coefficients \(\alpha _1\), \(\alpha _2\) and \(\alpha _a\) are determined by using the gradient method. Thus, the objective function (27) is now regarded as dependent on three decision variables: \(f(\alpha _1,\, \alpha _2,\, \alpha _a)\). As before, the optimization procedure is simply extended to the three-dimensional case. Since the vector of decision variables (32) becomes composed of the triple coefficients, vectors (33)–(35) are extended to have a third element, corresponding to \(\alpha _a\).
The results obtained for each length of the pendulum are given in Table 8. In all the cases, the following relation holds: \(\alpha _1< \alpha _2< \alpha _a\), which shows that the acceleration-related effect is not negligible. The total RMS error reach values below \(5^{\circ }\) while the total AVG errors are less than \(0.1^{\circ }\) (compare Tables 3, 4 and 7). In particular, the errors are at least 5 times smaller than those for the linear model and the gradient-based optimization. Apparently, the velocity and acceleration dependent damping model is most appropriate.
As can be seen in Fig. 12, there are relatively small phase shifts between the compared results. One can also notice just slight differences in the peak amplitudes. The numerical solutions of the equation of motion coincide quite accurately with the experimental observations.
The sequential visualization of the pendulum motion for \(L = 150\) mm and \(k = 2\) is shown in Fig. 13. The phase shift between the numerical and experimental results turns out to decrease with time. The angular difference (in absolute value) between the configuration pairs shown in Fig. 13a ranges approximately from \(0^{\circ }\) to \(5.3^{\circ }\) whereas the difference in Fig. 13b ranges from \(0^{\circ }\) to \(1^{\circ }\). It is worth noting that in the initial phase of motion the real pendulum is potentially exposed to certain types of disturbances such as out-of-plane motion (due to the manual release of the pendulum end) or torsional vibration (due to the uneliminated twist of the cord). In a further stage, the system motion is observed to stabilize.
In order to examine the importance of the damping effect, the total generalized dissipative force versus time is depicted in Fig. 14 for \(L = 150\) mm and two initial angles. Similarly to \(\varphi (t)\), the function \(Q_d(t)\) decays, and their peak values are larger for greater \(\varphi _0\). For this example, the maximum absolute values are \(Q_d^{\max } \approx 4.8\times 10^{-6}\) Nm and \(Q_d^{\max } \approx 10.4\times 10^{-6}\) Nm when \(k = 1\) and \(k = 3\), respectively. It is worth noting that the generalized gravity forces reach much higher levels—the extreme absolute values are about 1100 and 605 greater than \(Q_d^{\max }\). Additionally, the particular components of the damping force
included on the right-hand-side of Eq. (9), are plotted in a narrower time interval. As can be seen, the velocity-proportional term is the dominant one; the relative contributions of all the components as well as the character of \(Q_a(t)\) are affected by the initial angle \(\varphi _0\).
Position of the pendulum at particular time instants (the time given in seconds)—numerical solution (solid line) and experimental data (markers): a the swing of the pendulum from the initial position (top right) to the furthest left position, b the swing of the pendulum from the furthest right to the furthest left position in the later phase of motion. Results obtained for \(L = 150\) mm, \(k = 2\) and the three combined types of damping
6.2 Gradient method for the overall optimization
At the final stage, our studies are focused on the most effective damping model, but the aim is to define such damping parameters that are independent of the pendulum length, and to find their optimal values. By the term “overall optimization”, we mean that the distance between numerical solutions and the experimental data is minimized simultaneously for all the values of both \(\varphi _0\) and L.
First, we try to express the original (dimensional) coefficients \(c_1\), \(c_2\) and \(c_a\) as a product of two factors: affected and non-affected by the leading dimension L of the pendulum. Let us consider the distributions of the linear velocity v(r) and acceleration a(r) along the rod (\(0 \le r \le L\)). The moments of the frictional forces exerted on the pendulum, related to the three damping terms, are given by
where \(\omega = {\dot{\varphi }}\) and \(\varepsilon = {\ddot{\varphi }}\), while \({\hat{c}}_1\), \({\hat{c}}_2\), \({\hat{c}}_a\) are the coefficients (dimensional) independent of L, i.e. common for pendula of various length. It is obvious that \(M_1 = -Q_1\), \(M_2 = -Q_2\), \(M_a = -Q_a\), and all the moments are present in the equation of motion (9). Thus, we can clearly see that
Now, we introduce the radius of gyration \(r_O\) of the rod to write its moment of inertia as \(I_O= m r_O^2\). Taking into account the non-dimensional Eq. (12) together with definitions (13), and using the new expressions (40) for \(c_1\), \(c_2\) and \(c_a\), we obtain
where
Mathematical model (41) of the system is just the one in which the parameters \({\hat{c}}_1\), \({\hat{c}}_2\) and \({\hat{c}}_a\) should not depend on the pendulum length.
Such a reformulation of the dynamic equation allows us to solve the overall optimization problem. More precisely, the gradient-based procedure can be applied simultaneously to the whole set of time series collected experimentally. Thus, Eq. (41) must be integrated numerically at each step, and the new coefficients play the role of the decision variables. The objective function has the form
where \(L \in \{100,\, 150,\, 200,\, 300\}\) mm, and \(f_{k,\,L}\) denotes the numerical-experimental distance of type (24) specified for certain k and L.
The proposed optimization procedure provides the following values of the damping parameters:
and the total mean errors—calculated for all k and L, by analogy to (43)—have the values: \({\hat{e}}_{{\text {tot}}}^{{\text {rms}}}= 0.165\) rad, \({\hat{e}}_{{\text {tot}}}^{{\text {avg}}}= 0.0034\) rad. Finally, we can return to the dimensional damping coefficients by using relationships (40). The optimization results are presented in Table 9. The total errors for each pendulum length, \(e_{{\text {tot}}}^{{\text {rms}}}\) and \(e_{{\text {tot}}}^{{\text {avg}}}\), are given for comparison purposes. As can be seen, these quantities reach higher values than before (compare to Table 8). The distances \(e_k^{{\text {rms}}}\) and \(e_k^{{\text {avg}}}\) are also larger almost for every k.
The prediction quality of this approach can be assessed from Fig. 15, where the numerical and experimental responses of the system are shown for \(L = 100\) mm and \(L = 300\) mm at \(k = 1,\, 2,\, 4\). This time, the plots are focused on the first 6 s of motion. When it comes to the shortest pendulum, slight phase and amplitude differences can be observed for every initial configuration. In the second case, the amplitude discrepancy is higher, and the phase shift between the angular displacements intensifies with time, particularly for larger values of \(\varphi _0\). It seems that the overall optimization leads to a worse match of the model to the experimental data, which can be regarded as the cost of determining just a single set of parameters values (\({\hat{c}}_1,\, {\hat{c}}_2,\, {\hat{c}}_a\)), uniform for every pendulum.
6.3 Some remarks on the models quality
The described procedures for estimation of the damping parameters have been based on the Euclidean distance between data points: the experimental and numerical results. Also, the quality of the optimal solutions has been assessed by means of the related RMS and AVG errors. Such an approach seems to be natural and most widely used.
However, the classical distance means a point-to-point comparison of oscillations. It represents a very precise difference between two data sets, calculated sequentially along the time axis. Unfortunately, the general, shape-related similarity of the displacement time histories is not evaluated in this way. Consequently, even a slight phase shift can produce relatively high values of the RMS error.
In order to cast light on the quality of approximation of the real oscillations decay by numerical solutions, we will use the concept of the amplitude envelope [27, 37]. More precisely, we assume that the decaying character of the pendulum motion can be approximated by the time-dependent exponential function:
where A, \(\beta\), B are constants. Thus, given the peaks of the system responses found experimentally and numerically, \(\varphi ^{{\text {exp}}}\) and \(\varphi ^{{\text {num}}}\), their upper envelopes are fitted in the least-squares sense:
Now, the difference between the curves can be measured in many ways. By analogy to the RMS and AVG errors involved up to now, the following integral forms of the envelope errors are introduced:
where \(t_{e}\) denotes the end time of motion. It should be emphasized that, in contrast to \(e_k^{{\text {rms}}}\) and \(e_k^{{\text {avg}}}\), the new quantities (47) are non-dimensional, since they represent the relative errors of \(\Phi ^{{\text {num}}}\).
The percentage values of \({\widetilde{e}}_k^{{\text {rms}}}\) and \({\widetilde{e}}_k^{{\text {avg}}}\) corresponding to the results discussed in Sects. 6.1 and 6.2 are presented in Tables 10 and 11, respectively. The integrals occurring in formula (47) are evaluated numerically. The total mean errors are specified in the same manner as given in Eq. (26). As can be seen, the RMS and AVG distances between the envelopes for the numerical and experimental results are much lower in the case of the optimization conducted separately for each pendulum length. The \({\widetilde{e}}_k^{{\text {rms}}}\) values lie in the range between 0.4 and 9.1%, but most of them are less than 2%. The interenvelope distance per sample, in turn, does not exceed 1%. For the overall optimization, the ranges for the envelope errors are about two times wider. The \({\widetilde{e}}_k^{{\text {rms}}}\) values lie between 4.7 and 18.6% (many of them exceed 10%), whereas \({\widetilde{e}}_k^{{\text {avg}}}< 2\%\). Thus, the results generally confirm the previous observations.
However, it is worth noting that the envelope-based errors do not coincide with the point-to-point ones. Usually the greatest values of \({\widetilde{e}}_k^{{\text {rms}}}\) and \({\widetilde{e}}_k^{{\text {avg}}}\) for some L are related to the smallest values of \(e_k^{{\text {rms}}}\) and \(e_k^{{\text {avg}}}\), and vice versa (e.g. see \(L = 100\) mm, \(k = 1,\, 4\) in Tables 8 and 10, or \(L = 300\) mm, \(k = 1,\, 4\) in Tables 9 and 11). These two types of criteria for evaluation of similarity between \(\varphi ^{{\text {exp}}}\) and \(\varphi ^{{\text {num}}}\) seem to contradict each other, at least partially. As results from our trials to incorporate the interenvelope distance into the optimization procedures, this kind of objective function could slightly improve the amplitude match between the model and the experimental data, but at the cost of phase difference. The classical point-to-point distance, on the other hand, leads to a compromise between the amplitude and phase match.
Figures 16 and 17 allow for a graphical comparison between the envelopes related to the two types of optimization. Two examples are shown: \(L = 100\) mm, \(k = 4\) and \(L = 300\) mm, \(k = 1\). Apart from the exponential curves over the whole time range (\(0 \le t \le 12\) s), their clipped views for the last 3 s of motion are presented. When dealing with the separate optimization, the difference between envelopes \(\Phi ^{{\text {num}}}\) and \(\Phi ^{{\text {epx}}}\) is practically negligible in both cases. The overall optimization, in turn, leads to a worse approximation of the oscillation decay: the interenvelope distance grows gradually with time. In the second example (see Fig. 17b), the difference becomes very large (\({\widetilde{e}}_k^{{\text {rms}}}= 18.6\%\)).
7 Conclusions
In this work, we have focused our attention on planar free vibrations of a single physical pendulum. Such a system has been investigated both experimentally and numerically. The laboratory experiments were performed with pendula of different lengths, for various initial swing angles. It should be emphasized that our studies have not been restricted to the small-vibration case. The system motions were recorded by a high speed camera. In order to approximate the air resistance, three models of damping have been examined—involving the three components of the resistive force: linear (proportional to velocity), quadratic (velocity-squared) and acceleration-dependent (proportional to acceleration). A series of numerical simulations has been discussed, in which the corresponding damping coefficients have been estimated by means of several computational methods. The root-mean-square distance and the average distance per sample, evaluated between the numerical and experimental results, have been treated as the error measures.
The simplest, linear damping model is associated with the highest errors between the numerical solutions and the experimental data. The linear-quadratic model leads to non-physical results, i.e. negative values of one damping parameter; the only option is to use the velocity-squared part. The third variant of the resistance force, that is velocity and acceleration-dependent, turns out to be the most appropriate. The term proportional to acceleration, that may be tied to the empirical Morison equation, seems to be indispensable for the successful approximation of the real pendulum motion.
Obviously, there are certain discrepancies between the numerical and experimental results. In particular, the overall optimization leads to significant errors, higher than for the optimization performed separately for each length variant. In some degree, the differences might be attributed to friction at the pendulum support. However, due to a small diameter of the cord and its smooth surface, this effect is assumed to be much weaker than the air resistance. But the capability of the cord to twist and the out-of-plane vibration of the pendulum, especially in the initial phase of motion, may be of much greater importance. And last but not least, all the damping coefficients have been assumed constant, independent of the Reynolds number that is proportional to velocity. All in all, despite such strict assumptions, the considered models allow for quite accurate approximation of the pendulum motion.
When it comes to the computational approaches to the problem, the gradient method for optimization has been chosen as the major one on the path towards determination of a single set of damping parameters, independent of the system’s initial configuration. The other techniques, such as the bisection method or the successive search and the intersection technique, are quite well-suited for the simpler (one- and two-dimensional) estimation problems.
All the calculations have been conducted using the Wolfram Mathematica software. Many tasks, such as numerical integration of differential equations of motion, the least-squares curve fitting, or numerical evaluaton of integrals, have been accomplished by means of the built-in functions. However, the optimization procedures have been implemented by the authors.
The path of the computational studies reported in this paper, and the presented results indicate that both the modelling of damping and the parameters estimation are not a trivial task, even for relatively simple (but nonlinear) systems. Our future works will be devoted to the problem of this type for the case of three-dimensional motion, and for more complex systems such as multiple pendula.
References
Baker GL, Blackburn JA (2005) The pendulum: a case study in physics. Oxford University Press, Oxford
Beards CF (1996) Structural vibration: analysis and damping. Arnold, London
Braun S (ed) (2002) Encyclopedia of vibration. Academic Press, San Diego
Butenko S, Pardalos PM (2014) Numerical methods and optimization: an introduction. CRC Press, Boca Raton
Chapra SC, Canale RP (2010) Numerical methods for engineers. McGraw-Hill, Boston
Dahmen SR (2015) On pendulums and air resistance: the mathematics and physics of Denis Diderot. Eur Phys J H 40(3):337–373
de Silva CW (ed) (2007) Vibration and shock handbook. CRC Press, Boca Raton
Franklin J (2020) Mathematical methods for oscillations and waves. Cambridge University Press, Cambridge
Fritzkowski P, Kamiński H (2009) Dynamics of a rope modeled as a discrete system with extensible members. Comput Mech 44(4):473–480
Fritzkowski P, Kamiński H (2011) A discrete model of a rope with bending stiffness or viscous damping. Acta Mech Sin 27(1):108–113
Gatti PL, Ferrari V (2017) Applied structural and mechanical vibrations: theory and methods. CRC Press, London
Gauld CF (2009) Newton’s use of the pendulum to investigate fluid resistance: a case study and some implications for teaching about the nature of science. Sci Educ 18:383–400
Gill PE, Murray W (eds) (1974) Numerical methods for constrained optimization. Academic Press, London
Greiner W (2004) Classical mechanics: point particles and relativity. Springer, New York
Kaushal RS (2005) The pendula in mathematical sciences. Indian J Pure Appl Phys 43:479–488
Ladino LA, Rondon HS (2017) Determining the damping coefficient of a simple pendulum oscillating in air. Phys Educ 52:033007
Landau LD, Lifshitz EM (1976) Mechanics. Course of theoretical physics. Butterworth-Heinemann, Oxford
Landau LD, Lifshitz EM (1987) Fluid mechanics. Course of theoretical physics. Pergamon Press, Oxford
Lee JW, Kim HW, Ku HC, Yoo WS (2009) Comparison of external damping models in a large deformation problem. J Sound Vib 325:722–741
Lee W (2003) Analytically approximate solutions for vibrations of a long discrete chain. J Appl Mech 70:302–304
LeVeque RJ (2007) Finite difference methods for ordinary and partial differential equations: steady-state and time-dependent problems. SIAM, Philadelphia
Matthews MR, Gauld CF, Stinner A (eds) (2005) The pendulum: scientific, historical philosophical and educational perspectives. Springer, Dordrecht
McCreesh JP, Goodfellow TL, Seville AH (1975) Vibrations of a hanging chain of discrete links. Am J Phys 43:646–648
Mohazzabi P, Shankar SP (2017) Damping of a simple pendulum due to drag on its string. J Appl Math Phys 5:122–130
Nakayama Y, Boucher RF (2000) Introduction to fluid mechanics. Butterworth-Heinemann, Oxford
Nelson RA, Olsson MG (1986) The pendulum—rich physics from a simple system. Am J Phys 54(2):112–121
Newland DE (1989) Mechanical vibration analysis and computation. Dover Publications, Mineola
Ott E (1993) Chaos in dynamical systems. Cambridge University Press, New York
Patel MH (1989) Dynamics of offshore structures. Butterworths, London
Pook LP (2011) Understanding pendulums: a brief introduction. Springer, Dordrecht
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in fortran: the art of scientific computing. Cambridge University Press, Cambridge
Robson JM (1990) The physics of fly casting. Am J Phys 58:234–240
Sarpkaya T (2010) Wave forces on offshore structures. Cambridge University Press, Cambridge
Schagerl M, Steindl A, Steiner W, Troger H (1997) On the paradox of the free falling folded chain. Acta Mech 125:155–168
Shapiro IL, de Berredo-Peixoto G (2013) Lecture notes on Newtonian mechanics: lessons from modern concepts undergraduate. Lecture notes in physics. Springer, New York
Taylor JR (2005) Classical mechanics. University Science Books, Sausalito
Thornton ST, Marion JB (2004) Classical dynamics of particles and systems. Brooks/Cole, Belmont
Tomaszewski W, Pierański P, Geminard JC (2006) The motion of the freely falling chain tip. Am J Phys 74:776–783
Török JS (2000) Analytical mechanics with an introduction to dynamical systems. Wiley, New York
Wang CY (1994) Stability and large displacements of a heavy rotating linked chain with an end mass. Acta Mech 107:205–214
White FM (1999) Fluid mechanics. WCB/McGraw-Hill, New York
Zonetti LFC, Camargo ASS, Sartori J, de Sousa DF, Nunes LAO (1999) A demonstration of dry and viscous damping of an oscillating pendulum. Eur J Phys 20:85–88
Funding
This study was partially funded by 0612/SBAD/3558 and 0612/SBAD/3566 grants from the Ministry of Science and Higher Education in Poland.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Salamon, R., Kamiński, H. & Fritzkowski, P. Estimation of parameters of various damping models in planar motion of a pendulum. Meccanica 55, 1655–1677 (2020). https://doi.org/10.1007/s11012-020-01197-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-020-01197-z