Abstract
The nonlinearities of geometric nature that is characteristic for pendulum-type systems are expressed by the trigonometric functions. In order to apply the method of multiple scales in time domain to solve problems concerning such systems, the trigonometric functions of the generalised coordinates are usually approximated by a few terms of their Taylor series. In the paper we apply the polynomial approximation in quadratic means. In contrast to the approximation by Taylor series, the proposed manner approximates the trigonometric functions not around a given point but on the given interval. Quality and accuracy of the solutions obtained using the multiple scales method based on such approach have been tested. The steady state responses in the main resonance have been also examined and compared with their counterparts obtained using the method of multiple scales based on the Taylor series.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In general, nonlinearities in mechanical systems can result from nonlinear constitutive laws, from nonlinear geometric relationships and due to the design constraints. In the case of discrete mechanical systems consisting of rigid bodies, spring elements and dampers, the constitutive relationships for elastic and damping forces have usually the form of the higher-order power laws. Nonlinearities of the geometric nature are often manifested in the form of the trigonometric functions of unknown generalised coordinates. The two circumstances significantly affect the character of the mathematical governing equations as well as the methods of their solutions, especially in the case of employment of the approximate analytical methods.
One of such methods quite commonly used in the dynamics of discrete mechanical systems is the method of multiple scales in time domain (MMS), which belongs to the broad class of perturbation methods, and at the same time falls under the mainstream of multiscale modelling [1]. The perturbation approach consists in replacing an original nonlinear problem with a simpler one which is solvable analytically or partly analytically. Constructing the mathematical model of the simpler problem using the equations of the harmonic oscillator seems to be a natural way in the case of the vibrating mechanical systems [2]. The nonlinear terms occurring in the constitutive equations for springs can usually be treated as small contribution into the dominant linear relationship. This provides both the opportunity to build the differential operator of the harmonic oscillator equation and makes that all nonlinear terms in the equations of the approximated problem have the character of small perturbations.
In the case of the geometric nonlinearities typical for systems with pendulums, the restoring forces are described by the trigonometric functions of unknown generalised coordinates which excludes the direct applicability of the previously mentioned way of creating the approximated model. A widely used solution to this problem consists in the approximation of the trigonometric functions by few terms of their Taylor series. The functions sine and cosine are expanded in the Taylor series around a characteristic value of the argument, and then the series are truncated to a finite number of their terms. The choice of the point around which the functions are expanded in the Taylor series is dependent on the purpose of the analysis. It often corresponds to the equilibrium position around which the system oscillates. The number of the terms of the Taylor series taken into account affects the accuracy of the approximation, and strictly the size of the interval on which it is valid. In turn, for the reasons closely related with the character of the method of multiple scales this number is rather small [2,3,4]. The expansion in the Taylor series up to third order is usually applied, although the expansions both up to lower and higher orders are also used.
The mechanical systems of several degrees of freedom with pendulums serve as relatively simple models of many mechanisms and devices. Eissa et al. [4, 5] used the spring pendulum in order to model the ship’s roll motion. They dealt with the problem of the passive reduction of the vibration of the pendulum subjected to multi-parametric excitation forces with use the tuned absorber acting in the direction transversal to the swing vibration, in [4], and in the longitudinal direction, in [5]. The method of multiple scales with three time variables was applied, and the trigonometric functions of the a priori small angle were expanded in the Taylor series up to third order around zero.
The method of multiple scales has been successfully applied in the studies of chaotic behaviour of weakly nonlinear systems with the geometric nonlinearities in order to predict the chaotic responses. Lee and Park [6] investigated the chaotic resonant responses of a weakly nonlinear spring pendulum excited by harmonically changing force and torque. Applying of the method of multiple scales with two time variables allowed for obtaining uniformly valid asymptotic expansions corresponding to the conditions simultaneously occurring internal and external resonances. The trigonometric functions were approximated by the Taylor series truncation to the terms of the second order which significantly limited the area in which the chaotic responses were sought. Alasty and Shabani [7] basing on the asymptotic solutions given in [6] and conducting an extended analysis of the pendulum behaviour in the area of the internal and external resonances, showed the possibility of the occurrence of both chaotic and quasi-periodic responses. They also pointed to the high sensitivity of the pendulum’’ behaviour to small changes in attenuation parameters. However, it should be noted that the analysed area around the resonance was expanded in relation to the area adopted in [6] without changing the assumptions regarding the order of the approximation and the Taylor series.
Lee and Park [8] studied the responses of the forced weakly nonlinear spring pendulum again, this time using the variant of the method of the multiple scales with three time variables which is also called the second order approximation. In this variant, it is purposeful to expand the trigonometric functions in the Taylor series up to third order. They focused on the internal and external responses occurring at the same time and without enlarging the resonant area observed that the second-order approximation gives better qualitative agreement with the original system than the first-order approximation. In turn, Amer et al. [9] investigated the chaotic responses of the weakly nonlinear spring pendulum which is not only forced harmonically but also subjected to the kinematic excitation because its pivot point moves along a circular path. They considered the same type of resonances as the one studied in [6,7,8] but applied the method of multiple scales in the form of the third order approximation, i.e. the variant with four time variables. However, the trigonometric nonlinearities have been approximated by the terms of the Taylor series only up to the third order.
Starosta and co-authors [10, 11] dealt with the dynamics of the forced spring pendulum with viscous damping under the action of non-stationary constraints which are performed in such a way that the suspension point moves with the predetermined movement. They studied the behaviour of the spring pendulum whose suspension point moves with a constant angular velocity along a fixed circular path of a small radius [10] or along a closed Lissajous curve [11]. The investigations that focused on the resonant regular responses at the external and parametric simultaneously occurring resonances were based on the uniformly valid asymptotic expansions obtained using the second order variant of the multiple scales method i.e. the variant with three time scales. The trigonometric nonlinearities have been approximated by the terms of the Taylor series up to the third order, i.e. the highest order possible in this variant of the method.
The approach based on the limiting phase trajectories (LPT) idea was employed in the papers [12, 13] in order to study the non-steady resonance states of the harmonically forced and weakly nonlinear spring pendulum. Such states are accompanied by intensive energy exchange between the system and external source and in the case of the multi-degree of freedom systems also between the particular modes which manifests oneself among other in the strong modulation of the amplitude and phases. The shape of the modulation curves highly depends on the nonlinear features of the spring. The variant of the method of multiple scales with time variables was necessary to guarantee preserving the crucial nonlinear parameter in the considerations. In agreement with this variant, the trigonometric functions were expanded in the Taylor series up to third order. The conception of the limiting phase trajectories was proposed by Manevitch [14, 15] and applied firstly as a means to analyse non-steady vibration accompanied by intensive energy exchange between weakly coupled oscillators.
Another kind of simple mechanical system with geometric nonlinearities is the spring physical pendulum. Different aspects of its behaviour in small oscillations around the stable equilibrium position have been considered in [16,17,18]. From the point of view of this review, it is worth emphasizing that the common element of these works is the employment of the method of multiple scales with three time variables. The trigonometric functions have been approximated by the Taylor series truncated to the terms of the third order.
Salahshoor et al. [19] analysed vibration of the sliding pendulum with clearances ignoring the horizontal motion of the system. They proposed two models simulating the clearances occurring in the system. The simpler model has two degrees of freedom while the more complicated one is of three-degree-of-freedom. The clearances are modelled employing nonlinear springs and dampers. Primary resonance and internal resonance are discussed in detail on the base of approximate analytical solutions obtained using the method of multiple scales with three time variables. This variant of the method applied imply the expanding of the trigonometric nonlinearities in the Taylor series up to third order.
Container cranes dynamics is the subject of works [20, 21], where the double pendulum with assumed geometric constraint serves as the simplified model of the crane. In both works, the trigonometric nonlinearities occurring in the governing equations have been approximated by expansion of them in the Taylor series up to third order. Daqaq and Masoud [20] aiming at finding the approximation of the pendulum frequency necessary to design the nonlinear input-shaping controller used the method of multiple scales in the variant with three time variables. Nayfeh and Baumann [21] determined the normal form of the Hopf bifurcation applying the method of multiple scales with two time variables.
The double pendulum is another example of the mechanical system with nonlinearities of geometric type. Sado and Gajos [22] investigated the behaviour of a three-degree-of-freedom system with the double pendulum focusing on the vibration in the neighborhood of the internal and external resonances occurring at the same time. The equations governing the modulation of the amplitudes and phases as well as the resonance response functions in the implicit form were obtained employing the method of multiple scales with three time variables. Both the angle generalised coordinates have been approximated by the Taylor series keeping the terms up to the third order.
Sartorelli and Lacarbonara [23] investigated, both theoretically and experimentally, the parametric resonances of the double pendulum subjected to the kinematic excitation in the vertical direction. The theoretical part consisted in employing the method of multiple scales in order to obtain the differential equations of the slow time evolution of the amplitudes and phases for a priori assumed conditions of the both parametric resonances. Authors took into account the effects of higher orders by using the non-classical approach consisting in the introduction of three time variables proportional to the first, second and fourth powers of a small parameter. In the framework of this formulation they conducted three stages of the perturbation procedure corresponding to the odd powers of the small parameter. The trigonometric functions were approximated by the fifth order polynomial resulting from their expanding in the Taylor series around the stable equilibrium position.
Summing up, the method of multiple scales, but also other perturbative methods, cannot be applied directly for the governing equations for the systems with geometric nonlinearities. The approximation of the trigonometric nonlinearities with a polynomial composed of several terms of the Taylor series is commonly used for such systems. The accuracy of this approximation decreases with the distance from the point around which the function is expanded. The accuracy of the approximation can of course be increased by using higher order polynomials, but in the case of the perturbation methods this leads to a significant increase of the computational complexity. Regardless of the order of the approximation by the Taylor series one should be aware of the restrictions which result from it. These restrictions mainly apply to the size of the vibration amplitude. Any extrapolation beyond the interval on which the approximation is valid seems to be unjustified.
In the present work, we propose the application of the polynomial approximation in quadratic meaning in order to formulate the approximate governing equations for the systems with trigonometric nonlinearities. In contrast to the approximation realised by Taylor series, the proposed novel approach makes that the functions sine and cosine are approximated with sufficiently accuracy not only around a given point but on the whole predefined interval. The size of the interval one should a priori determine appropriately to the aim of investigations and to the expected range of the variability of angle coordinates. Therefore, the proposed approximation may be the solution which guarantee to obtain better predictions for resonance responses for mechanical systems with geometric nonlinearities.
The further part of the paper is organised in the following way. The mathematical foundations of the proposed polynomial approximation are described briefly in Sect. 2. The system chosen to examine the effects of the proposed approach is described in Sect. 3, where equations of motion are also derived. Section 4 reports the approximation of the governing equations with the use of the polynomial approximation. Resonant vibrations for the primary resonance are studied in Sect. 5. Section 6 is devoted to investigation of the steady state resonant responses. In Sect. 7, the results of simulations done are discussed. Concluding remarks are presented in Sect. 8.
2 Polynomial approximation in quadratic meaning
The issue of finding for a given real-valued function \( f \) the best approximation on a given finite interval we realize in a Hilbert space U, i.e. in the sense of \( L^{2} \)-norm. The \( L^{2} \)-norm is defined as follows
where \( \left( {f,f} \right) \) denotes the inner (or scalar) product.
Due to the fact that the \( L^{2} \)-norm is the generalised Euclidean norm, the best approximation problem in the Hilbert space is often called the approximation in quadratic sense.
Let \( I = \left[ {a,b} \right] \) be the interval on which the function f is determined. The solution, \( h_{0} , \) of the problem of the best approximation of f in U fulfills equation [24, 25]
Limiting the search to an n-dimensional subspace of U, with the basis \( \left\{ {\mu_{1} , \mu_{2} , \ldots ,\mu_{n} } \right\} \), one can effectively find the solution to the best approximation problem [25]. The solution h to the problem formulated in this mean satisfies equation
We assume that the solution sought is a linear combination of the base functions in the form
where \( d_{j} , j = 1,2, \ldots ,n \) are unknown coefficients.
Substituting (4) into Eq. (3) gives the system of n linear equations
with n unknown coefficients \( dj \).
Thus, the problem of the best approximation of the given function f consists in the solving the system of n linear equations.
Some details of the realisation of the procedure of the best approximation result from the purpose which is assumed in the paper. We seek the best approximation of the functions sine and cosine of the generalised coordinate which changes its values in some range around the stable equilibrium position. Therefore, the interval \( I \) should be symmetrical relative to zero. Thus, we postulate \( I = \left[ { - p,p} \right]. \) In the most commonly used variant of the method of multiple scales, three time variables proportional to the successive powers of the small parameter are introduced, and thus all terms of the order higher than third one are neglected in the solution. Focusing on the approach competitive for this variant we introduce the following basis \( \left\{ {1,x,x^{2} ,x^{3} } \right\}. \) Taking all this into account, we obtain
where \( f \) denotes the sine or the cosine, depending on the need.
Solving the system of Eq. (4) yields the following coefficients for the approximation of the sineFootnote 1
while for the approximation of the cosine the coefficients are
Therefore, we obtain the approximation formulas for the sine and cosine of the following form
where \( \beta_{1} = d_{2}^{s} , \beta_{2} = d_{4}^{s} , \beta_{3} = d_{1}^{c} , \beta_{4} = d_{3}^{c} . \)
Let us consider additionally the another manner of the approximation of the sine and cosine in the quadratic sense. Suppose that for some reasons it is desirable that the sine around zero to be close to the function x, and the cosine to the value one. We take, then, the \( \left\{ {x^{2} ,x^{3} } \right\} \) as the basis, and postulate that
where \( \gamma_{1} ,\gamma_{2} \) are to be found. With employment of the best approximation in quadratic meaning we obtain
In Table 1 are gathered the values of the relative error for the polynomial approximation of the sine and cosine in quadratic meaning, i.e. according to formulas (10)–(11), for some values of the parameter p which determines the length of the approximation interval. For comparison, the relative error values for the approximation carried out using the Taylor series truncated to the terms of third order are also given in the two last rows of the table. The relative errors are calculated using the \( L^{2} \)-norm according to the following formulas
where
Some regularities one can note. The accuracy estimated according to the proposed measure decreases with the growth of the value of the parameter p. Regardless of the length of the interval, both approaches basing on the polynomial approximation in quadratic sense give the more accurate results. The accuracy of the approximation of the cosine is significantly lower than the one for the sine, in the case of all approaches.
The quantitative and qualitative differences between the considered kinds of the approximation of the sine and cosine one can observe in Figs. 1 and 2 which present the graphs of the approximation error \( e_{i} \) on the right half of the whole approximation interval for \( p = 2 \).
In both figures, the dot-dashed line is used to draw the error concerning the approximation according to formula (10), the solid line presents the error of the approximation done according to (11), whereas the dashed line concern the error of the approximation with use of the Taylor series up to third order.
3 Problem formulation and equations of motion
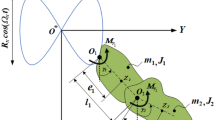
Plane motion of the body of mass m connected via a spring-damper suspension with the immovable point O is studied. The shape and the size of the body are negligible, so it is treated as a point mass. The scheme of the system is presented in Fig. 3. The spring is assumed to be massless, and its elastic properties are nonlinear with the nonlinearity of the cubic type. By L0 we denote the spring length in the non-stretched state. There are assumed two purely viscous dampers in the system. The resistance force R depends on the point velocity v according to the relation \( {\mathbf{R}} = - C_{2} {\mathbf{v}} . \) The system is loaded by the torque whose magnitude varies harmonically \( M\left( t \right) = M_{0} \sin \left( {\Omega _{2} t} \right) \) and by the force F with the magnitude changing harmonically, i.e. \( F\left( t \right) = F_{0} \sin \left( {\Omega _{1} t} \right) \). The total spring elongation \( X\left( t \right) \) and the angle \( \Phi \left( t \right) \) are assumed as the generalised coordinates.
The kinetic energy of the pendulum relative to the immovable reference frame is
where the dot over a symbol means the derivative with respect to time.
The potential energy of the conservative forces acting on the pendulum is described as follows
where \( g \) denotes the gravitational acceleration.
All other forces acting on the pendulum are introduced into consideration as the generalised forces corresponding to the generalised coordinates, so we have
where \( C_{1} = C + C_{2} . \)
In the conditions without the external loading, the pendulum reaches its stable equilibrium position when \( \Phi = 0 \) and \( X = X_{e} \), where the elongation of the spring at the static equilibrium \( X_{e} \) satisfies the equation
The Lagrange equations of the second kind yield the pendulum motion equations. Taking into account condition (18), we get the equations describing the motion of the pendulum around the stable equilibrium position
where \( X_{1} \left( t \right) = X\left( t \right) - X_{e} , L = L_{0} + X_{e} . \)
In order to transform Eqs. (19)–(20) into the dimensionless form, the length of the spring at the stable equilibrium position \( \omega_{1}^{ - 1} \). and the characteristic time \( \omega_{1}^{ - 1} , {\text{where}}\, \omega_{1} = \sqrt {\frac{{k_{1} }}{m}} \) is the frequency of the simple harmonic oscillator of mass m and stiffness k1, are chosen as the reference quantities. The dimensionless motion equations of the spring pendulum are as follows
where
The functions \( x\left( \tau \right), \varphi \left( \tau \right) \) are the dimensionless counterparts of the generalised coordinates \( X_{1} \left( t \right), \Phi \left( t \right). \) Equations (21)–(22) are supplemented with the following initial conditions
where \( x_{0} , v_{0} , \varphi_{0} , \omega_{0} \) are known.
The dimensionless static elongation \( x_{e} \) of the spring satisfies the equilibrium condition in the dimensionless form
4 Approximation of the governing equations
In Fig. 4 are presented results of the numerical experiment done using the standard procedure NDSolve of the Mathematica software. Assuming the resonant conditions, the original problem described by Eqs. (21)–(23) has been solved. The solution is drawn by the solid line. Then, the trigonometric functions occurring in the original problem have been approximate according to the formula (11), formula (12) and finally by the Taylor series terms up to third order. The solutions to these approximate equations are depicted in Fig. 4 by the dotted line (A1), the dashed line (A2), and the dot-dashed line (T), respectively.
The following values of the parameters which have the impact on the pendulum motion have been assumed for the numerical simulation
The following initial values are assumed:
The values of the coefficients occurring in approximations formulas (11)–(12) have been calculated for the fixed value \( p = 2 \) which is in agreement with the expected range of the oscillations.
One can note that the approximation of the sine and cosine with use of the third order Taylor series, in contrast to the both approaches basing on the polynomial approximation in the \( L^{2} \)-norm sense, definitely fails in the case of high amplitude vibrations.
Taking into account the error analysis discussed in Sect. 3 as well as the conclusions following from the afore numerical simulation, we employ the approximation of the trigonometric functions in the sense of the \( L^{2} \)-norm. Admittedly, the best results are guaranteed by the approximation according to formulas (11), but there is some problem with this variant of approximation. It does not satisfy strictly the equilibrium condition, because the polynomial approximating the cosine does not equal 1 at zero. The inability to satisfy this condition, strongly inscribed in the nature of the vibration of the pendulum, can significantly mishandle the intended effect. Thus, we decide for the variant of the approximation determined by formulas (12) which does not violate the equilibrium condition and seems to be a compromise between the best polynomial approximation and the approximation with using the Taylor series truncated to the terms of the third order.
The trigonometric nonlinearities in motion Eqs. (21)–(22) are approximated according to (12), thus
Substituting Eq. (25) into (21)–(22) gives the approximate motion equations of the form
Equations (26)–(27) together with the conditions (23) form the initial value problem whose mathematical form allows for employment of the method of multiple scales in order to obtain the approximate solution.
5 Asymptotic solution to resonant vibration problem
The weak character of the nonlinearities that is assumed in the model of the pendulum causes that all couplings occurring in the system also become weak. Therefore, the natural frequencies do not modify oneself as a result of the couplings and are close to the natural frequencies of the linear oscillator and the usual pendulum.
We consider the case of two external resonances occurring simultaneously, which happens when
The standard manner of the study of the resonance states using MMS consists in the introduction of the detuning parameters. Introducing the detuning parameters \( \sigma_{1} \) and \( \sigma_{2} \), we can rewrite the resonance conditions (28) as follows
where \( \sigma_{1} \) and \( \sigma_{2} \) as dimensionless quantities can be any small numbers. We assume that they are of the order \( O\left( {\varepsilon^{2} } \right) , \) thus
We substitute the relations (29)–(30) in Eqs. (26)–(27), and then employ the method of multiple scales in time domain.
In accordance with the MMS rules, we introduce three time variables \( \tau_{0} , \tau_{1} , \tau_{2} \) that describe the system evolution in time. In contrast to the description with use only one time variable, i.e. the original time \( \tau \), such an approach allows for separating the fast and slow processes from each other. For this reason the variables introduced are called the time scales. They are related to the dimensionless time \( \tau \) in the following manner
where the small \( \varepsilon \) parameter should satisfy the double inequality \( 0 < \varepsilon \ll 1. \)
The time variable \( \tau_{0} \) is usually called the fast time scale, and the others time variables are regarded as the slow time scales.
The consequence of introducing several time variables is the need to replace the ordinary differential operators with the partial ones. According to the chain rule, we can write
The functions \( x\left( \tau \right), \varphi \left( \tau \right) \) are approximated by the following asymptotic expansions
where the functions \( \xi_{k} \left( {\tau_{0} , \tau_{1} , \tau_{2} } \right), \phi_{k} \left( {\tau_{0} , \tau_{1} , \tau_{2} } \right), k = 1, \ldots , 3 \) are to find.
The assumptions about weak nonlinearities one can strictly express by the following relations
The coefficients \( \hat{\alpha }, \hat{c}_{1} , \hat{c}_{2} , \hat{c}_{3} , \hat{f}_{1} , \hat{f}_{2} \) are understood as O(1) when \( \varepsilon \to 0. \)
Substituting Eqs. (29)–(36) into governing Eqs. (26)–(27) yields the equations in which the small parameter appears in a few different powers. In accordance with the order of approximation of the variant of MMS used, all terms of the order \( O\left( {\varepsilon^{4} } \right) \) should be omitted. The terms of the equations obtained should be ordered according to the powers of the small parameter. Both equations should be satisfied for any value of the small parameter. The requirement leads to the set of six differential equations with unknown functions \( \xi_{k} \left( {\tau_{0} , \tau_{1} , \tau_{2} } \right), \) \( \phi_{k} \left( {\tau_{0} , \tau_{1} , \tau_{2} } \right), \) \( k = 1, \ldots , 3 \). The equations of the system are organised into three groups, depending on the exponent of the power of the small parameter accompanying the terms occurring in the equation. Two of them belong to the homogeneous equations containing the terms standing at \( \varepsilon \). Therefore, they are called the first order approximation equations. They are as follows
The equations of the second order approximation containing the terms standing at \( \varepsilon^{2} \) have the form
The coefficients that are accompanied by \( \varepsilon^{3} \) form the following equations of the third order approximation
The equations of system (37)–(42) are solved recursively starting from the equations of the first order approximation whose general solutions are
where the functions \( B_{1} \left( {\tau_{1} , \tau_{2} } \right), B_{2} \left( {\tau_{1} , \tau_{2} } \right) \) and their complex conjugates \( \bar{B}_{1} \left( {\tau_{1} , \tau_{2} } \right),\bar{B}_{2} \left( {\tau_{1} , \tau_{2} } \right) \) are unknown.
After substituting solutions (43)–(44) into equations of the second order approximation we obtain the following solvability conditions
The particular solutions to Eqs. (39)–(40) are
Substituting solutions (43)–(44) and (46)–(47) into equations of the third order approximation imply occurrence of secular terms again. They must be eliminated from the equations which leads to the following solvability conditions
The particular solutions to the equations of the third order approximation, i.e. (41)–(42), are
The unknown functions \( B_{j} , \bar{B}_{j} ,j = 1,2, \) should satisfy the solvability conditions. According to conditions (45) each of them does not depend on the time variable \( \tau_{1} . \) Let us present the unknown functions in the exponential form
where the functions \( b_{1} \left( {\tau_{2} } \right), b_{2} \left( {\tau_{2} } \right), \psi_{1} \left( {\tau_{2} } \right), \psi_{2} \left( {\tau_{2} } \right) \) are real-valued.
Taking into account the independence of the time variable \( \tau_{1} , \) one can regard solvability conditions (48)–(51) as the set of four ordinary differential equations of the first order with respect to the functions \( B_{1} ,B_{2} \) and their complex conjugates. Inserting relationships (54) into differential Eqs. (48)–(51), solving the latter with respect to the derivatives, and finally, using relationships (30)–(33) and (36), we obtain
where \( a_{j} \left( \tau \right) = \varepsilon b_{j} \left( \tau \right), j = 1, 2. \)
The initial conditions
where the known quantities \( a_{10} , a_{20} , \psi_{10} , \psi_{20} \) are compatible with the initial values \( x_{0} , v_{0} , \varphi_{0} , \omega_{0} \), complete the formulation of the initial-value problem.
The real-valued functions \( a_{j} , \psi_{j} , j = 1,2, \) present the amplitudes and phases of the pendulum oscillations, respectively. In the original formulation of modulation equations derived directly from the solvability conditions (48)–(49), there are derivatives relative to the slowest time scale. Employment of the relationships (32)–(33) transform this formulation to another one with the sole time variable \( \tau . \) Therefore, Eqs. (55)–(58) describe the slow modulation of the amplitudes and phases.
Inserting solutions (43)–(44), (46)–(47) and (52)–(53) into asymptotic expansions (34)–(35), one can obtain the approximate solution to the problem
where the functions \( a_{1} \left( \tau \right), a_{2} \left( \tau \right), \psi_{1} \left( \tau \right), \psi_{2} \left( \tau \right) \) stand for numerically obtained solutions of modulation Eqs. (55)–(58).
6 Steady state resonant responses
In order to study the steady states, it is convenient to introduce into consideration the modified phases. The modified phases \( \theta_{1} \) and \( \theta_{2} \) are associated with the phases \( \psi_{1} , \psi_{2} \) in the following way
Substituting relations (62) into Eqs. (55)–(58) yields
According to the assumptions about the steady state vibration, we postulate that the time derivatives of the amplitudes and the modified phases become equal to zero, and the amplitudes \( a_{1} , a_{2} \) and the modified phases \( \theta_{1} ,\theta_{2} \) are constant quantities. The steady state vibration is governed by the following equations
The modified phases can be eliminated from Eqs. (66)–(69) using the trigonometric identities which allows for expressing the dependence between the amplitudes and the frequencies as a system of two algebraic equations
where \( \Gamma = 3\gamma_{1} + w^{2} \left( {8w^{2} \left( {1 + \gamma_{2} } \right) + \gamma_{2} - 12\gamma_{1} - 5} \right). \)
Each of the polynomials occurring on the left sides of Eqs. (71)–(72) is of degree six, hence the number of the solutions of the system, understood as the pairs (\( a_{1} , a_{2} \)), equals thirty-six. Observe that not all of these solutions are the real numbers. In order to find the values of the amplitudes and phases appropriate for the steady state vibration we solve the aforementioned equations in the numerically with a use of the standard procedure NSolve of the Mathematica program. In this way, the resonance response curves are constructed by the multiple numerical solving Eqs. (71)–(72) for various values of the detuning parameters. However, the stability analysis of the resonance response curves demands also the knowledge of the values of the modified phases. Therefore, the fixed points of the modulation equations are determined numerically by solving Eqs. (67)–(70).
7 Examples and results analysis
In order to test the proposed approach consisting in the approximation of the trigonometric functions in the quadratic sense and show how it does in the association with the method of multiple scales, several simulations have been carried out. The results are compared with the numerical results and the results obtained using MMS, but combined with the commonly used approximation of the trigonometric nonlinearities by the third order Taylor series. The solutions obtained using MMS in the case when the trigonometric functions are approximated by the truncated Taylor series one can derive from Eqs. (60)–(61), assuming that
Similarly, substituting Eq. (73) into Eqs. (55)–(58) yields the modulation equations adequate for the approach with the Taylor series.
Due to the assumed purpose, we focus on the pendulum oscillations with relatively large amplitudes, especially concerning the vibration in the transversal direction. Let us start yet with the case when the amplitudes are rather small. We assume the following values of the parameters:
The initial values are as follows:
Moreover, the value of the parameter p which determines the interval of the approximation of the trigonometric functions in the \( L^{2} \)-norm sense has been set to 0.45.
The time variability of the generalised coordinates \( x\left( \tau \right) \) and \( \varphi \left( \tau \right) \) are presented in Figs. 5 and 6. Two first of them are related to the initial stage of motion in which the transient vibration is realised. Figures 7 and 8 concern the pendulum oscillations at the end of simulation. The pendulum oscillations in the longitudinal direction do not fix oneself on the simulation interval. In each of these group of graphs two curves are depicted. The approximate analytical solution obtained using MMS is drawn using solid red line, whereas the dotted line in black is used to draw the numerical solution obtained by means of the standard NDSolve of the Mathematica software. In all cases presented, one can observe a high compliance between the both solution.
Quantitative analysis of the effectiveness of the proposed approach to the approximation the trigonometric functions is carried out with using the measure of error of the satisfying the governing equations. Let \( G_{1} \) and \( G_{2} \) denote the differential operator of the first or the second of governing Eqs. (21)–(22), respectively. The measure proposed evaluates the error of the fulfilment of the governing equations in the following way
where \( x_{a} \left( \tau \right),\varphi_{a} \left( \tau \right) \) denote the approximate solutions to the considered initial-value problem obtained by means of the MMS, irrespectively of the manner of the approximation of trigonometric nonlinearities, \( \tau_{s} , \tau_{e} \) are the instants chosen from the interval of simulation, and \( \tau_{s} < \tau_{e} . \)
The values of the error calculated according to (74) are gathered in Table 2.
In the case of resonant vibration when the amplitudes of the pendulum oscillations in both direction are rather small, there is not significantly difference between the results obtained using polynomial approximation in quadratic sense and the ones that are calculated using the approximation with the Taylor series.
The next example is conceived as a test of the approach proposed in the case of the resonant motion with large amplitudes of swing vibration. The following values of the parameters are fixed:
The initial values are as follows:
Additionally, the parameter \( p = 1.8. \)
Let us start the discussion from the error analysis. The values of the error determined according to (74) are presented in Table 3.
The results are much less accurate than the ones discussed in the previous example. However, one can note that the approximation in the quadratic sense works better, in the range of steady state vibration, than this one basing on the Taylor series. Graphs presented in the Fig. 9 show the nature of the noticeable difference. In this figure, a fragment of the whole time history of the generalised coordinate \( \varphi \left( \tau \right) \) is shown. The time history is obtained numerically by means of the NDSolve procedure. The vibration on the interval is almost steady. The dotted red line, lying upper, presents the time course of the amplitude \( a_{2} \left( \tau \right) \) which is obtained using the proposed approach of the approximation in the \( L^{2} \)-norm sense. The graph of the amplitude is strictly the envelope of the first term of the solution (61), i.e. \( a_{2} \cos \left( {w\tau + \psi_{2} } \right). \) This term is the solution of the first order approximation Eq. (44). The dashed blue line also depicted the amplitude of the first term of the whole solution, but obtained using the approximation of the trigonometric functions by the Taylor series. The fixed values of the amplitudes of the first approximation solutions are taken as the steady-state resonance responses. Thus, one can note that the prediction of the resonant responses based on the proposed approach to the approximation of the trigonometric nonlinearities is more accurate. The graphs of the approximate solution obtained according to Eq. (61) and the solution calculated numerically are shown in Fig. 10. The first of them is depicted by the solid red line, the second one by the dotted black line.
Continuing the matter of the prediction of the steady states let us determine the resonance response curve assuming the following data:
Focusing on the relationship between the amplitude \( a_{2} \) and the detuning parameter \( \sigma_{2} \) we assume additionally that the detuning parameter \( \sigma_{1} = - 0.008. \)
In Fig. 11 two resonance response curves are shown. One of them presents the dependence obtained by solving Eqs. (71)–(72), i.e. in the \( L^{2} \)-norm sense. The second one is related to the approach consisting in employment of the approximation based on the Taylor series. For small values of the swing vibration amplitudes both approaches give consistent results. The significant difference occurs in the range when the values of the amplitudes are greater than 0.5 which essentially coincides with the range of the applicability of the Taylor series expansions up to third order (see Table 1). Resonance response curves obtained using the approach proposed in the paper indicate that the nonlinear resonance response of the spring pendulum is less flexible.
The stability in the sense of Lyapunov of the resonance response curve related to the proposed approach shown in Fig. 11 has been evaluated. Results of this study are presented in Fig. 12. The stable branches of the resonance response curves are depicted using filled squares, whereas the small circles present the fixed points that are unstable.
8 Conclusions
The geometric nonlinearity is an inherent feature of many mechanical systems and devices. In the case of the pendulum-like systems, nonlinear relationships of the trigonometric form describe the restoring forces that are of the crucial meaning for the motion and is impossible to treat them as small nonlinear contributions into motion equations. The occurrence of the trigonometric functions in the equations of the mathematical model excludes the direct applicability of the perturbation methods in order to find approximate analytical solutions. A widely used solution to this problem consists in the approximation of the trigonometric functions by few terms of their Taylor series.
In the present work, we propose the application of the polynomial approximation in the \( L^{2} \)-norm sense in order to formulate the approximate governing equations for the systems with trigonometric nonlinearities. In contrast to the approximation realised by using the Taylor series, the proposed approach makes that the functions sine and cosine are approximated with sufficiently accuracy not only around a given point but on the whole predefined interval.
We have employed the polynomial approximation in the \( L^{2} \)-norm meaning in connection with the method of multiple scales in time domain. The pendulum spring, which is relatively simple mechanical system of 2-dof, has been chosen by us in order to apply and test the approach proposed. The approximate solution in the analytical form for the case of two simultaneously occurring resonances has been derived. The focusing on the resonance study was conditioned by the fact that a significant advantage of the proposed approximation is expected in the case of large oscillations.
The results of the simulations carried out confirm that the approximation in the \( L^{2} \)-norm sense works just as well as the approximation basing on the Taylor series in the case of oscillations with rather small amplitudes. The advantage of the solution proposed, among other in prediction of the steady state resonant vibration, becomes significantly visible when the amplitudes of the swing oscillations beyond the threshold of about 0.5 rad. The resonance response curves obtained using the approach proposed in the paper indicate that the nonlinear resonance response of the spring pendulum is less flexible than it results from the commonly used solutions basing on the Taylor series. It is worth underlying that in both approximation the degrees of polynomials are equal to each other.
References
Weinan E (2011) Principles of multiscale modeling. Cambridge University Press, Cambridge
Nayfeh AH, Mook DT (1995) Nonlinear oscillations. Wiley, New York
Awrejcewicz J, Krysko VA (2006) Introduction to asymptotic methods. Chapman and Hall, Boca Raton
Eissa E, Kamel M, El-Sayed AT (2010) Vibration reduction of multi-parametric excited spring pendulum via a transversally tuned absorber. Nonlinear Dyn 61:109–121
Eissa E, Kamel M, El-Sayed AT (2011) Vibration reduction of a nonlinear spring pendulum under multi external and parametric excitations via a longitudinal absorber. Meccanica 46:325–340
Lee WK, Park HD (1997) Chaotic dynamics of a harmonically excited spring-pendulum system with internal resonance. Nonlinear Dyn 14:211–229
Alasty A, Shabani R (2006) Chaotic motions and fractal basin boundaries in spring-pendulum system. Nonlinear Anal Real World Appl 7:81–95
Lee WK, Park HD (1999) Second-order approximation for chaotic responses of a harmonically excited spring-pendulum system. Int J Non Linear Mech 34:749–757
Amer TS, Bek MA (2009) Chaotic responses of a harmonically excited spring pendulum moving in circular path. Nonlinear Anal Real World Appl 10:3196–3202
Starosta R, Sypniewska-Kamińska G, Awrejcewicz J (2011) Parametric and external resonances in kinematically and externally excited nonlinear spring pendulum. Int J Bifurcat Chaos 21(10):3013–3021
Starosta R, Sypniewska-Kamińska G, Awrejcewicz J (2012) Asymptotic analysis of kinematically excited dynamical systems near resonances. Nonlinear Dyn 68(4):459–469
Starosta R, Sypniewska-Kamińska G, Awrejcewicz J (2014) Asymptotic analysis and limiting phase trajectories in the dynamics of spring pendulum. In: Awrejcewicz J (ed) Applied non-linear dynamical systems springer proceedings, vol 93, pp 161–173
Awrejcewicz J, Starosta R, Sypniewska-Kamińska G (2016) Stationary and transient resonant response of a spring pendulum. Procedia IUTAM 19(2016):201–208
Manevitch LI (2007) New approach to beating phenomenon in coupled nonlinear oscillatory chains. Arch Appl Mech 77(5):301–312
Manevitch LI, Musienko AI (2009) Limiting phase trajectories and energy exchange between anharmonic oscillator and external force. Nonlinear Dyn 58:633–642
Awrejcewicz J, Starosta R, Sypniewska-Kamińska G (2013) Asymptotic analysis of resonances in nonlinear vibrations of the 3-dof Pendulum. Differ Equ Dyn Syst 21(1–2):123–140
Amer TS, Bek MA, Abouhmr MK (2018) On the vibrational analysis for the motion of a harmonically damped rigid body pendulum. Nonlinear Dyn 91:2485–2502
Amer TS, Bek MA, Abouhmr MK (2019) On the motion of a harmonically excited damped spring pendulum in an elliptic path. Mech Res Commun 95:23–34
Salahshoor E, Ebrihimi S, Maasoomi M (2016) Nonlinear vibration analysis of mechanical systems with multiple joint clearances using the method of multiple scales. Mech Mach Theory 105:495–509
Daqaq MF, Masoud ZN (2006) Nonlinear input-shaping controller for quay-side container cranes. Nonlinear Dyn 45:149–170
Nayfeh NA, Baumann WT (2008) Nonlinear analysis of time-delay position feedback control of container cranes. Nonlinear Dyn 53:75–88
Sado D, Gajos K (2008) Analysis of vibration of three-degree-of-freedom dynamical system with double pendulum. J Theor Appl Mech Pol 46:141–156
Sartorelli JC, Lacarbonara W (2012) Parametric resonances in a base-excited double pendulum. Nonlinear Dyn 69:1679–1692
Larson MG, Bengzon F (2013) The finite element method. Theory, implementation and applications. Texts in Computational Science and Engineering, vol 10. Springer, Berlin
Zeidler E (ed) (2004) Oxford users’ guide to mathematics. Oxford University Press, New York
Acknowledgements
This work was supported by the Grant of the Ministry of Science and Higher Education in Poland, 02/21/DSPB/3544 and 02/21/SBAD/3558 and by the Grant of the Polish National Science Centre OPUS 14 No. 2017/27/B/ST8/01330.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sypniewska-Kamińska, G., Awrejcewicz, J., Kamiński, H. et al. Resonance study of spring pendulum based on asymptotic solutions with polynomial approximation in quadratic means. Meccanica 56, 963–980 (2021). https://doi.org/10.1007/s11012-020-01164-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-020-01164-8