Skip to main content
SpringerLink
Log in

Dynamic response analysis of helical gear pair considering the interaction between friction and mesh stiffness

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

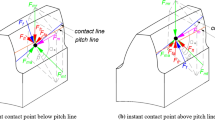
This work investigates the dynamic responses of a pair of helical gears considering the interaction between friction and time-varying mesh stiffness (TVMS). Firstly, governing equations with 8 degree-of-freedom, including friction excitations, are established. Then, the calculation methods for friction excitation and TVMS including friction are briefly introduced and influences of working conditions such as surface roughness, transmitted load and rotating speed on coefficient of friction, TVMS of a helical gear pair are revealed. Next, dynamic responses under steady state through numerical algorithm are obtained and the effects of the interaction between friction and TVMS are discussed under different working conditions. The results indicate that the effect brought by the interaction on dynamic responses except the linear vibration displacement along off-line-of-action is not consistent in a whole meshing period, and related to specific working condition. This work provides a more comprehensive way to understand dynamics behaviors of gear pairs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Ma H, Song R, Pang X et al (2014) Time-varying mesh stiffness calculation of cracked spur gears. Eng Fail Anal 44:179–194

    Article  Google Scholar 

  2. Ma H, Zeng J, Feng R et al (2015) Review on dynamics of cracked gear systems. Eng Fail Anal 55:224–245

    Article  Google Scholar 

  3. Wu Y, Wang J, Han Q (2012) Contact finite element method for dynamic meshing characteristics analysis of continuous engaged gear drives. J Mech Sci Technol 26(6):1671–1685

    Article  Google Scholar 

  4. Ma H, Pang X, Feng R et al (2015) Fault features analysis of cracked gear considering the effects of the extended tooth contact. Eng Fail Anal 48:105–120

    Article  Google Scholar 

  5. Munro RG, Palmer D, Morrish L (2001) An experimental method to measure gear tooth stiffness throughout and beyond the path of contact. Proc IMechE C J Mech Eng Sci 215(7):793–803

    Article  Google Scholar 

  6. Pandya Y, Parey A (2013) Experimental investigation of spur gear tooth mesh stiffness in the presence of crack using photoelasticity technique. Eng Fail Anal 34:488–500

    Article  Google Scholar 

  7. Raghuwanshi N, Parey A (2018) Experimental measurement of mesh stiffness by laser displacement sensor technique. Measurement 128:63–70

    Article  Google Scholar 

  8. Ma H, Zeng J, Feng R et al (2016) An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech Mach Theory 98:64–80

    Article  Google Scholar 

  9. Ma H, Feng M, Li Z et al (2017) Time-varying mesh characteristics of a spur gear pair considering the tip-fillet and friction. Meccanica 52:1695–1709

    Article  MathSciNet  Google Scholar 

  10. Sun Y, Ma H, Huangfu Y et al (2018) A revised time-varying mesh stiffness model of spur gear pairs with tooth modifications. Mech Mach Theory 129:261–278

    Article  Google Scholar 

  11. Chang L, Liu G, Wu L (2015) A robust model for determining the mesh stiffness of cylindrical gears. Mech Mach Theory 87:93–114

    Article  Google Scholar 

  12. Huangfu Y, Chen K, Ma H et al (2019) Investigation on meshing and dynamic characteristics of spur gears with tip relief under wear fault. Sci China Technol Sci. https://doi.org/10.1007/s11431-019-9506-5

    Article  Google Scholar 

  13. Chen K, Huangfu Y, Ma H et al (2019) Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths. Mech Syst Signal Process 130:273–292

    Article  Google Scholar 

  14. Wan Z, Cao H, Zi Y et al (2015) Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears. Mech Mach Theory 92:447–463

    Article  Google Scholar 

  15. Feng M, Ma H, Li Z et al (2018) An improved analytical method for calculating time-varying mesh stiffness of helical gears. Meccanica 53:1131–1145

    Article  Google Scholar 

  16. Wang Q, Zhao B, Fu Y et al (2018) An improved time-varying mesh stiffness model for helical gear pairs considering axial mesh force component. Mech Syst Signal Process 106:413–429

    Article  ADS  Google Scholar 

  17. Huangfu Y, Chen K, Ma H et al (2019) Deformation and meshing stiffness analysis of cracked helical gear pairs. Eng Fail Anal 95:30–46

    Article  Google Scholar 

  18. Han L, Xu L, Qi H (2017) Influences of friction and mesh misalignment on time-varying mesh stiffness of helical gears. J Mech Sci Technol 31(7):3121–3130

    Article  Google Scholar 

  19. He S, Singh R (2008) Dynamic transmission error prediction of helical gear pair under sliding friction using Floquet theory. ASME J Mech Des 130:052603-1–052603-9

    Google Scholar 

  20. Wei J, Gao P, Hu X et al (2014) Effects of dynamic transmission errors and vibration stability in helical gears. J Mech Sci Technol 28(6):2253–2262

    Article  Google Scholar 

  21. Jiang H, Shao Y, Mechefske C (2014) Dynamic characteristics of helical gears under sliding friction with spalling defect. Eng Fail Anal 39:92–107

    Article  Google Scholar 

  22. Jiang H, Liu F (2016) Dynamic features of three-dimensional helical gears under sliding friction with tooth breakage. Eng Fail Anal 70:305–322

    Article  Google Scholar 

  23. Brethee K, Gu F, Ball A (2016) Frictional effects on the diagnostics of helical gear tooth defects. In: IncoME 2016, 30th–31st Augues 2016, Manchester Conference Centre, Manchester

  24. Wang Q, Li Z, Ma H et al (2017) Effects of different coupling models of a helical gear system on vibration characteristics. J Mech Sci Technol 31(5):2143–2154

    Article  Google Scholar 

  25. Xu H (2005) Development of a generalized mechanical efficiency prediction methodology for gear pairs. Doctor of Philosophy, Ohio State University, Ohio, USA

  26. He S, Cho S, Singh R (2008) Prediction of dynamic friction forces in spur gears using alternate sliding friction formulations. J Sound Vib 309:843–851

    Article  ADS  Google Scholar 

  27. Pedrero J, Pleguezuelos M, Artes M et al (2010) Load distribution model along the line of contact for involute external gears. Mech Mach Theory 45:780–794

    Article  Google Scholar 

  28. Han L, Niu W, Zhang D et al (2013) An improved algorithm for calculating friction force and torque in involute helical gears. Math Probl Eng, Article ID 575302

  29. He S, Gunda R, Singh R (2007) Effect of friction on the dynamics of spur gear pair with realistic time-varying stiffness. J Sound Vib 301:927–949

    Article  ADS  Google Scholar 

Download references

Funding

This study was funded by Natural Science Foundation of Tianjin (Grant No. 18JCQNJC75200) and Tianjin Municipal Education Commission (Grant No. JWK1601), China.

Author information

Authors and Affiliations

  1. Tianjin Key Laboratory of High Speed Cutting and Precision Machining, Tianjin University of Technology and Education, Tianjin, 300222, China

    Lin Han & Houjun Qi

Authors
  1. Lin Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Houjun Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lin Han.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, L., Qi, H. Dynamic response analysis of helical gear pair considering the interaction between friction and mesh stiffness. Meccanica 54, 2325–2337 (2019). https://doi.org/10.1007/s11012-019-01088-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-019-01088-y

Keywords

Search

Navigation