An improved analytical method for calculating time-varying mesh stiffness of helical gears

Abstract

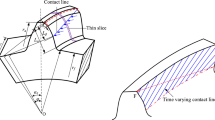
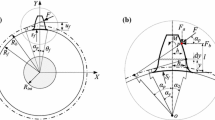
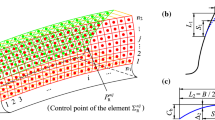
A “slice method” is adopted to calculate the time-varying mesh stiffness (TVMS) of helical gear pairs, where the tooth is divided into many individual sliced spur gears along the tooth width, and the TVMS of helical gear pairs is obtained by accumulating the TVMS of the sliced spur gear pairs. Based on the slice method, an improved analytical method (IAM) is proposed to calculate TVMS of the helical gear pairs. The proposed method is also verified by comparing TVMS obtained from IAM with that obtained from references and the finite element method. Based on the proposed IAM, the effects of the helix angle, gear width, modification coefficient and friction coefficient on mesh characteristics are also discussed. The results show that the total contact ratio of helical gear changes under different helix angles and gear tooth widths, and the fluctuation of mesh stiffness will reduce when the overlap contact ratio approaches an integer. Meanwhile, addendum modifications can not only change the total contact ratio but also affect the mean mesh stiffness of gear pairs. Furthermore, not only will the friction coefficients affect the mean mesh stiffness, and it can lead to an abrupt change of TVMS in double-teeth engagement region.

Appendices

Appendix 1: Calculation formulas for contact ratio

The transverse contact ratio ε _α and the overlap contact ratio ε _β can be calculated by:

$$\varepsilon_{\alpha } = \frac{{\tan \alpha_{\hbox{max} } - \tan \alpha_{\hbox{min} } }}{{2\uppi}}Z_{1} ,\,\,\varepsilon_{\beta } = \frac{{Z_{1} L\tan \beta_{b} }}{{2\uppi\,r_{b1} }}$$

(13)

where Z ₁ is the tooth number of the driving gear; L is the tooth width, r _b1 is the radius of the base circle of driving gear, β _b is the helix angle of the base circle. α _max is the maximum pressure angle, which corresponds to the pressure angle of the meshing point D (see Fig. 13). α _min is the minimum pressure angle, which corresponds to the pressure angle of the meshing point A (see Fig. 13). β _b, α _max and α _min can be calculated as follows:

$$\tan \beta_{\text{b}} = \tan \beta \cdot \frac{{r_{{{\text{b}}1}} }}{{r_{1} }},$$

(14)

$$\alpha_{\hbox{min} } = \angle {\kern 1pt} {\kern 1pt} NOA = \arctan \frac{NA}{{r_{{{\text{b}}1}} }},$$

(15)

$$\alpha_{\hbox{max} } = \alpha_{{{\text{a}}1}} = \arctan \frac{ND}{{r_{{{\text{b}}1}} }} = \arccos \frac{{r_{{{\text{b}}1}} }}{{r_{{{\text{a}}1}} }},$$

(16)

$$NA = NP - AP = r_{{{\text{b}}1}} \cdot \tan \alpha_{\text{t}} - r_{{{\text{b}}2}} \cdot (\tan \alpha_{{{\text{a}}2}} - \tan \alpha_{\text{t}} ),$$

(17)

$$ND = NA + AD = r_{{{\text{b}}1}} \cdot (\tan \alpha_{{{\text{a}}1}} - \tan \alpha_{\text{t}} ) + r_{{{\text{b}}2}} \cdot (\tan \alpha_{{{\text{a}}2}} - \tan \alpha_{\text{t}} ),$$

(18)

where r ₁ is the radius of the pitch circle, r _b1 and r _b2 are the radii of the base circles of the driving and driven gears, r _a1 and r _a2 are the radii of the addendum circle of the driving and driven gears, α _t is the transverse pressure angle, α _a1 and α _a2 are the pressure angles of addendum circles of the driving and driven gears, respectively, and they can be calculated by: $\alpha_{{{\text{a}}1}} = \arccos (r_{{{\text{b}}1}} /r_{{{\text{a}}1}} ),\,\,\alpha_{{{\text{a}}2}} = \arccos (r_{{{\text{b}}2}} /r_{{{\text{a}}2}} )$.

Fig. 13

Schematic of the driving gear

Appendix 2: Tooth stiffness calculation considering the effects of the friction coefficient and the addendum modification coefficient

Considering the effects of the friction coefficient [33] and the addendum modification coefficient [31], the bend stiffness k _b, the shear stiffness k _s and the axial compressive stiffness k _a can be given as follow:

$$\frac{1}{{(k_{b1}^{n} )_{j} }} = \left\{ \begin{aligned} & \int_{{\frac{\pi }{2}}}^{{\alpha_{t} }} {\frac{{[(\cos (\tau_{1,i}^{n} )_{j} - \mu \sin (\tau_{1,i}^{n} )_{j} )(y_{\tau } - y_{1} ) - x_{\tau } (\sin (\tau_{1,i}^{n} )_{j} + \mu \cos (\tau_{1,i}^{n} )_{j} )]^{2} }}{{EI_{y1} }}} \frac{{dy_{1} }}{d\gamma }d\gamma \\ & + \quad \int_{{\tau_{C} }}^{{(\tau_{1,i}^{n} )_{j} }} {\frac{{[(\cos (\tau_{1,i}^{n} )_{j} - \mu \sin (\tau_{1,i}^{n} )_{j} )(y_{\tau } - y_{2} ) - x_{\tau } (\sin (\tau_{1,i}^{n} )_{j} + \mu \cos (\tau_{1,i}^{n} )_{j} )]^{2} }}{{EI_{y2} }}\frac{{dy_{2} }}{d\tau }d\tau ,\quad (\theta_{1} < \theta_{P} )} \\ & \int_{{\frac{\pi }{2}}}^{{\alpha_{t} }} {\frac{{[(\cos (\tau_{1,i}^{n} )_{j} + \mu \sin (\tau_{1,i}^{n} )_{j} )(y_{\tau } - y_{1} ) - x_{\tau } (\sin (\tau_{1,i}^{n} )_{j} - \mu \cos (\tau_{1,i}^{n} )_{j} )]^{2} }}{{EI_{y1} }}} \frac{{dy_{1} }}{d\gamma }d\gamma \\ & + \quad \int_{{\tau_{C} }}^{{(\tau_{1,i}^{n} )_{j} }} {\frac{{[(\cos (\tau_{1,i}^{n} )_{j} + \mu \sin (\tau_{1,i}^{n} )_{j} )(y_{\tau } - y_{2} ) - x_{\tau } (\sin (\tau_{1,i}^{n} )_{j} - \mu \cos (\tau_{1,i}^{n} )_{j} )]^{2} }}{{EI_{y2} }}\frac{{dy_{2} }}{d\tau }d\tau ,\quad (\theta_{1} > \theta_{P} )} \\ \end{aligned} \right.,$$

(19)

$$\frac{1}{{(k_{{{\text{s}}1}}^{n} )_{j} }} = \left\{ \begin{aligned} \int_{{\frac{\uppi}{2}}}^{{\alpha_{\text{t}} }} {\frac{{1.2({\text{cos(}}\tau_{ 1 ,i}^{n} )_{j} - \mu \sin (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{GA_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma + \int_{{\tau_{C} }}^{{ (\tau_{ 1 ,i}^{n} )_{j} }} {\frac{{1.2({\text{cos(}}\tau_{ 1 ,i}^{n} )_{j} - \mu \sin (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{GA_{y2} }}} \frac{{{\text{d}}y_{2} }}{{{\text{d}}\tau }}{\text{d}}\tau ,\quad (\theta_{ 1} < \theta_{P} ) \hfill \\ \int_{{\frac{\uppi}{2}}}^{{\alpha_{\text{t}} }} {\frac{{1.2({\text{cos(}}\tau_{ 1 ,i}^{n} )_{j} + \mu \sin (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{GA_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma + \int_{{\tau_{C} }}^{{ (\tau_{ 1 ,i}^{n} )_{j} }} {\frac{{1.2({\text{cos(}}\tau_{ 1 ,i}^{n} )_{j} + \mu \sin (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{GA_{y2} }}} \frac{{{\text{d}}y_{2} }}{{{\text{d}}\tau }}{\text{d}}\tau ,\quad (\theta_{ 1} > \theta_{P} ) \hfill \\ \end{aligned} \right.,$$

(20)

$$\frac{1}{{(k_{{{\text{a}}1}}^{n} )_{j} }} = \left\{ \begin{aligned} \int_{{\frac{\uppi}{2}}}^{{\alpha_{\text{t}} }} {\frac{{ ( {\text{sin(}}\tau_{ 1 ,i}^{n} )_{j} + \mu \cos (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{EA_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma + \int_{{\tau_{C} }}^{{ (\tau_{ 1 ,i}^{n} )_{j} }} {\frac{{ ( {\text{sin(}}\tau_{ 1 ,i}^{n} )_{j} + \mu \cos (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{EA_{y2} }}} \frac{{{\text{d}}y_{ 2} }}{{{\text{d}}\tau }}{\text{d}}\tau {\kern 1pt} ,\quad (\theta_{ 1} < \theta_{P} ) \hfill \\ \int_{{\frac{\uppi}{2}}}^{{\alpha_{\text{t}} }} {\frac{{ ( {\text{sin(}}\tau_{ 1 ,i}^{n} )_{j} - \mu \cos (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{EA_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma + \int_{{\tau_{C} }}^{{ (\tau_{ 1 ,i}^{n} )_{j} }} {\frac{{ ( {\text{sin(}}\tau_{ 1 ,i}^{n} )_{j} - \mu \cos (\tau_{ 1 ,i}^{n} )_{j} )^{2} }}{{EA_{y2} }}} \frac{{{\text{d}}y_{ 2} }}{{{\text{d}}\tau }}{\text{d}}\tau {\kern 1pt} ,\quad (\theta_{ 1} > \theta_{P} ) \hfill \\ \end{aligned} \right.,$$

(21)

where α _t denotes the transverse pressure angle, $(\tau_{ 1 ,i}^{n} )_{j}$ denotes the operating pressure angle of the ith tooth pair of the nth gear slice of the driving gear at meshing position j, γ and τ denote the angular displacements of arbitrary point at the transition curve and the involute curve, E and G are Young’s modulus and Shear modulus, θ ₁ and θ _P can be found in Fig. 13. τ _C denotes the meshing angle at the position of the involute starting point, and $\tau_{C} = \arccos (r_{\text{b1}} /r_{C} ) - \theta_{\text{b1}} + {\text{inv(}}\arccos (r_{\text{b1}} /r_{C} ) ) ,$ $r_{C} = \sqrt {(r_{\text{b1}} \tan \alpha_{\text{t}} - (h_{\text{at}} - \chi_{1} )m_{\text{t}} /\sin \alpha_{\text{t}} )^{2} + r_{\text{b1}}^{2} }$. I _y1, I _y2, A _y1, A _y2, x ₁, y ₁, x ₂, y ₂, x _τ , y _τ , dy ₁/dγ, dy ₂/dτ can be expressed as:

$$I_{y1} = \frac{2}{3}x_{1}^{3} l,{\kern 1pt} {\kern 1pt} {\kern 1pt} I_{y2} = \frac{2}{3}x_{2}^{3} l,{\kern 1pt} {\kern 1pt} {\kern 1pt} A_{y1} = 2x_{1} l,{\kern 1pt} {\kern 1pt} {\kern 1pt} A_{y2} = 2x_{2} l,$$

(22)

$$x_{1} = r_{1} \times \sin \varPhi - (a_{1} /\sin \gamma + r_{\rho } ) \times \cos (\gamma - \varPhi ), y_{1} = r_{1} \times \cos \varPhi - (a_{1} /\sin \gamma + r_{\rho } ) \times \sin (\gamma - \varPhi )$$

(23)

$$x_{2} = r_{\text{b1}} [(\tau + \theta_{{{\text{b}}1}} )\cos \tau - \sin \tau ],\,\,\,\,\,y_{2} = r_{\text{b1}} [(\tau + \theta_{{{\text{b}}1}} )\sin \tau + \cos \tau ]$$

(24)

$$x_{\tau } = r_{\text{b1}} [( (\tau_{ 1 ,i}^{n} )_{j} + \theta_{{{\text{b}}1}} )\cos (\tau_{ 1 ,i}^{n} )_{j} - \sin (\tau_{ 1 ,i}^{n} )_{j} ],\,\,\,\,\,y_{\tau } = r_{\text{b1}} [( (\tau_{ 1 ,i}^{n} )_{j} + \theta_{{{\text{b}}1}} )\sin (\tau_{ 1 ,i}^{n} )_{j} + \cos (\tau_{ 1 ,i}^{n} )_{j} ],$$

(25)

$$\begin{aligned} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }} & = \frac{{a_{1} { \sin }\left( {\frac{{a_{1} /{ \tan }\gamma + b_{1} }}{{r_{1} }}} \right) (1 + { \tan }^{2} \gamma )}}{{{ \tan }^{2} \gamma }} \quad+ \frac{{a_{1} { \cos }\gamma }}{{{ \sin }^{2} \gamma }}{ \sin }\left( {\gamma - \frac{{a_{1} /{ \tan }\gamma + b_{1} }}{{r_{1} }}} \right){ ,} \\ & \quad- \left( {\frac{{a_{1} }}{{{ \sin }\gamma }} + r_{\rho } } \right){ \cos }\left( {\gamma - \frac{{a_{1} /{ \tan }\gamma + b_{1} }}{r}} \right)\quad\left( {1 + \frac{{a_{1} \left( {1 + { \tan }^{2} \gamma } \right)}}{{r_{1} { \tan }^{2} \gamma }}} \right) \\ \end{aligned}$$

(26)

$$\frac{{{\text{d}}y_{2} }}{{{\text{d}}\tau }} = r_{\text{b1}} (\tau + \theta_{\text{b1}} )\cos \tau ,$$

(27)

where $\varPhi = (a_{1} /\tan \gamma + b_{1} )/r_{1}$, $\theta_{{{\text{b}}1}} = (\uppi + 2\chi_{1} \tan \alpha_{\text{t}} )/2Z_{1} + {\text{inv}}\alpha_{\text{t}}$ denotes the half tooth angle corresponding to base circle of the driving gear with addendum coefficient, r ₁ denotes the radius of the pitch circle of the driving gear, $r_{\rho } = c_{\text{t}} m_{\text{t}} /(1 - \sin \alpha_{\text{t}} )$, $a_{1} = (h_{\text{at}} + c_{\text{t}} )m_{\text{t}} - r_{\rho } - \chi_{1} m_{\text{t}}$, $b_{1} =\uppi\,m_{\text{t}} /4 + h_{\text{at}} m_{\text{t}} \tan \alpha_{\text{t}} + r_{\rho } \cos \alpha_{\text{t}}$, h _at denotes transverse addendum coefficient, c _t denotes the transverse tip clearance coefficient, m _t denotes the transverse module, and χ ₁ denotes the addendum modification coefficient of driving gear.