Analysis of water wave scattering by a submerged perforated reef ball using multipole method

Abstract

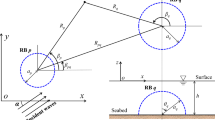
Based on linear potential theory, this study develops an analytical solution to water wave scattering by a submerged perforated reef ball. The series solutions for velocity potentials in the external and internal fluid domains of the perforated reef ball are developed using the multipole expansions and the separation of variables, respectively. The unknowns in the series solutions are determined by matching the porous boundary condition on the perforated reef ball. Also a numerical solution using three-dimensional multi-domain boundary element method (BEM) is developed. The special case of an impermeable reef ball is also examined. The calculation methods for the horizontal and vertical wave forces acting on the reef ball and the free surface elevation around the reef ball are given. The convergence of the calculation results is very rapid, and the results with five-figure accuracy are obtained using a few truncated terms in the series solution. The results by the analytical solution agree well with that by the multi-domain BEM solution. Typical calculation examples are presented to examine the effects of reef ball radius, porous effect parameter of reef ball and incident wave frequency on the wave forces and the free surface elevation. The results of analysis are valuable for engineering design and application of reef balls. The present analytical solution gives a new reliable benchmark for three-dimensional numerical models to wave interactions with perforated structures. Moreover, better understanding on wave scattering by perforated structures can be obtained during the analytically solving procedure.

Appendix: Three-dimensional multi-domain BEM solution

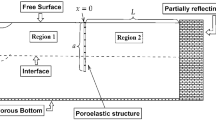
The whole fluid domain is still divided into two regions, which are the same as those in Sect. 2. As shown in Fig. 17, the closed boundary of region 1 is defined as: S₁ = S_F + S_D1 + S_B + S_∞, where S_F, S_D, S_B and S_∞ are respectively the free surface boundary, the water bottom boundary, the surface boundary of the reef ball and the far field boundary. The closed boundary of region 2 is defined as: S₂ = S_D2 + S_B.

Fig. 17

The sketch of three-dimensional multi-domain BEM solution

Applying the second Green theorem, the solution of Laplace equation can be converted into the solution of the following boundary integral equation [47]:

$$\alpha_{j} (\varvec{x}_{0} )\phi_{j} (\varvec{x}_{0} ) = \iint_{{\text{S}_{j} }} {\left[ {\phi_{j} (\varvec{x})\frac{{\partial \tilde{G}_{j} (\varvec{x};\varvec{x}_{0} )}}{{\partial \varvec{n}_{j} }} - \tilde{G}_{j} (\varvec{x};\varvec{x}_{0} )\frac{{\partial \phi_{j} (\varvec{x})}}{{\partial \varvec{n}_{j} }}} \right]\text{d} \text{S}_{j} (\varvec{x})},\quad \, j = 1,2,$$

(44)

where x = (x, y, z) and x₀ = (x₀, y₀, z₀) are the field and source points, respectively; α_j(x₀) is the interior angle; n_j denotes the unit normal vector on the boundary S_j and points away from fluid region j; and $\tilde{G}_{j} \left( {\varvec{x};\varvec{x}_{0} } \right)$ is the Green function, which satisfies

$$\nabla^{2} \tilde{G}_{j} = \delta (\varvec{x} - \varvec{x}_{0} ).$$

(45)

For the fluid region 1, the Green function is chosen as [48]:

$$\begin{aligned} \tilde{G}_{1} (\varvec{x};\varvec{x}_{0} ) & = - \frac{1}{4\pi }\left( {\frac{1}{{r_{0} }} + \frac{1}{{r_{1} }}} \right) \\ & \quad + \frac{1}{2\pi }\int_{0}^{\infty } {\frac{{(K + \mu )\text{e}^{ - \mu h} \cosh (\mu (z + h))\cosh (\mu (z_{0} + h))}}{K\cosh (\mu h) - \mu \sinh (\mu h)}J_{0} (\mu R_{0} )\text{d} \mu ,} \\ \end{aligned}$$

(46)

where $r_{0} = [R_{0}^{2} + (z - z_{0} )^{2} ]^{1/2}$, $r_{1} = [R_{0}^{2} + (z + z_{0} + 2h)^{2} ]^{1/2}$ and $R_{0}^{2} = (x - x_{0} )^{2} + (y - y_{0} )^{2}$. The path of the integration on the right hand of Eq. (46) passes below the point at μ = k. We split ϕ₁ as ϕ₁ = ϕ₀+ ϕ_d with ϕ₀ being the incident velocity potential given in Eq. (8), and ϕ_d being the diffraction velocity potential to be determined. We note that both the Green function $\tilde{G}_{1}$ and ϕ_d satisfy Eqs. (4)–(6). Thus, Eq. (44) can be reduced to

$$\alpha_{1} (\varvec{x}_{0} )\phi_{1} (\varvec{x}_{0} ) = \iint_{{\text{S}_{\text{B} } }} {\left[ {\phi_{1} (\varvec{x})\frac{{\partial \tilde{G}_{1} (\varvec{x};\varvec{x}_{0} )}}{{\partial \varvec{n}_{1} }} - \tilde{G}_{1} (\varvec{x};\varvec{x}_{0} )\frac{{\partial \phi_{1} (\varvec{x})}}{{\partial \varvec{n}_{1} }}} \right]\text{d} \text{S}_{\text{B} } (\varvec{x})} + \phi_{0} (\varvec{x}_{0} ).$$

(47)

For the fluid region 2, the Green function only satisfying the water bottom condition is given by

$$\tilde{G}_{2} (\varvec{x};\varvec{x}_{0} ) = - \frac{1}{4\pi }\left( {\frac{1}{{r_{0} }} + \frac{1}{{r_{1} }}} \right).$$

(48)

Then, Eq. (44) is reduced to

$$\alpha_{2} (\varvec{x}_{0} )\phi_{2} (\varvec{x}_{0}) = \iint_{{\text{S}_{\text{B}} }} {\left[ {\phi_{2} (\varvec{x})\frac{{\partial \tilde{G}_{2} (\varvec{x};\varvec{x}_{0} )}}{{\partial \varvec{n}_{2} }} - \tilde{G}_{2} (\varvec{x};\varvec{x}_{0} )\frac{{\partial \phi_{2} (\varvec{x})}}{{\partial \varvec{n}_{2} }}} \right]\text{d} \text{S}_{\text{B}} (\varvec{x})}.$$

(49)

The surface of the reef ball S_B is divided into I elements. Both velocity potential and its normal derivative on each element are assumed to be constants. Then, all the interior angles equal to 0.5. Now, Eqs. (47) and (49) can be, respectively, discretized into the following linear equations:

$$\left[ {\mathbf{A}} \right](\phi_{1}^{1} ,\phi_{1}^{2} , \ldots ,\phi_{1}^{I} )^{\text{T} } + \left[ {\mathbf{B}} \right](\bar{\phi }_{1}^{1} ,\bar{\phi }_{1}^{2} , \ldots ,\bar{\phi }_{1}^{I} )^{\text{T} } = \left\{ {\mathbf{f}} \right\},$$

(50)

$$\left[ {\mathbf{C}} \right](\phi_{2}^{1} ,\phi_{2}^{2} , \ldots ,\phi_{2}^{I} )^{\text{T} } + \left[ {\mathbf{D}} \right](\bar{\phi }_{2}^{1} ,\bar{\phi }_{2}^{2} , \ldots ,\bar{\phi }_{2}^{I} )^{\text{T} } = {\mathbf{0}}\text{,}$$

(51)

where $\phi_{j}^{m}$ and $\bar{\phi }_{j}^{m}$ are respectively the velocity potential and its normal derivative on the center of mth element of the body surface in region j. The matrix coefficients in Eqs. (50) and (51) are given by

$$A_{mn} = \iint_{{\text{S}_{\text{B}}^{n} }} {\left[ {\partial \tilde{G}_{1} (\varvec{x}^{n} ;\varvec{x}_{0}^{m} )/\partial \varvec{n}_{1} } \right]\text{d} \text{S}_{\text{B}}^{n} (\varvec{x})} - 0.5\delta_{mn} ,\quad m,n = 1,2, \ldots ,I,$$

(52)

$$B_{mn} = - \iint_{{\text{S}_{\text{B}}^{n} }} {\tilde{G}_{1} (\varvec{x}^{n} ;\varvec{x}_{0}^{m} )\text{d} \text{S}_{\text{B}}^{n} (\varvec{x})},\quad m,n = 1,2, \ldots ,I,$$

(53)

$$f_{m} = - \phi_{0} (\varvec{x}_{0}^{m} ),\quad m = 1,2, \ldots ,I,$$

(54)

$$C_{mn} = \iint_{{\text{S}_{\text{B}}^{n} }} {\left[ {\partial \tilde{G}_{2} (\varvec{x}^{n} ;\varvec{x}_{0}^{m} )/\partial \varvec{n}_{2} } \right]\text{d} \text{S}_{\text{B}}^{n} (\varvec{x})} - 0.5\delta_{mn} ,\quad m,n = 1,2, \ldots ,I,$$

(55)

$$D_{mn} = - \iint_{{\text{S}_{\text{B}}^{n} }} {\tilde{G}_{2} (\varvec{x}^{n} ;\varvec{x}_{0}^{m} )\text{d} \text{S}_{\text{B}}^{n} (\varvec{x})},\quad m,n = 1,2, \ldots ,I,$$

(56)

where δ_mn = 0 for m ≠ n and δ_mn = 1 for m = n. When the value of R₀/h is greater than 0.1, the Green function in Eq. (45) is calculated using a series method according to that in John [48]. Otherwise, the Green function in Eq. (45) is calculated using the methods described in Chapman [21, Chapter 4], Linton [41, Eqs. (3.7) and (4.11)] and Liu and Li [42, Appendix].

Applying the porous boundary condition on the hemispherical shell

$$- \frac{{\partial \phi_{1} }}{{\partial \varvec{n}_{1} }} = \frac{{\partial \phi_{2} }}{{\partial \varvec{n}_{2} }} = \text{i} kG(\phi_{2} - \phi_{1} ),\quad \text{on} \;\;{\text{S}}_{\text{B}} ,$$

(57)

the system of linear equations in Eqs. (49) and (50) can be simplified as

$$\left[ {\begin{array}{*{20}c} {{\mathbf{A}} + \text{i} kG{\mathbf{B}}} & { - \text{i} kG{\mathbf{B}}} \\ { - \text{i} kG{\mathbf{D}}} & {{\mathbf{C}} + \text{i} kG{\mathbf{D}}} \\ \end{array} } \right]\left\{ \begin{aligned} {\varvec{\upphi}}_{1} \hfill \\ {\varvec{\upphi}}_{2} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} {\mathbf{f}} \hfill \\ {\mathbf{0}} \hfill \\ \end{aligned} \right\}.$$

(58)

The velocity potentials on all element of the body surface S_B are determined after solving Eq. (58), and their normal derivatives are determined by Eq. (57).

The horizontal and vertical wave forces are respectively calculated by

$$F_{x} = \frac{\rho gH}{2}\iint_{{\text{S}_{\text{B}} }} {(\phi_{2} - \phi_{1} )n_{x} \text{dS} } = \frac{\rho gH}{2}\sum\limits_{m = 1}^{I} {(\phi_{2}^{m} - \phi_{1}^{m} )n_{x}^{m}\,S_{\text{B}}^{m}} ,$$

(59)

$$F_{z} = \frac{\rho gH}{2}\iint_{{\text{S}_{\text{B}} }} {(\phi_{2} - \phi_{1} )n_{z} \text{dS} } = \frac{\rho gH}{2}\sum\limits_{m = 1}^{I} {(\phi_{2}^{m} - \phi_{1}^{m} )n_{z}^{m}\,S_{\text{B}}^{m}} ,$$

(60)

where $n_{x}^{m}$ and $n_{z}^{m}$ are respectively the components along x- and z-directions of the unit normal vector on the mth element pointing to region 2, and $S_{\text{B}}^{m}$ is the area of the mth element on S_B.