Abstract
A three-dimensional modelling of free vibrations and static response of functionally graded material (FGM) sandwich plates is presented. Natural frequencies and associated mode shapes as well as displacements and stresses are determined by using the finite element method within the ABAQUS™ code. The three-dimensional (3-D) brick graded finite element is programmed and incorporated into the code via the user-defined material subroutine UMAT. The results of modal and static analyses are demonstrated for square metal-ceramic functionally graded simply supported plates with a power-law through-the-thickness variation of the volume fraction of the ceramic constituent. The through-the-thickness distribution of effective material properties at a point are defined based on the Mori-Tanaka scheme. First, exact values of displacements, stresses and natural frequencies available for FGM sandwich plates in the literature are used to verify the performance and estimate the accuracy of the developed 3-D graded finite element. Then, parametric studies are carried out for the frequency analysis by varying the volume fraction profile and value of the ceramic volume fraction.
Similar content being viewed by others

Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Sandwich panels are promising thin-walled structural elements combining high performance with lightweight. This is due to their excellent strength-to-weight and stiffness-to-weight ratios, acoustic and thermal insulation, protection against impacts and a possibility of tailoring properties for optimizing structural responses [1]. Conventional sandwich plates are tri-layer structures consisting of two thin, strength face sheets (skins) and a thick, lightweight core [2]. However, when dissimilar materials are joined, a high mismatch in material and geometrical properties between them leads to an inter-laminar stress concentration at the face sheet-to-core interface and as a result sandwich composites often suffer from premature failure caused by debonding the face sheet from the core. This issue has already become one of major topics extensively studied over the past several decades involving static, dynamic and fracture problems, e.g. recent papers [3,4,5,6,7,8,9,10,11,12]. Another important aspect is that usual sandwich materials have no high service temperature capabilities. These disadvantages of the sandwich structure can be reduced or eliminated by using a functionally graded material (FGM) as constitutive layers.
FGMs are a new type of composite materials, which were initially developed as thermal barrier coatings to minimize thermal and residual stresses as well as to prevent large deflections under high temperature in aerospace structures and fusion reactors [13]. The original idea was to use heat resistant ceramic on a high-temperature side and, then, to gradually reduce its volume fraction to metal on the other side. Nowadays, this FGM concept has received a wide spreading in automotive, optoelectronic, biomedical and sport industries. Combining two or more material phases often with incompatible properties of individual materials, the specific features desirable for certain engineering applications are accomplished. Thus, with spatially varying volume fraction of one of the constituents from the bottom to top face sheets of the sandwich material, the bond strength enhancement, removing interface stress concentration, providing multi-functionality and ability to control deformation, dynamic response, etc. can be achieved [14]. Since the use of FGMs as a branch of advanced composite materials, in particular functionally graded sandwich plates, increases, there is a high demand in predictions of their responses at a design stage to ensure their reliable exploitation. In this respect, many studies have been performed to estimate the thermal-mechanical behaviour of FGM plates including fracture, e.g. [15,16,17,18,19,20] among of the latest. On the other hand, the analysis of free vibrations and static response of FGM plates is of primary importance for their performance assessment.
A considerable amount of research on free vibrations and static analysis studies of FGM plates and shells can be found in the literature. Various analytical (or semi-analytical) and numerical methods have been developed for this, as recently reviewed in [21]. The main idea of many of them is to incorporate some new methodologies into known methods with appropriate minimal modifications, if needed. In most of analytical approaches, through-the-thickness assumptions of two-dimensional (2-D) plate/shell theories such as classic (CPT), first order shear deformation (FSDT) and high order shear deformation (HSDT) theories in conjunction with a given variation of elastic constants along the thickness direction are used to obtain the solution, e.g. [22,23,24,25,26,27] among of the many others. As concluded in [28], the material gradient along the thickness direction leads to complex deformations of the core that require the use at least a HSDT theory. An improvement of the 2-D FGM theories so-called quasi-three dimensional (3-D) theories accounting for the effect of both shear and normal deformations in the thickness direction to analyse FGM sandwich plates have been proposed in [29,30,31,32,33]. Analytical 3-D solutions for FGM sandwich plates have also been developed, e.g. in [34,35,36,37,38,39]. Although such approaches are sophisticated and require much efforts, they accurately describe complicating effects, do not call for additional assumptions and are usually used as a benchmarks for 2-D solutions and numerical results. Besides, the complexity of analytic solutions for FGM plates which is associated with their geometry different from rectangular, can be successfully overcome by using semi-analytic approaches. For instance, a numerical-analytical approach based on R-functions theory and the Ritz method has been worked out for studying geometrically nonlinear vibrations of functionally graded shallow shells of complex planform in [40]. An approach implementing the differential transform method for free vibration analysis of non-uniform cross-section of functionally graded beams has been presented, e.g. in [41, 42].
Nevertheless, the analysis of more general FGM plate shapes as well as loading and boundary conditions requires the use of numerical tools such as the finite element method (FEM). Conventional finite elements are typically formulated assuming constant elastic properties over the whole element. The modelling of FGM structures with such elements is related to the presentation of a graded region by a number of homogeneous strips. This approach requires a fine enough mesh discretization to accurately capture the gradient in materials properties as well as the gradients in calculated strain and stress fields. As a result, layered models are quite cumbersome in preparation of the input data and lead to excessive computational costs, especially in the case of 3-D modelling. Another approach adopting conventional finite elements for modelling FGM plates is based on the assumption that a FGM plate behaves like a homogenous with corrected location of the neutral axis, e.g. [43]. However, this technique is suitable only for 2-D modelling. Alternatively, to improve the efficiency of the FEM for modelling FGM structures, finite elements that include the gradient in material properties at the element level so-called graded elements have been proposed in literature. There are two approaches to model the material gradient within the finite element. In the first one, element material properties are approximated by using the same interpolation functions used for the displacement field as done e.g. in [44, 45], whereas in the second one, the material parameters are sampled directly at the integration points of the element, thereby the inhomogeneity is distributed, e.g. [46].
In recent years, commercially available finite element code ABAQUS™[47] has become popular among engineers and researchers due to its versatility and high accuracy. However, the package presents a difficulty in implementation of a spatial variation of material properties into FE models. To solve this issue, some existing works suggest to use the ABAQUS’ UEL subroutine implementing a material gradation in FGM plates via a user-developed finite element, e.g. [48]. While this approach gives a high flexibility in modelling, it requires the knowledge of an experienced user and extensive benchmarks of the element performance before simulations. Alternatively, to assign the gradation of properties in ABAQUS, a user-defined material subroutine UMAT can be used. This option allows exploiting conventional finite elements from ABAQUS’ library that do not need to be tested, but which are endowed with necessary properties at the Gauss points. Such approach for implementation of varying material properties has been reported for ABAQUS’ 2-D plane strain elements in [49,50,51], where the strain-stress state of FGM pavement and the thermo-mechanical behaviour of FGM plate have been analysed, respectively. Also, this modelling technique has been extended on 2-D plate/shell and 3-D models of FGM plates in [52, 53], respectively, however only the static bending analysis has been simulated there.
Despite a substantial volume of works and developed finite elements for the modelling of FGM structures, the literature search reveals that 3-D finite element models are still high required for predictions of dynamic and static responses of FGM sandwich plates. This is primarily motivated by the fact that 3-D solutions are direct outcomes of the analysis and no any assumptions on through-the-thickness deformations like in 2-D models are needed. Thus, the development of 3-D finite elements for high-fidelity dynamic and static predictions of FGM sandwich plates is of importance. In the present work, we propose a simple formulation of the 3-D brick graded finite element within the ABAQUS code for its application to modal dynamic and static analyses of FGM sandwich plates. For this purpose, the user-defined material subroutine UMAT is programmed to assign a smooth variation of elastic properties in a conventional 3-D brick finite element and an averaging procedure is proposed for obtaining the mass density equivalent to its actual gradation profile within the element. This modelling technique is simpler than the UEL option and is efficient compared with analytical solutions because the FE scheme can be applied to any complicated configurations and boundary conditions in sandwich plates. The performance of the 3-D graded element has been demonstrated by the 3-D modelling of free vibrations and static response of simply supported rectangular metal-ceramic FGM sandwich plates. The material is assumed to be linearly isotropic with mechanical properties varying across the plate thickness in accordance with a power-law. The accuracy of the graded element has been validated by comparisons with the results available in the literature for FGM sandwich plates. Parametric studies have also been carried out to find out the effect of varying volume fraction profiles and ceramic volume fractions on natural frequencies and associated mode shapes.
2 Problem statement
For the sake of completeness, the standard mechanical initial boundary value problem is briefly summarized in the section. Throughout this section we adopt the notations usual in most of the books on Continuum Mechanics, to which we address the reader for more details.
2.1 Equations of motion
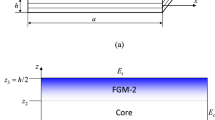
Let us consider a FGM sandwich plate as a 3-D deformable medium occupying the domain \(\Omega \in [0,a]\times [0,b]\times [-\frac{h}{2},+\frac{h}{2}]\) bonded by the surface \(\partial \Omega \subset \Omega \) at an instant of time \(t\in [0,T]\). The plate is defined in the unstressed reference configuration with respect to a rectangular Cartesian co-ordinate system \(x_i=(x,y,z)\) with the z-axis aligned along the plate thickness and with the plane \(z=0\) coinciding with the mid-plane of the sandwich plate. Also, the planes \(z=\pm h/2\) refer to the bottom \(\partial \Omega ^-\) and the top \(\partial \Omega ^+\) plate surfaces, respectively, where \(\partial \Omega \setminus (\partial \Omega ^-\cup \partial \Omega ^+)=[-\frac{h}{2},+\frac{h}{2}]\), and \(z\in [-\frac{h}{2},+\frac{h}{2}]\) as shown in Fig. 1a.
The motion of the plate is described by a displacement field \( {\mathbf {u}}\) at time \( t\in [0,T]\). Assume that during the motion the plate experiences only infinitesimal deformations with a strain measure defined by a tensor \(\pmb {\varepsilon }=\frac{1}{2}\left( \nabla {\mathbf {u}}+ (\nabla {\mathbf {u}})^T \right) \), and the stress state associated with the deformations is described by the Cauchy stress tensor \(\pmb {\sigma }\). Also, the plate is subjected to prescribed displacements \({\bar{\mathbf {u}}}\) on the boundary \(\partial \Omega _u\) and prescribed surface traction \( {\bar{\mathbf {t}}} \) on the boundary \(\partial \Omega _t\), the boundaries are such that \(\partial \Omega _t\cup \partial \Omega _u=\partial \Omega \) and \(\partial \Omega _t\cap \partial \Omega _u=\oslash \). Neglecting the body forces, the deformations of the sandwich plate during its motion have to obey the following system of equations [54]:
where \(\rho ({\mathbf {x}})\) is the density of material, and the superscript dot means a time derivative, i.e. \({\dot{\mathbf{u}}}\) and \({\ddot{\mathbf{u}}}\) stand for a velocity and an acceleration, respectively, \({\mathbf {n}}\) is an outward unit normal to the boundary surface \(\partial \Omega \).
Using the dynamic principle of virtual work, the system of Eq. (1) can be rewritten in weak form as follows:
for all virtual (kinematically admissible) displacement fields \(\delta {\mathbf {u}}\).
2.2 Constitutive equations and FGM
Let the plate be made of a functionally graded material, which, without loss of generality, is a mixture of two material phases such as metal and ceramic. The composite material is assumed to be linearly isotropic with smoothly varying mechanical properties in the z-direction only, Fig. 1b. The skins are homogeneous, pure metallic on the bottom side and pure ceramic on the top side with negligible small thickness in comparison with the thick metallic-ceramic FGM core. The constitutive equation of the linear isotropic FGM material is defined by the generalized Hooke’s law:
where the Lamé constants \(\lambda ({\mathbf {x}})\) and \(\mu ({\mathbf {x}})\) of the elasticity tensor \({\mathbb {C}}\) are point-wise functions of location. Since the gradient in properties occurs only along the plate thickness direction, then the material tensor in (3) in the Voigt notation reads as [54]:
Further, following the homogenization technique, the two-constituent microscopically inhomogeneous metallic-ceramic composite material is to be replaced by an equivalent macroscopically homogeneous FGM with effective material properties. The effective mechanical parameters of the FGM are usually evaluated based on the volume fraction distribution and the approximate shape of the dispersed phase [34]. It is assumed that the grading of the volume fraction of ceramic phase from the bottom to top plate surfaces is determined by a power-law function as follows:
where \(V_c^-\) and \(V_c^+\) are the volume fraction of ceramic on the bottom and top surfaces, respectively. The case of \(V_c^-=0\) and \(V_c^+=1\) refers to the gradation profile from pure metal on \(z=-h/2\) to pure ceramic on \(z=+h/2\).
There exist different approaches to estimate the effective properties of such equivalent FGM. The Mori-Tanaka homogenization method is the most popular among others in literature. In this scheme, the effective Lamé constants are computed from corresponding effective bulk modulus K and shear modulus \(\mu \) as follows:
where \(f_m=\mu _m(9K_m+8\mu _m)/6(K_m+2\mu _m)\); the subscripts ’m’ and ’c’ stand for the metallic and ceramic phases, respectively, and \(V_m + V_c = 1\). From (5) it follows that the FGM is ceramic rich when the parameter \(p < 1\) and metal rich when the parameter \(p > 1\). Figure 1c shows the volume fraction variation of the ceramic phase along the plate thickness for various values of the power-law index p.
Finally, the effective mass density at a point of the FGM is calculated using the ’rule of mixture’ in the form:
2.3 Finite element solution procedure
A displacement-based FEM framework is used for solving the problem formulated above. Accordingly to this method, the actual continuous model of the sandwich plate is idealized by an assemblage of arbitrary non-overlapping finite elements \(\Omega =\bigcup _{e=1}^N\Omega ^{(e)}\) interconnected at nodal points. In each a base element the components of the displacement field are approximated by suitable interpolation functions such that a vector of the displacement field \({{\varvec{u}}}\) at an arbitrary point of the element can be written in the matrix form as follows:
Here, the summation over all nodal points of the base element is intended. Also, \({{\varvec{N}}}=[N_I({\mathbf {x}})]\) is a matrix of the shape functions \(N_I\) for the displacements associated with a certain node I and \({{\varvec{U}}}^{(e)}\) is a vector of the nodal unknowns.
With the adopted displacement approximation (8), the strain-displacement relations can be rewritten through the nodal unknowns in the matrix notation as the following: \(\pmb {\varepsilon }={{\varvec{B}}}{{\varvec{U}}}\), where \({{\varvec{B}}}=[B_I]\) is the matrix of gradients of the shape functions, i.e. \(B_I={N_I}_{,{\mathbf {x}}}\). Inserting all these matrix relations into the variational equality (2) and taking into account a linear elastic material definition (3), we arrive at the system of semi-discrete equations of motion at the element level as:
where \({{\varvec{M}}}^{(e)}\), \({{\varvec{K}}}^{(e)}\) and \({{\varvec{F}}}^{(e)}\) are the mass matrix, the stiffness matrix and the force vector, defined by the expressions [55]:
Thereafter, the use of the assembly operation \((\bullet )={\mathbb {A}}_{e=1}^N(\circ )\) over all the finite elements leads us to the global system of finite element semi-discrete equations of motion:
It should be noted that damping is not included in the dynamic system of Eq. (11). The governing system of Eq. (11) can be employed to study the statics and free vibrations by ignoring the time and excluding the appropriate terms. For the static (or quasi-static) analysis, the problem reduces to the system of algebraic equations:
In the case of free vibration analysis, the governing system of equations should be stated in the form of the eigenvalue problem as follows:
where \(\omega \) is an undamped circular frequency and \(\pmb {\phi }\) is a vector of mode shape associated with found frequency \(\omega \).
3 Three-dimensional graded finite element
The modal analysis for extraction of natural frequencies and associated mode shapes and the static analysis of FGM sandwich plates are carried out with the ABAQUS/Standard code using three-dimensional models. Conventional 3-D finite elements available in the ABAQUS’ finite element library do not enable to model variation of mechanical properties within the element volume. To eliminate this inconvenience, we have developed within the package environment a graded 3-D finite element incorporating gradients of material properties. For this purpose, either eight-node linear C3D8 or twenty-node quadratic C3D20 brick isoparametric finite elements can be used as a base element, Fig. 2. Since the quadratic elements usually yield better results at less expense than their linear counterparts [55], C3D20 elements will be used in the succeeding calculations. Isoparametric interpolation within the element volume is defined in terms of the natural coordinates \((\xi ,\eta ,\zeta )\) each spanning the range from \(-1\) to \(+1\), as shown in Fig. 2a. The node numbering convention used for these elements with either full or reduced integration is also demonstrated in Fig. 2b, c. The shape functions of both the 8-node and 20-node brick elements can be presented as follows:
Isoparametric 3-D brick finite elements after [47]: a master elements; b 8-node linear element with reduced and full integration schemes; and c 20-node quadratic element with reduced and full integration schemes (Numbering of integration points for output is shown in the element layer closest to the face 1, and the integration points in the other layers are numbered consecutively)
The spatial variation of the material parameters have been achieved by coding the user-defined material subroutine UMAT. The routine evaluates the increments of strain and stress vectors and the material Jacobian to provide an implementation of the incremental form of a defined mechanical constitutive law into the code solver. At the end, it updates the stress and strain vectors, and other solution dependent variables over the element volume at the Gauss points, [47]. Since the material constants depend on the position within the element, the calculations of the constitutive material relation will assign the material parameters directly at different integration points of the element. Finally, by means of numerical integration of the tangential stiffness matrix of the finite element as:
the actual gradient of material properties is completely specified within the element. In this expression, i, j and k are the Gauss points, \(|J_{ijk}|\) is the determinant of the Jacobian matrix and \(w_i\) are the Gaussian weights. The matrix \({{\varvec{C}}}\) given in (15) contains the material constants \(\lambda \) and \(\mu \) depending on the position as shown in (4).
To complete the development of the graded finite element, the mass density, which is also a function of position for the FGM plate, should be incorporated into the element formulation. However, there is a complication in terms of formulating the element mass matrix with sampling the density values at the Gauss points similar to (15). The frequency extraction procedure is a linear perturbation analysis in ABAQUS. The perturbations are assumed to be about the base state of a model and ignore any inelastic effects and any parametric dependencies of the model on temperature or other field and solution dependent variables [47]. Moreover, the code does not provide a direct access to the computation of elements of the mass matrix. The latter is formed with the conventional homogeneous elements, where the element volume is simply multiplied by a given constant mass density. Herein, we suggest a simple “engineering solution” to account for changes in inertial properties due to the use of FGMs. A constant value of the mass density required by ABAQUS can be obtained by averaging a proper density distribution over the whole volume of the FGM plate, V as follows:
Although the density in the form of an integrated value averaged over the volume (16), does not reflect its actual gradual change, this formula can reasonably approximate the inertial property of a FGM sandwich plate, as shown in all the frequency analyses below.
4 Numerical results
In this section numerical results for studying the static behaviour and free vibrations of two-constituent metallic-ceramic functionally graded sandwich plates are presented. In each the analysis presented below, first, convergence studies with mesh refinement have been conducted. An optimal mesh was selected from the conditions that differences between the results, namely, a displacement of the central point in the case of static analysis and a fundamental frequency in the case of eigenfrequency problem, obtained with current and finer meshes are no more than 5%, but from the other hand, the calculations should be the best compromise between computational cost and solution accuracy.
4.1 Static analysis
The accuracy of the 3-D graded finite element programmed via UMAT in the ABAQUS environment is verified, first, performing the static analysis of a FGM sandwich plate. A simply supported Al/SiC square sandwich plate subjected to a normal pressure given by \(q_0\mathrm {sin}\frac{\pi x}{a}\mathrm {sin}\frac{\pi y}{b}\) on the top surface was considered. We accepted the parameters of (5) as \(V_c^{-}=0\), \(V_c^{+}=1\) and \(p=2\), the plane dimensions and the thickness-to-length ratio as \(a=b=100\) mm and \(\frac{h}{a}=0.2\), respectively, and \(q_0=1\) MPa. The material constants used in the calculations are listed in Table 1. The numerically calculated results are compared with those obtained analytically in [34].
A 3-D finite element model of the FGM sandwich plate considered in the present work is illustrated in Fig. 3a. The meshes, optimal from the standpoint of the convergence analysis mentioned above, for both the developed 3-D FGM elements with six elements through-the-thickness and the conventional homogeneous 3-D elements with ten elements through-the-thickness are shown in Fig. 3b, c, respectively. It should be noted that the latter model requires a tedious and cumbersome procedure for preparing and, then, introducing the input data different for each the layer of elements in the mesh, while the former one uses a simpler pre-processing, i.e. the input data are assigned on the whole finite element model at once.
The physical quantities compared with the solutions reported in [34] are presented in a dimensionless form as follows:
The results of comparison between the analytic solutions in [34] and the results obtained from the both graded and layered models in the static analysis are summarized in Table 2, where \(\Delta , \%\) denotes relative errors between the reference data and the results of the model with FGM elements and the layered model with homogeneous elements, relatively. A good agreement with the analytic solutions can be seen for both the finite element models. However, the graded model is superior to the layered one because it is more accurate and efficient, i.e. gives better results with less number of the elements and is more convenient for using. The minor discrepancies between the results of the model with FGM elements and the reference values may be addressed to the problem of non-equivalency between the ways of applying the boundary conditions to plate edges in 3-D analytic and FEM models, as discussed elsewhere in literature, e.g. in [56, 57].
The distributions of the dimensionless deflection and longitudinal \(\sigma _{xx}\) and transverse normal \(\sigma _{zz}\) stresses through-the-thickness of the FGM sandwich plate, computed at a point \((\frac{a}{2},\frac{b}{2},z)\) using both the FGM elements in the continuous model and the homogeneous elements in the layered model, in comparison with some known analytic values given in [34] are shown in Fig. 4. One can see that the numerical models have very close results to the analytic solutions and they are able to accurately reproduce the through-the-thickness behaviours. Although both the numerical models are slightly stiffer than the analytical one due to the discretized nature of the models, they give the exact result for the transverse normal stress and the results which are very close to the exact solution for the longitudinal stress. In doing so, the layered model is a bit stiffer compared with the graded elements and exhibits a stepwise change of the longitudinal stress (see Fig. 4d). Such a step-type variation with constant longitudinal stress in each element is inherently related to homogeneous elements and cannot be avoided in modelling with layered models. In contrast to this, the graded model provides a continuous stress variation through the plate thickness.
To show the efficiency of the developed graded 3-D finite element for studying FGM sandwich plates, the influence of the gradation profile on the static response of the simply supported square FGM sandwich plate is further analysed. Figure 5 depicts the through-the-thickness variations of normalized deflection, \({\bar{w}}\), and longitudinal \({\bar{\sigma }}_{xx}\) and transverse normal \({\bar{\sigma }}_{zz}\) stresses, calculated at the centre point of the sandwich plate, for different values of the power index p. For the sake of clarity, the behaviour of these quantities at bottom, middle and top layers of the plate with increasing the exponent p are illustrated there as well. From the plots it is clearly seen that the deflections of the FGM sandwich plates are not symmetrical with respect to the plate midplane and this non-symmetry is larger when more aluminum phase is in the graded material. The stresses have also nonlinear patterns across the thickness. These conclusions are in a compliance with the results in [29, 36]. With increasing the exponent p the deflections of the bottom, middle and top layers are reduced smoothly and same manner to the values close to deflections of the metallic plate (Fig. 5d), whereas the longitudinal stress on those layers varies in a more complicated way (Fig. 5e). The tensile longitudinal stress \({\bar{\sigma }}_{xx}\) at the bottom layer first a bit reduces with increasing the metal phase and, then, its value smoothly rises with growing the index p and, finally, tends to the magnitude of stress in the metallic plate. In contrast to this, the compressive longitudinal stress \({\bar{\sigma }}_{xx}\) at the top layer first remarkably increases with increasing the metal phase and, then, it gradually decreases with increasing the exponent p nearly to the stress of the metallic plate. The transverse normal stress \({\bar{\sigma }}_{zz}\) at bottom and top layers almost does not depend on the gradation profile, and its behaviour at the midplane is similar to the longitudinal stress at this layer, i.e., first, increases and, then, slowly tends to the stress of the metal plate, as seen in Fig. 5e, f.
The distributions of the dimensionless quantities through-the-thickness of the FGM sandwich plate at a point \((\frac{a}{2},\frac{b}{2},z)\): a deflection; b longitudinal stress \(\sigma _{xx}\); c transverse normal stress \(\sigma _{zz}\); and the variations of the dimensionless quantities at bottom \(z=-\frac{h}{2}\), middle \(z=0\) and top \(z=+\frac{h}{2}\) layers with increasing the power index p: d deflection; e longitudinal stress \(\sigma _{xx}\); and f transverse normal stress \(\sigma _{zz}\)
4.2 Free vibration analysis
The correctness of the developed 3-D graded finite element in conjunction with the proposed procedure of the mass density averaging for finite element modelling of free vibrations has been verified by comparing the fundamental frequency, displacements and stresses of a simply supported square \(\hbox {Al}/\hbox {ZrO}_2\) sandwich plate with the results available in [36]. The material properties of the FGM plate studied are listed in Table 1. The dimensions and the parameters of the power-law given by (5) for this FGM sandwich plate are taken the same as the previous static analysis. Table 3 shows the comparisons between the reference values and the results obtained with the 3-D FGM elements model and the layered model with the conventional homogeneous 3-D elements.
It is known that besides standard flexural and in-plane predominant modes resulted from 2-D models of FGM sandwich panels, the 3-D solution predicts additionally thickness-stretching predominant modes [35]. Thus, to validate the ability of the proposed graded element for producing such response, the deflection and stresses at several points of the thickness have also been considered for comparison with analytical values in [36]. All the compared quantities have been nondimensionalized by the formulae:
A glance at the values in Table 3 reveals that the computed results are in satisfactory agreement with those presented in [36]. The finite element solutions of the both models with FGM and homogeneous elements are almost the same, and they slightly overestimate the analytical reference values. The sources of these discrepancies could be, first, the normalization formulae involve a deflection which is not exact value itself, but being calculated. Second, not actual distribution of the mass density, but its average value is implemented into the model. Finally, because of an incompatibility between the ways of applying boundary conditions in the FEM and analytical techniques. It should be noted that for the sake of simplicity, needed to carry out a large number of computations, the simply supported conditions in the present research have been realised using the nodal displacement constraints applied over each a whole edge of the sandwich plate.
As expected, the 3-D finite element frequency analysis has been able to reveal the existence of peculiar mode shapes associated with the natural frequencies of the thick sandwich plate. That is apart from the usual bending or flexural mode shapes, one has been observed the following additional modes: the pumping or thickness-stretching mode, where the deflections are predominant and are symmetric with respect to the mid-plane; the in-plane or extensional modes, where one of longitudinal displacements prevails; and finally so-called bi-inplane modes or extensional modes, where two longitudinal displacements act simultaneously and either symmetrically or anti-symmetrically. Such mode shapes have been mentioned, but not exhibited in [35]. These types of the mode shapes and the differences between them for metallic, \(\hbox {Al}/\hbox {ZrO}_2\) sandwich and ceramic plates are illustrated in Fig. 6. One can clearly see that those peculiar mode shapes are different between the two homogeneous plates and they, in turn, differ from the functionally graded plate. The latter has the configurations of the mode shapes which are intermediate between the metallic and ceramic plates. Herewith, the influence of the material gradation is more evident on thickness-stretching and bi-inplane extensional mode shapes than on in-plane extensional ones.
The ability of the developed 3-D graded element to properly capture the gradation profile across the plate thickness for the frequency analysis has also been examined. The fundamental frequency of the simply supported \(\hbox {Al}/\hbox {ZrO}_2\) square thick sandwich plate considered above is calculated for different values of the power index p. The results of calculations are compared with those known in [29]. The values of the frequencies normalized by \({\bar{\omega }}=\omega h\sqrt{\rho _m/E_m}\) are exhibited in Table 4, where the numerical results obtained by using both the FGM elements and the homogeneous elements in the layered model are compared with the analytic solutions.
It is obviously that the numerical results show a good agreement with the analytic solutions. This confirms the accurate performance of the developed 3-D graded finite element. Moreover, it should be mentioned that due to the convergence requirement, the element size of the layered model was smaller than the size of the graded element as 1 mm and 2.5 mm, respectively. As a result, the total CPU time of calculations with homogeneous elements was about 3 times longer than the computations with the graded elements. This demonstrates the efficiency of the 3-D graded element in the predictions. For this FGM sandwich plate, the first sixteen dimensionless natural frequencies depending on the power index p are computed and summarized in Table 5.
For the sake of better illustration of the power-index dependence of the natural frequencies of the \(\hbox {Al}/\hbox {ZrO}_2\) sandwich plate, the evolutions of four frequencies with increasing the metal phase are depicted in Fig. 7. One can see that, first, quantitatively the natural frequencies of the FGM sandwich plate are between those of the same metallic and ceramic plates. Second, the power-index or an assumption about the material phase distribution through-the-thickness of the FGM sandwich plate affects its natural frequencies such that with increasing p the frequencies tend to values close to those of the metallic plate. However, the rate of this trend is different for the lower frequencies, as illustrated in Fig. 7a, b and for the higher ones, as shown in Fig. 7c, d. The former ones are slightly changed at the small p and, then, slowly are reduced to the frequencies of the metallic plate with growing the exponent to infinity. In contrast to this, the latter ones decrease quickly enough with increasing the metal phase and tend to the frequencies of the metal plate.
Finally, the influence of both the ceramic volume fraction on the top surface and the metal phase in the sandwich core on the modal dynamics of FGM sandwich plates have been studied. The same \(\hbox {Al}/\hbox {ZrO}_2\) sandwich plate as considered above was modeled. Different values of \(V_c^+\) such as 0.0, 0.3, 0.5, 0.7 and 1.0 at a zero-value of \(V_c^-\) were used in the simulations. The variations of four natural frequencies depending on the both parameters of \(V_c^+\) and p are shown in Fig. 8 as 2-D and 3-D plots. As is evident from these plots, the natural frequencies of the simply supported \(\hbox {Al}/\hbox {ZrO}_2\) square thick sandwich plate regardless the position in the frequency spectrum become less sensitive to increasing the metallic phase in the gradation profile with decreasing the volume fraction of ceramic on the top surface. Thus, the concentration of the ceramic constituent is an important factor for the dynamic design of FGM sandwich plates. More detailed studies of the role of different constituents on the modal dynamics of FGM sandwich plates are still needed, but they are out of the scope of this work.
5 Conclusions
The static response and free vibrations of simply supported metal-ceramic FGM square thick sandwich plates have been analyzed by using the three-dimensional finite element modelling with the ABAQUS code. The effective material properties at a plate point were assumed to be defined in accordance with the Mori-Tanaka approach. A power-law variation of the volume fraction of the ceramic phase through-the-thickness of the sandwich plate was adopted. The 3-D brick graded finite element incorporating the variation of material properties in direction of the plate thickness was programmed and, then, was implemented into ABAQUS via the user-defined material subroutine UMAT (the code can be downloaded from http://polonez.pollub.pl/deliverables/). A simple procedure was proposed to estimate an average constant value of the mass density within the graded finite element. The use of this element in predictions turned out to be accurate and very efficient since the graded element unlike the layered model with conventional homogeneous elements neither requires extensive procedure of input data preparation nor fine enough mesh, but it allowed one using the whole power of the ABAQUS code.
With the 3-D graded finite element developed and implemented into ABAQUS, the calculated displacements and stresses in the static analysis and the computed natural frequencies in the free vibration analysis of the FGM sandwich plates have been found to match well the analytic solutions reported in literature. The minor discrepancies between the results of the finite element models and the reference values could be addressed to the problem of non-equivalency of boundary conditions applied to the plate edges between analytic and numerical 3-D modelling procedures. Also, the predictions showed that the deflections and the values of natural frequencies of the FGM sandwich plates are between those for pure ceramic and pure metallic plates. However, the stresses have a nonlinear pattern across the sandwich plate thickness and their variations with increasing the metallic phase have more sophisticated character, especially for the longitudinal stress. The gradients in the material properties affect the natural frequencies of a simply supported square FGM sandwich plate. The values of the natural frequencies with growing the metallic phase tend to those of a pure metallic plate. However, the lower frequencies are less sensitive to the power-law index than the higher ones. It was also found that the mode shapes associated with the frequencies of the thick sandwich plates exhibit not only flexural dominant deformations, but thickness-stretching dominant and extensional dominant deformations as well. Yet, it was found out that the volume fraction of ceramic on the top surface is an important factor for dynamic design of FGM sandwich plates. The predictions demonstrated that the less is the ceramic concentration on the top surface, the less sensitive are the frequencies to increasing the metallic phase in the sandwich core. Finally, it needs to mention that although the present results are demonstrated only for the simply supported metallic-ceramic FGM square sandwich plate, the graded 3-D element developed in this work can be used for the 3-D modelling of sandwich plates with any other geometry, gradation profile and boundary conditions. Thus, the results presented in this paper may provide a benchmark for studying statics and modal dynamics of the FGM sandwich plate by other methods and models.
References
Karlsson KF, Åström BT (1997) Manufacturing and applications of structural sandwich components. Compos Part A 28A:97–111
Altenbach H, Altenbach J, Kissing W (2018) Mechanics of composite structural elements, 2nd edn. Springer Nature, Singapore
Burlayenko VN, Sadowski T (2011) Dynamic analysis of debonded sandwich plates with flexible core: numerical aspects and simulation. In: Altenbach H, Eremeyev VA (eds) Shell-like structures, advanced structured materials 15. Springer, Berlin, pp 415–440
Burlayenko VN, Sadowski T (2011) Numerical modeling of sandwich plates with partially dedonded skin-to-core interface for damage detection. In: De Roeck G et al (eds) Proceedins of the 8th international conference on structural dynamics (EURODYN). Belgium, Leuven, pp 2242–2249
Rinker M, Ratcliffe JG, Adams DO, Kruger R (2013) Characterizing facesheet/core disbonding in honeycomb core sandwich structure. NASA/CR-2013-217959, Langley Research Center, Hampton, Virginia
Burlayenko VN, Sadowski T (2014) Simulations of post-impact skin/core debond growth in sandwich plates under impulsive loading. J Appl Nonlin Dyn 3(4):369–379
Qu Y, Meng G (2017) Nonlinear vibro-acoustic analysis of composite sandwich plates with skin-core debondings. AIAA J 55(5):1723–1733
Idriss M, El Mahi A (2017) Effects of debonding length on the fatigue and vibration behaviour of sandwich composite. J Compos Mater 51(13):1839–1847
Burlayenko VN, Sadowski T (2018) Linear and nonlinear dynamic analyses of sandwich panels with face sheet-to-core debonding. Shock Vib 2018, Article ID 5715863, 16 pages
Szekrényes A (2018) The role of transverse stretching in the delamination fracture of soft core sandwich plates. Appl Math Model 63:611–632
Funari MF, Greco F, Lonetti P (2018) Sandwich panels under interfacial debonding mechanisms. Compos Struct 203:310–320
Seguel F, Meruane V (2018) Damage assessment in a sandwich panel based on full-field vibration measurements. J Sound Vib 417(17):1–18
Miyamoto Y, Kaysser WA, Rabin BH, Kawasaki A, Ford RG (1999) Functionally graded materials design. Processing and applications. Springer, New York
Kanu NJ, Vates UK, Singh GK, Chavan S (2018) Fracture problems, vibration, buckling, and bending analyses of functionally graded materials: a state-of-the-art review including smart FGMs. Particulate Sci Technol (in press)
Sadowski T, Pietras D, Ivanov IV (2014) Estimation of thermal stress intensity factor in a strip with various property gradations subjected to thermal shock. Key Eng Mater 601:71–75
Favata A, Trovalusci P, Masiani R (2016) A multiphysics and multiscale approach for modeling microcracked thermo-elastic materials. Comput Mater Sci 116:22–31
Burlayenko VN, Altenbach H, Sadowski T, Dimitrova SD (2016) Computational simulations of thermal shock cracking by the virtual crack closure technique in a functionally graded plate. Comput Mater Sci 116:11–21
Petrova VE, Schmauder S (2017) Modeling of thermo-mechanical fracture of FGMs with respect to multiple cracks interaction. Phys Mesomech 20:241–249
Pathak H (2017) Three-dimensional quasi-static fatigue crack growth analysis in functionally graded materials (FGMs) using coupled FE-XEFG approach. Theor Appl Fract Mec 92:59–75
Zhang HH, Han SY, Fan LF, Huang D (2018) The numerical manifold method for 2D transient heat conduction problems in functionally graded materials. Eng Anal Bound Elem 88:145–155
Swaminathan K, Sangeetha DM (2017) Thermal analysis of FGM plates: a critical review of various modelling techniques and solution methods. Compos Struct 160:43–60
Ebrahimi F, Rastgo A (2008) An analytical study on the free vibration of smart circular thin FGM plate based on classical plate theory. Thin-Walled Struct 46(12):1402–1408
Tornabene F, Viola E (2009) Free vibration analysis of functionally graded panels and shells of revolution. Meccanica 44:255–281
Vo TP, Thai H-T, Nguyen T-K, Fawad I (2014) Static and vibration analysis of functionally graded beams using refined shear deformation theory. Meccanica 49(1):155–168
Viola E, Rossetti L, Fantuzzi N, Tornabene F (2014) Static analysis of functionally graded conical shells and panels using the generalized unconstrained third order theory coupled with the stress recovery. Compos Struct 112:44–65
Tornabene F, Fantuzzi N, Bacciocchi M (2014) Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories. Compos Part B-Eng 67:490–509
Lashkari MJ, Rahmani O (2016) Bending behavior of sandwich structures with flexible functionally graded core based on high-order sandwich panel theory. Meccanica 51(5):1093–1112
Zenkour AM (2005) A comprehensive analysis of functionally graded sandwich plates: part 2-Buckling and free vibration. Int J Solids Struct 42:5244–5258
Qian LF, Batra RC, Chen LM (2004) Static and dynamic deformations of thick functionally graded elastic plates by using higher-order shear and normal deformable plate theory and meshless local Petrov-Galerkin method. Compos Part B-Eng 35:685–697
Neves AMA, Ferreira AJM, Carrera E, Cinefra M, Roque CMC, Jorge RMN, Soares CMM (2013) Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique. Compos Part B-Eng 44(1):657–674
Zenkour AM (2013) Bending analysis of functionally graded sandwich plates using a simple four-unknown shear and normal deformations theory. J Sandwich Struct Mater 15:629–656
Fantuzzi N, Brischetto S, Tornabene F, Viola E (2016) 2D and 3D shell models for the free vibration investigation of functionally graded cylindrical and spherical panels. Compos Struct 154:573–590
Van Do VN, Lee C-H (2018) Quasi-3D higher-order shear deformation theory for thermal buckling analysis of FGM plates based on a meshless method. Aerosp Sci Technol 82–83:450–465
Vel SS, Batra RC (2002) Exact solution for thermoelastic deformations of functionally graded thick rectangular plates. AIAA J 40(7):1421–1432
Reddy JN, Cheng Z-Q (2003) Frequency of functionally graded plates with three-dimensional asymptotic approach. J Eng Mech 129(8):896–900
Vel SS, Batra RC (2004) Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J Sound Vib 272:703–730
Li Q, Iu VP, Kou KP (2008) Three-dimensional vibration analysis of functionally graded material sandwich plates. J Sound Vibr 311(1–2):498–515
Alibeigloo A, Liew KM (2014) Free vibration analysis of sandwich cylindrical panel with functionally graded core using three-dimensional theory of elasticity. Compos Struct 113:23–30
Brischetto S, Tornabene F, Fantuzzi N et al (2016) 3D exact and 2D generalized differential quadrature models for free vibration analysis of functionally graded plates and cylinders. Meccanica 51:2059–2098
Awrejcewicz J, Kurpa L, Shmatko T (2017) Analysis of geometrically nonlinear vibrations of functionally graded shallow shells of a complex shape. Lat Am J Solids Struct 14:1648–1668
Rajasekaran S, Tochaei EN (2014) Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-order. Meccanica 49:995–1009
Ghazaryan D, Burlayenko VN, Avetisyan A, Bhaskar A (2018) Free vibration analysis of functionally graded beams with non-uniform cross-section using the differential transform method. J Eng Math 110:97–121
Ramu I, Mohanty SC (2014) Modal analysis of functionally graded material plates using finite element method. Proc Mater Sci 6:460–467
Zhang Z, Paulino GH (2007) Wave propagation and dynamic analysis of smoothly graded heterogeneous continua using graded finite elements. Int J Solids Struct 44(11–12):3601–3626
Asemi K, Salehi M, Akhlaghi M (2015) Three dimensional graded finite element elasticity shear buckling analysis of FGM annular sector plates. Aerosp Sci Technol 43:1–13
Santare MH, Thamburaj P, Gazonas GA (2003) The use of graded finite elements in the study of elastic wave propagation in continuously nonhomogeneous materials. Int J Solids Struct 40(21):5621–5634
ABAQUS User’s manual, ver. 2016 (2016) Dassault Systémes Simulia Corp., Providence, RI, USA
Reinoso J, Blázquez A (2016) Geometrically nonlinear analysis of functionally graded power-based and carbon nanotubes reinforced composites using a fully integrated solid shell element. Compos Struct 152:277–294
Buttlar WG, Paulino GH, Song SH (2006) Application of graded finite elements for asphalt pavements. J Eng Mech 132(3):240–248
Burlayenko VN (2016) Modelling thermal shock in functionally graded plates with finite element method. Adv Mater Sci Eng 2016, Article ID 7514638, 12 pages
Burlayenko VN, Altenbach H, Sadowski T, Dimitrova SD, Bhaskar A (2017) Modelling functionally graded materials in heat transfer and thermal stress analysis by means of graded finite elements. Appl Math Model 45:422–438
Mars J, Koubaa S, Wali M, Dammak F (2017) Numerical analysis of geometrically non-linear behavior of functionally graded shells. Lat Am J Solids Struct 14(11):1952–1978
Shiyekar SM, Lavate P (2015) Flexure of power law governed functionally graded plates using ABAQUS UMAT. Aerosp Sci Technol 46:51–59
Timoshenko S, Goodier JN (1970) Theory of elasticity. McGraw-Hill, New York
Bathe KJ, Wilson EL (1977) Numerical methods in finite element analysis. Prentice-Hall, Englewood Cliffs
Naumenko K, Altenbach H, Huang C-X, Burlayenko V (2001) Influence of the element type on the accuracy of creep–damage predictions in thin-walled structures. In: Proceedings of the European conference on computational mechanics (ECCM-3) June 26-29, 2001, Cracow, Poland
Tornabene F, Brischetto S, Fantuzzi N, Bacciocchi M (2016) Boundary conditions in 2D numerical and 3D exact models for cylindrical bending analysis of functionally graded structures. Shock Vibr 2016, Article ID 2373862, 17 pages
Acknowledgements
The authors would like to mention that this research has been done within the POLONEZ 2 Project, Grant Agreement No. UMO-2016/21/P/ST8/00790, supported by the National Science Centre of Poland within the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 665778.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Burlayenko, V.N., Sadowski, T. Free vibrations and static analysis of functionally graded sandwich plates with three-dimensional finite elements. Meccanica 55, 815–832 (2020). https://doi.org/10.1007/s11012-019-01001-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-019-01001-7