1 Introduction

The dynamics of pipes with flow have been studied intensively for over half a century [1]. The reasons for these studies include the practical importance of the problem—that is, they are widely used in various installations, cooling systems, pipelines, ocean mining—and also to collect knowledge that may be useful in other areas of fluid–structure interactions [2]. Moreover, numerous studies are related to the dynamics of fluid-conveying carbon nanotubes, whose nanostructural size poses non-classical mechanical problems which need to be solved to apply CNTs in, for example, gas storage or drug delivery [3, 4].

When the flow velocity inside the cantilever pipe exceeds the so-called critical value, self-excited flutter vibrations arise. This behavior is specific to cantilever pipes; that is, pipes which are supported at both ends are prone to a buckling type of instability [5]. This phenomenon can be observed in our daily life. For example, when a strong stream of water flows inside a garden hose, its free end makes a snake-like motion on the grass. These kind of systems are prone to changes of their physical parameters and to the introduction of new effects. For example, an effect of a viscous damping or a lumped mass attached to the pipe can both stabilize or destabilize the system, depending on the values of its parameters [6, 7]. Recently, the applications of functionally graded materials are investigated to enhance stability of fluid-conveying pipes [8, 9]. Moreover, the destabilizing effect of damping has also attracted attention of the researchers, due to its positive impact on devices used for energy harvesting [10].

Imbrahim’s [1] article lists over 30 research papers related to the control of fluid-conveying pipes. The vast majority of them describe the concept of generating transverse forces or bending moments acting on the system actively, depending on the state of the system in a closed feedback loop. Various actuators have been used to do this, some examples include servomotors stuck to a pipe [11,12,13], gyroscopic mechanisms [14], and piezoelements mounted on a pipe surface [15, 16] or embedded in its material [17]. A few of these papers aim at more general results, and the type of the actuator is not defined [18, 19].

A significant disadvantage of active methods is their ability to destabilize the system when a failure happens because the external action of forces or moments can put additional energy into the system. Thus, it is proposed to use a semi-active method that is based on an eddy-current damper, a.k.a. the motional (Lorentz) type of electromagnetic device. In numerous applications of structural control, the employment of the semi-active devices provided a good balance between the performance and robustness [20,21,22,23,24,25,26], reducing the amount of consumed energy compared to the active actuators.

The considered eddy-current damper consists of a conducting plate that moves within a perpendicular and (approximately) constant magnetic field as, for example, in an analogue electricity meter. As a consequence of the Lenz law, this motion generates eddy currents in the plate and a drag force that is approximately linear function of the plate’s velocity. Therefore, they are viscous-type dampers. The damping coefficient depends on the size of the plate and the induction of the magnetic field [27]. These devices were considered for use in vehicle suspension systems [28] and also to reduce the lateral vibrations of a rotating shaft [29]. They are contact-less, so they do not disturb the dynamics of the pipe, apart from introducing an additional mass. Moreover, they allow incorporating a control strategy in a convenient way—by changes of the voltage supplied to the actuators. Such actuators are reported to be usually more effective than the dampers of another popular category, i.e. transformer devices [30, 31], which showed mediocre effectiveness when applied for the passive stabilization of a pipe with flow [32]. Their numerous advantages make us believe that the obtained results may find other applications involving vibration suppression, which are not necessarily related to the pipes with flow.

In the present work, the idea of using eddy-current dampers for the semi-active control of a fluid-conveying pipe is evaluated. The idea has been initially studied by the present authors in [33], where they developed the model of the system and by means of numerical simulations demonstrated a general stabilizing performance of an open-loop switched control. In this work, a robust state-feedback control that aims at improving the stability of the system with the optimal state’s convergence measure is designed and validated experimentally. For that purpose the structure of the control acting as a solution to a convergence-related finite-horizon optimal control problem is investigated. Based on this structure, a parameterized state-dependent control function is constructed. The selection of the control function’s parameters is made based on the solution to the suboptimal control problem concerned with the assumed convergence measure. The efficiency and robustness of the designed controller are verified experimentally in a vast range of flow velocities. The experiments are conducted on a specially designed and manufactured test stand.

2 Mathematical model

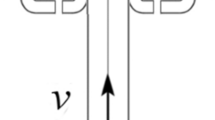
The dynamic behavior of a vertical pipe conveying fluid, which has its lower end mounted in a clamped configuration, see Fig. 1, is going to be studied. The electromagnetic devices of the motional type are attached at a selected position along the pipe. A general description of the dynamics of fluid-conveying pipes involves complex non-linear modeling, see, for example, [34, 35]. In this work, it is assumed that the pipe is slender and is subjected to small lateral oscillations in the plane of symmetry \(\xi -w\). Therefore, the linear Bernoulli–Euler model is valid. The selection of the linear model is also motivated by the needs of our control design. As will be demonstrated, the assumed model allows characterizing the bang–bang structure of the optimal open-loop stabilizing controls (see Sect. 4.1). This in turn enables choosing an appropriate state-dependent function for the suboptimal closed-loop controller (Sect. 4.2). The assumed linear structure’s model also allows building the computationally efficient optimization procedure (Sect. 4.3).

Fig. 1
figure 1

Schematic of the examined system: a standing cantilever pipe conveying fluid together with electromagnetic devices of motional type

Full size image

Let \(w=w(\xi ,t)\) stand for the pipe’s horizontal deflection. A viscous-type internal damping is considered. The gravity force acting downwards is taken into consideration. The mass of the actuators is included in a lumped form, however their rotatory inertia is disregarded in this study. The so called plug flow model is employed. This means that the flow velocity is constant across every cross-section that is perpendicular to the longitudinal axis of the pipe.

The resultant equation of the dynamics of the pipe is as follows

$$\begin{aligned}&EI \frac{\partial ^4 w}{\partial \xi ^4} + E^{*}I \frac{\partial ^5 w}{\partial \xi ^4 \partial t} \\&\quad + \left[ m_f v^2 + \left( m+m_f \right) \left( L-\xi \right) g + \mathbf {1}_{[0,\xi _a]}M_ag \right] \frac{\partial ^2 w}{\partial \xi ^2} \\&\quad + 2 m_f v \frac{\partial ^2 w}{\partial \xi \partial t} - \left( m + m_f + M_a\delta _a \right) g \frac{\partial w}{\partial \xi } \\&\quad + C \left( B_1^2 + B_2^2 \right) \delta _a \frac{\partial w}{\partial t} + \left( m + m_f + M_a\delta _a \right) \frac{\partial ^2 w}{\partial t^2} = 0,\end{aligned}$$
(1)

where L is the pipe’s length, EI and \(E^{*}I\)—the bending stiffness and bending damping of the pipe, m and \(m_f\)—the masses (per unit length) of the pipe and the fluid, \(M_a\)—the mass of the actuators attached at the distance \(\xi _a\) from the pipe’s support, v—the flow velocity, C—the constant of the viscous damping force generated by the actuators, \(B_1\) and \(B_2\)—the magnetic inductions in the electromagnets’ circuits, g—the gravitational acceleration, \(\delta _a\)—the Dirac delta function concentrated at \(\xi _a\), and \(\mathbf {1}_{[0,\xi _a]}\)—the indicator function over the interval \([0,\xi _a]\).

The clamped support leads to the following boundary conditions

$$\begin{aligned} w\Big \vert _{\xi =0}&= \frac{\partial w}{\partial \xi }\bigg \vert _{\xi =0} = \bigg ( EI \frac{\partial ^2 w}{\partial \xi ^2} + E^{*}I \frac{\partial ^3 w}{\partial \xi ^2 \partial t } \bigg )_{\xi =L} \\&= \bigg ( EI \frac{\partial ^3 w}{\partial \xi ^3} + E^{*}I \frac{\partial ^4 w}{\partial \xi ^3 \partial t} \bigg )_{\xi =L} = 0.\end{aligned}$$
(2)

Equation (1), the same as the equation used by the authors in the numerical study [33], is similar to the equation that was validated in [36]. What sets them apart is an incorporation of internal damping in the pipe and, obviously, the effect of the actuators—their mass and the drag force. Note that the flutter is a result of two opposite effects generated by the flow: the inertial force of the moving fluid \(m_fv^2\partial ^2 w/\partial \xi ^2\), which destabilizes the system, and the Coriolis force \(2m_fv\partial ^2 w/\partial \xi \partial t\), which exerts a damping effect.

To reduce the frequency of vibrations, the inertia of the system is increased by adding mass M at distance \(\xi _M\) from the support. Moreover, the pipe is restrained by a thread at location \(\xi _t\), so that the vibrations are planar, similar to [6, 37]. The additional mass is modeled analogously as the actuators, whereas the thread is treated as a linear spring of stiffness \(k_t\). The appropriate terms were incorporated into Eq. (1), yet they are not presented here to make the equation clearer.

The constant determining the viscous drag amounts to \(C = \sigma h S \left( \alpha _1 + \alpha _2 \right) \), where \(\sigma \) is the electric conductivity of the plate, h—the plate’s thickness, S—the cross-sectional area of the magnetic flux that crosses perpendicularly the plate (by assumption, the flux remains constant over the area of the plate during the vibrations), and \(\alpha _1,\, \alpha _2\)—the constants that depend on the size of the plate and the cross-section of the magnetic flux, see [27].

The control is going to be designed using a discretized system represented by a set of ordinary differential equations. Assume an approximate solution to the partial equation (1) in the form of a linear combination of cantilever’s eigenfunctions

$$\begin{aligned} w(\xi ,t)&= \sum _{j=1}^{n} W_j(\xi )Y_j(t), \end{aligned}$$
(3)
$$\begin{aligned} W_j(\xi )&= C_j \Big [ \cosh \frac{\lambda _j}{L}\xi - \cos \frac{\lambda _j}{L}\xi \nonumber \\&+ \frac{\sin \lambda _j - \sinh \lambda _j}{\cos \lambda _j + \cosh \lambda _j} \Big ( \sinh \frac{\lambda _j}{L}\xi - \sin \frac{\lambda _j}{L}\xi \Big ) \Big ], \end{aligned}$$
(4)

where \(\lambda _j\) are the consecutive roots of the characteristic equation \(\cos \lambda \cosh \lambda =-1\), and \(C_j\)—the constants that normalize the modal shapes with respect to the norm generated by the scalar product \(\int _0^L W_iW_j\). Applying the Galerkin procedure, a set of \(\,n\,\) second-order ODE’s for the vector of unknown generalized coordinates \(\,\mathbf {Y} = \left( Y_i \right) _{n \times 1}\,\) is obtained

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {Y}} + \left( \mathbf {D} + v\mathbf {D_{Cor}} + u\mathbf {D_{act}} \right) \dot{\mathbf {Y}} + \left( \mathbf {S} + v^2\mathbf {S_{in}} \right) \mathbf {Y} = \mathbf {0}, \end{aligned}$$
(5)

where \(\,\mathbf {M} = \big ( (m+m_f)\delta _{ij} + M_a W_i(\xi _a)W_j(\xi _a) \big )_{n \times n}\,\) is the mass matrix; \(\mathbf {D} = \big ( ( E^{*}I (\lambda _j/L)^4 \delta _{ij}\big )_{n \times n}\)—the structural damping matrix; \(\mathbf {D_{Cor}} = \big ( 2 m_f d_{ij} \big )_{n \times n}\)—the matrix that characterizes the effect of the Coriolis force; \(\,\mathbf {D_{act}} = \big ( CW_i(\xi _a)W_j(\xi _a) \big )_{n \times n}\)—the matrix describing the influence of the actuators; \(\mathbf {S} = \big ( EI (\lambda _j/L)^4 \delta _{ij} + \left( m+m_f \right) g b_{ij} + M_a g c_{ij} - \left( m+m_f \right) g d_{ij} - M_a g W_i(\xi _a)W_j'(\xi _a) \big )_{n \times n}\)—the structural stiffness matrix; \(\mathbf {S_{in}} = \big ( m_f a_{ij} \big )\)—the matrix characterizing the inertia of the moving fluid, \(\,a_{ij}=\int _0^L W_i W_j''\,\), \(\,b_{ij}=\int _0^L (L-\xi ) W_i W_j''\,\), \(\,c_{ij}=\int _0^L \mathbf {1}_{[0,\xi _a]} W_i W_j''\,\), \(\,d_{ij}=\int _0^L W_i W_j'\,\); and \(\delta _{ij}\) is Kronecker’s delta. The control variable u amounts to the sum of the squares of the inductions,

$$\begin{aligned} u=B_1^2+B_2^2, \quad u \in [0,u_{max}] \quad {\text {for}}\,{\text {all}}\ t. \end{aligned}$$
(6)

Reduce now the order of the problem by the substitution \(\,x_i=Y_i,\, x_{n+i}=\dot{Y_i},\,i=1,2,\ldots ,n\) and gather the variables into the vector \(\, \mathbf {x} = \left( x_i \right) _{2n \times 1}\). The dynamics of the control system are governed by the first-order bilinear differential equation

$$\begin{aligned} \dot{\mathbf {x}}(t)=\mathbf {A}\,\mathbf {x}(t)+u(t)\,\mathbf {B}\,\mathbf {x}(t)\, ,\,\,\mathbf {x}(0)=\mathbf {x}^0 \ne \mathbf {0}, \end{aligned}$$
(7)

where the following matrices allow us to separate the effects of the moving fluid and of the electromagnetic forces:

$$\begin{aligned} \mathbf {A}&= \begin{pmatrix} \mathbf {0} &{} \mathbf {I} \\ -\mathbf {M}^{-1} \left( \mathbf {S} - v^2\,\mathbf {S_{in}} \right) &{} - \mathbf {M}^{-1} \left( \mathbf {D} - v\,\mathbf {D_{Cor}}\right) \\ \end{pmatrix}, \end{aligned}$$
(8)
$$\begin{aligned} \mathbf {B}&= \begin{pmatrix} \mathbf {0} &{} \mathbf {0} \\ \mathbf {0} &{} - \mathbf {M}^{-1} \mathbf {D_{act}} \\ \end{pmatrix}. \end{aligned}$$
(9)

It has been found that \(n=10\) base functions are sufficient to describe the dynamics of the pipe, while keeping the number of equations reasonably low for efficient optimization.

3 Dynamic properties

3.1 The transition to flutter

Begin with the analysis of the situation when eddy-current dampers are absent. In time zero the pipe is deflected in the first cantilever mode. Figure 2 shows the phenomena that occur when the flow velocity is increased. When \(v=0\) the system oscillates like a vertically standing cantilever beam (a). For \(v>0\) two opposite phenomena occur. The Coriolis acceleration of the moving fluid generates force which impedes lateral motion of the pipe, and the inertia of the fluid leads to the centrifugal force which destabilizes the pipe. The former is a linear function of the flow velocity, whereas the latter depends on the square of it. Thus, the Coriolis effect dominates at low flows (b). For higher values of the flow velocity the inertial force dominates. This brings about a greater frequency of the vibrations and their weaker suppression. For v equal to the critical value (here \(347.12\hbox { m/s}\)) the system oscillates at a constant amplitude (c). When the flow is increased beyond \(v^{\mathrm {cr}}\), the straight equilibrium looses stability, and a small disturbance results in exponentially growing vibrations (d). Note that in reality the amplitude of these vibrations is restricted by geometrical and material non-linearities. However, this behavior is not captured by the linear model that is used, in which once the flow reaches the overcritical region, the amplitude starts growing boundlessly. Still, this simplified model is sufficient for developing the control strategy.

Fig. 2
figure 2

Arising of the flutter for the system without the actuators: a\(v=0\), b\(v=200\hbox { m/s}\), c\(v=v^{\mathrm {cr}}=347.12\) m/s, d\(v=347.5\hbox { m/s}\)

Full size image

Note that the effect of Coriolis acceleration was studied by Sugiyama et al. [38], who actively controlled the flow velocity in the pipe to suppress its lateral vibrations.

In the subsequent sections, the performance of the proposed control method is going to be studied in three cases: (A) no flow; (B) moderate flow, when the Coriolis damping dominates; and, (C) the flow just beneath the critical value, when inertia of the moving fluid significantly affects the dynamics of the pipe.

Now the dynamics of the pipe with the eddy-current dampers attached to it is going to be discussed. Figure 3 illustrates the effects of their location on the pipe \(\xi _a/L\) and the control \(u=B_1^2+B_2^2\) on the critical flow. The horizontal dashed line shows the critical flow velocity of the system without the actuators (\(v^{\mathrm {cr}}=347.12\hbox { m/s}\)). The solid line for \(u=0\) demonstrates the influence of the additional mass of the plates, which may both stabilize the system and decrease the critical flow, which is in accordance with [7]. The voltage supplied to the motional devices generates viscous damping that emphasizes this effect, see the lines for \(u>0\). Even low values of the magnetic field are able to improve the stability of the system. For example, assuming \(B_1=B_2=0.2\hbox { T}\), \(v_{0.08}^{\mathrm {cr}}=433.27\hbox { m/s}\) is obtained, which is approximately 25% greater than the reference level and 10% greater than \(v_{0}^{\mathrm {cr}}\).

Fig. 3
figure 3

Critical flow velocity \(v^{\mathrm {cr}}\) as a function of the actuators’ position \(x_a/L\) for selected values of the control input

Full size image

The control method will be evaluated for systems with actuators attached at \(\xi _a=0.6L\), where their efficiency is the highest, and for locations \(\xi _a=0.4L\) and \(\xi _a=0.8L\) to compare.

Note that the influence of the external damping greatly depends on the medium which flows throughout the pipe. It was shown many years ago that if the mass ratio of the fluid to the pipe is high, then increasing the external damping may actually destabilize the system [36]. Indeed, if water was used instead of air as a moving fluid, then high values of induction could lead to a decrease of the critical flow for the actuators attached relatively far from the support, see Fig. 4. This justifies the use of controllable devices for the stabilization purpose (instead of, for example, permanent magnets) because this system is adaptable to changes of working conditions. However, our experiments have been performed only with air because the use of water would require significant modifications of the test stand.

Fig. 4
figure 4

Critical flow velocity \(v^{\mathrm {cr}}\) as a function of the control variable \(u=B_1^2+B_2^2\) for selected positions of the actuators; a air and b water as a moving fluid

Full size image

3.2 The energy of the pipe

Write \(\mathbf {W}(\xi ) = \big [ W_1(\xi ),\ldots ,W_n(\xi ) \big ]^{\mathrm {T}}\), \(\mathbf {x_{I}} = \left[ x_1,\ldots ,x_n \right] ^{\mathrm {T}}\) and \(\mathbf {x_{II}} = \left[ x_{n+1},\ldots ,x_{2n} \right] ^{\mathrm {T}}\). The following formula defines the elastic (strain) energy of the pipe:

$$\begin{aligned} v^{\mathrm {pipe}}_{\mathrm {e}}(t)&= \int _0^L \frac{1}{2} EI \bigg ( \frac{\partial ^2 w}{\partial \xi ^2}(\xi ,t) \bigg )^2 \mathrm {d}\xi \\&= \frac{1}{2} EI \mathbf {x_{I}}^{\mathrm {T}}(t) \int _0^L \mathbf {W''}(\xi )\mathbf {W''}(\xi )^{\mathrm {T}} \mathrm {d}\xi \mathbf {x_{I}}(t) \\&= \frac{1}{2} \mathbf {x}^{\mathrm {T}}(t)\mathbf {Q}\mathbf {x}(t).\end{aligned}$$
(10)

Here, the energy matrix

$$\begin{aligned} \mathbf {Q} = \begin{bmatrix} EI \int _0^L \mathbf {W''}\mathbf {W''}^{\mathrm {T}}&\mathbf {0} \\ \mathbf {0}&\mathbf {0} \\ \end{bmatrix} \end{aligned}$$
(11)

is symmetric and positive semidefinite. A thorough description of the mechanical energy of the pipe with flow is complex, because it requires terms related to that flow (the analyzed system is not just the pipe, but a part of the space limited by it), see for example [5]. However, is has been found that the pipe’s potential energy allows finding a control method that works well. The stability of the system and the performance of the optimal control can be fairly justified using the potential energy.

4 Controller design

A typical approach to designing an optimal stabilizing controller for a vibrating structure described by the bilinear system as (7) is based on solving a finite horizon optimal control problem (see [21, 39]). The resulting control function is given in an open-loop form and it has a switched structure. The time instants of the control switches have been shown to be highly sensitive to a change of the model’s parameters (see for example [40]). Therefore, the use of the open-loop control is rather limited to perfectly identified systems with predictable excitation. Given that the information of the flow parameters may not be accessible, a closed-loop controller that provides a fair stabilizing performance for a wide range of flow velocity and based on an easy for implementation state-feedback loop is designed. In particular, a state-feedback control function \(u=u^*(\mathbf {x})\) that stabilizes the system (7) at the equilibrium \(\mathbf {x}=0\) with an optimal convergence measure is going to be found. First, the structure of the open-loop optimal control \(u=u^*(t)\) that minimize the convergence-related objective functional is recalled. Next, a parameterized state-feedback function \(u(\mathbf {x})\) that mimics the structure of the optimal open-loop solution \(u^*(t)\) is defined. For the optimal state-feedback control \(u^*(\mathbf {x})\), the solution to a suboptimal problem that establishes the selection of the parameters in the function \(u(\mathbf {x})\) is used.

4.1 Open-loop optimal control problem

Recall that \(\mathbf {Q}\) is the matrix that by the formula \(\mathbf {x}^T(t) \mathbf {Q} \mathbf {x}(t)\) characterizes the energy of the system (7) at time t. By selecting the time horizon \(T>0\), the problem of stabilization of (7) with the optimal convergence rates can be formulated as follows:

$$\begin{aligned}&\text{ Find }u(t)^*=\text{ argmin }\,J=\frac{1}{2}\int _0^{T} \mathbf {x}^T \mathbf {Q} \mathbf {x}\,\text{ d }t \\&\text{ Subject } \text{ to }\,\,\,\,\dot{\mathbf {x}}(t)=\mathbf {A}\,\mathbf {x}(t)+u(t)\,\mathbf {B}\,\mathbf {x}(t)\, ,\,\,\mathbf {x}(0)=\mathbf {x}^0\, ,\\& u(t) \in [0,u_{max}].\end{aligned}$$
(12)

The problem (12) is classified as a finite horizon bilinear optimal control problem. If the objective functional J does not explicitly dependent on the controls and the set of admissible controls is compact, then the solution to a bilinear optimal control problem is given by controls of the switching type (see [41]). This result follows immediately from the Pontryagin Maximum Principle [42]. Next, the key steps are going to be demonstrated.

Introduce now the adjoint state H and the Hamiltonian \(\mathbf {p}\) which are, respectively, defined by

$$\begin{aligned} H(\mathbf {x},\mathbf {p},u) = \mathbf {p}^T \left( \mathbf {A}\,\mathbf {x}+u\,\mathbf {B}\,\mathbf {x} \right) -\frac{1}{2} \mathbf {x}^T\,\mathbf {Q}\,\mathbf {x} \end{aligned}$$
(13)

and

$$\begin{aligned} \dot{\mathbf {p}}(t)=-\frac{\partial H}{\partial \mathbf {x}}\, ,\,\,\,\,\,\mathbf {p}(T)=0. \end{aligned}$$
(14)

Then, the Pontryagin Maximum Principle states that the solution to the problem (12) satisfies

$$\begin{aligned} u^*=\text{ argmax }_{u \in [0,u_{max}]} H(\mathbf {x},\mathbf {p},u). \end{aligned}$$
(15)

From (15) the switching law for the optimal controls is obtained

$$\begin{aligned} u^*(t)= \left\{ \begin{array}{ll} u_{max},\quad &{}\mathbf {p}^T(t)\,\mathbf {B}\,\mathbf {x}(t) > 0 \\ 0,\quad &{}\mathbf {p}^T(t)\,\mathbf {B}\,\mathbf {x}(t) < 0 \\ \text{ undetermined,}\quad &{}\mathbf {p}^T(t)\,\mathbf {B}\,\mathbf {x}(t) = 0 \\ \end{array} \right. \ \ . \end{aligned}$$
(16)

To determine the trajectory of \(u^*(t)\), one has to solve the Two-Point Boundary Value Problem consisting of (7), (14) and (16). Shooting [43] and relaxation [44] methods can be applied for this purpose.

4.2 State-feedback suboptimal control problem

Because our aim is to design the closed-loop control \(u^*(\mathbf {x})\) that mimics the solution to the open-loop problem (12), a state-feedback approximation of the switching law as given by (16) is going to be introduced. First, the following constants are introduced:

$$\begin{aligned} c_1=u_{max}/2\, ,\,\,\,c_2=u_{max}/ \pi \end{aligned}$$
(17)

and \(n \times n\) matrix \(\mathbf {K} \in \mathcal {K}\), where the set \(\mathcal {K}\) is defined by

$$\begin{aligned} \mathcal {K}=\left\{ [k_{ab}]: -k_{max} \le k_{ab} \le k_{max}\, ,\,\,\,k_{max}>0 \right\} . \end{aligned}$$
(18)

For the control function, the following state-feedback structure is assumed:

$$\begin{aligned} u(\mathbf {x})=c_1+c_2\,\text{ arctan }\left( \mathbf {x}^T \mathbf {K} \mathbf {x}\right) . \end{aligned}$$
(19)

The reader can verify that the selection of the constants \(c_1\) and \(c_2\) ensures the admissibility condition (6). Moreover, for a sufficiently large value of the quadratic term \(\mathbf {x}^T \mathbf {K} \mathbf {x}\) (positive or negative), the control \(u(\mathbf {x})\) operates near the extreme admissible values (\(u_{max}\) or 0) and, therefore, approximates the desired switching structure (16).

By relying on the control structure (19), our goal is to find matrix \(\mathbf {K}\) such that the closed-loop system

$$\begin{aligned} \dot{\mathbf {x}} &= \mathbf {A}\,\mathbf {x}+\left( c_1+c_2\,\text{ arctan }\left( \mathbf {x}^T \mathbf {K} \mathbf {x}\right) \right) \,\mathbf {B}\,\mathbf {x}\, ,\\&\mathbf {x}(0)=\mathbf {x}^0\end{aligned}$$
(20)

is stabilized with an optimal convergence rate. As in the case of the problem (12), the energy \(\mathbf {x}^T(t) \mathbf {Q} \mathbf {x}(t)\) as the measure of the state convergence is chosen. The following suboptimal control problem is considered:

$$\begin{aligned}&\text{ Find }\,\,\,\,\mathbf {K}^*=\text{ argmin }\,J=\frac{1}{2}\int _0^{T} \mathbf {x}^T \mathbf {Q} \mathbf {x}\,\text{ d }t \\&\text{ Subject } \text{ to }\,\,\,\,\dot{\mathbf {x}}=\mathbf {A}\,\mathbf {x}+\left( c_1+c_2\,\text{ arctan }\left( \mathbf {x}^T \mathbf {K} \mathbf {x}\right) \right) \,\mathbf {B}\,\mathbf {x}\, , \\&\mathbf {x}(0)=\mathbf {x}^0\, ,\,\, \mathbf {K} \in \mathcal {K}.\end{aligned}$$
(21)

The desired control \(u^*(\mathbf {x})\) is then given by (19), where \(\mathbf {K}=\mathbf {K}^*\). The existence of the solution to (21) follows from Filippov theorem, compactness of the set \(\mathcal {K}\) and continuity of the objective functional J (for details see [45]).

4.3 Solution to the problem (21)

To solve the problem (21), an iterative algorithm that is based on the method of steepest descent is developed. First, the relevant derivatives corresponding to the directions of the descent for the decision parameter; that is for matrix \(\mathbf {K}\), are estimated.

By introducing the Hamiltonian

$$\begin{aligned} H(\mathbf {x},\mathbf {p},\mathbf {K}) &= \mathbf {p}^T \left( \mathbf {A}\,\mathbf {x}+\left( c_1+c_2\,\text{ arctan }\left( \mathbf {x}^T\,\mathbf {K}\,\mathbf {x}\right) \right) \mathbf {B}\,\mathbf {x} \right) \\&-\frac{1}{2} \mathbf {x}^T\,\mathbf {Q}\,\mathbf {x}\end{aligned}$$
(22)

and the adjoint state \(\mathbf {p}=\mathbf {p}(t)\) given by

$$\begin{aligned} \dot{\mathbf {p}}&= -\frac{\partial H}{\partial \mathbf {x}}=-\mathbf {A}^T \mathbf {p}-\left( c_1+c_2\,\text{ arctan }\left( \mathbf {x}^T \mathbf {K} \mathbf {x}\right) \right) \mathbf {B}^T \mathbf {p} \\&- c_2\,\mathbf {p}^T \mathbf {B} \mathbf {x}\,\frac{\left( \mathbf {K}+\mathbf {K}^T\right) \mathbf {x}}{\left( \mathbf {x}^T\,\mathbf {K}\,\mathbf {x}\right) ^2+1} + \mathbf {Q} \mathbf {x}\, ,\,\,\,\mathbf {p}(T)=0.\end{aligned}$$
(23)

the objective functional in (21) can be represented by

$$\begin{aligned} J = \int _{0}^{T} \left( \mathbf {p}^T\,\dot{\mathbf {x}} - H(\mathbf {x},\mathbf {p},\mathbf {K})\right) \text{ d }t. \end{aligned}$$
(24)

An infinitesimal change \(\text{ d }\mathbf {K}\) causes variations of the functions \(\delta \mathbf {x}\), \(\delta \dot{\mathbf {x}}\), \(\delta \mathbf {p}\), which implies the following differential of the objective functional

$$\begin{aligned} \text{ d } J &= \int _{0}^{T} \left( - \frac{\partial H}{\partial \mathbf {K}}\,\text{ d }\mathbf {K} - \left( \frac{\partial H}{\partial \mathbf {x}} \right) ^T \delta \mathbf {x} \right) \, \text{ d } t \\&+ \int _{0}^{T} \left( \mathbf {p}^T \delta \dot{\mathbf {x}} + \left( \dot{\mathbf {x}} - \frac{\partial H}{\partial \mathbf {p}} \right) ^T \delta \mathbf {p} \right) \, \text{ d } t .\end{aligned}$$
(25)

The last term in (25) vanishes because

$$\begin{aligned} \dot{\mathbf {x}} = \frac{\partial H}{\partial \mathbf {p}}. \end{aligned}$$
(26)

Under the assumption

$$\begin{aligned} \delta \dot{\mathbf {x}} = \frac{d}{dt}\left( \delta \mathbf {x} \right) \end{aligned}$$
(27)

an integration by parts yields

$$\begin{aligned} \text{ d } J &= -\int _{0}^{T} \frac{\partial H}{\partial \mathbf {K}}\,\text{ d }\mathbf {K} \, \text{ d } t \\&-\int _{0}^{T} \left( \dot{\mathbf {p}} + \frac{\partial H}{\partial \mathbf {x}} \right) ^T \delta \mathbf {x}\, \text{ d } t + \left( \mathbf {p}^T \delta \mathbf {x} \right) _{0}^{T}.\end{aligned}$$
(28)

From (23), it can be observed that

$$\begin{aligned} \dot{\mathbf {p}} + \frac{\partial H}{\partial \mathbf {x}}=0\, ,\,\,\,\mathbf {p}(T)=0. \end{aligned}$$
(29)

Moreover, the initial condition in (7) implies \(\delta \mathbf {x}(0)=0\). Therefore, the two last terms in (28) vanish and, eventually, one obtains

$$\begin{aligned} \text{ d } J = - \int _{0}^{T} \frac{\partial H}{\partial \mathbf {K}}\,\text{ d }\mathbf {K} \, \text{ d } t. \end{aligned}$$
(30)

Finally, the derivative of the objective functional with respect to \(\mathbf {K}\) is given by

$$\begin{aligned} \frac{\text{ d }J}{\text{ d }\mathbf {K}} = - \int _{0}^{T} \frac{\partial H}{\partial \mathbf {K}}\, \text{ d } t= - c_2 \int _{0}^{T} \mathbf {p}^T\,\mathbf {B}\,\mathbf {x}\,\frac{\mathbf {x}\,\mathbf {x}^T}{{\left( \mathbf {x}^T\,\mathbf {K}\,\mathbf {x}\right) ^2+1}}\, \text{d} t. \end{aligned}$$
(31)

To guarantee that the matrix \(\mathbf {K}\) belongs to the admissible set 18, the following projection is introduced

$$\begin{aligned} \text{ Proj }(\mathbf {K})=[k_{ab}]: {\left\{ \begin{array}{ll} k_{ab}\,\,\,\,\,\text{ if }\,\,\,\,\,-k_{max} \le k_{ab} \le k_{max}\, ,\\ -k_{max}\,\,\,\,\,\text{ if }\,\,\,\,\,k_{ab}<-k_{max}\, ,\\ k_{max}\,\,\,\,\,\text{ if }\,\,\,\,\,k_{ab}>k_{max}.\\ \end{array}\right. } \end{aligned}$$
(32)

Assuming the maximal number of iterations \(l_{max}\), the matrix \(\mathbf {K}\) will be updated by using the following sequence:

$$\begin{aligned} \mathbf {K}^{l+1} &= \text{ Proj }\left( \mathbf {K}^{l}- \gamma \,\left( \frac{\text{ d }J}{\text{ d }\mathbf {K}} \right) \right) \, ,\\&\,\,\gamma >0\, ,\,\,\,l=0,1,\ldots ,l_{max}.\end{aligned}$$
(33)

The optimization algorithm is composed of the following steps:

  1. 1.

    Set \(l=0\) and the initial matrix \(\mathbf {K}^l=0\).

    Assume that \(\gamma \) and \(\epsilon \) are small positive numbers.

    Assume the maximal number of iterations \(l_{max}\). Select \(\kappa \in (0,1)\).

  2. 2.

    Solve the state equation (7) by substituting:

    \(\mathbf {K}=\mathbf {K}^l\), \(u=c_1+c_2\,\text{ arctan }\left( \mathbf {x}^T \mathbf {K} \mathbf {x}\right) \).

  3. 3.

    By backward integration, solve the adjoint state equation (23) by substituting the solution to the state equation (Step 2) and \(\mathbf {K}=\mathbf {K}^l\).

  4. 4.

    Evaluate the derivatives (31) by substituting the solution to the state equation (Step 2), the solution to the adjoint state equation (Step 3) and \(\mathbf {K}=\mathbf {K}^l\).

    Compute the value of the objective function \(J(\mathbf {K}^{l})\).

  5. 5.

    Update the matrix \(\mathbf {K}^{l+1}\) using (33).

  6. 6.

    Compute the value of the objective function \(J(\mathbf {K}^{l+1})\).

    If \(J(\mathbf {K}^{l+1}) < J(\mathbf {K}^{l})\), then set \(l=l+1\) and go to Step 7.

    Otherwise, modify the step-size \(\gamma \) by \(\gamma =\kappa \cdot \gamma \), and go to Step 4.

  7. 7.

    Check if any of the terminal conditions are fulfilled: \(|J(\mathbf {K}^{l+1})-J(\mathbf {K}^{l})|/J(\mathbf {K}^{l}) < \epsilon \) or \(l = l_{max}\)

    If not, then go to Step 2. Otherwise, set \(\mathbf {K}^*=\mathbf {K}^l\) and STOP.

5 Experimental results

In this section, the control method that was previously presented will be tested experimentally. The performance of the method for various flows in the tested pipe is going to be assessed. To do this, two different damping cases are evaluated. Then the motion of the pipe conveying air controlled in the optimal way is compared with the one when the actuators operate under the constant control. The same energy consumption is assumed in both cases.

5.1 The test stand

Designing and manufacturing of the test stand was a demanding engineering task due to numerous limitations, related to the free space available in the lab, the budged assumed for the experimental works, availability of commercially manufactured tubes, heat generated by the actuators, and others. Furthermore, the flow velocity, masses of the fluid, the pipe and the actuators, and the length of the pipe should be such that the system exhibits periodic planar oscillations that could be captured by linear model (1), and the external damping actually stabilizes the system (please refer to Fig. 4b and [6]).

Note that if one wanted to expand applicability of the proposed control strategy for flows beyond the critical value, the choice of parameters should be such that the system exhibits periodic and in-plane oscillations which characterize the behavior of majority of the flutter-induced structures:

  • The flow velocity should not exceed the critical value by too much, because in a presence of a mass attached to the pipe a sufficiently high flow yields quasi-periodic or chaotic vibrations [46].

  • The ratio of the masses of the fluid and the pipe \(\beta =m_f/(m_f+m)\) should be appropriate. In certain ranges of this parameter the post-critical vibrations are non-planar or non-periodic, even if there is no lumped mass attached to the pipe [47].

  • The ratio of the masses of the actuators and the pipe \(\Gamma =M_a/((m_f+m)L)\) should be such that for flows slightly exceeding the critical value the resultant bifurcation is planar and periodic [48, 49].

To design the test rig, many numerical simulations were first performed using the already presented model simulating the dynamics of the pipe during the air flow, see Sect. 2. A few pipes of various geometry were tested under a range of the flow velocities. After these preliminary investigations, the laboratory test stand with a single pipe was manufactured.

The studied pipe is made of ABS styrene of density \(\rho =1.17 \hbox { g/cm}^3\) and it has nominal length \(L=958\hbox { mm}\), external diameter \(D=9.05\hbox { mm}\) and internal diameter \(d=7.85\hbox { mm}\). The Young’s modulus \(E=2.22\hbox { GPa}\) and the damping coefficient \(E^{*}=4.46\hbox { MPa}\,\hbox {s}\) of the material were determined during free vibration tests. The pipe was stuck by the grip handle to a composite wooden plate that was mounted on the aluminum truss frame. Conical shanks were used to connect the truss frame components, which ensured high stiffness of the structure by eliminating unnecessary clearances between the truss elements. This prevented any unfavorable additional vibrations. The grip handle was connected to the air compressor, which allowed us to supply compressed air from the tank to the interior of the pipe. Here, a fast pneumatic valve and a flow meter between the air compressor and the grip handle were used. The fast pneumatic valve and an electromagnet were used to impose a fixed initial deflection on the pipe. They were controlled by a real time unit and activated simultaneously to initiate the experimental trial. A view of the test stand and its 3D CAD model are shown in Fig. 5

Fig. 5
figure 5

Laboratory test rig of the standing cantilever pipe conveying air together with electromagnetic devices of motional type (on the left) and the 3D CAD model of the considered system (on the right)

Full size image

The scheme of the real-time measurement and control system installation is presented in Fig. 6. It is based on a PC equipped with an I/O data acquisition card (NI PCI-6251), four laser displacement sensors (OADM 12I6430/S35A made by Baumer) of maximum measurement resolution equal to 0.01 mm, a two-way current amplifier and electromagnetic devices of the motional type (i.e. EM actuators). Laser sensors were mounted at heights of \(\xi _1=1/4\), \(\xi _2=2/4\), \(\xi _3=3/4\) and \(\xi _4=4/4\) of the pipe’s length to measure the deflection of the structure. The optimal control signals were computed by the real time unit and magnified by the amplifier, which is able to provide an operating current of 0.1–5 A. These signals were sent to the electromagnetic devices, which generated the damping force that acted on a rectangular aluminum plate attached to the pipe. The plate has dimensions of 140 mm \(\times \) 30 mm \(\times \) 1.6 mm, mass \(M_a=18.5\hbox { g}\) and is located at a selected distance from the support. Experiments are conducted for three positions of the actuators: \(\xi _a = 0.4L, 0.6L \text { and } 0.8L\). The C-shaped EM actuator was formed from iron to create a closed loop with an air gap. It has dimensions of 80 mm \(\times \) 65 mm, the air gap cross-sectional area is 10 mm \(\times \) 10 mm, and the gap width amounts to 8 mm. The coil was wound from an insulated copper wire of diameter 0.6 mm, which was wrapped 600 times around the core. The total length of the wire carrying current was approximately 33 m. To prevent impacts between the plate and the core, the shape of the plate was curved. The plate curvature amounts to 1/450 [1/mm]. The magnetic flux value in the gap was measured by the GM08 Gaussmeter made by Hirst Magnetic. This instrument has a measurement range of 0.0–3.0 T and a frequency range DC of 15 Hz–10 kHz. The maximum induction of the magnetic field used in the experiments was approximately 0.2 T.

Fig. 6
figure 6

Scheme of the measurement and the control system used in the test rig

Full size image

The parameters of the system that appear in the Eq. (1) are listed in Table 1.

Table 1 Parameters of the examined system
Full size table

5.2 Empirical verification of the control strategy

Experiments were conducted with no air flow (Case A), moderate (B) and subcritical flow velocity (C). In Case B the air flow was such that the Coriolis damping was predominant in the system, whereas in C the air flow was just beneath the critical one. The actual values of the static inlet air pressure varied depending on the position of the actuators, and they are presented in Table 2.

Table 2 The values of static inlet air pressure (bar) for various positions of actuators and simulation scenarios
Full size table

A constant initial deflection of 3 cm was imposed at the tip of the pipe using an electromagnet. The system was then released, and—at the same time—the inlet valve was opened, which initiated the air flow. The vibrations were recorded for 6 s.

First, the system with the optimal control of the actuators was investigated. In each case, the dynamics generated by the suboptimal solution \(u^*(\mathbf {x})\) was compared with that generated by the passive control \(u_{pass}\), which was defined as a constant control consuming the same amount of electric energy as the optimal solution. From \(u=B_1^2+B_2^2\), it can be concluded that the value of the passive control can be computed as

$$\begin{aligned} u_{pass}=\frac{1}{T}\int _0^T u^*(\mathbf {x})\,\text{ d }t. \end{aligned}$$
(34)

The entire procedure was conducted multiple times to ensure that the results are repeatable.

The potential energy of the pipe averaged over the 6-s time horizon was computed for the suboptimal and passive cases to assess the performance of the control method. Table 3 contains the average ratio of these two values for the considered cases. The optimal control outperforms the corresponding passive strategy by 6–23% depending on the position of the actuators and the air flow velocity.

Table 3 Comparison of the performance of the optimal control for the considered air flow velocities
Full size table

The performance of the control method for the system with no flow and with subcritical flow velocity is greater than for the case with moderate flow. This is because the effect of the Coriolis acceleration of the moving fluid is the predominant mechanism of energy dissipation in Case B, see Sect. 3.1, which overshadows both the passive and the active action of the actuators and narrows the advantage of the latter. Moreover, when the actuators are attached at \(\xi _a=0.6L\) the performance of the suboptimal control is greater than the passive strategy much more than for two other positions of the actuators. This is in accordance with the results presented in Fig. 3, Sect. 3.1, which showed that this location of the actuators provides the highest possible critical flow velocity, so it increases the difference between passive and active approach as well.

Figures 7, 8 and 9 compare the suboptimal control of the system with the corresponding passive strategies, i.e. the solutions with constant control that consumes the same amount of energy as the active solution, for three analyzed positions of the actuators. Time series of the tip deflection (figures on the left) indicate that the improvement brought about by the suboptimal control over the passive action of the actuators is always present, and in some cases—significant.

Fig. 7
figure 7

Tip deflection (left) and the normalized control variable (right) of the system with suboptimal and constant passive control, for no flow (a), moderate (b) and subcritical (c) flow velocity; \(\xi _a=0.4L\)

Full size image
Fig. 8
figure 8

Tip deflection (left) and the normalized control (right) of the system with suboptimal and constant passive control, for no flow (a), moderate (b) and subcritical (c) flow velocity; \(\xi _a=0.6L\)

Full size image
Fig. 9
figure 9

Tip deflection (left) and the normalized control (right) of the system with suboptimal and constant passive control, for no flow (a), moderate (b) and subcritical (c) flow velocity; \(\xi _a=0.8L\)

Full size image

The values of the control variable normalized with respect to the maximum are depicted in figures on the right side. Actually, these are the values established by the control algorithm; however, it has been confirmed that the latency of the induction flux in magnetic circuits can be neglected. Note that, in general, the control reduces the induction at the time moments of the extreme deflection. This is understandable because it allows saving energy when very little motion of the pipe takes place, thus damping—which is proportional to the velocity—is small. Another consequence of the switching pattern of the control is the fact that the performance of the active method for near-critical flow velocities is, in general, lower than in scenarios A and B. This is because in Case C high frequency vibrations occur, so the control is turned off for very little time, and the passive control is nearly the maximum one.

6 Summary and conclusions

This paper has investigated the application of eddy-current dampers to improve the stability of the cantilever pipe discharging fluid. A linear model of the system was applied. It was first used to find the position of the actuators which provides the highest increase of the flow velocity leading to the flutter. The attachment of the actuators at around 60% of the pipe’s length can increase the critical flow velocity by 25% using moderate and easy to achieve intensities of the magnetic flux in the electromagnets’ cores.

The model was then used to develop an optimal closed-loop control to improve the stability of the system. Then, the state-feedback parametrization of the optimal control scheme was performed, which enabled designing a practical and robust closed-loop control system. This controller was experimentally verified on the test stand, which was especially designed and built for this purpose. The controlled strategy can stabilize the system more efficiently than the passive method. The improvement amounted to 6–23% depending on the flow velocity and position of the actuators. The optimal performance was achieved for either zero or subcritical flow velocity and the location of actuators at 60% of the pipe’s length. In each of the considered cases, it was assumed that the designed controller consumed the same amount of electrical energy as in the case of the passive method. Therefore, basing on the analyzed results, it can be stated that comparing to the passive method, the designed control guarantees equivalent stabilizing performance with less amount of the wasted energy.

The proposed method of stabilization is based on contactless devices, thus its application may be especially advisable for slender structures whose stability could be affected by the use of force actuators directly attached to the structure. Moreover, it can be easily adapted to changes of the working conditions. This is a significant advantage of the method because it is already known that in certain situations (e.g. when the mass ratio of the fluid and the pipe is high) an increase of the damping can actually destabilize the system.