Hard loss of stability of Ziegler’s column with nonlinear damping

Abstract

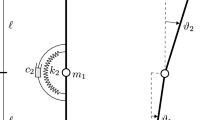
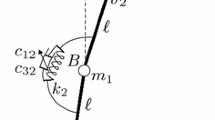
The paper is devoted to discuss the effects of nonlinear damping on the post-critical behavior of the Ziegler’s column. The classical Ziegler’s double-pendulum is considered in regime of finite displacements, in which, moreover, nonlinear damping of Van der Pol-type is introduced at the hinges. A second-order Multiple Scale analysis is carried out on the equations of motion expanded up to the fifth-order terms. The nature of the Hopf bifurcation, namely, supercritical or subcritical, as well as the occurrence of the ‘hard loss of stability’ phenomenon, are investigated. The effects of the nonlinear damping on the amplitude of the limit-cycle are finally studied for different linearly damped columns.

Appendices

Appendix 1: Details on the Multiple Scale algorithm

This Appendix is devoted to furnish some detail on the perturbation algorithm presented in Sect. 3.

Once the generating solution of Eq. (11a), which is expressed by Eq. (12), is substituted in Eq. (11b), the following non-homogeneous problem is obtained:

$$\begin{aligned} \mathcal {L}\mathbf {q}_{1}&= \left( -2i\omega _{d}{\mathrm {d}}_{1}A\mathbf {M}\mathbf {u}_{d}-{\mathrm {d}}_{1}A\mathbf {C}\mathbf {u}_{d}-\delta \mu \mathbf {H}\mathbf {u}_{d}A\right) e^{i\omega _{d}t_{0}}\nonumber \\&\quad+\left[ 3\mu _{d}\mathbf {F}_{1}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) +\omega _{d}^{2}\mathbf {F}_{2}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \right] A^{2}\bar{A}e^{i\omega _{d}t_{0}}\nonumber \\&\quad-\left[ 3\omega _{d}^{2}\mathbf {F}_{3}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) -i\omega _{d}\mathbf {F}_{4}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \right] A^{2}\bar{A}e^{i\omega _{d}t_{0}}\nonumber \\&\quad+\left[ \mu _{d}\mathbf {F}_{1}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) -\omega _{d}^{2}\mathbf {F}_{2}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) \right] A^{3}e^{3i\omega _{d}t_{0}}\nonumber \\&\quad-\left[ \omega _{d}^{2}\mathbf {F}_{3}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) -i\omega _{d}\mathbf {F}_{4}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) \right] A^{3}e^{3i\omega _{d}t_{0}}\nonumber \\&\quad+{\mathrm {c.c.}} \end{aligned}$$

(18)

Solvability condition of this latter, furnishes an equation for the unknown ${\mathrm {d}}_{1}A$ of the type of Eq. (13), namely:

$$\begin{aligned} {\mathrm {d}}_{1}A&= -\delta \mu \,\frac{\mathbf {v}_{d}^{H}\mathbf {H}\mathbf {u}_{d}}{2i\Omega _{d}}A+\frac{3\mu _{d}}{2i\Omega _{d}}\mathbf {v}_{d}^{H}\mathbf {F}_{1}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) A^{2}\bar{A}\nonumber \\&\quad+\frac{\omega _{d}^{2}}{2i\Omega _{d}}\left[ \mathbf {v}_{d}^{H}\mathbf {F}_{2}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) -3\mathbf {v}_{d}^{H}\mathbf {F}_{3}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \right] A^{2}\bar{A}\nonumber \\&\quad+\frac{\omega _{d}}{2\Omega _{d}}\mathbf {v}_{d}^{H}\mathbf {F}_{4}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) A^{2}\bar{A} \end{aligned}$$

(19)

where the apex H denotes the conjugate transpose, the normalization condition $\mathbf {v}_{d}^{H}\mathbf {M}\mathbf {u}_{d}=1$ is accounted for, and $\Omega _{d}:=\omega _{d}-i\left( \mathbf {v}_{d}^{H}\mathbf {C}\mathbf {u}_{d}\right) /2$ is introduced.

Once Eq. (19) is substituted in the $\varepsilon$-order problem (18), this latter reads:

$$\mathcal {L}\mathbf {q}_{1} =\left( \delta \mu \,A\,\mathbf {z}_{1}+A^{2}\bar{A}\,\mathbf {z}_{2}\right) e^{i\omega _{d}t_{0}}+A^{3}\mathbf {z}_{3}e^{3i\omega _{d}t_{0}}+{\mathrm {c.c.}}$$

(20)

where the following definitions hold:

$$\begin{aligned} \mathbf {z}_{1}&:= \frac{\mathbf {v}_{d}^{H}\mathbf {H}\mathbf {u}_{d}}{2i\Omega _{d}}\left( 2i\omega _{d}\mathbf {M}\mathbf {u}_{d}+\mathbf {C}\mathbf {u}_{d}\right) -\mathbf {H}\mathbf {u}_{d}\nonumber \\ \mathbf {z}_{2}&:= -\frac{3\mu _{d}}{2i\Omega _{d}}\mathbf {v}_{d}^{H}\mathbf {F}_{1}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \left( 2i\omega _{d}\mathbf {M}\mathbf {u}_{d}+\mathbf {C}\mathbf {u}_{d}\right) \nonumber \\&\quad-\frac{\omega _{d}^{2}}{2i\Omega _{d}}\mathbf {v}_{d}^{H}\mathbf {F}_{2}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \left( 2i\omega _{d}\mathbf {M}\mathbf {u}_{d}+\mathbf {C}\mathbf {u}_{d}\right) \nonumber \\&\quad+\frac{3\omega _{d}^{2}}{2i\Omega _{d}}\mathbf {v}_{d}^{H}\mathbf {F}_{3}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \left( 2i\omega _{d}\mathbf {M}\mathbf {u}_{d}+\mathbf {C}\mathbf {u}_{d}\right) \nonumber \\&\quad-\frac{\omega _{d}}{2\Omega _{d}}\mathbf {v}_{d}^{H}\mathbf {F}_{4}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \left( 2i\omega _{d}\mathbf {M}\mathbf {u}_{d}+\mathbf {C}\mathbf {u}_{d}\right) \nonumber \\&\quad+3\mu _{d}\mathbf {F}_{1}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) +\omega _{d}^{2}\mathbf {F}_{2}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \nonumber \\&\quad-3\omega _{d}^{2}\mathbf {F}_{3}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) +i\omega _{d}\mathbf {F}_{4}\left( \mathbf {u}_{d},\mathbf {u}_{d},\bar{\mathbf {u}}_{d}\right) \nonumber \\ \mathbf {z}_{3}&:= \mu _{d}\mathbf {F}_{1}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) -\omega _{d}^{2}\mathbf {F}_{2}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) \nonumber \\&\quad-\omega _{d}^{2}\mathbf {F}_{3}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) +i\omega _{d}\mathbf {F}_{4}\left( \mathbf {u}_{d},\mathbf {u}_{d},\mathbf {u}_{d}\right) \end{aligned}$$

(21)

The solution of the equation (20) is in the form of Eq. (14), where $\mathbf {w}_{1}$, $\mathbf {w}_{2}$ and $\mathbf {w}_{3}$ are obtained by resolving the following algebraic problems:

$$\begin{aligned} \left[ -\omega _{d}^{2}\mathbf {M}+i\omega _{d}\mathbf {C}+\left( \mathbf {K}+\mu _{d}\mathbf {H}\right) \right] \mathbf {w}_{1}&= \mathbf {z}_{1}\nonumber \\ \left[ -\omega _{d}^{2}\mathbf {M}+i\omega _{d}\mathbf {C}+\left( \mathbf {K}+\mu _{d}\mathbf {H}\right) \right] \mathbf {w}_{2}&= \mathbf {z}_{2}\nonumber \\ \left[ -9\omega _{d}^{2}\mathbf {M}+3i\omega _{d}\mathbf {C}+\left( \mathbf {K}+\mu _{d}\mathbf {H}\right) \right] \mathbf {w}_{3}&= \mathbf {z}_{3} \end{aligned}$$

(22)

In particular $\mathbf {w}_{1}$ and $\mathbf {w}_{2}$ are solutions of singular problems, normalized according to $\mathbf {v}_{d}^{H}\mathbf {w}_{j}=0,\;j=1,2$, while $\mathbf {w}_{3}$ is the solution of a non-singular problem.

Finally, Eq. (15) is obtained by straightforwardly extending the above discussed procedure to the $\varepsilon ^{2}$-order problem: Eqs. (12) and (14) are substituted in Eq. (11c) and solvability condition of this latter is enforced. However, this step of the algorithm entails cumbersome final expressions, which do not provide any further qualitative information on the perturbation solution; therefore, the relevant equations, which can be easily obtained through a software for symbolic calculation, are not reported here.

Appendix 2: Derivation of the equations of motion of the nonlinearly damped visco-elastic Beck’s beam

The relevant steps for deriving the equations of motion of the nonlinearly damped visco-elastic Beck’s beam are reported, in order to render the present paper self-contained. For further details the reader is referred to [39].

The beam is modeled as one-dimensional, internally constrained, polar continuum (see, e.g., [47]), embedded in the plane spanned by the unit vectors $\bar{\mathbf {a}}_{x}$, $\bar{\mathbf {a}}_{y}$. The rotation angle of the point P around the $\bar{\mathbf {a}}_{z}$-axis, namely $\theta \left( s,t\right)$, maps the reference basis $\left( \bar{\mathbf {a}}_{x},\bar{\mathbf {a}}_{y},\bar{\mathbf {a}}_{z}\right)$, attached to P, into the current one $\left( \mathbf {a}_{x},\mathbf {a}_{y},\bar{\mathbf {a}}_{z}\right)$; $\theta$ is taken as configuration variable. Moreover, the unshearability constraint, entails that $\mathbf {a}_{x}$ is tangent to the beam axis.

The curvature of the beam is introduced as a measure of strain; it reads:

$$\chi \left( s,t\right) =\theta '\left( s,t\right)$$

(23)

The inextensibility condition entails:

$$\begin{aligned} u'\left( s,t\right)&= \cos \theta \left( s,t\right) -1\nonumber \\ v'\left( s,t\right)&= \sin \theta \left( s,t\right) \end{aligned}$$

(24)

where u, v are scalar function which describe the longitudinal and transverse displacement of the beam axis, respectively. The geometrical boundary conditions at the clamp are:

$$\begin{aligned} u\left( 0,t\right)&= 0\nonumber \\ v\left( 0,t\right)&= 0\nonumber \\ \theta \left( 0,t\right)&= 0 \end{aligned}$$

(25)

The fields u, v are then rewritten as functions of $\theta$: indeed, by integrating with respect to s Eq. (24), and by taking into account for Eq. (25), the following conditions hold:

$$\begin{aligned} u\left( s,t\right)&= \int _{0}^{s}\left[ \cos \theta \left( \hat{s},t\right) -1\right] \,{\mathrm {d}}\hat{s}\nonumber \\ v\left( s,t\right)&= \int _{0}^{s}\sin \theta \left( \hat{s},t\right) \,{\mathrm {d}}\hat{s} \end{aligned}$$

(26)

being $\hat{s}$ a dummy variable. The balance equations in the reference basis $\left( \bar{\mathbf {a}}_{x},\bar{\mathbf {a}}_{y},\bar{\mathbf {a}}_{z}\right)$ read:

$$\begin{aligned}&R'\left( s,t\right) +p_{x}\left( s,t\right) =0\nonumber \\&S'\left( s,t\right) +p_{y}\left( s,t\right) =0\nonumber \\&M'\left( s,t\right) +S\left( s,t\right) \cos \theta \left( s,t\right) -R\left( s,t\right) \sin \theta \left( s,t\right) =0 \end{aligned}$$

(27)

where R, S are the extrinsic component of the force-stress vector, M is the bending moment and $p_{x},p_{y}$ are the external distributed loads. The mechanical boundary conditions at the free end are:

$$\begin{aligned} R\left( \ell ,t\right)&= -F\cos \theta \left( \ell ,t\right) \nonumber \\ S\left( \ell ,t\right)&= -F\sin \theta \left( \ell ,t\right) \nonumber \\ M\left( \ell ,t\right)&= 0 \end{aligned}$$

(28)

Then, by integrating Eqs. (27a, b) with respect to s, and by taking into account for Eqs. (28a, b), the extrinsic components are rewritten as:

$$\begin{aligned} R\left( s,t\right)&= -F\cos \theta \left( \ell ,t\right) +\int _{s}^{\ell }p_{x}\left( \hat{s},t\right) \,{\mathrm {d}}\hat{s}\nonumber \\ S\left( s,t\right)&= -F\sin \theta \left( \ell ,t\right) +\int _{s}^{\ell }p_{y}\left( \hat{s},t\right) \,{\mathrm {d}}\hat{s} \end{aligned}$$

(29)

When Eqs. (29) are substituted in Eq. (27c), this latter becomes:

$$\begin{aligned}&M'\left( s,t\right) +\cos \theta \left( s,t\right) \int _{s}^{\ell }p_{y}\left( \hat{s},t\right) \,{\mathrm {d}}\hat{s}-\sin \theta \left( s,t\right) \int _{s}^{\ell }p_{x}\left( \hat{s},t\right) \,{\mathrm {d}}\hat{s}\nonumber \\&\quad +F\left[ \cos \theta \left( \ell ,t\right) \sin \theta \left( s,t\right) -\sin \theta \left( \ell ,t\right) \cos \theta \left( s,t\right) \right] =0 \end{aligned}$$

(30)

Once the inertia forces and the external damping are introduced, i.e. $p_{x}=-m\ddot{u},\,p_{y}=-m\ddot{v}-b\dot{v}$, and use of Eqs. (26) and (4) is made, Eq. (30) is transformed into:

$$\begin{aligned}&EI\theta ''+\eta _{1}I\dot{\theta }''+\eta _{3}I\left( \theta '^{2}\dot{\theta }'\right) '-b\cos \theta \intop _{s}^{\ell }\intop _{0}^{\check{s}}\dot{\theta }\cos \theta d\hat{s}d\check{s}\nonumber \\&\quad +m\cos \theta \intop _{s}^{\ell }\intop _{0}^{\check{s}}\left( \dot{\theta }^{2}\sin \theta -\ddot{\theta }\cos \theta \right) d\hat{s}d\check{s}\nonumber \\&\quad -m\sin \theta \intop _{s}^{\ell }\intop _{0}^{\check{s}}\left( \dot{\theta }^{2}\cos \theta +\ddot{\theta }\sin \theta \right) d\hat{s}d\check{s}\nonumber \\&\quad +F\left[ \cos \theta \left( \ell ,t\right) \sin \theta \left( s,t\right) -\sin \theta \left( \ell ,t\right) \cos \theta \left( s,t\right) \right] =0 \end{aligned}$$

(31)

being $\check{s}$ a dummy variable. Equation (31) must be sided by the two remaining (i.e. not used) boundary conditions, namely Eqs. (25c) and (28c), which read:

$$\begin{aligned}&\theta \left( 0,t\right) =0\nonumber \\&EI\theta '\left( \ell ,t\right) +\eta _{1}I\dot{\theta }'\left( \ell ,t\right) +\eta _{3}I\left[ \theta '^{2}\left( \ell ,t\right) \dot{\theta }'\left( \ell ,t\right) \right] =0 \end{aligned}$$

(32)

Finally, by introducing the quantities (6) in Eqs. (31) and (32), Eqs. (5) are obtained (tilde removed).