On kinks and other travelling-wave solutions of a modified sine-Gordon equation

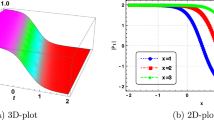
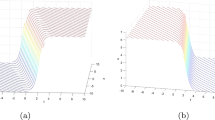
Abstract

We give an exhaustive, non-perturbative classification of exact travelling-wave solutions of a perturbed sine-Gordon equation (on the real line or on the circle) which is used to describe the Josephson effect in the theory of superconductors and other remarkable physical phenomena. The perturbation of the equation consists of a constant forcing term and a linear dissipative term. On the real line candidate orbitally stable solutions with bounded energy density are either the constant one, or of kink (i.e. soliton) type, or of array-of-kinks type, or of “half-array-of-kinks” type. While the first three have unperturbed analogs, the last type is essentially new. We also propose a convergent method of successive approximations of the (anti)kink solution based on a careful application of the fixed point theorem.

Appendix

Proof of Proposition 1

Let $0\le z_{0,2}<z_{0,1}, z_j(g):=z(g;g_0,z_{0,j};\mu ,\gamma )$ ($j=1,2$) be the corresponding solutions of (15) and $G_j$ the corresponding intervals giving their (maximal) domains. By continuity the inequality

$$ z_1-z_2>0 $$

(65)

will hold in a neighbourhood of $g_0$ within $G_1\cap G_2$. In fact, it will hold for all $g\in G_1\cap G_2$. If ad absurdum this were not the case, denote by $\bar{g}\in G_1\cap G_2$ the least $g>g_0$ (resp. largest $g<g_0$) where $z_1-z_2$ vanishes: $z_1(\bar{g})-z_2(\bar{g})=0$; then the problem (15) with initial (resp. final) condition $z(\bar{g})=z_1(\bar{g})\equiv z_2(\bar{g})$ would admit the two different solutions $z_1, z_2$, against the existence and uniqueness theorem. As for the monotonicity of $g_{\pm }$, by the same theorem $z_1(g_{2\pm })>z_2(g_{2\pm })=0$ implies $g_{1+}>g_{2+}$ if $g_{2+}<\infty$, otherwise $g_{1+}=g_{2+}=\infty$, and $g_{1-}<g_{2-}$ if $g_{2-}>-\infty$, otherwise $g_{1-}=g_{2-}=-\infty$. $\square$

Proof of Proposition 2

Let $\mu _1\le \mu _2, \gamma _1\epsilon \ge \gamma _2\epsilon$, with one of the two inequalities being strict; for $j=1,2$ let $u_j(g):=u(g;g_0,u_0;\mu _j,\gamma )$ be the corresponding solutions of (15) with the same condition $u_j(g_0) =u_0$, and $G_j$ the intervals giving their (maximal) domains. We find

$$ u_{2g}=-\mu _2+\frac{\gamma _2-\sin g}{u_2}<-\mu _1+\frac{\gamma _1-\sin g}{u_2}. $$

By the comparison principle⁶ (see e.g. [42]) it follows, as claimed,

$$\begin{aligned} u_1(g) >u_2(g) & \quad g\in ]g_0,g_+[, \\ u_1(g) <u_2(g) &\quad g\in ]g_-,g_0[. \end{aligned}$$

(66)

If $\epsilon >0$, this implies: $\lim _{g\downarrow g_{2+}}u_1(g)\ge \lim _{g\downarrow g_{2+}}u_2(g)=0$ and therefore $g_{1+}\ge g_{2+}$ (the inequalities being strict as long as $g_{2+}<\infty$); $\lim _{g\uparrow g_{1-}}u_2\ge 0$ and therefore $g_{1,-}\ge g_{2-}$ (the inequalities being strict as long as $g_{1-}>-\infty$). Moreover, let $g_j(\xi )=g(\xi ;g_0,u_0;\mu _j,\gamma _j)$ be the corresponding two solutions of (16), i.e. the solutions of (10). We find

$$ g_2'(\xi )=u_2\big (g_2(\xi )\big ) \left\{ \begin{array}{ll} <u_1\big (g_2(\xi )\big ),& \quad \forall \xi >\xi _0,\\ >u_1\big (g_2(\xi )\big ), &\quad \forall \xi <\xi _0, \end{array}\right. $$

while $g_2(\xi _0)=g_0=g_1(\xi _0)$. By the comparison principle this implies as claimed $g_2(\xi )<g_1(\xi )$ for all $\xi \in X_1\cap X_2$. Similarly one argues if $\epsilon <0$. $\square$

Proof of Proposition 3

Consider the Cauchy problem (15) in subsequent intervals $]g_k,g_{k+1}[ \subset G$. Since the equation is invariant under $g\rightarrow g+2\pi$, by Proposition 1 if $z(g_1)$ is respectively larger, equal, smaller than $z(g_0)$ then so are $z(g_{k+1}),I_{k+1}$ in comparison with $z(g_k),I_k$ respectively, for all $k\in K$; in other words, the sequences $\{z(g_k)\}, \{I_k\}$ are either constant, or strictly monotonic. Equation (21) follows from (19) applied in $]g_k,g_{k+1}[$.

If $\epsilon =-$, then rhs (21)$>2\pi \gamma >0$ for any k, so that the sequences are strictly increasing and diverging as $k\rightarrow \infty$, whereas K must have a lower bound, otherwise $z(g_k)$ would become negative for sufficiently low k.

If $\epsilon =+$, then the two terms at the rhs (21) have opposite sign and can compensate each other. If the sequences are strictly increasing, the sides of (21) are positive for all k and $I_k<2\pi \gamma /\mu$. Applying (19) to the interval $[g_k,g_k+\Delta g]$ for any $\Delta g\le 2\pi$ we find

$$\begin{aligned} z(g_k+\Delta g)-z(g_k) & =U(g_k)-U(g_k+\Delta g) \\ &\quad-\,\mu \int \limits _{g_k}^{g_k+\Delta g}ds\sqrt{2z(s)}. \end{aligned}$$

But $|U(g_k)-U(g_k+\Delta g)|$ is upper bounded, e.g. by $2+2\pi \gamma$, whence

$$ |z(g_k+\Delta g)-z(g_k)|\le 2+2\pi \gamma +\mu I_k< 2+4\pi \gamma.$$

(67)

If ad absurdum $z(g_k)$ diverged as $k\rightarrow \infty$, then also $z(g_k+\Delta g)$ and in turn $I_k$ [by (20)] would diverge, in contrast with $I_k<2\pi \gamma /\mu$; so it must converge. Moreover, as before, K must have a lower bound. On the other hand, rewriting (21) in the form $z(g_{k-1})-z(g_k)=\mu I_{k-1}-2\pi \gamma$, we see that if the sequences $\{z(g_k)\},\{I_k\}$ are strictly decreasing, the sides are positive for all k and larger than $\mu I_0-2\pi \gamma >0$ for all negative k; this implies that they diverge as $k\rightarrow -\infty$, and again by (67) so do $z(g),I(z,g)$. Whereas they must either converge as $k\rightarrow \infty$, or K must have an upper bound. $\square$