Equations of motion of rotating composite beam with a nonconstant rotation speed and an arbitrary preset angle

Abstract

In the presented paper the equations of motion of a rotating composite Timoshenko beam are derived by utilising the Hamilton principle. The non-classical effects like material anisotropy, transverse shear and both primary and secondary cross-section warpings are taken into account in the analysis. As an extension of the other papers known to the authors a nonconstant rotating speed and an arbitrary beam’s preset (pitch) angle are considered. It is shown that the resulting general equations of motion are coupled together and form a nonlinear system of PDEs. Two cases of an open and closed box-beam cross-section made of symmetric laminate are analysed in details. It is shown that considering different pitch angles there is a strong effect in coupling of flapwise bending with chordwise bending motions due to a centrifugal force. Moreover, a consequence of terms related to nonconstant rotating speed is presented. Therefore it is shown that both the variable rotating speed and nonzero pitch angle have significant impact on systems dynamics and need to be considered in modelling of rotating beams.

1 Introduction

Rotating beams are important structures widely used in mechanical and aerospace engineering as turbine blades, various cooling fans, windmill blades, helicopter rotor blades, airplane propellers etc. Introduction of composite materials technology has significantly influenced their design and opened new research areas. Various elastic couplings, resulting from the directional-dependent properties of composites and ply-stacking sequences combinations might be exploited to enhance their response. A profound understanding of rotating composite beams dynamics is essential towards taking the full advantage of their design potential and avoiding failures.

An interest of modelling composite rotating beams started in mid 80s and increasing number of research work led to several review papers, where different approaches to rotating composite beam modelling were discussed. In 1994 Kunz [17] and later Volovoi et al. [32] made an extended assessment of rotating beam modelling methods with special regard to helicopter rotor blades.

Currently available approaches to analysis of composite beams fall in one of the three cases [13]: (a) theories in which some a’priori cross-sectional deformation is assumed leading to 1-D governing equations; (b) theories based on equations for the blade as a one-dimensional continuum, the cross-section properties of which are obtained from separate source e.g. [12]; (c) approach where the beam and cross-sectional governing equations are rigorously reduced from three-dimensional elasticity theory. Although ‘ad hock’ theories (a) have some drawbacks (see [36]) they still stay to be one of the most common ones.

A very extensive work devoted to thin-walled composite beam analysis was done by Librescu and Song [21, 28, 29] and their co-workers e.g. [23, 24]. Authors developed and refined a theory of beams modelled as thin-walled structures of an arbitrary, closed or open cross-section. The work-out theory encompassed a number of non-classical effects such as the anisotropy and heterogeneity of constituent materials, transverse shear, primary and secondary warping phenomena (Vlasov effect) etc. under assumption of the cross-section to be rigid in its own plane. In the performed analysis of rotating systems [29] the effects of the centrifugal and Coriolis forces were taken into account. Furthermore, the importance of shear effects in composite material was emphasized.

Kaya and Ozgumus in [15] performed an analysis of the free vibration response of an axially loaded, closed-section composite Timoshenko beam which featured material coupling between flapwise bending and torsional vibrations due to ply orientation. The governing differential equations of motion were derived and the impact of the various couplings, as well as the slenderness ratio on the natural frequencies were investigated. Although only the cases of constant rotating speed and zero pitch angle were considered.

Sina et al. [27] analysed a rotating tapered thin-walled composite Timoshenko beam in linear regime following Librescu’s approach. In the performed analysis centrifugal and Coriolis forces were taken into account; however no beam presetting angle nor variable rotating speed were considered in that paper. A discussion of taper and slenderness ratio impact on natural frequencies and mode shapes was furthermore presented.

Jun et al. [14] studied the dynamics of axially loaded thin-walled beams of open, mono-symmetrical section. The studies considered the effect of warping stiffness, but were restricted to Euler–Bernoulli beam theory and isotropic material only. An impact of axial force and warping stiffness on the coupled bending torsional natural frequencies with various boundary conditions is examined.

The analysis of a nonlinear rotating thin-walled composite beam was presented by e.g. Arvin and Bakhtiari-Nejad [2]. Authors developed a model for rotating composite Timoshenko beam considering centrifugal forces by means of von-Karmans strain–displacement relationships. The system was studied using the multiple time scales method and nonlinear normal modes theory. Again assumptions regarding zero pitch angle and constant rotation speed were made. Ghorasi [11] developed a nonlinear model of the rotating thin-walled composite Euler–Bernoulli beam using the previously mentioned variational asymptotic method elaborated by Cesnik and Hodges [6]. He considered a non-zero pitch angle but again only in parallel with constant rotating speed case. Avramov et al. [4] modelled rotating Euler–Bernoulli beams made by isotropic material with asymmetric cross-sections considering non-zero pitch angle but constant rotation speed. The study of flexural-flexural-torsional nonlinear vibrations using nonlinear normal modes approach were presented.

Effect of an initial beam pre-twist was examined by several researchers too. Chandiramani et al. [7] studied free linear vibrations of the rotating pre-twisted thin-walled composite Timoshenko beams considering a non-zero pitch angle but a constant rotating speed. Also Oh et al. [23] modelled and studied the similar system, but again following an assumption of the constant rotation speed.

Possible interactions and mode couplings observed in rotating ‘smart’ beams gained attention of several researchers in recent years too. Na et al. [22] addressed the problem of modelling and bending vibration control of tapered rotating blades represented as nonuniform thin-walled beams and incorporating adaptive capabilities. The blade model incorporated most non-classical features and their assessment on system dynamics including the taper characteristics was accomplished. Ren et al. [25] modelled a rotating thin-walled shape memory alloy composite Euler–Bernoulli beam, considering centrifugal and Coriolis forces with non-zero pitch angle but constant rotating speed. Free vibrations of the system were studied. Choi et al. [8] modelled rotating thin walled composite Timoshenko beams with macro fiber composite actuators and sensors using Librescu’s approach. Again zero pitch angle and constant rotating speed assumptions were made.

The research on free vibrations of the rotating inclined cantilever beam was done by Lee and Sheu [20]. Influence of the beam setting angle and the inclination angle on the first two natural frequencies of the system were examined. Moreover different hub radius to beam length ratios were tested. This study was limited to isotropic materials, so only very little of possible internal couplings observed in the case of composite materials were recorded and commented.

A nonlinear model of rotating isotropic blades based on the Cosserat theory of rods without restrictions on the geometry of deformation was presented in [18]. The roles of internal kinematic constraints such as unshearability of the slender blades, coupling between flapping, lagging, axial and torsional deformations were studied. The authors showed an influence of the angular velocity on the possible internal resonances which may occur in the considered rotating structure. The method of multiple time scales was applied directly to PDE of motion in order to determine the back-bone curves of the flapping modes out of internal resonance [3]. The hardening and softening effect was shown for selected angular velocities, and the importance of 2:1 internal resonance between flapping and axial modes leading to additional interactions and changing dynamics was demonstrated. As results from the paper the angular speed may be treated as the geometrical tuning mechanics leading to specific dynamic interactions between modes. As in the case of previously mentioned papers the assumption of constant rotating speed stayed in force.

Case of non-constant rotating speed with respect to isotropic material blade was examined by Vyas and Rao [33]. The equations of motion of a Timoshenko beam mounted on a disk rotating with constant acceleration were given. In the derivation higher order effects due to Coriolis forces were included, but impact of non-zero presetting angle was ignored; moreover no numerical examples were given. Warmiński and Balthazar [34] modelled a rotating Euler–Bernoulli beam made of isotropic material with a tip mass. In the analysis geometrical nonlinearities and nonconstant rotating speed were taken into account, but an impact of pitch angle has been neglected. The authors showed transitions through the resonances for a reduced order discrete system. This topic was also investigated and continued afterwards by Fenili and Balthazar [9, 10]. Authors considered the non-ideal system’s power supply where the response of the excited beam affected the behaviour of the energy source. The performed simulations led to the observation, that this interaction caused a damping of the beam response.

Apart from analytical based models composite thin walled beams are studied also by means of finite element method. Altenbach et al. [1] developed a generalized Vlasov theory for thin-walled composite beam and next an isoparametric finite element with arbitrary nodal degrees of freedom. The element was tested for multiple cases of open and closed cross-section cantilever designs, although only static cases were considered. The 3D model of a rotating beam with geometric nonlinearities was investigated in [30] by the p-version of finite element method. The two models, Bernoulli-Euler and Timoshenko, were studied and the importance of warping function for different rectangular cross-sections was shown. Moreover, authors concluded that additional shear stresses which appeared while bending and torsion were coupled have an essential influence on the beam’s dynamics. In the latest paper [31] the p-version of finite element was used for 3D Timoshenko beam model in which two types of nonlinearity were considered, a nonlinear strain-displacement relation and inertia forces due to rotation. The deformation in a longitudinal direction due to warping was taken into account. Dynamics was studied for constant and nonconstant rotation speed and for harmonic external loading.

A very comprehensive theory of rotating slender beams has been developed since the nineties by Hodges and his co-workers. It was presented in a series of papers and later collected in a book by Hodges [13]. In order to derive the equations of motions they used Cosserat theory (a director theory) for the determination of generalized strains. The modelling was based on asymptotic procedures that exploited the smallness of system’s parameters such as strain and slenderness. The approach extracted from a three-dimensional elasticity formulation the two sets of analyses: one over the cross section, providing elastic constants that might be used in a suitable set of beam equations, and the other set beeing the beam equations themselves. Authors developed a software called variational asymptotic beam section analysis (VABS) which used the originally worked-out analysis method. The VABS software was later verified and validated within the frame of several works e.g. by Yu et al. [36], by Kovvali et al. [16]. The worked out theory is especially well suited for helicopter rotor blades modelling since it accounts for initial twist and geometrical nonlinearities (i.e. large displacements and rotations caused by deformation) preserving small strain condition. It allows for arbitrary cross-sectional geometry and material properties as well. In spite of the fact that authors have not assumed constant angular velocity there is a lack of explicit dependencies in the case when nonlinear couplings arise from nonconstant angular velocity. This phenomenon is essential in case of study of so called non-ideal system when energy source e.g. DC motor interacts with the power-driven structure. Nonlinear coupling terms may be observed by Sommerfeld effect [5, 34].

Although of evident practical importance, to the best of the authors knowledge, no studies on possible interactions occurring in composite beams rotating with nonconstant speed have been found in the specialised literature. Also the assumption of the arbitrary pitch angle in the performed analysis still leaves some space for discussion. To address this situation a derivation of equations of motion of the rotating thin-walled composite Timoshenko beam is presented. In the performed analysis most non-classical effects like material anisotropy, transverse shear and both primary and secondary cross-section warpings are taken into account, as well as arbitrary pitch angle and nonconstant rotating speed. The resulting general equations form a system of nonlinear PDEs that are coupled together. To illustrate the potential of this study a more detailed examination of two cases of open and closed box-beam cross-sections made of symmetric laminate is performed. It is shown that considering different pitch angles one observes a strong effect in coupling of flapwise bending and choordwise bending motions due to centrifugal force. Moreover, the consequence of terms related to nonconstant rotating speed is exemplified.

2 Theory

2.1 Problem formulation

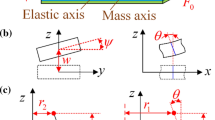
Let us consider a slender, straight and elastic composite thin-walled beam clamped at the rigid hub of radius ${R_0}$ experiencing rotational motion as shown in Fig. 1. The length of the beam is denoted by l, its wall thickness by h and it is assumed to be constant spanwise. The composite material is linearly elastic (Hookean) and its properties may vary in directions orthogonal to the middle surface.

Fig. 1

Rotating thin-walled beam under consideration and reference frames

2.1.1 Coordinate systems

Four coordinate systems are defined to describe the motion of the beam:

• global and fixed in space Cartesian coordinate system $(X_0,Y_0,Z_0)$ attached at the center of the hub $O$ (Fig. 1a),

• beam Cartesian coordinate system $(X_1,Y_1,Z_1)$ with origin $O$ set at the center of the hub, rotating with arbitrary angular velocity $\dot{\psi }(t)$ about axis $OZ_1=OZ_0$ (Fig. 1a),

• beam Cartesian coordinate system $(x,y,z)$ located at the blade root and oriented with respect to plane of rotation ($X_1Y_1$) at angle $\theta$ denoting blade presetting (pitch) angle (Fig. 1b). Axis $ox$ is directed along beam span and $oz$ axis is normal to the beam chord. The origin $o$ of the $(x,y,z)$ coordinates is set at the center of the beam cross-section, therefore axes $ox$ and $OX_1$ coincide,

• local, curvilinear coordinate system $(x,n,s)$ related to blade cross-section—see Fig. 1c. Its origin is set conveniently at the point on a mid-line contour. The circumferential coordinate $s$ is measured along the tangent to the middle surface in a counter-clockwise direction, whereas $n$ points outwards and along the normal to the middle surface.

2.1.2 Assumptions

For the development of the equations of motion the following kinematic and static assumptions are postulated:

• (a) the original shape of the cross-section is maintained in its plane, but is allowed to warp out of the plane,

• (b) the concept of the Saint-Venant torsional model is discarded in the favour of the non-uniform torsional one. Therefore the rate of beam twist $\varphi ^{\prime }={d\varphi }/{d x}$ depends in general on the spanwise coordinate $x$,

• (c) in addition to the primary warping effects (related to the cross-section shape) the secondary warping related to the wall thickness is also considered,

• (d) the transverse beam shear deformations $\gamma _{xy}$, $\gamma _{xz}$ are taken into account. These are assumed to be uniform over the beam cross-section,

• (e) the ratio of wall thickness to the radius of curvature at any point of the beam wall is negligibly small while compared to unity. In a special case of the prismatic beams made of planar segments this ratio is exactly 0,

• (f) the stress in transverse normal ($\sigma _{nn})$ direction and the hoop stress resultant ($N_{ss})$ are very small and can be neglected.

2.2 Beam model

The equations of motion of the rotating beam are derived according to the extended Hamilton’s principle of the least action

$$\begin{aligned} \delta J=\int \limits _{t_{1}}^{t_{2}} \big ( \delta T-\delta U+\delta W_{ext} \big )dt=0, \end{aligned}$$

(1)

where $J$ is the action, $T$ is the kinetic energy, $U$ is the potential energy and the work of the external forces is given by the $W_{ext}$ term. One of the key steps of the derivation procedure is associated with the definition of a position vector and subsequently velocity and acceleration ones.

2.2.1 Position vector

Let us consider any arbitrary point A located on the beam’s profile mid-line specified by its position vector ${\mathbf{r}}= \lbrace{x,y,z}\rbrace^{\text {T}}$ in the local beam’s coordinate system—Fig. 2. As the system rotates and A experiences displacement ${\mathbf{D}}= \lbrace{D_{x},D_{y},D_{z}}\rbrace^{\text {T}}$ it occupies a new position $\text {A}^{\prime }$ given by a position vector $\mathbf {R}$ defined in fixed inertial frame.

Fig. 2

a Position vectors of point A in reference frames; b transformation of an arbitrary cross-section as rigid body motion; point P denotes cross-section pole and $v_P, w_P$ its transversal displacements while $\varphi (x,t)$ is cross-section rotation

To find the position vector $\mathbf {R}$ in the global coordinate system transformation matrices defining transitions to subsequent reference frames need to be defined. For this purpose the method of four dependent Euler parameters is used—see e.g. Shabana [26].

Transformation between $X_0Y_0Z_0$ and $X_1Y_1Z_1$ frames

Transformation between $X_0Y_0Z_0$ and $X_1Y_1Z_1$ frames is related to the rotation through angle $\psi (t)$ about $OZ_1=OZ_0$ axis. Therefore a transformation matrix is given as

$$ {\mathbf {A}}^{\text {(I)}}= \left[ \begin{array}{lll} \cos \psi (t) &{} -\sin \psi (t) &{} 0\\ \sin \psi (t) &{} \cos \psi (t) &{} 0\\ 0 &{} 0 &{} 1\\ \end{array} \right]$$

(2)

Transformation between ($xyz$) and ($X_1Y_1Z_1$) frames

Transformation from beam’s local $xyz$ frame to $X_1Y_1Z_1$ one is related to the rotation about $OX_1$ axis through angle $\theta$ (see Fig. 1) corresponding to beam’s pitch angle and next the translation along the hub radius $R_0$. So the second rotation matrix is

$$ {\mathbf {A}}^{\text {(II)}}= \left[ \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} \cos \theta &{} -\sin \theta \\ 0 &{} \sin \theta &{} \cos \theta \\ \end{array}\right]$$

(3)

In the following discussion, to distinguish between coordinates associated with cross-section’s mid-line points and off-mid line ones lower ($y$, $z$) and capital ($Y$, $Z$) letters are used correspondingly. Following this notation setting (in beam’s local coordinate system) the initial position vector $\mathbf {r}$ of any arbitrary point of the cross-section

$${\mathbf {r}}= x {\mathbf {i}} + Y {\mathbf {j}} + Z {\mathbf {k}}$$

(4)

and applying subsequent transformations the position vector $\mathbf {R}$ in inertial (global) frame is

$$ {\mathbf {R}}={\mathbf {A}}^{\text {(I)}}\big [{\mathbf {A}}^{\text {(II)}}({\mathbf {r}}+{\mathbf {D}}) + {\mathbf {R}}_0\big ]$$

(5)

Substituting (2), (3) and (4) into the above relation one obtains

$$\begin{aligned} {\mathbf{R}}=\left\{ \begin{array}{l} (D_x+x+R_0)\cos \psi (t) - (D_y+Y)\cos \theta \sin \psi (t) + (D_z + Z)\sin \theta \sin \psi (t)\\ (D_x+x+R_0)\sin \psi (t) + (D_y+Y)\cos \theta \cos \psi (t) - (D_z + Z)\sin \theta \cos \psi (t)\\ (D_y+Y)\sin \theta + (D_z + Z)\cos \theta \\ \end{array} \right\} \end{aligned}$$

(6)

where $D_x$, $D_y$ and $D_z$ are individual terms of deformation vector $\mathbf {D}$ in local coordinates as defined later in (9).

2.2.2 Velocity vector

The velocity vector of an arbitrary point A of the elastic body in the inertial frame can be obtained by differentiating the position vector (6) with respect to time. This requires evaluating the time derivative of the transformation matrix. Next a skew symmetric matrix needs to be defined to formulate an angular velocity vector in a global coordinate system as described in e.g. [26]. After appropriate manipulations one arrives at

$$\begin{aligned} \dot{R}_x =&\big [-\!(D_x + x + R_0)\sin \psi (t)- (D_y+Y)\cos \theta \cos \psi (t)+ (D_z+Z)\sin \theta \cos \psi (t)\big ]\dot{\psi }(t)\nonumber \\&+ \dot{D}_x\cos \psi (t)- \dot{D}_y\cos \theta \sin \psi (t)+ \dot{D}_z\sin \theta \sin \psi (t)\nonumber \\ \dot{R}_y =&\big [ (D_x + x + R_0)\cos \psi (t)- (D_y+Y)\cos \theta \sin \psi (t)+ (D_z+Z)\sin \theta \sin \psi (t)\big ]\dot{\psi }(t)\nonumber \\&+ \dot{D}_x\sin \psi (t)+ \dot{D}_y\cos \theta \cos \psi (t)- \dot{D}_z\sin \theta \cos \psi (t)\nonumber \\ \dot{R}_z =&\dot{D}_y\sin \theta + \dot{D}_z\cos \theta \end{aligned}$$

(7)

where overdot means time derivative, so $\dot{D}_x$, $\dot{D}_y$ and $\dot{D}_z$ terms correspond to velocities of deformation.

2.2.3 Acceleration vector

Following the same approach as the above one an acceleration vector is obtained:

$$\begin{aligned} \ddot{R}_x =&\big [-\!\!(D_x\!+\!x\!+\!R_0)\sin \psi (t)- (D_y\!+\!Y)\cos \theta \cos \psi (t)+ (D_z\!+\!Z)\sin \theta \cos \psi (t)\big ]{\ddot{\psi }}(t)\nonumber \\&+ \big [-\!\!(D_x \!+\!x\!+\!R_0)\cos \psi (t)+ (D_y\!+\!Y)\cos \theta \sin \psi (t)- (D_z\!+\!Z)\sin \theta \sin \psi (t)\big ]{\dot{\psi }}^2(t)\nonumber \\&+ 2\big [-\!\!\dot{D}_x\sin \psi (t)- \dot{D}_y\cos \theta \cos \psi (t)+ \dot{D}_z\sin \theta \cos \psi (t)\big ]\dot{\psi }(t)\nonumber \\&+ \ddot{D}_x\cos \psi (t)- \ddot{D}_y\cos \theta \sin \psi (t)+\ddot{D}_z\sin \theta \sin \psi (t)\nonumber \\ \ddot{R}_y =&\big [(D_x\!+\!x\!+\!R_0)\cos \psi (t)- (D_y\!+\!Y)\cos \theta \sin \psi (t)+ (D_z\!+\!Z)\sin \theta \sin \psi (t)\big ]{\ddot{\psi }}(t)\nonumber \\&+ \big [ -\!\!(D_x \!+\!x\!+\!R_0)\sin \psi (t)- (D_y\!+\!Y)\cos \theta \cos \psi (t)+ (D_z\!+\!Z)\sin \theta \cos \psi (t)\big ]{\dot{\psi }}^2(t)\nonumber \\&+ 2\big [\dot{D}_x\cos \psi (t)- \dot{D}_y\cos \theta \sin \psi (t)+ \dot{D}_z\sin \theta \sin \psi (t)\big ]\dot{\psi }(t)\nonumber \\&+ \ddot{D}_x\sin \psi (t)+ \ddot{D}_y\cos \theta \cos \psi (t)- \ddot{D}_z\sin \theta \cos \psi (t)\nonumber \\ \ddot{R}_z = &\ddot{D}_y\sin \theta + \ddot{D}_z\cos \theta \end{aligned}$$

(8)

Commenting on the velocity relation (7) and the acceleration formula (8) one can notice that supposing constant angular velocity condition $\dot{\psi }(t)=const.$ and zero pitch angle $\theta =0$ these simplify exactly to the formulations given for cases examined by other researchers e.g. by Choi et al. [8], Librescu and Song [21] or Sina et al. [27].

2.2.4 Displacement field

Following the assumptions given in the section 2.1.2 the displacements of an arbitrary point of the cross-section are defined as (Librescu and Song [21])

$$\begin{aligned} D_x&= u_0(x,t) + \vartheta _y(x,t) \Big (z - n\dfrac{d y}{d s}\Big ) + \vartheta _z(x,t)\Big (y + n\dfrac{d z}{d s}\Big ) - G(n,s)\varphi ^\prime (x,t) \nonumber \\&= u_0(x,t) + \vartheta _y(x,t)\,Z + \vartheta _z(x,t)\,Y - G(n,s)\,\varphi ^\prime (x,t) \nonumber \\ D_y&= v_p\,(x,t) - (Y - y_p)\big (1-\cos \varphi (x,t)\big ) - (Z - z_p)\sin \varphi (x,t) \nonumber \\&\approx v_p\,(x,t) - \frac{1}{2}(Y-y_p)\big (\varphi (x,t)\big )^2 - (Z - z_p)\varphi (x,t) \nonumber \\ D_z&= w_p\,(x,t) + (Y - y_p)\sin \varphi (x,t) - (Z - z_p)\big (1-\cos \varphi (x,t)\big ) \nonumber \\&\approx w_p\,(x,t) + (Y - y_p)\varphi (x,t) - \frac{1}{2}(Z-z_p)\big (\varphi (x,t)\big )^2 \end{aligned}$$

(9)

where $G(s,n)$ is a warping function formulated in Appendix 1, $\varphi (x,t)$ denotes rotation of the cross-section (twist angle) as seen in Fig. 2 and prime denotes differentiation with respect to the span coordinate ($x$). Angles $\vartheta _y(x,t)=\gamma _{xz}-w_p^\prime$ and $\vartheta _z(x,t)=\gamma _{xy}-v_p^\prime$ represent cross-sections’ rotations about respective axes $y$ and $z$ at pole P. The coordinates associated with off-mid-line points are denoted by capital letters ($Y$, $Z$), while mid-line ones are denoted by small $y$ and $z$ as already has been explained. Moreover, in the above formula the moderately large rotations are allowed by the approximation $\cos \varphi \approx 1 - \varphi ^2/2$. The later linearisation of the respective resulting equations is performed after incorporation of this approximation.

2.2.5 Strains

We restrict our modelling to linear elastic range, therefore we consider only linear strains. The axial and circumferential-axial ones are split into mid-line terms (superscript $( \cdot)^{(0)}$) and off-mid-line ones (superscript $(\cdot )^{(1)}$) as proposed by Librescu and Song [21]

$$\begin{aligned} \varepsilon _{xx} =\varepsilon _{xx}^{(0)} + n\varepsilon _{xx}^{(1)} \end{aligned}$$

(10a)

$$\begin{aligned} \gamma _{xs} = \gamma _{xs}^{(0)} + n\gamma _{xs}^{(1)} \end{aligned}$$

(10b)

$$\begin{aligned} \gamma _{xn} = \gamma _{xn}^{(0)} \end{aligned}$$

(10c)

It should be noted that considering linearised displacement field of equations (9) the following strains $(\varepsilon _{yy}=\varepsilon _{zz}=\gamma _{yz})$ are identically zero. The respective parts are defined in terms of mid-line coordinates

$$\begin{aligned} \varepsilon _{xx}^{(0)} = u_{0}^{\prime } + z\vartheta _y^{\prime } + y\vartheta _z^{\prime } - G^{(0)}(s)\varphi ^{\prime \prime } \end{aligned}$$

(11a)

$$\begin{aligned} \varepsilon _{xx}^{(1)} = -\frac{dy}{ds}\vartheta _y^{\prime } + \frac{dz}{ds}\vartheta _z^{\prime } - G^{(1)}(s)\varphi ^{\prime \prime } \end{aligned}$$

(11b)

$$\begin{aligned} \gamma _{xs}^{(0)} = \bar{\gamma }_{xs}^{(0)} + g^{(0)}(s)\varphi ^{\prime } \end{aligned}$$

(11c)

$$\begin{aligned} \bar{\gamma }_{xs}^{(0)} = (\vartheta _y+ w_{p}^{\prime })\frac{dz}{ds} + (\vartheta _z+ v_{p}^{\prime })\frac{dy}{ds} \end{aligned}$$

(11d)

$$\begin{aligned} \gamma _{xs}^{(1)} = g^{(1)}(s)\varphi ^{\prime } \end{aligned}$$

(11e)

$$\begin{aligned} \gamma _{xn}^{(0)} =-(\vartheta _y+ w_{p}^{\prime })\frac{dy}{ds} + (\vartheta _z+ v_{p}^{\prime } )\frac{dz}{ds}, \end{aligned}$$

(11f)

and primary and secondary warping functions $G^{(0)}(s)$, $G^{(1)}(s)$ and $g^{(0)}$, $g^{(1)}$ functions formulas are given explicitly in the Appendix 1.

2.3 Energies

Following the displacement field, the position vector formula and acceleration dependencies (see Sects. 2.2.1, 2.2.2 and 2.2.3) the formulas for the appropriate energies are derived in subsequent paragraphs.

2.3.1 Potential energy

The potential energy of the elastic system under consideration is given by

$$\begin{aligned} U&= \frac{1}{2}\int \limits _0^{\!\!l}\!\!\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \big (\sigma _{xx}\varepsilon _{xx} + \sigma _{xn}\gamma _{xn} + \sigma _{xs}\gamma _{xs} \big ) dndsdx= \nonumber \\&\frac{1}{2}\int \limits _0^{l}\!\!{\int \limits _c \big [ N_{xx}\varepsilon _{xx}^{(0)} + L_{xx}\varepsilon _{xx}^{(1)} + N_{xn}\gamma _{xn}^{(0)} + N_{xs}\gamma _{xs}^{(0)} + L_{xs}\gamma _{xs}^{(1)} \big ] dsdx} \end{aligned}$$

(12)

whereas formulations for stress resultants and stress couples (see Fig. 3) as defined in (95–97) were used. Integral’s subscript $c$ denotes integration along the mid-line contour. The variation of the potential energy arising from Eq. (12) is

$$\begin{aligned} \delta U=\int \limits _0^{l}\!\!\int \limits _c \big [ N_{xx}\delta \varepsilon _{xx}^{(0)} + L_{xx}\delta \varepsilon _{xx}^{(1)} + N_{xn}\delta \gamma _{xn}^{(0)} + N_{xs}\delta \gamma _{xs}^{(0)} + L_{xs}\delta \gamma _{xs}^{(1)} \big ] dsdx. \end{aligned}$$

(13)

Fig. 3

In-plane and transversal stress resultants and stress couples acting on a beam’s wall element

The requested variations of strains given by formulas (11) are

$$\begin{aligned} \delta \varepsilon _{xx}^{(0)} = \delta u_{0}^{\prime } + z\delta \vartheta _y^{\prime } + y\delta \vartheta _z^{\prime } - G^{(0)}(s)\delta \varphi ^{\prime \prime } \end{aligned}$$

(14a)

$$\begin{aligned} \delta \varepsilon _{xx}^{(1)} = - \frac{dy}{ds}\delta \vartheta _y^{\prime } + \frac{dz}{ds}\delta \vartheta _z^{\prime } - G^{(1)}(s)\delta \varphi ^{\prime \prime } \end{aligned}$$

(14b)

$$\begin{aligned} \delta \gamma _{xs}^{(0)} =\frac{dz}{ds}\delta \vartheta _y+ \frac{dz}{ds}\delta w_{p}^{\prime } + \frac{dy}{ds}\delta \vartheta _z+ \frac{dy}{ds}\delta v_{p}^{\prime } + g^{(0)}(s)\delta \varphi ^{\prime } \end{aligned}$$

(14c)

$$\begin{aligned} \delta \gamma _{xs}^{(1)} = g^{(1)}(s)\delta \varphi ^{\prime } \end{aligned}$$

(14d)

$$\begin{aligned} \delta \gamma _{xn}^{(0)} = - \frac{dy}{ds}\delta \vartheta _y- \frac{dy}{ds}\delta w_{p}^{\prime } + \frac{dz}{ds}\delta \vartheta _z+ \frac{dz}{ds}\delta v_{p}^{\prime } \end{aligned}$$

(14e)

Integrating given in Appendix 2 formulas for stress resultants (95, 96) and stress couples (97) along the mid-line contour the following one-dimensional stress measures are introduced

$$\begin{aligned} T_{x}&= \int \limits _c N_{xx} ds \quad \quad \quad \text {the\,axial\,force} \end{aligned}$$

(15)

$$\begin{aligned} Q_{y}&= \int \limits _c \Big ( N_{xs}\frac{dy}{ds} + N_{xn}\frac{dz}{ds} \Big )ds \quad \quad \quad {\text {the\,shear\,force\,in}}\,y\hbox {-direction} \end{aligned}$$

(16)

$$\begin{aligned} Q_{z}&= \int \limits _c \Big ( N_{xs}\frac{dz}{ds} - N_{xn}\frac{dy}{ds} \Big )ds \quad \quad \quad {\text {the\,shear\,force\,in}}\,z\hbox {-direction} \end{aligned}$$

(17)

$$\begin{aligned} M_{x} &= \int \limits_c \Big ( g^{(0)}(s)N_{xs} + g^{(1)}(s)L_{xs} \Big ) ds \quad \quad \quad {\text {the\,twisting\,moment\,about}}\,x\hbox {-axis} \end{aligned}$$

(18)

$$\begin{aligned} M_{y}&= \int \limits _c \Big ( zN_{xx} - L_{xx}\frac{dy}{ds}\Big ) ds \quad \quad \quad {\text {the\,bending\,moment\,in}}\, y\hbox {-axis} \end{aligned}$$

(19)

$$\begin{aligned} M_{z}&= \int \limits _c \Big ( yN_{xx} + L_{xx}\frac{dz}{ds}\Big ) ds \quad \quad \quad {\text {the\,bending\,moment\,in}} \,z\hbox {-axis} \end{aligned}$$

(20)

$$\begin{aligned} B_{w}&= \int \limits _c \big (G^{(0)}(s)N_{xx} + G^{(1)}(s)L_{xx} \big ) ds \quad \quad \quad \text {the\,warping\,torque,\, bimoment} \end{aligned}$$

(21)

Therefore considering equations (14a) and the above given stress measures, relation (13) after integration by parts and reordering takes the final form

$$\begin{aligned} \delta U = \int \limits _{0}^{l} \Big \lbrace&-T_{x}^{\prime }\delta u_{0} - Q_{y}^{\prime }\delta v_{p} - Q_{z}^{\prime }\delta w_{p} - \nonumber \\&\big (Q_{z} - M_{y}^{\prime }\big )\delta \vartheta _y- \big (Q_{y} - M_{z}^{\prime }\big )\delta \vartheta _z- \big (M_{x}^{\prime } + B_{w}^{\prime \prime }\big )\delta \varphi \Big \rbrace dx\! + \nonumber \\&T_{x}\delta u_{0}\Big |_{x=0}^{x=l} + Q_{y}\delta v_{p} \Big |_{x=0}^{x=l} + Q_{z}\delta w_{p} \Big |_{x=0}^{x=l} + \nonumber \\&M_{y}\delta \vartheta _y\Big |_{x=0}^{x=l} + M_{z}\delta \vartheta _z\Big |_{x=0}^{x=l} + \big (M_{x} + B_{w}^{\prime }\big )\delta \varphi \Big |_{x=0}^{x=l} - B_{w}\delta \varphi ^{\prime }\Big |_{x=0}^{x=l} \end{aligned}$$

(22)

Appearing in the above one-dimensional stress measures might be expressed in terms of basic unknown functions of the problem (or their spatial derivatives) i.e. $u_0(x,t)$, $v_p(x,t)$, $w_p(x,t)$, $\vartheta _y(x,t)$, $\vartheta _z(x,t)$ and $\varphi (x,t)$. To do this the strain definitions (11) are substituted into stress resultants and stress couples definitions as given in (104)

$$\begin{aligned} N_{xx}(s,x)&= K_{11}\varepsilon _{xx}^{(0)} + K_{12}\bar{\gamma }_{xs}^{(0)} + K_{13}\varphi ^\prime + K_{14}\varepsilon _{xx}^{(1)} \end{aligned}$$

(23)

$$\begin{aligned} N_{xs}(s,x)&= K_{21}\varepsilon _{xx}^{(0)} + K_{22}\bar{\gamma }_{xs}^{(0)} + K_{23}\varphi ^\prime + K_{24}\varepsilon _{xx}^{(1)} \end{aligned}$$

(24)

$$\begin{aligned} L_{xx}(s,x)&= K_{41}\varepsilon _{xx}^{(0)} + K_{42}\bar{\gamma }_{xs}^{(0)} + K_{43}\varphi ^\prime + K_{44}\varepsilon _{xx}^{(1)} \end{aligned}$$

(25)

$$\begin{aligned} L_{xs}(s,x)&= K_{51}\varepsilon _{xx}^{(0)} + K_{52}\bar{\gamma }_{xs}^{(0)} + K_{53}\varphi ^\prime + K_{54}\varepsilon _{xx}^{(1)} \end{aligned}$$

(26)

$$\begin{aligned} N_{xn}(s,x)&= C_{44}\gamma _{xn}^{(0)} \end{aligned}$$

(27)

$$\begin{aligned} N_{sn}(s,x)&= C_{45}\gamma _{xn}^{(0)} \end{aligned}$$

(28)

and next substituted in (15–21). After unknowns reordering one arrives at final formulas for one-dimensional stress measures

$$\begin{aligned} T_{x}=&a_{11}u_{0}^{\prime } + a_{15}\vartheta _y+ a_{13}\vartheta _y^{\prime } + a_{14}\vartheta _z+ a_{12}\vartheta _z^{\prime } + a_{14}v_{p}^{\prime } + a_{15}w_{p}^{\prime } + a_{17}\varphi ^{\prime } - a_{16}\varphi ^{\prime \prime }, \nonumber \\ Q_{y}=&a_{14}u_{0}^{\prime } + a_{45}\vartheta _y+ a_{34}\vartheta _y^{\prime } + a_{44}\vartheta _z+ a_{24}\vartheta _z^{\prime } + a_{44}v_{p}^{\prime } + a_{45}w_{p}^{\prime } + a_{47}\varphi ^{\prime } - a_{46}\varphi ^{\prime \prime }, \nonumber \\ Q_{z}=&a_{15}u_{0}^{\prime } + a_{55}\vartheta _y+ a_{35}\vartheta _y^{\prime } + a_{45}\vartheta _z+ a_{25}\vartheta _z^{\prime } + a_{45}v_{p}^{\prime } + a_{55}w_{p}^{\prime } + a_{57}\varphi ^{\prime } - a_{56}\varphi ^{\prime \prime }, \nonumber \\ M_{x}=&a_{17}u_{0}^{\prime } + a_{57}\vartheta _y+ a_{37}\vartheta _y^{\prime } + a_{47}\vartheta _z+ a_{27}\vartheta _z^{\prime } + a_{47}v_{p}^{\prime } + a_{57}w_{p}^{\prime } + a_{77}\varphi ^{\prime } - a_{67}\varphi ^{\prime \prime }, \nonumber \\ M_{y}=&a_{13}u_{0}^{\prime } + a_{35}\vartheta _y+ a_{33}\vartheta _y^{\prime } + a_{34}\vartheta _z+ a_{23}\vartheta _z^{\prime } + a_{34}v_{p}^{\prime } + a_{35}w_{p}^{\prime } + a_{37}\varphi ^{\prime } - a_{36}\varphi ^{\prime \prime }, \nonumber \\ M_{z}=&a_{12}u_{0}^{\prime } + a_{25}\vartheta _y+ a_{23}\vartheta _y^{\prime } + a_{24}\vartheta _z+ a_{22}\vartheta _z^{\prime } + a_{24}v_{p}^{\prime } + a_{25}w_{p}^{\prime } + a_{27}\varphi ^{\prime } - a_{26}\varphi ^{\prime \prime }, \nonumber \\ B_{w}=&a_{16}u_{0}^{\prime } + a_{56}\vartheta _y+ a_{36}\vartheta _y^{\prime } + a_{46}\vartheta _z+ a_{26}\vartheta _z^{\prime } + a_{46}v_{p}^{\prime } + a_{56}w_{p}^{\prime } + a_{67}\varphi ^{\prime } - a_{66}\varphi ^{\prime \prime }. \end{aligned}$$

(29)

where the coefficients $a_{ij}$ ($i,j=1,\ldots 7$) are defined in Appendix 2.

2.3.2 Kinetic energy

The kinetic energy of the system is defined

$$\begin{aligned} T = \dfrac{1}{2}\int \limits _{V}\!\!\rho \, \dot{\mathbf {R}}^ {\text T}\dot{\mathbf {R}}\, dV \end{aligned}$$

(30)

where designation $\rho$ refers to average composite material density and $V$ refers to volume element and $dV=dndsdx$. From the above we obtain the variation

$$\delta T = \int\limits _{V}\!\!\rho \, \dot{\mathbf {R}}{{}^{\text {T}}}\delta \dot{\mathbf {R}} dV = \int \limits _{V}\!\!\rho \frac{\partial }{\partial t}\Big (\dot{\mathbf {R}}{{}^{\text {T}}}\delta {\mathbf {R}}\Big ) dV - \int \limits _{V}\!\!\rho \ddot{\mathbf {R}}{{}^\text {T}}\delta {\mathbf {R}} dV$$

(31)

Integration of the above relation over the time interval $\langle t_1,t_2\rangle$ and keeping in mind that $\delta R_i$ vanishes at time $t=t_1$ and $t=t_2$, yields the kinetic energy variation term for the Hamiltonian principle (1)

$$\int \limits _{t_1}^{t_2}\!\!\delta T d t = -\int \limits _{t_1}^{t_2}\!\!\int \limits _{V}\!\!\rho\,{\ddot{\mathbf {R}}^{\text {T}}}\delta {\mathbf {R}} d V d t = -\int \limits _{t_1}^{t_2}\!\!\int \limits _{V}\!\!\rho \big (\ddot{R}_x\delta R_x + \ddot{R}_y\delta {R}_y + \ddot{R}_z\delta R_z\big )d V d t$$

(32)

Cartesian coordinates of the position vector variation $\delta \mathbf {R}$, as well as appropriate basic unknowns terms are given in Appendix 3.

2.3.3 Work of external forces

Consider the general case of beam loading expressed in terms of

• $F_{i}$—body forces per unit mass, with corresponding external work $W_{ext,1}$,

• $q_{i}$—surface loads per unit area applied at the beam’s middle surface with external work $W_{ext,2}$,

• $t_{i}$—traction loads per unit area applied at longitudinal (side) sections of open cross-section beams with resulting external work $W_{ext,3}$,

• $\hat{t}_{i}$—traction loads per unite area applied in beams with open cross-sections of at free edges of the cross-section with external work $W_{ext,4}$,

• $T_{ext,z}$—torque applied at hub for nonconstant rotational speed, $W_{ext,5}$.

The respective terms are as follows

$$\begin{aligned} W_{ext,1}& = \int \limits _0^{l}\!\!\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} {\rho _{0}\big (F_{x}D_{x}+F_{y}D_{y} +F_{z}D_{z} \big )} dndsdx \nonumber \\ W_{ext,2}&= \int \limits _0^{l}\!\!\int \limits _c \big (q_{x} \overline{D}_{x} + q_{y} \overline{D}_{y} + q_{z} \overline{D}_{z} \big ) dsdx \nonumber \\ W_{ext,3}& = n_{x}\bigg [\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \big (t_{x}D_{x}+t_{y}D_{y}+t_{z}D_{z} \big ) dnds \bigg ]\!\bigg |_{x=0}^{x=l} \qquad {\text{with}}\quad n_{x}= {\left\{ \begin{array}{ll} -1 & x=0\\ 1 & x=l\\ 0 & {\text{elsewhere}}\\ \end{array}\right. } \nonumber \\ W_{ext,4}&= n_{s}\bigg [\int \limits _0^{\;l}\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \big(\hat{t}_{x}D_{x}+\hat{t}_{y}D_{y}+\hat{t}_{z}D_{z} \big ) dndx \bigg ]\!\bigg |_{s=s_{1}}^{s=s_{2}}\qquad {\text{with}}\quad n_{s}={\left\{ \begin{array}{ll} -1 & s=s_{1}\\ 1 & s=s_{2}\\ 0 &{\text{elsewhere}}\\ \end{array}\right. } \nonumber \\ W_{ext,5}& = T_{ext,z}\psi (t) \end{aligned}$$

(33)

whereas superposed bar indicates displacements of the mid-surface contour points ($n=0$). Therefore, the total work and its perturbation are as follows

$$\begin{aligned} W_{ext} =&W_{ext,1} + W_{ext,2} + W_{ext,3} + W_{ext,4} + W_{ext,5} \nonumber \\ \delta W_{ext} =&\delta W_{ext,1}+\delta W_{ext,2}+\delta W_{ext,3}+\delta W_{ext,4}+\delta W_{ext,5} \end{aligned}$$

(34)

Then the external works equations system (33) using also displacement relations (9) takes the form

$$\begin{aligned} W_{ext,1}&= \int \limits _0^{l}\!\!\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}}\!\! \rho _{0} \Big [F_{x}u_{0}+F_{x}Z\vartheta _y+F_{x}Y\vartheta _z-F_{x}G(n,s)\varphi ^{\prime } + F_{y}v_{p} + F_{z}w_{p} + \nonumber \\&\quad \quad \quad [F_{z}( Y-y_{p})-F_{y}(Z-z_{p})]\varphi \Big ]dndsdx \nonumber \\ W_{ext,2}&= \int \limits _0^{l}\!\!\int \limits _c \Big [q_{x}u_{0} + q_{x}z\vartheta _y+ q_{x}y\vartheta _z- q_{x}G^{(0)}(s)\varphi ^{\prime } + q_{y}v_{p} + q_{z}w_{p} + \nonumber \\&\quad \quad \quad [q_{z}(y-y_{p}) - q_{y}(z-z_{p}) ]\varphi \Big ]dsdx \nonumber \\ W_{ext,3}&= \bigg [n_{x}\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \big [t_{x}u_{0}+t_{x}Z\vartheta _y+t_{x}Y\vartheta _z-t_{x}G(n,s)\varphi ^{\prime } + t_{y}v_{p} + t_{z}w_{p} + \nonumber \\&\quad \quad \quad [t_{z}(Y-y_{p}) - t_{y}(Z-z_{p})]\varphi \big ]dnds \bigg ] \bigg |_{x=0}^{x=l} \nonumber \\ W_{ext,4}&= \delta _{0}n_{s}\bigg [\int \limits _0^{l}\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \big [\hat{t}_{x}u_{0}+\hat{t}_{x}Z\vartheta _y+ \hat{t}_{x}Y\vartheta _z- \hat{t}_{x}G(n,s)\varphi ^{\prime } + \hat{t}_{y}v_{p}+\hat{t}_{z}w_{p} + \nonumber \\&\quad \quad \quad [\hat{t}_{z}(Y-y_{p})-\hat{t}_{y}(Z-z_{p}) ]\varphi \big ]dndx \bigg ]\bigg |_{s=s_{1}}^{s=s_{2}} \end{aligned}$$

(35)

where $\delta _0$ is a tag indicting case of open ($\delta _0=1$) or closed case ($\delta _0=0$). Formulas for the appropriate work terms in (35) are given in Appendix 4.

2.4 Equations of motion

In this section the final form of the equations of motions of the system is derived. Starting from Eq. (1) and considering Eqs. (32), (13), and (121) the least action principle results in the relation

$$\begin{aligned} \delta J&= \int \limits _{t_{1}}^{t_{2}}\Bigg \{ -\int \limits _0^{l}\!\! \int \limits _c\! \int \limits _{{-h}/{2}}^{{h}/{2}}{\rho \ddot{\mathbf {R}}}^{\text {T}}\delta {\mathbf {R}} dndsdx\\&-\int \limits _0^{l}\!\!\int \limits _c \big [ N_{xx}^{m}\delta \varepsilon _{xx}^{(0)} + L_{xx}^{m}\delta \varepsilon _{xx}^{(1)} + N_{xn}^{m} \delta \gamma _{xn}^{(0)} + N_{xs}^{m}\delta \gamma _{xs}^{(0)} + L_{xs}^{m} \delta \gamma _{xs}^{(1)} \big ] dsdx \\&+ \delta W_{ext,1}+\delta W_{ext,2} +\delta W_{ext,3}+\delta W_{ext,4}+\delta W_{ext,5} \Bigg \} dt =0. \end{aligned}$$

(36)

Considering for variation of potential energy (22), variation of kinetic energy Eqs. (110)–(115) and variation of external work equation (122), the least action principle equation (36), after integration with respect to time leads to the following equations with respect to variation of problem’s independent variables

• $\delta \psi (t)$

  $$\begin{aligned} -& B_{22}{\ddot{\psi }}(t)- B_{14}l{\ddot{\psi}}(t)\cos ^{2}\theta - B_{13}l{\ddot{\psi }}(t)\sin ^{2}\theta + 2B_{15}l{\ddot{\psi }}(t)\cos \theta \sin \theta \nonumber \\&- \int \limits _0^{l} \Big [2 B_{1}(R_{0} + x)u_{0}{\ddot{\psi }}(t)+ 2 \big (B_{12}\cos ^{2}\theta - B_{11}\sin \theta \cos \theta \big )v_{p}{\ddot{\psi }}(t)\nonumber \\&+ 2 \big (B_{11}\sin ^{2}\!\theta - B_{12}\sin \theta \cos \theta \big )w_{p}{\ddot{\psi }}(t)+ 2 B_{11}(R_{0}+x)\vartheta _y{\ddot{\psi }}(t)\nonumber \\&+ 2B_{12}(R_{0}\!+\!x)\vartheta _z{\ddot{\psi }}(t)+ 2\big (B_{17}\sin ^{2}\!\theta \! -\! B_{18}\cos ^{2}\theta \big )\varphi {\ddot{\psi }}(t)\nonumber \\&- 2B_{7}(R_{0}\!+\!x)\varphi ^{\prime } + 2 \big (B_{16} - B_{19}\big )\varphi {\ddot{\psi }}(t)\sin \theta \cos \theta \Big ]dx \nonumber \\&- \int \limits _0^{l}\!\Big [\big (B_{11}\sin \theta \! - \!B_{12}\cos \theta \big )\ddot{u}_{0} \! +\! B_{1}(R_{0}+x)\ddot{v}_{p}\cos \theta - B_{1}(R_{0}+x)\ddot{w}_{p}\sin \theta \nonumber \\&+ \big (B_{13}\sin \theta - B_{15}\cos \theta \big ){\ddot{\vartheta }}_y+ \big (B_{15}\sin \theta - B_{14}\cos \theta \big ){\ddot{\vartheta }}_z\nonumber \\&+ \big (B_{9}\cos \theta - B_{8}\sin \theta \big )\ddot{\varphi }^{\prime } - \big (B_{3}\sin \theta + B_{2}\cos \theta \big )(R_{0} + x)\ddot{\varphi } \Big ]dx \nonumber \\&-\int \limits _0^{l} \Big [2 B_{1}(R_{0}+x)\dot{u}_{0}\dot{\psi }(t)- 2B_{11}\dot{v}_{p}\dot{\psi }(t)\sin \theta \cos \theta + 2B_{12}\dot{v}_{p}\dot{\psi }(t)\cos ^{2}\theta \nonumber \\&- 2B_{12}\dot{w}_{p}\dot{\psi }(t)\sin \theta \cos \theta + 2B_{11}\dot{w}_{p}\dot{\psi }(t)\sin ^{2}\theta + 2 B_{11}(R_{0}+x){\dot{\vartheta }}_y\dot{\psi }(t)\nonumber \\&+ 2 B_{12}(R_{0}+x){\dot{\vartheta }}_z\dot{\psi }(t)- 2 B_{7}(R_{0}+x)\dot{\varphi }^{\prime }\dot{\psi }(t)+ 2 B_{17}\dot{\varphi }\dot{\psi }(t)\sin ^{2}\theta \nonumber \\&- 2 B_{18}\dot{\varphi }\dot{\psi }(t)\cos ^{2}\theta + 2(B_{16}-B_{19})\dot{\varphi }\dot{\psi }(t)\sin \theta \cos \theta \Big ]dx + T_{ext,z} = \;0 \end{aligned}$$

  (37)

• $\delta u_{0}$,

  $$\begin{aligned}&- B_{1} \ddot{u}_0 - B_{12}{\ddot{\vartheta }}_z- B_{11}{\ddot{\vartheta }}_y+ B_{7}\ddot{\varphi }^\prime + 2 B_{1}\dot{v}_p\dot{\psi }(t)\cos \theta - 2 B_{2}\dot{\varphi }\dot{\psi }(t)\cos \theta \nonumber \\&- 2B_{1}\dot{w}_p\dot{\psi }(t)\sin \theta - 2B_{3}\dot{\varphi }\dot{\psi }(t)\sin \theta + B_{1} (R_0+x+u_0){\dot{\psi }}^2(t)+ B_{12}\vartheta _z{\dot{\psi }}^2(t)\nonumber \\&+ B_{11}\vartheta _y{\dot{\psi }}^2(t)- B_{7}\varphi ^\prime {\dot{\psi }}^2(t)- B_{1} w_p{\ddot{\psi }}(t)\sin \theta - B_{3}\varphi {\ddot{\psi }}(t)\sin \theta - B_{11}{\ddot{\psi }}(t)\sin \theta \nonumber \\&+ B_{1} v_p {\ddot{\psi }}(t)\cos \theta - B_{2}\varphi {\ddot{\psi }}(t)\cos \theta + B_{12}{\ddot{\psi }}(t)\cos \theta + T_{x}^{\prime }+P_{ext,x}+\delta _{0}\hat{P}_{ext,x} = 0 \end{aligned}$$

  (38)

  with boundary conditions,

  $$\begin{aligned} u_{0} \big |_{x=0}=0, \qquad \left[ T_{x} + n_{x}Q_{ext\mathrm {,}x}\right] \!\big |_{x=l}=0 \end{aligned}$$

  (39)

• $\delta v_{p}$

  $$\begin{aligned}B_1 \ddot{v}_p + B_{2}\ddot{\varphi } - 2 B_{1} \dot{u}_0\dot{\psi }(t)\cos \theta - 2 B_{12}{\dot{\vartheta }}_z\dot{\psi }(t)\cos \theta \\- 2 B_{11}{\dot{\vartheta }}_y\dot{\psi }(t)\cos \theta \nonumber + 2 B_{7}\dot{\varphi }^\prime \dot{\psi }(t)\cos \theta \\- B_{1} w_p{\dot{\psi }}^2(t)\sin \theta \cos \theta - B_{3}\varphi {\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\- B_{11}{\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{1}v_p{\dot{\psi }}^2(t)\cos ^2\theta \\- B_{2}\varphi {\dot{\psi}}^2(t)\cos ^2\theta \nonumber + B_{12}{\dot{\psi }}^2(t)\cos ^2\theta - B_{1} (R_0 + x + u_0)\\{\ddot{\psi }}(t)\cos \theta - B_{12}\vartheta _z{\ddot{\psi }}(t)\cos \theta \nonumber - B_{11}\vartheta _y{\ddot{\psi }}(t)\cos \theta \\ + B_{7}\varphi ^\prime {\ddot{\psi }}(t)\cos \theta + Q_{y}^{\prime } + P_{ext,y} + \delta _{0}\hat{P}_{ext,y} = 0 \end{aligned}$$

  (40)

  with boundary conditions,

  $$\begin{aligned} v_{p} \big |_{x=0}=0,\qquad \left[ Q_{y} + n_{x}Q_{ext,y}\right] \! \big |_{x=l} = 0 \end{aligned}$$

  (41)

• $\delta w_{p}$

  $$\begin{aligned}&- B_{1}\ddot{w}_p - B_{3}\ddot{\varphi } + 2 B_{1}\dot{u}_0\,\dot{\psi }(t)\sin \theta + 2 B_{12}{\dot{\vartheta }}_z\dot{\psi }(t)\sin \theta + 2 B_{11}{\dot{\vartheta }}_y\dot{\psi }(t)\sin \theta \nonumber \\&- 2 B_{7}\dot{\varphi }^\prime \dot{\psi }(t)\sin \theta + B_{1}w_p{\dot{\psi }}^2(t)\sin ^2\theta + B_{3}\varphi {\dot{\psi }}^2(t)\sin ^2\theta + B_{11}{\dot{\psi }}^2(t)\sin ^2\theta \nonumber \\&- B_{1}v_p{\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{2}\varphi {\dot{\psi }}^2(t)\sin \theta \!\cos \theta - B_{12}{\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\&+ B_{1} (R_0\!+\!x\!+\!u_0) {\ddot{\psi }}(t)\sin \theta + B_{12}\vartheta _z{\ddot{\psi }}(t)\sin \theta + B_{11}\vartheta _y{\ddot{\psi }}(t)\sin \theta \nonumber \\&- B_{7}\varphi ^\prime {\ddot{\psi }}(t)\sin \theta + Q_{z}^{\prime } + P_{ext,z}+\delta _{0}\hat{P}_{ext,z} = 0 \end{aligned}$$

  (42)

  with boundary conditions,

  $$\begin{aligned} w_{p} \big |_{x=0}=0, \qquad \left[ Q_{z} + n_{x}Q_{ext,z} \right] \!\big |_{x=l}=0 \end{aligned}$$

  (43)

• $\delta \vartheta _y$

  $$\begin{aligned}&-B_{11}\ddot{u}_0 - B_{13}{\ddot{\vartheta }}_y- B_{15}{\ddot{\vartheta }}_z+ B_{8} \ddot{\varphi }^\prime + 2 B_{11}\,\dot{v}_p\,\dot{\psi }(t)\cos \theta - 2 B_{16}\dot{\varphi }\dot{\psi }(t)\cos \theta \nonumber \\&- 2 B_{11}\dot{w}_p\dot{\psi }(t)\sin \theta - 2 B_{17}\dot{\varphi }\dot{\psi }(t)\sin \theta + B_{11}(R_0 + x + u_0){\dot{\psi }}^2(t)+ B_{15}\vartheta _z{\dot{\psi }}^2(t)\nonumber \\&+ B_{15}\vartheta _y{\dot{\psi }}^2(t)- B_{8}\varphi ^\prime {\dot{\psi }}^2(t)- B_{11}w_p{\ddot{\psi }}(t)\sin \theta - B_{17}\varphi {\ddot{\psi }}(t)\sin \theta + B_{11}v_p{\ddot{\psi }}(t)\cos \theta \nonumber \\&- B_{16}\varphi {\ddot{\psi }}(t)\cos \theta - B_{13}{\ddot{\psi }}(t)\sin \theta + B_{15}{\ddot{\psi }}(t)\cos \theta - Q_{z}+M_{y}^{\prime } + m_{ext,y} + \delta _{0}\hat{m}_{ext,y} = 0 \end{aligned}$$

  (44)

  with boundary conditions,

  $$\begin{aligned} \vartheta _y\big |_{x=0}=0, \qquad \left[ M_{y}+n_{x}M_{ext,y} \right] \! \big |_{x=l} = 0 \end{aligned}$$

  (45)

• $\delta \vartheta _z$

  $$\begin{aligned}&- B_{12}\ddot{u}_0 - B_{15}{\ddot{\vartheta }}_y- B_{14}{\ddot{\vartheta }}_z+ B_{9} \ddot{\varphi }^\prime + 2 B_{12}\dot{v}_p\,\dot{\psi }(t)\cos \theta - 2 B_{18}\dot{\varphi }\dot{\psi }(t)\cos \theta \nonumber \\&- 2 B_{12}\dot{w}_p\dot{\psi }(t)\sin \theta - 2 B_{19}\dot{\varphi }\dot{\psi }(t)\sin \theta + B_{12}(R_0 + x + u_0){\dot{\psi }}^2(t)+ B_{14}\vartheta _z{\dot{\psi }}^2(t)\nonumber \\&+ B_{15}\vartheta _y{\dot{\psi }}^2(t)- B_{9}\varphi ^\prime {\dot{\psi }}^2(t)- B_{12}w_p{\ddot{\psi }}(t)\sin \theta - B_{19}\varphi {\ddot{\psi }}(t)\sin \theta + B_{12}v_p{\ddot{\psi }}(t)\cos \theta \nonumber \\&- B_{18}\varphi {\ddot{\psi }}(t)\cos \theta - B_{15}{\ddot{\psi }}(t)\sin \theta + B_{14}{\ddot{\psi }}(t)\cos \theta - Q_{y}+M_{z}^{\prime } + m_{ext,z} + \delta _{0}\hat{m}_{ext,z} = 0 \end{aligned}$$

  (46)

  with boundary conditions,

  $$\begin{aligned} \vartheta _z\big |_{x=0}=0, \qquad \left[ M_{z} + n_{x}M_{ext,z} \right] \! \big |_{x=l}=0 \end{aligned}$$

  (47)

• $\delta \varphi$

  $$\begin{aligned}&B_{2}\ddot{v}_{p} - B_{4}\ddot{\varphi } - B_{3}\ddot{w}_{p} - B_{5}\ddot{\varphi } \nonumber \\&+ B_{3}(R_{0}+x)\varphi {\ddot{\psi }}(t)\cos \theta + B_{2}(R_{0}+x+u_{0}){\ddot{\psi }}(t)\cos \theta \nonumber \\&- B_{2}(R_{0}+x)\varphi {\ddot{\psi }}(t)\sin \theta + B_{3}(R_{0}+x+u_{0}){\ddot{\psi }}(t)\sin \theta \nonumber \\&+ B_{16}\vartheta _y{\ddot{\psi }}(t)\cos \theta + B_{17}\vartheta _y{\ddot{\psi }}(t)\sin \theta + B_{18}\vartheta _z{\ddot{\psi }}(t)\cos \theta + B_{19}\vartheta _z{\ddot{\psi }}(t)\sin \theta \nonumber \\&- B_{20}\varphi ^{\prime }{\ddot{\psi }}(t)\cos \theta - B_{21}\varphi ^{\prime }{\ddot{\psi }}(t)\sin \theta \nonumber \\&- B_{18}{\dot{\psi }}^2(t)\cos ^{2}\theta + B_{17}{\dot{\psi }}^2(t)\sin ^{2}\theta + \big (B_{16} - B_{19}\big ){\dot{\psi }}^2(t)\cos \theta \sin \theta \nonumber \\&- B_{2}v_{p}{\dot{\psi }}^2(t)\cos ^{2}\theta - B_{3}v_{p}{\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{2}w_{p}{\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\&+ B_{3}w_{p}{\dot{\psi }}^2(t)\sin ^{2}\theta + B_{4}\varphi {\dot{\psi }}^2(t)\cos ^{2}\theta - B_{19}\varphi {\dot{\psi }}^2(t)\cos ^{2}\theta + B_{5}\varphi {\dot{\psi }}^2(t)\sin ^{2}\theta \nonumber \\&- B_{16}\varphi {\dot{\psi }}^2(t)\sin ^{2}\theta + B_{17}\varphi {\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{18}\varphi {\dot{\psi }}^2(t)\cos \theta \sin \theta \nonumber \\&+ 2 B_{2}\dot{u}_{0}\dot{\psi }(t)\cos \theta + 2 B_{3}\dot{u}_{0}\dot{\psi }(t)\sin \theta \nonumber \\&+ 2 B_{16}{\dot{\vartheta }}_y\dot{\psi }(t)\cos \theta + 2 B_{17}{\dot{\vartheta }}_y\dot{\psi }(t)\sin \theta + 2 B_{18}{\dot{\vartheta }}_z\dot{\psi }(t)\cos \theta + 2 B_{19}{\dot{\vartheta }}_z\dot{\psi }(t)\sin \theta \nonumber \\&+ 2 B_{6}\varphi {\dot{\psi }}^2(t)\sin \theta \cos \theta - 2 B_{20}\dot{\varphi }^{\prime }\dot{\psi }(t)\cos \theta - 2 B_{21}\dot{\varphi }^{\prime }\dot{\psi }(t)\sin \theta \nonumber \\&+ \big [B_{7}(R_{0}+x + u_0)\big ]^{\prime }{\dot{\psi }}^2(t)+ \big (B_{7}v_{p}\big )^{\prime }{\ddot{\psi }}(t)\cos \theta - \big (B_{7}w_{p}\big )^{\prime }{\ddot{\psi }}(t)\sin \theta \nonumber \\&+ \big (B_{8}\vartheta _y\big )^{\prime }{\dot{\psi }}^2(t)+ \big (B_{9}\vartheta _z\big )^{\prime }{\dot{\psi }}^2(t)- \big (B_{20}\varphi \big )^{\prime }{\ddot{\psi }}(t)\cos \theta - \big (B_{21}\varphi \big )^{\prime }{\ddot{\psi }}(t)\sin \theta \nonumber \\&+ 2\big (B_{7}\dot{v}_{p}\big )^{\prime }\dot{\psi }(t)\cos \theta -2\big (B_{7}\dot{w}_{p}\big )^{\prime }\dot{\psi }(t)\sin \theta - 2\big (B_{20}\dot{\varphi }\big )^{\prime }\dot{\psi }(t)\cos \theta \nonumber \\&- 2\big (B_{21}\dot{\varphi }\big )^{\prime }\dot{\psi }(t)\sin \theta - \big (B_{8}{\ddot{\vartheta }}_y\big )^{\prime } - \big (B_{9}{\ddot{\vartheta }}_z\big )^{\prime } - \big (B_{7}\ddot{u}_{0}\big )^{\prime } + \big (B_{10}\ddot{\varphi }^{\prime }\big )^{\prime } - \big (B_{10}\varphi ^{\prime }\big )^{\prime }{\dot{\psi }}^2(t)\nonumber \\&+ M_{x}^{\prime } + B_{w}^{\prime \prime } + m_{ext,x}+m_{ext,w}^{\prime } + \delta _{0}\hat{m}_{ext,x} + \delta _{0}\hat{m}_{ext,w}^{\prime } = \;0 \end{aligned}$$

  (48)

  with boundary conditions,

  $$\begin{aligned}&\varphi ^{\prime }\big |_{x=0} = 0, \qquad \varphi \big |_{x=0} = 0,\nonumber \\&\big [B_{9}{\ddot{\psi }}(t)\cos \theta - B_{8}{\ddot{\psi }}(t)\sin \theta + B_{7}v_{p}{\ddot{\psi }}(t)\cos \theta - B_{20}\varphi {\ddot{\psi }}(t)\cos \theta \nonumber \\&- B_{7}w_{p}{\ddot{\psi }}(t)\sin \theta - B_{21}{\ddot{\psi }}(t)\varphi \sin \theta \big ]\!\big |_{x=l} \nonumber \\&+ \big [(R_{0} + x + u_{0})B_{7}{\dot{\psi }}^2(t)+ B_{8}\vartheta _y{\dot{\psi }}^2(t)+ B_{9}\vartheta _z{\dot{\psi }}^2(t)- B_{10}\varphi ^{\prime }{\dot{\psi }}^2(t)\big ]\!\big |_{x=l} \nonumber \\&+ \big [2 B_{7}\dot{\psi }(t)\dot{v}_{p}\cos \theta - 2 B_{20}\dot{\psi }(t)\dot{\varphi }\cos \theta - 2 B_{7}\dot{\psi }(t)\dot{w}_{p}\sin \theta - 2 B_{21}\dot{\psi }(t)\dot{\varphi }\sin \theta \big ]\! \big |_{x=l} \nonumber \\&+ \big [B_{10}\ddot{\varphi }^{\prime }-B_{7}\ddot{u}_{0} - B_{8}{\ddot{\vartheta }}_y- B_{9}{\ddot{\vartheta }}_z\big ]\!\Big |_{x=l} \nonumber \\&+\big [M_{x} + B_{w}^{\prime } - m_{ext,w} - \hat{m}_{ext,w} + n_{x}M_{ext,x}\big ]\!\big |_{x=l} = 0 \nonumber \\&-\big [B_{w}+n_{x}M_{ext,w}\big ]\! \big |_{x=l} = 0 \end{aligned}$$

  (49)

Relations (37)–(49) form a nonlinear system of PDEs with all equations coupled together. It should be noted that in a case of the nonrotating beam and zero pitch angle the above system of equations corresponds exactly to the particular case given by Librescu and Song in [21]. The equations derived in this paper take into account nonconstant angular velocity and also arbitrary pitch angle of the beam. These two effects are essential for the study of dynamics of rotating blades.

3 Results

In this section two cases of composite beams are examined in order to study the impact of the variable rotating speed and the pitch angle on system’s motion. The geometries of both cross-sections are presented in Fig. 4. To simplify the evaluation a symmetrically lay-up composite material is considered for both beams. Therefore the coupling stiffness matrix coefficients $B_{ij}$ [see definition (99)] vanish. Moreover it is assumed that the cross-section pole coincides with the spanwise axis $x$; therefore $v_p\rightarrow v_0$, $w_p\rightarrow w_0$. This results in simplification

$$\begin{aligned} y_{p} = z_{p} = 0 \end{aligned}$$

(50)

Fig. 4

Beam cross-sections to be considered: a blade (open section) b closed box beam

3.1 Symmetric composite blade

A symmetric composite beam with rectangular open cross-section as indicated in Fig. 4a is examined. In this case, considering the inertia and stiffness coefficients given in Appendix 5, Tables 1 and 2 individual equations of motion are given by

• $\delta \psi$

  $$\begin{aligned}&- B_{22}{\ddot{\psi }}(t)- B_{14}l{\ddot{\psi }}(t)\cos ^{2}\theta - B_{13}l{\ddot{\psi }}(t)\sin ^{2}\theta \nonumber \\&- \int \limits _0^{l} \big [2B_{1}(R_{0}+x)u_{0}{\ddot{\psi }}(t)+ 2(B_{16}-B_{19})\varphi {\ddot{\psi }}(t)\sin \theta \cos \theta \big ]dx\nonumber \\&-\int \limits _0^{l} \big [2B_{1}(R_{0}+x)\dot{u}_{0}\dot{\psi }(t)+ 2(B_{16}-B_{19})\dot{\varphi }\dot{\psi }(t)\sin \theta \cos \theta \big ]dx\nonumber \\&- \int \limits _0^{l} \big [B_{1}(R_{0}\!+\!x)\ddot{v}_{0}\cos \theta - B_{1}(R_{0}\!+\!x)\ddot{w}_{0}\sin \theta + B_{13}{\ddot{\vartheta }}_y\sin \theta - B_{14}{\ddot{\vartheta }}_z\cos \theta \big ]dx + T_{ext,z} = 0 \end{aligned}$$

  (51)

• $\delta u_{0}$

  $$\begin{aligned}&- B_{1} \ddot{u}_{0} + 2 B_{1}\dot{v}_{0}\dot{\psi }(t)\cos \theta - 2B_{1}\dot{w}_{0}\dot{\psi }(t)\sin \theta + B_{1} (R_0+x+u_{0}){\dot{\psi }}^2(t)\nonumber \\&- B_{1} w_{0}{\ddot{\psi }}(t)\sin \theta + B_{1} v_{0} {\ddot{\psi }}(t)\cos \theta \nonumber \\&+ \big (a_{11}u_{0}^\prime \big )^\prime + \big (a_{14}\vartheta _{z}\big )^\prime + \big (a_{14}v_{0}^\prime \big )^\prime + P_{ext,x} + \delta _{0}\hat{P}_{ext,x} =0 \end{aligned}$$

  (52)

  with boundary conditions,

  $$\begin{aligned} u_{0} \big |_{x=0}=0,\quad \big [ a_{11}u_{0}^\prime + a_{14}\vartheta _{z} + a_{14}v_{0}^\prime + n_{x}Q_{ext,x} \big ]\! \big |_{x=l}=0, \end{aligned}$$

  (53)

• $\delta v_{0}$

  $$\begin{aligned}&- B_{1} \ddot{v}_{0} - 2 B_{1} \dot{u}_{0}\dot{\psi }(t)\cos \theta - B_{1} w_{0}{\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{1}v_{0}{\dot{\psi }}^2(t)\cos ^2\theta - B_{1} (R_{0}\!+\!x\!+\!u_{0}){\ddot{\psi }}(t)\cos \theta \nonumber \\&+ \big (a_{14}u_{0}^{\prime }\big )^{\prime } + \big [a_{44}(\vartheta _z+ v_{0}^{\prime })\big ]^{\prime } + P_{ext,y} + \delta _{0}\hat{P}_{ext,y} = 0 \end{aligned}$$

  (54)

  with boundary conditions,

  $$\begin{aligned} v_{0} \big |_{x=0}=0,\qquad \big [ a_{14}u_{0}^{\prime } + a_{44}(\vartheta _z+ v_{0}^{\prime }) + n_{x}Q_{ext,y}\big ]\!\big |_{x=l} = 0 \end{aligned}$$

  (55)

• $\delta w_{0}$

  $$\begin{aligned}&- B_{1}\ddot{w}_{0} + 2 B_{1}\dot{u}_{0}\,\dot{\psi }(t)\sin \theta + B_{1}w_{0}{\dot{\psi }}^2(t)\sin ^2\theta - B_{1}v_{0}{\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\&+ B_{1} (R_{0}\!+\!x\!+\!u_{0}) {\ddot{\psi }}(t)\sin \theta + \big [a_{55}(\vartheta _y+ w_{0}^{\prime })\big ]^{\prime } + P_{ext,z}+\delta _{0}\hat{P}_{ext,z} = 0 \end{aligned}$$

  (56)

  with boundary conditions,

  $$\begin{aligned} w_{0} \big |_{x=0}=0, \qquad \big [a_{55}(\vartheta _y+ w_{0}^{\prime }) + n_{x}Q_{ext,z} \big ]\!\big |_{x=l}=0 \end{aligned}$$

  (57)

• $\delta \vartheta _y$

  $$\begin{aligned}&- B_{13}{\ddot{\vartheta }}_y- 2 B_{16}\dot{\varphi }\dot{\psi }(t)\cos \theta + B_{13}\vartheta _y{\dot{\psi }}^2(t)- B_{16}\varphi {\ddot{\psi }}(t)\cos \theta - B_{13}{\ddot{\psi }}(t)\sin \theta \nonumber \\&+ m_{ext,y}+\delta _{0}\hat{m}_{ext,y}-a_{55}\vartheta _{y} - a_{55}w_{0}^{\prime } + \big (a_{33}\vartheta _{y}^{\prime } \big )^{\prime } + \big ( a_{37}\varphi ^{\prime } \big )^{\prime } = 0 \end{aligned}$$

  (58)

  with boundary conditions,

  $$\begin{aligned} \left. \vartheta _{y} \right| _{x=0}=0, \quad \big [a_{33}\vartheta _{y}^{\prime } + a_{37}\varphi ^{\prime } + n_{x}M_{ext,y} \big ]\! \big |_{x=l}=0, \end{aligned}$$

  (59)

• $\delta \vartheta _z$

  $$\begin{aligned}&- B_{14}{\ddot{\vartheta }}_z- 2 B_{19}\dot{\varphi }\dot{\psi }(t)\sin \theta + B_{14}\vartheta _z{\dot{\psi }}^2(t)- B_{19}\varphi {\ddot{\psi }}(t)\sin \theta + B_{14}{\ddot{\psi }}(t)\cos \theta \nonumber \\&+ m_{ext,z}+\delta _{0}\hat{m}_{ext,z} - a_{14}u_{0}^{\prime } - a_{44}\vartheta _{z} - a_{44}v_{0}^{\prime } + \big ( a_{22}\vartheta _{z}^{\prime } \big )^{\prime } = 0 \end{aligned}$$

  (60)

  with boundary conditions,

  $$\begin{aligned} \left. \vartheta _{z} \right| _{x=0}=0, \quad \big [ a_{22}\vartheta _{z}^{'}{+n}_{x}M_{ext,z} \big ]\!\big |_{x=l}=0, \end{aligned}$$

  (61)

• $\delta \varphi$

  $$\begin{aligned}&-B_{4}\ddot{\varphi }-B_{5}\ddot{\varphi } + B_{16}\vartheta _y{\ddot{\psi }}(t)\cos \theta + B_{19}\vartheta _z{\ddot{\psi }}(t)\sin \theta + \big (B_{16} - B_{19}\big ){\dot{\psi }}^2(t)\cos \theta \sin \theta \nonumber \\&+ B_{4}\varphi {\dot{\psi }}^2(t)\cos ^{2}\theta - B_{19}\varphi {\dot{\psi }}^2(t)\cos ^{2}\theta +B_{5}\varphi {\dot{\psi }}^2(t)\sin ^{2}\theta - B_{16}\varphi {\dot{\psi }}^2(t)\sin ^{2}\theta + 2 B_{16}{\dot{\vartheta }}_y\dot{\psi }(t)\cos \theta \nonumber \\&+ 2 B_{19}{\dot{\vartheta }}_z\dot{\psi }(t)\sin \theta + \big (B_{10}\ddot{\varphi }^{\prime }\big )^{\prime } - \big (B_{10}\varphi ^{\prime }\big )^{\prime }{\dot{\psi }}^2(t)+ m_{ext,x} + m_{ext,w}^{\prime } + \delta _{0}\hat{m}_{ext,x} + \delta _{0}\hat{m}_{ext,w}^{\prime } \nonumber \\&+ \big (a_{37}\vartheta _{y}^{\prime } \big )^{\prime } + \big ( a_{77}\varphi ^{\prime }\big )^{\prime } - \big ( a_{66}\varphi ^{\prime \prime } \big )^{\prime \prime } =0, \end{aligned}$$

  (62)

  with boundary conditions,

  $$\begin{aligned} \varphi \big |_{x=0}=0, \qquad \varphi ^{\prime } \big |_{x=0}=0, \qquad \big [- a_{66}\varphi ^{\prime \prime } + n_{x}M_{ext,w} \big ]\!\big |_{x=l}=0,\nonumber \\ \big [-B_{10}\varphi ^{\prime }{\dot{\psi }}^2(t)+B_{10}\ddot{\varphi }^{\prime }+a_{37}\vartheta _{y}^{\prime }+a_{77}\varphi ^{\prime } - \big ( a_{66}\varphi ^{\prime \prime } \big )^{\prime } \nonumber \\ - m_{ext,w} - \hat{m}_{ext,w} + n_{x}M_{ext,x}\big ]\!\big |_{x=l} = 0, \end{aligned}$$

  (63)

It should be noted that in relations (52)–(63) in all equations there is a term which corresponds to nonconstant rotation. Therefore all equations are coupled together and form a nonlinear system of PDEs. Detailed analysis of the above equations is given together with a set arising for the box-beam case.

3.2 Symmetric composite uniform box-beam

In this section a composite symmetric beam with rectangular closed cross-section as indicated in Fig. 4b is examined; the circumferentially uniform stiffness (CUS) composite configuration is assumed, which is achievable via usual filament winding technology. In this case, considering the inertia and stiffness coefficients given in Appendix 5 Tables 1 and 2 respectively the equations of motion are given by

• $\delta \psi$

  $$\begin{aligned}&-I_{2}{\ddot{\psi }}(t)- B_{14}l{\ddot{\psi }}(t)\cos ^{2}\theta - B_{13}l{\ddot{\psi }}(t)\sin ^{2}\theta \nonumber \\&- \int \limits _{0}^{l} \big [2B_{1}(R_{0}+x)u_{0}{\ddot{\psi }}(t)+ 2(B_{16}-B_{19})\varphi {\ddot{\psi }}(t)\sin \theta \cos \theta \big ]dx\nonumber \\&-\int \limits _{0}^{l} \big [2B_{1}(R_{0}+x)\dot{u}_{0}\dot{\psi }(t)+ 2(B_{16}-B_{19})\dot{\varphi }\dot{\psi }(t)\sin \theta \cos \theta \big ]dx \nonumber \\&- \int \limits _{0}^{l} \big [B_{1}(R_{0}\!+\!x)\ddot{v}_{0}\cos \theta - B_{1}(R_{0}\!+\!x)\ddot{w}_{0}\sin \theta + B_{13}{\ddot{\vartheta }}_y\sin \theta - B_{14}{\ddot{\vartheta }}_z\cos \theta \big ]dx + T_{ext,z} = 0 \end{aligned}$$

  (64)

• $\delta u_{0}$,

  $$\begin{aligned}&- B_{1} \ddot{u}_{0} + 2 B_{1}\dot{v}_{0}\dot{\psi }(t)\cos \theta - 2B_{1}\dot{w}_{0}\dot{\psi }(t)\sin \theta + B_{1} (R_{0}+x+u_{0}){\dot{\psi }}^2(t)\nonumber \\&- B_{1} w_{0}{\ddot{\psi }}(t)\sin \theta + B_{1} v_{0} {\ddot{\psi }}(t)\cos \theta + \big (a_{11}u_{0}^{\prime }\big )^{\prime } + \big (a_{17}\varphi ^{\prime }\big )^\prime + P_{ext,x}+\delta _{0}\hat{P}_{ext,x} = 0 \end{aligned}$$

  (65)

  with boundary conditions,

  $$\begin{aligned} u_{0} \big |_{x=0}=0, \qquad \left[ a_{11}u_{0}^{\prime } + a_{17}\varphi ^{\prime } + n_{x}Q_{ext\mathrm {,}x}\right] \!\big |_{x=l}=0 \end{aligned}$$

  (66)

• $\delta v_{0}$

  $$\begin{aligned}&- B_{1} \ddot{v}_{0} - 2 B_{1} \dot{u}_{0}\dot{\psi }(t)\cos \theta - B_{1} w_{0}{\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{1}v_{0}{\dot{\psi }}^2(t)\cos ^2\theta \nonumber \\&- B_{1} (R_{0}\!+\!x\!+\!u_{0}){\ddot{\psi }}(t)\cos \theta +\big [a_{44}(\vartheta _{z} + v_{0}^{\prime })\big ]^{\prime } + \big (a_{34}\vartheta _{y}^{\prime }\big )^{\prime } + P_{ext,y} + \delta _{0}\hat{P}_{ext,y} = 0 \end{aligned}$$

  (67)

  with boundary conditions,

  $$\begin{aligned} v_{0} \big |_{x=0}=0,\qquad \left[ a_{44}(\vartheta _{z} + v_{0}^{\prime }) + a_{34}\vartheta _{y}^{\prime } + n_{x}Q_{ext,y}\right] \! \big |_{x=l} = 0 \end{aligned}$$

  (68)

• $\delta w_{0}$

  $$\begin{aligned}&- B_{1}\ddot{w}_{0} + 2 B_{1}\dot{u}_{0}\,\dot{\psi }(t)\sin \theta + B_{1}w_{0}{\dot{\psi }}^2(t)\sin ^2\theta - B_{1}v_{0}{\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\&+ B_{1} (R_{0}\!+\!x\!+\!u_{0}) {\ddot{\psi }}(t)\sin \theta + \big (a_{\!25}\vartheta _z^\prime \big )^{\prime } + \big [a_{\!55}(\vartheta _y+ w_{0}^{\prime })\big ]^{\prime } + P_{ext,z}+\delta _{0}\hat{P}_{ext,z} = 0 \end{aligned}$$

  (69)

  with boundary conditions,

  $$\begin{aligned} w_{0} \big |_{x=0}=0, \qquad \left[ a_{25}\vartheta _z^\prime + a_{55}(\vartheta _y+ w_{0}^{\prime }) + n_{x}Q_{ext,z} \right] \!\big |_{x=l}=0 \end{aligned}$$

  (70)

• $\delta \vartheta _y$

  $$\begin{aligned}&- B_{13}{\ddot{\vartheta }}_y- 2 B_{16}\dot{\varphi }\dot{\psi }(t)\cos \theta + B_{13}\vartheta _y{\dot{\psi }}^2(t)- B_{16}\varphi {\ddot{\psi }}(t)\cos \theta - B_{13}{\ddot{\psi }}(t)\sin \theta \nonumber \\&- a_{55}\vartheta _y- a_{25}\vartheta _z^\prime - a_{55}w_{0}^{\prime } + \big (a_{33}\vartheta _y^{\prime } \big )^{\prime } + \big ( a_{34}v_{0}^{\prime } \big )^{\prime } + \big (a_{34}\vartheta _z\big )^{\prime } + m_{ext,y}+\delta _{0}\hat{m}_{ext,y} = 0 \end{aligned}$$

  (71)

  with boundary conditions,

  $$\begin{aligned} \vartheta _y\big |_{x=0}=0, \qquad \big (a_{33}\vartheta _y^{\prime } + a_{34}v_{0}^{\prime } + a_{34}\vartheta _z+ n_{x}M_{ext,y} \big )\!\big |_{x=l} = 0 \end{aligned}$$

  (72)

• $\delta \vartheta _z$

  $$\begin{aligned}&- B_{14}{\ddot{\vartheta }}_z- 2 B_{19}\dot{\varphi }\dot{\psi }(t)\sin \theta + B_{14}\vartheta _z{\dot{\psi }}^2(t)- B_{19}\varphi {\ddot{\psi }}(t)\sin \theta + B_{14}{\ddot{\psi }}(t)\cos \theta \nonumber \\&- a_{44}\vartheta _z- a_{34}\vartheta _y^\prime - a_{44}v_{0}^{\prime } + \big (a_{25}\vartheta _y\big )^{\prime } + \big (a_{25}w_{0}^{\prime } \big )^{\prime } + \big ( a_{22}\vartheta _z^\prime \big )^{\prime } + m_{ext,z}+\delta _{0}\hat{m}_{ext,z} = 0 \end{aligned}$$

  (73)

  with boundary conditions,

  $$\begin{aligned} \vartheta _z\big |_{x=0}=0, \qquad \big (a_{25}\vartheta _y+ a_{25}w_{0}^{\prime } + a_{22}\vartheta _z^\prime + n_{x}M_{ext,z} \big )\!\big |_{x=l}=0 \end{aligned}$$

  (74)

• $\delta \varphi$

  $$\begin{aligned}&- B_{4}\ddot{\varphi }-B_{5}\ddot{\varphi } + B_{16}\vartheta _y{\ddot{\psi }}(t)\cos \theta + B_{19}\vartheta _z{\ddot{\psi }}(t)\sin \theta + \big (B_{16} - B_{19}\big ){\dot{\psi }}^2(t)\cos \theta \sin \theta \nonumber \\&+ (B_{4}- B_{19})\varphi {\dot{\psi }}^2(t)\cos ^{2}\theta + (B_{5}- B_{16})\varphi {\dot{\psi }}^2(t)\sin ^{2}\theta + 2 B_{16}{\dot{\vartheta }}_y\dot{\psi }(t)\cos \theta + 2 B_{19}{\dot{\vartheta }}_z\dot{\psi }(t)\sin \theta \nonumber \\&+ \big (B_{10}\ddot{\varphi }^{\prime }\big )^{\prime } - \big (B_{10}\varphi ^{\prime }\big )^{\prime }{\dot{\psi }}^2(t)+ m_{ext,x} + m_{ext,w}^{\prime } + \delta _{0}\hat{m}_{ext,x} + \delta _{0}\hat{m}_{ext,w}^{\prime } \nonumber \\&+ \big (a_{17}u_{0}^{\prime } \big )^{\prime } + \big ( a_{77}\varphi ^{\prime }\big )^{\prime } - \big ( a_{66}\varphi ^{\prime \prime } \big )^{\prime \prime } =0, \end{aligned}$$

  (75)

  with boundary conditions,

  $$\begin{aligned} \varphi \big |_{x=0}=0, \qquad \varphi ^{\prime } \big |_{x=0}=0, \qquad \big [- a_{66}\varphi ^{\prime \prime } + n_{x}M_{ext,w} \big ]\!\big |_{x=l}=0,\nonumber \\ \big [-B_{10}\varphi ^{\prime }{\dot{\psi }}^2(t)+B_{10}\ddot{\varphi }^{\prime } + a_{17}u_{0}^{\prime } + a_{77}\varphi ^{\prime } - \big ( a_{66}\varphi ^{\prime \prime } \big )^{\prime } \nonumber \\ - m_{ext,w} - \hat{m}_{ext,w} + n_{x}M_{ext,x}\big ]\!\big |_{x=l} = 0, \end{aligned}$$

  (76)

Considering equations (64)–(76), similarly with open cross-section case, they form a nonlinear system of all equations coupled.

4 Discussion

Looking at relations (51)–(63) and (65)–(76) one observes in all these equations there is at least one term where the angular acceleration ${\ddot{\psi }}(t)$ is multiplied by a certain problem variable (or it’s spatial derivative). Therefore all the resulting equations are coupled together and form a nonlinear system of PDEs. Similar terms have also arised in paper [34], where a case of Euler–Bernoulli beam made of isotropic material rotating with nonconstant velocity has been considered. It is worth to note here that assuming temporary the zero value for the pitch angle and the constant rotating speed case (and position vector restricted to the middle-line contour material points) the obtained system of equations (64)–(76) coincides exactly with the one reported by Librescu and Song in [21].

Analysing the derived axial displacement equation in both of the considered cross-section cases [see eqs. (52) and (65)] one can notice that $u$ is coupled to transverse displacements ($v$ and $w$ DOFs) not only by Coriolis terms but by nonconstant rotation velocity ${\ddot{\psi }}(t)$ terms as well. In these two equations fixing the preset position of a structure at $\theta =0$ makes the terms corresponding to beam’s vertical movement (i.e. flapping $w$) to disappear.

In the second limit case of $\theta ={\pi }/{2}$ presetting the axial dynamics of the box-beam [Eq. (65)] is similar because all $v$ originating terms disappear. Since transverse displacements $v$ and $w$ are defined in local coordinate system one can conclude, that in both of the two discussed limit cases ($\theta =0,{\pi }/{2}$) only the lead-lag plane displacement enters the axial equation of a box-beam.

For the symmetric blade and limit case of $\theta ={\pi }/{2}$ presetting the axial dynamics is different. This is related to the presence of a coupling term $(a_{14} v_p^\prime )^\prime$ in (52) which does not depend on presetting angle. It means that apart from the discussed special case of $\theta =0$ both lead-lag and flapping couplings are always present in (52). Also for the box-beam case coupling terms originating from both transverse displacements are present in axial equation (65) for the general presetting $\theta \ne (0,{\pi }/{2})$.

It should be noted that the numerical modal analysis of the rotating symmetric composite beam with open section for $0^\circ$, $45^\circ$ and $90^\circ$ pitch angles has been presented by authors in paper [19]. In case of $0^\circ$ and $90^\circ$ presettings the observed free vibration bending modes correspond to either flapwise of choordwise bendings. However in case of analysed $45^\circ$ pitch angle free vibration bending modes exhibit mixed flapwise and with chordwise displacements. Hence the impact of arbitrary presetting angle modelled in this article is in full agreement with the findings reported in [19].

Studying the transverse displacement equations (54)/(67) and (56)/(69) one observes that the nonconstant rotation velocity introduces additional inertia terms rendering coupling to the axial displacement $u$. Considering special cases of $\theta =0,{\pi }/{2}$ presetting one observes that these terms affect only the lead-lag displacements (i.e. parallel to the plane of rotation). This coupling scheme is also confirmed by the appropriate terms in torsion equation (62)/(75).

Analysis of eqs. (58)/(71) and (60)/(73) reveals the considered nonconstant rotating speed to introduce additional coupling terms also between the rotatory DOFs. Discussion of the special cases $\theta =0,{\pi }/{2}$ yields that the additional coupling term involving torsion angle $\varphi$ impacts only flapping cross-section rotation (i.e. about horizontal axis) and is not present in lead-lag plane. This is also confirmed by the detailed analysis of torsion equation (62)/(75).

Further analysis of the pitch angle impact on the systems dynamics reveals that its non-zero value introduces new additional coupling between transverse displacements. The terms incorporating $\sin \theta \cos \theta$ product that are not present in case of zero or ${\pi }/{2}$ presetting appear in transverse displacement formulas (54)/(67) and (56)/(69) formulas. This renders the bendings in both planes to be coupled. The similar $\sin \theta \cos \theta$ product appears also in the equation of torsion as an additional centrifugal term.

5 Conclusions

The equations of motion of composite Timoshenko beam experiencing variable angular velocity were derived. In the performed analysis also the general case of non-zero pitch angle and arbitrary hub’s radius were taken into account. The equations of motion form a nonlinear system of PDEs coupled together. Detailed analysis of symmetric layup of the composite beam of rectangular open and closed cross-section cases showed similar characteristics considering nonconstant rotating speed and the effect of pitch angle. Considering nonconstant angular velocity in both cases the nonlinear system of PDEs with all equations coupled together arises. Non-zero pitch angle results in direct coupling of flapwise bending motion with choordwise bending motion. As it was shown the nonconstant rotating speed introduces additional couplings to the system of equations of motion, which are not observed in $\psi (t)=const.$ cases discussed in the literature. Therefore nonconstant angular velocity and non-zero pitch angle have to be considered in modelling of rotating beams and in examination of their dynamics.

The equations derived in this paper are fundamental for further study of dynamics of rotating blade systems. The investigations will be developed in (a) the aspect of variable pitch angle which takes place in e.g. helicopter rotor dynamics and (b) the aspect of non-ideal systems where the structure interacts with the energy source [5, 35].

Appendices

Appendix 1

The primary and secondary warping functions and torsional functions for open and closed section beams are defined as given in [21]. The warping function $G(n,s)$ is the sum of primary $G^{(0)}(s)$ and secondary one $nG^{(1)}(s)$

$$\begin{aligned} G(n, s) = G^{(0)}(s) + nG^{(1)}(s) \end{aligned}$$

(77)

To simplify further expressions the following quantities are defined (see also Fig. 2)

$$\begin{aligned} r_{t}(s)&= R_{t}(s) = (z - z_{p})\frac{dz}{ds} + (y - y_{p})\frac{dy}{ds} \end{aligned}$$

(78)

$$\begin{aligned} R_{n}(s)&= (Y - y_{p})\frac{dz}{ds} - (Z - z_{p})\frac{dy}{ds} \end{aligned}$$

(79)

$$\begin{aligned} r_{n}(s)&= (y - y_{p})\frac{dz}{ds} - (z - z_{p})\frac{dy}{ds} \end{aligned}$$

(80)

to represent distances from pole P to the tangent and to the normal of the mid-line beam contour as shown in Fig. 2.

In case of open section one gets

$$\begin{aligned} G_{o}^{(0)}(s) = \int \limits _0^s {r_{n}(\bar{s})d\bar{s}} = {2\mathrm {\Omega }}_{os} \qquad G_{o}^{(1)}(s) = - r_{t}(s) \end{aligned}$$

(81)

whereas $\Omega _{0s}$ is the area enclosed by the center line and $\overline{s}$ is a dummy variable measured along centerline till the point of interest. The torsional function $g_{o}^{(0)}(s)$ and $g_{o}^{(1)}$ one for this case are given by

$$\begin{aligned} g_{o}^{(0)}(s) = 0 \qquad g_{o}^{(1)}(s) = 2 \end{aligned}$$

(82)

In case of closed sections both warping functions take the form

$$\begin{aligned} G_{c}^{(0)}(s)&= \int \limits _0^s {r_{n}(\bar{s})d\bar{s}} - \int \limits _0^s{\Big (\frac{\oint {r_{n}(s)ds} }{\oint {(\frac{1}{h(s)G_{xs}(s)})ds} }\frac{1}{h(\bar{s})G_{xs}(\bar{s})}\Big )d\bar{s}}=2\Omega _{os}-\dfrac{2\Omega }{\beta }s \end{aligned}$$

(83)

$$\begin{aligned} G_{c}^{(1)}(s)&= -r_{t}(s) - 2\int \limits _0^s {\Big (\frac{\oint {ds}}{\oint {(\frac{1}{h(s)G_{xs}(s)})ds}}\frac{1}{h(\bar{s})G_{xs}(\bar{s})} - 1\Big )d\bar{s}}=-r_t(s) \end{aligned}$$

(84)

where $h(s)$ is the thickness, $G_{xs}(s)$ is the shear modulus of the cross-section in circumferential surface and $\beta$ denotes mid-line contour perimeter and the $g_{c}^{(.)}(s)$ functions are given by,

$$\begin{aligned} g_{c}^{(0)}(s) = \frac{\oint {r_{n}(\bar{s})d\bar{s}} }{\oint {(\frac{d\bar{s}}{h(\bar{s})G_{xs}(\bar{s})})}}\cdot \frac{1}{h(s)G_{xs}(s)}=\dfrac{2 \Omega }{\beta } \end{aligned}$$

(85)

$$\begin{aligned} g_{c}^{(1)}(s) = 2\frac{\oint {d\bar{s}} }{\oint {(\frac{d\bar{s}}{h(\bar{s})G_{xs}(\bar{s})})}}\cdot \frac{1}{h(s)G_{xs}(s)}=2 \end{aligned}$$

(86)

whereas the last equalities are true in case of uniform $h(s) G_{xs}$ product with respect to $s$ coordinate.

Appendix 2

The constitutive equations for the $k$ th laminate orthotropic layer in reference system out of its principal axis have the form

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{ss}\\ \sigma _{xx}\\ \sigma _{nn}\\ \sigma _{xn}\\ \sigma _{sn}\\ \sigma _{xs}\\ \end{array}\right\} _{\!(k)}\! =\, \left[ \begin{array}{llllll} C_{11}^{(k)} &{} C_{12}^{(k)} &{} C_{13}^{(k)} &{} 0 &{} 0 &{} C_{16}^{(k)}\\ C_{12}^{(k)} &{} C_{22}^{(k)} &{} C_{23}^{(k)} &{} 0 &{} 0 &{} C_{26}^{(k)}\\ C_{13}^{(k)} &{} C_{23}^{(k)} &{} C_{33}^{(k)} &{} 0 &{} 0 &{} C_{36}^{(k)}\\ 0 &{} 0 &{} 0 &{} C_{44}^{(k)} &{} C_{45}^{(k)} &{} 0\\ 0 &{} 0 &{} 0 &{} C_{45}^{(k)} &{} C_{55}^{(k)} &{} 0\\ C_{16}^{(k)} &{} C_{26}^{(k)} &{} C_{36}^{(k)} &{} 0 &{} 0 &{} C_{66}^{(k)}\\ \end{array} \right] \cdot \, \left\{ \begin{array}{l} \varepsilon _{ss}\\ \varepsilon _{xx}\\ \varepsilon _{nn}\\ \gamma _{xn}\\ \gamma _{sn}\\ \gamma _{xs}\\ \end{array}\right\} _{\!(k)} \end{aligned}$$

(87)

Considering the assumption of the normal stress $\sigma _{nn}$ to be negligible (see Sect. 2.1, item (f)) the corresponding strain in wall thickness direction can be defined as

$$\begin{aligned} \varepsilon _{nn}=-\frac{C_{13}^{(k)}}{C_{33}^{(k)}}\varepsilon _{ss}-\frac{C_{23}^{(k)}}{C_{33}^{(k)}}\varepsilon _{xx}-\frac{C_{36}^{(k)}}{C_{33}^{(k)}}\gamma _{xs} \end{aligned}$$

(88)

Setting the above into (87) and using the cross-section non-deformability condition $\gamma _{yz} = \gamma _{sn} = 0$ [Sect. 2.1, item (a)] results in the system of reduced equations

$$\begin{aligned} \sigma _{ss}^{(k)}&= \overline{Q}_{11}^{(k)}\varepsilon _{ss}+\overline{Q}_{12}^{(k)}\varepsilon _{xx}+\overline{Q}_{16}^{(k)}\gamma _{xs} \end{aligned}$$

(89)

$$\begin{aligned} \sigma _{xx}^{(k)}&= \overline{Q}_{12}^{(k)}\varepsilon _{ss}+\overline{Q}_{22}^{(k)}\varepsilon _{xx}+\overline{Q}_{26}^{(k)}\gamma _{xs} \end{aligned}$$

(90)

$$\begin{aligned} \sigma _{xn}^{(k)}&= \overline{Q}_{44}^{(k)}\gamma _{xn} \end{aligned}$$

(91)

$$\begin{aligned} \sigma _{sn}^{(k)}&= \overline{Q}_{45}^{(k)}\gamma _{xn} \end{aligned}$$

(92)

$$\begin{aligned} \sigma _{xs}^{(k)}&= \overline{Q}_{16}^{(k)}\varepsilon _{ss}+\overline{Q}_{26}^{(k)}\varepsilon _{xx}+\overline{Q}_{66}^{(k)}\gamma _{xs} \end{aligned}$$

(93)

where

$$\begin{aligned} \overline{Q}_{ij}^{(k)} = \overline{Q}_{ji}^{(k)} = C_{ij}^{(k)}-\frac{C_{i3}^{(k)}C_{j3}^{(k)}}{C_{33}^{(k)}} \quad {\text {for}}\quad i,j = 1,2,6;\qquad \overline{Q}_{4i} = C_{4i}\quad{ \text {for}}\quad i = 4,5 \end{aligned}$$

(94)

are reduced stiffness coefficients for $k$-th laminate layer.

Define the following 2-D stress resultants:

• membraine

  $$\begin{aligned} \left\{ \begin{array}{l} N_{ss}\\ N_{xx}\\ N_{xs} \end{array} \right\} =\sum _{k=1}^{N}\int \limits _{\ n_{(k-1)}}^{\ n_k}\!\! \left\{ \begin{array}{l} \sigma _{ss}^{(k)}\\ \sigma _{xx}^{(k)}\\ \sigma _{xs}^{(k)} \end{array} \right\} dn \end{aligned}$$

  (95)

• transverse

  $$\begin{aligned} \left\{ \begin{array}{l} N_{xn}\\ N_{sn} \end{array} \right\} = \sum _{k=1}^{N}\int \limits _{\ n_{(k-1)}}^{\ n_k}\!\! \left\{ \begin{array}{l} \sigma _{xn}^{(k)}\\ \sigma _{sn}^{(k)} \end{array} \right\} dn \end{aligned}$$

  (96)

• stress couples

  $$\begin{aligned} \left\{ \begin{array}{l} L_{xx}\\ L_{xs} \end{array} \right\} =\sum _{k=1}^{N}\int \limits _{\ n_{(k-1)}}^{\ n_k}\!\! \left\{ \begin{array}{l} \sigma _{xx}^{(k)}\\ \sigma _{xs}^{(k)} \end{array} \right\} n dn \end{aligned}$$

  (97)

  where $L_{ss}$ term is set to 0 due to shallow shell assumption [Sect. 2.1, item (e)].

According to the above $N_{ss}$ definition and also considering the (f) assumption and equations (10a, b), (89) one gets

$$\begin{aligned} N_{ss}=\sum _{k=1}^N \int \limits _{\;n_{(k-1)}}^{\ n_{k}}\!\! \sigma _{ss}^{(k)}dn =\,&0 \Longleftrightarrow \sum \limits _{k=1}^N \int \limits _{\;n_{(k-1)}}^{\ n_{k}} {\left( \overline{Q}_{11}^{(k)}\varepsilon _{ss} + \overline{Q}_{12}^{(k)}\varepsilon _{xx} + \overline{Q}_{16}^{(k)}\gamma _{xs} \right) dn = 0\Longleftrightarrow } \nonumber \\ \varepsilon _{ss}&= -\frac{A_{12}}{A_{11}}\varepsilon _{xx}^{(0)} - \frac{B_{12}}{A_{11}}\varepsilon _{xx}^{(1)} - \frac{A_{16}}{A_{11}}\gamma _{xs}^{(0)} - \frac{B_{16}}{A_{11}}\gamma _{xs}^{(1)} \end{aligned}$$

(98)

whereas

$$\begin{aligned} A_{ij} =\sum \limits _{k=1}^N \int \limits _{\;n_{(k-1)}}^{\ n_{k}}\!\!\!\! {\overline{Q}_{ij}^{(k)}dn} \qquad B_{ij} =\sum \limits _{k=1}^N \int \limits _{\;n_{(k-1)}}^{\ n_{k}}\!\!\!\! {n \overline{Q}_{ij}^{(k)}dn} \qquad D_{ij} =\sum \limits _{k=1}^N \int \limits _{\;n_{(k-1)}}^{\ n_{k}}\!\!\!\! {n^{2}\overline{Q}_{ij}^{(k)}dn} \end{aligned}$$

(99)

Therefore using relation (98) the constitutive equations (89)– (92) are:

$$\begin{aligned} \sigma _{xx}^{(k)}&= \bigg (\overline{Q}_{22}^{(k)} - \frac{\overline{Q}_{12}^{(k)}A_{12}}{A_{11}}\bigg )\varepsilon _{xx}^{(0)} + \bigg (n \overline{Q}_{22}^{(k)} - \frac{\overline{Q}_{12}^{(k)}B_{12}}{A_{11}}\bigg )\varepsilon _{xx}^{(1)} + \nonumber \\&\bigg (\overline{Q}_{26}^{(k)} - \frac{\overline{Q}_{12}^{(k)}A_{16}}{A_{11}}\bigg )\gamma _{xs}^{(0)} + \bigg (n\overline{Q}_{26}^{(k)} - \frac{\overline{Q}_{12}^{(k)}B_{16}}{A_{11}}\bigg )\gamma _{xs}^{(1)} \end{aligned}$$

(100)

$$\begin{aligned} \sigma _{xn}^{(k)}&= \, \overline{Q}_{44}^{(k)}\gamma _{xn}^{(0)} \end{aligned}$$

(101)

$$\begin{aligned} \sigma _{sn}^{(k)}&= \, \overline{Q}_{45}^{(k)}\gamma _{xn}^{(0)} \end{aligned}$$

(102)

$$\begin{aligned} \sigma _{xs}^{(k)}&= \bigg (\overline{Q}_{26}^{(k)} - \frac{\overline{Q}_{16}^{(k)}A_{12}}{A_{11}}\bigg )\varepsilon _{xx}^{(0)} + \bigg (n \overline{Q}_{26}^{(k)} - \frac{\overline{Q}_{16}^{(k)}B_{12}}{A_{11}}\bigg )\varepsilon _{xx}^{(1)} + \nonumber \\&\bigg (\overline{Q}_{66}^{(k)} - \frac{\overline{Q}_{16}^{(k)}A_{16}}{A_{11}}\bigg )\gamma _{xs}^{(0)} + \bigg (n\overline{Q}_{66}^{(k)} - \frac{\overline{Q}_{16}^{(k)}B_{16}}{A_{11}}\bigg )\gamma _{xs}^{(1)} \end{aligned}$$

(103)

and subsequently after re-ordering and using (11d) the 2-D stress resultants and stress couples are

$$\begin{aligned} \left\{ \begin{array}{l} N_{xx}\\ N_{xs}\\ L_{xx}\\ L_{xs}\\ N_{xn}\\ N_{sn} \end{array} \right\} = \left[ \begin{array}{lllll} K_{11} &{} K_{12} &{} K_{13} &{} K_{14} &{} 0\\ K_{21} &{} K_{22} &{} K_{23} &{} K_{24} &{} 0\\ K_{41} &{} K_{42} &{} K_{43} &{} K_{44} &{} 0\\ K_{51} &{} K_{52} &{} K_{53} &{} K_{54} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} A_{44}\\ 0 &{} 0 &{} 0 &{} 0 &{} A_{45}\\ \end{array} \right] \cdot \left\{ \begin{array}{l} \varepsilon _{xx}^{(0)}\\ \bar{\gamma }_{xs}^{(0)}\\ \varphi ^{\prime }\\ \varepsilon _{xx}^{(1)}\\ \gamma _{xn}^{(0)} \end{array} \right\} \end{aligned}$$

(104)

where the beam effective stiffness coefficients $K_{ij}$ are given as follows

$$\begin{aligned} K_{11}&= \left( A_{22}-\frac{A_{12}A_{12}}{A_{11}} \right) \quad K_{12} = \left( A_{26}-\frac{A_{12}A_{16}}{A_{11}} \right) \\ K_{14}&= \left( B_{22}-\frac{A_{12}B_{12}}{A_{11}} \right) \quad K_{21} = \left( A_{26}-\frac{A_{16}A_{12}}{A_{11}} \right) \\ K_{22}&= \left( A_{66}-\frac{A_{16}A_{16}}{A_{11}} \right) \quad K_{24} = \left( B_{26}-\frac{A_{16}B_{12}}{A_{11}} \right) \\ K_{41} &= \left( B_{22}-\frac{B_{12}A_{12}}{A_{11}} \right) \quad K_{42} = \left( B_{26}-\frac{B_{12}A_{16}}{A_{11}} \right) \\ K_{44} &= \left( D_{22}-\frac{B_{12}B_{12}}{A_{11}} \right) \quad K_{51}= \left( B_{26}-\frac{A_{12}B_{16}}{A_{11}} \right) \\ K_{52} &= \left( B_{66}-\frac{A_{16}B_{16}}{A_{11}} \right) \quad K_{54} = \left(D_{26}-\frac{B_{12}B_{16}}{A_{11}} \right) \end{aligned}$$

(105)

In the above relations symmetry is preserved for terms $K_{12}=K_{21}$, $K_{14}=K_{41}$ and $K_{24}=K_{42}$. The remaining $K_{i3}, i=1,2,4,5$ terms depend whether the cross-section is open or closed one. General formulas have the form

$$\begin{aligned} K_{13} = g^{(0)}\!\left( A_{26}-\frac{A_{12}A_{16}}{A_{11}} \right) + g^{(1)}\!\left( B_{26}-\frac{A_{12}B_{16}}{A_{11}} \right) \nonumber \\ K_{23} = g^{(0)}\!\left( A_{66}-\frac{A_{16}A_{16}}{A_{11}} \right) + g^{(1)}\!\left( B_{66}-\frac{A_{16}B_{16}}{A_{11}} \right) \nonumber \\ K_{43} = g^{(0)}\!\left( B_{26}-\frac{A_{16}B_{12}}{A_{11}} \right) + g^{(1)}\!\left( D_{26}-\frac{B_{12}B_{16}}{A_{11}} \right) \nonumber \\ K_{53} = g^{(0)}\!\left( B_{66}-\frac{A_{16}B_{16}}{A_{11}} \right) + g^{(1)}\!\left( D_{66}-\frac{B_{16}B_{16}}{A_{11}} \right) \end{aligned}$$

(106)

In case of open sections, according to (82) relation, the above expressions simplify to

$$\begin{aligned} K_{13} = g^{(1)}\left( B_{26}-\frac{A_{12}B_{16}}{A_{11}} \right)&\qquad K_{23} = g^{(1)} \left( B_{66}-\frac{A_{16}B_{16}}{A_{11}} \right) \nonumber \\ K_{43} = g^{(1)}\left( D_{26}-\frac{B_{12}B_{16}}{A_{11}} \right)&\qquad K_{53} = g^{(1)} \left( D_{66}-\frac{B_{16}B_{16}}{A_{11}} \right) \end{aligned}$$

(107)

Appendix 3

Following the position vector $\mathbf {R}$ as defined by (6) and displacement field (Sect. 2.2.4) the components of $\delta \mathbf {R}$ are

$$\begin{aligned} \delta R_x =&-\big [x+R_0+u_0(x,t) + \vartheta _y(x,t)\,Z + \vartheta _z(x,t)\,Y - G(n,s)\,\varphi ^\prime (x,t)\big ]\sin \psi (t)\delta \psi (t)\nonumber \\&- \big [Y + v_p(x,t) - \frac{\varphi ^2(x,t)}{2}(Y-y_p) - (Z - z_p)\varphi (x,t)\big ]\cos \theta \cos \psi (t)\delta \psi (t)\nonumber \\&+ \big [Z + w_p(x,t) + (Y - y_p)\varphi (x,t) - \frac{\varphi ^2(x,t)}{2}(Z-z_p) \big ]\sin \theta \cos \psi (t)\delta \psi (t)\nonumber \\&+ \cos \psi (t)\delta u_0(x,t) - \cos \theta \sin \psi (t)\delta v_p(x,t) + \sin \theta \sin \psi (t)\delta w_p(x,t)\nonumber \\&+ Z\cos \psi (t)\delta \vartheta _y(x,t) + Y\!\cos \psi (t)\delta \vartheta _z(x,t) - G(n,s)\cos \psi (t)\delta \varphi ^\prime (x,t)\nonumber \\&+ \big [(Y-y_p)\varphi (x,t)\cos \theta \sin \psi (t)+ (Z-z_p)\cos \theta \sin \psi (t)\nonumber \\&+ (Y-y_p)\sin \theta \sin \psi (t)- (Z-z_p)\sin \theta \sin \psi (t)\varphi (x,t)\big ]\delta \varphi (x,t)\nonumber \\ \delta R_y =&\big [x+R_0+u_0(x,t) + \vartheta _y(x,t)\,Z + \vartheta _z(x,t)\,Y - G(n,s)\,\varphi ^\prime (x,t)\big ]\cos \psi (t)\delta \psi (t)\nonumber \\&- \big [Y + v_p(x,t) - \frac{\varphi ^2(x,t)}{2}(Y-y_p) - (Z - z_p)\varphi (x,t)\big ]\cos \theta \sin \psi (t)\delta \psi (t)\nonumber \\&+ \big [Z + w_p(x,t) + (Y - y_p)\varphi (x,t) - \frac{\varphi ^2(x,t)}{2}(Z-z_p) \big ]\sin \theta \sin \psi (t)\delta \psi (t)\nonumber \\&+ \sin \psi (t)\delta u_0(x,t) + \cos \theta \cos \psi (t)\delta v_p(x,t) - \sin \theta \cos \psi (t)\delta w_p(x,t)\nonumber \\&+ Z\sin \psi (t)\delta \vartheta _y(x,t) + Y\!\sin \psi (t)\delta \vartheta _z(x,t) - G(n,s)\sin \psi (t)\delta \varphi ^\prime (x,t)\nonumber \\&+ \big [-(Y-y_p)\varphi (x,t)\cos \theta \cos \psi (t)- (Z-z_p)\cos \theta \cos \psi (t)\nonumber \\&- (Y-y_p)\sin \theta \cos \psi (t)+ (Z-z_p)\sin \theta \cos \psi (t)\varphi (x,t)\big ]\delta \varphi (x,t)\nonumber \\ \delta R_z&= \sin \theta \, \delta v_p + \cos \theta \,\delta w_p -\big [(Z-z_p)\sin \theta - (Y-y_p)\cos \theta \big ]\,\delta \varphi (x,t)\nonumber \\&- \big [(Z-z_p)\cos \theta + (Y-y_p)\sin \theta \big ]\varphi (x,t)\,\delta \varphi (x,t) \end{aligned}$$

(108)

Inserting the above terms (108) and accelerations (8) into energy variation time integral (32) and rearranging all the terms according to variations of respective basic unknowns of the problem and skipping higher order terms resulting from cosine approximation, yields

• $\delta \psi (t)$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \Big \lbrace&B_{22}{\ddot{\psi }}(t)+ B_{14}l{\ddot{\psi }}(t)\cos ^{2}\theta + B_{13}l{\ddot{\psi }}(t)\sin ^{2}\theta - 2 B_{15} l{\ddot{\psi }}(t)\cos \theta \sin \theta \nonumber \\&+ \int \limits _0^{l} \Big [2 B_{1}(R_{0} + x)u_{0}{\ddot{\psi }}(t)- 2 B_{7}(R_{0}+x)\varphi ^{\prime }{\ddot{\psi }}(t)+ 2 B_{11}(R_{0}+x)\vartheta _y{\ddot{\psi }}(t)\nonumber \\&+ 2 B_{12}(R_{0}+x)\vartheta _z{\ddot{\psi }}(t)+ 2 B_{12}v_{p}{\ddot{\psi }}(t)\cos ^{2}\theta - 2 B_{11}v_{p}{\ddot{\psi }}(t)\sin \theta \cos \theta \nonumber \\&+ 2 B_{11}w_{p}{\ddot{\psi }}(t)\sin ^{2}\theta - 2 B_{12}w_{p}{\ddot{\psi }}(t)\sin \theta \cos \theta - 2 B_{18}\varphi {\ddot{\psi }}(t)\cos ^{2}\theta \nonumber \\&+ 2 B_{17}\varphi {\ddot{\psi }}(t)\sin ^{2}\theta - 2 B_{19}\varphi {\ddot{\psi }}(t)\sin \theta \cos \theta + 2 B_{16}\varphi {\ddot{\psi }}(t)\sin \theta \cos \theta \Big ]dx\nonumber \\&+ \int \limits _0^{l}\!\Big [\big (B_{11}\sin \theta - B_{12}\cos \theta \big )\ddot{u}_{0} + B_{1}(R_{0}+x)\ddot{v}_{p}\cos \theta - B_{1}(R_{0}+x)\ddot{w}_{p}\sin \theta \nonumber \\&+ \big (B_{13}\sin \theta - B_{15}\cos \theta \big ){\ddot{\vartheta }}_y+ \big (B_{15}\sin \theta - B_{14}\cos \theta \big ){\ddot{\vartheta }}_z\nonumber \\&- \big (B_{3}\sin \theta + B_{2}\cos \theta \big )(R_{0} + x)\ddot{\varphi } + \big (B_{9}\cos \theta - B_{8}\sin \theta \big )\ddot{\varphi }^{\prime } \Big ]dx\nonumber \\&+ \int \limits _0^{l} \Big [2 B_{1}(R_{0}+x)\dot{u}_{0}\dot{\psi }(t)+ 2\big (B_{12}\cos ^{2}\theta - B_{11}\sin \theta \cos \theta \big )\dot{v}_{p}\dot{\psi }(t)\nonumber \\&+ 2\big (B_{11}\sin ^{2}\theta - B_{12}\sin \theta \cos \theta \big )\dot{w}_{p}\dot{\psi }(t)+ 2 B_{11}(R_{0}+x){\dot{\vartheta }}_y\dot{\psi }(t)\nonumber \\&+ 2 B_{12}(R_{0}+x){\dot{\vartheta }}_z\dot{\psi }(t)- 2 B_{7}(R_{0}+x)\dot{\varphi }^{\prime }\dot{\psi }(t)\nonumber \\&+ 2 \big (B_{17}\sin ^{2}\theta - B_{18}\cos ^{2}\theta \big )\dot{\varphi }\dot{\psi }(t)+ 2(B_{16}-B_{19})\dot{\varphi }\dot{\psi }(t)\sin \theta \cos \theta \Big ]dx \Big \rbrace \end{aligned}$$

  (109)

• $\delta u_0$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \!\int \limits _0^l\Big [&B_{1} \ddot{u}_0 + B_{12}{\ddot{\vartheta }}_z+ B_{11}{\ddot{\vartheta }}_y- B_{7}\ddot{\varphi }^\prime - 2 B_{1}\dot{v}_p\dot{\psi }(t)\cos \theta + 2 B_{2}\dot{\varphi }\dot{\psi }(t)\cos \theta \nonumber \\&+ 2 B_{1}\dot{w}_p\dot{\psi }(t)\sin \theta + 2 B_{3}\dot{\varphi }\dot{\psi }(t)\sin \theta - B_{1} (R_0+x+u_0){\dot{\psi }}^2(t)- B_{12}\vartheta _z{\dot{\psi }}^2(t)\nonumber \\&- B_{11}\vartheta _y{\dot{\psi }}^2(t)+ B_{7}\varphi ^\prime {\dot{\psi }}^2(t)+ B_{1} w_p{\ddot{\psi }}(t)\sin \theta + B_{3}\varphi {\ddot{\psi }}(t)\sin \theta + B_{11}{\ddot{\psi }}(t)\sin \theta \nonumber \\&- B_{1} v_p {\ddot{\psi }}(t)\cos \theta + B_{2}\varphi {\ddot{\psi }}(t)\cos \theta - B_{12}{\ddot{\psi }}(t)\cos \theta \Big ] d x \end{aligned}$$

  (110)

• $\delta v_p$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \!\int \limits _0^l\Big [&B_{1} \ddot{v}_p - B_{2}\ddot{\varphi } + 2 B_{1} \dot{u}_0\dot{\psi }(t)\cos \theta + 2 B_{12}{\dot{\vartheta }}_z\dot{\psi }(t)\cos \theta + 2 B_{11}{\dot{\vartheta }}_y\dot{\psi }(t)\cos \theta \nonumber \\&- 2 B_{7}\dot{\varphi }^\prime \dot{\psi }(t)\cos \theta + B_{1} w_p{\dot{\psi }}^2(t)\sin \theta \cos \theta + B_{3}\varphi {\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\&+ B_{11}{\dot{\psi }}^2(t)\sin \theta \cos \theta - B_{1}v_p{\dot{\psi }}^2(t)\cos ^2\theta + B_{2}\varphi {\dot{\psi }}^2(t)\cos ^2\theta \nonumber \\&- B_{12}{\dot{\psi }}^2(t)\cos ^2\theta + B_{1} (R_0 + x + u_0){\ddot{\psi }}(t)\cos \theta + B_{12}\vartheta _z{\ddot{\psi }}(t)\cos \theta \nonumber \\&+ B_{11}\vartheta _y{\ddot{\psi }}(t)\cos \theta - B_{7}\varphi ^\prime {\ddot{\psi }}(t)\cos \theta \Big ] d x \end{aligned}$$

  (111)

• $\delta w_p$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \!\int \limits _0^l\Big [&B_{1}\ddot{w}_p + B_{3}\ddot{\varphi } - 2 B_{1}\dot{u}_0\,\dot{\psi }(t)\sin \theta - 2 B_{12}{\dot{\vartheta }}_z\dot{\psi }(t)\sin \theta - 2 B_{11}{\dot{\vartheta }}_y\dot{\psi }(t)\sin \theta \nonumber \\&+ 2 B_{7}\dot{\varphi }^\prime \dot{\psi }(t)\sin \theta - B_{1}w_p{\dot{\psi }}^2(t)\sin ^2\theta - B_{3}\varphi {\dot{\psi }}^2(t)\sin ^2\theta - B_{11}{\dot{\psi }}^2(t)\sin ^2\theta \nonumber \\&+ B_{1}v_p{\dot{\psi }}^2(t)\sin \theta \cos \theta - B_{2}\varphi {\dot{\psi }}^2(t)\sin \theta \!\cos \theta + B_{12}{\dot{\psi }}^2(t)\sin \theta \cos \theta \nonumber \\&- B_{1} (R_0\!+\!x\!+\!u_0) {\ddot{\psi }}(t)\sin \theta - B_{12}\vartheta _z{\ddot{\psi }}(t)\sin \theta - B_{11}\vartheta _y{\ddot{\psi }}(t)\sin \theta \nonumber \\&+ B_{7}\varphi ^\prime {\ddot{\psi }}(t)\sin \theta \Big ] d x \end{aligned}$$

  (112)

• $\delta \vartheta _y$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \!\int \limits _0^l\!\Big [&B_{11}\ddot{u}_0 + B_{13}{\ddot{\vartheta }}_y+ B_{15}{\ddot{\vartheta }}_z- B_{8} \ddot{\varphi }^\prime - 2 B_{11}\,\dot{v}_p\,\dot{\psi }(t)\cos \theta + 2 B_{16}\dot{\varphi }\dot{\psi }(t)\cos \theta \nonumber \\&+ 2 B_{11}\dot{w}_p\dot{\psi }(t)\sin \theta + 2 B_{17}\dot{\varphi }\dot{\psi }(t)\sin \theta - B_{11}(R_0 + x + u_0){\dot{\psi }}^2(t)- B_{15}\vartheta _z{\dot{\psi }}^2(t)\nonumber \\&- B_{15}\vartheta _y{\dot{\psi }}^2(t)+ B_{8}\varphi ^\prime {\dot{\psi }}^2(t)+ B_{11}w_p{\ddot{\psi }}(t)\sin \theta + B_{17}\varphi {\ddot{\psi }}(t)\sin \theta \nonumber \\&- B_{11}v_p{\ddot{\psi }}(t)\cos \theta + B_{16}\varphi {\ddot{\psi }}(t)\cos \theta + B_{13}{\ddot{\psi }}(t)\sin \theta - B_{15}{\ddot{\psi }}(t)\cos \theta \Big ] d x \end{aligned}$$

  (113)

• $\delta \vartheta _z$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \!\int \limits _0^l\!\Big [&B_{12}\ddot{u}_0 + B_{15}{\ddot{\vartheta }}_y+ B_{14}{\ddot{\vartheta }}_z- B_{9} \ddot{\varphi }^\prime - 2 B_{12}\dot{v}_p\,\dot{\psi }(t)\cos \theta + 2 B_{18}\dot{\varphi }\dot{\psi }(t)\cos \theta \nonumber \\&+ 2 B_{12}\dot{w}_p\dot{\psi }(t)\sin \theta + 2 B_{13}\dot{\varphi }\dot{\psi }(t)\sin \theta - B_{12}(R_0 + x + u_0){\dot{\psi }}^2(t)\nonumber \\&- B_{14}\vartheta _z{\dot{\psi }}^2(t)- B_{15}\vartheta _y{\dot{\psi }}^2(t)+ B_{9}\varphi ^\prime {\dot{\psi }}^2(t)+ B_{12}w_p{\ddot{\psi }}(t)\sin \theta + B_{19}\varphi {\ddot{\psi }}(t)\sin \theta \nonumber \\&- B_{12}v_p{\ddot{\psi }}(t)\cos \theta + B_{18}\varphi {\ddot{\psi }}(t)\cos \theta + B_{15}{\ddot{\psi }}(t)\sin \theta - B_{14}{\ddot{\psi }}(t)\cos \theta \Big ] d x \end{aligned}$$

  (114)

• $\delta \varphi$ term

  $$\begin{aligned} -\int \limits _{t_1}^{t_2}\!\! d t \!\int \limits _0^l\!\Big [&-B_{2}\ddot{v}_p + B_{3}\ddot{w}_p + (B_{4}+B_{5})\ddot{\varphi }(t) - 2 (B_{2}\cos \theta + B_{3}\sin \theta )\dot{u}_0 \dot{\psi }(t)\nonumber \\&- 2 (B_{16}\cos \theta + B_{17}\sin \theta ){\dot{\vartheta }}_y\dot{\psi }(t)- 2 (B_{18}\cos \theta + B_{19}\sin \theta ){\dot{\vartheta }}_z\dot{\psi }(t)\nonumber \\&+ 2 (B_{20}\cos \theta + B_{21}\sin \theta )\dot{\varphi }^\prime \dot{\psi }(t)- (B_{3}\cos \theta - B_{2}\sin \theta )(R_0\!+\!x)\varphi {\ddot{\psi }}(t)\!\nonumber \\&+ (B_{2}\cos ^2\theta + B_{3}\sin \theta \cos \theta )v_p {\dot{\psi }}^2(t)- (B_{2}\sin \theta \cos \theta + B_{3}\sin ^2\theta )w_p{\dot{\psi }}^2(t)\nonumber \\&- (B_{18}\sin \theta \cos \theta + B_{17}\sin \theta \cos \theta - B_{16}\sin ^2\theta - B_{19}\cos ^2\theta )\varphi {\dot{\psi }}^2(t)\nonumber \\&- (2 B_{6}\sin \theta \cos \theta + B_{5}\sin ^2\theta + B_{4}\cos ^2\theta )\varphi {\dot{\psi }}^2(t)\nonumber \\&+ (B_{18}\cos ^2\theta - B_{17}\sin ^2\theta + B_{9}\sin \theta \cos \theta - B_{16}\sin \theta \cos \theta ){\dot{\psi }}^2(t)\nonumber \\&- (B_{2}\cos \theta \!+\!B_{3}\sin \theta )(R_0\!+\!x\!+\!u_0){\ddot{\psi }}(t)- (B_{16}\cos \theta + B_{17}\sin \theta )\vartheta _y{\ddot{\psi }}(t)\nonumber \\&- (B_{18}\cos \theta \!+\!B_{19}\sin \theta )\vartheta _z{\ddot{\psi }}(t)+ (B_{20}\cos \theta + B_{21}\sin \theta )\varphi ^\prime {\ddot{\psi }}(t)\nonumber \\&+ (B_{7} \ddot{u}_0)^\prime \! +\! (B_{8}{\ddot{\vartheta }}_y)^\prime + (B_{9}{\ddot{\vartheta }}_z)^\prime \! -\! (B_{10}\ddot{\varphi })^\prime \! +\! 2[(B_{20}\dot{\varphi })^\prime \!\cos \theta + (B_{21}\dot{\varphi })^\prime \!\sin \theta ]\dot{\psi }(t)\nonumber \\&- 2 (B_{7} \dot{v}_p)^\prime \dot{\psi }(t)\cos \theta + 2 (B_{7}\dot{w}_p)^\prime \dot{\psi }(t)\sin \theta - [B_{7}(R_0+x+u_0)]^\prime {\dot{\psi }}^2(t)\nonumber \\&- (B_{8} \vartheta _y)^\prime {\dot{\psi }}^2(t)- (B_{9} \vartheta _z)^\prime {\dot{\psi }}^2(t)+ (B_{10}\varphi ^\prime )^\prime {\dot{\psi }}^2(t)- (B_{7} v_p)^\prime {\ddot{\psi }}(t)\cos \theta \nonumber \\&+ (B_{7} w_p)^\prime {\ddot{\psi }}(t)\sin \theta + (B_{20}\varphi )^\prime {\ddot{\psi }}(t)\cos \theta + (B_{21}\varphi )^\prime {\ddot{\psi }}(t)\sin \theta \Big ] d x\nonumber \\ -\int \limits _{t_1}^{t_2}\!\!\Big [&- B_{7}\ddot{u}_0 - B_{8}{\ddot{\vartheta }}_y- B_{9}{\ddot{\vartheta }}_z+ B_{10} \ddot{\varphi }^\prime + 2 B_{7}\dot{v}_{\!p}\dot{\psi }(t)\cos \theta - 2 B_{7}\dot{w}_{\!p}\dot{\psi }(t)\sin \theta \nonumber \\&-2 \big (B_{20} \cos \theta + B_{21}\sin \theta \big )\dot{\varphi }\dot{\psi }(t)+ B_{7} (R_0+x+u_0){\dot{\psi }}^2(t)+ B_{8} \vartheta _y{\dot{\psi }}^2(t)\nonumber \\&+ B_{9}\vartheta _z{\dot{\psi }}^2(t)- B_{10}\varphi ^\prime {\dot{\psi }}^2(t)+ B_{7}v_p{\ddot{\psi }}(t)\cos \theta - B_{7}w_p{\ddot{\psi }}(t)\sin \theta \nonumber \\&- (B_{20}\cos \theta + B_{21}\sin \theta )\varphi {\ddot{\psi }}(t)+ (B_{9}\cos \theta - B_{8}\sin \theta ){\ddot{\psi }}(t)\Big ] d t\; \delta \varphi \Big |_{x=0}^{x=l} \end{aligned}$$

  (115)

where, in order to simplify the notation, inertia $I_i$ terms are given in Table 2 in 1. A reader may easily notice in the foregoing equations terms related to nonconstant angular velocity and terms corresponding to Coriolis and centrifugal accelerations.

Appendix 4

According to the assumed general loading conditions the following external loads are defined

• Shear forces

  $$\begin{aligned} \begin{array}{ll} P_{ext,y} = \int \limits _c\! \int \limits _{{-h}/{2}}^{{h}/{2}} \rho _{0}F_{y}\, dnds + \int \limits _c q_{y} ds &{} P_{ext,z} = \int \limits _c\! \int \limits _{{-h}/{2}}^{{h}/{2}} \rho _{0}F_{z}\, dnds + \int \limits _c q_{z} ds \\ Q_{ext,y} = n_{x}\int \limits _c\!\int \limits _{{-h}/{2}}^{{h}/{2}} t_{y}\, dnds &{} Q_{ext,z} = n_{x}\int \limits _c\!\int \limits _{{-h}/{2}}^{{h}/{2}} t_{z}\, dnds \\ \hat{P}_{ext,y} = \bigg [n_{s}\int \limits _{{-h}/{2}}^{{h}/{2}} \hat{t}_{y}\, dn \bigg ]\!\bigg |_{s=s_{1}}^{s=s_{2}} &{} \hat{P}_{ext,z} = \bigg [n_{s}\int \limits _{{-h}/{2}}^{{h}/{2}} \hat{t}_{z}\, dn \bigg ]\!\bigg |_{s=s_{1}}^{s=s_{2}} \end{array} \end{aligned}$$

  (116)

• Axial forces

  $$\begin{aligned} P_{ext,x}&= \int \limits _c\!\! \int \limits _{{-h}/{2}}^{{h}/{2}} \rho _{0}F_{x}\,dnds + \int \limits _c q_{x} ds \qquad Q_{ext,x} =n_{x}\int \limits _c\!\int \limits _{{-h}/{2}}^{{h}/{2}} t_{x}\, dnds \\ \hat{P}_{ext,x}&= \bigg [n_{s}\int \limits _{{-h}/{2}}^{{h}/{2}} \hat{t}_{x}\,dn\bigg ]\!\bigg |_{s=s_{1}}^{s=s_{2}} \end{aligned}$$

  (117)

• Bending moments

  $$\begin{aligned} m_{ext,x}&= \int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \rho _{0}[ F_{z} (Y-y_{p}) - F_{y}(Z-z_{p})]dnds\! + \!\int \limits _c [q_{z}(y-y_{p})-q_{y}(z-z_{p})] ds \nonumber \\ M_{ext,x}&= n_{x}\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}}[t_{z}(Y-y_{p})-t_{y}(Z-z_{p})]dnds \nonumber \\ \hat{m}_{ext,x}&= \bigg [ n_{s}\int \limits _{{-h}/{2}}^{{h}/{2}} \big [\hat{t}_{z}(Y-y_{p})-\hat{t}_{y}(Z-z_{p}) \big ] dn \bigg ]\!\bigg |_{s=s_{1}}^{s=s_{2}} \end{aligned}$$

  (118)

• Bi-moments

  $$\begin{aligned} m_{ext,w}&= \int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}}\!\!\rho _{0} F_{x}G(n,s) dnds + \int \limits _c\!\! q_{x}G^{(0)}(s)ds \quad M_{ext,w} = n_{x}\!\!\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}}\!\! t_{x}G(n,s)\, dnds \nonumber \\ \hat{m}_{ext,w}&= \bigg [n_{s}\int \limits _{{-h}/{2}}^{{h}/{2}} \hat{t}_{x}G(n,s)\, dn \bigg ] \!\bigg |_{s=s_{1}}^{s=s_{2}} \end{aligned}$$

  (119)

• Bending moments

  $$\begin{aligned} \begin{array}{ll} m_{ext,y} = \int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \rho _{0}F_{x} Z\, dnds + \int \limits _c q_{x} z\, ds &{} m_{ext,z} = \int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} \rho _{0}F_{x} Y\, dnds + \int \limits _c q_{x} y\, ds \\ M_{ext,y} = n_{x}\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} t_{x}Z\, dnds &{} M_{ext,z} = n_{x}\int \limits _c\!\!\int \limits _{{-h}/{2}}^{{h}/{2}} t_{x}Y\, dnds\\ \hat{m}_{ext,y} = \bigg [n_{s}\int _{{-h}/{2}}^{{h}/{2}} \hat{t}_{x}Z\, dn \bigg ] \!\bigg |_{s=s_{1}}^{s=s_{2}} &{} \hat{m}_{ext,z} = \bigg [n_{s}\int _{{-h}/{2}}^{{h}/{2}} \hat{t}_{x}Y\, dn \bigg ] \!\bigg |_{s=s_{1}}^{s=s_{2}} \end{array} \end{aligned}$$

  (120)

Using equations (116)–(120) the work defining equations (35) take the form

$$\begin{aligned} W_{ext,1} + W_{ext,2}&= \int \limits _0^{\quad l} \big [P_{ext,x}u_{0}+m_{ext,y}\vartheta _y+m_{ext,z}\vartheta _z+P_{ext,y}v_{p} \nonumber \\&+P_{ext,z}w_{p}+m_{ext,x}\varphi -m_{ext,w}\varphi ^{\prime }\big ]dx \nonumber \\ W_{ext,3}&= \Big [ n_{x} \big (Q_{ext,x}u_{0} + M_{ext,y}\vartheta _y+ M_{ext,z}\vartheta _z- M_{ext,w}\varphi ^{\prime } \nonumber \\&+Q_{ext,y}v_{p} + Q_{ext,z}w_{p} + M_{ext,x}\varphi \big ) \Big ]\Big |_{x=0}^{x=l} \nonumber \\ W_{ext,4}&= \int \limits _{0}^{\quad l} \Big [\hat{P}_{ext,x}u_{0} + \hat{m}_{ext,y}\vartheta _y+ \hat{m}_{ext\mathrm {,}z} \vartheta _z+ \hat{P}_{ext,y}v_{p} + \hat{P}_{ext,z}\delta w_{p} \nonumber \\&+ \hat{m}_{ext,x}\varphi - \hat{m}_{ext,w}\varphi ^{\prime }\Big ] dx \end{aligned}$$

(121)

The variation of the total external work expressed by all its components takes the form

$$\begin{aligned} \delta W_{ext,1} + \delta W_{ext,2}&= \int \limits _{0}^{l} \big [ P_{ext,x}\delta u_{0} + m_{ext,y}\delta \vartheta _y+ m_{ext,z}\delta \vartheta _z+ P_{ext,y}\delta v_{p} \nonumber \\&+P_{ext,z}\delta w_{p} + \big (m_{ext,x} + m_{ext,w}^{\prime }\big )\delta \varphi \big ]dx - \big [m_{ext\mathrm {,}w}\delta \varphi \big ]\! \Big |_{x=0}^{x=l}, \nonumber \\ \delta W_{ext,3}&= \big [n_{x}\big ( Q_{ext,x}\delta u_{0} + M_{ext,y}\delta \vartheta _y+ M_{ext,z}\delta \vartheta _z- M_{ext,w}\delta \varphi ^{\prime } \nonumber \\&+Q_{ext,y}\delta v_{p} + Q_{ext,z}\delta w_{p} + M_{ext,x}\delta \varphi \big ) \big ]\! \Big |_{x=0}^{x=l}, \nonumber \\ \delta W_{ext,4}&= \int \limits _{0}^{l} \big [\hat{P}_{ext,x}\delta u_0 + \hat{m}_{ext,y}\delta \vartheta _y+ \hat{m}_{ext,z}\delta \vartheta _z+ \hat{P}_{ext,y}\delta v_{p} \nonumber \\&+\hat{P}_{ext,z}\delta w_{p} + \big (\hat{m}_{ext,x} + \hat{m}_{ext,w}^{\prime }\big )\delta \varphi \big ] dx - \big [\hat{m}_{ext\mathrm {,}w}\delta \varphi \big ]\! \Big |_{x=0}^{x=l},\nonumber \\ \delta W_{ext,5}&= \;T_{ext,z}\delta \psi (t), \end{aligned}$$

(122)

Appendix 5

In order to provide a self-contained theory and a system of equations the inertia coefficients requested for kinetic energy (110)–(115) and stiffness coefficients of the system are given in explicit form. Setting the terms

$$\begin{aligned} m_{0}=\int \limits _{{-h}/{2}}^{{h}/{2}} \!\!\!\varrho dn \qquad m_{2}=\int \limits _{{-h}/{2}}^{{h}/{2}} \!\!\!\varrho n^{2} dn \end{aligned}$$

(123)

the definitions of inertia coefficients $B_i$ are summarised in Table 1. The definition of introduced stiffness coefficients are given in Table 2.

Table 1 General definitions of inertia coefficients $B_{i}$ and formulas for beams made of symmetric laminate with rectangular cross-section

Table 2 Definitions of stiffness coefficients $a_{ij}$