On controlling the response of primary and parametric resonances of a nonlinear magnetic levitation system

Abstract

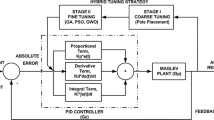
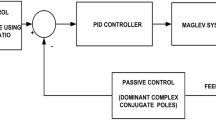
In this paper, a proportional-derivative controller is proposed to reduce the horizontal vibration of a magnetically levitated system having quadratic and cubic nonlinearities to primary and parametric excitations. A second order approximate solution is sought using the method of multiple scales perturbation technique to clarify the nonlinear behavior for both amplitude and phase of the system. The effect of feedback signal gain is studied to indicate the optimum values for best performance. Validation curves are included to compare the approximate solution and the numerical simulation. A comparison with previously published work is included.

Appendix

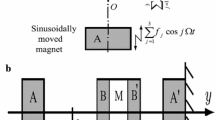
The incoming derivation of the magnetic levitation model has been mentioned before in Ref. [1]. From Fig. 31, the repulsive force in the $\eta$ direction between the total magnetic poles on the surface $S_{2}$ of magnet A and the total magnetic poles on the surface $S_{3}$ of magnet B is obtained from Coulomb’s law as mentioned in [1] as follows:

$$ F(\delta ) = \frac{{\lambda_{A} \lambda_{B} l_{B} }}{2\pi \mu }\left[ \begin{aligned} &2h_{A} \tan^{ - 1} \left( {\frac{{h_{A} + h_{B} }}{\delta }} \right) + 2h_{B} \tan^{ - 1} \left( {\frac{{h_{A} + h_{B} }}{\delta }} \right) \hfill \\& - 2h_{A} \tan^{ - 1} \left( {\frac{{h_{A} - h_{B} }}{\delta }} \right) - 2h_{B} \tan^{ - 1} \left( {\frac{{h_{A} - h_{B} }}{\delta }} \right) \hfill \\ &- \delta \,\,\,\,\,\,\log \left( {1 + \left( {\frac{{h_{A} + h_{B} }}{\delta }} \right)^{2} } \right) + \delta \,\,\,\,\log \left( {1 + \left( {\frac{{h_{A} - h_{B} }}{\delta }} \right)^{2} } \right) \hfill \\ \end{aligned} \right] $$

(40)

where $\delta$ denotes the gap between magnets A and B. In addition, $\lambda_{A} ,\lambda_{B}$ and $\mu$ respectively signify the magnetic flux densities of magnets A and B, and the magnetic permeability. The repulsive force acting between surfaces S1&S4 and the absorptive forces acting between surfaces S1&S3, and S2&S4 must be also calculated. Taking into account the thickness $C_{A}$ and $C_{B}$ of the magnets, the four forces for the four sets of surfaces are calculated using Eq. (40). Summing the four forces where the repulsive forces are regarded as positive and the absorptive ones are regarded as negative yields the repulsive force acting on magnets A and B with gap $\delta$, then a nonlinear restoring force acting on the main system is derived. Here, the forces between the magnets A&A′, B&B′, A&B′, A′&B are neglected.

Fig. 31

Repelling magnets on the main system

In Fig. 32, the magnet A is moved with an external sinusoidal excitation E. Another static Cartesian coordinate system has been considered whose O` is at the upper area of the sinusoidally moved magnet A in the initial static equilibrium state. Here, $l$ is the constant gap between magnets A and A′ in the initial static equilibrium state. In addition, $l_{0}$ denotes the width of a mass M including magnets B and B′. The motion of the main system is considered around $Y_{st}$, which is the gap between magnets A and B in the initial static equilibrium state. The forces acting on magnets B and B′ are $F(Y - E)$ and $F(l - l_{0} - Y)$ respectively, and they are expanded with respect to $\frac{y}{{Y_{st} }}$, where $Y = y + Y_{st}$ and $\left| {\frac{y}{{Y_{st} }}} \right| \ll 1$ are assumed. By considering the Maclaurin expansion up to the third power of $\frac{y - E}{{Y_{st} }}$ and $\frac{y}{{Y_{st} }}$ for the forces $F_{B} \& F_{B^{\prime}}$ respectively, the following equation of motion can be obtained by applying Newton’s second law of motion as follows:

$$ M\frac{{d^{2} y}}{{dt^{2} }} = F_{B} - F_{B`} = F(Y - E) - F(l - l_{0} - Y) = F(Y_{st} + y - E) - F(l - l_{0} - Y_{st} - y) = - (K_{R1} + K_{L1} )y - (K_{R2} - K_{L2} )y^{2} - (K_{R3} + K_{L3} )y^{3} + K_{R1} E + 2K_{R2} Ey - K_{R2} E^{2} + 3K_{R3} Ey^{2} - 3K_{R3} E^{2} y + K_{R3} E^{3} $$

(41)

where

$$ \begin{gathered} K_{R1} = \left. { - \frac{{dF_{B} }}{dy}} \right|_{y = 0} ,\quad K_{R2} = \left. { - \frac{1}{2!}\frac{{d^{2} F_{B} }}{{dy^{2} }}} \right|_{y = 0} ,\hfill \\ K_{R3} = \left. { - \frac{1}{3!}\frac{{d^{3} F_{B} }}{{dy^{3} }}} \right|_{y = 0} \hfill \\ \hfill \\ \end{gathered} $$

$$ \begin{gathered} K_{L1} = \left. { - \frac{{dF_{B`} }}{dy}} \right|_{y = 0} ,\quad K_{L2} = \left. { - \frac{1}{2!}\frac{{d^{2} F_{B`} }}{{dy^{2} }}} \right|_{y = 0} ,\hfill \\ K_{L3} = \left. { - \frac{1}{3!}\frac{{d^{3} F_{B`} }}{{dy^{3} }}} \right|_{y = 0} \hfill \\ \hfill \\ \end{gathered} $$

Fig. 32

Analytical model of the nonlinear magnetic levitation system. a Equilibrium state, b sinusoidally excited state

In Eq. (41), the variable y can be normalized w.r.t the value $Y_{st}$ and the variable $t$ can be normalized w.r.t the value $T = \sqrt {\frac{M}{{K_{R1} + K_{L1} }}}$ as follows:

$$ y^{*} = \frac{y}{{Y_{st} }},\quad t^{*} = \frac{t}{T} $$

(42)

Inserting Eq. (42) into (41) yields:

$$ {\ddot{y}}^{*} + 2\mu {\dot{y}}^{*} + y^{*} + \alpha_{2} y^{*2} + \alpha_{3} y^{*3} = 2k_{2} y^{*} E^{*} + 3k_{3} y^{*2} E^{*} - 3k_{3} y^{*} E^{*2} + k_{1} E^{*} - k_{2} E^{*2} + k_{3} E^{*3} $$

(43)

where the dot indicates the derivative w.r.t the dimensionless time $t^{*}$, and $\mu$ denotes the main system damping coefficient due to the friction. Hereinafter in this discussion, the asterisk (*) is omitted for simplification. The dimensionless parameters in (43) are as follows:

$$ \begin{gathered} \alpha_{2} = \frac{{(K_{R2} - K_{L2} )Y_{st} }}{{K_{R1} + K_{L1} }},\quad \alpha_{3} = \frac{{(K_{R3} + K_{L3} )Y_{st}^{2} }}{{K_{R1} + K_{L1} }},\hfill \\ k_{1} = \frac{{K_{R1} }}{{K_{R1} + K_{L1} }},\quad k_{2} = \frac{{K_{R2} Y_{st} }}{{K_{R1} + K_{L1} }} \hfill \hfill \\ \end{gathered} $$

$$ k_{3} = \frac{{K_{R3} Y_{st}^{2} }}{{K_{R1} + K_{L1} }},\quad y^{*} = \frac{y}{{Y_{st} }},\quad t^{*} = \frac{t}{T},\quad E^{*} = \frac{E}{{Y_{st} }} $$

The external excitation E is assumed as a single force as was assumed in [1]. So we can suppose the excitation as $E = f\cos (\Omega t)$, and Eq. (43) can be as follows:

$$ \begin{aligned} {\ddot{y}} + 2\mu {\dot{y}} + y + \alpha_{2} y^{2} + \alpha_{3} y^{3} &= 2k_{2} yf\,\,\cos (\Omega t) + 3k_{3} y^{2} f\,\,\,\cos (\Omega t) - 3k_{3} yf^{2} \cos^{2} (\Omega t) \hfill \\ \, &\quad + k_{1} f\,\,\,\cos (\Omega t) - k_{2} f^{2} \,\,\,\cos^{2} (\Omega t) + k_{3} f^{3} \cos^{3} (\Omega t) \hfill \\ \end{aligned} $$

(44)

After applying the PD control signal, Eq. (44) will be as follows:

$$ \begin{aligned} {\ddot{y}} + 2\mu {\dot{y}} + y + \alpha_{2} y^{2} + \alpha_{3} y^{3} &= 2k_{2} yf\,\,\,\cos (\Omega t) + 3k_{3} y^{2} f\,\,\cos (\Omega t) - 3k_{3} yf^{2} \cos^{2} (\Omega t) \hfill \\ \, &\quad + k_{1} f\,\,\,\cos (\Omega t) - k_{2} f^{2} \,\,\cos^{2} (\Omega t) + k_{3} f^{3} \,\,\,\cos^{3} (\Omega t) - (py + d\dot{y}) \hfill \\ \end{aligned} $$

(45)

which is Eq. (1) stated at the start of this paper.